Web Semántica:
Unidad 4 - Ontologías
Gustavo Andrés Uribe Gómez
guribe@unicomfacauca.edu.co
+572 8220517 Ext. 130

¿Qué son?
“Formal ontologies are theories that attempt to give precise mathematical formulations of the properties and relations of certain entities”
(Hofweber, 2012)
¿Qué son?
“Ontology is the study of the most general classes or categories of everything that exists, their dependencies and relations. An ontology is a set of claims about these classes of beings and the relations among them”
(Schulz S., 2012)
¿Qué son?
“An ontology defines (or specifies) the concepts, relationships, and other distinctions that are relevant for modeling a domain. The specification of an ontology takes the form of the definitions of representational vocabulary (classes, relations, and so forth) that provide meanings for the vocabulary and formal constraints on its coherent use.”
(Gruber, 1993)
¿Qué son?
“Ontologies are information artefacts that attempt to give precise formulations of the properties and relations of certain types of entities" (Hofweber, 2012)
¿Qué deben ser?
- Formales
- Explicitas
- Adecuadas al conocimiento actual
Todo esto garantiza inferencias adecuadas
¿Qué no son?
- Representaciones léxico-semánticas: terminologías y tesauros.
- Lo que es típicamente cierto: conocimiento del contexto
- Conocimiento acerca de individuos: bases de datos
¿Qué no deberían ser?
Componentes
- Clases
- Relaciones
- Taxonómicas
- Metadatos
Lógica Descriptiva

Formalidad en Lenguajes
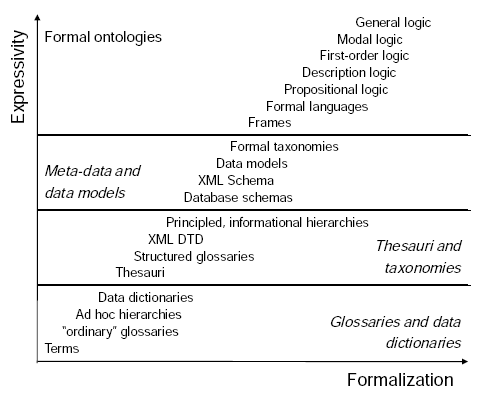
(Rebstock, 2008) modificado por B. Blobel
Componentes
- Clases / Conceptos (TBox)
- Relaciones / Roles
- Individuos (ABox)
- Conexiones lógicas entre ellos
(WaterMolecule subClassOf hasPhysicalPart some OyxgenAtom)
WaterMolecule subClassOf bearerOf some
( PhysicalMass and molecularWeightQuantityLocated
value 18.01528 ^^xsd:double)
Sintaxis
- Matemática
- Manchester
- XML (OWL)
- Turtle
Introducir los ejemplos de la anterior diapositiva en Protégé y visualizar las diferentes sintaxis
Descriptores de Clases
Text
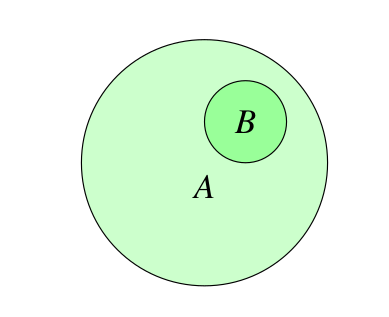
( B subClassOf A )
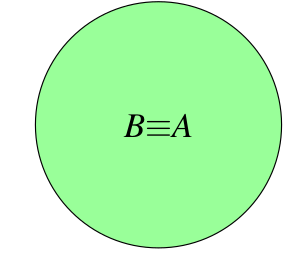
Descriptores de Clases
Text
( B equivalentTo A )
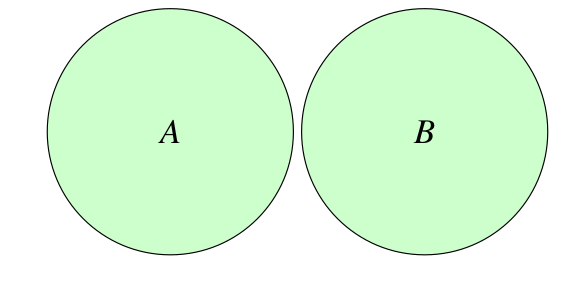
Descriptores de Clases
( B DisjointWith: A )
( CuerpoMasculino DisjointWith: CuerpoFemenino )
Descriptores de Clases
( A DisjointUnionOf: B,C )
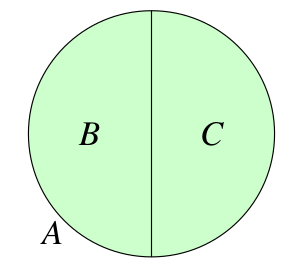
( PartículaSubAtómica DisjointUnionOf: Proton , Electron , Neutron )
Descriptores de Clases
( C equivalentTo (A and B))
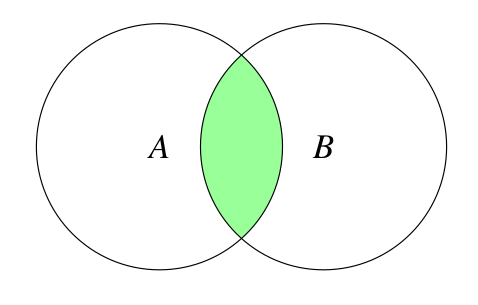
C
Descriptores de Clases
( C equivalentTo ( A or B ))
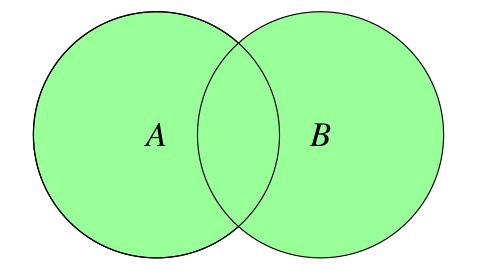
Descriptores de Clases
( C equivalentTo (not A))
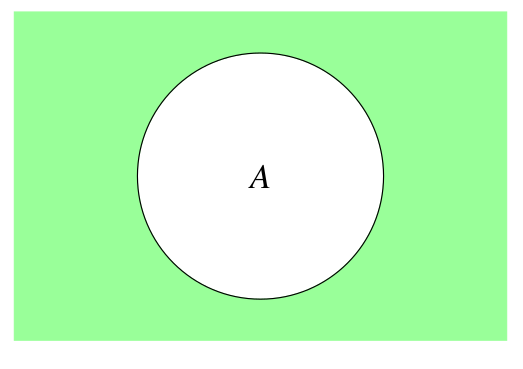
Descriptores de Propiedades
ObjectProperty: hasParticipant
Domain: Process
Range: MaterialObject
Descriptores de Propiedades
hasAgent subPropertyOf hasParticipant
A subPropertyOf B
A equivalentTo B
A DisjointWith: B
Descriptores de Propiedades
| Característica | Definición |
|---|---|
| Funcional | Para cada x, y1, y2 , si xRy1 y xRy2 entonces y1 = y2 |
| FuncionalInversa | Para cada x1, x2, y, si x1Ry y x2Ry, entonces x1 = x2 |
| Transitiva | Para cada x,y,z, si xRy y yRz, entonces xRz |
| Symetrica | Para cada x,y si xRy entonces yRx |
| Asimetrica | Para cada x,y si xRy entonces not yRx |
| Reflexiva | Para cada x,xRx. |
| Irreflexiva | Para cada x, not xRx. |
Descriptores de Propiedades
Restricciones de valor - Restricciones Universales
( R only C )
( hasProperPhysicalPart only SubAtomicParticle )
Descriptores de Propiedades
Restricciones númericas
( R exactly num C )
( R exactly min C )
( R exactly max C )
( hasPhysicalPart exactly 2 HydrogenAtom )
Descriptores de Propiedades
Valores Concretos
( R value num^^datatype )
( molecularWeightQuantityLocated value 18.01528^^xsd:double)
Nivel de Expresividad
Lenguaje Atributivo
- Negación atómica
- Intersección de clases
- Restricciones universales (para todo se cumple ..., only)
- Cuantificador existencial limitado (existe algún ..., some)
- Limitado implica que el conjunto de búsqueda de la existencia debe ser el Universal
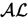
Nivel de Expresividad
Frame-based description logic
- Intersección de clases
- Restricciones universales
- Cuantificador existencial limitado
- Restricción de propiedades
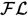
Nivel de Expresividad
Lenguaje existencial
- Intersección de clases
- Cuantificador existencial completo
- Se puede garantizar la existencia en un conjunto más pequeño
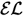
Nivel de Expresividad
Extensiones
- Propiedades funcionales
- Cuantificado existencial completo
- Unión de clases
- Negación de clases compuestas
- Jerarquía de propiedades
- Reflexividad e irreflexividad, propiedades disyuntas
- Nominales (value, owl:oneOf = {} //In manchester syntax)
- Propiedades Inversas
- Restricción en cardinalidad (min, max, exactly)
- Restricciones de cardinalidad cuantificados (exactly 2 HydrogenAtom)
- Uso de tipos de datos y propiedades de datos
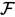

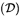
Nivel de Expresividad
Extensiones
- con propiedades transitivas
- sin restricción de propiedades
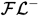
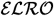
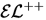
- Protégé soporta
- OWL-2
- OWL-DL
- OWL-Lite
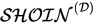
Lenguaje OWL

OWL
Lenguaje diseñado para la descripción de ontologías mediante el uso de la lógica descriptiva, con el objetivo de que el contenido Web sea más accesible por las máquinas
Perfiles
- OWL 1.0
- OWL-DL
- OWL-Lite
- OWL-Full
-
OWL 2.0
- OWL 2 EL (algoritmos complejidad polinomial)
- OWL 2 QL
- Algoritmos complejidad logarítmica
- Consultas bases de datos relacionales
- Usada para muchos individuos
- OWL 2 RL (algoritmos complejidad polinomial por medio de definición de reglas)
- OWL 2 DL (Semántca directa)
- OWL 2 Full (Semántica RDF)
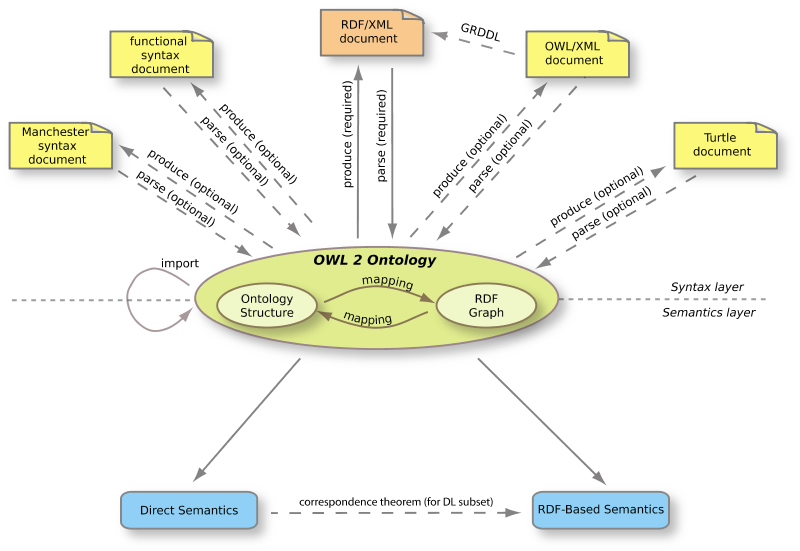
Fuente: w3c
Ontologías de Nivel Superior

Tipos de Ontologías
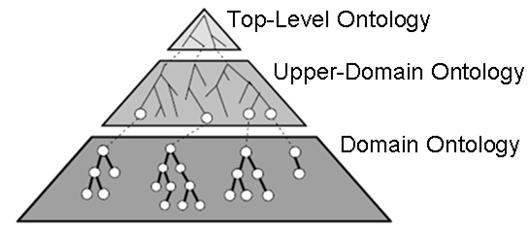
(Stefan, 2012)
Top-level Ontologies
- BFO (Basic Formal Ontology)
- GFO (General Formal Ontology)
- DOLCE (Descriptive Ontology for Linguitic and Cognitive Engineering)
BFO
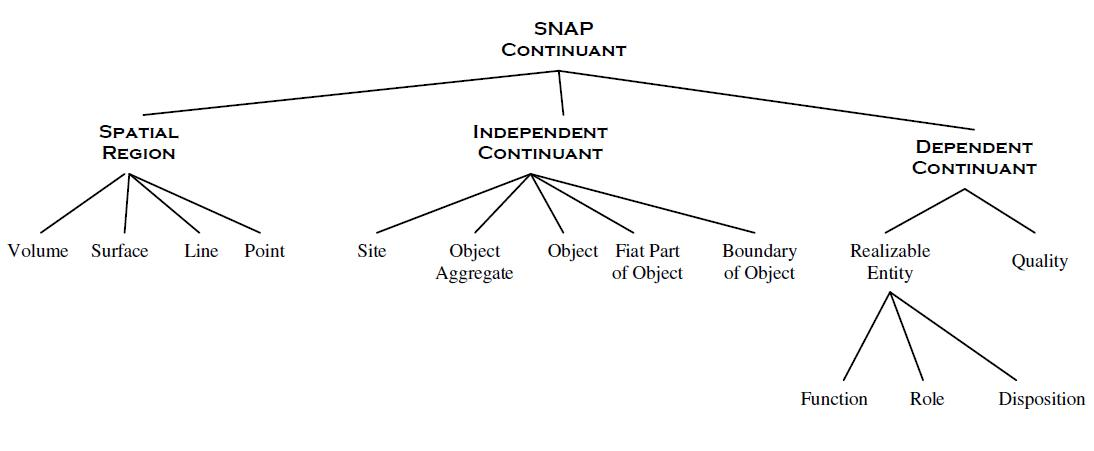
BFO

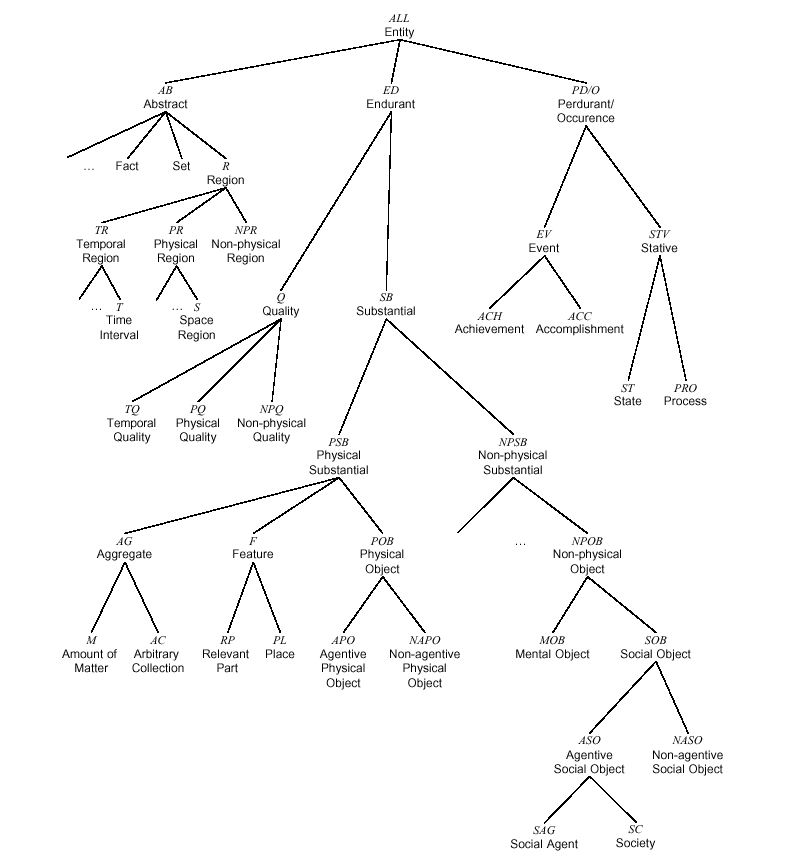
DOLCE
BioTop
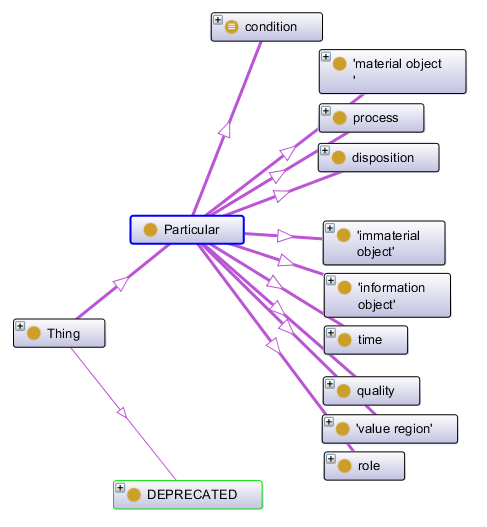
Recomendaciones

Principios para Estar Conforme a la Realidad
- Dos clases no pueden referirse a la misma entidad en la realidad
- Incluir en una clase don entidades no relacionadas
- Introducir clases que no correspondan a entidades en la realidad
- Clases que se refieren a un número finito de individuos
- No incluir clases que relacionadas con un individuo. e.j.: "Person infected by patient #431"
Principios para Definir las Clases
- No metaclasses
- No clases ambiguas, que puedan referir a dos tipos de entidades. E.j.: Cáncer; puede referirse a un proceso o a un tejido
- No usar clases que se refieran a individuos no incluidos en otras clases. E.j.: otros.
- No definir clases con contenido epistémicos. E.j.: "ProbableCáncer", "InfecciónBacterialIdenficadaPorLaCulturaSputum"
Principios para los Nombre
- Claros y sin ambigüedad
- Usar nombres explícitos y concisos
- Usar nombres independientes del contexto
- No usar palabras con muchos significados
- No incluir información administrativa en los nombres
- Ser inequivoco
- Evitar homonimos
- Usar palabras en singular
- Evitar negaciones
- Evitar conjunciones
Principios para los Nombre
- Reducir la variación de los términos
- Reciclar términos
- En las etiquetas usar espacio para separa palabras
- No usar abreviaciones y acrónimos
- Pasar los símbolos a palabras
- Usar el estilo genus-differentia (general a específico)
- Alinear la tipografía
- En las etiquetas preferir iniciar en minúsculas
- Evitar el formato en las caracteres
- Los nombres de las propiedades inician en minúscula
- Los nombres de las clases inician en Mayúscula
Principios para Taxonomías
- Exhaustividad: Las subclases deben definirse partiendo de la superclase. Ej: Para definir los mamíferos sería: Animal and ( tieneComponenteFísico GlándulaMamaria)
- Disjunción: En lo posible obtener subclases que no compartan individuos.
- Estructuración: Debe escogerse un número adecuado de subclases. Las clases en un mismo nivel de generalidad deberían presentar alguna relación.
- Sistematicidad: La división en subclases debe seguir unos principios definidos. Por ejemplo los animales se pueden clasificar de dos maneras, por su fisiología o por su grado de domesticación. Es conveniente solo clasificar por una de las dos.