シンボリック実行および SMT Solver を用いた
JavaScriptプログラムの自動モデル検査および
自動反例生成手法の提案および実装
2020-02-14 東京大学工学部電気電子工学科
2019年度卒業論文本審査報告スライド
坂井・入江研究室 学部4年 高橋光輝

Agenda
- 背景
- 提案手法
- 評価
- まとめ
背景
近年、ソフトウェアセキュリティ及びソフトウェア
テスティングの観点から、シンボリック実行を用いた
静的解析の手法が注目されている。
- ソフトウェアセキュリティ関連
- Angr [Shoshitaishvili, 2016]
- Driller [Stephens, 2016]
- ソフトウェアテスティング関連
- KLEE [Cader, 2008]
- CREST [Burnim, 2008]
- SAGE [Godefroid, 2008]
- SPF [Păsăreanu, 2010]
シンボリック実行とは
- シンボリック実行 [King, 1976] は、プログラムに登場する変数をシンボルとして表現し、
具体的な値を仮定せずシンボルのまま変数に対する演算を追跡するプログラムの解析手法 - ホワイトボックステストの一種
- 結果を一階の論理式ないし命題論理式に変形し、
SAT Solverなどのプログラムに与えることによって、どのような入力のときにどのような出力が得られるのかを論理的に解くことが目的
(a, b) => {
let x = a * 2 + 100;
//=> x : a * 2 + 100
let y = x * 3 - b;
//=> y : a * 6 - b + 300
let z = x + y;
//=> z : a * 8 - b + 400
return x + y + z;
//=> a * 16 - b * 2 + 700
}背景
- これら既存のシンボリックな解析手法は、多くが
CやJavaなどの静的にコンパイルされる言語を
対象としたものである。 - しかし、特にWebセキュリティなどの分野においては
RubyやPythonなどのスクリプト言語や
ブラウザで動作するJavaScriptなどの言語を
解析できることが望ましい。 - 本研究ではその中でも特にJavaScript言語に対する
シンボリック実行を研究対象とする。
関連研究
- JavaScriptコードに対するシンボリック実行の
重要な関連研究として、Liらの
SymJS [Li, 2014] が挙げられる。 - Liらは、独自の SMT Solver [Li, 2013] を用いて、
Rhinoのバイトコードに対してシンボリックな
解析を行った。
[Li, 2014] より作成
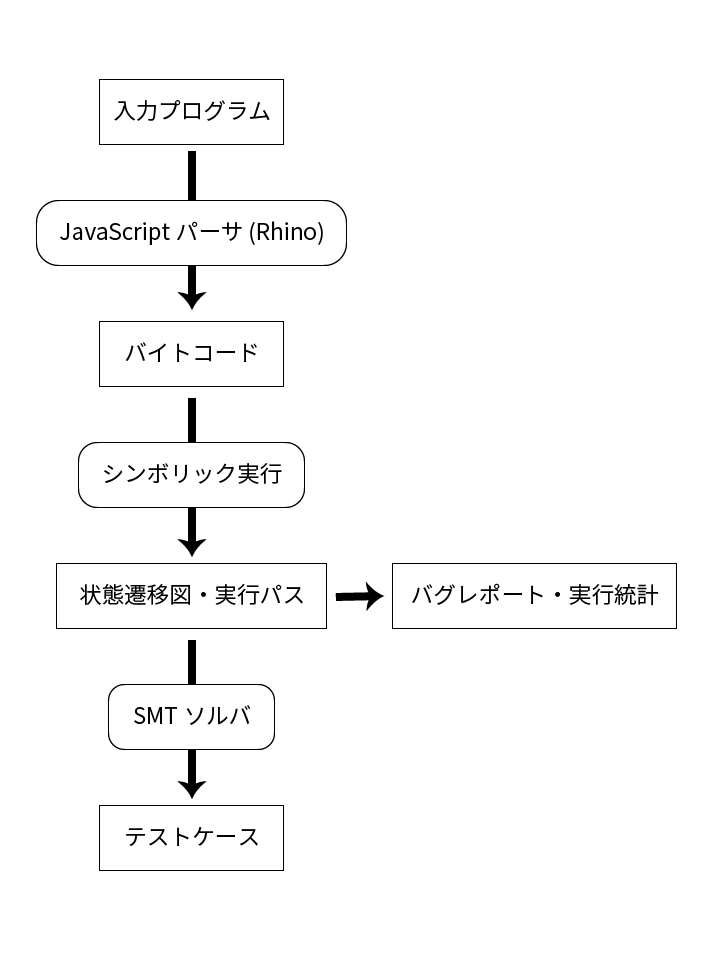
関連研究
- 生のJavaScriptコードではなく変換後のバイトコードに
対して解析を行うのはシンボリック実行に置いて重要な
命令の原子性を維持するという点からも妥当である。 - しかし解析対象のJavaScriptエンジンにRhinoを用いるのは
速度面や最新仕様への追従といった観点から疑問が残る。
Agenda
- 背景
- 提案手法
- 評価
- まとめ
提案手法
本研究では、先行研究であるSymJSを踏まえ、
新たにSpiderMonkeyのバイトコードを利用する
手法を提案するとともに、
自動モデル検査および自動反例生成の手法を
このフレームワークに適用する方法を示す。
提案手法 (1)
- 本研究では、JavaScriptプログラムのシンボリック実行に
用いるバイトコードのセットとして
SpiderMonkeyを用いる手法を提案する。 - SpiderMonkeyはFirefoxに組み込まれている
最新のJavaScript文法への対応が進んでいる。 - また、バイトコードもJITへの2重変換を前提としており
比較的単純な分岐命令を生成する。
提案手法 (2)
- また、Liらの研究では
コード網羅率を向上させる
テストケースの自動生成が
目的だった。 - 本研究では、これを一歩進め、
新たに論理式による
モデル仕様の記述を用いて
SMTソルバで解くことにより
JavaScriptプログラムの
自動モデル検査および
自動反例生成を行う手法を
提案する。
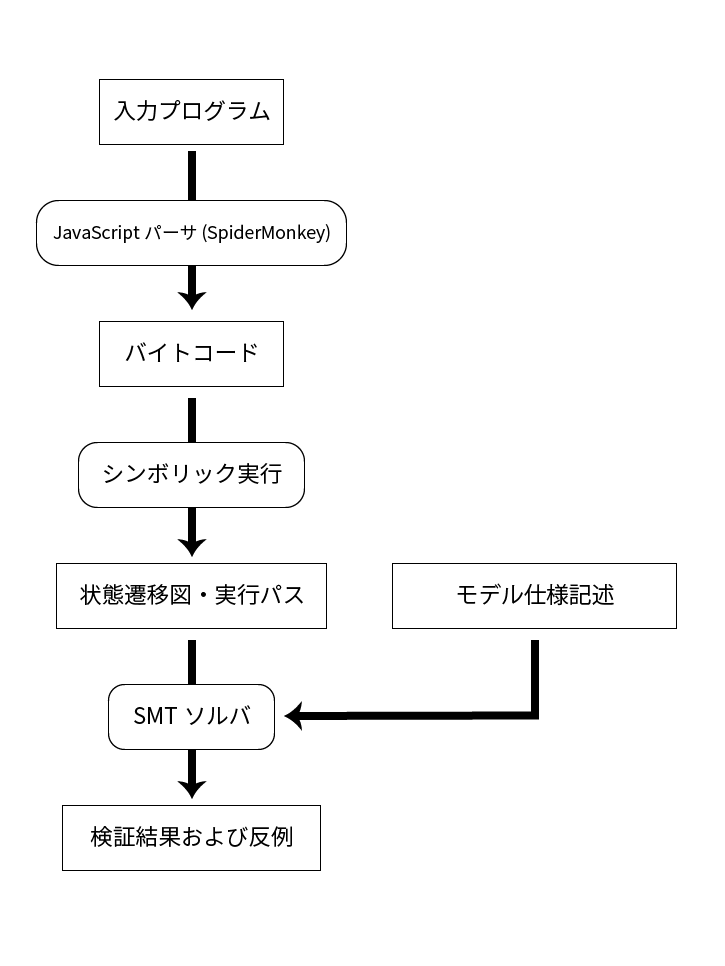
提案手法 (2)

以下の手順でモデル検査および
反例生成を行う。
- プログラムに要求する
入力、および出力の制約を
論理式の形で書き下す - プログラムの実行パスを列挙し
入力に対応する出力シンボル
および分岐条件を抽出する - 分岐条件および入力・出力の
結果を制約と組み合わせ解き
存在量化子を用いて
反例生成式を得る - 適切なSMTソルバを用いて解く
モデル検査の例
仕様
整数 \(x\) と \(y\) が与えられる。
1, 2, 3 のうち \(x\) とも \(y\) とも異なる整数を出力せよ。
制約
- \(x, y\) は 1, 2, 3 のいずれか
- \(x\) と \(y\) は異なる
モデル仕様記述
本問に対応するモデル仕様は、
一階の論理式を用いて以下のように表現することができる。
検査対象のプログラム
この問題に対する正当な実装の例、および
SpiderMonkeyによるそのコンパイル結果を示す。
(x, y) => {
if (x === 1) {
if (y === 2) {
return 3;
} else if (y === 3) {
return 2;
}
} else if (x === 2) {
if (y === 1) {
return 3;
} else if (y === 3) {
return 1;
}
} else if (x === 3) {
if (y === 1) {
return 2;
} else if (y === 2) {
return 1;
}
}
return 0;
};00000: GetArg 0
00003: One
00004: StrictEq
00005: IfEq 73
00015: GetArg 1
00018: Int8 2
00020: StrictEq
00021: IfEq 39
00031: Int8 3
00034: Goto 63
00044: GetArg 1
00047: Int8 3
00049: StrictEq
00050: IfEq 63
00060: Int8 2
00062: Return
00068: Goto 217
00078: GetArg 0
00081: Int8 2
00083: StrictEq
00084: IfEq 150
00094: GetArg 1
00097: One
00098: StrictEq
00099: IfEq 117
00109: Int8 3
00111: Return
00112: Goto 140
00122: GetArg 1
00125: Int8 3
00127: StrictEq
00128: IfEq 140
00138: One
00139: Return
00145: Goto 217
00155: GetArg 0
00158: Int8 3
00160: StrictEq
00161: IfEq 217
00171: GetArg 1
00174: One
00175: StrictEq
00176: IfEq 194
00186: Int8 2
00188: Return
00189: Goto 217
00199: GetArg 1
00202: Int8 2
00204: StrictEq
00205: IfEq 217
00215: One
00216: Return
00222: Zero
00223: Return
00224: RetRval実行パス探索
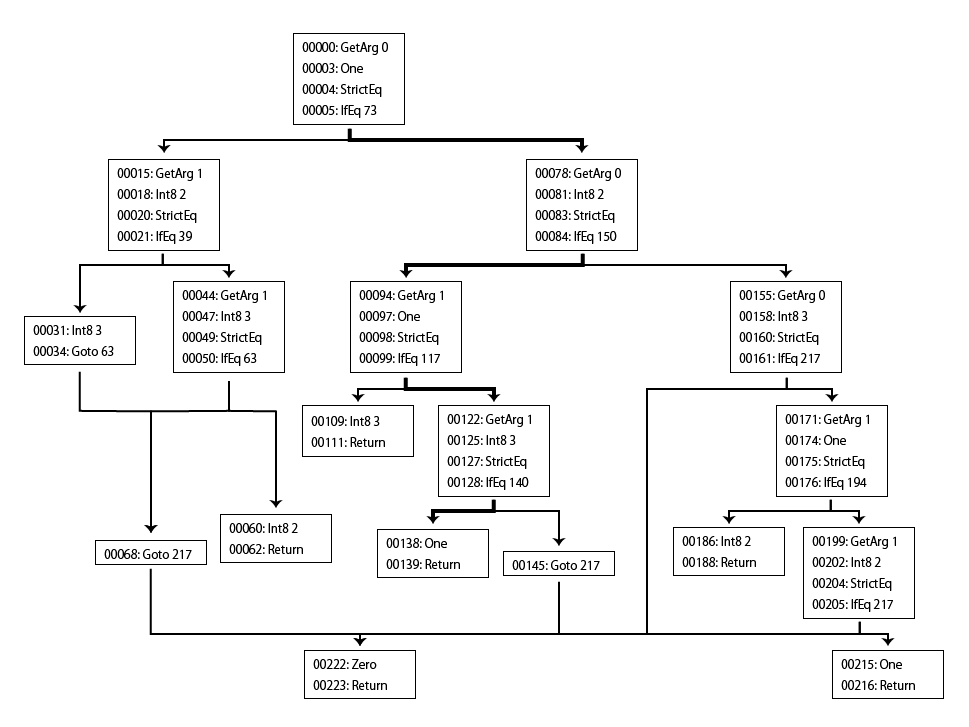
SMT Solver を用いた求解
先に示した実行パスでは、4つの分岐命令を通過している。
これらの分岐条件はそれぞれ \(x\neq1,x=2,y\neq1,y=3\) と
表現できる。
これと先のモデル仕様記述を組み合わせ、反例生成式
を得る。
SMT Solver を用いた求解
以上の条件を SMT-LIB 2.0 の
形式で書き下したのが
左の記述である。
これをSMTソルバCVC4を
用いて解くことによって
「充足不可能」の結果を得た。
反例が存在しない、
すなわち与えたプログラムが
モデル記述に対する
正当な実装であることが
保証された。
(set-logic ALL)
(set-option :produce-models true)
(define-sort FP () (_ FloatingPoint 11 53))
(define-fun toFP ((n Real)) FP ((_ to_fp 11 53) RNE n))
(declare-const x FP)
(declare-const y FP)
(assert
(and
(fp.gt x (toFP 0))
(fp.leq x (toFP 3))
(fp.eq (fp.roundToIntegral RNE x) x)
(fp.gt y (toFP 0))
(fp.leq y (toFP 3))
(fp.eq (fp.roundToIntegral RNE y) y)
(not (fp.eq x (toFP 1)))
(fp.eq x (toFP 2))
(not (fp.eq y (toFP 1)))
(fp.eq y (toFP 3))
(not (fp.eq x y))
(not
(let ((ans (toFP 1)))
(and
(fp.gt ans (toFP 0))
(fp.leq ans (toFP 3))
(fp.eq (fp.roundToIntegral RNE ans) ans)
(not (fp.eq ans x))
(not (fp.eq ans y)))))))
(check-sat)
(get-model)Agenda
- 背景
- 提案手法
- 評価
- まとめ
評価手法
-
以上の分析をJavaScriptプログラムに対して自動で行う
モデル検査機を実装した。 -
実験にはプログラミングコンテストAtCoderへの提出プログラムをスクレイピングして用いた。
-
AtCoderで過去に開催されたプログラミングコンテストの問題から検証に適していると思われるものを選択し、これらの要求仕様を SMT-LIB 2.0 の形で書き下した。
-
またそれぞれの問題に対するJavaScriptによる提出プログラムをスクレイピングし、実装したモデル検査機への入力として与える。
実験結果
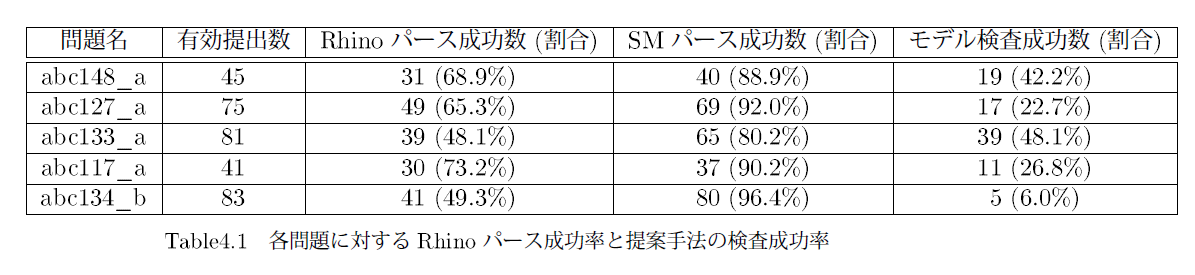
-
Rhinoに対してSpiderMonkeyを用いることによってすべてのケースにおいてパース成功率の向上がみられた
- SpiderMonkeyを利用することによるモデル検査機としての優位性が裏付けられた
-
最大で半分程度の提出に対して提案手法を用いたモデル検査を適用することができた
- これらのケースはいずれも変数として数値型のみを扱い、ループや非同期処理などの複雑な動作を含まず、単純な入出力のみを扱うものであった
- そのため相当に限定的なケースに限られるものの、提案手法が実際にすでに存在するプログラムに対して適用可能なものであることが示された
Agenda
- 背景
- 提案手法
- 評価
- まとめ
まとめ
-
JavaScriptプログラムのシンボリック実行を用いたプログラム解析という問題に対して、
新たにSpiderMonkeyを用いてバイトコードの適用を行う手法を示した -
また、さらにこの手法がJavaScriptプログラムの
モデル検査に応用できることを示した -
今後の展望としては、文字列型やオブジェクト型などのより高度なデータ型に対するシンボリック実行を実装し、さらに多くのJavaScriptプログラムを解析できるようにすることが考えられる
Appendix
実装
- 入力プログラムをSpiderMonkeyでパースする
- 上で得た命令列を適切なコードブロック単位に分割し、分岐命令によって起こりうるブロック間の遷移を列挙する
- プログラムの取りうる実行パスを深さ優先探索を用いて列挙し、それぞれに対するシンボリック実行を用いた入力値解析を行う
- シンボル化された出力値および条件分岐を充足するための条件をSMT-LIB 2.0の形式に変換し、CVC4を用いて充足可能性の判定を行う。
- この結果、充足不可能であれば正当な実装であると判定して終了する。充足可能であればその値を仕様に対する反例として出力する。
検査対象のプログラムの出力が
シンボルを含む場合
(x, y) => {
const z = x + y;
return 6 - z;
};SMT Solver を用いた求解
この例では条件分岐を
含まないため、
実行パスに対応する分岐条件は存在しない。
出力に入力に基づく
シンボルが含まれるため
これを含めてSMTソルバで
求解する。
実行すると同じく
「充足不可能」の結果を得る
(set-logic ALL)
(set-option :produce-models true)
(define-sort FP () (_ FloatingPoint 11 53))
(define-fun toFP ((n Real)) FP ((_ to_fp 11 53) RNE n))
(declare-const x FP)
(declare-const y FP)
(assert
(and
(fp.gt x (toFP 0))
(fp.leq x (toFP 3))
(fp.eq (fp.roundToIntegral RNE x) x)
(fp.gt y (toFP 0))
(fp.leq y (toFP 3))
(fp.eq (fp.roundToIntegral RNE y) y)
(not (fp.eq x y))
(not
(let ((ans (fp.sub RNE (toFP 6) (fp.add RNE x y))))
(and
(fp.gt ans (toFP 0))
(fp.leq ans (toFP 3))
(fp.eq (fp.roundToIntegral RNE ans) ans)
(not (fp.eq ans x))
(not (fp.eq ans y)))))))
(check-sat)
(get-model)References (1)
- [Shoshitaishvili, 2016] Shoshitaishvili, Yan, et al. "Sok:(state of) the art of war: Offensive techniques in binary analysis." 2016 IEEE Symposium on Security and Privacy (SP). IEEE, 2016.
- [Stephens, 2016] Stephens, Nick, et al. "Driller: Augmenting Fuzzing Through Selective Symbolic Execution." NDSS. Vol. 16. No. 2016. 2016.
- [Cader, 2008] Cadar, Cristian, Daniel Dunbar, and Dawson R. Engler. "KLEE: Unassisted and Automatic Generation of High-Coverage Tests for Complex Systems Programs." OSDI. Vol. 8. 2008.
- [Burnim, 2008] Burnim, Jacob, and Koushik Sen. "Heuristics for scalable dynamic test generation." Proceedings of the 2008 23rd IEEE/ACM international conference on automated software engineering. IEEE Computer Society, 2008.
- [Codefroid, 2008] Godefroid, Patrice, Michael Y. Levin, and David A. Molnar. "Automated Whitebox Fuzz Testing." NDSS. Vol. 8. 2008.
- [Păsăreanu, 2010] Păsăreanu, Corina S., and Neha Rungta. "Symbolic PathFinder: symbolic execution of Java bytecode." Proceedings of the IEEE/ACM international conference on Automated software engineering. ACM, 2010.
- [Saxena, 2010] Saxena, Prateek, et al. "A symbolic execution framework for javascript." 2010 IEEE Symposium on Security and Privacy. IEEE, 2010.
- [Li, 2014] Li, Guodong, Esben Andreasen, and Indradeep Ghosh. "SymJS: automatic symbolic testing of JavaScript web applications." Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering. ACM, 2014.
- [Mirshokraie, 2015] Mirshokraie, Shabnam, Ali Mesbah, and Karthik Pattabiraman. "Jseft: Automated javascript unit test generation." 2015 IEEE 8th International Conference on Software Testing, Verification and Validation (ICST). IEEE, 2015.
References (2)
- [Li, 2013] Li, Guodong, and Indradeep Ghosh. "PASS: string solving with parameterized array and interval automaton." Haifa Verification Conference. Springer, Cham, 2013.
- [Deng, 2007] Deng, Xianghua, and John Hatcliff. "Kiasan/KUnit: Automatic test case generation and analysis feedback for open object-oriented systems." Testing: Academic and Industrial Conference Practice and Research Techniques-MUTATION (TAICPART-MUTATION 2007). IEEE, 2007.
- [Andreasen, 2017] Andreasen, Esben, et al. "A survey of dynamic analysis and test generation for JavaScript." ACM Computing Surveys (CSUR) 50.5 (2017): 66.
- [Chaudhuri, 2010] Chaudhuri, Avik, and Jeffrey S. Foster. "Symbolic security analysis of ruby-on-rails web applications." Proceedings of the 17th ACM conference on Computer and communications security. ACM, 2010.
- [Milicevic, 2014] Milicevic, Aleksandar, Ido Efrati, and Daniel Jackson. "αRby—An embedding of Alloy in Ruby." International Conference on Abstract State Machines, Alloy, B, TLA, VDM, and Z. Springer, Berlin, Heidelberg, 2014.
- [Tanida, 2014] Tanida, Hideo, et al. "Automatic unit test generation and execution for javascript program through symbolic execution." Proceedings of the Ninth International Conference on Software Engineering Advances. 2014.
- [King, 1976] King, James C. "Symbolic execution and program testing." Communications of the ACM 19.7 (1976): 385-394.