Ultimate

TIC-TAC-TOE

Hexanome 4405

Disponible sur: https://github.com/halflings/ultimate-tictactoe

Ultimate Tic-tac-Toe ?

  • Un champ de jeu composé de 9 grilles.

  • Chaque grille se joue comme un tic-tac-toe normal.

  • Jouer une case envoie le joueur suivant sur la grille équivalente.

  • Le champ de jeu est en lui même une grille géante.





Une partie ;-) ?

Pourquoi ce jeu?


  • Jeu méconnu = Plus de challenge. (Pas de stratégie optimale connue)

  • "Un jeu dans le jeu" : IA prenant en compte deux niveaux de jeu (local et global)

  • Parce qu'il est amusant !

    Structure du jeu

    Le champ de jeu est représenté par une matrice. Cette structure... 
    [[0,2,1,0,1,2,0,0,0],[1,1,2,2,1,0,0,1,2],[0,1,2,0,1,2,2,1,1],[1,0,1,2,0,0,1,1,1],[0,1,1,0,2,2,1,2,0],[2,1,2,1,1,2,0,0,1],[0,2,1,2,1,0,0,2,0],[2,1,0,2,2,1,1,0,0],[1,0,0,1,0,1,2,2,2]]

    ...est équivalente à la grille suivante:

    Une "API" complète


    Un ensemble  de prédicats permettent d'examiner le jeu et ses différents paramètres:
    playableGrid(N) :- getGridsState(State), allowedGrids(Allowed,State), member(N, Allowed).
playableCell(N, M) :- playableGrid(N), gameField(D), nth1(N, D, G), nth1(M, G, 0).

nextPlayer(X) :- lastMove(_,_,-1), X is 1.
nextPlayer(X) :- lastMove(_,_,P), P > 0, X is 3-P.


playMove(N,M,J) :- gameField(D), /* ... */
                   retract(gameField(D)), assert(gameField(NewD)), 
					           lastMove(A,B,C), retract(lastMove(A,B,C)),
                    asserta(lastMove(N,M,J)).

    Chaque IA implémente un prédicat  nextMove donnant le coup à jouer.

    Fonctionnement du programme

    • En entrée: État du champ de jeu (matrice), dernier coup joué et IA utilisée dans un fichier 
      input.pl 
    :- ['ai.pl'].
:- asserta(gameField([[1, 0, 2, 0, 1, 2, 0, 0, 2], [1, 2, 1, 2, 2, 2, 2, 0, 0], [2, 1, 1, 2, 0, 0, 2, 0, 0], [1, 1, 1, 2, 0, 0, 0, 2, 0], [1, 1, 0, 2, 2, 0, 1, 0, 2], [1, 1, 2, 1, 1, 2, 2, 1, 0], [1, 1, 1, 0, 1, 0, 0, 2, 2], [1, 1, 1, 2, 2, 0, 0, -1, 1], [1, 1, 1, 0, 0, 2, 0, 2, 0]])).
:- asserta(lastMove(5, 5, 2)).
    • En sortie: Nouvel état du champ de jeu et d'autres informations (dernier coup, état des grilles, ...)
    [[1,0,2,0,1,2,0,0,2],[1,2,1,2,2,2,2,0,0],[2,1,1,2,0,0,2,0,0],[1,1,1,2,0,0,0,2,0],[1,1,1,2,2,0,1,0,2],[1,1,2,1,1,2,2,1,0],[1,1,1,0,1,0,0,2,2],[1,1,1,2,2,0,0,-1,1],[1,1,1,0,0,2,0,2,0]] [] [2,2,2,1,1,1,1,1,1] [5,3,1]

    Des IAs de poids

    Des IAs basées sur un système de poids et de priorités:

    • Divers critères sur ce qu'est "un bon coup"

    • Critères défensifs vs Critères offensifs

    • Le poids d'un coup est la somme des poids de tous les critères qu'il vérifie

    • Les critères de priorité plus élevée dominent les autres

    • Le coup au poids le plus grand est joué à chaque tour

    Exemple de critères


    • Coup gâchant une victoire locale à l'adversaire: + 32 
    • Coup n'amenant pas l'adversaire à gagner une grille: + 64

       
    spoilWinWeight(N, M, J, 32) :- NJ is 3 - J, isWinningMove(N, M, NJ).
spoilWinWeight(_, _, _, 0).

avoidWinWeight(M, J, 64) :- NJ is 3 - J, not(isWinningMove(M, _, NJ)).
avoidWinWeight(_, _, 0).

    Une IA " LearninG "


    Son principe :

    Etudier les victoires des parties jouées.


    L'objectif :

    Ne pas jouer de coups faisant gagner l'adversaire.


    La solution :

     Cataloguer les coups faisant perdre les parties, et ne pas les rejouer si on est dans une situation identique.


    Évaluation des IA


    Pour évaluer l'efficacité de l'IA de manière automatisée:

    • Parties contre un joueur humain
    • Parties contre un jeu 'aléatoire'
    • Parties entre IAs différentes

      Interfaçage et Tests


      Une première interface (Python), en ASCII
      Pas pratique pour jouer et visualiser le jeu

      INTERFAÇAGE ET TESTS


      Interface web (Python/Javascript)
      Permet de comparer les IAs et de jouer.

      Plusieurs stratégies


      Chaque IA a une stratégie de jeu différente:

      • IA locale
      • IA agressive
      • IA défensive
      • IA globale/hybride
      • IA "learning"

      On lance quelques milliers de parties pour comparer les IAs entre elles.

      Résultats

      IA Agressive vs IA Défensive

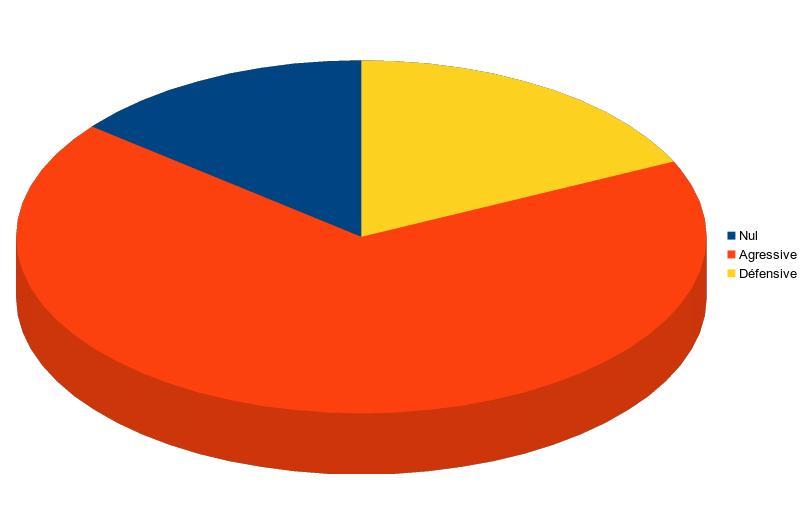
      Résultats

      IA Agressive vs IA Globale/Hybride

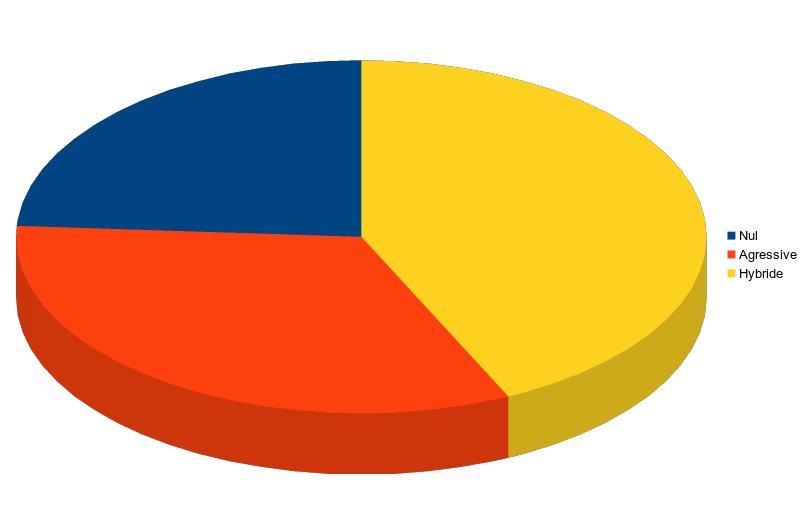
      RÉSULTATS

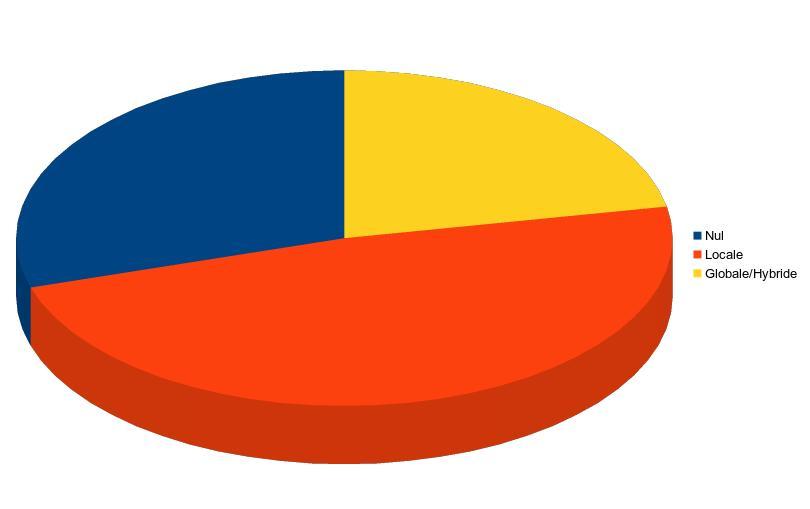
      IA Locale vs IA Globale/Hybride





      Démonstration :-) !

      Synthèse


      • Aucune IA ne sort réellement du lot !

      • Chaque IA est efficace contre certaines stratégies de jeu et faible contre d'autres.

      • Raison: IAs bâties sur l'axiome d'un joueur 'intelligent' et adoptant une stratégie particulière.

      • L'IA qui apprend n'amène pas de résultats satisfaisants : pas assez de combinaisons perdantes trouvées.
      Made with Slides.com