A gentle introduction to Particle Filters

EA503 - DSP - Prof. Luiz Eduardo

Watch

Student Dave

Channel!

Agenda

  1. Tools from statistics + Recap
  2. Particle filters and its components
  3. An algorithm (In Python)

Classical statistics

We place probability distributions on data

(only data is random)

Bayesian statistics

We place probability distributions in the model and in parameters

Probability represents uncertainty

P(Hypothesis|Data)
P(Hypothesis∣Data)P(Hypothesis|Data)

Posterior

Probability

P(Data|Hypothesis)
P(Data∣Hypothesis)P(Data|Hypothesis)

Likelihood

P(Hypothesis)
P(Hypothesis)P(Hypothesis)

Prior

Bayesian statistics

P(Hypothesis|Data) = \frac{P(Hypothesis)*P(Data|Hypothesis)}{P(Data)}
P(Hypothesis∣Data)=P(Hypothesis)∗P(Data∣Hypothesis)P(Data)P(Hypothesis|Data) = \frac{P(Hypothesis)*P(Data|Hypothesis)}{P(Data)}

Recursively, 

P(Hypothesis|Data) = P(H_t|H_{t-1}, D_t)
P(Hypothesis∣Data)=P(Ht∣Ht−1,Dt)P(Hypothesis|Data) = P(H_t|H_{t-1}, D_t)

Bayesian statistics

P(Hypothesis|Data) = P(H_t|H_{t-1}, D_t)
P(Hypothesis∣Data)=P(Ht∣Ht−1,Dt)P(Hypothesis|Data) = P(H_t|H_{t-1}, D_t)

Every time we get a new step, we should be able to improve our state estimation

Kalman Filter

P(H_t|H_{t-1}, A_t, D_t)
P(Ht∣Ht−1,At,Dt)P(H_t|H_{t-1}, A_t, D_t)

Prediction + correction

Constraint: It needs to be a Gaussian distribution

It is also a recursive structure

Can we represent these recursive models as chains?

X_{t-1}
Xt−1X_{t-1}
X_{t}
XtX_{t}
X_{t+1}
Xt+1X_{t+1}

Markov chain

X is the true information

P(X_t|X_{t-1})
P(Xt∣Xt−1)P(X_t|X_{t-1})

We may not have access to the true information, but to a measured (estimated) value

X_{t-1}
Xt−1X_{t-1}
X_{t}
XtX_{t}
X_{t+1}
Xt+1X_{t+1}
Y_{t-1}
Yt−1Y_{t-1}
Y_{t}
YtY_{t}
Y_{t+1}
Yt+1Y_{t+1}

Hidden Markov chain

P(Y_t|X_{t})
P(Yt∣Xt)P(Y_t|X_{t})
X_{t-1}
Xt−1X_{t-1}
X_{t}
XtX_{t}
X_{t+1}
Xt+1X_{t+1}
Y_{t-1}
Yt−1Y_{t-1}
Y_{t}
YtY_{t}
Y_{t+1}
Yt+1Y_{t+1}

What can we say about this model in terms of P?

X_{t-1}
Xt−1X_{t-1}
X_{t}
XtX_{t}
X_{t+1}
Xt+1X_{t+1}
Y_{t-1}
Yt−1Y_{t-1}
Y_{t}
YtY_{t}
Y_{t+1}
Yt+1Y_{t+1}

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})

Consider all the observations for the estimation

[marginal distribution]

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})

We know

P(X_t|X_{t-1})
P(Xt∣Xt−1)P(X_t|X_{t-1})
P(Y_t|X_{t})
P(Yt∣Xt)P(Y_t|X_{t})

and

Considering that this is a recursive process,

P(X_{t-1}|Y_1,...,Y_{t-1})
P(Xt−1∣Y1,...,Yt−1)P(X_{t-1}|Y_1,...,Y_{t-1})

Combining these Probabilities:

P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})
P(Yt,Xt,Xt−1∣Y1,...,Yt−1)P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})

We know

P(X_t|X_{t-1})
P(Xt∣Xt−1)P(X_t|X_{t-1})
P(Y_t|X_{t})
P(Yt∣Xt)P(Y_t|X_{t})

and

Considering that this is a recursive process,

P(X_{t-1}|Y_1,...,Y_{t-1})
P(Xt−1∣Y1,...,Yt−1)P(X_{t-1}|Y_1,...,Y_{t-1})

Combining these Probabilities:

P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})
P(Yt,Xt,Xt−1∣Y1,...,Yt−1)P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})

We know

P(X_t|X_{t-1})
P(Xt∣Xt−1)P(X_t|X_{t-1})
P(Y_t|X_{t})
P(Yt∣Xt)P(Y_t|X_{t})

and

Considering that this is a recursive process,

P(X_{t-1}|Y_1,...,Y_{t-1})
P(Xt−1∣Y1,...,Yt−1)P(X_{t-1}|Y_1,...,Y_{t-1})

Combining these Probabilities:

P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})
P(Yt,Xt,Xt−1∣Y1,...,Yt−1)P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})

We know

P(X_t|X_{t-1})
P(Xt∣Xt−1)P(X_t|X_{t-1})
P(Y_t|X_{t})
P(Yt∣Xt)P(Y_t|X_{t})

and

Considering that this is a recursive process,

P(X_{t-1}|Y_1,...,Y_{t-1})
P(Xt−1∣Y1,...,Yt−1)P(X_{t-1}|Y_1,...,Y_{t-1})

Combining these Probabilities:

P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})
P(Yt,Xt,Xt−1∣Y1,...,Yt−1)P(Y_{t},X_{t},X_{t-1}|Y_1,...,Y_{t-1})

Not

Relevant in this formula

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})

In a particular point,

P(Y_{t}=y,X_{t},X_{t-1}=x|Y_1,...,Y_{t-1})
P(Yt=y,Xt,Xt−1=x∣Y1,...,Yt−1)P(Y_{t}=y,X_{t},X_{t-1}=x|Y_1,...,Y_{t-1})

Sum x (it'll remove                 )

X_{t-1}
Xt−1X_{t-1}
\sum_{x} P(Y_{t}=y,X_{t},X_{t-1}=x|Y_1,...,Y_{t-1})
∑xP(Yt=y,Xt,Xt−1=x∣Y1,...,Yt−1)\sum_{x} P(Y_{t}=y,X_{t},X_{t-1}=x|Y_1,...,Y_{t-1})
P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1}) =
P(Yt=y,Xt∣Y1,...,Yt−1)=P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1}) =

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})

Get rid of  

Y_{t} = y
Yt=yY_{t} = y
\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})
∑xP(Yt=y,Xt=x∣Y1,...,Yt−1)\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})
P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})
P(Yt=y,Xt∣Y1,...,Yt−1)P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})

Current:

Another manipulation

P(Y_{t}=y|Y_1,...,Y_{t-1}) =
P(Yt=y∣Y1,...,Yt−1)=P(Y_{t}=y|Y_1,...,Y_{t-1}) =

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})
\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}
P(Yt=y,Xt∣Y1,...,Yt−1)∑xP(Yt=y,Xt=x∣Y1,...,Yt−1)\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}

Final

arrangement:

And this is the set of ideas we need for understanding...

[joint distribution]

Agenda

  1. Tools from statistics + Recap
  2. Particle filters and its components
  3. An algorithm (In Python)

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})
\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}
P(Yt=y,Xt∣Y1,...,Yt−1)∑xP(Yt=y,Xt=x∣Y1,...,Yt−1)\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}

Final

arrangement:

This computation can be REALLY heavy (O^2)

[joint distribution]

Let's use points (particles) to represent our space

Let's estimate this joint distribution as a sum of weighted trajectories of this particles

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})
\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}
P(Yt=y,Xt∣Y1,...,Yt−1)∑xP(Yt=y,Xt=x∣Y1,...,Yt−1)\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}

Final

arrangement:

https://www.youtube.com/watch?v=lzN18y_z6HQ

In pictures

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})
\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}
P(Yt=y,Xt∣Y1,...,Yt−1)∑xP(Yt=y,Xt=x∣Y1,...,Yt−1)\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}

Final

arrangement:

https://www.youtube.com/watch?v=lzN18y_z6HQ

In pictures

Goal:

P(X_t|Y_1,...,Y_{t})
P(Xt∣Y1,...,Yt)P(X_t|Y_1,...,Y_{t})
\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}
P(Yt=y,Xt∣Y1,...,Yt−1)∑xP(Yt=y,Xt=x∣Y1,...,Yt−1)\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})}

Final

arrangement:

In formulas

\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})} \overset{\Delta}{=}
P(Yt=y,Xt∣Y1,...,Yt−1)∑xP(Yt=y,Xt=x∣Y1,...,Yt−1)=Δ\frac{P(Y_{t}=y,X_{t}|Y_1,...,Y_{t-1})}{\sum_{x} P(Y_{t}=y,X_{t}=x|Y_1,...,Y_{t-1})} \overset{\Delta}{=}
\sum_{i=1}^{NumParticles} weight^{i} \delta(X_{t-1} - X_{t}^i)
∑i=1NumParticlesweightiδ(Xt−1−Xti)\sum_{i=1}^{NumParticles} weight^{i} \delta(X_{t-1} - X_{t}^i)

The sum of these weights is 1

The joint distribution becomes a sum of impulses with weights

The weight is proportional to three components:

1.

P(Y_{t}|X_{t})
P(Yt∣Xt)P(Y_{t}|X_{t})

Observation probability

2.

P(X_{t}|X_{t-1}=x)
P(Xt∣Xt−1=x)P(X_{t}|X_{t-1}=x)

Transition probability

3.

P(X_{t}|X_{t-1}=x_0,Y_1,...,Y_{t-1})
P(Xt∣Xt−1=x0,Y1,...,Yt−1)P(X_{t}|X_{t-1}=x_0,Y_1,...,Y_{t-1})

Computation

from previous step

We can build a recursive formula for the weight of a given particle i

P(Y_{t}|X_{t})
P(Yt∣Xt)P(Y_{t}|X_{t})
P(X_{t}|X_{t-1}=x)
P(Xt∣Xt−1=x)P(X_{t}|X_{t-1}=x)
P(X_{t}|X_{t-1}=x_0,Y_1,...,Y_{t-1})
P(Xt∣Xt−1=x0,Y1,...,Yt−1)P(X_{t}|X_{t-1}=x_0,Y_1,...,Y_{t-1})
w_{t}^{i} =
wti=w_{t}^{i} =
w_{t-1}^{i}
wt−1iw_{t-1}^{i}

The steps to the algorithm

1. Use n particles to represent distributions over hidden states; create initial values

2. Transition probability: Sample the next state from each particle

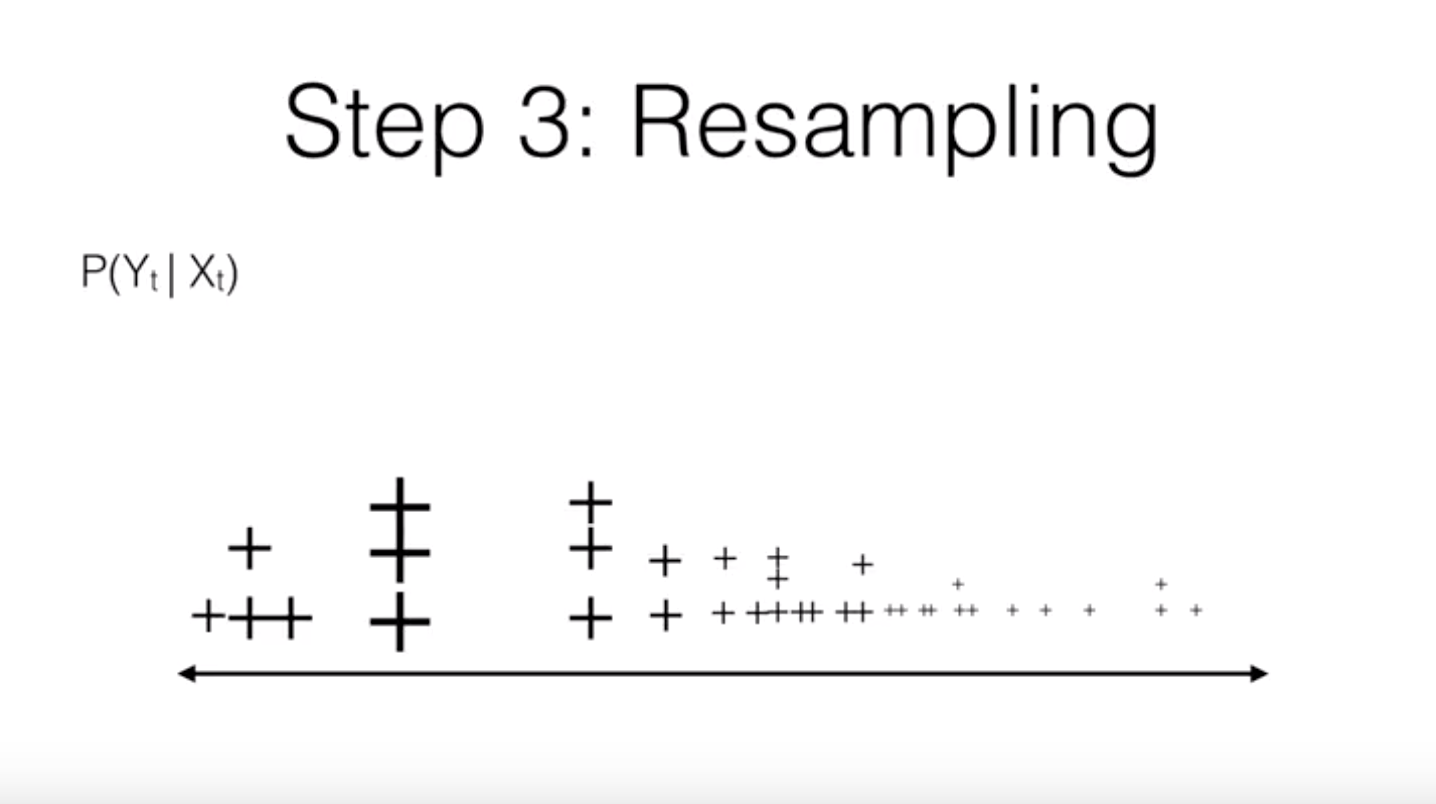
3. Calculate the weights and normalize them

4. Resample: generate a new distribution of particles

loop

https://www.youtube.com/watch?v=lzN18y_z6HQ

In pictures

https://www.youtube.com/watch?v=lzN18y_z6HQ

In pictures

https://www.youtube.com/watch?v=lzN18y_z6HQ

In pictures

https://www.youtube.com/watch?v=lzN18y_z6HQ

In pictures

A concrete example

https://www.youtube.com/watch?v=lzN18y_z6HQ​

1 sample/s

A concrete example

https://www.youtube.com/watch?v=lzN18y_z6HQ​
\phi_n
ϕn\phi_n

is a phase angle, given

y_n = \theta_n + v_n
yn=θn+vny_n = \theta_n + v_n
v_n \approx \Nu(0.5^2)
vn≈N(0.52)v_n \approx \Nu(0.5^2)

A concrete example

https://www.youtube.com/watch?v=lzN18y_z6HQ​

This is the measurement model

A concrete example

https://www.youtube.com/watch?v=lzN18y_z6HQ​

This is the measurement model

(it comes from domain knowledge)

A concrete example

https://www.youtube.com/watch?v=lzN18y_z6HQ​

This is the process model

w_n \approx \Nu(0, \sigma_{w}^2)
wn≈N(0,σw2)w_n \approx \Nu(0, \sigma_{w}^2)

A concrete example

https://www.youtube.com/watch?v=lzN18y_z6HQ​

This is state space - now we apply the algorithm

Agenda

  1. Tools from statistics + Recap
  2. Particle filters and its components
  3. An algorithm (In Python)

Modified example based on SciPy

References