Quantum Symmetry and Hopf Algebras
Harshit Yadav
Rice University
Part I:
Classical and Quantum Symmetries
Symmetries


Why do we want to find symmetries?

Since, this image is symmetric, it suffices to know just the left half of it.
The symmetries of an object make it easier to analyze it.
Why do we want to find symmetries?

A symmetry of an object \( X \) is an invertible property-preserving transformation of \( X\).
The symmetries of an object make it easier to analyze it.
Since, this image is symmetric, it suffices to know just the left half of it.
flipping the picture around the red line is a symmetry of this picture
Why do we want to find symmetries?
The symmetries of an object make it easier to analyze it.


Since, this image is symmetric, it suffices to know just the left half of it.
A symmetry of an object \( X \) is an invertible property-preserving transformation of \( X\).
How to quantify symmetries?
A coarse measure would be to look at the size \(|Sym(X)|\). But this set has much more structure.
Idea - look at the collection of all symmetries
\(Sym(X) =\) the set of symmetries of \(X\)
How to quantify symmetries?
a
b
d
c
A coarse measure would be to look at the size \(|Sym(X)|\). But this set has much more structure.
Idea - look at the collection of all symmetries
\(Sym(X) =\) the set of symmetries of \(X\)
Example: Consider the symmetries of the rectangle
A coarse measure would be to look at the size \(|Sym(X)|\). But this set has much more structure.
How to quantify symmetries?
Idea - look at the collection of all symmetries
\(Sym(X) =\) the set of symmetries of \(X\)
Example: Consider the symmetries of the rectangle
- We always have the transformation \(Id\) which leaves the rectangle unchanged.
a
b
d
c
A coarse measure would be to look at the size \(|Sym(X)|\). But this set has much more structure.
How to quantify symmetries?
Idea - look at the collection of all symmetries
\(Sym(X) =\) the set of symmetries of \(X\)
Example: Consider the symmetries of the rectangle
- We always have the transformation \(Id\) which leaves the rectangle unchanged.
a
b
d
c
a
b
d
c
- We can rotate it by \(180^{\circ}\) to get
\( R_{180}\)
a
b
d
c
d
c
a
b
\( H\)
a
b
d
c
d
c
a
b
\( H\)
b
a
c
d
\(V\)
\( Sym(X) = \{ Id, R_{180}, H, V \} \)
a
b
d
c
Thus, \( VH =R_{180} \).
d
c
a
b
\( H\)
b
a
c
d
\(V\)
\( Sym(X) = \{ Id, R_{180}, H, V \} \)
\( H\)
a
b
d
c
c
b
a
d
\(V\)
d
a
b
c
b
c
d
a
- \( \cdot \) is associative: \( g_1\cdot (g_2\cdot g_3) = (g_1 \cdot g_2) \cdot g_3 \)
- There is an element \(e\in G\) satisfying \( e\cdot g =g=g\cdot e \)
- For every element \(g \in G\), there is an element \( g^{-1}\) such that \( g\cdot g^{-1} = e = g^{-1}\cdot g\)
Groups
A Group is a set \( G\) with a function \( \cdot:G\times G \rightarrow G \) such that:
Example 1: \( G = Sym( \) \( ) =\{Id, R_{180}, H, V \}\)
Groups
- \( \cdot \) is associative: \( g_1\cdot (g_2\cdot g_3) = (g_1 \cdot g_2) \cdot g_3 \)
- There is an element \(e\in G\) satisfying \( e\cdot g =g=g\cdot e \)
- For every element \(g \in G\), there is an element \( g^{-1}\) such that \( g\cdot g^{-1} = e = g^{-1}\cdot g\)
A Group is a set \( G\) with a function \( \cdot:G\times G \rightarrow G \) such that:
Example 2: \( D_6 = Sym ( \) \( ) =\{ Id, R_{120}, R_{120}^2, A,B,C \} \)
Example 1: \( G = Sym( \) \( ) =\{Id, R_{180}, H, V \}\)
Groups
- \( \cdot \) is associative: \( g_1\cdot (g_2\cdot g_3) = (g_1 \cdot g_2) \cdot g_3 \)
- There is an element \(e\in G\) satisfying \( e\cdot g =g=g\cdot e \)
- For every element \(g \in G\), there is an element \( g^{-1}\) such that \( g\cdot g^{-1} = e = g^{-1}\cdot g\)
A Group is a set \( G\) with a function \( \cdot:G\times G \rightarrow G \) such that:
Example 2: \( D_6 = Sym ( \) \( ) =\{ Id, R_{120}, R_{120}^2, A,B,C \} \)
where \(R_{120}\) is the \(120^{\circ}\) rotation, \(A\) is the flip along the dotted line.
Example 1: \( G = Sym( \) \( ) =\{Id, R_{180}, H, V \}\)
Groups
- \( \cdot \) is associative: \( g_1\cdot (g_2\cdot g_3) = (g_1 \cdot g_2) \cdot g_3 \)
- There is an element \(e\in G\) satisfying \( e\cdot g =g=g\cdot e \)
- For every element \(g \in G\), there is an element \( g^{-1}\) such that \( g\cdot g^{-1} = e = g^{-1}\cdot g\)
A Group is a set \( G\) with a function \( \cdot:G\times G \rightarrow G \) such that:
Symmetries of Vector Spaces
Symmetries of vector spaces generalize the study of symmetries of objects and sets.
Still, why generalize?
Here's an motivation from Machine Learning
Symmetries of Vector Spaces
Symmetries of vector spaces generalize the study of symmetries of objects and sets.
Still, why generalize?
Here's an application from Machine Learning
In a black and white image of 3x3 resolution, we have 9 pixels where each black pixel corresponds to 1 and each white pixel to 0. Such an image is represented by a vector in \(\mathbb{R}^9\). Thus to understand its symmetries, we need to study symmetries of \(\mathbb{R}^9\).

Symmetries of Vector Spaces
Symmetries of vector spaces generalize the study of symmetries of objects and sets.
Still, why generalize?
Here's an application from Machine Learning
In a black and white image of 3x3 resolution, we have 9 pixels where each black pixel corresponds to 1 and each white pixel to 0. Such an image is represented by a vector in \(\mathbb{R}^9\). Thus to understand its symmetries, we need to study symmetries of \(\mathbb{R}^9\).

\( (1, 0, 1, 1, 0, 1, 0, 1, 0) \in \mathbb{R}^9 \)
Symmetries of Vector Spaces
Symmetries of vector spaces generalize the study of symmetries of objects and sets.
Still, why generalize?
Here's an application from Machine Learning
In a black and white image of 3x3 resolution, we have 9 pixels where each black pixel corresponds to 1 and each white pixel to 0. Such an image is represented by a vector in \(\mathbb{R}^9\). Thus to understand its symmetries, we need to study symmetries of \(\mathbb{R}^9\).

\( (1, 0, 1, 1, 0, 1, 0, 1, 0) \in \mathbb{R}^9 \)
A symmetry of a vector space \(V\) is an invertible linear transformation \(f: V\rightarrow V\) of \(V\). We denote the set of all symmetries as \( GL(V) \).
The set \(GL(V)\) is quite large and we are more interested in certain subsets of it.
In the example of the pixelated picture, we are only interested in symmetries of \(\mathbb{R}^9\) that keep the picture unchanged.
Thus, one can study nice subsets of \(GL(V)\); but this is difficult.
Better approach: Group actions on vector spaces
An action* of a group \(G\) on a vector space \(V\) is defined as a map \( \phi: G \rightarrow GL(V) \) which satisfies \( \phi(g\cdot g') = \phi(g) \phi(g') \).
*In CS literature, the terminology '\(V\) is \(G\)-equivariant' is used more prominently.
Developing Group Equivariant Neural Networks is a hot area these days


Cons of groups
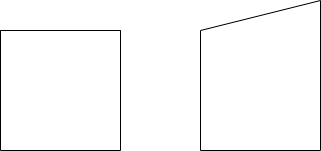
\( X \)
\( X^{def} \)
Deform
\( Sym(X) =\{ Id, R,R^2,R^3,\)
\(A,B,C,D \} \)
\(Sym(X^{def})= \{ Id\}\)
This is inconvenient when generalizing to the quantum setting.
When trying to formalize Quantum Physics, we encounter quantum versions of vector spaces which are deformations of usual vector spaces.
\(V\)
\(V_q\)
Deform
V has symmetries given by some group \(G\)
Want some deformed group \(G_q\) which gives us symmetries of \(V_q\)
It turns out that Hopf algebras provide the right setting for addressing this problem.
Because of the rigid nature of groups, in most examples, we are not able to find any such group \(G_q\). Thus, we have to broaden our framework.
When trying to formalize Quantum Physics, we encounter quantum versions of vector spaces which are deformations of usual vector spaces.
Since, Hopf algebra generalize groups to address problems from Quantum Physics, they are also referred to as quantum groups.
When a vector space admits actions by Hopf algebras which are not coming from groups, we say they admit quantum symmetries.
Groups
Hopf algebras
- \(G\)-action on \(V\)
- \(V\) deforms to \(V_q\)
- Do not get any non-trivial groups action on \(V_q\)
- \(H\)-action on \(V\)
- \(V\) deforms to \(V_q\)
- Have nice deformations \(H_q\) of \(H\) of which act on \(V_q\)
Part II:
Defining Hopf
algebras
\( \mathbb{R}[x] =\) the set of polynomials in the variable \( x\)
- Naturally a vector space over \( \mathbb{R} \)
- Can multiply two polynomials to get a new one
- Have the polynomial \( f(x)=1\) which satisfies \( fg=g=gf \) for any other polynomial \( g\)
Combining elements
\(Mat_n(\mathbb{R}) =\) the set of \( n\times n\) matrices
- Vector space over \( \mathbb{R} \)
- Matrix multiplication
- The \(n \times n\) identity matrix \( I_n\) satisfies \( I_n M = M = M I_n\)

\(x+1\)
\(x\)
\(x^2+x\)
Algebras
An algebra over \( \mathbb{R}\) is a tuple \( (A,m,u)\) where:


- \(A \) is an \( \mathbb{R}\)-vector space
- \( m=\) \(: A\otimes A \rightarrow A\) is a linear map, and
- \(u=\) \(:\mathbb{R} \rightarrow A\) is a linear map
Algebras
An algebra over \( \mathbb{R}\) is a tuple \( (A,m,u)\) where:


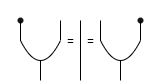
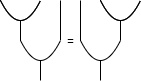
associativity
unitality
\(f\)
\(g\)
\(h\)
\(f\)
\(g\)
\(h\)
\(gh\)
\(f(gh)\)
\((fg)h\)
\(fg\)
\(f\)
\(f\)
\(f\)
\(f\)
\(fe\)
\(ef\)
\(1\)
\(1\)
\(e\)
\(e\)
- \(A \) is an \( \mathbb{R}\)-vector space
- \( m=\) \(: A\otimes A \rightarrow A\) is a linear map, and
- \(u=\) \(:\mathbb{R} \rightarrow A\) is a linear map
satisfying:
Given a group \(G\), the group algebra \( \mathbb{R}G\) is a:
- \( \mathbb{R}\) vector space with basis \(x_g\) for all \( g \in G\),
- with multiplication \(x_g x_{g'} =x_{g\cdot g'}\), and
- unit \(x_{e}\) where \(e\) is the identity element of \(G\).
By working with groups algebras, we do not lose anything. In fact,
\(G\)-actions on vector spaces
\( f: G \rightarrow GL(V)\)
\( \mathbb{R}G\)-actions on vector spaces
\(F: \mathbb{R}G \rightarrow \text{End}(V) \)

\(x_g\)
\(x_{g'}\)
\(x_{g\cdot g'}\)

\(1\)
\(x_e\)
End\((V)=\) the set of all linear maps \(V \rightarrow V\)
Breaking up elements into two
\( \mathbb{R}[x] =\) the set of polynomials in the variable \(x\)
- Break up \(x^n \) as \( \Delta(x^n) = \sum_{k=0}^n {n\choose k} x^k \otimes x^{n-k} \), extend.
\(\mathbb{R}G = \) the group algebra of a group \(G\)
Most natural example come from different kinds of graphs.
- Naturally a \(\mathbb{R}\)-vector space
- Break up \(x_g\) as \( \Delta(x_g) = x_g\otimes x_g\), then extend to \( \mathbb{R}[G] \).
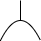
\(x_g\)
\(x_g\)
\(x_g\)

\(x^n\)
\(x^{k}\)
\(x^{n-k}\)
\(\sum_k\)
Coalgebras
An coalgebra over \( \mathbb{R}\) is a tuple \( (C,\Delta,\varepsilon)\) where:
- \(C \) is an \( \mathbb{R}\)-vector space
- \( \Delta=\) \(: A \rightarrow A \otimes A \) is a linear map, and
- \( \varepsilon = \) \(: C \rightarrow \mathbb{R} \) is a linear map
such that \(\Delta\) and \( \varepsilon\) satisfy

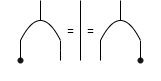
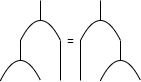

coassociativity
counitality

Vector Spaces
Vector Spaces
Algebras
Vector Spaces
Algebras
Coalgebras


Vector Spaces
Algebras
Coalgebras
Groups


Vector Spaces
Algebras
Coalgebras
Groups
Group algebras


Vector Spaces
Algebras
Coalgebras
Groups
Group algebras
\(\mathbb{R}[x]\)
Group algebras have the structure of both an algebra and a coalgebra.

\(x_g\)
\(x_{g'}\)
\(x_{g\cdot g'}\)

\(1\)
\(x_e\)

\(x_g\)
\(x_g\)
\(x_g\)

\(x_g\)
\(\delta_{x,e}\)
However, a group had an inverse for each element and we have not used that information. Define the map:
\(S=\) \(:\mathbb{R}G \rightarrow \mathbb{R}G \)
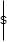
\( x_g \mapsto x_{g^{-1}} \)
Then we set up the definition of a Hopf algebras so that group algebras are an example.
Hopf algebras
A Hopf algebra is a tuple \( (H,m=\) \(,u=\) \(,\Delta=\) \(, \varepsilon=\) \(,\) \(S=\) \(:H \rightarrow H) \) such that:
- \( (H,m,u) \) is an algebra,
- \( (H,\Delta,\varepsilon) \) is a coalgebra,
- Algebra and coalgebra structures are compatible
- \( S:H \rightarrow H \) is a linear map which satisfies




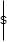




\(Id_{\mathbb{R}} \)
Algebras
Coalgebras
Vector Spaces
Hopf
Algebras
Group
Algebras

Groups
Symmetries of
vector spaces
Group actions on
vector spaces
Symmetries of objects
Actions of group algebras on vector spaces
do not behave well under deformations
of the algebra
Actions of group algebras on algebras
broaden framework to consider Hopf action
Actions of Hopf
algebras on
algebras
pixelated
image example
need only certain
symmetries
equivalent
problem
in all interesting
examples, underlying vector space has algebra structure
Symmetries of
vector spaces
Group actions on
vector spaces
Symmetries of objects
Actions of group algebras on vector spaces
do not behave well under deformations
of the algebra
Actions of group algebras on algebras
broaden framework to consider Hopf action
Actions of Hopf
algebras on
algebras
pixelated
image example
need only certain
symmetries
equivalent
problem
in all interesting
examples, underlying vector space has algebra structure
UPSHOT:
By going to the world of Hopf algebras, we are able to find to find (quantum) symmetries of deformations of algebras.
Symmetries of
vector spaces
Group actions on
vector spaces
Symmetries of objects
Actions of group algebras on vector spaces
do not behave well under deformations
of the algebra
Actions of group algebras on algebras
broaden framework to consider Hopf action
Actions of Hopf
algebras on
algebras
pixelated
image example
need only certain
symmetries
equivalent
problem
in all interesting
examples, underlying vector space has algebra structure
Invariants of spaces
Hopf algebras provide us ways to distinguish 3-dimensional spaces.
The problem of distinguishing shapes comes under the field of topology. In topology, we consider two shapes to be the same if we can smoothly deform one shape into the another.

These two shapes are
considered the same

These are considered
different
No holes/punctures
One hole
No holes/punctures

For \(3\)-dimensional shapes, we can no longer eye-ball the number of holes to distinguish shapes.
Distinguishing shapes in higher dimensions is very difficult problem and many mathematicians have won the Fields medal for work in this area.
Jones polynomial
Input: \(K=\)

Output: \(V_K(t) =t+t^3-t^4 \)
If two knots \(K,K' \) have different Jones polynomials \(V_K(t), V_{K'}(t) \), then the knots are different from each other.
In fact, the Jones polynomial is a special case of a powerful algorithm that distinguishes shapes that uses Hopf algebras as input.
Thank you for your attention!
Email : hy39@rice.edu
Slides: tinyurl.com/yg577z4h
Feel free to contact with question/comments.