Lecture 2

Data

λ Haskell Beginners 2022

Pattern Matching

Patterns

📜 Pattern — specific value or shape of input.

case-of

f :: type
f ... = case var of
    pat1 -> result1
    pat2 -> result2
    ...
    patN -> resultN

Syntax

f :: type
f pat1 = result1
f pat2 = result2
...
f patN = resultN

Examples

not :: Bool -> Bool
not True  = False
not False = True

isZero :: Int -> Bool
isZero 0 = True
isZero n = False

eval :: Char -> Int -> Int -> Int
eval op x y = case op of
    '+' -> x + y
    '-' -> x - y
    '*' -> x * y
    '/' -> div x y
    _ -> 0

    ^ watch for indentation!

Patterns on lists

isEmpty :: [Int] -> Bool
isEmpty [] = True
isEmpty _  = False

sumOfTwoInThree :: [Int] -> Int
sumOfTwoInThree [x, _, y] = x + y
sumOfTwoInThree _         = 0

oneOrTwoZeroes :: [Int] -> Bool
oneOrTwoZeroes l = case l of
    [0]    -> True
    [0, 0] -> True
    _      -> False

-- check if a list has at least two elements
atLeastTwo :: [Int] -> Bool
atLeastTwo [_, _] = True
atLeastTwo _      = False

Does the following work?

❌ No! Because it checks only on lists of size two.

Structural List Patterns

[]      
x : xs

A list can be only one of those two:

1️⃣ Empty list

2️⃣ An element prepended to a list

      ┌── connecting head and tail
      │   `:` is both operator and pattern
      │
    x : xs
    │   │
    │   └── tail
  head

Wait! What about list literals [x, y, z]?

Syntax sugar 🍬

[ 3 ,  1 , 2 ]

  3 :  1 :  2 : []

  3 : (1 : (2 : []))

🪙 Heads or Tails?

headOrDef :: Int -> [Int] -> Int
headOrDef def []      = def
headOrDef _   (x : _) = x

dropHead :: [Int] -> [Int]
dropHead []       = []
dropHead (_ : xs) = xs

secondIsZero :: [Int] -> Bool
secondIsZero (_ : 0 : _) = True
secondIsZero _ = False

🔄 List Recursion

sum :: [Int] -> Int
sum      []  = 0
sum (x : xs) = x + sum xs

⚠️ Warning!

🐌 Slow implementation!

count :: Int -> [Int] -> Int
count n list = go 0 list
  where
    go :: Int -> [Int] -> Int
    go acc list =
        if null list
        then result
        else if head list == n
        then go (acc + 1) (tail list)
        else go  acc      (tail list)

count :: Int -> [Int] -> Int
count n list = go 0 list
  where
    go :: Int -> [Int] -> Int
    go acc [] = acc
    go acc (x : xs)
        | x == n    = go (acc + 1) xs
        | otherwise = go  acc      xs

Improving previous examples

👩‍🔬 Always use pattern matching on lists instead of unsafe

head and tail functions whenever you need either of them.

What's wrong, Haskell?

isEmpty :: [Int] -> True
isEmpty _  = False
isEmpty [] = True

same :: Int -> Int -> True
same x x = True
same _ _ = False

💻 Code

🚫 Error

headOrDef :: Int -> [Int] -> Int
headOrDef def l       = def
headOrDef _   (x : _) = x

👩‍🔬 Incorrect order of patterns

👩‍🔬 Variable is a "catch-all" pattern

👩‍🔬 Patterns on variable names are not supported

head :: [Int] -> Int
head (x : _) = x

👩‍🔬 Patterns don't cover all possible cases

isGreeting :: String -> Bool
isGreeting str = case str of
    'H' : 'i' : '!' : _ -> True
    _ -> False

👩‍🔬 No errors here,

just looks ugly.

Totality

example :: Bool -> [Int] -> Int
example True  []     = 0
example False [x, y] = x + y

📜 A function is total if it is defined for all inputs of its corresponding type, or in other words, if a function returns the output on any possible values of the input types.

⚗️ GHC checks if a function is partial due to non-exhaustive patterns.

📜 Partial — non-total.

<interactive>:32:1: warning: [-Wincomplete-patterns]
    Pattern match(es) are non-exhaustive
    In an equation for ‘example’:
        Patterns not matched:
            True (_:_)
            False (_:_:_:_)
            False [_]
            False []

Data

Tuples

ghci> :t ('x', True)
('x', True) :: (Char, Bool)

ghci> :t ([True, False], "abc", 'F')
([True, False], "abc", 'F') :: ([Bool], [Char], Char)

ghci> fst ('x', True)
'x'

ghci> snd ('x', True)
True

ghci> fst (3, True, False)

<interactive>:39:5: error:
    • Couldn't match expected type ‘(a, b0)’
                  with actual type ‘(a0, Bool, Bool)’

Working with tuples

splitAtPos3 :: [Int] -> ([Int], [Int])
splitAtPos3 l = (take 3 l, drop 3 l)

ghci> splitAtPos3 [1..10]
([1,2,3],[4,5,6,7,8,9,10])
ghci> splitAtPos3 [3, 1]
([3,1],[])

Returning

Matching

showTriple :: (Bool, Int, String) -> String
showTriple (b, n, string) =
    if b
    then "The number is: " ++ show n
    else "The string is: " ++ string

ghci> showTriple (True, 42, "hello")
"The number is: 42"
ghci> showTriple (False, 42, "hello")
"The string is: hello"

Algebraic Data Type (ADT)

ADT — a type formed by combing other types using either

product or sum types.

Product type

Sum type

Combining types using both

Choice of types, either one or another

Product Type

Product type — zero or more types combined

String

Int

Bool

"Hello!"

True

("Hello!", 42, True)
("Byeeee", 15, False)
("", 0, True)

All possible combinations including values of all types

data: Product

      ┌── data type name
      │
      │       ┌── Constructor name
      │       │
data User = MkUser String Int Bool
                     │     │    │
                     └─────┼────┘
                           │
                           │
                      Field types

data: Working with data

data User = MkUser String Int Bool
    deriving (Show)  -- to display our type in GHCi

Getters

getUserName :: User -> String
getUserName (MkUser name _ _) = name

Setters

setUserName :: String -> User -> User
setUserName name (MkUser _ age isTired) = MkUser name age isTired

ghci> :t MkUser
MkUser :: String -> Int -> Bool -> User

ghci> getUserName (MkUser "John" 29 True)
"John"

ghci> setUserName "Ivan" (MkUser "John" 29 True)
MkUser "Ivan" 29 True

getUserAge :: User -> Int
getUserAge (MkUser _ age _) = age

data: Records

ghci> john = MkUser {userAge = 29, userIsTired = True, userName = "John"}
ghci> john
MkUser {userName = "John", userAge = 29, userIsTired = True}

ghci> userName john
"John"

ghci> ivan = john { userName = "Ivan", userIsTired = False }
ghci> ivan
MkUser {userName = "Ivan", userAge = 29, userIsTired = False}

data User = MkUser
    { userName    :: String
    , userAge     :: Int 
    , userIsTired :: Bool
    }

userName    :: User -> String
userAge     :: User -> Int
userIsTired :: User -> Bool

Generates the following top-level functions

➕ Initialization using names

➕ Record-update syntax

Sum Type

Sum type — choice of zero or more types

String

Int

Bool

"Hello!"

True

"Hello!"
42
True

Any possible option of a value from each type

Sum Types: Enumerations

data Color
    = Red
    | Green
    | Blue

data Bool
    = False
    | True

showColor :: Color -> String
showColor color = case color of
    Red   -> "red"
    Green -> "green"
    Blue  -> "blue"

ghci> showColor Blue
"blue"

ghci> map showColor [Red, Green, Blue, Green]
["red","green","blue","green"]

Sum Types

data Result
    = Error String
    | Ok Int

divide :: Int -> Int -> Result
divide _ 0 = Error "Division by zero!"
divide x y = Ok (div x y)

ghci> showResult (divide 15 0)
"Error: Division by zero!"

ghci> showResult (divide 15 3)
"Ok: 5"

showResult :: Result -> String
showResult (Error msg) = "Error: " ++ msg
showResult (Ok result) = "Ok: " ++ show result

A data type with 2 constructors

Each constructor has one field

data Answer
    = NoResult
    | Result Int

data Property
    = Padding Int
    | Clickable Bool Int
    | Description String

Recursive data types

data IntList
    = Empty
    | Cons Int IntList

length :: IntList -> Int
length Empty = 0
length (Cons _ xs) = 1 + length xs

1️⃣ Empty list

2️⃣ An element prepended to a list

nzeroes :: Int -> IntList
nzeroes 0 = Empty
nzeroes n = Cons 0 (nzeroes (n - 1))

ghci> nzeroes 3
Cons 0 (Cons 0 (Cons 0 Empty))

ghci> length (nzeroes 126)
126

type

type MyTriples = [(Int, Bool, String)]
type IntPredicate = Int -> Bool

ℹ️ Use the type keyword to give another name to an existing type

type String = [Char]
type FilePath = String

Standard type aliases

⚠️ The type is the same! It's just a different name.

type Attack  = Int
type Defense = Int
type Health  = Int

damage :: Attack -> Defense -> Health -> Health
damage atk def hp = hp + def - atk

newtype

newtype — lightweight wrapper for an existing type. Can only have:

Exactly one constructor
Exactly one field

type Attack  = Int
type Defense = Int
type Health  = Int

newtype Attack  = MkAttack Int
newtype Defense = MkDefense Int
newtype Health  = MkHealth Int

damage :: Attack -> Defense -> Health -> Health
damage (MkAttack atk) (MkDefense def) (MkHealth hp) =
    MkHealth (hp + def - atk)

🔰 Benefits

No runtime cost
Literally new type

💰 Costs

Wrapping and unwrapping

Polymorphism

Parametric polymorphism

dup :: a -> (a, a)
dup x = (x, x)

⬆️ Specific types start with an upper letter: String, Int, Bool, ...

⬇️ Type variables start with a lower letter: a, b, c, f, m, ...

ghci> dup 'x'
('x','x')

ghci> :t dup 'x'
dup 'x' :: (Char, Char)

ghci> dup True
(True,True)

ghci> :t dup True
dup True :: (Bool, Bool)

Real types

fst :: (a, b) -> a
snd :: (a, b) -> b

(++) :: [a] -> [a] -> [a]
(:)  ::  a  -> [a] -> [a]

head    :: [a] ->  a
tail    :: [a] -> [a]
reverse :: [a] -> [a]

take :: Int -> [a] -> [a]
drop :: Int -> [a] -> [a]

zip :: [a] -> [b] -> [(a, b)]

map    :: (a -> b)    -> [a] -> [b]
filter :: (a -> Bool) -> [a] -> [a]

Hoogle

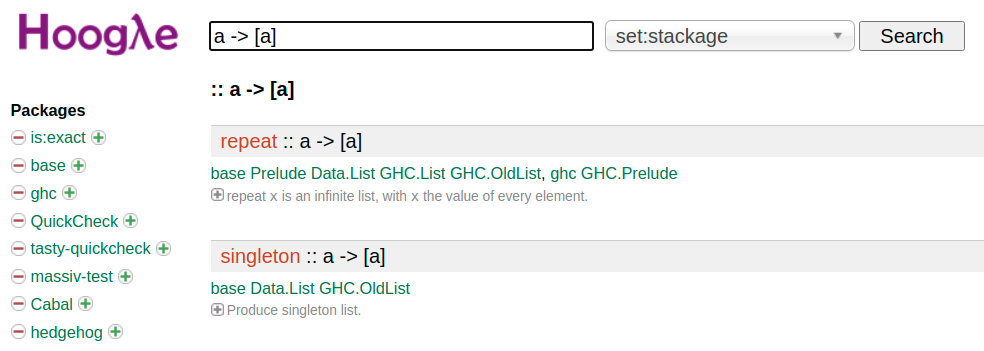
Hoogle — Haskell search engine to search Haskell package database by name, module or even type.

Polymorphic types

🐉 A treasure chest always contains gold and some reward

data Chest a = MkChest
    { chestGold     :: Int
    , chestTreasure :: a
    }

type BronzeChest = Chest Armor
type SilverChest = Chest (Sword, Armor)
type GoldenChest = Chest (Artifact, Sword, [Gemstone])

ghci> :t MkChest
MkChest :: Int -> a -> Chest a

ghci> MkChest 100 True
MkChest { chestGold = 100
        , chestTreasure = True}

data RewardChest
    = Bronze BronzeChest
    | Silver SilverChest
    | Golden GoldenChest

reward :: Dragon -> RewardChest
reward ... = ...

Common types

data Maybe a
    = Nothing
    | Just a

data Either a b
    = Left a
    | Right b

ℹ️ Optional value

ℹ️ Choice between two types

ℹ️ List

data [] a
    = []
    | a : [a]

data List a
    = Empty
    | Cons a (List a)

Simpler version (not in base)

Common functions

find :: (a -> Bool) -> [a] -> Maybe a

ghci> find (> 4) [3, 1, 2]
Nothing
ghci> find (> 4) [3, 5, 1, 2, 10]
Just 5

ℹ️ Find an optional value

fromMaybeInt :: Maybe Int -> Int
fromMaybeInt Nothing  = 0
fromMaybeInt (Just n) = n

ℹ️ Optional number to zero default

ℹ️ Lists of different types

partitionEithers :: [Either a b] -> ([a], [b])

ghci> partitionEithers [Left 3, Right "hi!", Left 5]
([3,5],["hi!"])

Back to Functions

Eta-reduction, part 1

\forall x : f(x) \equiv g(x)\ \ \mathrm{means}\ \ f \equiv g

showInt :: Int -> String
showInt n = show n

showInt :: Int -> String
showInt = show

η-reduction, part 2

onlyEven :: [Int] -> [Int]
onlyEven xs = filter even xs

onlyEven :: [Int] -> [Int]
onlyEven = filter even

prod :: [Int] -> [Int] -> [Int]
prod xs ys = zipWith (*) xs ys

prod :: [Int] -> [Int] -> [Int]
prod = zipWith (*)

ghci> :t zipWith
zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]

ghci> zipWith (*) [3, 1, 2] [10, 20, 30]
[30,20,60]

👩‍🔬 You don't always want to eta-reduce because variable names can be helpful in some situations

Function Composition

☎️ Function composition operator: the dot (.) operator

(.) :: (b -> c) -> (a -> b) -> a -> c
(.) f g = \x -> f (g x)

ELI5 Composition

\mathrm{defrost} :: 🧊 \rightarrow 🥦

\mathrm{cook} :: 🥦 \rightarrow 🥘

\mathrm{cookFrozen} :: 🧊 \rightarrow 🥘

\mathrm{cookFrozen} = \mathrm{cook}\ .\ \mathrm{defrost}

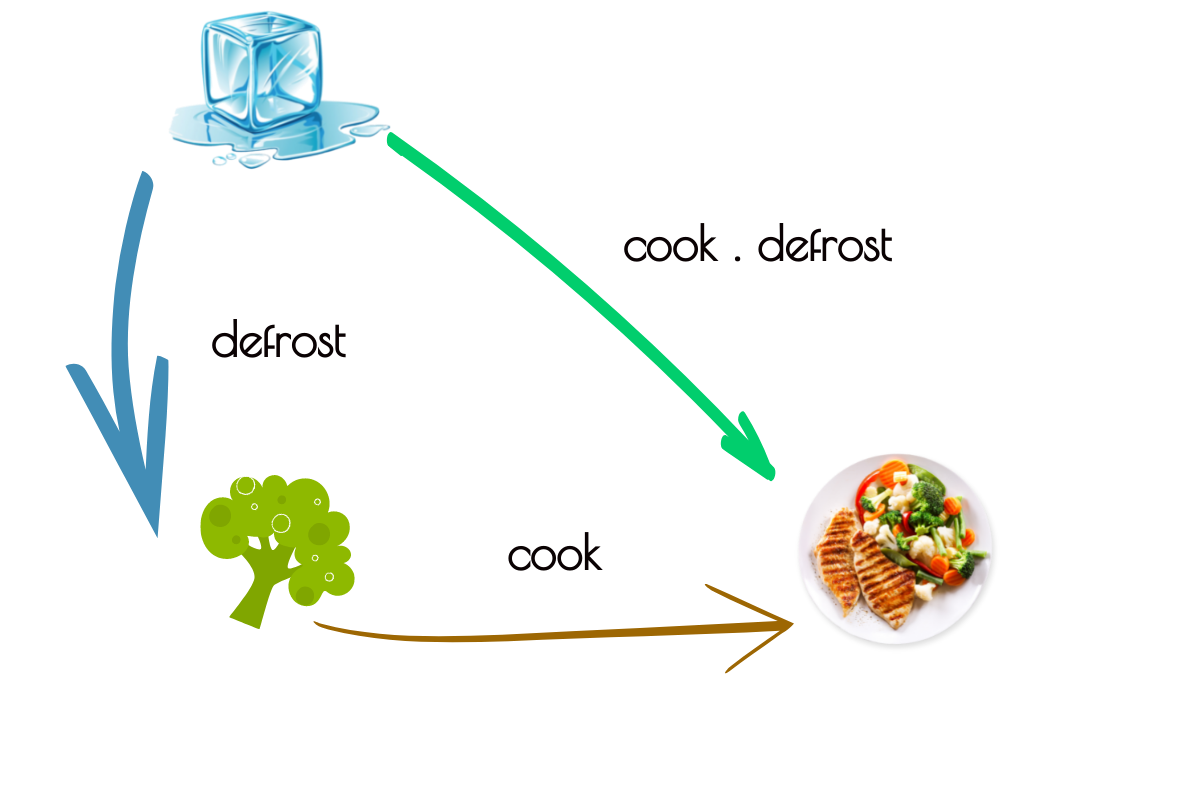
Function Composition

(.) :: (b -> c) -> (a -> b) -> a -> c
(.) f g = \x -> f (g x)

Examples

ghci> (length . show) True
4

ghci> map (length . words) ["Hi all", "bi dup boo", "x"]
[2,3,1]

ghci> map (even . length . words) ["Hi all", "bi dup boo", "x"]
[True,False,False]

Composition + Eta-reduction

🛠 A function that returns first 5 lists of even length

takeEven5 :: [[a]] -> [[a]]
takeEven5 list = take 5 (filter (\l -> even (length l)) list)

1️⃣ Rewrite lambda to composition

takeEven5 list = take 5 (filter (\l -> (even . length) l) list)

2️⃣ Eta-reduce lambda

takeEven5 list = take 5 (filter (even . length) list)

3️⃣ Rewrite main function to composition

takeEven5 list = (take 5 . filter (even . length)) list

takeEven5 = take 5 . filter (even . length)

4️⃣ Eta-reduce main function

More sources

🔗 TypeClasses: Beginner crash course (Types and functions)

🔗 Cube Composer (game)

🔗 YouTube: Point-Free or Die