トポロジカル・ガロア理論による
アーベル・ルフィニの定理の証明
n次方程式の解の公式は
長年にわたり研究されてきた

2次方程式の解の公式
2000 BC
バビロニアで発見される
3,4 次方程式の解の公式
1540 年
カルダノ,フェラーリらにより発見
5 次方程式の解の公式
1820 年
アーベルにより解の公式が存在しないことが証明される。
このスライドでは
五次方程式の解の公式が
存在しないことを証明します
複素関数としてのn次方程式
n次方程式を複素関数として表すと、解と係数は互いに関係をもつ複素平面上の点として表される。
解の連続的な交換により係数は閉ループを描く
解の連続的な交換
解の連続的な交換
-
解を連続的に交換すると、多項式は解の交換により変化しないため、係数は連続的な軌跡を描いて元に返ってくる。しかし、交換された2つの解は元に戻ってこない。
係数を用いて解を表すためには
解の交換により元に戻ってくる数から
解の交換により元に戻ってこない数を作る必要がある。
閉ループを開く必要がある。
解の公式に必要な演算
- 加減乗除は同じ入力に対して同じ出力を返す一価関数である。
- 一価関数は閉ループを開くことができない。
べき根の性質
べき根は多価関数である。
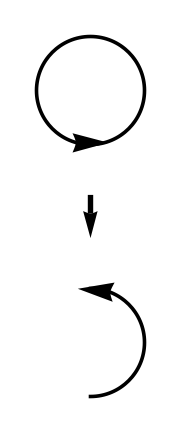
べき根は閉ループを開くことができる
べき根は閉ループを開くことができる
べき根の能力
- n乗根は複素平面上の1点をn個の点に写す。
-
n乗根の中身が元に戻ってくるとき、n乗根は実質的にn個の
巡回的並び替えを行う。
1個のn乗根にできる並び替え :
周期nの巡回的な並び替え + 恒等置換
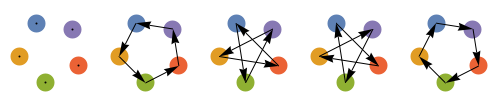

1個のべき根ではできない並び替え
1個のべき根にできる並び替えは限られている
交換子

...




解
係数
係数と
四則演算
べき根
置換
交換子

- x,yが巡回的な並び替えであるとき、それらの合成 xy は順序を交換したyxと結果が同じになる。このとき [x,y] は恒等置換になる。
- よって、解の置換の交換子により、べき根を一回使う式が閉ループを
描くようにすることができる。
2つの置換 x, y による交換子 [x,y] を以下のように定義する
交換子によりべき根を
1回使った式は閉ループを描く
交換子の交換子



...


| ... |








交換子によりべき根を1回使った式は閉ループを描く
交換子の交換子によりべき根の中のべき根を使った式は閉ループを描く
解
係数
係数と
四則演算
べき根
べき根の中のべき根
n次方程式の解の公式が存在する条件
- 交換子を繰り返すことでべき根を使ったどんな式も閉ループを描くようにすることができる。
- 解がこの式と同じ性質を持つためには、解の置換の集合が
交換子の繰り返しによって恒等置換のみになる必要がある。
n = 2 の場合
解の2つを {α,β} と置く。解の置換は
の2つ。交換子は
となり、全て恒等置換になる。
つまり、2次方程式の解は交換子1回により閉ループを描く。
これはべき根を一回使った式と同じ性質であるため、
2次方程式の解はべき根1回と係数を使った式により表せる
可能性がある。
交換子
交換子の交換子
n = 3 の場合
交換子を繰り返すと解の置換の数は
6 → 3 → 1
と減り、最後に恒等置換だけになる。
3次方程式の解は交換子の交換子により閉ループになる。このため、
べき根の中のべき根と係数を使った式で表せる可能性がある。
n = 4 の場合
交換子
交換子の交換子
交換子の交換子の交換子
交換子を繰り返すと解の置換の数は
24 → 12 → 4 → 1
と減り、最後に恒等置換だけになる。
4次方程式の解は交換子の交換子の交換子により閉ループになる。このため、
べき根の中のべき根の中のべき根と
係数を使った式で表せる可能性がある。
n = 5 の場合
交換子
交換子の交換子
n = 5 の場合
5次方程式の場合、交換子を繰り返したとき、解の置換は
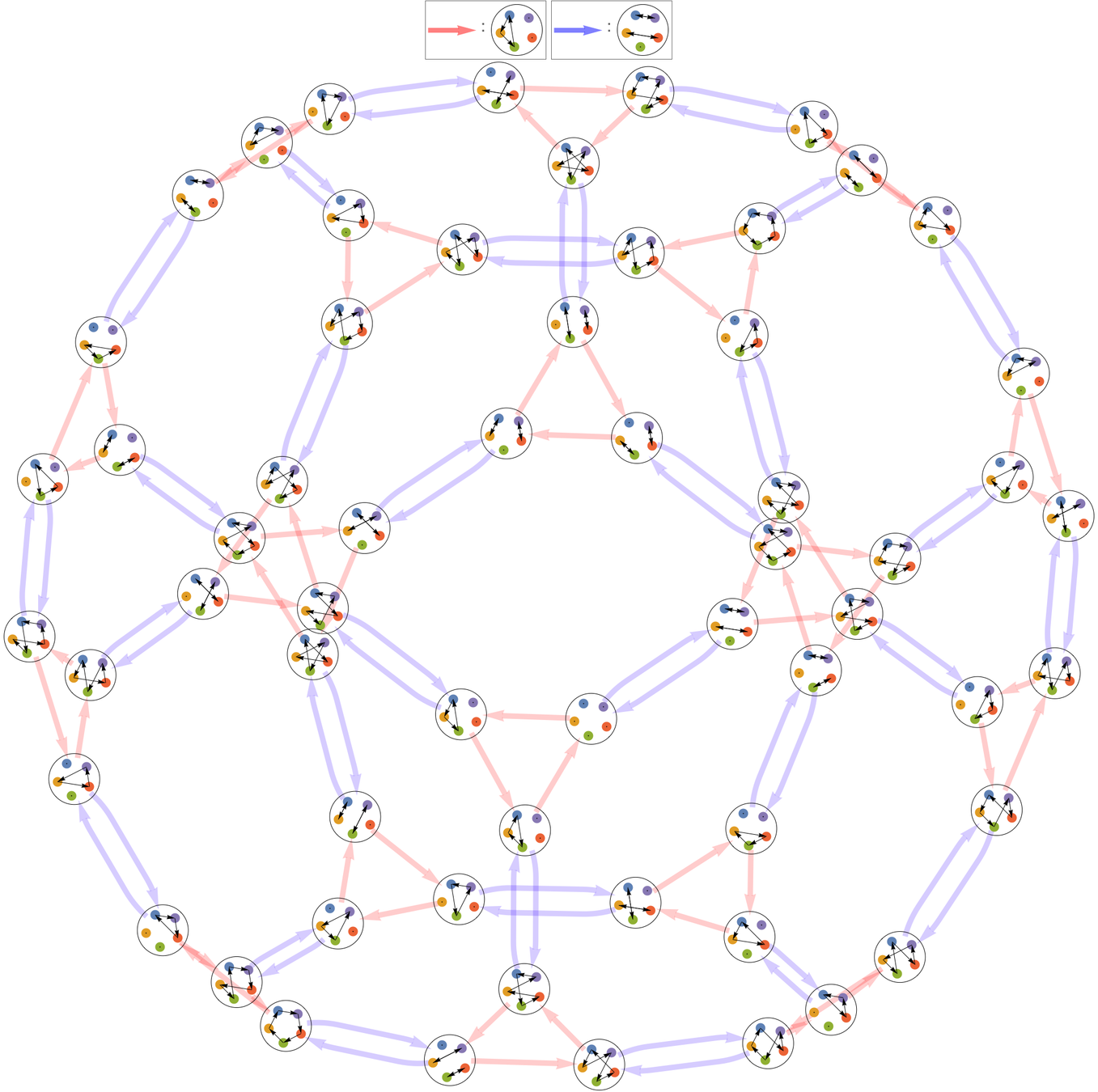
120 → 60 → 60 → ...
となり、置換の数は60からいつまでも減ることがない。
よって、5次方程式の解は交換子を何回繰り返しても元に戻ってこないようにすることができる。つまり、5次方程式の解はべき根をいくら使っても係数により表すことができない。
交換子の繰り返しによる解の置換の集合の変化
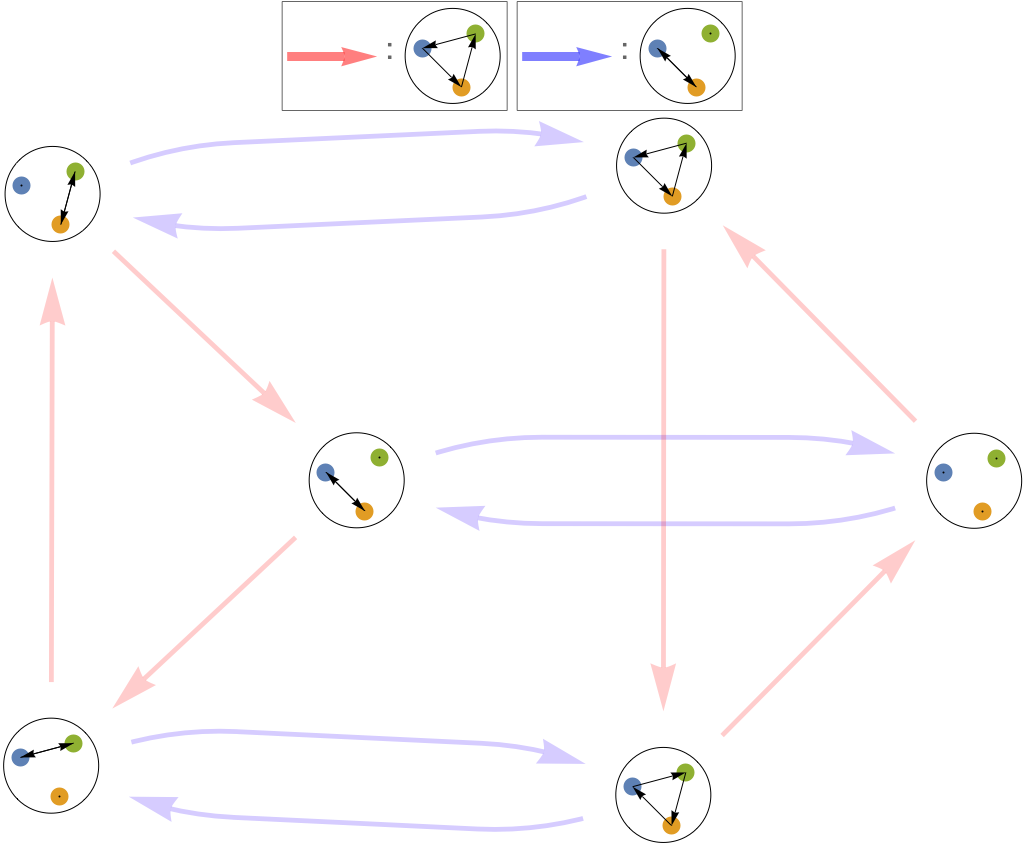
- 2次:2 → 1
- 3次:6 → 3 → 1
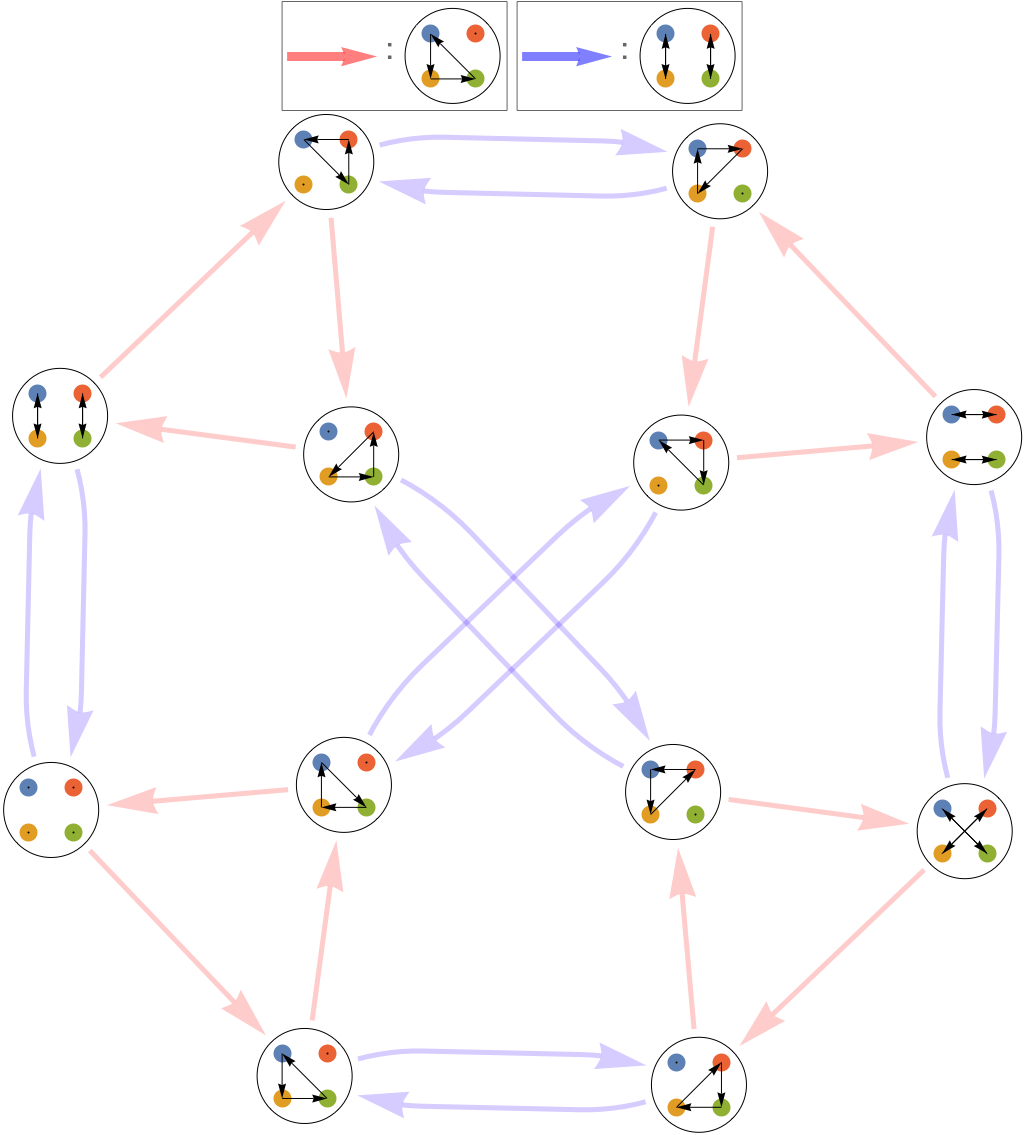
- 4次:24 → 12 → 4 → 1
- 5次:120 → 60 → 60 → ...
まとめ
- n次方程式の解を交換したとき、係数は閉ループを描く
- 解の公式をつくるためには、閉ループを開くことのできるべき根を使う必要がある。
- 交換子により、べき根を一回使った式が閉ループを描くようにすることができる。交換子を繰り返すことで、べき根を何回使った式も閉ループを描くようにすることができる。
- 交換子の繰り返しにより解の置換の集合が恒等置換だけになる場合のみ、n次方程式の解は係数とべき根により表せる可能性がある。
- 5次方程式は交換子を何回繰り返しても解の置換の集合を恒等置換だけにすることはできない。よって5次方程式の解の公式は存在しない。
群論
n個のものの並び替え全体を、並び替えどうしがどどう繋がっているかということも含めた数学的対象とみる。これを n次対称群 と呼ぶ。
の要素の交換子からなる群を、n次交代群 と呼ぶ。
交代群に対して、それの交換子からなる群を考え、またその群に対しても、再びそれの交換師からなる群を考え、ということを繰り返して最終的に群が恒等変換になるとき、
そのような群を可解群と呼ぶ。これまで見てきたとおり、 , , は可解群である。
交換子をいくら繰り返しても群の元が恒等変換だけにならないものを非可解群と呼ぶ。 は非可解群である。