COMP2521
Data Structures & Algorithms
Week 3.1
Trees & Binary Search Trees
Author: Hayden Smith 2021
In this lecture
Why?
- To understand the what, how, and why of what binary tree data structures are, as they are a fundamental set of data structure + algorithms for efficient programs
What?
- Trees
- Binary Search Trees (BST)
- Operations on BSTs
- Representing BSTs in code
"Trees"

Computer-y "Trees"
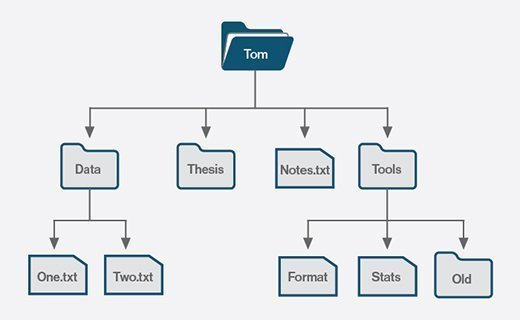
Source: https://searchstorage.techtarget.com/definition/file-system
Data Structure "Trees"
- Trees are connected graphs that:
- has edges (lines) and nodes (circles)
- has no cycles (can't get caught in loops)
- for each node with a particular data value
- for each node links to up to k children
- In this case, k = 2
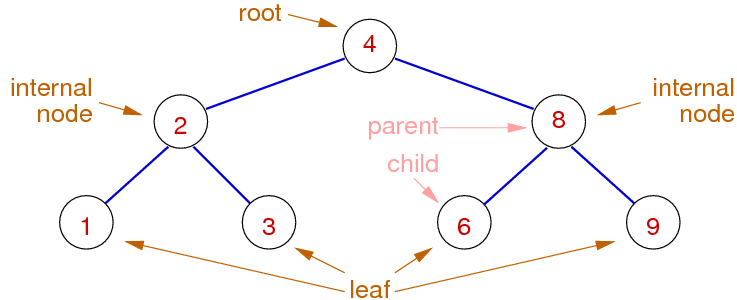
Binary Search "Trees"
Binary search trees (BSTs) are able to be searched with a binary search, and are easy to maintain / modify
So why BSTs?
Let's establish a few key facts:
- Binary search is a necessary algorithm to use for large sets of numbers (substantially quicker than linear search)
- Maintaining an ordered array is hard (shuffling), but binary searching an ordered array is very doable
- Maintaining an ordered linkedlist is easy (direct insertion), but binary searching on an ordered linkedlist is hard (will always have to traverse linearly, no random access)
So why BSTs?
BSTs provide us the best of both worlds:
- If ordered, their structure is essentially built kind-of like a binary search flow
- Because of its linkedlist-style approach, it's easy to make big modifications just by swapping/adding pointers, rather than re-shuffling everything
BST Rules
BSTs are ordered trees, which means:
- Each node is the root of 2 subtrees (which are potentially null)
- All values in the left subtree are less than the root
- All values in the right subtree are greater than the root
- These rules apply for all nodes in the tree
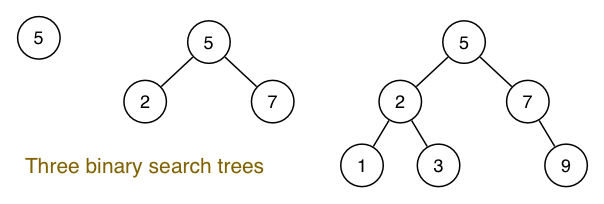
BST Structure
Binary search trees are either:
- empty; or
- consist of a node with two subtrees:
- node contains a value
- left and right subtrees are also BSTs (recursive)
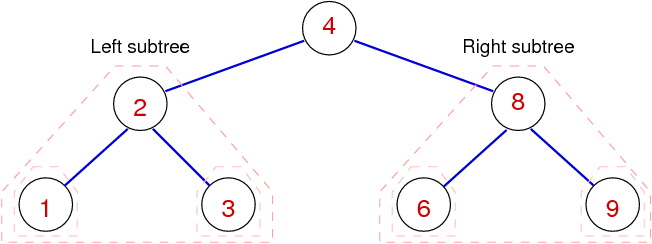
BST Structure
Two key concepts with tree structures:
- Level of a node: Path length from root to node
- Height/depth of tree: max path length from root to leaf
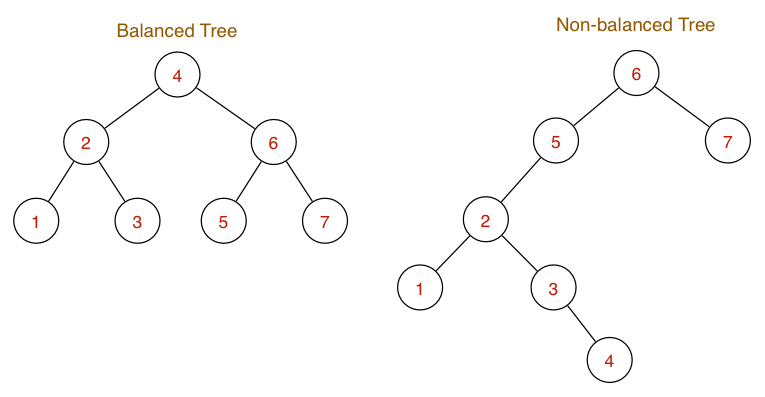
Balanced BST
A tree becomes weight-balanced once there are equal number of nodes between the left and right subtree, for all nodes in the tree.
BST Operations
- There are a few key operations we will focus on:
- insert(Tree, item)
- delete(Tree, item)
- search(Tree, item)
- print(Tree)
- (create + destroy)
However, there are many more operations for BSTs
BST Insertion
This BST is initially empty, then we insert [3, 2, 4, 5, 1] in that order.
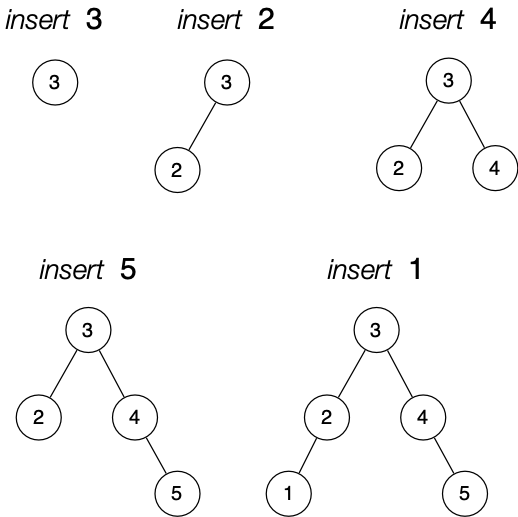
Insert does not guarantee to maintain a balanced tree.
BST Insertion
So what kind of algorithm is this actually using?
TreeInsert(Tree, item):
if Tree is empty:
return new root node containing item
else if item < Tree's node value:
Tree's left child = TreeInsert(Tree's left child, item)
else if item > Tree's node value:
Tree's right child = TreeInsert(Tree's right child, item)
return TreeBST Insert
BST Insertion
This BST is initially empty, then we insert [4, 2, 6, 5, 1, 7, 3] in that order.
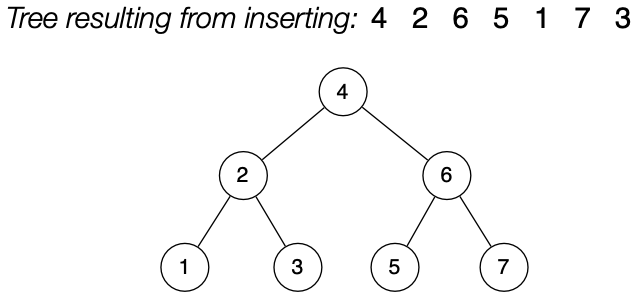
BST Insertion
This BST is initially empty, then we insert [5, 6, 2, 3, 4, 7, 1] in that order.
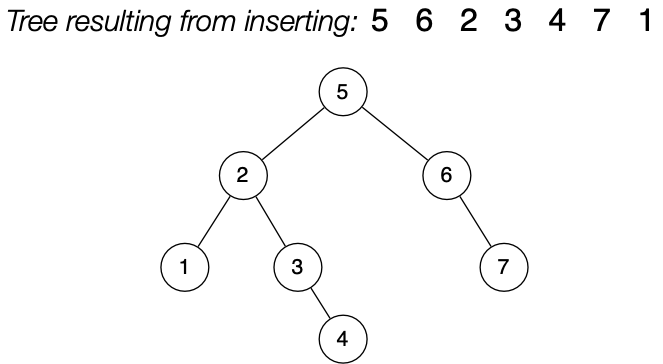
BST Insertion
This BST is initially empty, then we insert [1, 2, 3, 4] in that order.
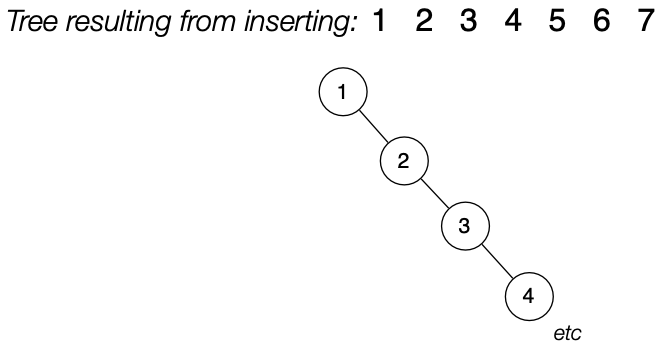
Time Complexity
BST Insertion is typically O(h), where h is the height of the BST. In general, the time complexity is simply the time it takes to traverse down to the place that the node needs to be inserted.
For a balanced tree, O(h) = O(log2(n))
BST Representation in code
Binary tree representations are very similar to Linked List structures, with one exception: Instead of only "1" next pointer, there are 2 - one for each child (left / right)
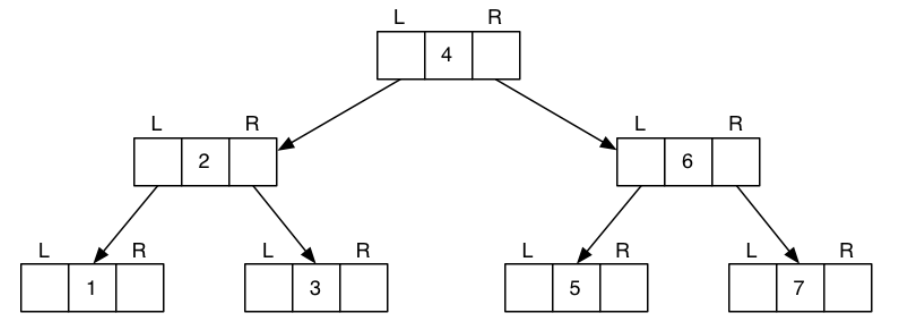
BST Representation in code
Abstract vs concrete data
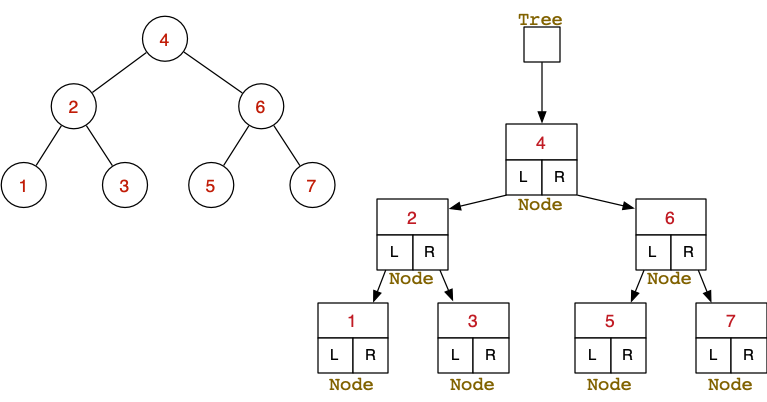
BST Representation in code
typedef struct Node *Tree;
typedef int Item;BSTree.h
#include "BSTree.h"
typedef struct Node {
int data;
Tree left
Tree right;
} Node;BSTree.c
Let's get coding!
typedef struct Node *Tree;
typedef int Item;
Tree TreeCreate(Item it);
void TreeDestroy(Tree t);
Tree TreeInsert(Tree t, Item it);
void TreePrint(Tree t);
BSTree.h
#include "BSTree.h"
typedef struct Node {
int data;
Tree left
right;
} Node;
Tree TreeCreate(Item it) {
// TODO
}
void TreeDestroy(Tree t) {
// TODO
}
Tree TreeInsert(Tree t, Item it) {
// TODO
}
void TreePrint(Tree t) {
// TODO
}
BSTree.c
+ a makefile...
#include "BSTree.h"
int main(int argc, char* argv[]) {
Tree t = TreeCreate(1);
TreeInsert(t, 2);
TreePrint(t);
TreeInsert(t, 4);
TreePrint(t);
TreeInsert(t, 5);
TreePrint(t);
TreeInsert(t, 3);
TreePrint(t);
TreeDestroy(t);
return 0;
}main.c
BST Traversal
There are 4 different ways to traverse a tree:
- Preorder: Visit root, then left subtree, then right subtree
- Inorder: Visit left subtree, then root, then right subtree
- Postorder: Visit left subtree, then right subtree, then root
- Level order: Visit root, then all its children, then all their children etc (we won't look at this as it's covered in Graphs) - you implement this in lab04
BST Traversal
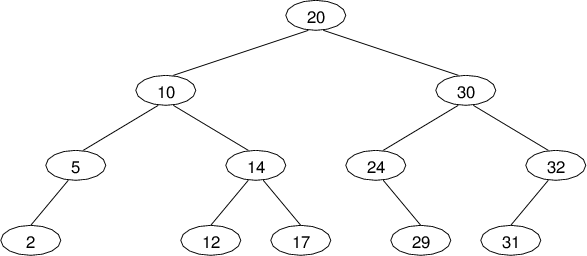
- Preorder: 20 10 5 2 14 12 17 30 24 29 32 31
-
Inorder: 2 5 10 12 14 17 20 24 29 30 31 32
-
Postorder: 2 5 12 17 14 10 29 24 31 32 30 20
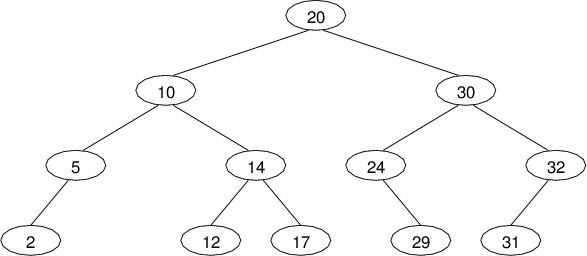
BST Traversal
preorder
BSTTraverse(tree):
if tree is empty, return
print tree's data
BSTTraverse(tree's left child)
BSTTraverse(tree's right child)BSTTraverse(tree):
if tree is empty, return
BSTTraverse(tree's left child)
print tree's data
BSTTraverse(tree's right child)BSTTraverse(tree):
if tree is empty, return
BSTTraverse(tree's left child)
BSTTraverse(tree's right child)
print tree's data
inorder
postorder
BTS Traversals are fascinating because all 3 algorithms are content-wise the same, just structurally different.
Time Complexity
BST Traversal for search is:
- Best case O(1) - what you are looking for is at the root
- Worst case O(h), where h is the height of the BST
BST Traversal for printing is:
- Always O(n) where n is the number of nodes in the tree
BST Join
How do we join two trees?
t = TreeJoin(t1, t2)
Take two BSTs, join and return a single one that contains all items correctly ordered
Join does not guarantee to maintain a balanced tree.
BST Join
Method:
- Find the min node in the right subtree (t2)
- Replace min node by its right subtree (if not empty)
- Elevate min node to be new root of both trees
BST Join
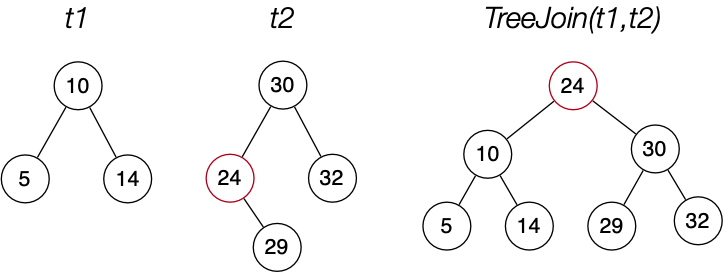
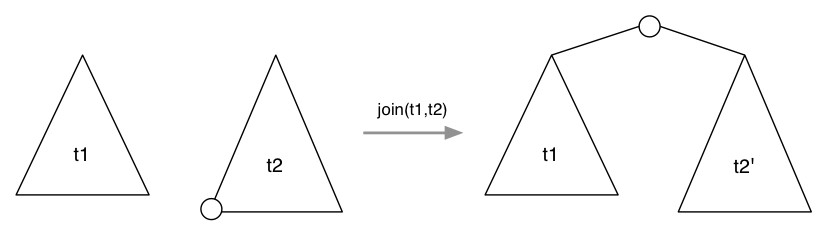
BST Join
Pseudocode
TreeJoin(tree1, tree2):
if tree1 is empty, return tree2
if tree2 is empty, return tree1
current = tree2
parent = NULL
while current's left child is not empty:
parent = current
current = current's left child
if parent is not NULL:
parent's left child = current's right child
current's right child = tree2
current's left child = tree1
return current (new root)Time Complexity
BST Join is typically O(m), where m is the height of the right subtree.
BST Delete
Deleting from a binary tree is not as conceptually easy as some other tasks. There are 4 key cases to consider:
| Case | Case for a "node" to delete | Action |
|---|---|---|
| 1 | Empty tree | New tree is also empty |
| 2 | Zero subtrees | Unlink node from parent |
| 3 | One subtree | Replace by child |
| 4 | Two subtrees | Replace by successor, join two subtrees |
Deletion does not guarantee to maintain a balanced tree.
BST Delete - Case 1 - Empty tree
Well this is easy, just return NULL
BST Delete - Case 2 - Zero subtrees
This is also easy, just unlink the node from the parent and free the node.
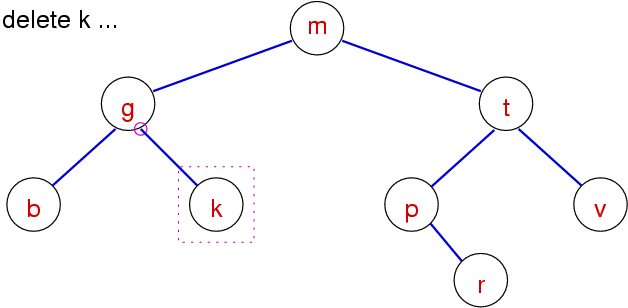
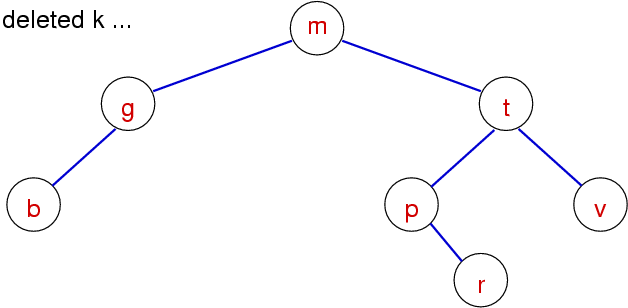
BST Delete - Case 3 - One subtree
A tiny bit harder, replace the node with its child, then free the original node.
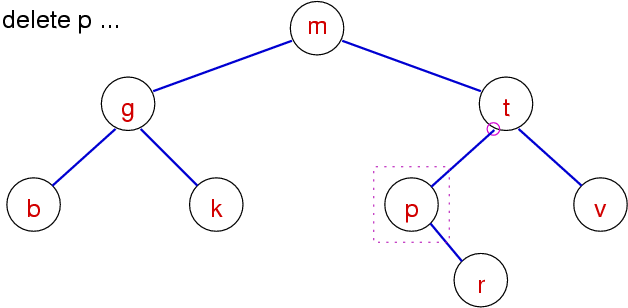
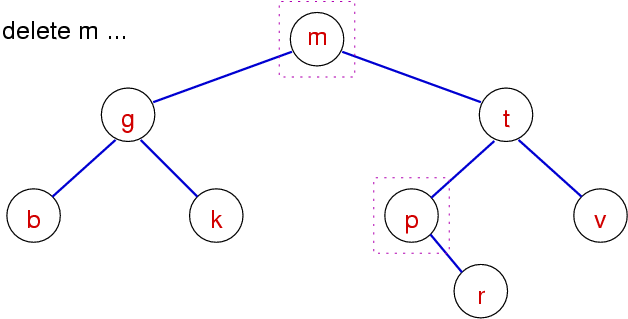
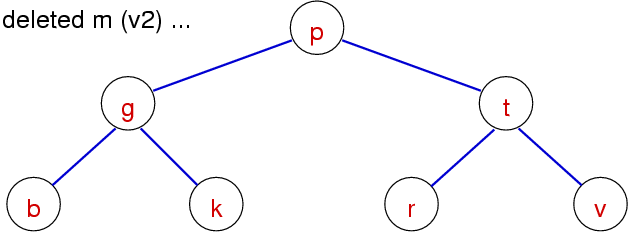
BST Delete - Case 4 (Method 1 - Join)
Simply join the two subtrees that are left after you delete the node
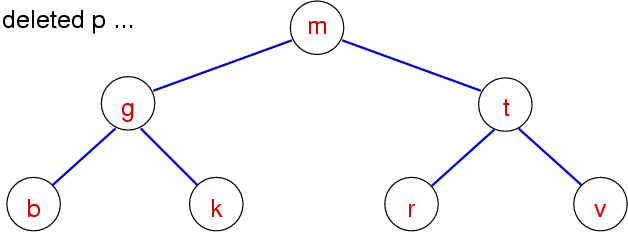
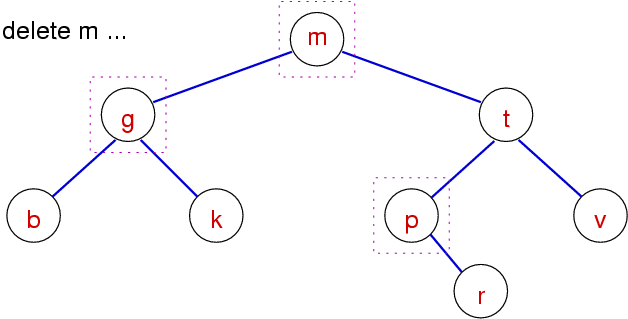
BST Delete - Case 4 (Method 2 - Successor)
For the node, its right child becomes new root, then attach the node's left subtree to the minimum element of the right subtree
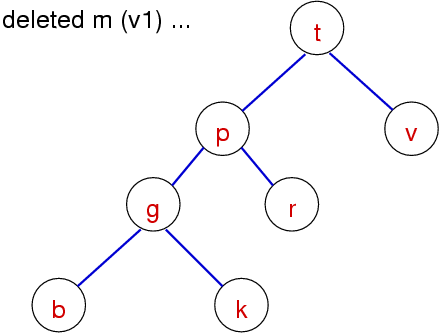
BST Delete
Pseudocode
TreeDelete(tree,item):
if t is not empty:
if item < data(t):
left(t)=TreeDelete(left(t), item)
else if item > data(t):
right(t)=TreeDelete(right(t), item)
else:
if left(t) and right(t) are empty:
new = empty tree // 0 children
else if left(t) is empty:
new = right(t) // 1 child
else if right(t) is empty:
new = left(t) // 1 child
else:
new = TreeJoin(left(t), right(t)) // 2 children
free memory allocated for t
t = newTime Complexity
BST Deletion is typically O(h), where h is the height of the BST. In general, the time complexity is simply the time it takes to traverse down to the place that the node needs to be deleted.
Helpful Macros
We can make use of C macros to abstract repeated code out and make our code easier to read.
// a Node contains its data, plus left and right subtrees
typedef struct Node {
int data;
Tree left, right;
} Node;
// some macros that we will use frequently
#define data(node) ((node)->data)
#define left(node) ((node)->left)
#define right(node) ((node)->right)BSTree.c
Feedback
