COMP2521
Data Structures & Algorithms
Week 7.3
Minimum Spanning Trees
Author: Hayden Smith 2021
In this lecture
Why?
- We need efficient ways to generate minimum spanning trees from a graph
What?
- Minimum Spanning Trees
- Kruskal's Algorithm
- Prim's Algorithm
Minimum Spanning Tree
-
Spanning Tree (ST) of a graph G = (V, E):
- Contains all vertices (spanning)
- Contains no cycles (tree)
- ST is a connected subgraph of G
-
Minimum Spanning Tree (MST) of a graph G = (V, E)
- MST is a spanning tree of G
- Sum of edge weights is no larger than any other ST
Applications? Electrical grids, networks. Essentially anything where we want to connect nodes assuming that edge lengths are costly.
Minimum Spanning Tree

Minimum Spanning Tree
How do we find the MSTs for a Graph?
One possible strategy is to just brute force: Generate all spanning trees, calculate total weight of each, and find the minimum. However, this is very expensive.
Thankfully, others have developed algorithms for us. Today we will explore just two of them.
Kruskal's Algorithm
Kruskal's algorithm is one approach for computing an MST:
- Start with an empty MST
- Consider edges in increasing weight order:
- Add edge if it does not form a cycle in the MST
- Repeat until V-1 edges are added
Kruskal's Algorithm
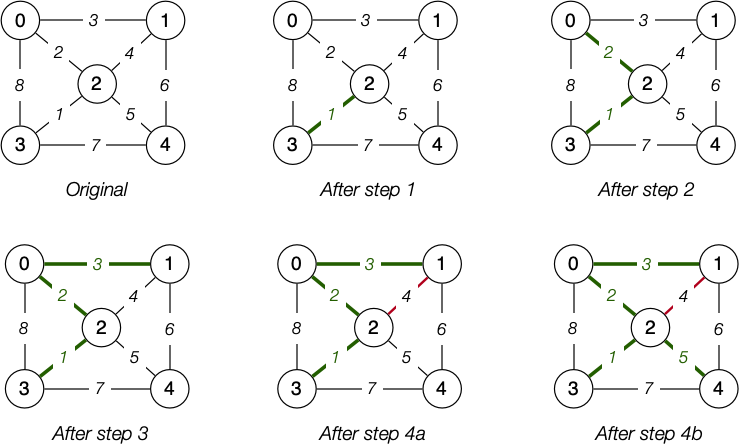
Kruskal's Algorithm
KruskalMST(G):
MST=empty graph
sort edges(G) by weight
for each e ∈ sortedEdgeList:
MST = MST ∪ {e} // add edge
if MST has a cyle:
MST = MST \ {e} // drop edge
if MST has n-1 edges:
return MST
Kruskal's Algorithm
Rough time complexity analysis …
- sorting edge list is O(E·log E)
- at least V iterations over sorted edges
- on each iteration …
- getting next lowest cost edge is O(1)
- checking whether adding it forms a cycle: cost = O(V^2)
Possibilities for cycle checking: Use DFS?
Prim's Algorithm
Prim's algorithm is one approach for computing an MST:
- start from any vertex v and empty MST
- choose edge not already in MST to add to MST; must be:
- connects a vertex in MST to a vertex not in MST
- minimal weight of all such edges
- repeat until MST covers all vertices
Prim's Algorithm
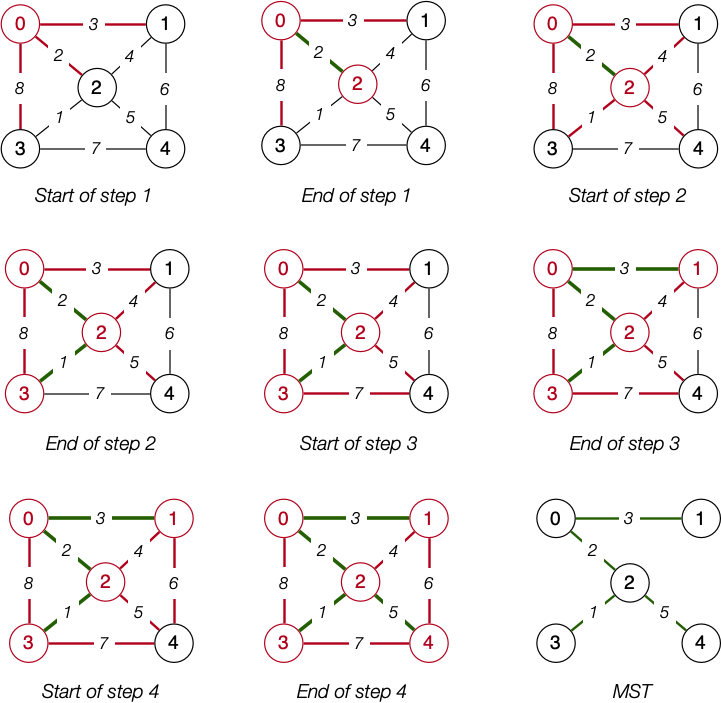
Prim's Algorithm
PrimMST(G):
MST = empty graph
usedV = {0}
unusedE = edges(g)
while |usedV| < n:
find e = (s,t,w) ∈ unusedE such that {
s ∈ usedV ∧ t ∉ usedV
(∧ w is min weight of all such edges)
}
MST = MST ∪ {e}
usedV = usedV ∪ {t}
unusedE = unusedE \ {e}
return MSTPrim's Algorithm
Rough time complexity analysis …
- V iterations of outer loop
- in each iteration, finding min-weighted edge …
- with set of edges is O(E) ⇒ O(V·E) overall
- with priority queue is O(log E) ⇒ O(V·log E) overall
Note:
- have seen stack-based (DFS) and queue-based (BFS) traversals
- using a priority queue gives another non-recursive traversal
Prim's V Kruskal's
Read more about a comparison here.
Feedback
