COMP2521
Data Structures & Algorithms
Week 8.3
Merge Sort
Author: Hayden Smith 2021
In this lecture
Why?
- We need some algorithms better than O(n^2) for large data sets.
What?
- Merge sort
Mergesort Overview
The key of this approach is that it's recursive.
- Split the array into two roughly equal sized partitions
- Recursively sort each of the partitions
- Merge the two partitions into a new sorted array
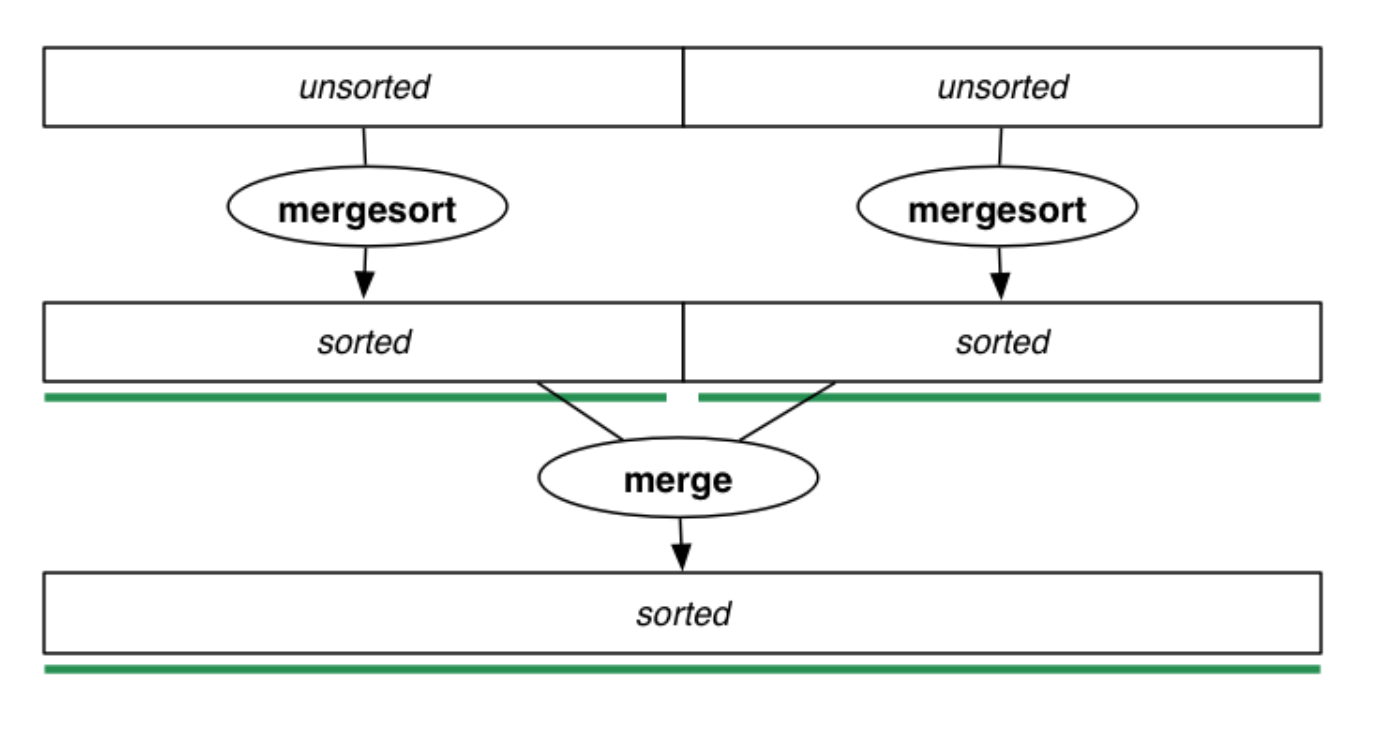
Mergesort Overview
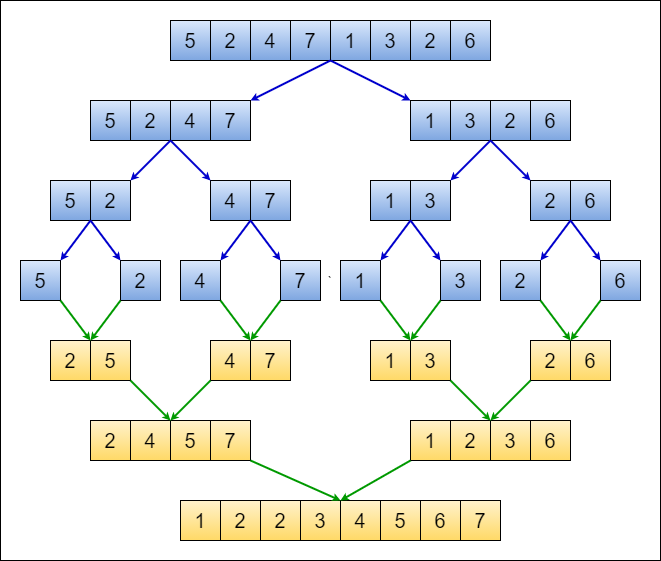
Source: https://levelup.gitconnected.com/visualizing-designing-and-analyzing-the-merge-sort-algorithm-cf17e3f0371f
Split / Divide
Merge
Implementation
void mergesort(Item a[], int lo, int hi)
{
int mid = (lo + hi) / 2; // mid point
if (hi <= lo) return;
mergesort(a, lo, mid);
mergesort(a, mid+1, hi);
merge(a, lo, mid, hi);
}
int main() {
int nums[10] = {32,45,17,22,94,78,64,25,55,42};
mergesort(nums, 0, 9);
}Merge sort is kind of like a binary tree split where the re-merging happens post-fix.
The function "merge" has to merge two sorted arrays back together.
Implementation
void merge(Item a[], int lo, int mid, int hi) {
int i, j, k, nitems = hi - lo + 1;
Item *tmp = malloc(nitems * sizeof(Item));
i = lo; j = mid + 1; k = 0;
// scan both segments, copying to tmp
while (i <= mid && j <= hi) {
if (leq(a[i], a[j]))
tmp[k++] = a[i++];
else
tmp[k++] = a[j++];
}
// copy items from unfinished segment
while (i <= mid) tmp[k++] = a[i++];
while (j <= hi) tmp[k++] = a[j++];
//copy tmp back to main array
for (i = lo, k = 0; i <= hi; i++, k++)
a[i] = tmp[k];
free(tmp);
}The merge function
Performance

Split / Divide
We have to split our list log(N) times
Merge
We have to merge N numbers exactly log(N) times
This part requires extra memory :(
O(log(N))
O(N * log(N))
Performance
Mergesort has both a best and worst case of O(N*log(N))
Whether the list is fully sorted, or fully reverse sorted, the same steps are taken
This makes it time-wise generally better than quicksort - however - we need extra memory for this.
Linked Lists
Whilst mergesort typically operates on arrays, it's also possible to do it on linkedlists. We won't go into any detail on this.
Feedback
