COMP2521
Data Structures & Algorithms
Week 9.2
Hashing
Author: Hayden Smith 2021
In this lecture
Why?
- Associate data structures (as opposed to ordered data structures) are a core data structure that needs exploration
What?
- Hashing
- Hash Table ADT
- Hash Collisions
Ordered & Associative Containers
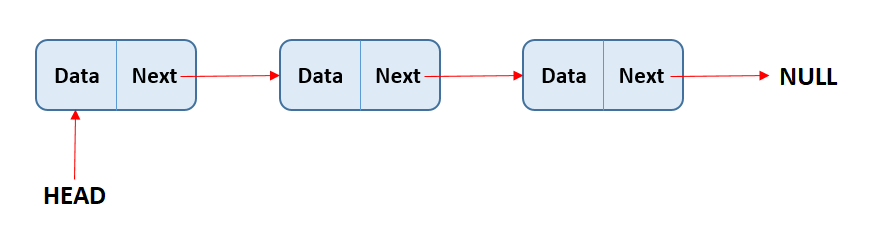
So far we've mainly explored ordered containers (linked lists, arrays, trees).
Ordered containers have a sense of order between elements, and typically you can assign a meaningful index to each element that denotes order.

Ordered & Associative Containers
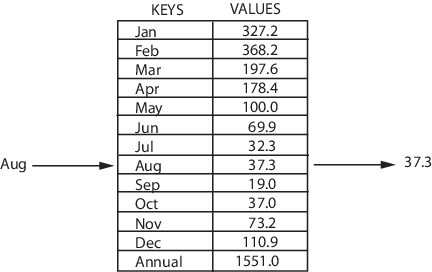
Associative containers map "keys" to various values, and items in associative containers have no sense of order. Keys are typically strings.
You can think of these a little like structs (conceptually). Identified by name.
Hashing
We need a way for this to make sense
courses["COMP3311"] = "Database Systems";
printf("%s\n", courses["COMP3311"]);courses[h("COMP3311")] = "Database Systems";
printf("%s\n", courses[h("COMP3311")]);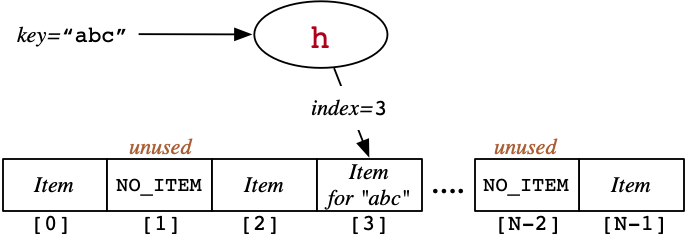
Let's define a function h that converts a string to a number
Hashing
In reality we do this
key = "COMP3311";
item = {"COMP3311","Database Systems",...};
courses = HashInsert(courses, key, item);
printf("%s\n", HashGet(courses, "COMP3311"));
To use arbitrary values as keys, we need ...
- Set of Key (strings) values dom(Key), each key identifies one Item
- An array (of size N ) to store Items
- A hash function h() of type dom(Key) → [0..N-1]
- requirement: if (x = y) then h(x) = h(y)
- requirement: h(x) always returns same value for given x
- One issue: Array is size N, but dom(Key) > N in nearly all cases
- Therefore collisions are inevitable (we will discuss this later)
Hash Table ADT
typedef struct HashTabRep *HashTable;
// make new empty table of size N
HashTable newHashTable(int);
// add item into collection
void HashInsert(HashTable, Item);
// find item with key
Item *HashGet(HashTable, Key);
// drop item with key
void HashDelete(HashTable, Key);
// free memory of a HashTable
void dropHashTable(HashTable);Hash Table ADT Implementation
typedef struct HashTabRep {
Item **items; // array of (Item *)
int N; // size of array
int nitems; // # Items in array
} HashTabRep;
HashTable newHashTable(int N)
{
HashTable new = malloc(sizeof(HashTabRep));
new->items = malloc(N*sizeof(Item *));
new->N = N;
new->nitems = 0;
for (int i = 0; i < N; i++) new->items[i] = NULL;
return new;
}
void HashInsert(HashTable ht, Item it) {
int h = hash(key(it), ht->N);
// assume table slot empty!?
ht->items[h] = copy(it);
ht->nitems++;
}
Item *HashGet(HashTable ht, Key k) {
int h = hash(k, ht->N);
Item *itp = ht->items[h];
if (itp != NULL && equal(key(*itp),k))
return itp;
else
return NULL;
}This assumes no collisions
void HashDelete(HashTable ht, Key k) {
int h = hash(k, ht->N);
Item *itp = ht->items[h];
if (itp != NULL && equal(key(*itp),k)) {
free(itp);
ht->items[h] = NULL;
ht->nitems--;
}
}
void dropHashTable(HashTable ht) {
for (int i = 0; i < ht->N; i++) {
if (ht->items[i] != NULL) free(ht->items[i]);
}
free(ht);
}
// key() and copy() come from Item type; equal() from Key type Hash Functions
Basic mechanism of hash functions
int hash(Key key, int N)
{
int val = convert key to 32-bit int;
return val % N;
}
- If keys are ints, conversion is easy (identity function)
- How to convert keys which are strings? (e.g. "COMP1927" or "John")
- Definitely prefer that hash("cat",N) ≠ hash("dog",N)
- Prefer that hash("cat",N) ≠ hash("act",N) ≠ hash("tac",N)
Hash Function Examples
Universal hashing function
int hash(char *key, int N)
{
int h = 0, a = 31415, b = 21783;
char *c;
for (c = key; *c != '\0'; c++) {
a = a*b % (N-1);
h = (a * h + *c) % N;
}
return h;
}Hashing function (Postgresql dbms)
hash_any(unsigned char *k, register int keylen, int N)
{
register uint32 a, b, c, len;
// set up internal state
len = keylen;
a = b = 0x9e3779b9;
c = 3923095;
// handle most of the key, in 12-char chunks
while (len >= 12) {
a += (k[0] + (k[1] << 8) + (k[2] << 16) + (k[3] << 24));
b += (k[4] + (k[5] << 8) + (k[6] << 16) + (k[7] << 24));
c += (k[8] + (k[9] << 8) + (k[10] << 16) + (k[11] << 24));
mix(a, b, c);
k += 12; len -= 12;
}
// collect any data from remaining bytes into a,b,c
mix(a, b, c);
return c % N;
}
#define mix(a,b,c) \
{ \
a -= b; a -= c; a ^= (c>>13); \
b -= c; b -= a; b ^= (a<<8); \
c -= a; c -= b; c ^= (b>>13); \
a -= b; a -= c; a ^= (c>>12); \
b -= c; b -= a; b ^= (a<<16); \
c -= a; c -= b; c ^= (b>>5); \
a -= b; a -= c; a ^= (c>>3); \
b -= c; b -= a; b ^= (a<<10); \
c -= a; c -= b; c ^= (b>>15); \
}Problems with Hashing
In ideal scenarios, search cost in hash table is O(1).
Problems with hashing:
- Hash function relies on size of array (⇒ can't expand)
- Changing size of array effectively changes the hash function
- If change array size, then need to re-insert all Items
- Items are stored in (effectively) random order
- If size(KeySpace) size(IndexSpace), collisions inevitable
- Collision: k ≠ j && hash(k,N) = hash(j,N)
- If nitems > nslots, collisions inevitable
Hash Collisions
How do we deal with collisions?
-
Separate Chaining: allow multiple Items at a single array location
- E.g. array of linked lists (but worst case is O(N))
-
Linear Probing: systematically compute new indexes until find a free slot
- Need strategies for computing new indexes (aka probing)
-
Double Hashing: increase the size of the array
- Needs a method to "adjust" hash() (e.g. linear hashing)
Hash Collisions - Separate Chaining
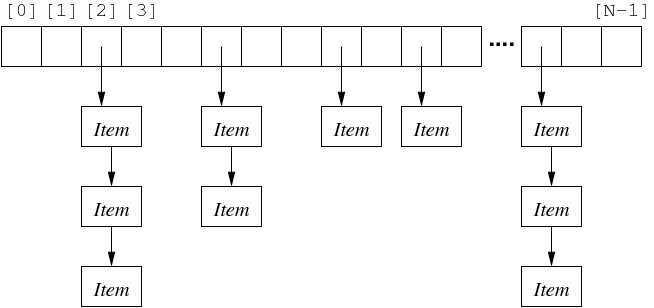
Solve collisions by having multiple items per array entry.
Make each element the start of linked-list of Items.
All items in a given list have the same hash() value
Hash Collisions - Separate Chaining
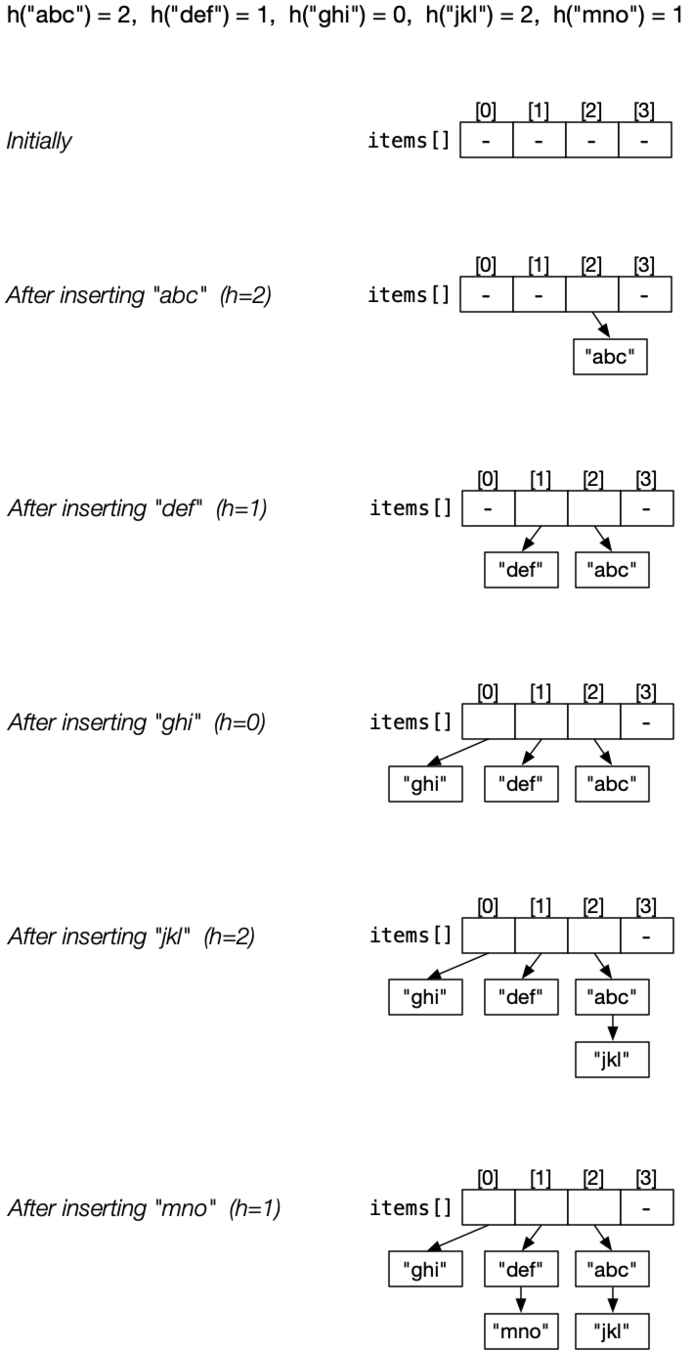
Solve collisions by having multiple items per array entry.
Make each element the start of linked-list of Items.
All items in a given list have the same hash() value

Hash Collisions - Separate Chaining
typedef struct HashTabRep {
List *lists; // array of Lists of Items
int N; // # elements in array
int nitems; // # items stored in HashTable
} HashTabRep;
HashTable newHashTable(int N) {
HashTabRep *new = malloc(sizeof(HashTabRep));
assert(new != NULL);
new->lists = malloc(N*sizeof(List));
assert(new->lists != NULL);
for (int i = 0; i < N; i++)
new->lists[i] = newList();
new->N = N; new->nitems = 0;
return new;
}Item *HashGet(HashTable ht, Key k) {
int i = hash(k, ht->N);
return ListSearch(ht->lists[i], k);
}
void HashInsert(HashTable ht, Item it) {
Key k = key(it);
int i = hash(k, ht->N);
ListInsert(ht->lists[i], it);
}
void HashDelete(HashTable ht, Key k) {
int i = hash(k, ht->N);
ListDelete(ht->lists[i], k);
}Hash Collisions - Separate Chaining
Cost analysis:
- N array entries (slots), M stored items
- Average list length L = M/N
- Best case: all lists are same length L
- Worst case: one list of length M (h(k)=0 )
- searching within a list of length n :
- best: 1, worst: n, average: n/2 ⇒ O(n)
- if good hash and M≤N, cost is 1
- if good hash and M>N, cost is (M/N)/2
Complexity = O(M/N/2)
Ratio of items/slots is called load α = M/N
Hash Collisions - Linear Probing
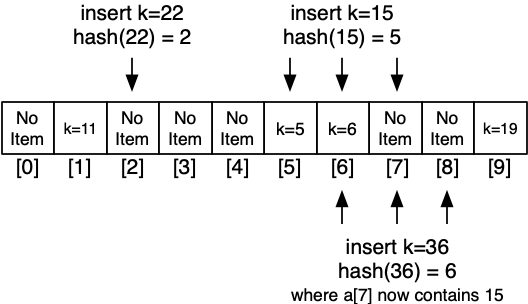
Collision resolution by finding a new location for Item
- Hash indicates slot i which is already used
- Try next slot, then next, until we find a free slot
- Insert item into available slot
Because the value at every index stores the original hash value, it's easy to tell when we've found it
Hash Collisions - Linear Probing
typedef struct HashTabRep {
Item **items; // array of pointers to Items
int N; // # elements in array
int nitems; // # items stored in HashTable
} HashTabRep;
HashTable newHashTable(int N)
{
HashTabRep *new = malloc(sizeof(HashTabRep));
assert(new != NULL);
new->items = malloc(N*sizeof(Item *));
assert(new->items != NULL);
for (int i = 0; i < N; i++) new->items[i] = NULL;
new->N = N; new->nitems = 0;
return new;
}void HashInsert(HashTable ht, Item it)
{
assert(ht->nitems < ht->N);
int N = ht->N;
Key k = key(it);
Item **a = ht->items;
int i = hash(k,N);
for (int j = 0; j < N; j++) {
if (a[i] == NULL) break;
if (equal(k,key(*(a[i])))) break;
i = (i+1) % N;
}
if (a[i] == NULL) ht->nitems++;
if (a[i] != NULL) free(a[i]);
a[i] = copy(it);
}
Item *HashGet(HashTable ht, Key k)
{
int N = ht->N;
Item **a = ht->items;
int i = hash(k,N);
for (int j = 0; j < N; j++) {
if (a[i] == NULL) break;
if (equal(k,key(*(a[i]))))
return a[i];
i = (i+1) % N;
}
return NULL;
}Creation, insertion, search
Hash Collisions - Linear Probing
void HashDelete(HashTable ht, Key k)
{
int N = ht->N;
Item *a = ht->items;
int i = hash(k,N);
for (int j = 0; j < N; j++) {
if (a[i] == NULL) return; // k not in table
if (equal(k,key(*(a[i])))) break;
i = (i+1) % N;
}
free(a[i]); a[i] = NULL; ht->nitems--;
// clean up probe path
i = (i+1) % N;
while (a[i] != NULL) {
Item it = *(a[i]);
a[i] = NULL; // remove 'it'
ht->nitems--;
HashInsert(ht, it); // insert 'it' again
i = (i+1) % N;
}
}
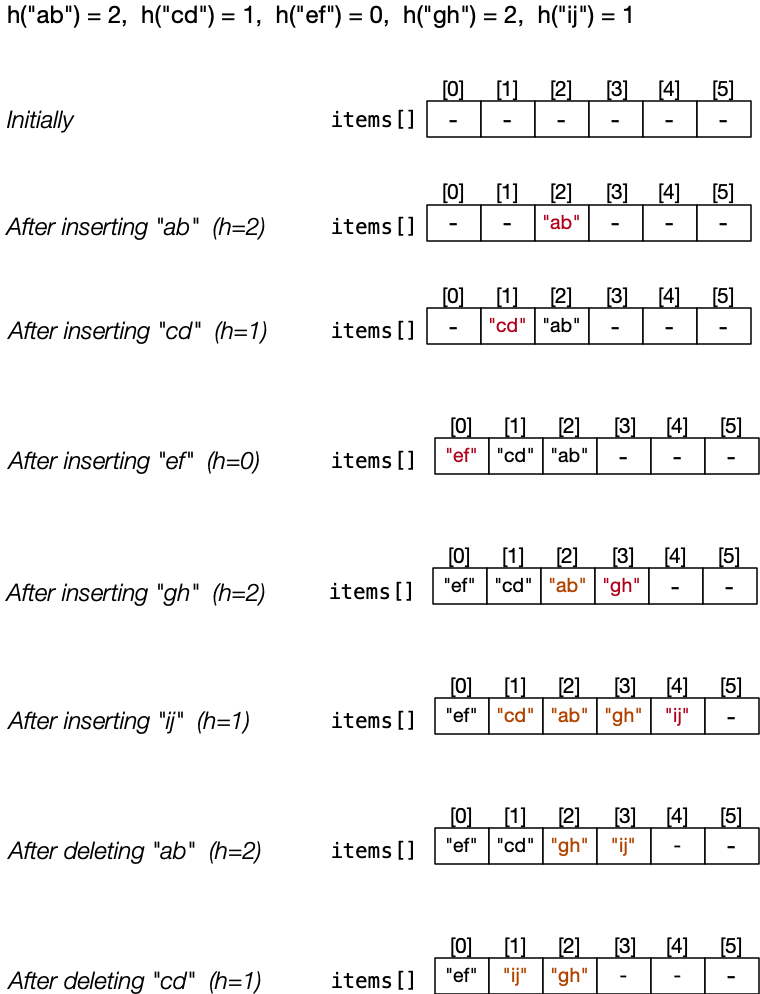
Deletion is tricky,
Need to ensure no NULL in middle of "probe path"
(i.e. previously relocated items moved to appropriate location)
Hash Collisions - Linear Probing

Hash Collisions - Linear Probing
Search cost analysis:
- Cost to reach first Item is O(1)
- Subsequent cost depends how much we need to scan
- Affected by load α = M/N (i.e. how "full" is the table)
- Average cost for successful search = 0.5*(1 + 1/(1-α))
- Average cost for unsuccessful search = 0.5*(1 + 1/(1-α)^2)
Example costs (assuming large table, e.g. N>100 ):
| load (α) | 0.50 | 0.67 | 0.75 | 0.90 |
| search hit | 1.5 | 2.0 | 3.0 | 5.5 |
| search miss | 2.5 | 5.0 | 8.5 |
55.5
|
Assumes reasonably uniform data and good hash function.
Hash Collisions - Double Hashing
Double hashing improves on linear probing:
- By using an increment which ...
- Is based on a secondary hash of the key
- Ensures that all elements are visited
(can be ensured by using an increment which is relatively prime to N)
- Tends to eliminate clusters ⇒ shorter probe paths
To generate relatively prime
- Set table size to prime e.g. N=127
- Hash2() in range [1..N1] where N1 < 127 and prime
Hash Collisions - Double Hashing
typedef struct HashTabRep {
Item **items; // array of pointers to Items
int N; // # elements in array
int nitems; // # items stored in HashTable
int nhash2; // second hash mod
} HashTabRep;
#define hash2(k,N2) (((k)%N2)+1)
HashTable newHashTable(int N)
{
HashTabRep *new = malloc(sizeof(HashTabRep));
assert(new != NULL);
new->items = malloc(N*sizeof(Item *));
assert(new->items != NULL);
for (int i = 0; i < N; i++)
new->items[i] = NULL;
new->N = N; new->nitems = 0;
new->nhash2 = findSuitablePrime(N);
return new;
}Item *HashGet(HashTable ht, Key k)
{
Item **a = ht->items;
int N = ht->N;
int i = hash(k,N);
int incr = hash2(k,ht->nhash2);
for (int j = 0, j < N; j++) {
if (a[i] == NULL) break; // k not found
if (equal(k,key(*(a[i]))) return a[i];
i = (i+incr) % N;
}
return NULL;
}void HashInsert(HashTable ht, Item it)
{
assert(ht->nitems < ht->N); // table full
Item **a = ht->items;
Key k = key(it);
int N = ht->N;
int i = hash(k,N);
int incr = hash2(k,ht->nhash2);
for (int j = 0, j < N; j++) {
if (a[i] == NULL) break;
if (equal(k,key(*(a[i])))) break;
i = (i+incr) % N;
}
if (a[i] == NULL) ht->nitems++;
if (a[i] != NULL) free(a[i]);
a[i] = copy(it);
}
Hash Collisions - Double Hashing
Search cost analysis:
- cost to reach first Item is O(1)
- subsequent cost depends how much we need to scan
- affected by load α = M/N (i.e. how "full" is the table)
- average cost for successful search =
- Average cost for unsuccessful search =
Costs for double hashing (assuming large table, e.g. N>100 ):
| load (α) | 0.5 | 0.67 | 0.75 | 0.90 |
| search hit | 1.4 | 1.6 | 1.8 | 2.6 |
| search miss | 1.5 | 2.0 | 3.0 | 5.5 |
Can be significantly better than linear probing
Hash Collisions - Summary
Collision resolution approaches:
- chaining: easy to implement, allows α > 1
- linear probing: fast if α << 1, complex deletion
- double hashing: faster than linear probing, esp for α ≅ 1
Only chaining allows α > 1, but performance poor when α >> 1
For arrays, once M exceeds initial choice of N,
- Need to expand size of array (N)
- Problem: hash function relies on N, so changing array size potentially requires rebuiling whole table
Feedback
