INTEGRACIÓN NUMERÍCA
Análisis Numérico
INTEGRACIÓN NUMÉRICA
Los métodos de integración numérica se usan cuando ƒ(x) es difícil o imposible de integrar analíticamente, o cuando ƒ(x) esta dada como un conjunto de valores tabulados.
REGLA DEL TRAPECIO
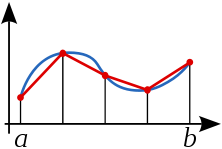
Se aproxima la función dividiendo el intervalo [a, b] en n intervalos de igual longitud y formando entonces trapecios por encima de cada intervalo.
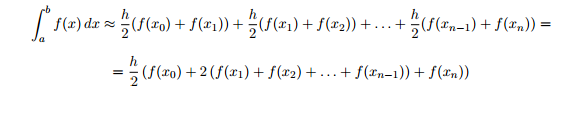
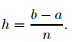
REGLA DEL SIMPSON
La regla de Simpson reemplaza la suma de áreas de los trapecios por la suma de las áreas situadas por debajo de las parábolas para aproximar la integral en un intervalo definido.
Al igual que en la regla de los trapecios dividimos el intervalo [a , b] en n intervalos de igual longitud ( n deberá ser un numero para).
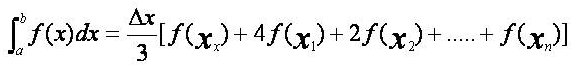
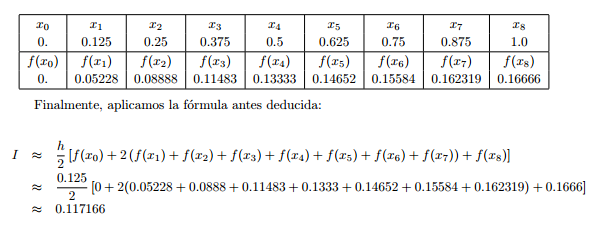
EJEMPLO CON TRAPECIO

EJEMPLO CON SIMPSON
