A possible mass distribution of primordial black holes implied by LIGO-Virgo

Heling Deng

Arizona State University

2101.11098

Outline

  • LIGO BHs
  • Primordial?
  • A simple model "fitting" LIGO
  • A possible mechanism

Outline

  • LIGO BHs
  • Primordial?
  • A simple model "fitting" LIGO
  • A possible mechanism

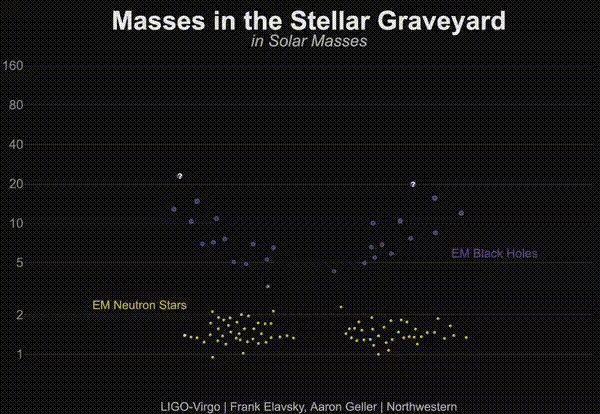
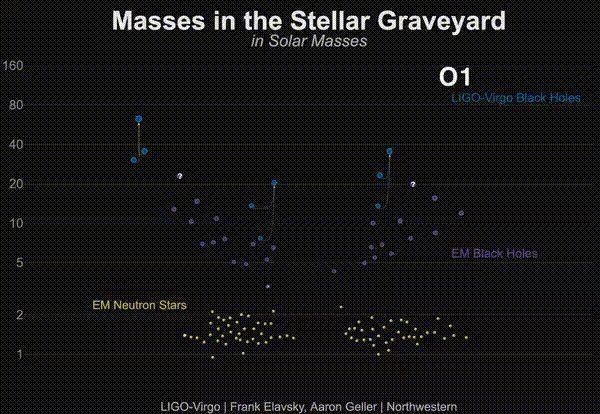
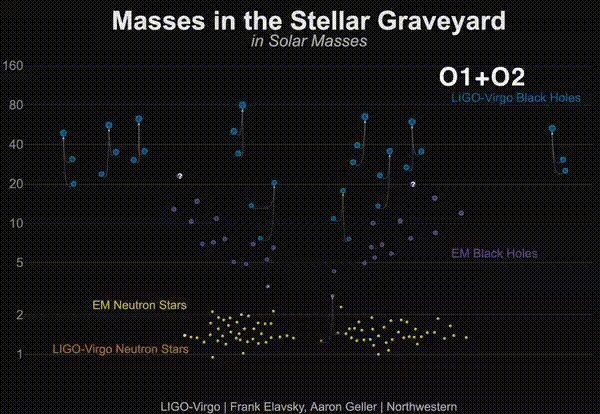
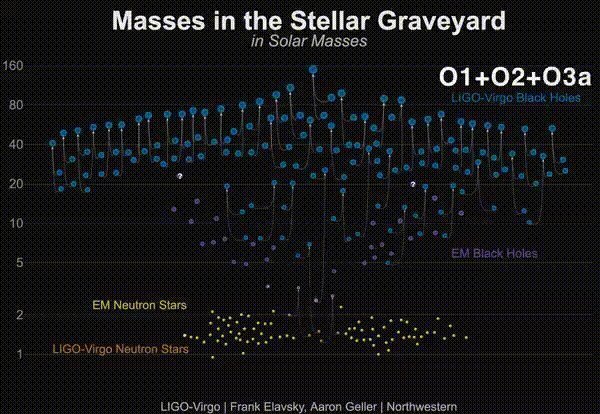
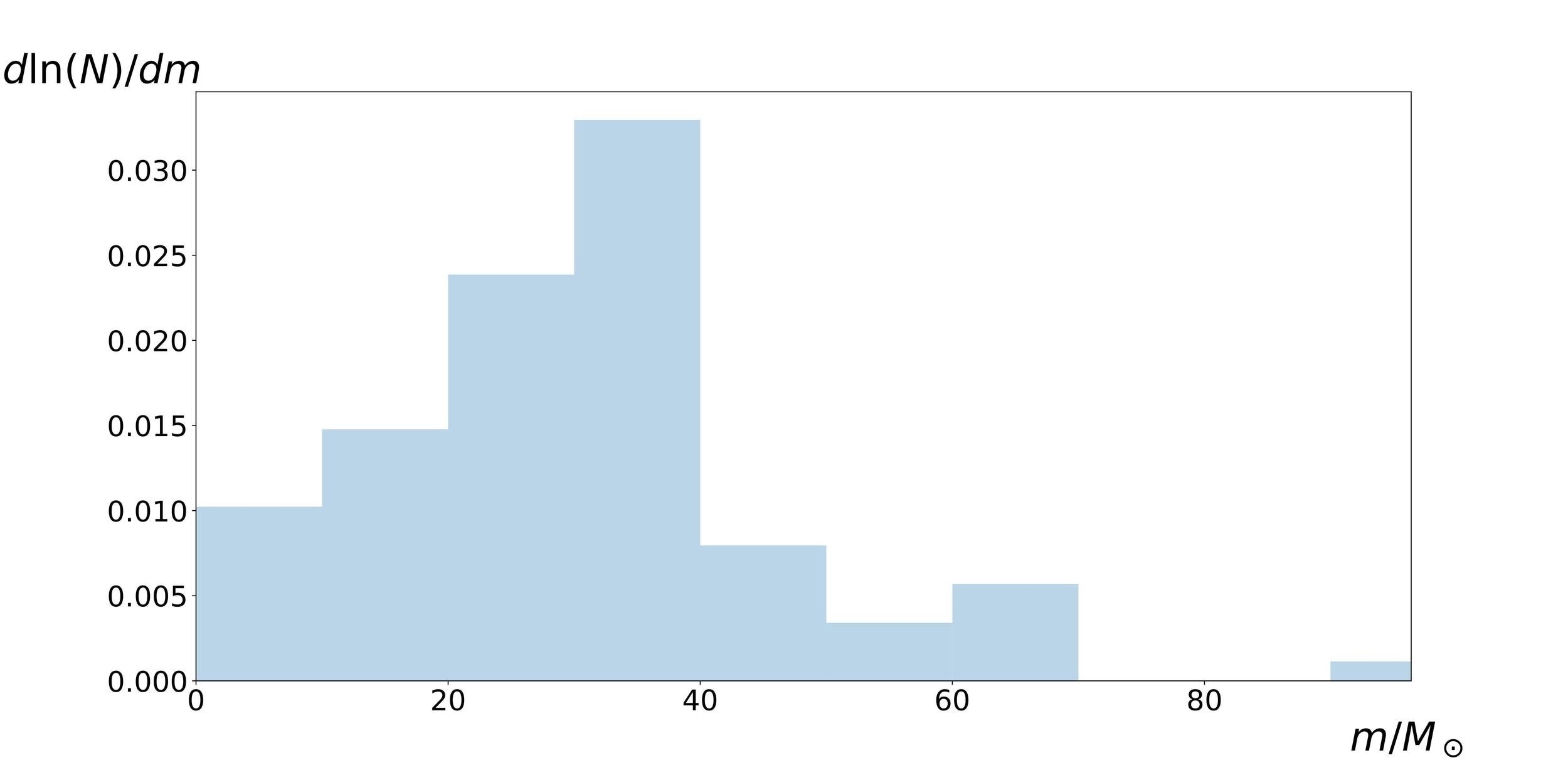
Mass distribution of LIGO BHs

BH mass

(BH number)

Outline

  • LIGO BHs
  • Primordial?
  • A simple model "fitting" LIGO
  • A possible mechanism
M_\text{Pl} \newline 10^{-5}\ \rm g
M_\text{evp} \newline 10^{15}\ \rm g
M_\odot \newline 10^{33}\ \rm g
M_\text{PBH}

LIGO BHs

  • Supermassive black holes
  • LIGO black holes
  • Dark matter
\mathcal O (10\text{-} 100)M_\odot

SMBH

\mathcal{O}(10^6 \text{-} 10^{10})M_\odot

...

...

Primordial black holes (PBHs) 

...

BHs formed during radiation era

Motivations

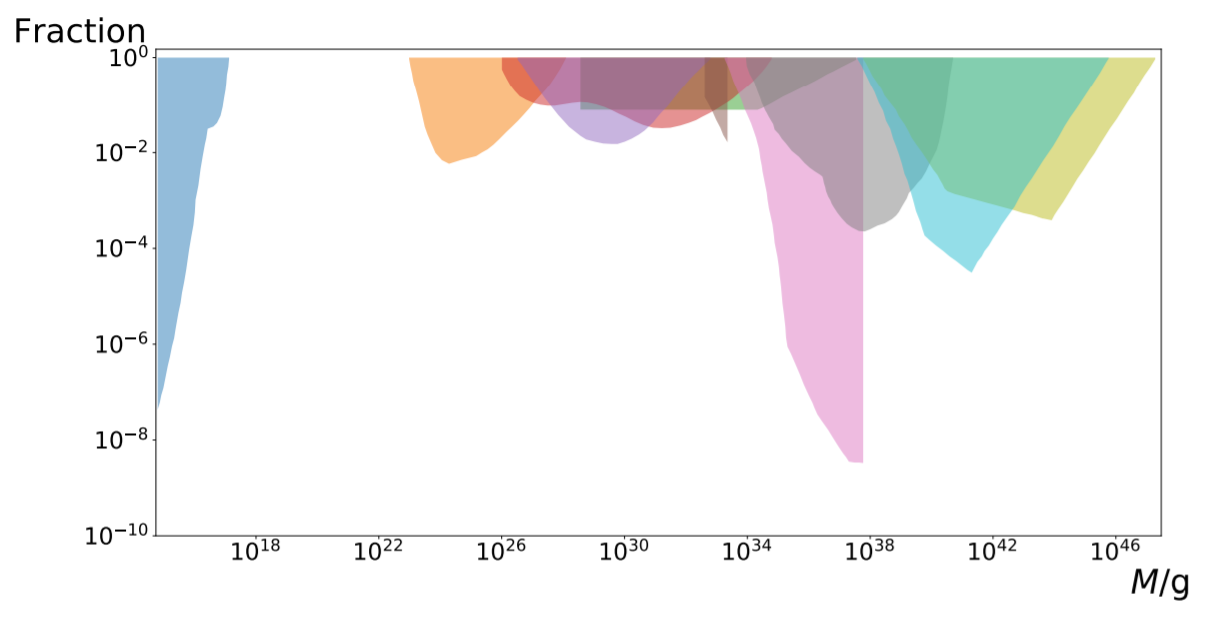
Observational constraints of PBHs as DM

PBH binary

PBH mass function

f_{PBH}\equiv\frac{\rho_{PBH}}{\rho_{CDM}} = \int \psi(m)\text{d}m
f(m)=m\psi(m)
\psi(m)\text{d}m=\frac{m}{\rho_{CDM}}\text{d}n

(Fraction of CDM in PBHs with \(\sim m\))

(Fraction of CDM in PBHs within (\(m, m+\text{d}m)\))

(Fraction of CDM in PBHs)

PBH mass function \( f(m)\)

Merger rate \(R(m_1,m_2,z) \propto f(m_1) f(m_2)\) 

Detection probability \(p_{det}(m_1,m_2,z)\)

Probability of each event \(p_i(m_1,m_2,z)\)

+

Likelihood of all LIGO events

+

Expected number of detection \(N_e\)

Signals follow a Poisson process

p_{Poisson}\propto N_e^{N_o}e^{-N_e}
\mathcal{L}\propto p_{Poisson}\prod_{i=1}^{N_o} p_i

Mergers reaching earth today

\(N(m_1,m_2,z) \propto R(m_1,m_2,z)\)

Outline

  • LIGO BHs
  • Primordial?
  • A simple model "fitting" LIGO
  • A possible mechanism

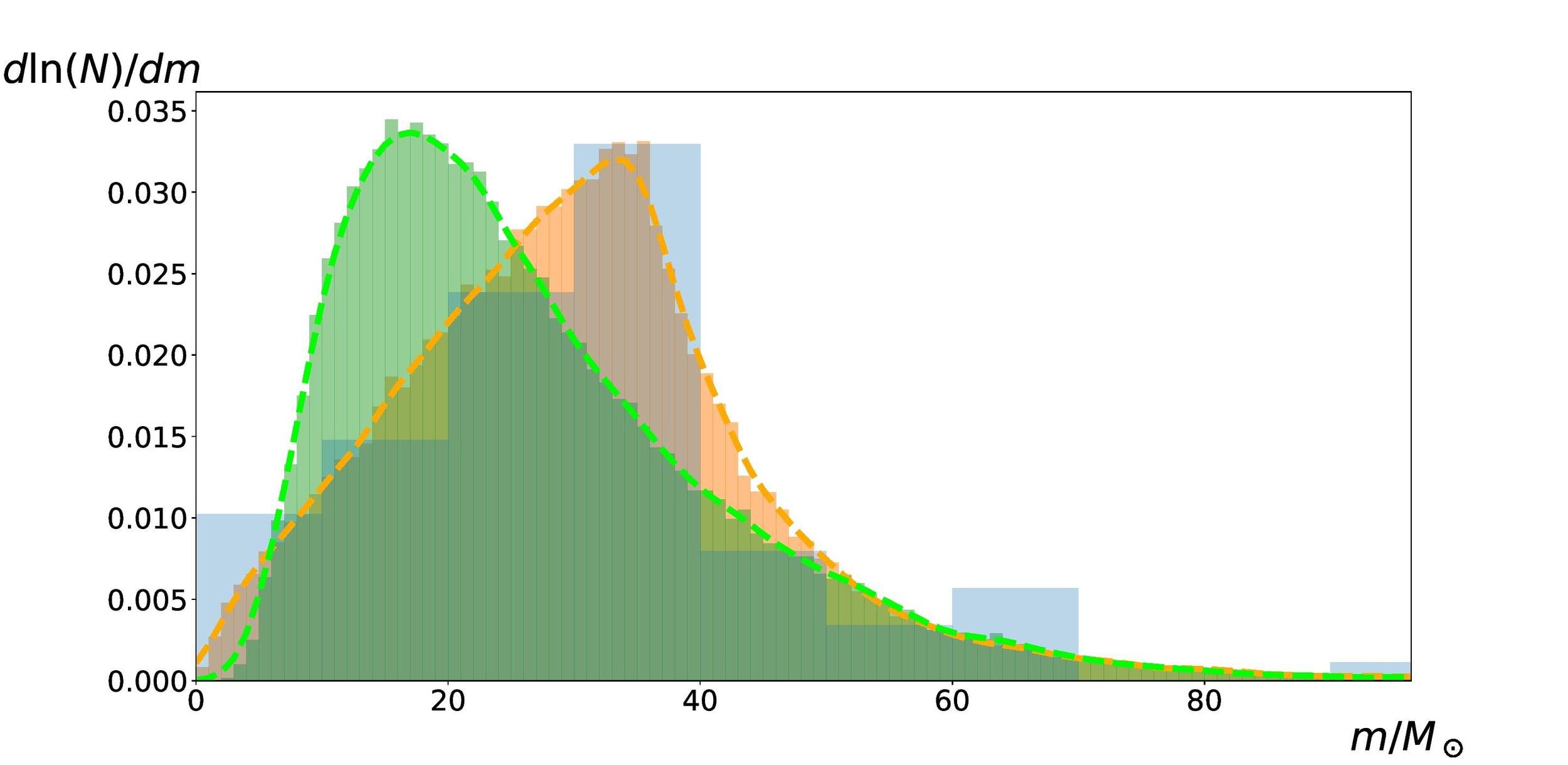
Mass distribution of LIGO BHs

m^{\alpha_1},\ \ \ m< m_*
m^{\alpha_2},\ \ \ m> m_*
f(m)\propto
\{

A simple mass function

\log(m)
\log(f)
m^{\alpha_1}
m^{\alpha_2}
m_*
f_{PBH}
f_{PBH}
f_{PBH}\approx 10^{-3}

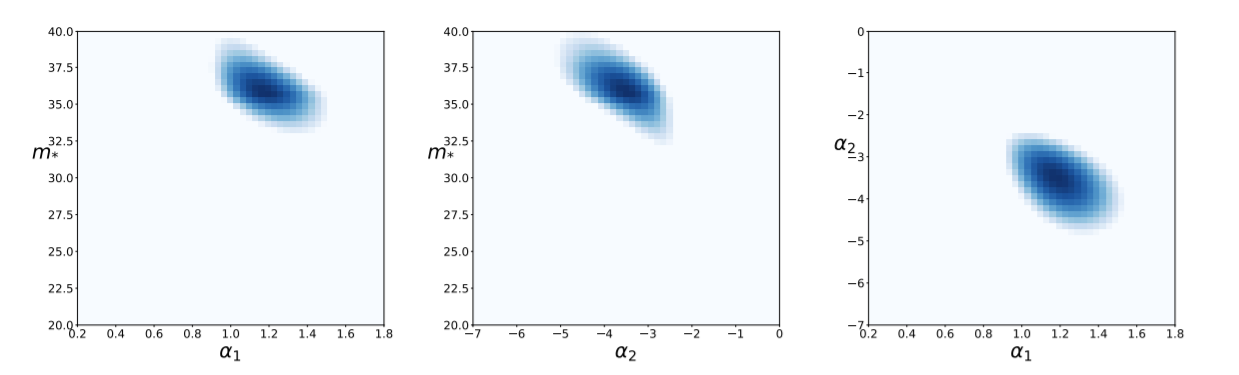
Maximizing \(\mathcal{L}\) in a 4-parameter space

\alpha_2 = -4
\alpha_1 = 1.2
m_*=35M_\odot
\log(m)
\log(f)
m^{1.2}
m^{-4}
35M_\odot
10^{-3}

Outline

  • LIGO BHs
  • Primordial?
  • A simple model "fitting" LIGO
  • A possible mechanism

A possible mechanism

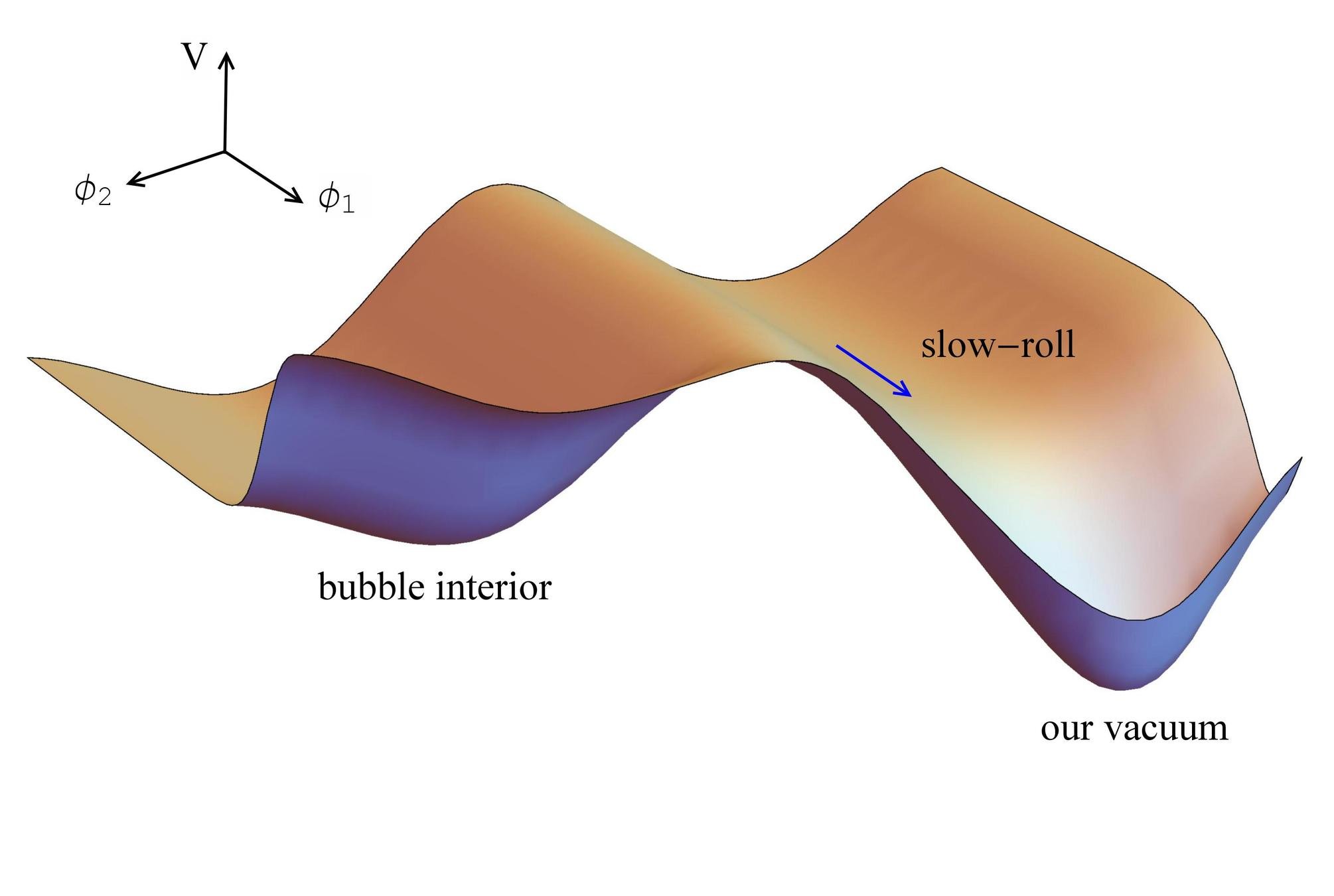
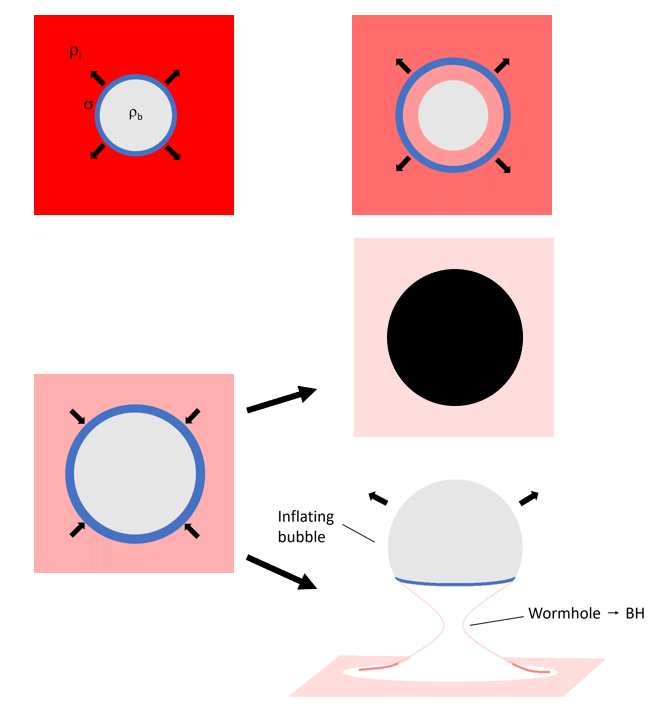
subcritical

supercritical

EOM of bubble from Israel's junction conditions

r

m\propto r^3
m\propto r^2

Size distribution of bubbles after inflation

Constant bubble nucleation rate \(\lambda\) during inflation

Evolution of bubbles in radiation background \(r\)(\(\gamma_i\), \(\rho_i\), \(\rho_b\), \(\sigma\))

BH mass distribution \(f(m)\)

Parameters: \(\lambda\), \(\gamma_i\), \(\sigma\), \(\rho_i\), \(\rho_b\)

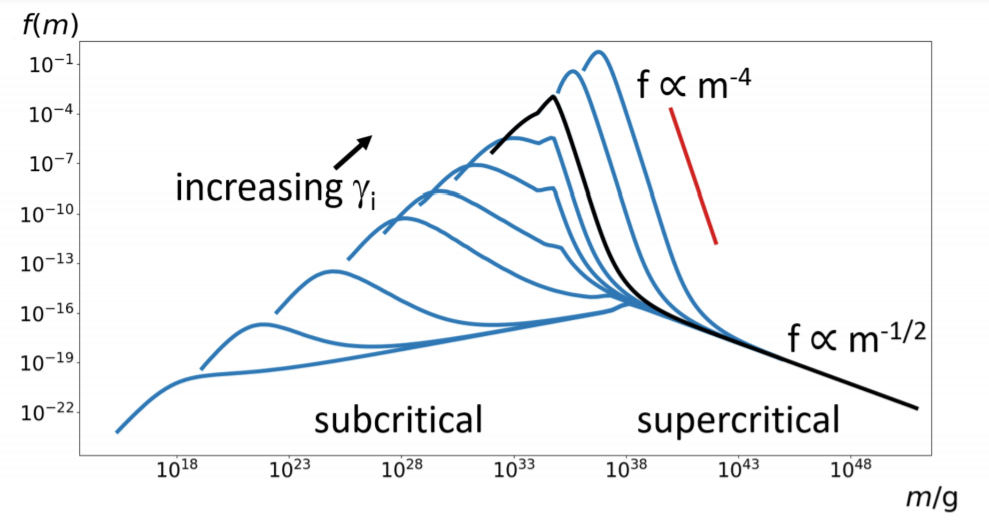
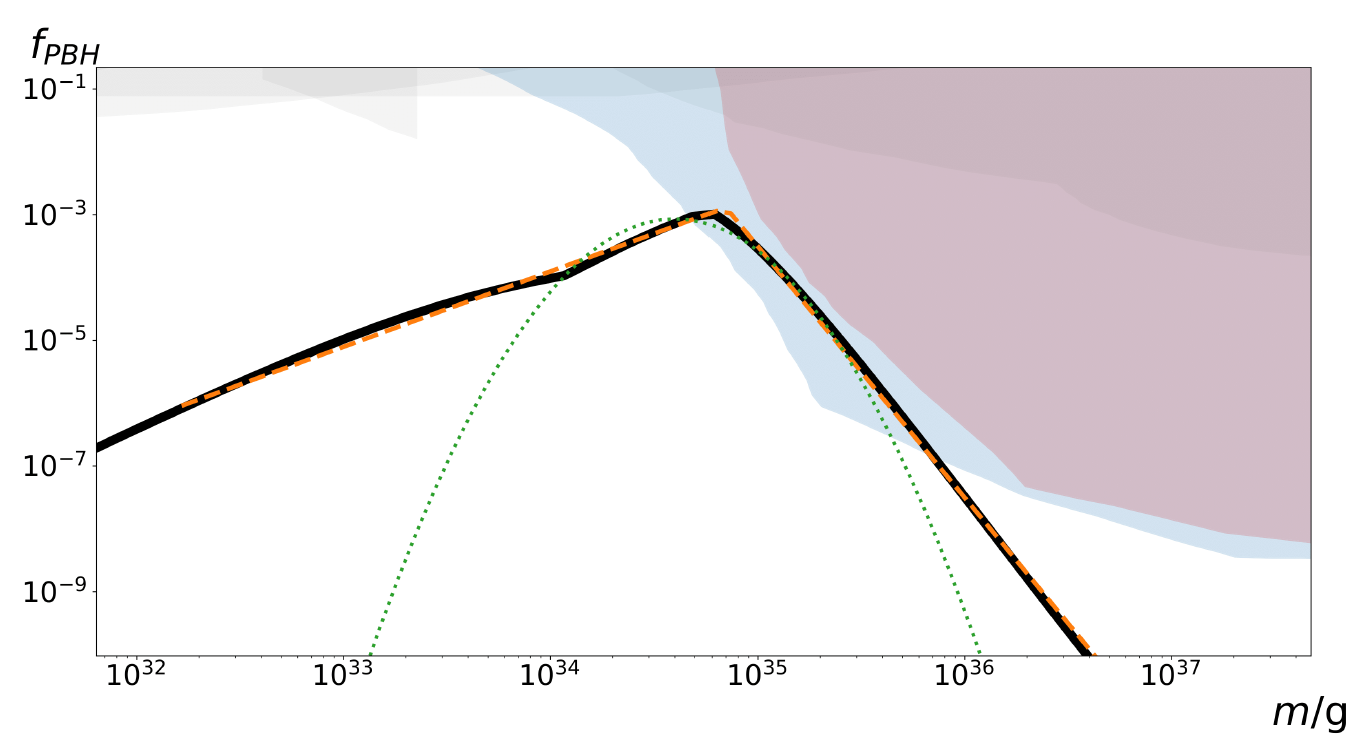
Conclusions

PBH mass function

Merger rate

Detection probability

Expected number of observable events

Probability of each detected event

p_i
p_{Poisson}\propto N_e^{N_o}e^{-N_e}
\mathcal{L}\propto p_{Poisson}\prod_{i=1}^{N_o} p_i
N_e

+

+

Likelihood of all LIGO events

Intrinsic PBH merger rate

\text{d}R(m_1,m_2,z)\propto f(m_1) f(m_2)

(Number of event  \((m_1,m_2,z)\) per unit volume per unit time)

Signals reaching earth 

\text{d}N(m_1,m_2,z)\propto \text{d}R(m_1,m_2,z)

(Number of event  \((m_1,m_2,z)\) reaching the earth per unit time)

Detection probability \(p_{det}(m_1,m_2,z)\)

\text{d}N_e(m_1,m_2,z)=p_{det}(m_1,m_2,z)\text{d}N\times T_o
Made with Slides.com