Primordial black holes from vacuum bubbles

邓鹤凌

Arizona State University

Outline

Primordial black holes

Fitting LIGO black holes

LIGO BHs from bubbles?

PBHs from bubbles

Outline

Primordial black holes

Fitting LIGO black holes

LIGO BHs from bubbles?

PBHs from bubbles

M_\text{Pl} \newline \sim10^{-5}\ \rm g

M_\text{evp} \newline \sim10^{15}\ \rm g

M_\odot \newline \sim10^{33}\ \rm g

M_\text{PBH}

LIGO BH

Supermassive black holes

\mathcal O (10\text{-} 100) \ M_\odot

SMBH

...

Primordial black holes (PBHs)

\mathcal{O}(10^6 \text{-} 10^{10})M_\odot

Astrophysical BHs

M_\text{Pl} \newline \sim10^{-5}\ \rm g

M_\text{evp} \newline \sim10^{15}\ \rm g

M_\odot \newline \sim10^{33}\ \rm g

M_\text{PBH}

LIGO BH

Supermassive black holes

LIGO black holes

\mathcal O (10\text{-} 100) \ M_\odot

SMBH

...

Primordial black holes (PBHs)

\mathcal{O}(10^6 \text{-} 10^{10})M_\odot

Astrophysical BHs

LIGO BHs

M_\text{Pl} \newline \sim10^{-5}\ \rm g

M_\text{evp} \newline \sim10^{15}\ \rm g

M_\odot \newline \sim10^{33}\ \rm g

M_\text{PBH}

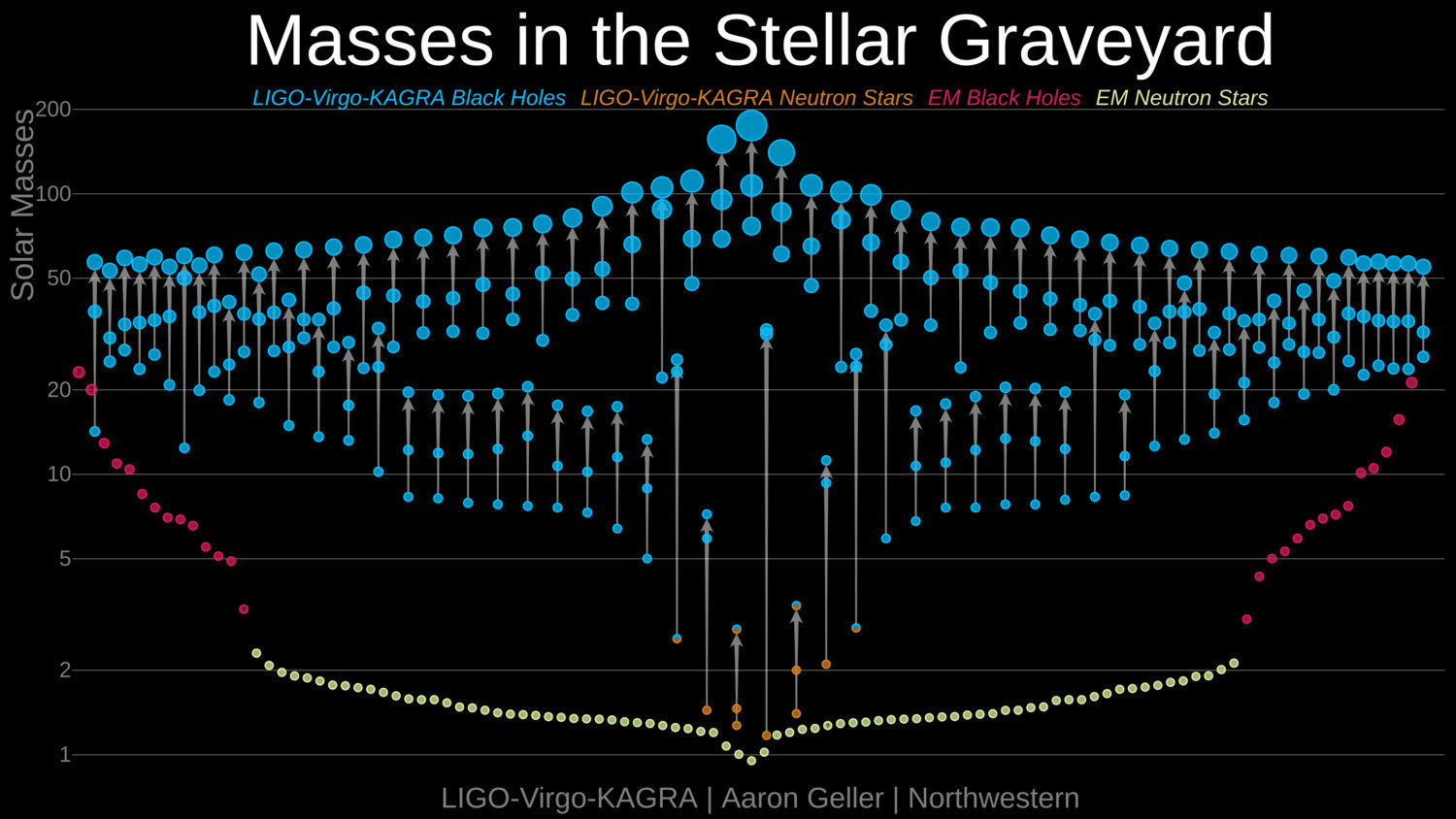
LIGO BH

Supermassive black holes

LIGO black holes

Dark matter

\mathcal O (10\text{-} 100) \ M_\odot

SMBH

...

Primordial black holes (PBHs)

\mathcal{O}(10^6 \text{-} 10^{10})M_\odot

Astrophysical BHs

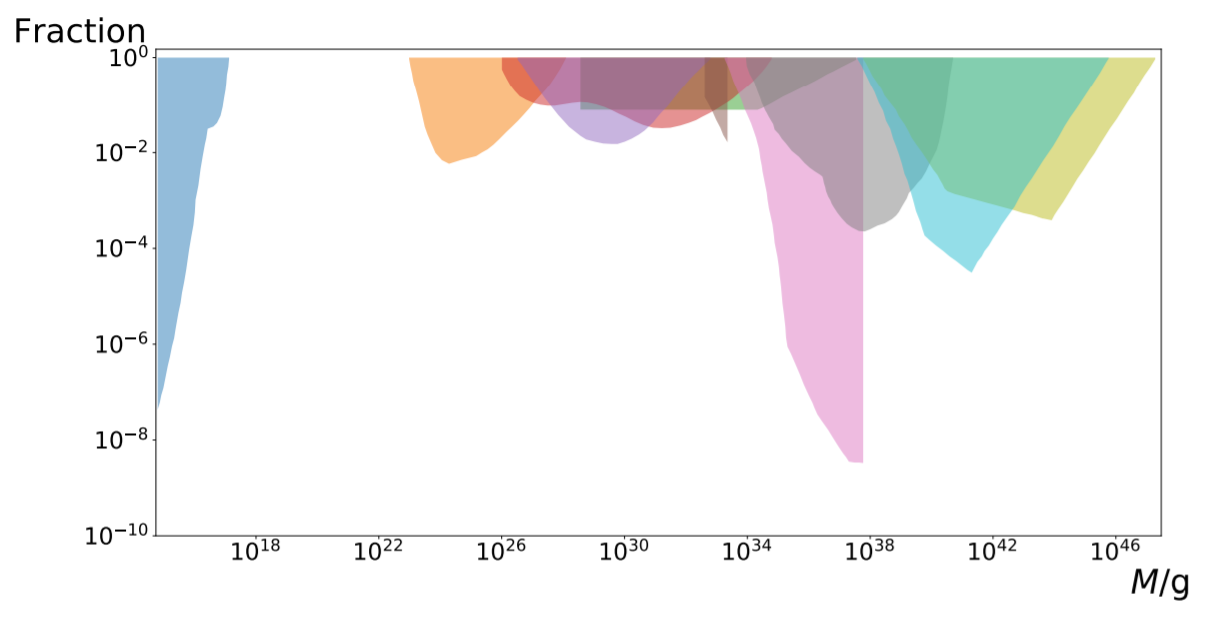
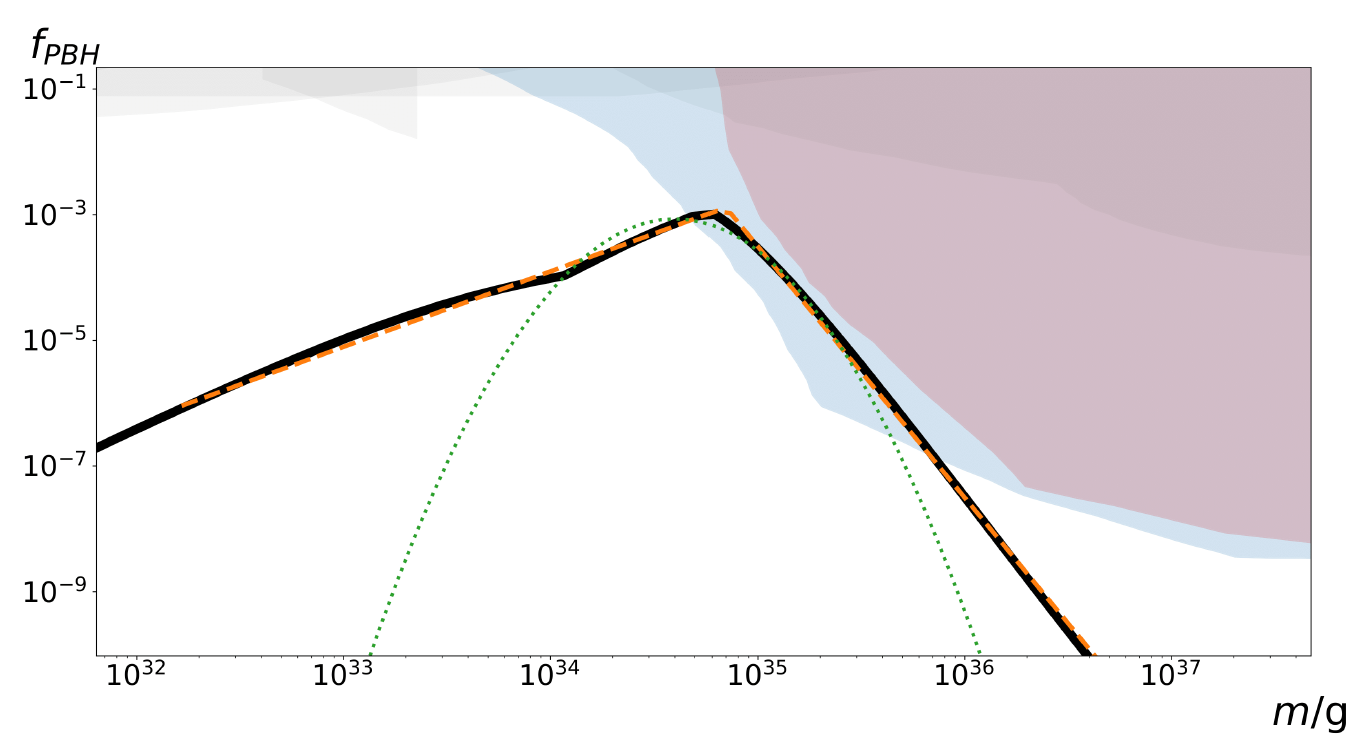
Observational constraints of PBHs as DM

Outline

Primordial black holes

Fitting LIGO black holes

LIGO BHs from bubbles?

PBHs from bubbles

\rho_i

\rho_b

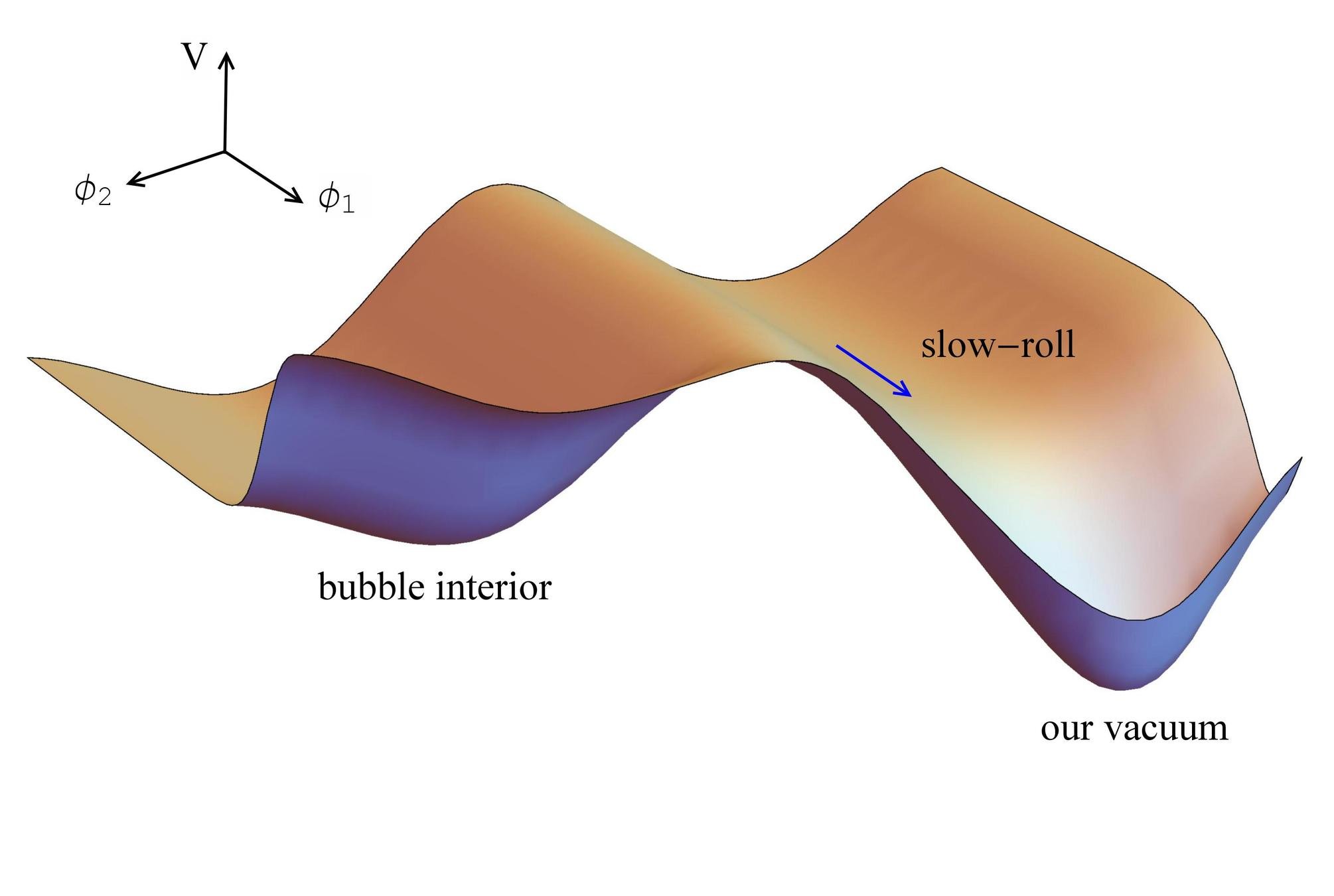
Inflation \(\rho_i \to\) radiation fluid \(\rho_i\)

\rho_b

Bubble interior \(\rho_b<\rho_i\)

\rho_i

H_b^{-1}

Subcritical

Supercritical

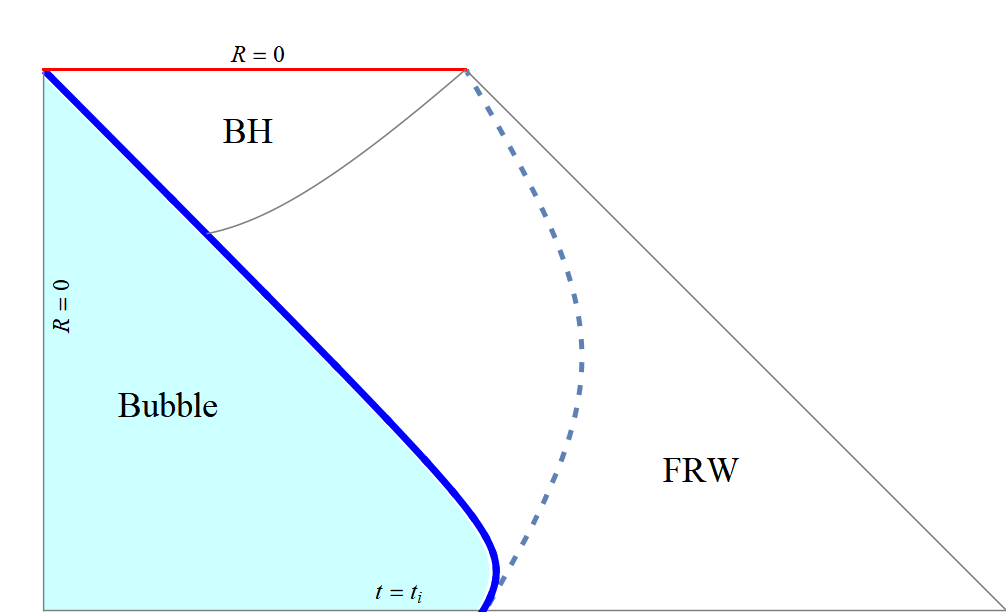
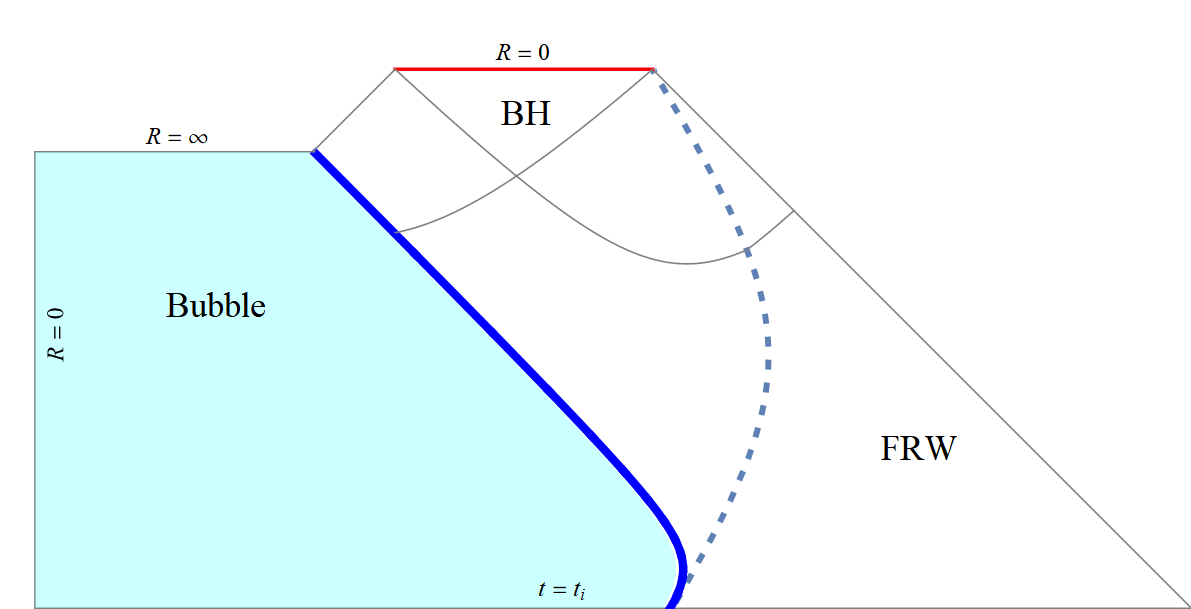
Wormhole \(\to\) BH

H_b^{-1}

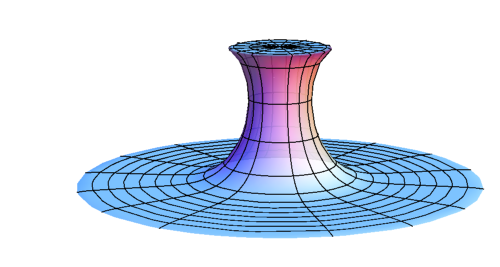
Used numerical simulations of full GR to find relation between BH mass and bubble size \(m(R)\)

subcritical

m\propto R^3

supercritical

m\propto R^2

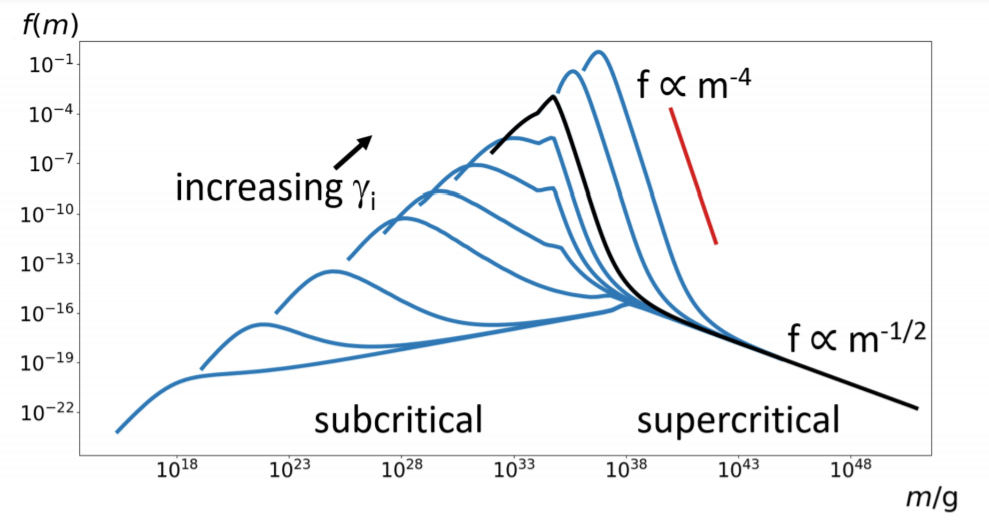
PBH mass function (fraction of DM in PBHs with mass \(\sim m\))

f(m)\equiv \frac{\rho_t(m)}{\rho_\text{CDM}}

PBH mass density

\rho_t(m)=mn_t(m)

Number density of bubbles (BHs)

n_t(R)\to n_t(m)

const over time

m^{0},\ \ \ m< m_*

m^{-1/2},\ \ \ m> m_*

f(m)\propto

\{

Broken power law

BH mass distribution from bubbles

\log(m)

\log(f)

m^{0}

m^{-1/2}

m_*

subcritical

supercritical

Outline

Primordial black holes

Fitting LIGO black holes

LIGO BHs from bubbles?

PBHs from bubbles

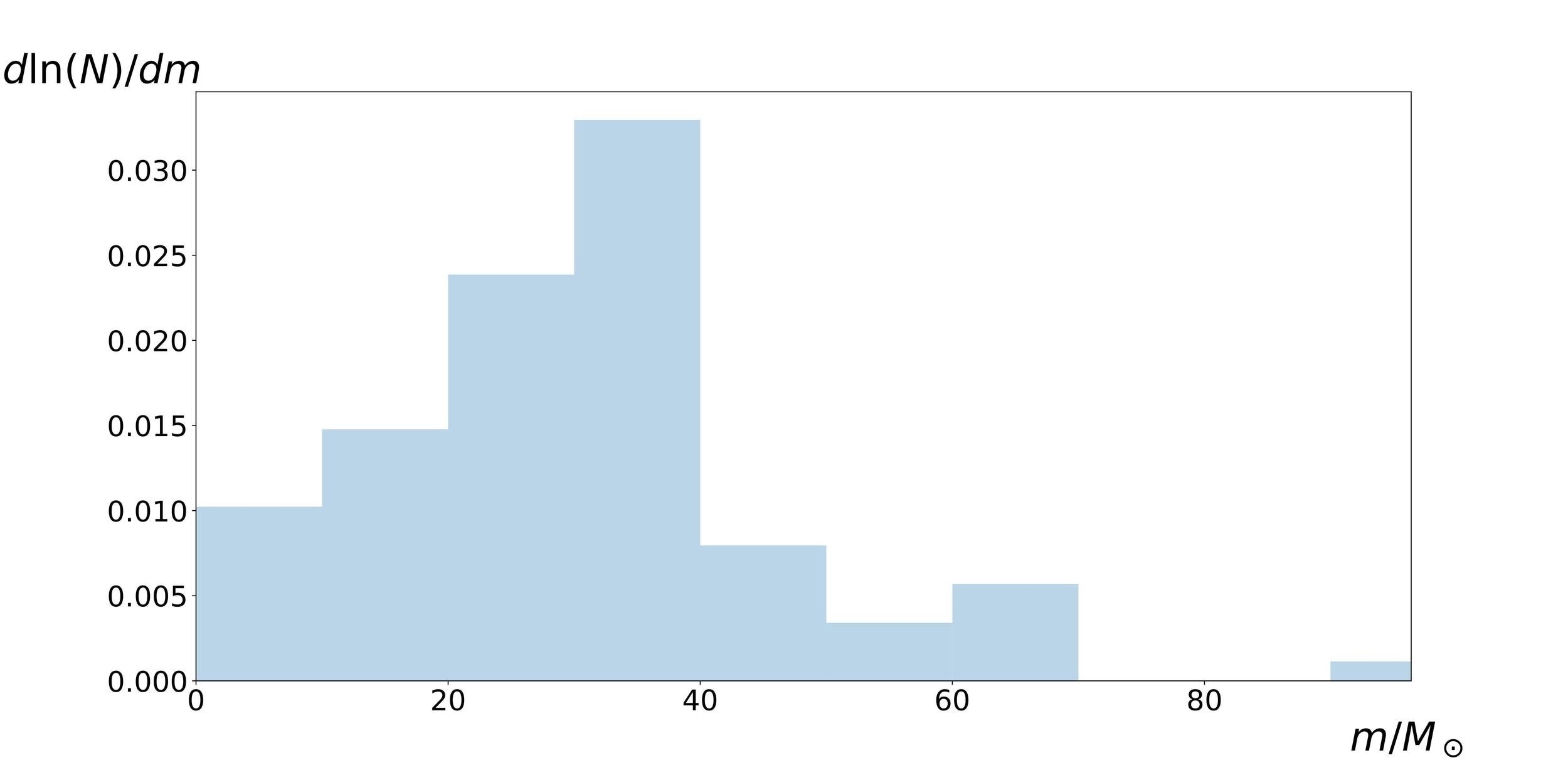
Mass distribution of LIGO BHs

m^{\alpha_1},\ \ \ m< m_*

m^{\alpha_2},\ \ \ m> m_*

f(m)\propto

\{

A simple mass function

\log(m)

\log(f)

m^{\alpha_1}

m^{\alpha_2}

m_*

f_{PBH}

PBH mass function

Merger rate

Detection probability

Probability of each event \(p_i(m_1,m_2,z)\)

+

Likelihood of all LIGO events

\mathcal{L}\propto \prod_{i=1}^{N_o} p_i

Mergers reaching earth today

\(f(m)\) characterized by \(f_{PBH}, \alpha_1, \alpha_2, m_*\)

f_{PBH}\approx 10^{-3}

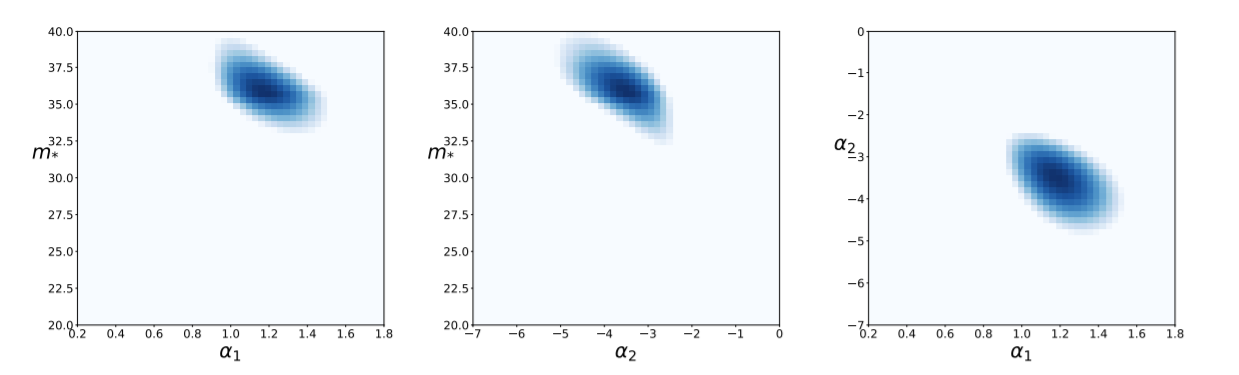
Maximizing \(\mathcal{L}\) in a 4-parameter space

\alpha_2 = -4

\alpha_1 = 1.2

m_*=35M_\odot

\log(m)

\log(f)

m^{1.2}

m^{-4}

35M_\odot

10^{-3}

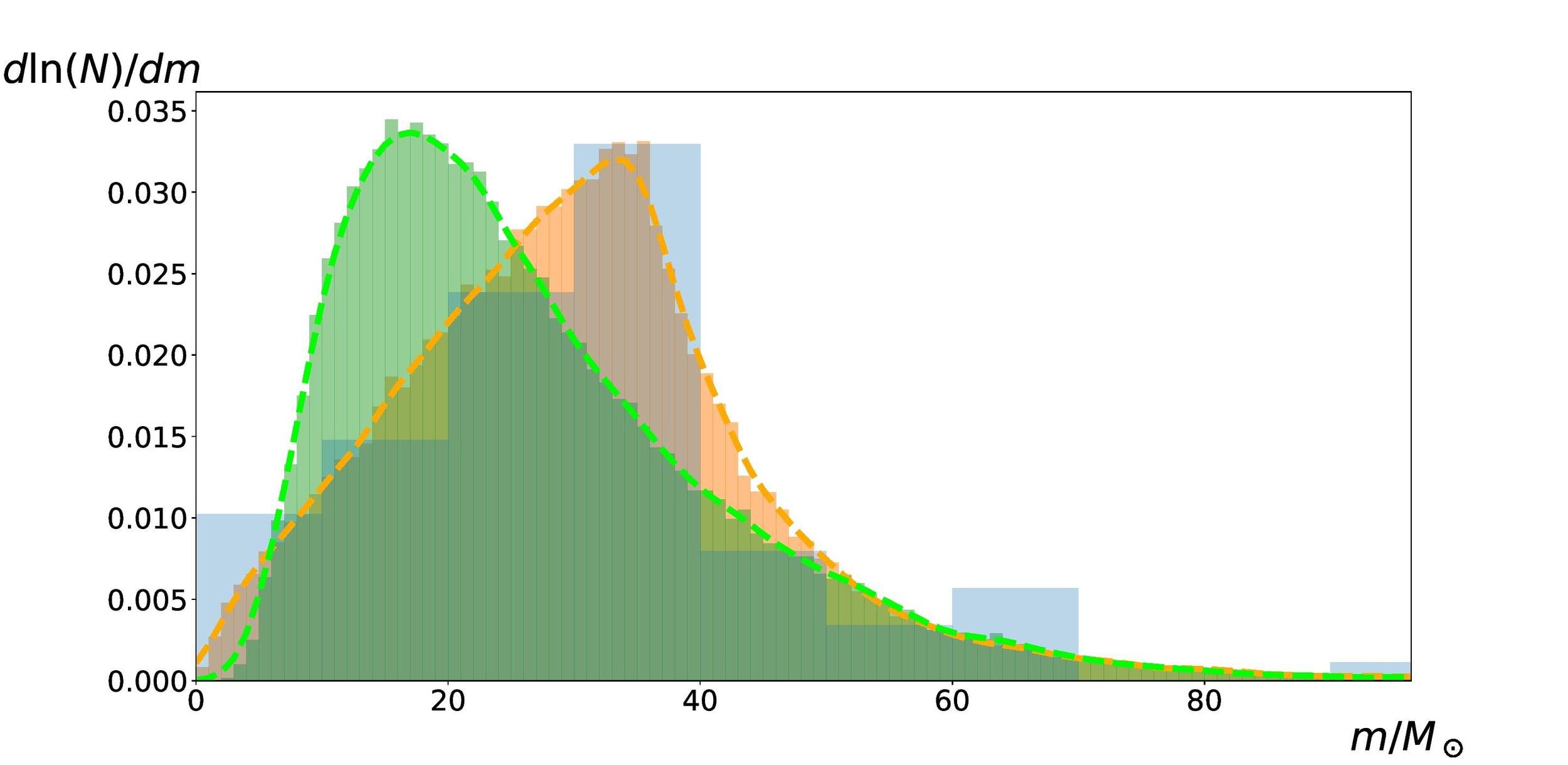
Is there a mechanism that can generate such a mass function?

Outline

Primordial black holes

Fitting LIGO black holes

LIGO BHs from bubbles?

PBHs from bubbles

\log(m)

\log(f)

m^{0}

m^{-1/2}

m_*

\log(f)

m^{1.2}

m^{-4}

35M_\odot

\log(m)

\log(f)

m^{0}

m^{-1/2}

m_*

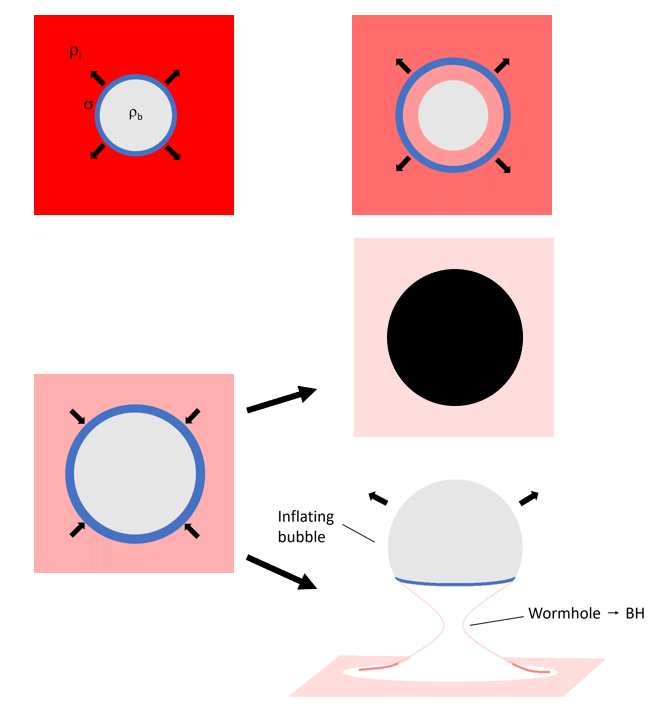
Fluid not get into bubble

Fluid gets into bubble

f\propto m^{1.2}

Observational constraints of PBHs as DM

m^{1.2}

m^{-4}

PBH mass function

Merger rate

Detection probability

Expected number of observable events

Probability of each detected event

p_i

p_{Poisson}\propto N_e^{N_o}e^{-N_e}

\mathcal{L}\propto p_{Poisson}\prod_{i=1}^{N_o} p_i

N_e

+

Likelihood of all LIGO events

\rho_b

Empty layer

Intrinsic PBH merger rate

\text{d}R(m_1,m_2,z)\propto f(m_1) f(m_2)

(Number of event \((m_1,m_2,z)\) per unit volume per unit time)

Signals reaching earth

\text{d}N(m_1,m_2,z)\propto \text{d}R(m_1,m_2,z)

(Number of event \((m_1,m_2,z)\) reaching the earth per unit time)

Detection probability \(p_{det}(m_1,m_2,z)\)

\text{d}N_e(m_1,m_2,z)=p_{det}(m_1,m_2,z)\text{d}N\times T_o