Primordial Black Hole Formation by Vacuum Bubbles
Heling Deng
1710.02865 with Alex Vilenkin
Tufts University
- dynamics & spacetime
- results
- simulation setup
- observations
- results
- simulation setup
- observations
- dynamics & spacetime
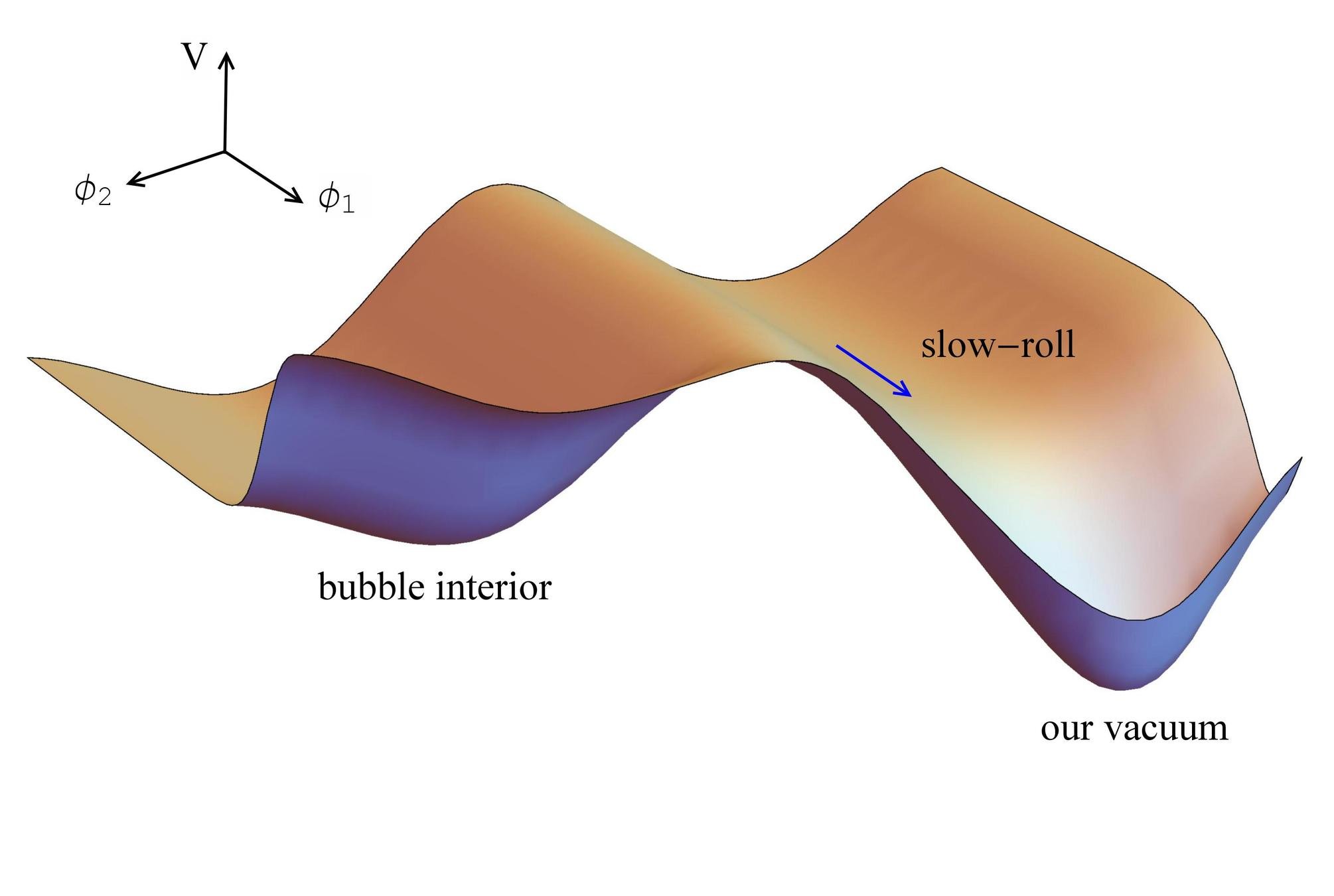
inflaton
radiation
BH
subcritical
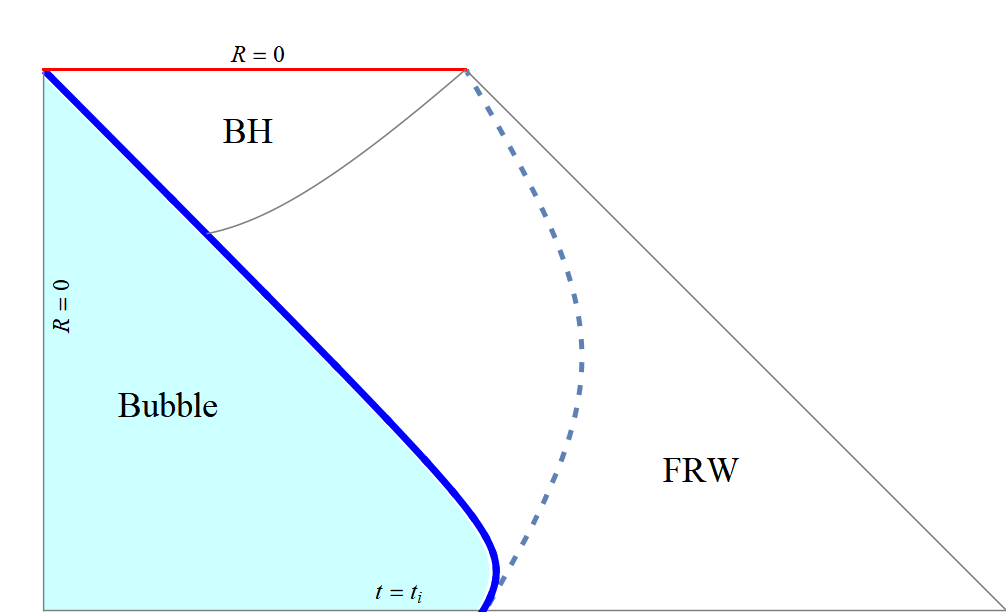
subcritical spacetime
subcritical BH mass
1512.01819 by Jaume Garriga, Alex Vilenkin and Jun Zhang (2016)
- bubble mass doesn't change much after bubble decouples from Hubble flow
- bubble doesn't grow much before it decouples from Hubble flow
supercritical
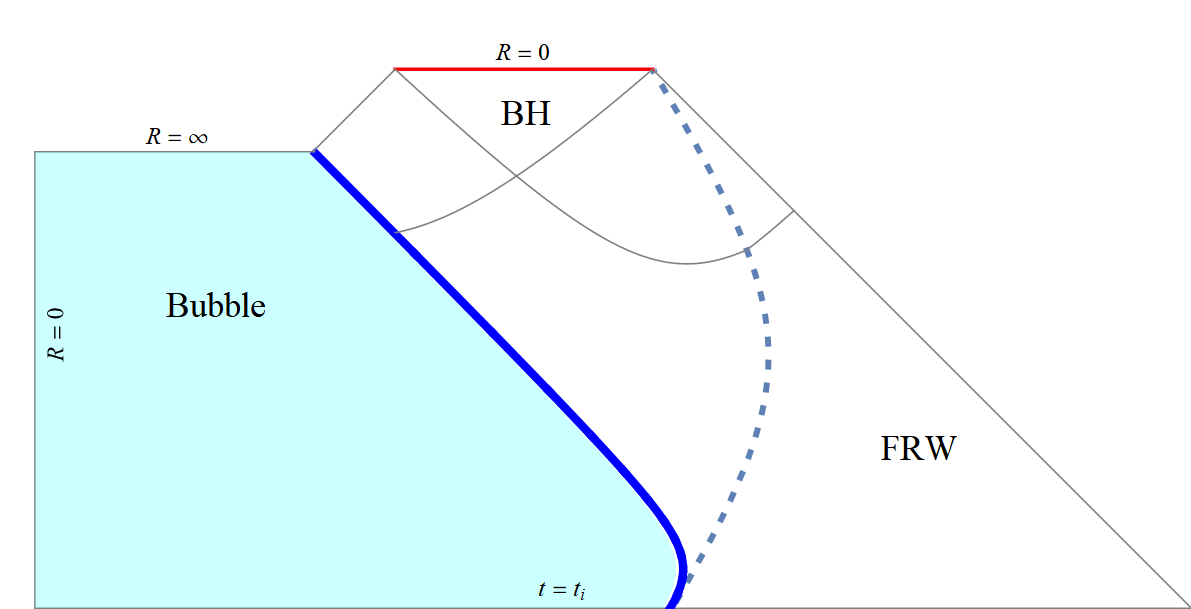
supercritical spacetime
supercritical BH mass
upper bound:
1612.03753 with Jaume Garriga and Alex Vilenkin (2016)
- results
- simulation setup
- observations
- dynamics & spacetime
metric
fluid
radiation
comoving gauge
BH apparent horizon
Misner-Sharp mass
boundary condition
outer: FRW solutions
inner: junction conditions
initial condition
...
- results
- simulation setup
- observations
- dynamics & spacetime
early stage of evolution of \(\rho \)
evolution of \(\rho \) after BH formation (subcritical)
evolution of \(\rho \) after BH formation (supercritical)
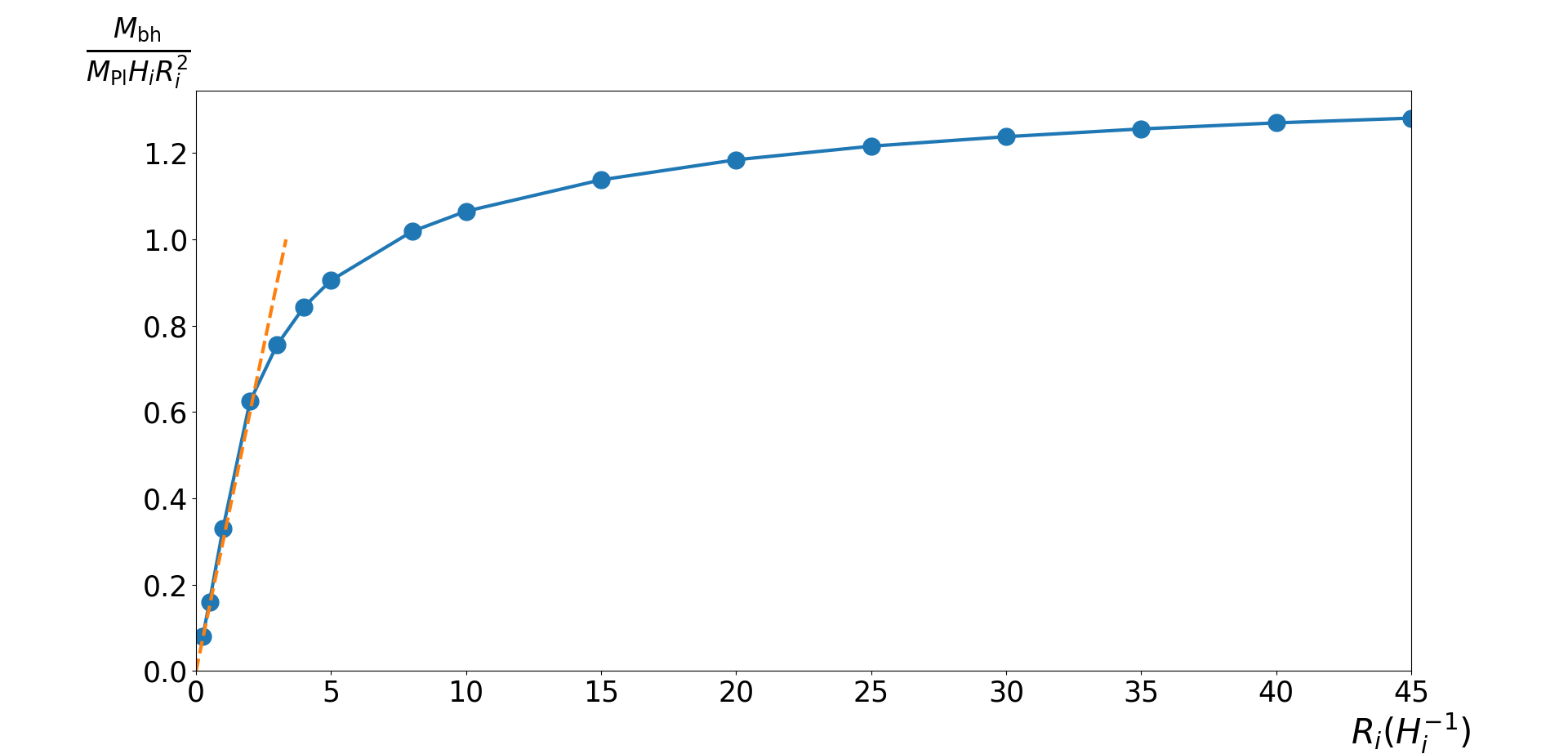
supercritical
subcritical
mass of BH formed by vacuum bubbles
where
bubble size distribution
number density
PBH mass function (fraction of CDM in PBH with mass ~ \(M\) )
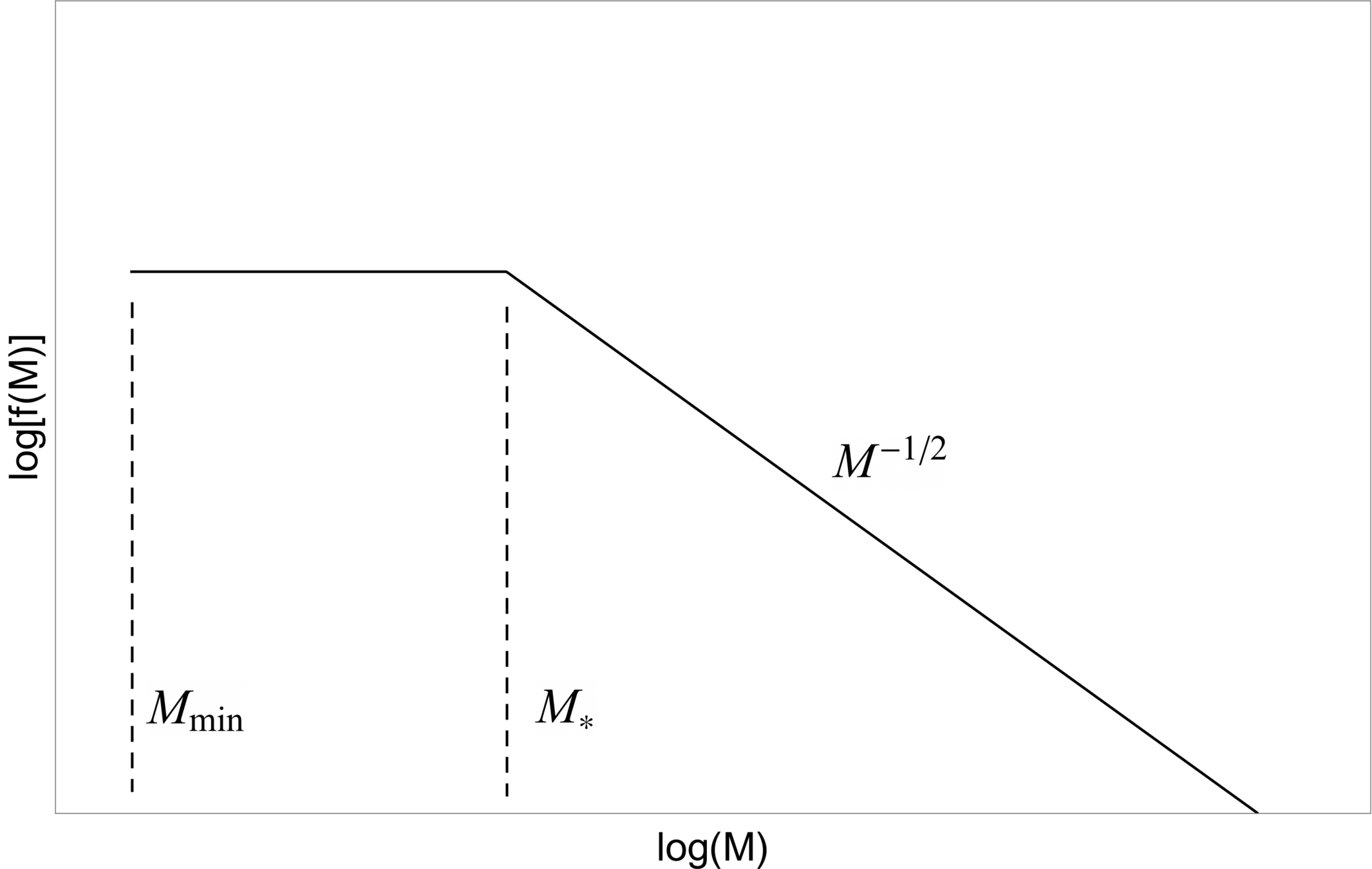
BH mass distribution
total fraction of CDM in PBH
- results
- simulation setup
- observations
- dynamics & spacetime
observational constraints on monochromatic PBH
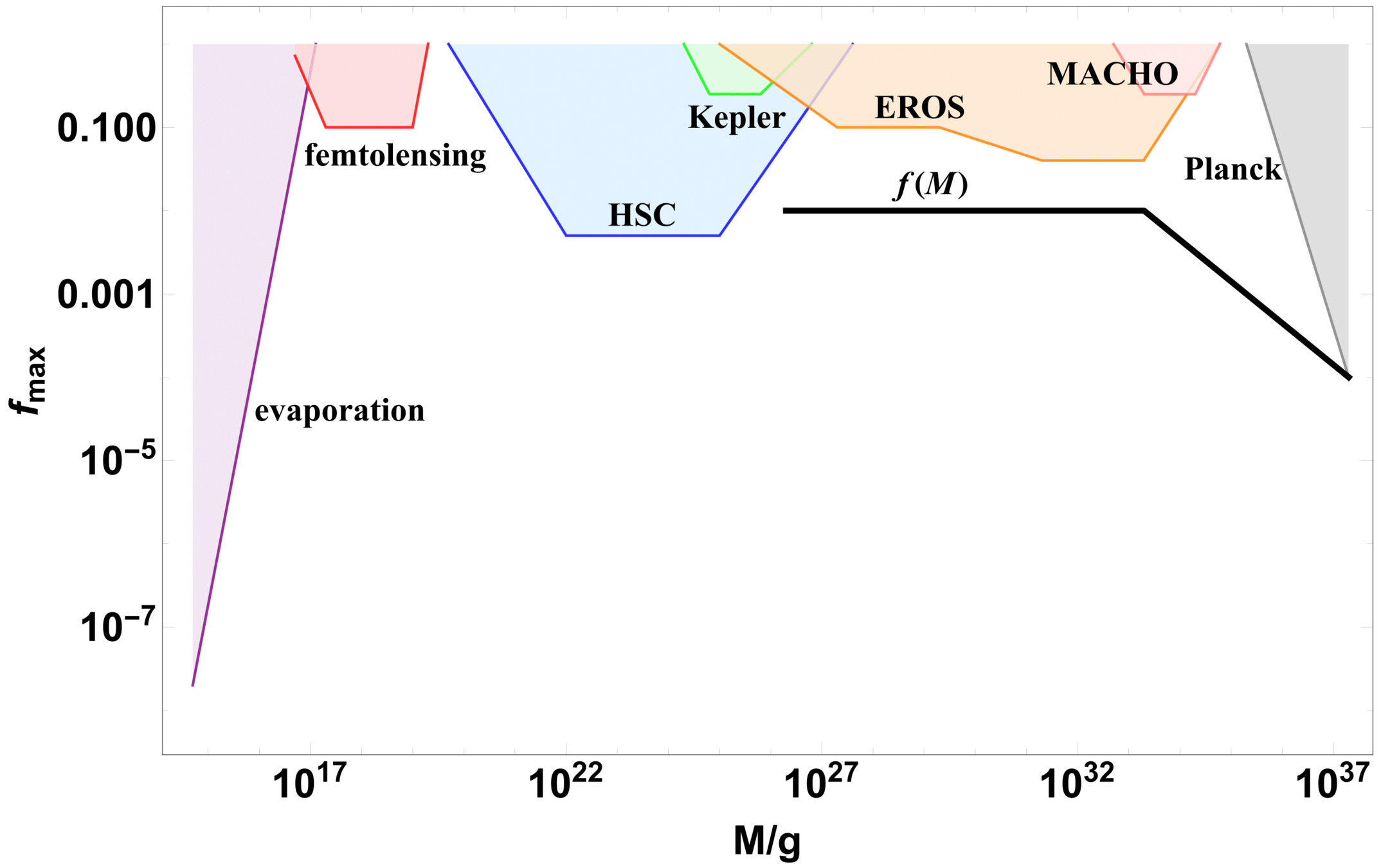
observational constraints \(\to\) our \(f_\text{PBH} \)
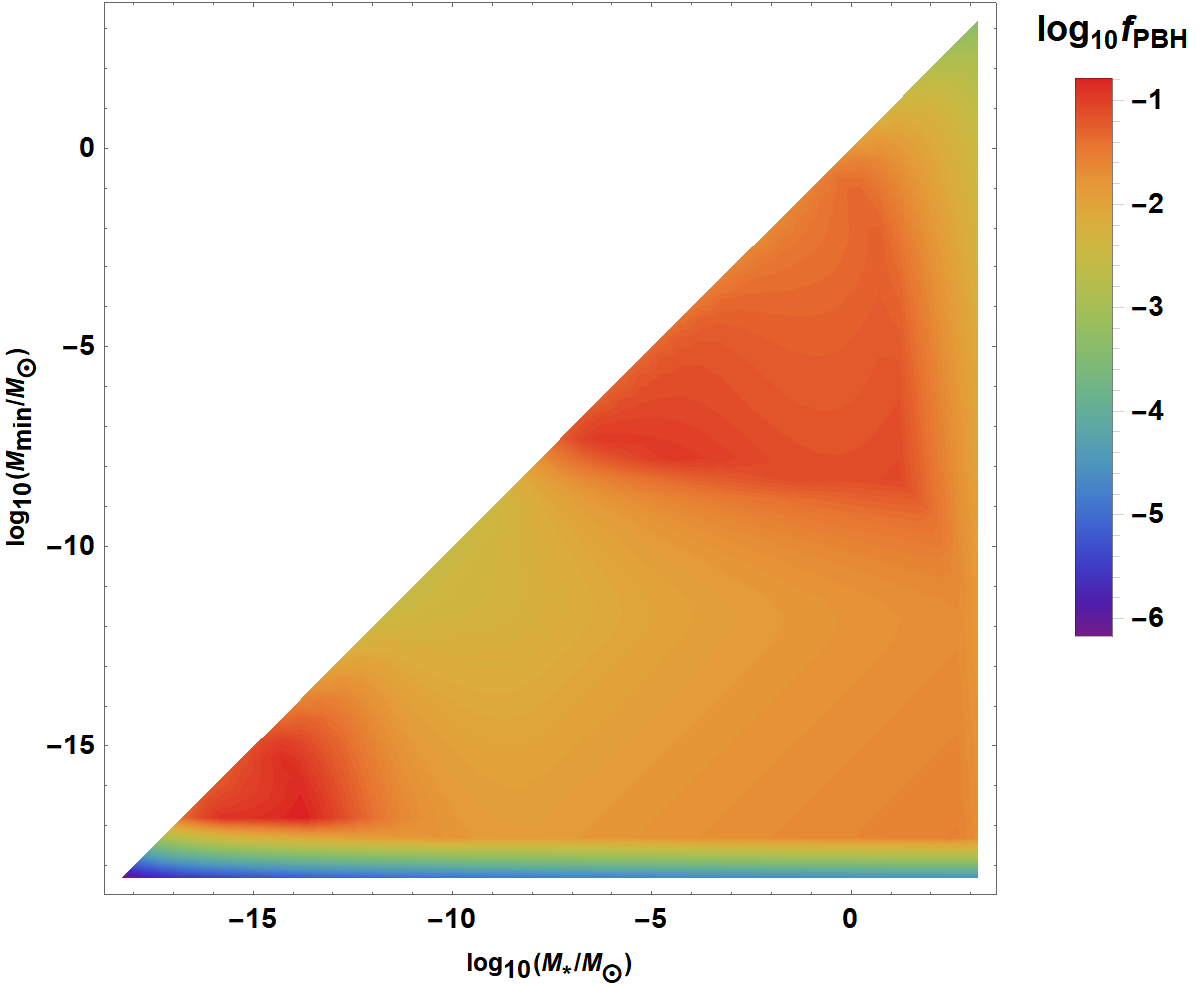
1705.05567 by Carr et al. (2017)
LIGO PBH?
\(f(M\sim 30\ M_\odot) \sim 10^{-3} \ \to \) merger rate for LIGO events
1603.08338 by Sasaki et al. (2016)

Conclusions
- a subcritical bubble collapses into an ordinary BH
- PBH formed by vacuum bubbles can have a distinct, wide range of mass spectrum
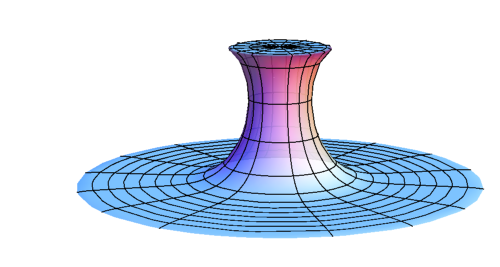
- a supercritical bubble has an inflating baby universe connected to our universe by a wormhole
- vacuum bubbles may nucleate during inflation, leading to the formation of BHs
- can make up 10% of DM and account for LIGO BHs