Huawei Research Talk

Henry Charlesworth, 31/08/23

Overview of this talk

Part I: Intrinsically Motivated Collective Motion - rich emergent collective dynamics from a simple, general decision making principle.

 

Part II: Solving Complex Dexterous Manipulation Tasks With Trajectory Optimisation and Deep RL

Part I: Intrinsically Motivated Collective Motion

"Intrinsically Motivated Collective Motion", Proceedings of the National Academy of Sciences 116 (31), 2019

Work carried out in 2016-2018 during PhD in the Centre for Complexity Science, University of Warwick

  • Layman's summary: "Taking all else to be equal, aim to keep your options open as much as possible".
  • Maximise the amount of control you have over the potential states that you are able to access in the future.
  • Rationale is that in an uncertain world this puts you in a position where you are best prepared to deal with the widest range of future scenarios you may end up encountering.
  • Quantative frameworks based on principle: "empowerment", "causal entropic forces".

"Future State Maximisation"

FSM - high-level examples

  • Owning a car vs. not owning a car
  • Going to university
  • Aiming to be healthy rather than sick
  • Aiming to be rich rather than poor
  • A concept introduced in the psychology literature to explain the incentive for behaviour which does not provide an immediate or obviously quantifiable benefit to the decision making agent, e.g. exploring novel environments, accumulating knowledge, play, etc.

Connection to "Intrinsic Motivation"

  • Can view FSM as a task-independent intrinsic motivation that encourages an agent to maximise the control over what it is able to do - hence "achieving mastery" over its environment
  • Concept of intrinsic motivation also started to appear a lot in RL literature:
    • Novelty/prediction based "intrinsic rewards" (count-based exploration, intrinsic curiosity module, random network distillation etc).
    • Skill-based intrinsic motivation (Diversity is all you Need, Variational Intrinsic Control, etc).
  • In principle, achieving "mastery" over your environment in terms of maximising the control you have over the future things that you can do should naturally lead to: developing re-usable skills, obtaining knowledge about how your environment works, etc.

Philosophy/ motivation behind FSM

How can FSM be useful?

  • If you accept this is often a sensible principle to follow, we might expect behaviours/heuristics to have evolved that make it seem like an organism is applying FSM.

Could be useful in explaining/understanding

certain animal behaviours.

  • Could also be used to generate behaviour for artificially intelligent agents.

Quantifying FSM

- "Causal Entropic Forces" (Approach based on thermodynamics)

 

- "Empowerment" (Information theoretic approach)

 

[1] "Empowerment: A Universal Agent-Centric Measure of Control" - Klyubin et al. 2005

[2] "Causal Entropic Forces" - Wissner-Gross and Freer, 2013

Empowerment

  • Formulates a measure of the amount of control an agent has over it's future in the language of information theory.
I(X;Y) = H(Y) - H(Y|X) = H(X) - H(X|Y)
  • Mutual information - measures how much information one variable tells you about the other:
  • Channel capacity:
C(X \to Y) = \max_{\mathbb{P}(x)} I(X;Y)

Empowerment

  • Consider an agent making decisions at discrete time steps. Let \( \mathcal{A} \) be the set of actions it can take, and \( \mathcal{S} \) be the set of possible states its "sensors" can be in.
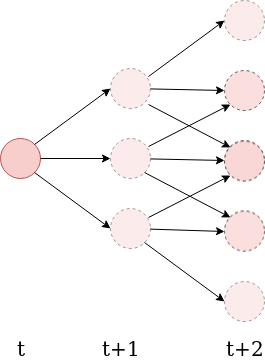
  • Define the n-step empowerment to be the channel capacity between the agent's available action sequences, and the possible states of its sensors at a later time \(t+n\):
\mathfrak{E}_n = C(A_t^n \to S_{t+n} | S_t) = \max_{\mathbb{P}(a_t^n)} I(A_t^n ; S_{t+n} | S_t)
  • Explicitly measures how much an agent's actions are capable of influencing the potential states its sensors can be in a later time.

Empowerment in Deterministic Environments

\mathfrak{E}_n = C(A_t^n \to S_{t+n} | S_t) = \max_{\mathbb{P}(a_t^n)} I(A_t^n ; S_{t+n} | S_t)
\mathfrak{E}_n = C(A_t^n \to S_{t+n} | S_t) = \max_{\mathbb{P}(a_t^n)} H(S_{t+n} | S_t) - H(S_{t+n} | A_n^t, S_t)

Deterministic environment implies:

H(S_{t+n} | A_n^t, S_t) = 0
\implies \mathfrak{E}_n = \max_{\mathbb{P}(a_t^n)} H(S_{t+n} | S_t)
\implies \mathfrak{E}_n = \log | \mathcal{S}_{t+n} |

Where            is the set of states that can be reached at time t + n

\mathcal{S}_{t+n}

"Variational Information Maximisation for Intrinsically Motivated Reinforcement Learning" - Mohamed and Rezende (2015)

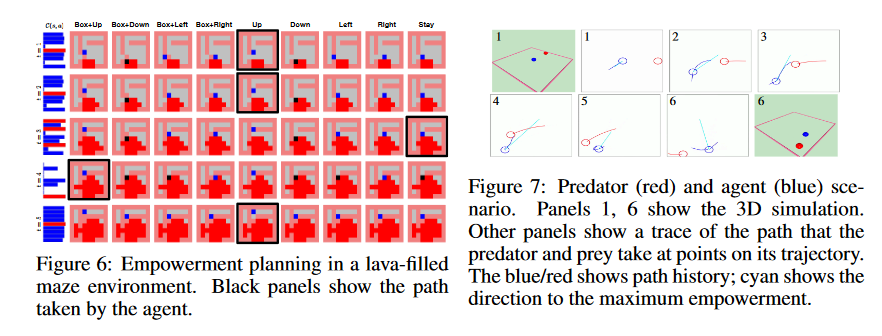
  • Use a variational bound on the mutual information to estimate the empowerment in examples with high-dimensional input spaces (images)
  • Use the empowerment as an intrinsic reward signal and apply reinforcement learning so that the agents learn to maximise their empowerment in some simple environments.

Ideas related to FSM in Reinforcement Learning

"Skew-fit: State-Covering Self-Supervised Reinforcement Learning" - Pong et al. 2019

  • Goal-conditioned RL where the aim is to explicitly maximise the coverage of the state space that can be reached - philosophy is very closely related to FSM.
  • Maximises an objective: \(I_{\pi}(S;G) = H(S) - H(S|G)\)

set diverse goals

Minimise uncertainty about final state

  • Aim for uniform exploration of state-space whilst learning a goal-conditioned policy that can be re-used for downstream tasks.
  • Equivalently: \(I_{\pi}(S;G) = H(G) - H(G|S)\)

Maximise coverage of state space

Learn how to achieve goals (minimise uncertainity about

Ideas related to FSM in Reinforcement Learning

given specified goal

which goal was specified given state reached)

Other Related RL Papers

  • "Efficient Exploration via State Marginal Matching" (2019) & "Provably Efficient Maximum Entropy Exploration" (2018) - Aim for  uniform exploration of state space.
  • "Variational Intrinsic Control" (2016), "Diversity is All you Need: Learning Skills without a Reward Function" (2018) & "Entropic Desired Dynamics for Intrinsic Control" (2021) - Aim to learn diverse skills (different skills visit different regions of state space).

How can FSM be useful in understanding collective motion?

"Intrinsically Motivated Collective Motion"

"Intrinsically Motivated Collective Motion" - Proceedings of the National Academy Of Sciences (PNAS), 2019 - https://www.pnas.org/content/116/31/15362 (Charlesworth and Turner)

What is Collective Motion?

  • Coordinated motion of many individuals all moving according to the same rules.
  • Occurs all over the place in nature at many different scales - flocks of birds, schools of fish, bacterial colonies, herds of sheep etc.

Previous Collective Motion Models

  • Often only include local interactions - do not account for long-ranged interactions, like vision.

 

 

​

 

 

  • Tend to lack low-level explanatory power - the models are essentially empirical in that they have things like co-alignment and cohesion hard-wired into them.

Example: Vicsek Model

T. Vicsek et al., Phys. Rev. Lett. 75, 1226 (1995).

R

\mathbf{v}_i(t+1) = \langle \mathbf{v}_k(t) \rangle_{|\mathbf{r}_k-\mathbf{r}_i| < R} + \eta(t)
\mathbf{r}_i(t+1) = \mathbf{r}_i(t) + \mathbf{v}_i(t)

Our approach

  • Based purely on a simple, low-level motivational principle - FSM.
  • No built in alignment/cohesive interactions - these things emerge spontaneously.

Our Model

  • Consider a group of circular agents equipped with simple visual sensors, moving around on an infinite 2D plane.

Possible Actions:

Visual State

Making a decision

Leads to robust collective motion!

  • Very highly ordered collective motion. (Average order parameter ~ 0.98)
  • Density is well regulated, flock is marginally opaque.
  • These properties are robust over variations in the model parameters!
\phi = \frac{1}{N} |\sum_i \mathbf{\hat{v}}_i |

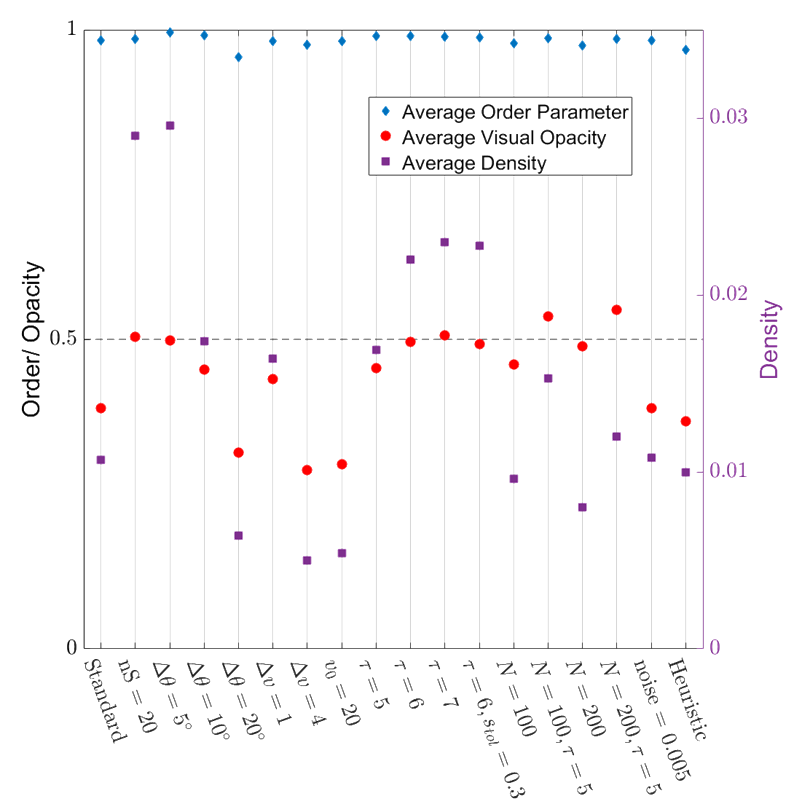
Order Parameter:

Also: Scale Free Correlations

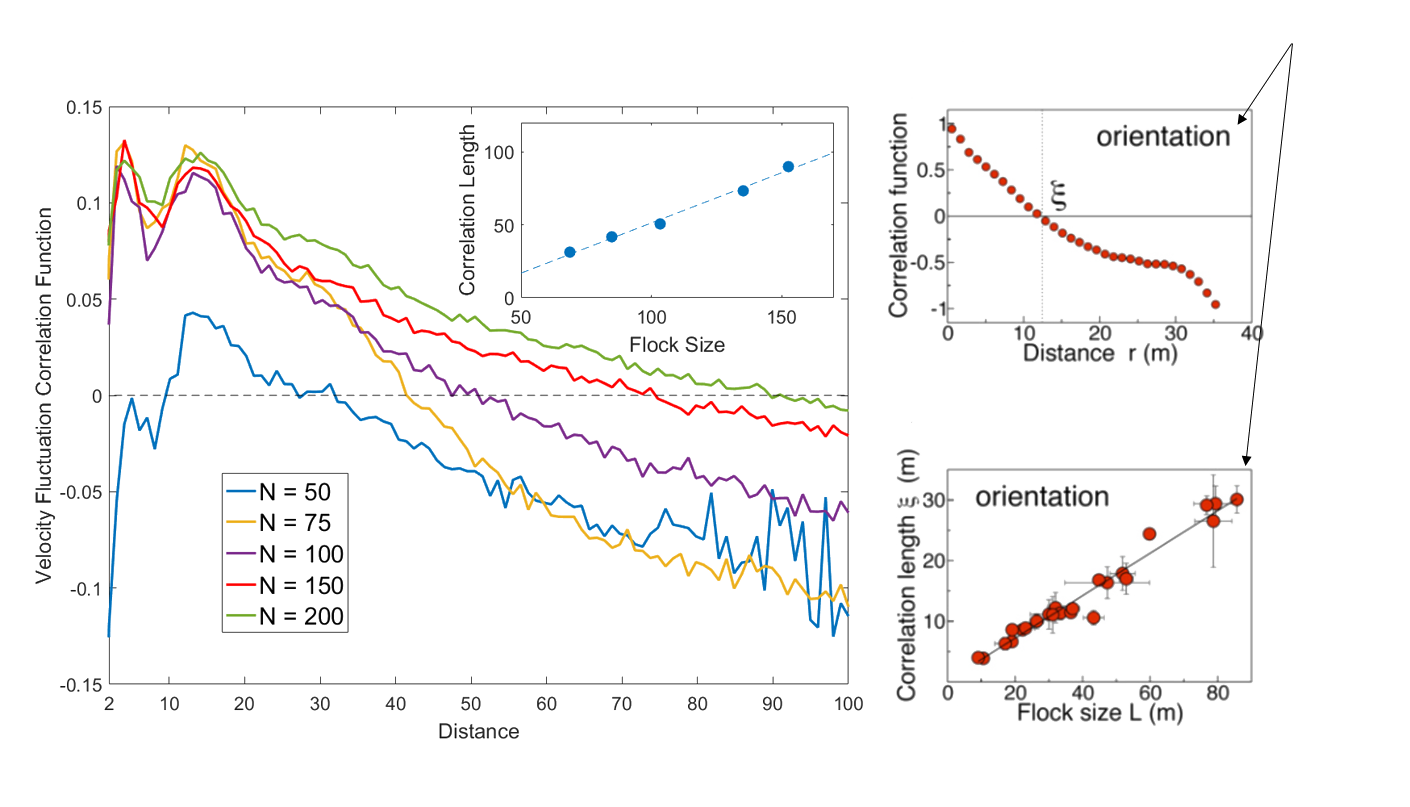
Real starling data (Cavagna et al. 2010)

Data from model

  • Scale free correlations mean an enhanced global response to environmental perturbations!
\mathbf{u_i} = \mathbf{v_i} - \langle \mathbf{v} \rangle

 correlation function:

C(r) = \langle \mathbf{u}_i(0) . \mathbf{u}_j(|r|) \rangle

velocity fluctuation

Result with a large flock - remarkably rich emergent dynamics

Conclusions

  • FSM is a general principle that could potentially be useful in a variety of different areas - indeed similar principles have found their way into RL in recent years.

 

  • A simple vision-based FSM model spontaneously leads to organised collective motion - collective motion emerges directly from the low-level principle.

Part II: Solving Complex Dexterous Manipulation Tasks With

"Solving Complex Dexterous Manipulation Tasks With Trajectory Optimisation and Deep Reinforcement Learning", Charlesworth & Montana, ICML (2021)

Trajectory Optimisation and Deep RL

Project website: https://dexterous-manipulation.github.io

Work carried out in 2019-2020 as a Postdoc with Professor Giovannia Montana at the University of Warwick

General Motivation

  • Develop more autonomous robots that can operate in unstructured and uncertain environments

Requires considerably more sophisticated manipulators than the typical "parallel jaw grippers" most robots in industry use today.

  • Human hand is the most versatile and sophisticated manipulator we know of!

Natural to build robotic hands that try and mimic the human hand and train them to perform complex manipulation tasks.

Why Dexterous Manipulation is Hard

  • Difficult to accurately model/optimise over Physics of complex, discontinuous contact patterns that occur between the hand and object(s).

Traditional robotics methods struggle. Motivates RL/ gradient-free trajectory optimisation.

  • High-dimensional state/action spaces. Tasks often require precise coordination of large number of joints in order to perform well.

Despite some successes, dexterous manipulation remains a significant challenge for RL (and other methods).

Background - Previous Work

  • Open AI Gym Environments (2018) - achieved partial success with "Hindsight Experience Replay".
  • Goal-conditioned RL - match orientation and/or position of target.

Background - Previous Work

  • "Learning Complex Dexterous Manipulation with Deep RL and Demonstrations" - 2018

Background - Previous Work

  • Open AI - Dactyl. Very large scale RL experiments trained purely in simulation. Transfer to real hardware with automatic domain randomisation.
  • Very impressive but required enormous amounts of compute (training Rubik's cube policy  involved 64 V100 GPUs and ~30,000 CPU cores for several months).

Our Contributions

1. Introduced "Dexterous Gym" - a suite of challenging extensions to the Gym manipulation environments.

2. Develop a gradient-free trajectory optimisation algorithm that can solve many of these tasks significantly more reliably than existing methods.

3. Demonstrated that the most challenging task, "Pen Spin", could be "solved" by combining examples generated by the trajectory optimisation method with off-policy deep RL.

Dexterous Gym

Trajectory Optimisation - MPPI (Model-Predictive Path Integral Control)

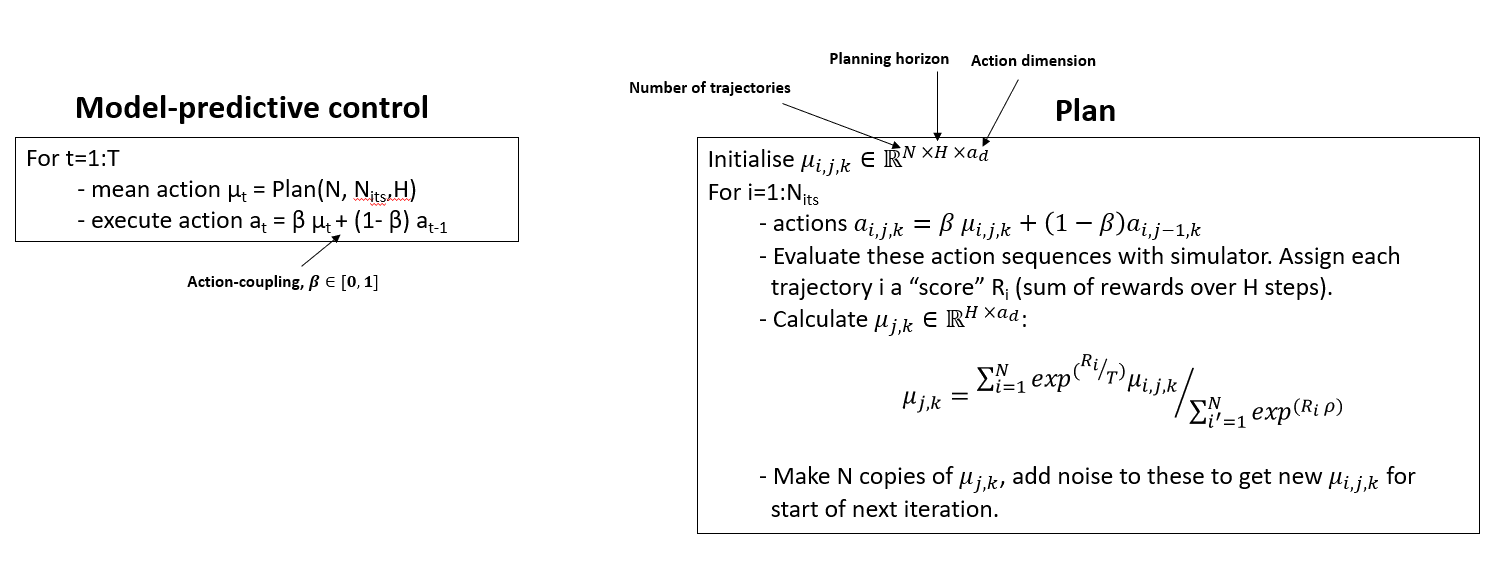
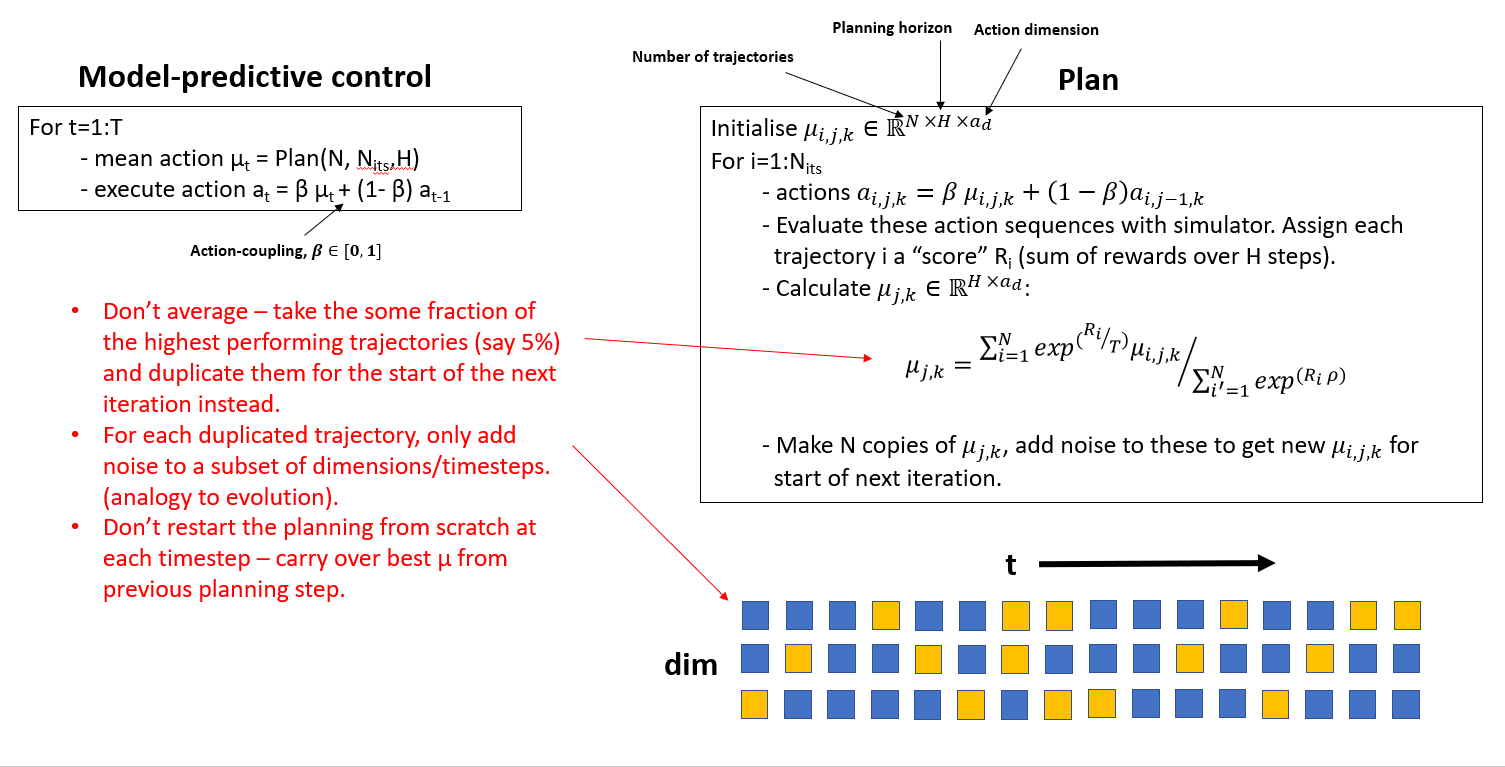
Trajectory Optimisation - Our Modifications (TOPDM)

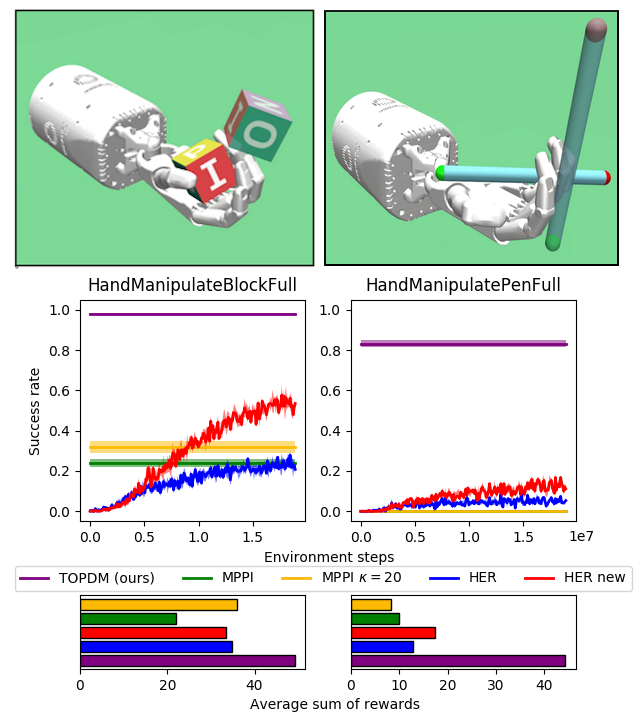
Results on Most Difficult OpenAI Gym Envs

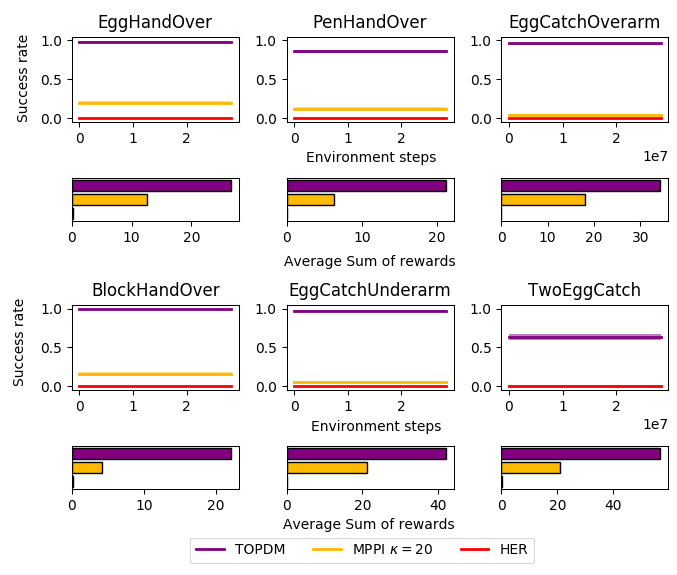
Results on Custom Environments (and Humanoid)

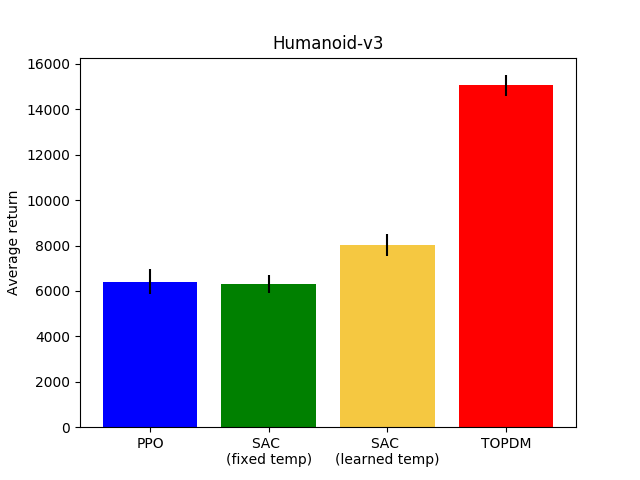
Combining TOPDM with Deep RL

  • Use example trajectories generated by TOPDM to "guide" the deep RL
  • Regularly re-load the simulator to states seen on the example trajectories. Gather short rollouts from there, train an off-policy RL algorithm (TD3) on these (and normal) trajectories.
  • Still fully autonomous - no expert/VR demonstrations required.
  • This approach works really well on the very challenging Pen Spin environment.
  • Build in the same action-smoothing "trick" used in MPPI into TD3 - makes a surprisingly big difference!

Combining TOPDM with Deep RL

TOPDM only

TD3 + TOPDM demos

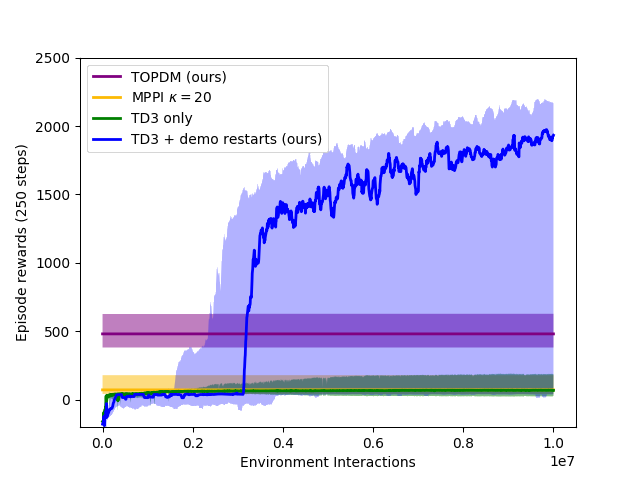
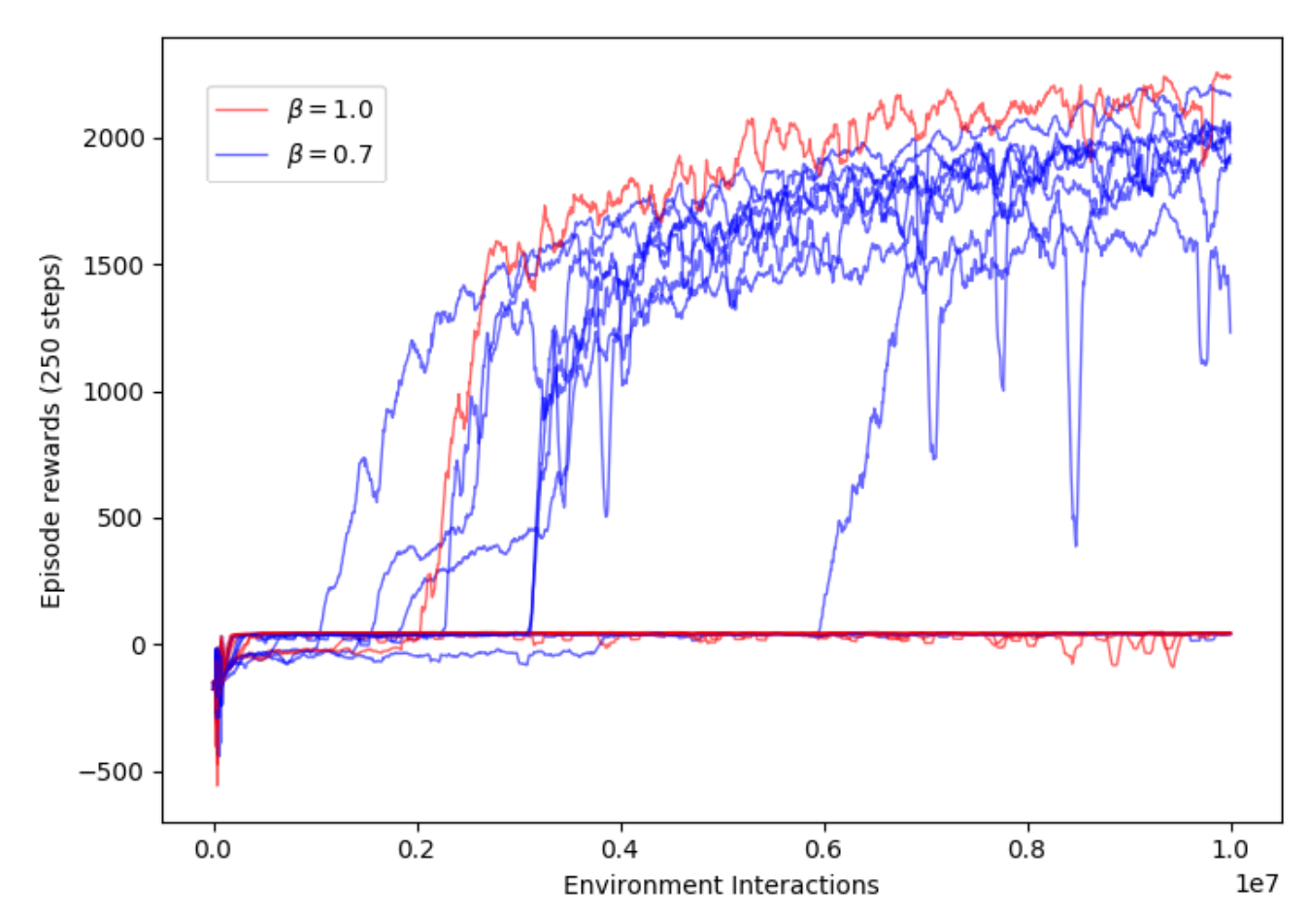
Conclusions

  • Relatively simple modifications to existing trajectory optimisation method leads to substantial improvement in performance on variety of dexterous manipulation tasks.
  • Can get best of both worlds (precise manipulation optimised over large time horizon) by combining examples generated with trajOpt into training an off-policy deep RL algorithm.

Extra Material (for questions, if relevant)

Continuous version of the model

  • Would be nice to not have to break the agents' visual fields into an arbitary number of sensors.
  • Calculating the mutual information (and hence empowerment) for continuous random variables is difficult - need to take a different approach.

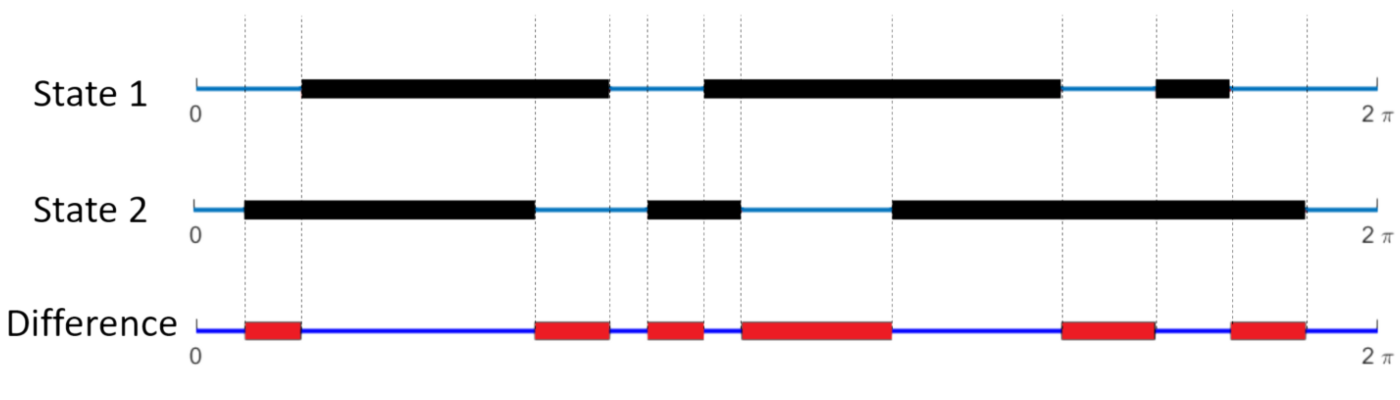
Continuous version of the model

  • Let \(f(\theta)\) to be 1 if angle \(\theta\) is occupied by the projection of another agent, or 0 otherwise
  • Define the "difference" between two visual states i and j to be:
d_{ij} = \frac{1}{2\pi} \int_0^{2\pi} [f_i(\theta)(1-f_j(\theta)) + f_j(\theta)(1-f_i(\theta))]d\theta
  • This is simply the fraction of the angular interval \([0, 2\pi)\) where they are different.

Continuous version of the model

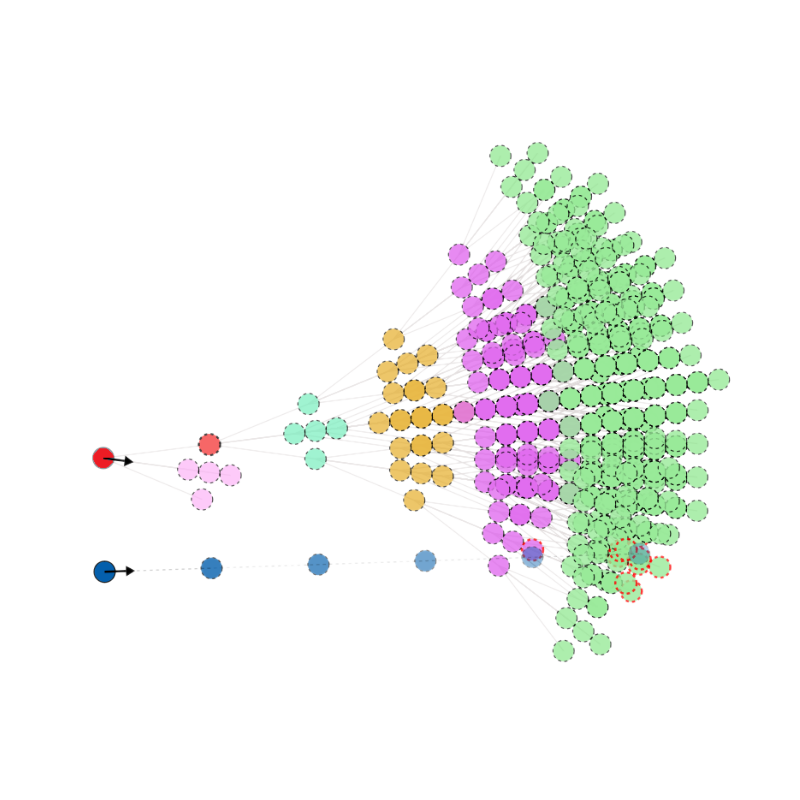
W_{\alpha} = \frac{1}{n_{\alpha}} \sum_{i=1}^{n_{\alpha}} \sum_{j=1}^{n_{\alpha}} d_{ij}

branch \(\alpha\)

For each initial move, \( \alpha \), define a weight as follows:

  • Rather than counting the number of distinct visual states on each branch, this weights every possible future state by its average difference between all other states on the same branch.
  • Underlying philosophy of FSM remains the same.

Can we do this without a full search of future

  • This algorithm is very computationally expensive. Can we generate a heuristic that acts to mimic this behaviour?
  • Train a neural network on trajectories generated by the FSM algorithm to learn which actions it takes, given only the currently available visual information (i.e. no modelling of future trajectories).

states?

Visualisation of the neural network

previous visual sensor input

current visual sensor input

hidden layers of neurons

output: predicted probability of action

non-linear activation function: f(Aw+b)

How does it do?

Some other things you can do

Making the swarm turn

Guiding the swarm to

follow a trajectory

A bit of fun: FSM at different scales:

Made with Slides.com