Analysis, Modelling and Protection of Online Private Data

Dr. Silvia Puglisi - me@hiro7.eu

The problem of web privacy

The problem of web privacy

In the early age of the Internet users enjoyed a large level of anonymity.

Users can't be anonymous online without a certain investment in time/skills/money.

The problem of web privacy

Traditional

Modern

Traditional

  • Market research
  • Census data
  • Public records
  • Surveys
  • Purchases
  • Loyalty programs
  • Clubs
  • Credit history
  • Insurances
  • Healthcare
  • Employers
  • Public web data
  • Social networks
  • Web activity
  • App statistics
  • Online shopping
  • Smart TV
  • Activity trackers
  • Cars
  • Smart watches
  • E-readers
  • ISPs

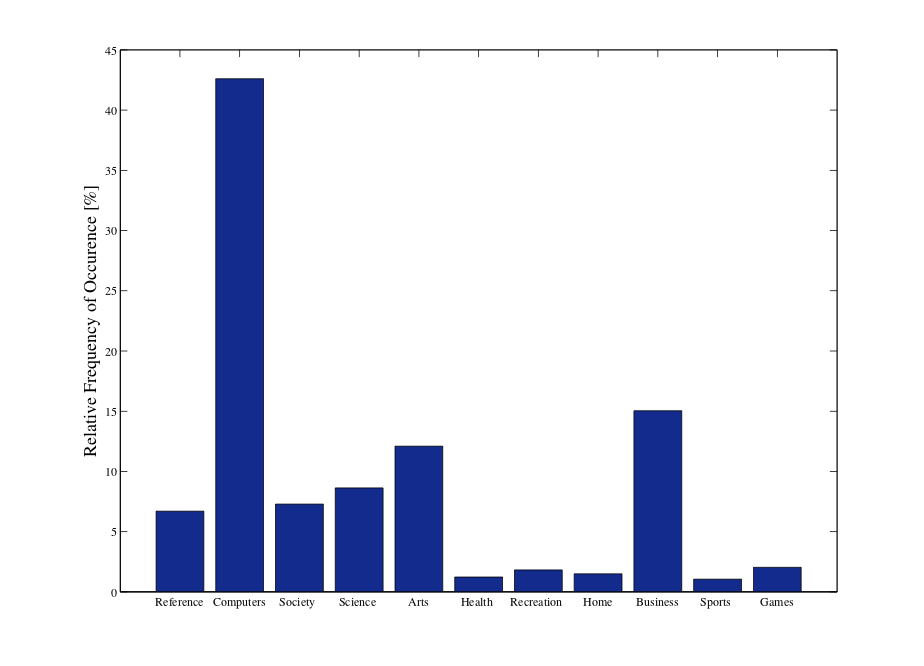
User Profiling

Trade-off between system utility and user privacy.

Classify privacy threats in social applications.

Mitigation possibilities.

p_m = (p_{m,1},...,p_{m,L})
pm=(pm,1,...,pm,L)p_m = (p_{m,1},...,p_{m,L})

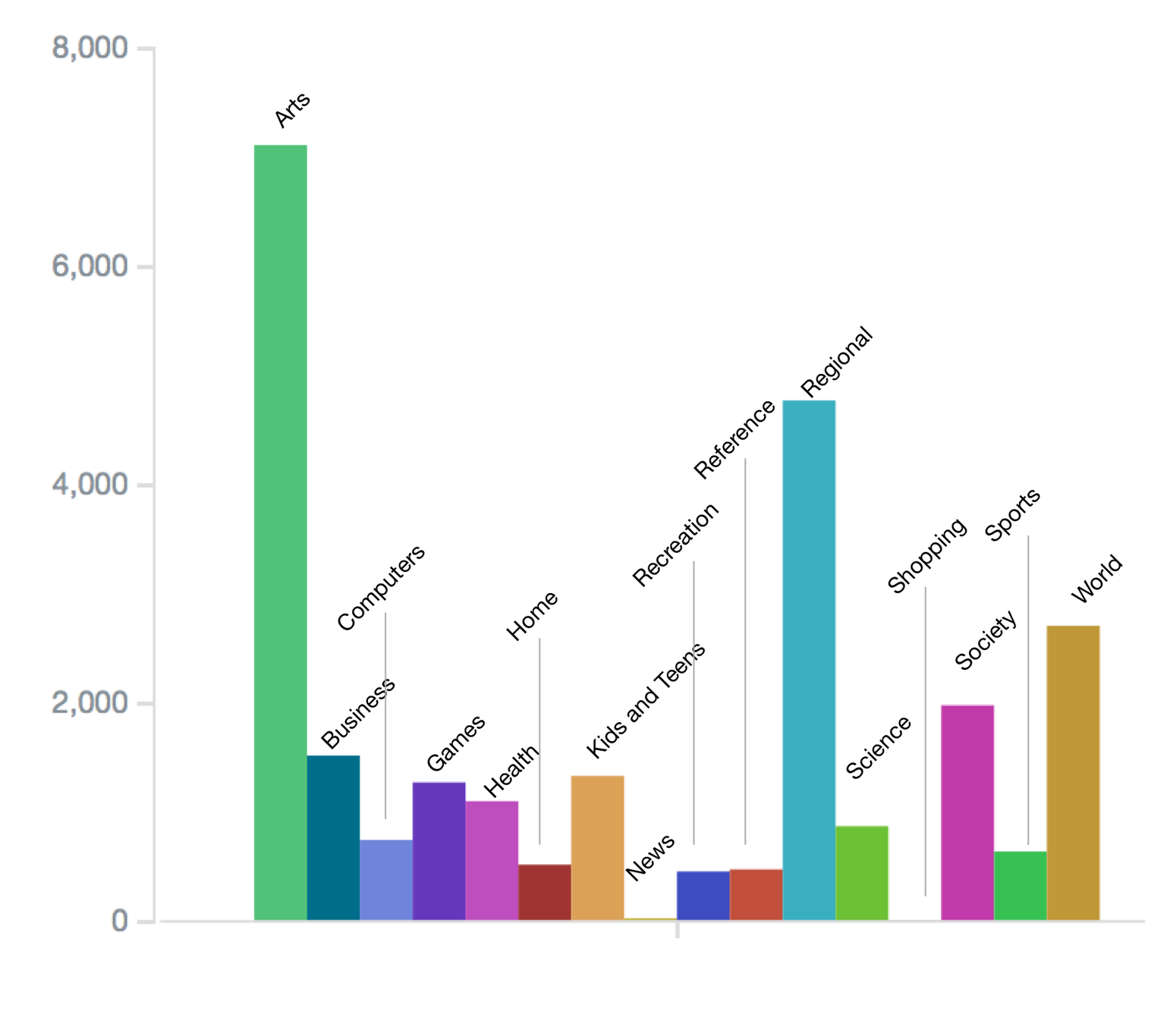
A metric of privacy

D(p \| u) = \log u - H(p) = - \sum{p_i \log{p_i}}
D(p∥u)=logu−H(p)=−∑pilogpiD(p \| u) = \log u - H(p) = - \sum{p_i \log{p_i}}
D(p\,\|\,q)=\sum p_i \log \frac{p_i}{q_i}
D(p∥q)=∑pilogpiqiD(p\,\|\,q)=\sum p_i \log \frac{p_i}{q_i}
R_0 = D(p_0\,\|\,q)
R0=D(p0∥q)R_0 = D(p_0\,\|\,q)
R = D(p\,\|\,q)
R=D(p∥q)R = D(p\,\|\,q)

T.M.Cover and J.A. Thomas. Elements of Information Theory. Wiley,New York, second edition, 2006.

Edwin T. Jaynes. On the rationale of maximum-entropy methods. Proceedings of the IEEE, 70(9):939–952, 1982.

JavierParra-Arnau, David Rebollo-Monedero, and Jordi Forne. Measuring the privacy of user profiles in personalized information systems. Future Generation Computer Systems, 33:53–63, 2014.

the Kullback–Leibler divergence is a measure of discrepancy between two probability distributions

The problem of web tracking

Tracking networks follow users' browsing habits while they surf the web.

 

The objective is collecting users' traces and surfing patterns.

 

These data constitute what is called the user's online footprint.

 

 

 

Objectives

  • Build a model of users' online footprints.
  • Measure how tracking network follow user browsing patterns.
  • Identify tracking networks from their network properties.
  • Measure the impact of tracking on user privacy.

 

 

 

Modelling the user profile

\hat{p} = (\hat{p}_1,\ldots, \hat{p}_L).
p^=(p^1,…,p^L).\hat{p} = (\hat{p}_1,\ldots, \hat{p}_L).
q =(q_1,\ldots, q_L)
q=(q1,…,qL)q =(q_1,\ldots, q_L)
p = (p_1,\ldots, p_L)
p=(p1,…,pL)p = (p_1,\ldots, p_L)

Partial user profile - what the tracker sees

Ad profile - what the tracker uses

Modelling users' activities

Users are connected to tracking networks through the pages they visit.

 

Tracker were categorised according to the average degree of the neighbourhood of each node.

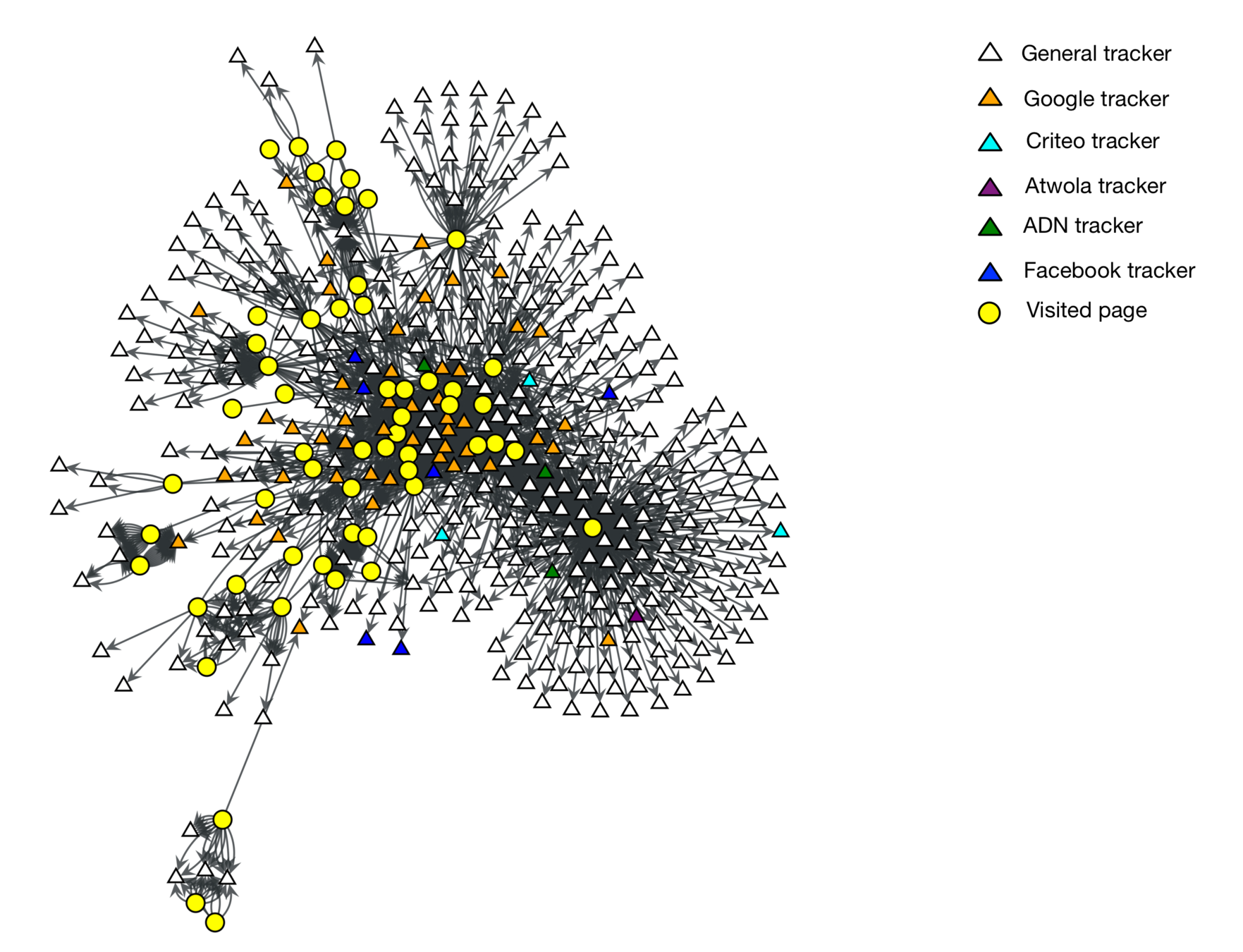
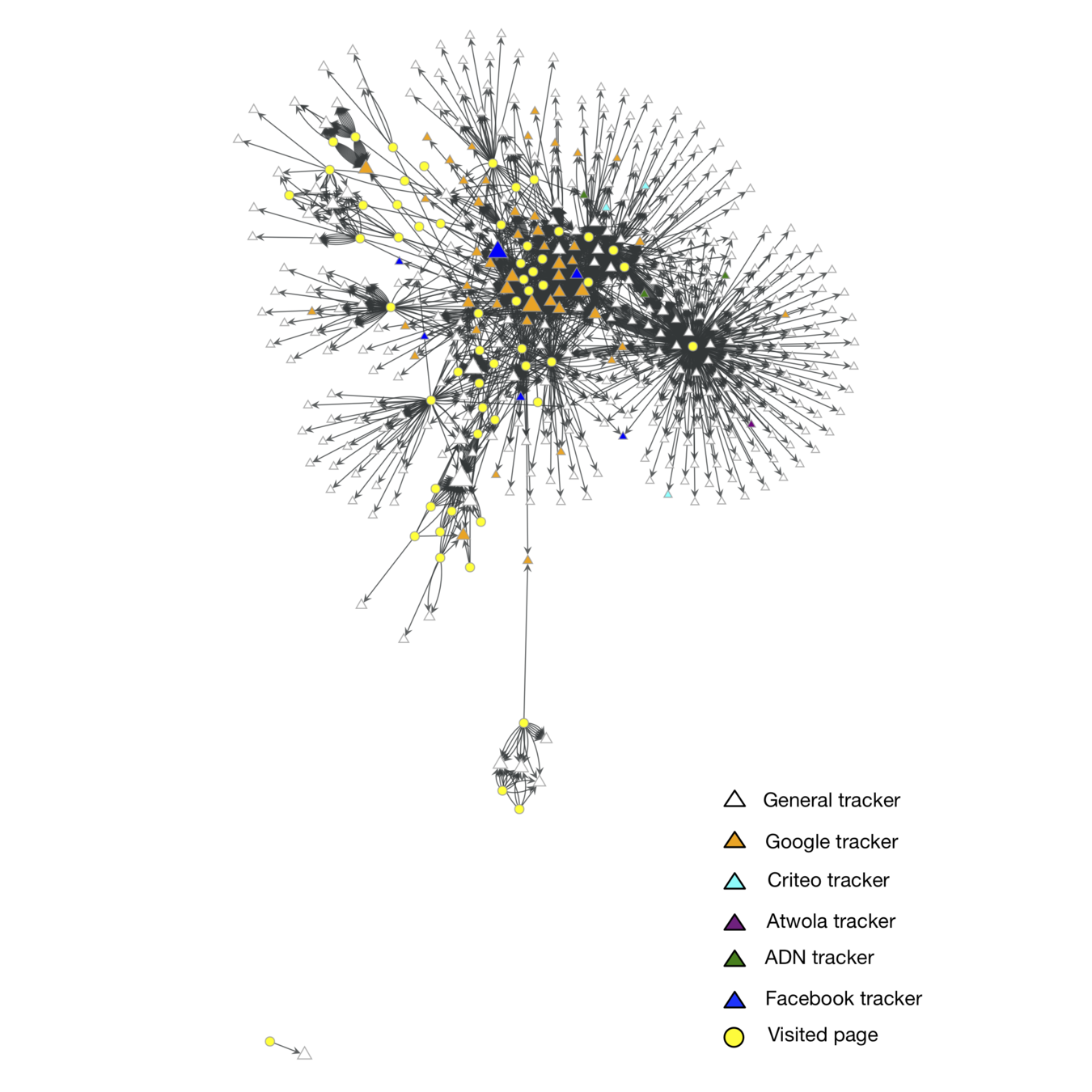
\langle k_{nn,i} \rangle= \frac{1}{| N(i) |} \sum_{j \in N(i) } {k_j}
⟨knn,i⟩=1∣N(i)∣∑j∈N(i)kj\langle k_{nn,i} \rangle= \frac{1}{| N(i) |} \sum_{j \in N(i) } {k_j}
Tracker domain avg k
tacoda.at.atwola.com 180
bcp.crwdcntrl.net 180
match.prod.bidr.io 180
glitter.services.disquis.com 180
ad.afy11.net 180
idsync.lcdn.com 180
mpp.vindicosuite.com 180
aka-cdn-ns.adtechus.com 180
client6.google.com
 180
i.simpli.fi
 180
ads.p161.net
 180
cms.quantserve.com
 180
ads.yahoocom
 129
graph.facebook.com
 118
ib.adnxs.com
 110
rs.gwallet.com
 108
bid.g.doubleclick.net
 98.333

for 1 user visiting 200 pages

Thank you

The only way to deal with an unfree world is to become so
absolutely free that your very existence is an act of rebellion.

Albert Camus

Made with Slides.com