Principle Component Analysis
講者:羅右鈞
日期:2016.10.27
地點:清華大學
Intuition
Let's say, we've collected some data with the following 4 attributes,
and aim to build model to perform some prediction tasks...
| height | dhuwur | altuera | teitei | |
|---|---|---|---|---|
| 0 | 159 | 4.77 | 5.247 | 62.5983 |
| 1 | 168 | 5.04 | 5.544 | 66.1416 |
| ... | ... | ... | ... | ... |
| N | 173 | 5.189 | 5.709 | 68.1101 |
Intuition
In fact ... all these attributes are same as "height" in different languages and be converted to different units
| height | dhuwur | altuera | teitei | |
|---|---|---|---|---|
| 0 | 159 | 4.77 | 5.247 | 62.5983 |
| 1 | 168 | 5.04 | 5.544 | 66.1416 |
| ... | ... | ... | ... | ... |
| N | 173 | 5.189 | 5.709 | 68.1101 |
- "tingg" = "dhuwur" = "altuera" = "teitei" = "height"
- In other words, all attributes are dependent on some quantity which aren't easy to be observed
- We can describe data by only 1 attribute!
Curse of dimensionality
As dimensionality grows: fewer observations per region.
(sparse data)


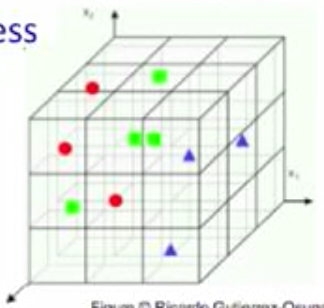
1-D: 3 regions
2-D: 9 regions
3-D: 27 regions
1000-D: GG
That's why dimension reduction is important
Dimension Reduction
Goal: represent instances with fewer variables
- try to preserve as much structure in the data as possible
- we want that structure is useful for specific tasks, e.g., regression, classification.
Feature selection
- pick a subset of the original dimensions X1, X2, X3, ..., Xd-1, Xd
- pick good class "predictors", e.g. information gain
Feature extraction
- Construct a new set of dimensions Ei = f(X1,X2...Xd)
- (linear) combinations of original dimensions
- PCA performs linearly combinations of orignal dimensions
PCA Ideas
Define a set of principle components
- 1st: direction of the greatest variance in data
- 2nd: perpendicular to 1st, greatest variance of what's left
First m << d components become m new dimensions
- You can then project your data with these new dimensions

Why greatest variance?
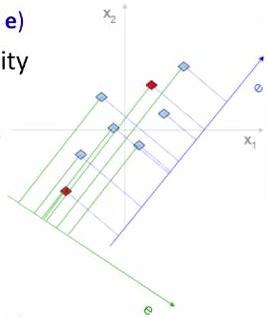
e preserves more structure than e
- distances between data points in original space remains in new space
How to compute Principle Components ?
- Center the data at zero (subtracted by mean)
- Compute covariance matrix Σ
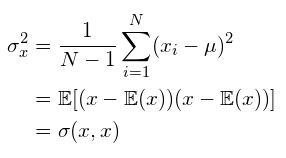
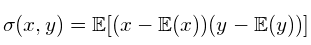
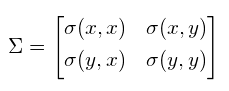
this computes sample variance (N-1 to estimate unbiased variance)
- Normalize(standardize) covariance matrix [-inf, inf] to [-1, 1], we get Pearson correlation coefficient (correlation matrix)
- The correlation coefficient between two random variables x and y are defined as:
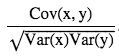
if computing population variance, you can just divide by N
How to compute Principle Components (cont.)?
Interesting observation:
- multiply a vector by covariance matrix
x1
x2
e1
e2
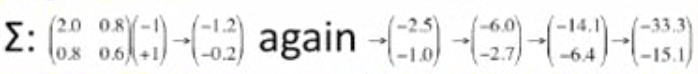
slope: 0.400 0.450 0.454... 0.454...
Want vectors e which aren't rotated: Σe = λe
- principle components = eigenvectors with largest eigenvalues
In fact ... (see Read more for proof)
- eigenvector = direction of greatest variance
- eigenvalue = variance along eigenvector
(-1.0, +1.0)
(-1.2, -0.2)
(-14.1 -6.4)
(-33.3 -15.1)
(-6.0, -2.7)

Finally, project original data points to new dimesions by dot product
Read more
- Principle Component Analysis (Main reference)
- A geometric interpretation of the covariance matrix
- Khanacademy: Introduction to eigenvalues and eigenvectors
- Quara: Why does repeatedly multiplying a vector by a square matrix cause the vector to converge on or along the matrix's eigenvector?
- Quara: What do eigenvalues and eigenvectors represent intuitively?
L1 sentence
Encoder
L1 encoded vector
L2 Decoder
L2
sentence
Encoder
L2
encoded vector
L1 Decoder
Inference
Training