Field-level inference from
galaxy redshift surveys
Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
2026/01/15

Field-level inference of primordial
non-Gaussianity from DESI:
Validation on simulations
Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
2026/01/15

Field-level inference of primordial non-Gaussianity from galaxy redshift surveys
Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
2025/11/27


Field-level inference of primordial non-Gaussianity from galaxy redshift surveys
Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
CoBALt, 2025/06/30



Field-level inference of primordial non-Gaussianity from galaxy redshift surveys
Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
CoBALt, 2025/06/30



Optimal extraction of primordial non-Gaussian signal from galaxy redshift survey
Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
Sesto, 2025/07/17


Field-level analysis of primordial non-Gaussianity with DESI tracers

Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
PNG Meeting, 2025/06/18

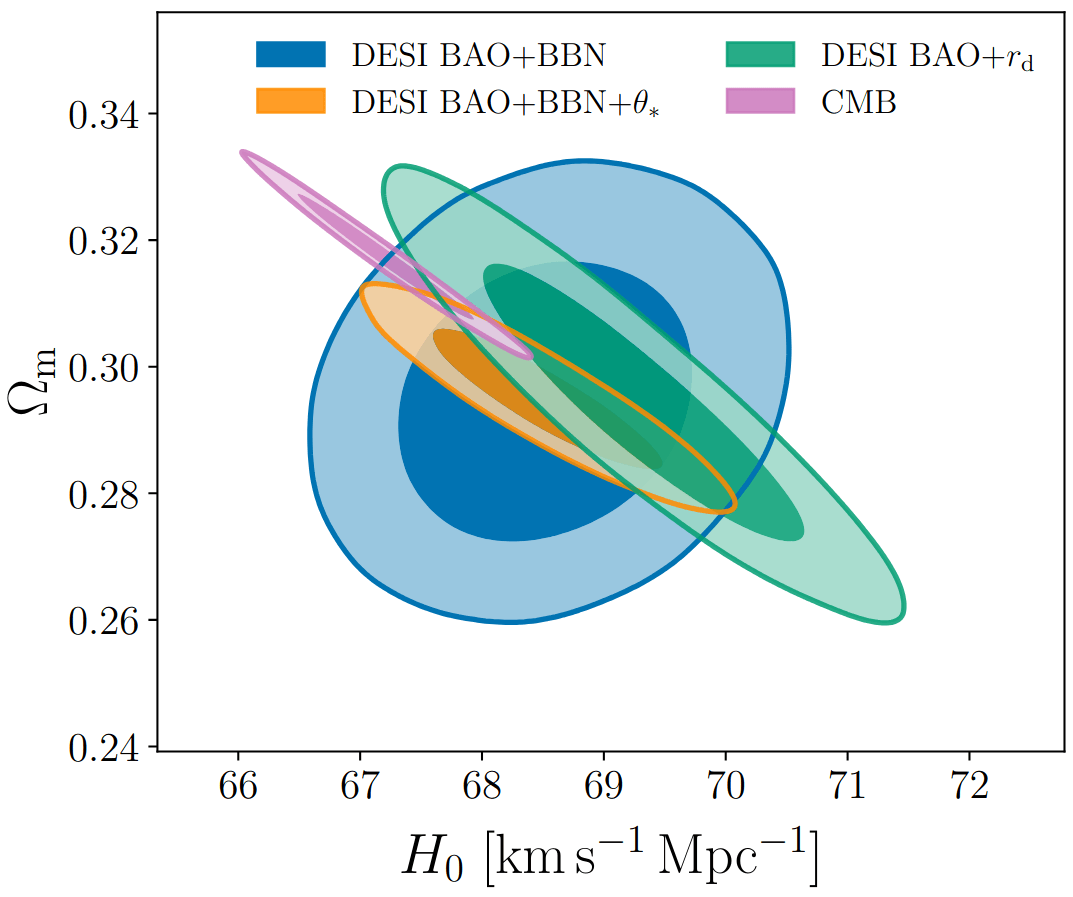
The universe recipe (so far)
$$\frac{H}{H_0} = \sqrt{\Omega_r + \Omega_b + \Omega_c+ \Omega_\kappa + \Omega_\Lambda}$$
instantaneous expansion rate
energy content
Cosmological principle + Einstein equation
+ Inflation
\(\delta_L \sim \mathcal G(0, \mathcal P)\)
\(\sigma_8:= \sigma[\delta_L * \boldsymbol 1_{r \leq 8}]\)
initial field
primordial power spectrum
std. of fluctuations smoothed at \(8 \text{ Mpc}/h\)

Cosmological inference
\(\Omega := \{ \Omega_m, \Omega_\Lambda, H_0, \sigma_8, f_\mathrm{NL},...\}\)
inference
\(P\)

\(\Omega\)
\(\delta_L\)
\(\delta_g\)

Cosmological inference
\(\Omega := \{ \Omega_m, \Omega_\Lambda, H_0, \sigma_8, f_\mathrm{NL},...\}\)
\(\Omega\)
\(\delta_L\)
\(\delta_g\)


inference

Cosmological inference
inference
\(\Omega := \{ \Omega_m, \Omega_\Lambda, H_0, \sigma_8, f_\mathrm{NL},...\}\)



\(\Omega\)
\(\delta_L\)
\(\delta_g\)
\(P\)

Cosmological inference
\(\Omega := \{ \Omega_m, \Omega_\Lambda, H_0, \sigma_8, f_\mathrm{NL},...\}\)
\(\Omega\)
\(\delta_L\)
\(\delta_g\)


inference


\(128^3\) PM on 8GPU:
4h MCLMC vs. \(\geq\) 80h HMC
Fast & differentiable model with

Cosmological inference
\(\Omega := \{ \Omega_m, \Omega_\Lambda, H_0, \sigma_8, f_\mathrm{NL},...\}\)
inference

\(P\)


\(\Omega\)
\(\delta_L\)
\(\delta_g\)



Cosmological inference
\(\Omega := \{ \Omega_m, \Omega_\Lambda, H_0, \sigma_8, f_\mathrm{NL},...\}\)
\(\Omega\)
\(\delta_L\)
\(\delta_g\)


inference



Field-level inference
Summary stat inference
\(\Omega\)
\(s\)
\(\delta_g\)
\(\Omega\)
\(\delta_L\)
\(s\)
marginalize
condition
marginalize
\(\Omega\)
\(s\)
\(\delta_g\)
\(\Omega\)
\(\delta_L\)
condition
Two approaches to cosmological inference
Cosmo model
\(\mathrm{p}(\Omega,s)\)
\(\mathrm{p}(\Omega \mid s)\)
\(\Omega\)
\(\delta_g\)
\(\mathrm{p}(\Omega,\delta_L,\delta_g, s)= \mathrm{p}(s \mid \delta_g) \, \mathrm{p}(\delta_g \mid \Omega,\delta_L)\, \mathrm{p}(\delta_L \mid \Omega)\, \mathrm{p}(\Omega)\)
\(\mathrm{p}(\Omega,\delta_L \mid \delta_g)\)
\(\mathrm{p}(\Omega \mid \delta_g)\)
\(\delta_g\)
\(\Omega\)
\(\delta_L\)
\(s\)
Two approaches to cosmological inference
Cosmo model
Problem:
- \(s\) is too simple \(\implies\) lossy compression
- \(s\) is too complex \(\implies\) intractable marginalization
The Problem:
- high-dimensional integral $$\mathrm{p}(\Omega \mid \delta_g) = \int \mathrm{p}(\Omega, \delta_L \mid \delta_g) \;\mathrm d \delta_L$$
- To probe scales of \(15\ \mathrm{Mpc}/h\) in DESI volume, \(\operatorname{dim}(\delta_L) \simeq 1024^3\)
The Promise:
- "lossless" explicit inference
Field-level inference
Summary stat inference
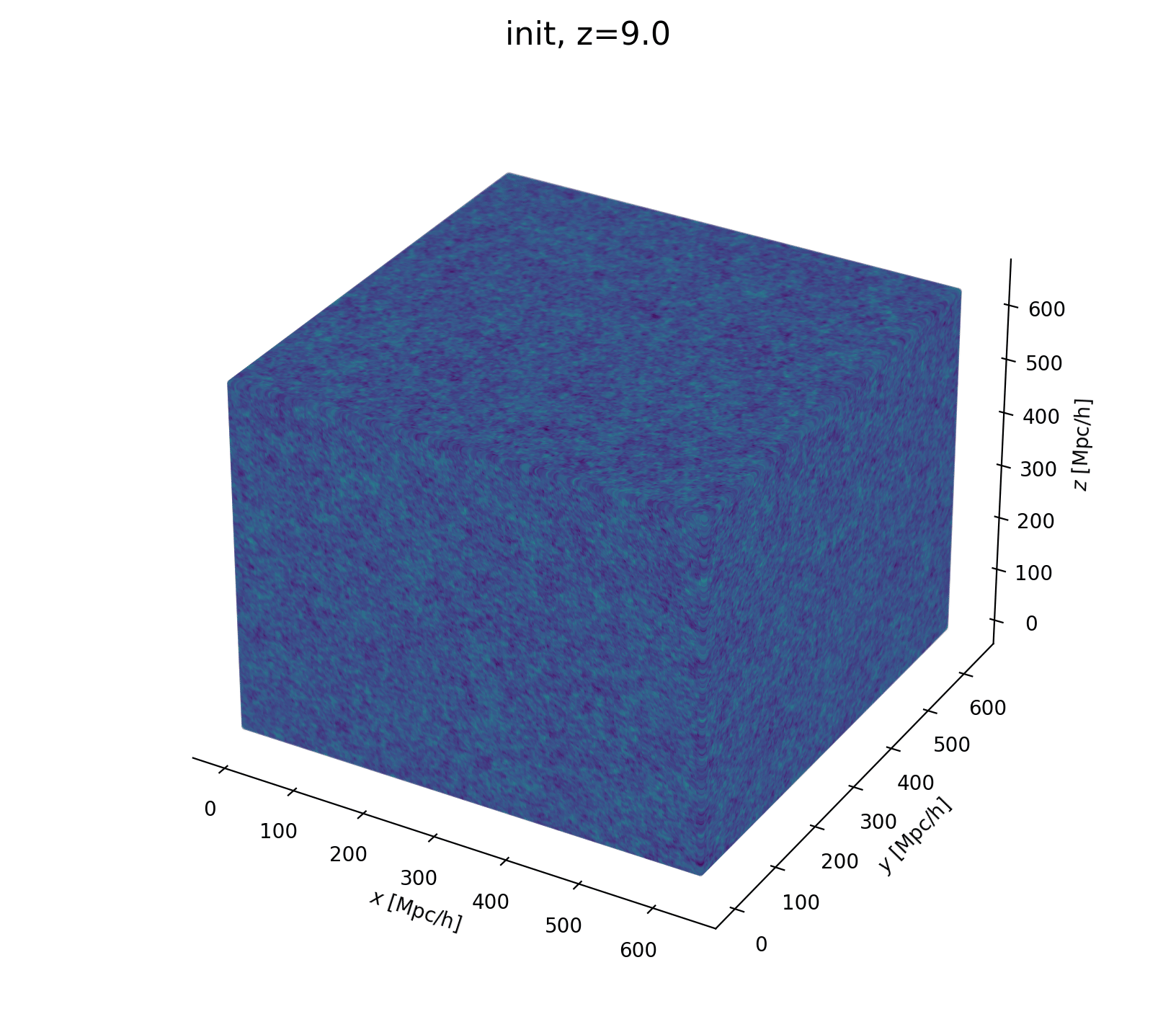
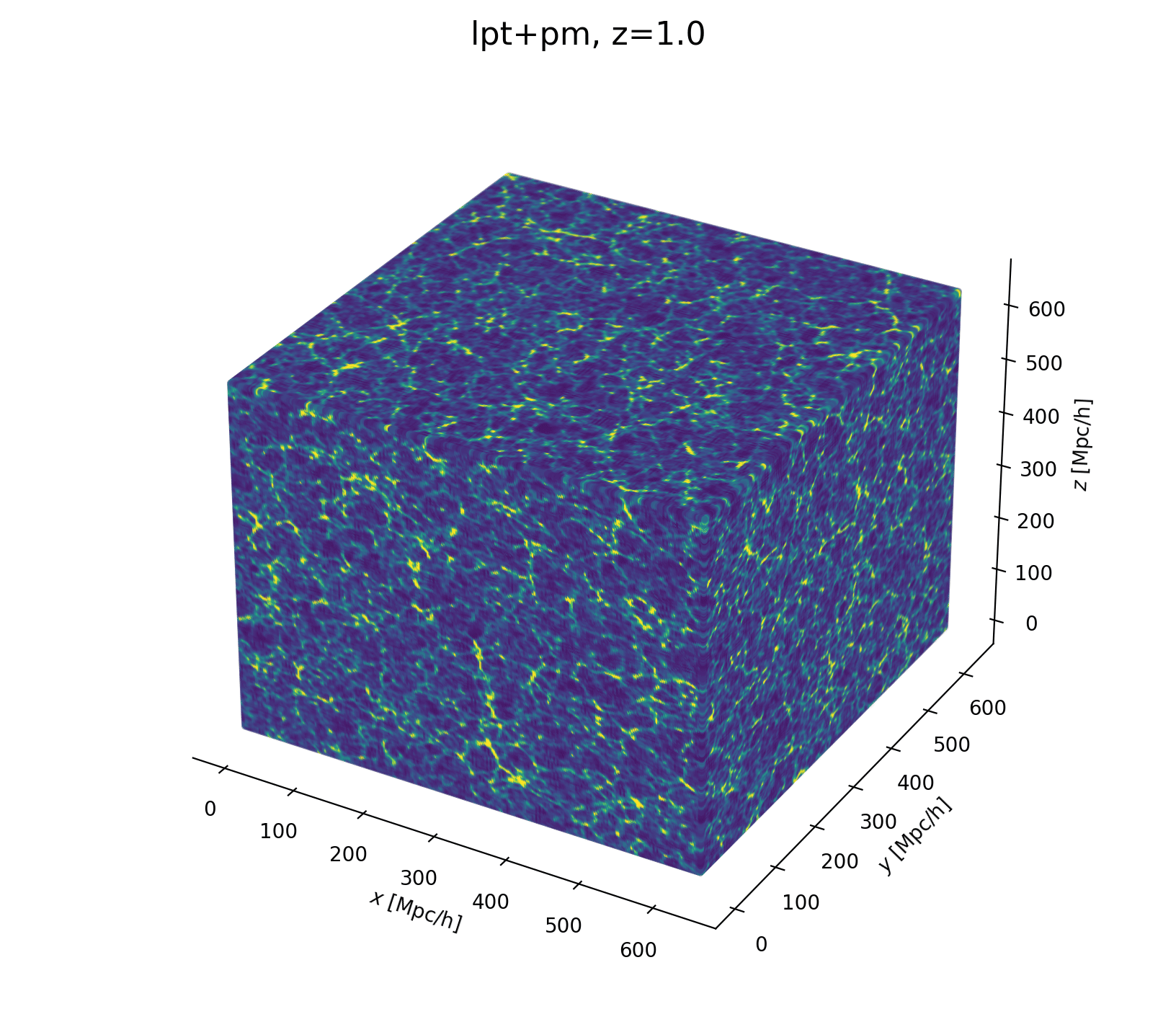
What it looks like
Inferring jointly cosmology, bias parameters, and initial matter field allows full universe history reconstruction


-
Prior on
- Cosmology \(\Omega\)
- Initial field \(\delta_L\)
- EFT parameters
(Dark matter-galaxy connection)
-
LSS formation: 2LPT or PM
(BullFrog or FastPM) - Apply galaxy bias
- Redshift-Space Distortions
- Observational noise
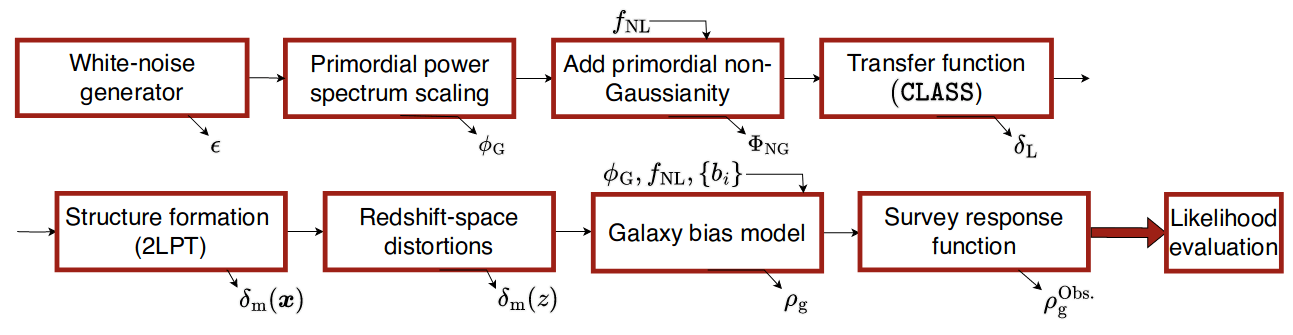
Field-Level Modeling
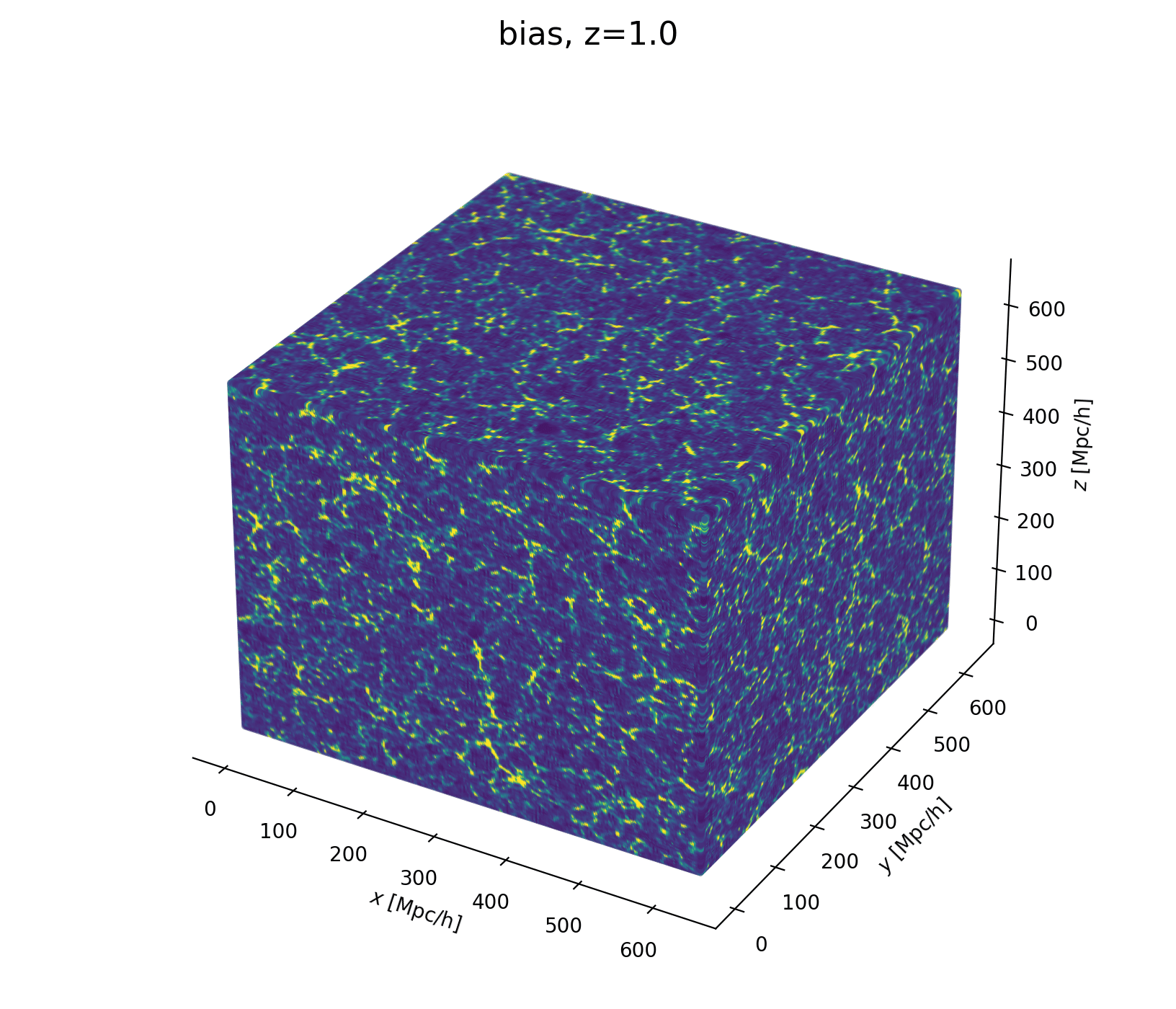
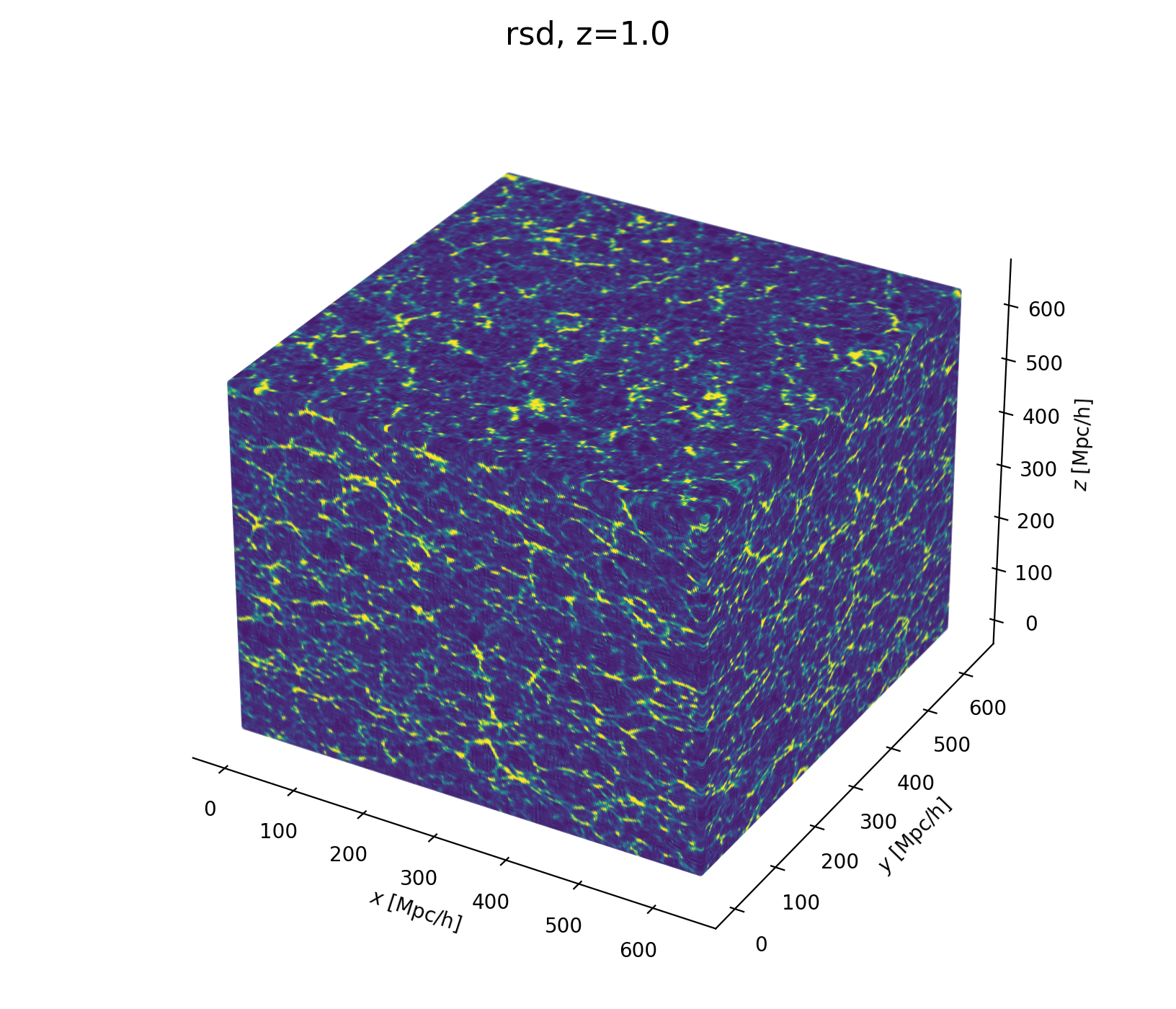
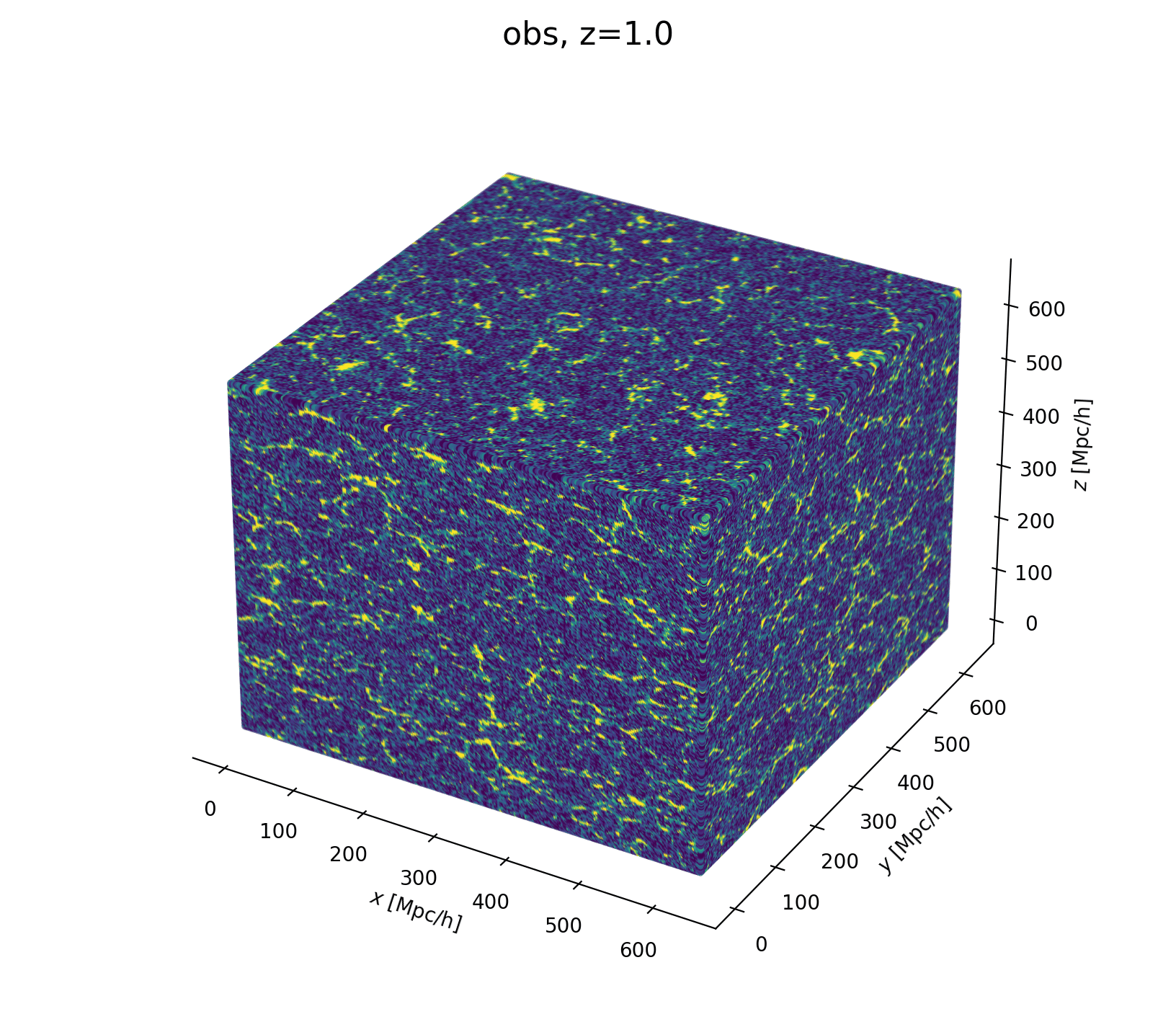
Fast and differentiable model thanks to (\(\texttt{NumPyro}\) and \(\texttt{JaxPM}\))

-
Sample initial conditions
-
LSS formation: 2LPT or N-body PM
(BullFrog or FastPM) lightcone - EFT-based galaxy bias
- Redshift-Space Distortions
- Observational noise and systematics
Field-Level Modeling and Inference





Fast and differentiable model with

+ field-level preconditioning = \(128^3\) PM inference in 4h on a single GPU node
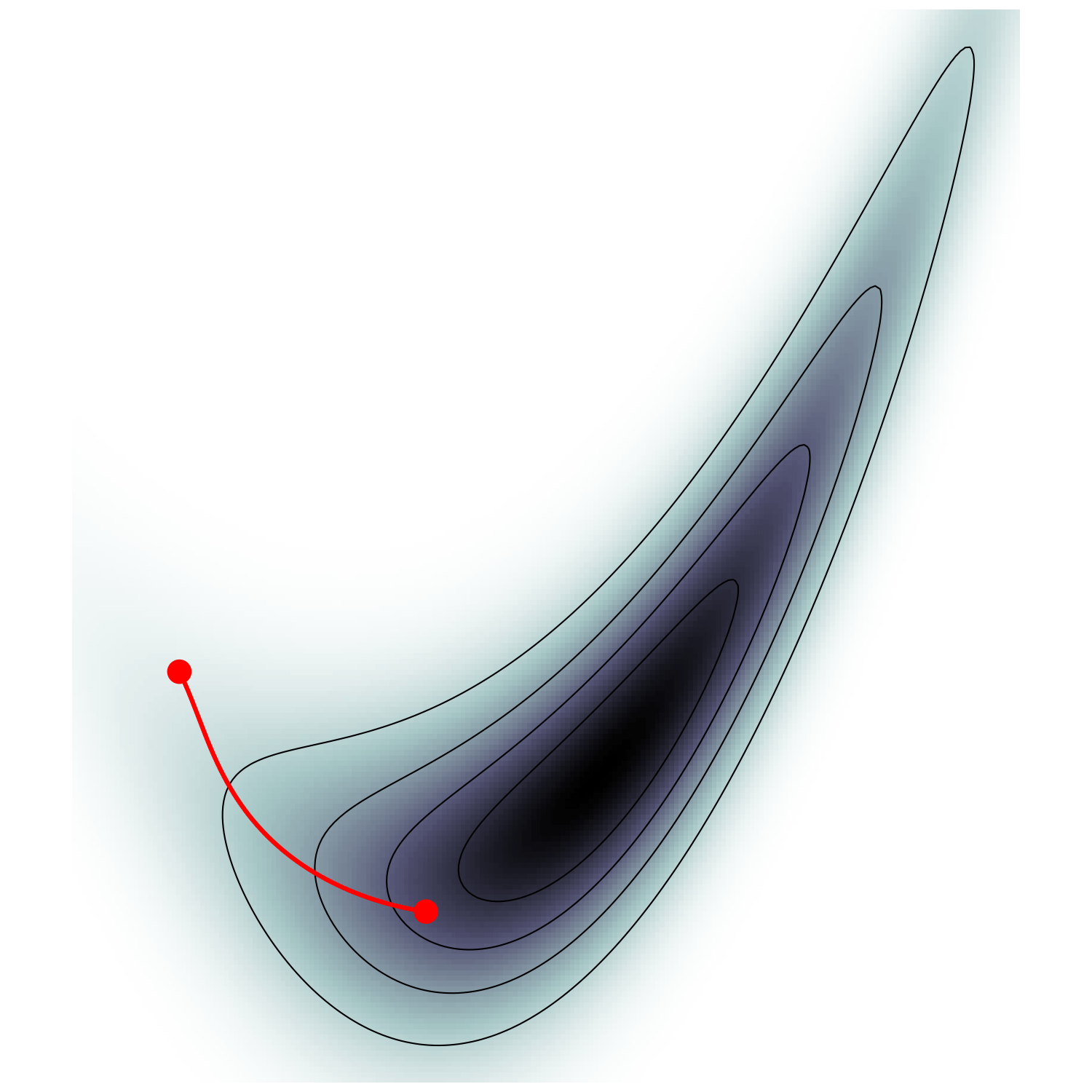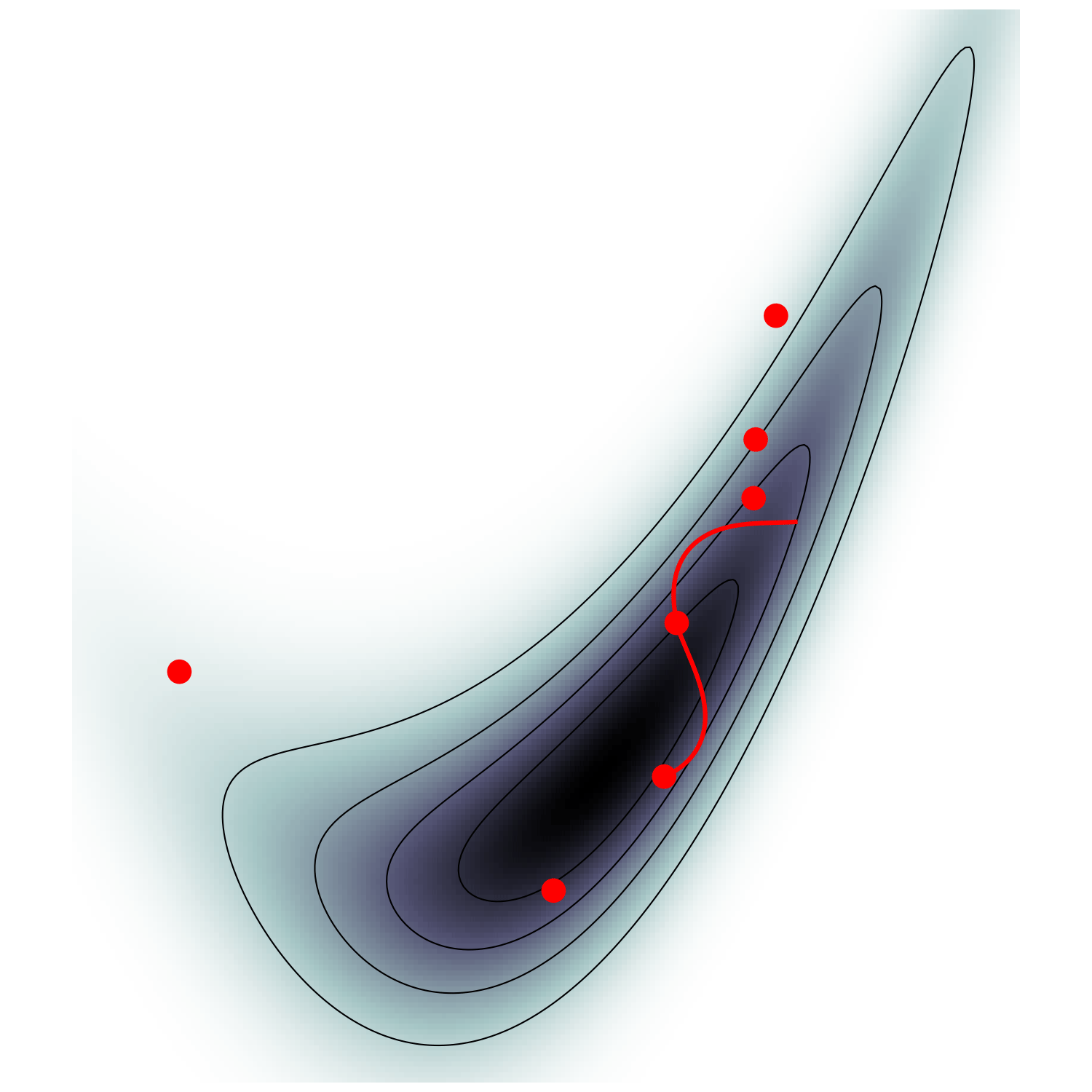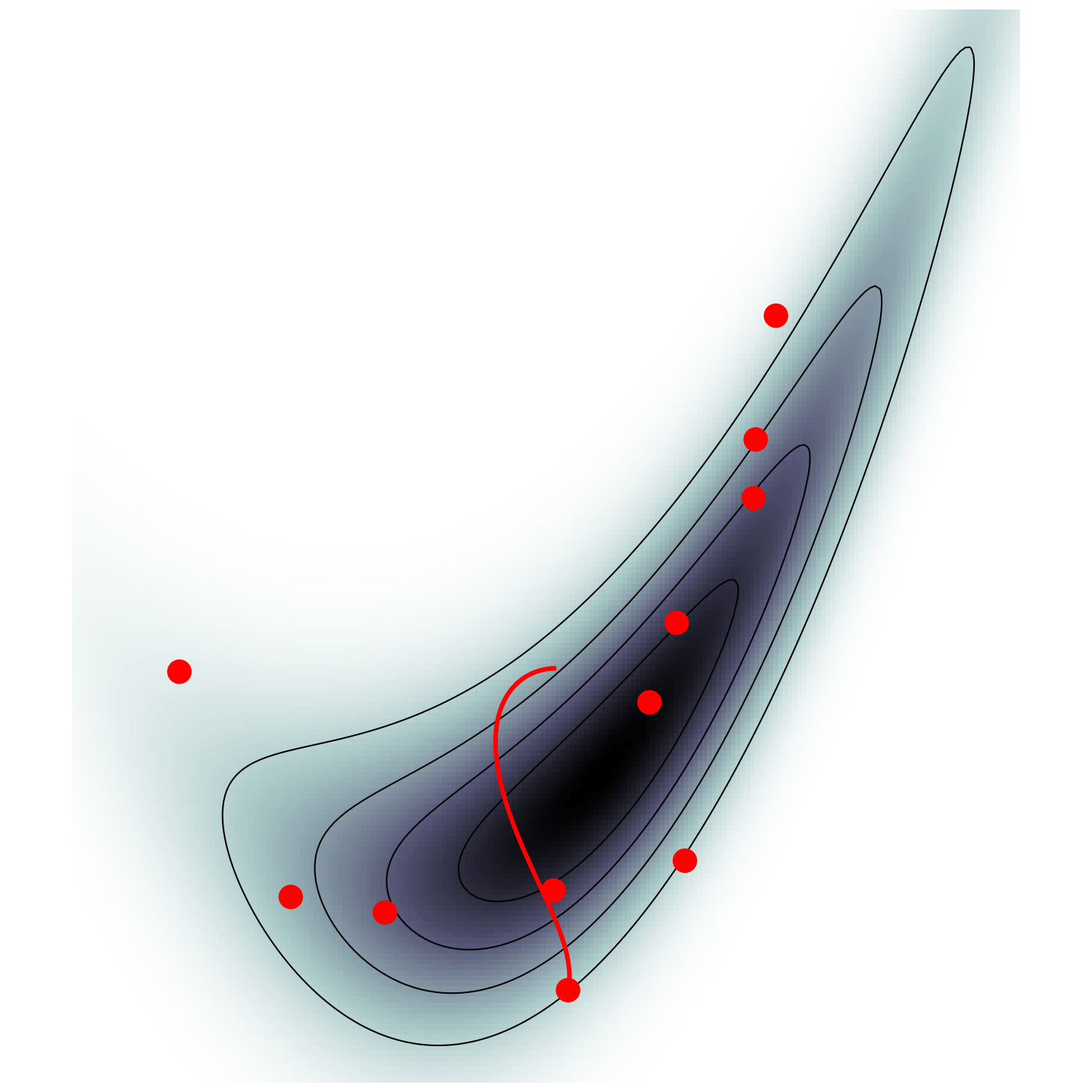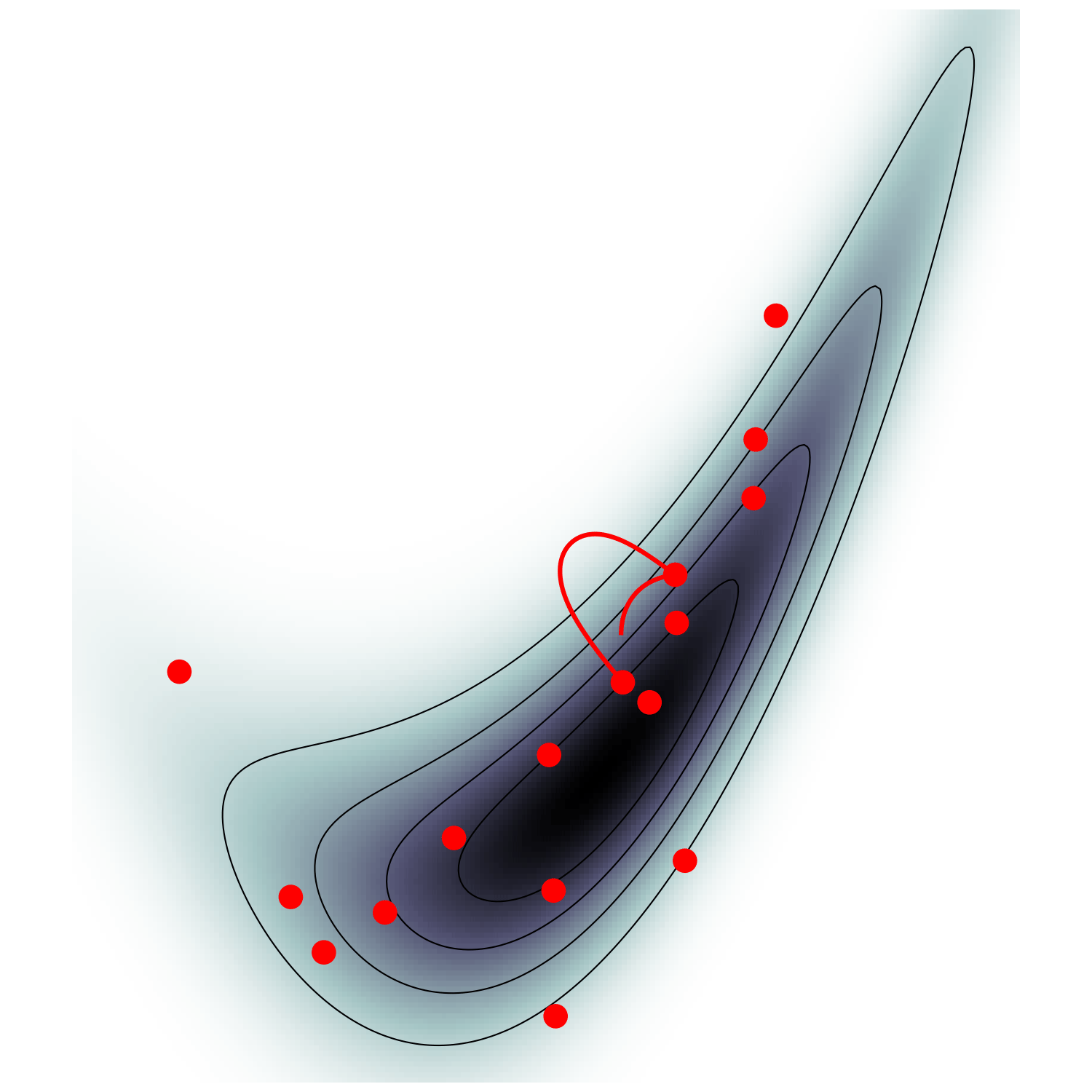
MicroCanonical sampling
+
-
Sample initial conditions
-
LSS formation: 2LPT or N-body PM
(BullFrog or FastPM) lightcone - EFT-based galaxy bias
- Redshift-Space Distortions
- Observational noise and systematics

Fast and differentiable model with

+ field-level preconditioning = \(128^3\) PM inference in 4h on a single GPU node

MicroCanonical sampling
+
Field-Level Modeling and Inference
How to N-body-differentiate?







\((\boldsymbol q, \boldsymbol p)\)
\(\delta(\boldsymbol x)\)
\(\delta(\boldsymbol k)\)
paint*
read*
fft*
ifft*
fft*
*: differentiable, e.g. with via \(\texttt{JaxPM}\), in \(\mathcal O(n \log n)\)
apply forces
to move particles
solve Vlasov-Poisson
to compute forces
\(\begin{cases}\dot {\boldsymbol q} \propto \boldsymbol p\\ \dot{\boldsymbol p} = \boldsymbol f \end{cases}\)
\(\begin{cases}\nabla^2 \phi \propto \delta\\ \boldsymbol f = -\nabla \phi \end{cases} \implies \boldsymbol f \propto \frac{i\boldsymbol k}{k^2} \delta\)
MCMC sampling
High-dimensional sampling is hard
𝓐 𝓭𝓻𝓾𝓷𝓴 𝓶𝓪𝓷 𝔀𝓲𝓵𝓵 𝓯𝓲𝓷𝓭 𝓱𝓲𝓼 𝔀𝓪𝔂 𝓱𝓸𝓶𝓮, 𝓫𝓾𝓽 𝓪 𝓭𝓻𝓾𝓷𝓴 𝓫𝓲𝓻𝓭 𝓶𝓪𝔂 𝓰𝓮𝓽 𝓵𝓸𝓼𝓽 𝓯𝓸𝓻𝓮𝓿𝓮𝓻 (\(\mathrm p \approx 0.66\))
🌸 𝓢𝓱𝓲𝔃𝓾𝓸 𝓚𝓪𝓴𝓾𝓽𝓪𝓷𝓲
\(-\nabla\)
\(d \approx 1\)

🏠
🚶♀️
To maintain constant move-away probability, step-size \(\simeq d^{-1/2}\)
\(d \gg 1\)

🪺
🐦
Canonical MCMC samplers
Recipe😋 to sample from \(\mathrm p \propto e^{-U}\)
- take particle with position \(\boldsymbol q\), momentum \(\boldsymbol p\), mass matrix \(M\), and Hamiltonian $$\mathcal H(\boldsymbol q, \boldsymbol p) = U(\boldsymbol q) + \frac 1 2 \boldsymbol p^\top M^{-1} \boldsymbol p$$
- follow Hamiltonian dynamics during time \(L\)
$$\begin{cases} \dot {{\boldsymbol q}} = \partial_{\boldsymbol p}\mathcal H = M^{-1}{{\boldsymbol p}}\\ \dot {{\boldsymbol p}} = -\partial_{\boldsymbol q}\mathcal H = - \nabla U(\boldsymbol q) \end{cases}$$and refresh momentum \(\boldsymbol p \sim \mathcal N(\boldsymbol 0,M)\)
- usually, perform Metropolis adjustment
- this samples canonical ensemble $$\mathrm p_\text{C}(\boldsymbol q, \boldsymbol p) \propto e^{-\mathcal H(\boldsymbol q, \boldsymbol p)} \propto \mathrm p(\boldsymbol q)\,\mathcal N(\boldsymbol 0, M)$$
gradient guides particle toward high density sets
scales poorly with dimension
must average over all energy levels
Hamiltonian Monte Carlo (e.g. Neal2011)
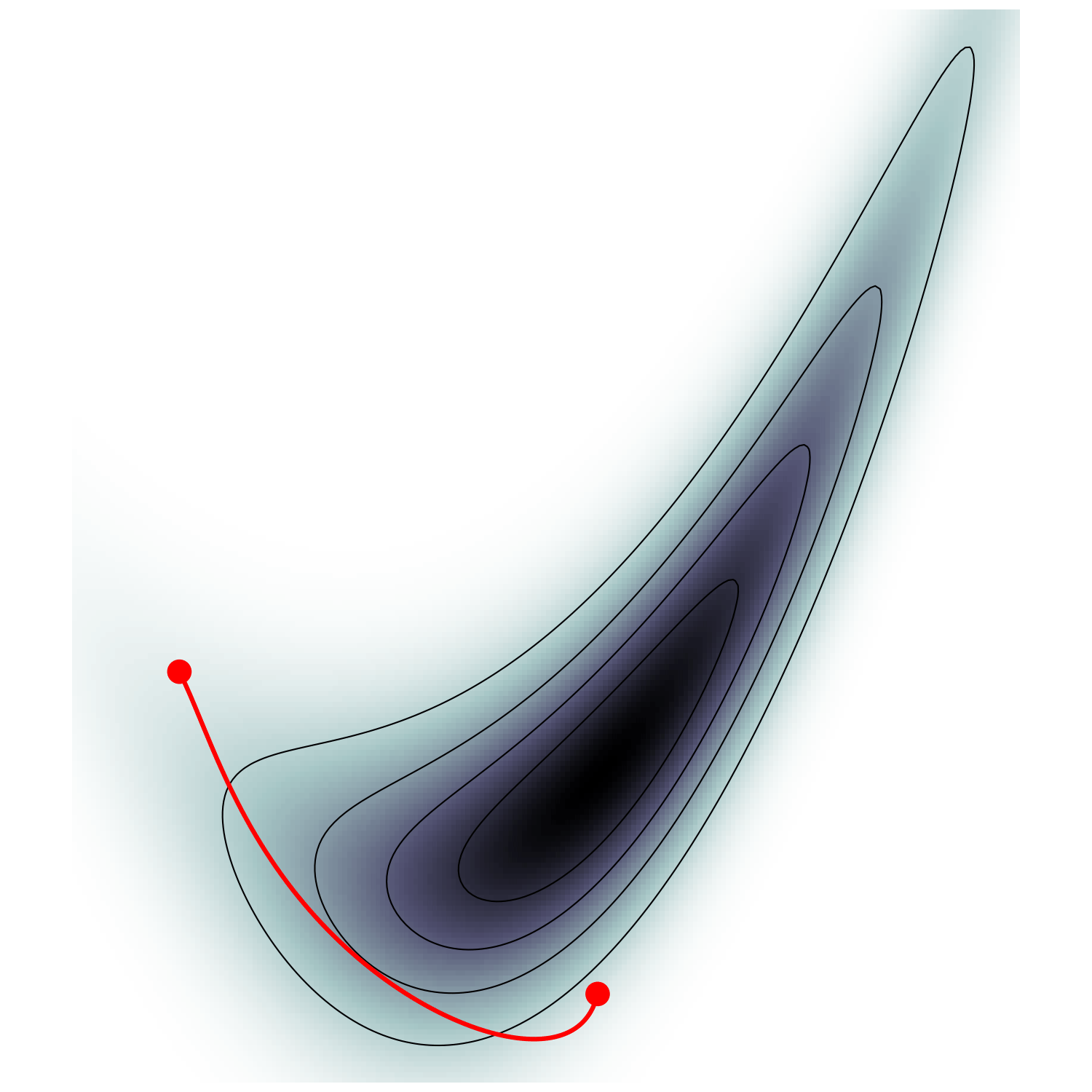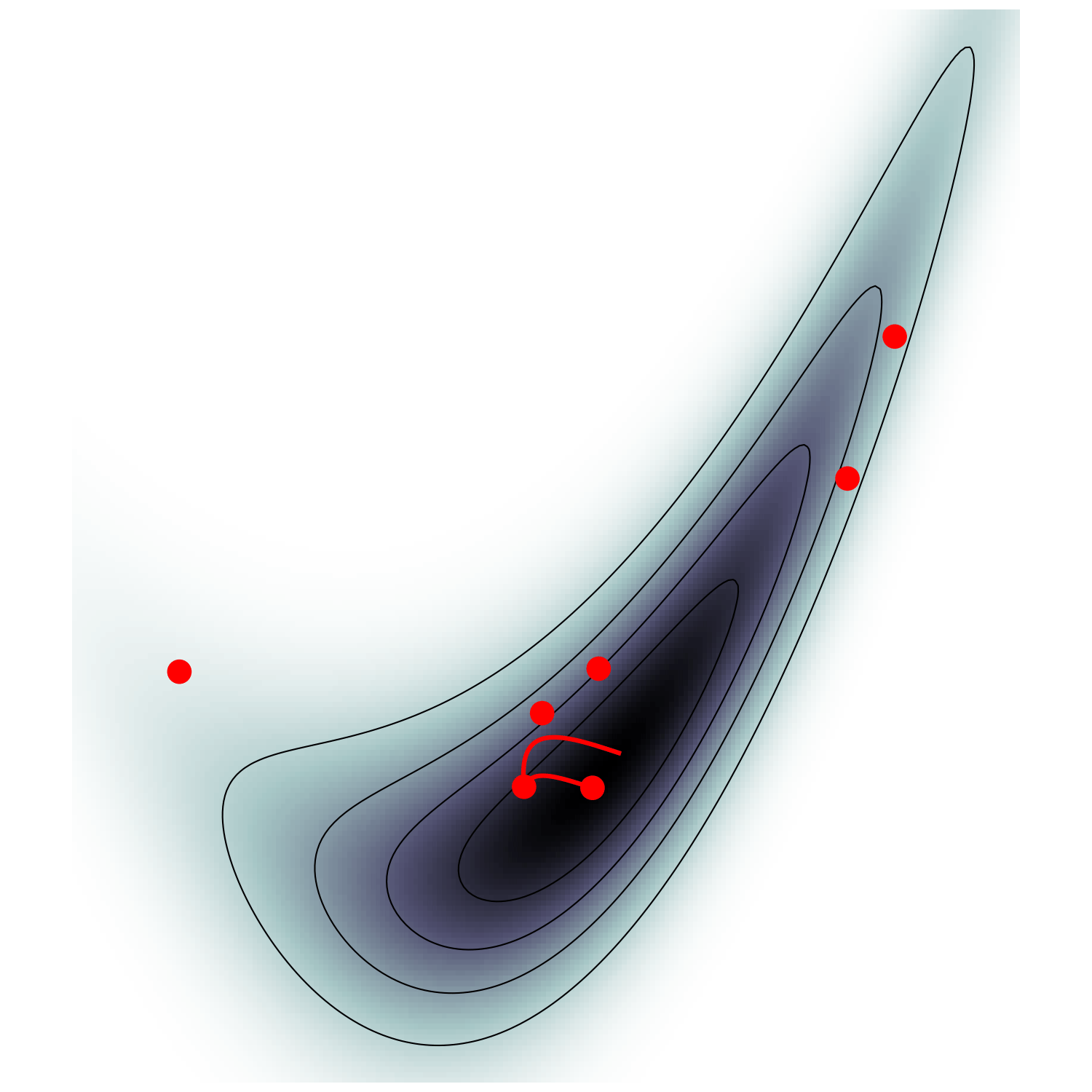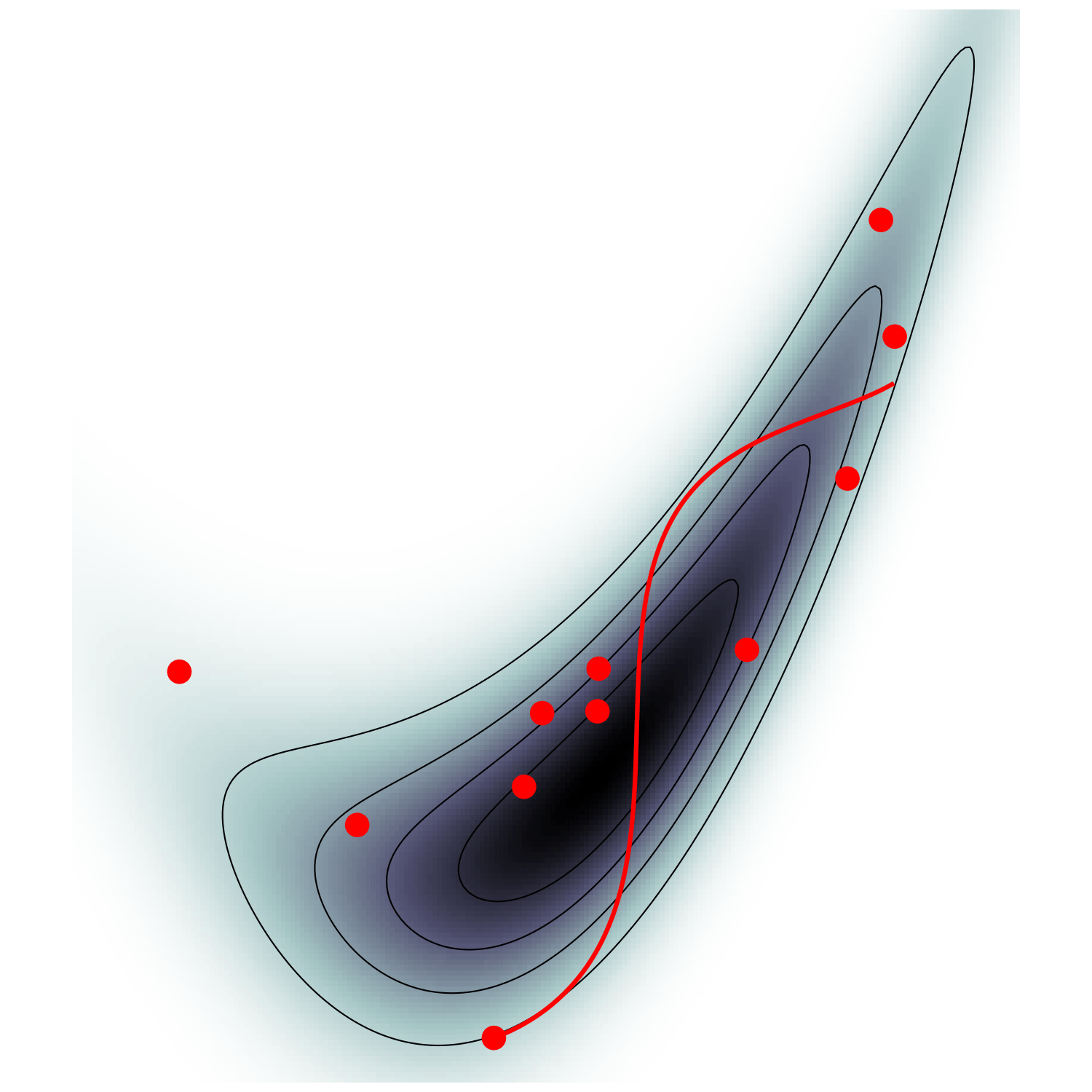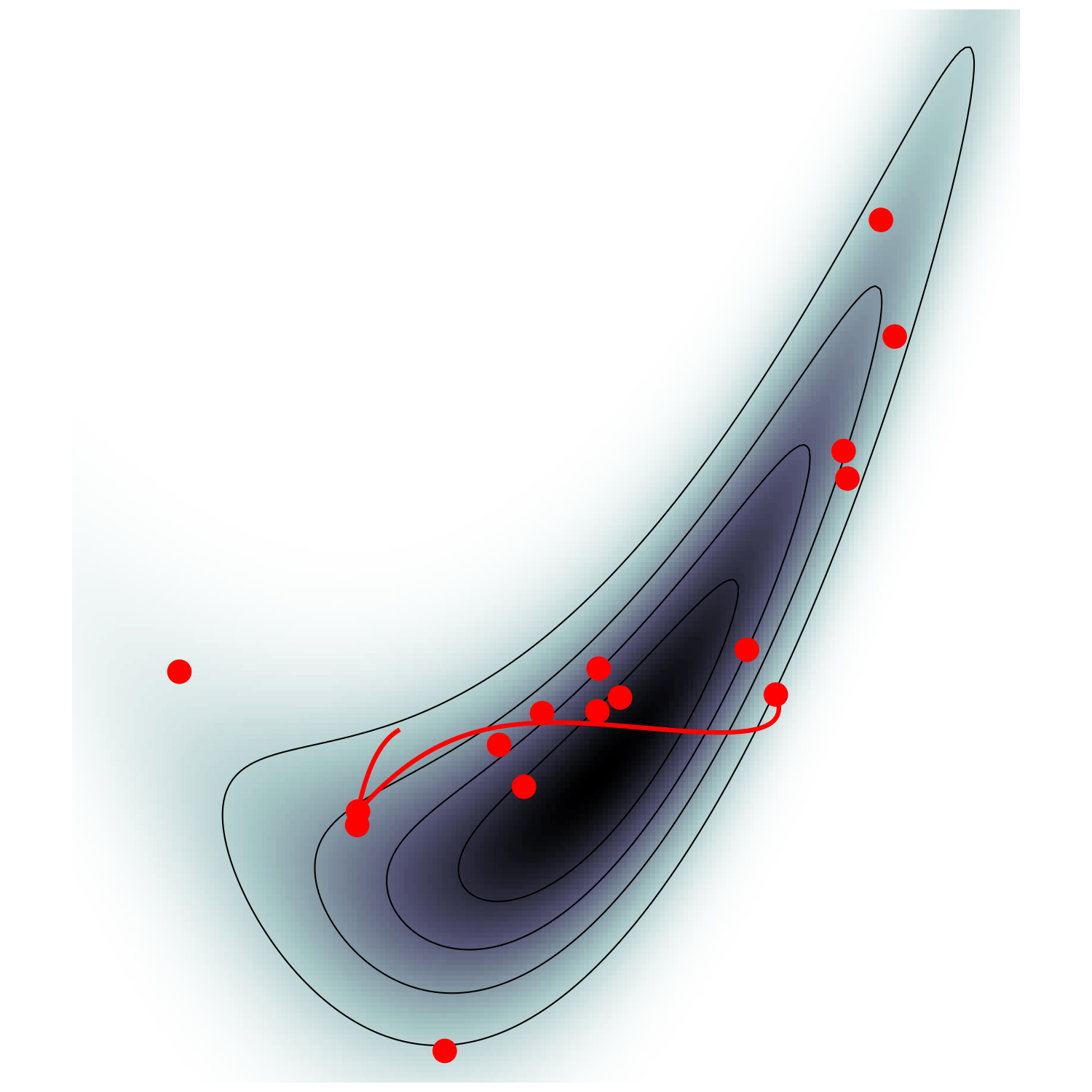
Microcanonical MCMC samplers
Recipe😋 to sample from \(\mathrm p \propto e^{-U}\)
-
take particle with position \(\boldsymbol q\), momentum \(\boldsymbol p\), mass matrix \(M\), and Hamiltonian $$\mathcal H(\boldsymbol q, \boldsymbol p) = \frac {\boldsymbol p^\top M^{-1} \boldsymbol p} {2 m(\boldsymbol q)} - \frac{m(\boldsymbol q)}{2} \quad ; \quad m=e^{-U/(d-1)}$$
-
follow Hamiltonian dynamics during time \(L\)
$$\begin{cases} \dot{\boldsymbol q} = M^{-1/2} \boldsymbol u\\ \dot{\boldsymbol u} = -(I - \boldsymbol u \boldsymbol u^\top) M^{-1/2} \nabla U(\boldsymbol q) / (d-1) \end{cases}$$ and refresh \(\boldsymbol u \leftarrow \boldsymbol z/ \lvert \boldsymbol z \rvert \quad ; \quad \boldsymbol z \sim \mathcal N(\boldsymbol 0,I)\)
-
usually, perform Metropolis adjustment
- this samples microcanonical/isokinetic ensemble $$\mathrm p_\text{MC}(\boldsymbol q, \boldsymbol u) \propto \delta(H(\boldsymbol q, \boldsymbol u)) \propto \mathrm p (\boldsymbol q) \delta(|\boldsymbol u|^2 - 1)$$

single energy/speed level
let's try avoiding that
gradient guides particle toward high density sets
MicroCanonical HMC (Robnik+2022)
Canonical/Microcanonical MCMC samplers
- \(\mathcal H(\boldsymbol q, \boldsymbol p) = \frac {\boldsymbol p^\top M^{-1} \boldsymbol p} {2 m(\boldsymbol q)} - \frac{m(\boldsymbol q)}{2} \quad ; \quad m:=e^{-U/(d-1)}\)
- samples microcanonical/isokinetic ensemble $$\mathrm p_\text{MC}(\boldsymbol q, \boldsymbol p) \propto \delta(\mathcal H(\boldsymbol q, \boldsymbol p)) \propto \mathrm p (\boldsymbol q) \delta(\dot{\boldsymbol q}^\top M \dot{\boldsymbol q} - 1)$$

Hamiltonian Monte Carlo (e.g. Neal2011)

MicroCanonical HMC (Robnik+2022)
- \(\mathcal H(\boldsymbol q, \boldsymbol p) = U(\boldsymbol q) + \frac 1 2 \boldsymbol p^\top M^{-1} \boldsymbol p\)
- samples canonical ensemble $$\mathrm p_\text{C}(\boldsymbol q, \boldsymbol p) \propto e^{-\mathcal H(\boldsymbol q, \boldsymbol p)} \propto \mathrm p(\boldsymbol q)\,\mathcal N(\boldsymbol 0, M)$$
Primordial Non-Gaussianity from galaxies
Local-type PNG is constrained by the induced scale-dependent bias
\(\phi_{\mathrm{NL}}=\phi+{\color{purple}f_{\mathrm{NL}}}\phi^{2}\)
\(\delta_g(\boldsymbol k)\simeq\left(b_{1}+ b_\phi {\color{purple}f_\mathrm{NL}}k^{-2} \right) \delta_L(\boldsymbol k)\)
Primordial Non-Gaussianity from galaxies
Local-type PNG is mostly constrained by the induced scale-dependent bias
\(\phi_{\mathrm{NL}}=\phi+{\color{purple}f_{\mathrm{NL}}}\phi^{2}\)
\(\delta_g(\boldsymbol k)\simeq\left(b_{1}+ b_\phi {\color{purple}f_\mathrm{NL}}k^{-2} \right) \delta_L(\boldsymbol k)\)
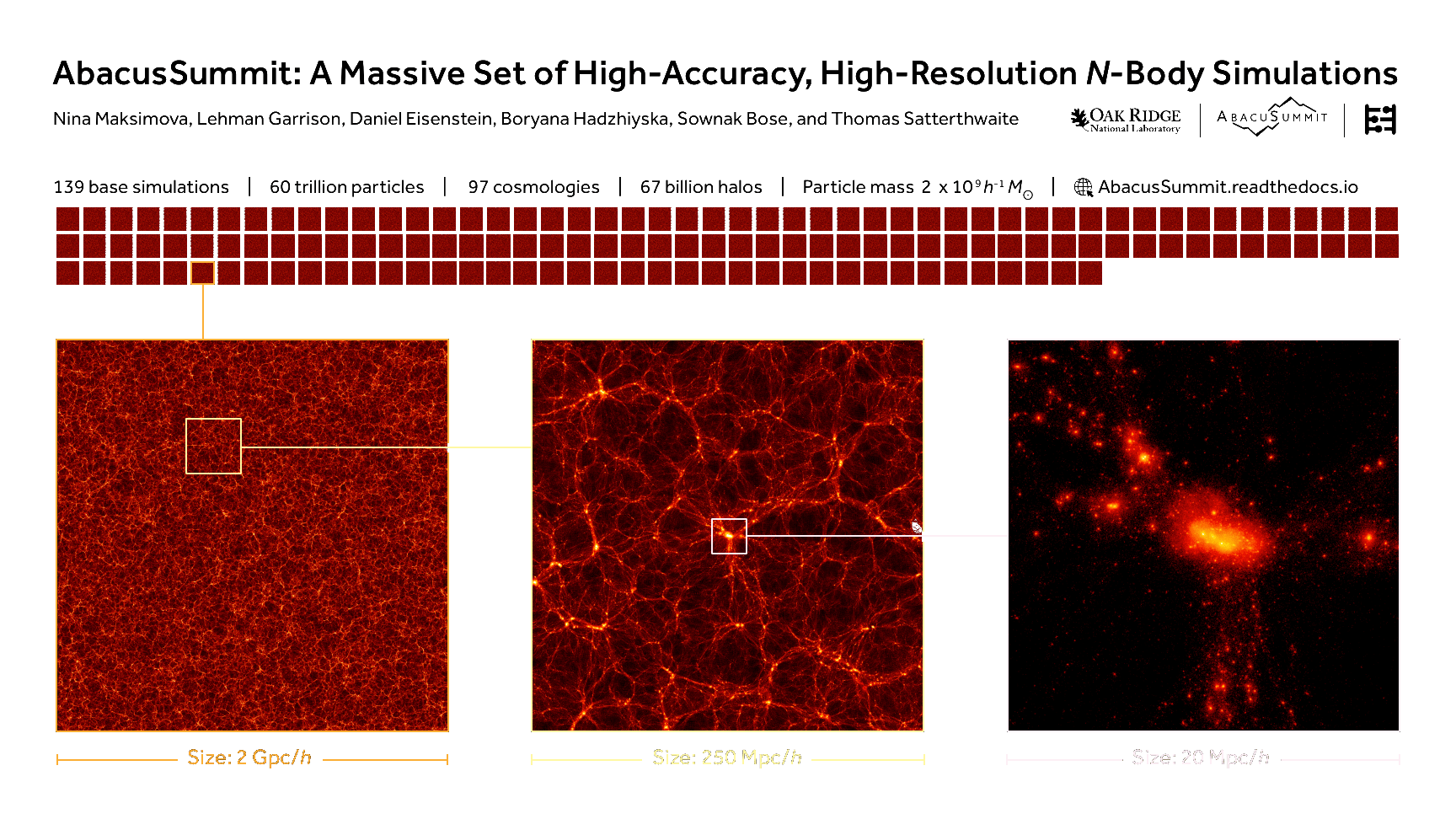
Ideal first demonstration for FLI
- Most of signal from easier large scales
- Result very sensitive to systematics, more directly implemented at field-level
- Bonus: fully explicit/explainable, no black box modeling
- Validate on DESI reference simulations: HOD-populated N-body AbacusSummit
Field-Level modeling of PNG
-
Sample initial conditions and add PNG
$$\phi_{\mathrm{NL}}=\phi+{\color{purple}f_{\mathrm{NL}}}\phi^{2}$$ - Compute Lagrangian bias of particles at \(\boldsymbol q^\mathrm{in}\) $$\mathcal O_{\rm L}=1+{\color{purple}b_{1}}\,\delta_{\rm L}+{\color{purple}b_{2}}\delta_{\rm L}^{2}+{\color{purple}b_{s^2}}s^{2}+ {\color{purple}b_{\nabla^2}} \nabla^2 \delta _{\rm L}\\\!\!\!\!\!\!\! + {\color{purple}f_{\rm NL} b_\phi}\phi + {\color{purple} f_{\rm NL} b_{\phi\delta}} \phi \delta_{\rm L}$$
-
Displace particles to \(\boldsymbol q^\mathrm{fin}\)
\(\boldsymbol q^\mathrm{fin} = \boldsymbol q^\mathrm{2LPT} + H^{-1}\dot {\boldsymbol q}^\mathrm{2LPT}_\parallel + {\color{purple}b_{\nabla_\parallel}} \nabla_\parallel \delta_\mathrm{L}(\boldsymbol q^\mathrm{in})\) -
Paint particles on grid with kernel \(K\) and weight \(\mathcal O_{\rm L}\)
$$(1+\delta_g)(\boldsymbol x) = \int K(\boldsymbol x - \boldsymbol q^\mathrm{fin}) \mathcal O_L(\boldsymbol q^\mathrm{in})\, \mathrm d \boldsymbol q^\mathrm{in}$$ -
Noise via galaxy stochasticity
$$n_g \sim \mathcal N({\color{purple} \bar n_g} (1+\delta_g),\, {\color{purple}\bar n_g \sigma_0}(1+{\color{purple}\sigma_\delta}\delta_g))$$
3 PNG parameters, 2 options:
- infer the 3 as independent
- assume "universality" relations
$$\begin{align*}b_\phi &=2\delta_c({\color{purple} b_1}+1-p)\\b_{\phi \delta} &=2 (\delta_c {\color{purple} b_2}+ {\color{purple} b_1})\end{align*}$$(Lagrangian form)
Fast and differentiable model with







-
Sample initial conditions and add PNG
$$\phi_{\mathrm{NL}}=\phi+{\color{purple}f_{\mathrm{NL}}}\phi^{2}$$ - Compute Lagrangian bias of particles at \(\boldsymbol q^\mathrm{in}\) $$\mathcal O_{\rm L}=1+{\color{purple}b_{1}}\,\delta_{\rm L}+{\color{purple}b_{2}}\delta_{\rm L}^{2}+{\color{purple}b_{s^2}}s^{2}+ {\color{purple}b_{\nabla^2}} \nabla^2 \delta _{\rm L}\\\!\!\!\!\!\!\! + {\color{purple}f_{\rm NL} b_\phi}\phi + {\color{purple} f_{\rm NL} b_{\phi\delta}} \phi \delta_{\rm L}$$
-
Displace particles to \(\boldsymbol q^\mathrm{fin}\)
\(\boldsymbol q^\mathrm{fin} = \boldsymbol q^\mathrm{2LPT} + H^{-1}\dot {\boldsymbol q}^\mathrm{2LPT}_\parallel + {\color{purple}b_{\nabla_\parallel}} \nabla_\parallel \delta_\mathrm{L}(\boldsymbol q^\mathrm{in})\) -
Paint particles on grid with kernel \(K\) and weight \(\mathcal O_{\rm L}\)
$$(1+\delta_g)(\boldsymbol x) = \int K(\boldsymbol x - \boldsymbol q^\mathrm{fin}) \mathcal O_L(\boldsymbol q^\mathrm{in})\, \mathrm d \boldsymbol q^\mathrm{in}$$ -
Noise via galaxy stochasticity
$$n_g \sim \mathcal N({\color{purple} \bar n_g} (1+\delta_g),\, {\color{purple}\bar n_g \sigma_0}(1+{\color{purple}\sigma_\delta}\delta_g))$$
Fast and differentiable model with

In practice, discreteness reduction: oversampling, deconvolution, interlacing, kernel choice (NUFFT-like)









\(k_\mathrm{evolve}\)
(LPT, bias)
\(k_\mathrm{paint}\)
\(k_\mathrm{final}\)
\(k_\mathrm{init}\)




Field-Level modeling of PNG
EFT-based Field-Level modeling
-
Sample initial conditions and add PNG
$$\phi_{\mathrm{NL}}=\phi+{\color{purple}f_{\mathrm{NL}}}\phi^{2}$$ - Initialize particles at \(\boldsymbol q^\mathrm{in}\)
- Compute their Lagrangian bias expansion
$$\mathcal O_{\rm L}=1+{\color{purple}b_{1}}\,\delta_{\rm L}+{\color{purple}b_{2}}\delta_{\rm L}^{2}+{\color{purple}b_{s^2}}s^{2}+ {\color{purple}b_{\nabla^2}} \nabla^2 \delta _{\rm L}\\\!\!\!\!\!\!\! + {\color{purple}f_{\rm NL} b_\phi \phi} + {\color{purple} f_{\rm NL} b_{\phi\delta}} \phi \delta_{\rm L}$$ -
Displace particles to \(\boldsymbol q^\mathrm{fin}\)
\(\boldsymbol q^\mathrm{fin} = \boldsymbol q^\mathrm{LPT} + H^{-1}\dot {\boldsymbol q}^\mathrm{LPT}_\parallel + {\color{purple}b_{\nabla_\parallel}} \nabla_\parallel \delta_\mathrm{L}(\boldsymbol q^\mathrm{in})\),
with \(\boldsymbol q^\mathrm{LPT} = \boldsymbol q^\mathrm{in} + \Psi^\mathrm{LPT}(\boldsymbol q^\mathrm{in}, \delta_{\rm NL})\) -
Paint particles on grid with kernel \(K\) and weight \(\mathcal O_{\rm L}\)
$$(1+\delta_g)(\boldsymbol x) = \int K(\boldsymbol x - \boldsymbol q^\mathrm{fin}) \mathcal O_L(\boldsymbol q^\mathrm{in})\, \mathrm d \boldsymbol q^\mathrm{in}$$ -
Noise via galaxy stochasticity
$$n_g \sim \mathcal N({\color{purple} \bar n_g} (1+\delta_g),\, {\color{purple}\bar n_g \sigma_0}(1+{\color{purple}\sigma_\delta}\delta_g))$$









\(k_\mathrm{evolve}\)
(LPT, bias)
\(k_\mathrm{paint}\)
\(k_\mathrm{final}\)
\(k_\mathrm{init}\)




In practice, discreteness reduction: oversampling, deconvolution, interlacing, kernel choice (NUFFT-like, see e.g. Stadler+2024)
3 PNG parameters, 2 options:
- infer the 3 as independent
- assume "universality" relations
$$\begin{align*}b_\phi &=2\delta_c({\color{purple} b_1}+1-p)\\b_{\phi \delta} &=2 (\delta_c {\color{purple} b_2}- {\color{purple} b_1})\end{align*}$$(Lagrangian form)
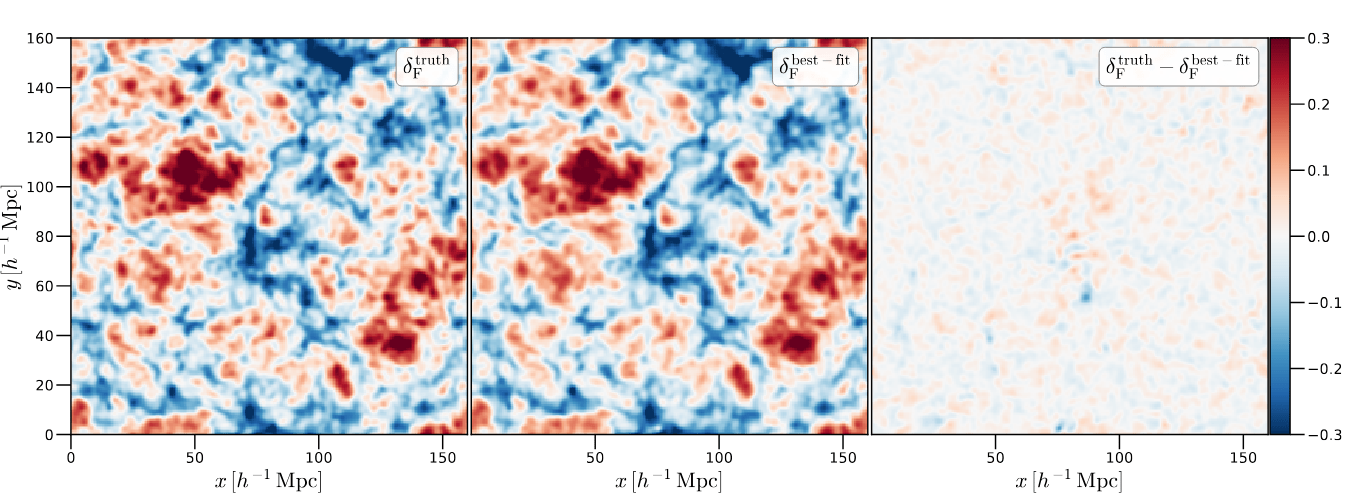
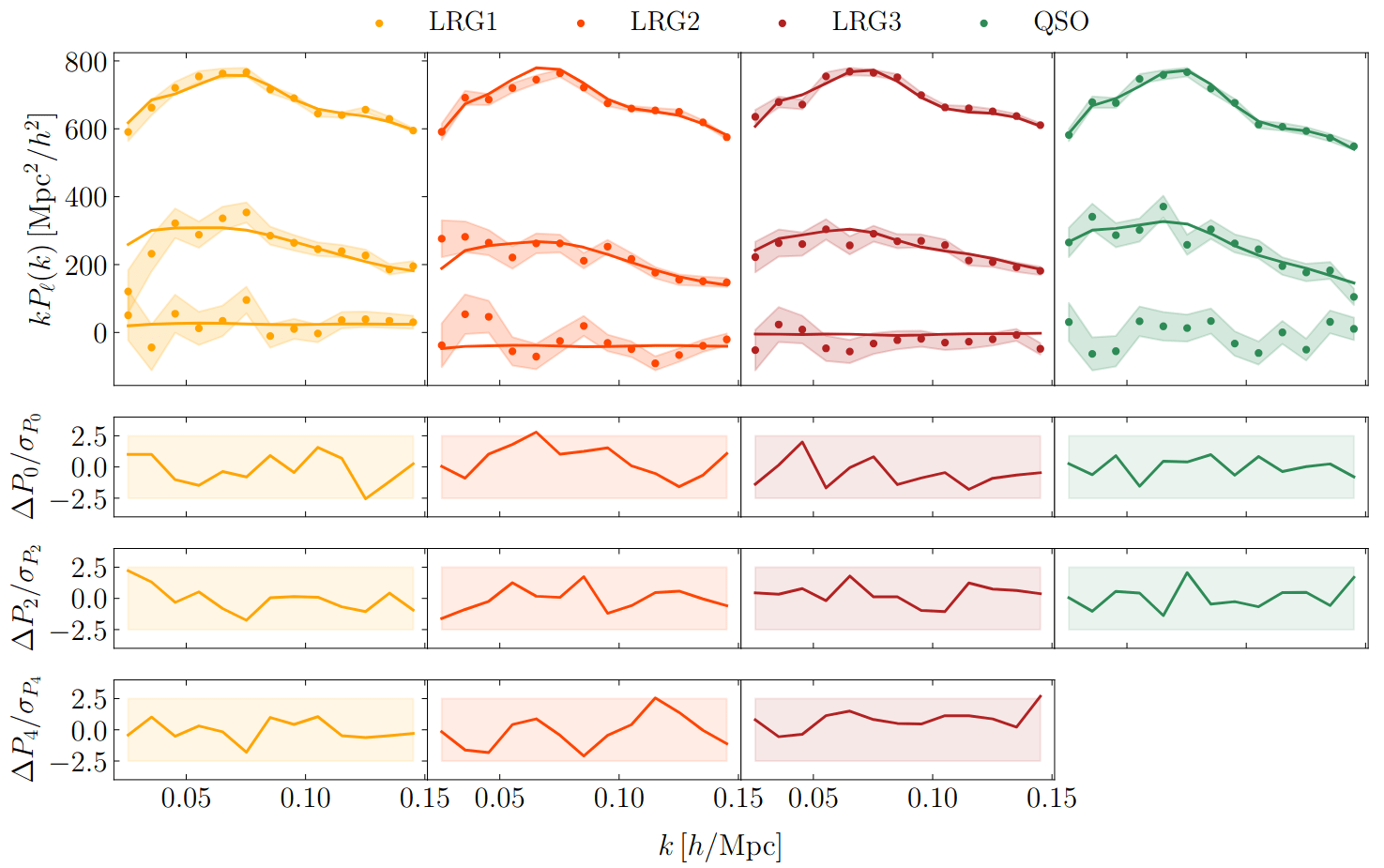
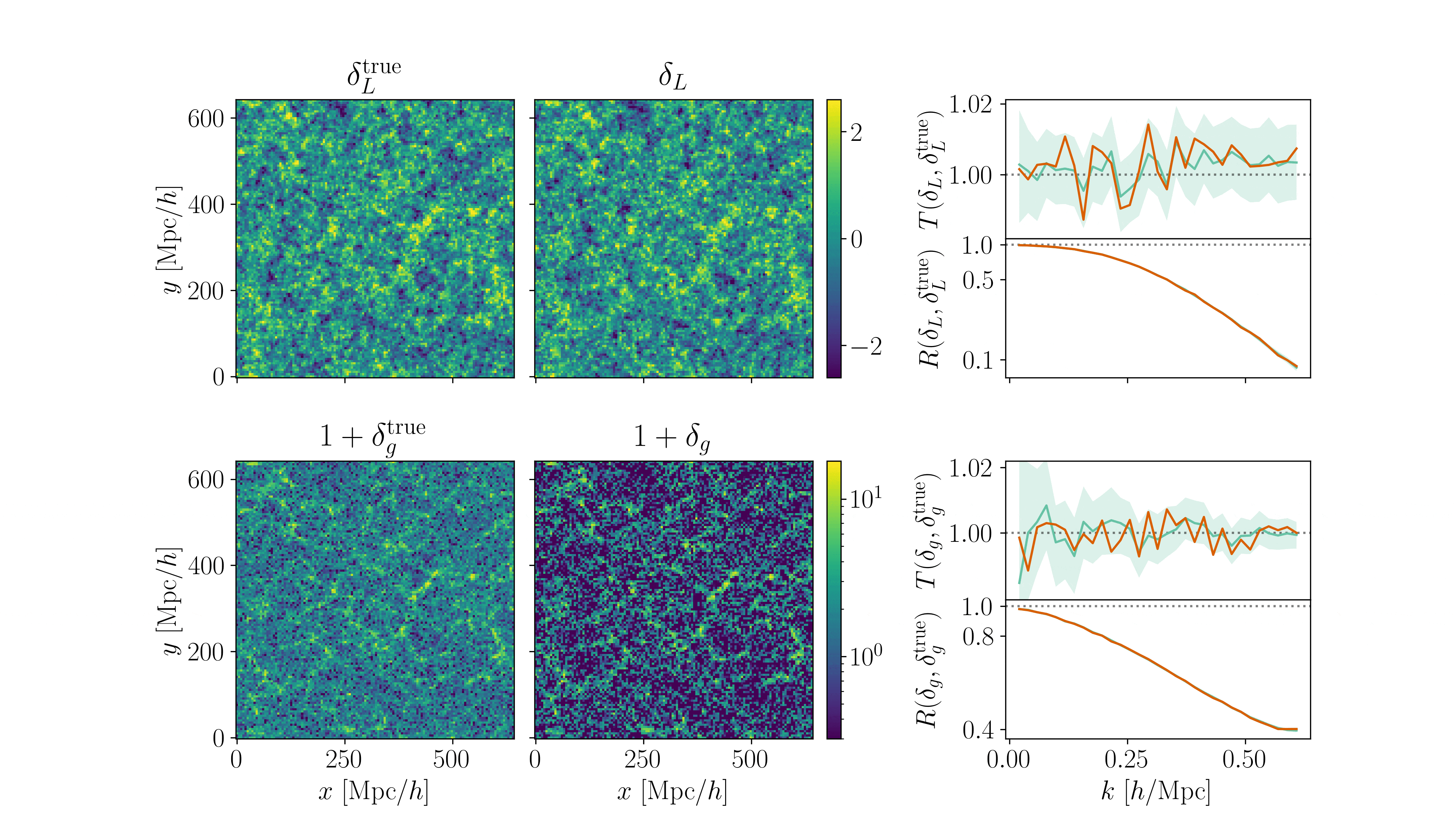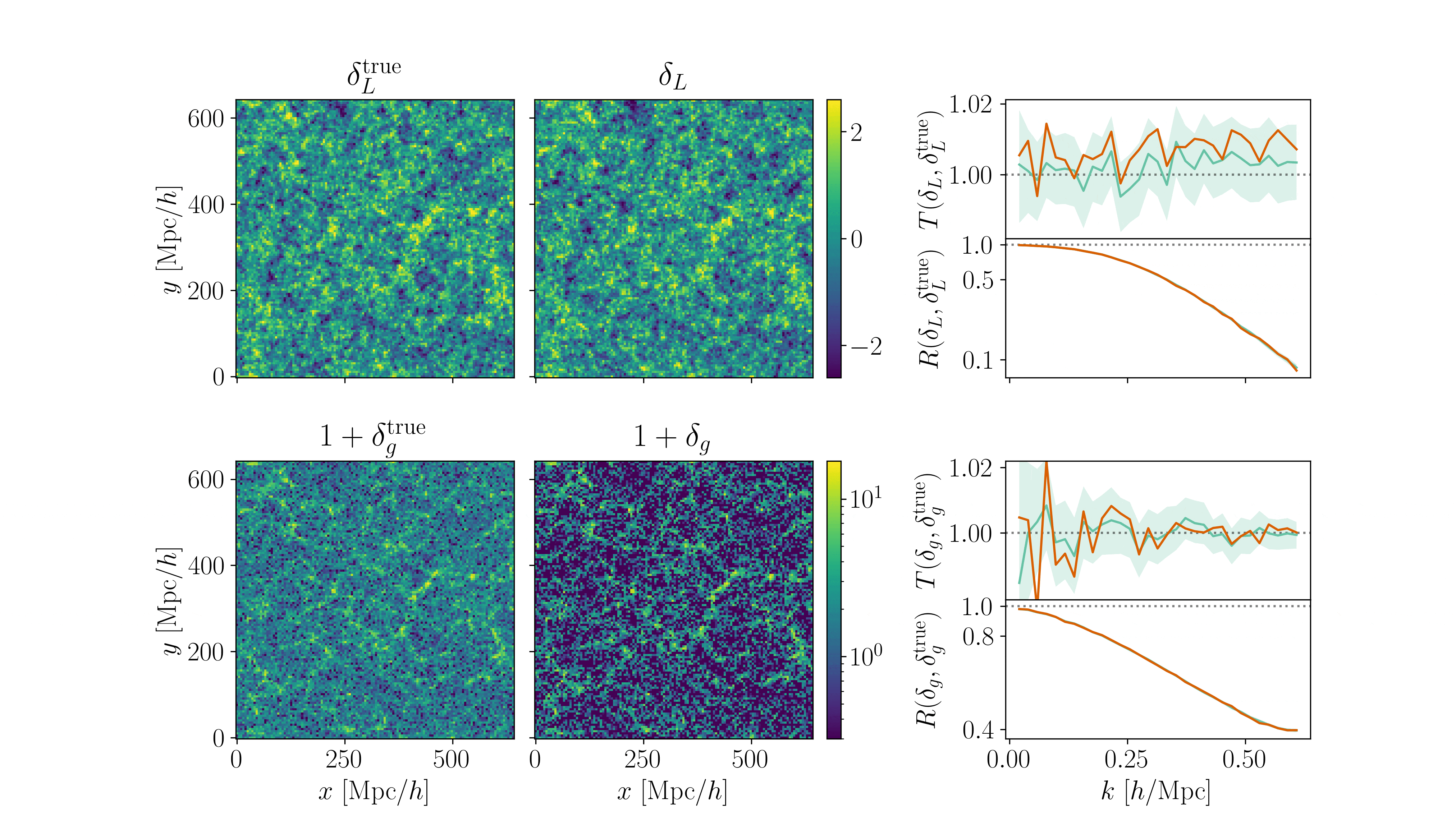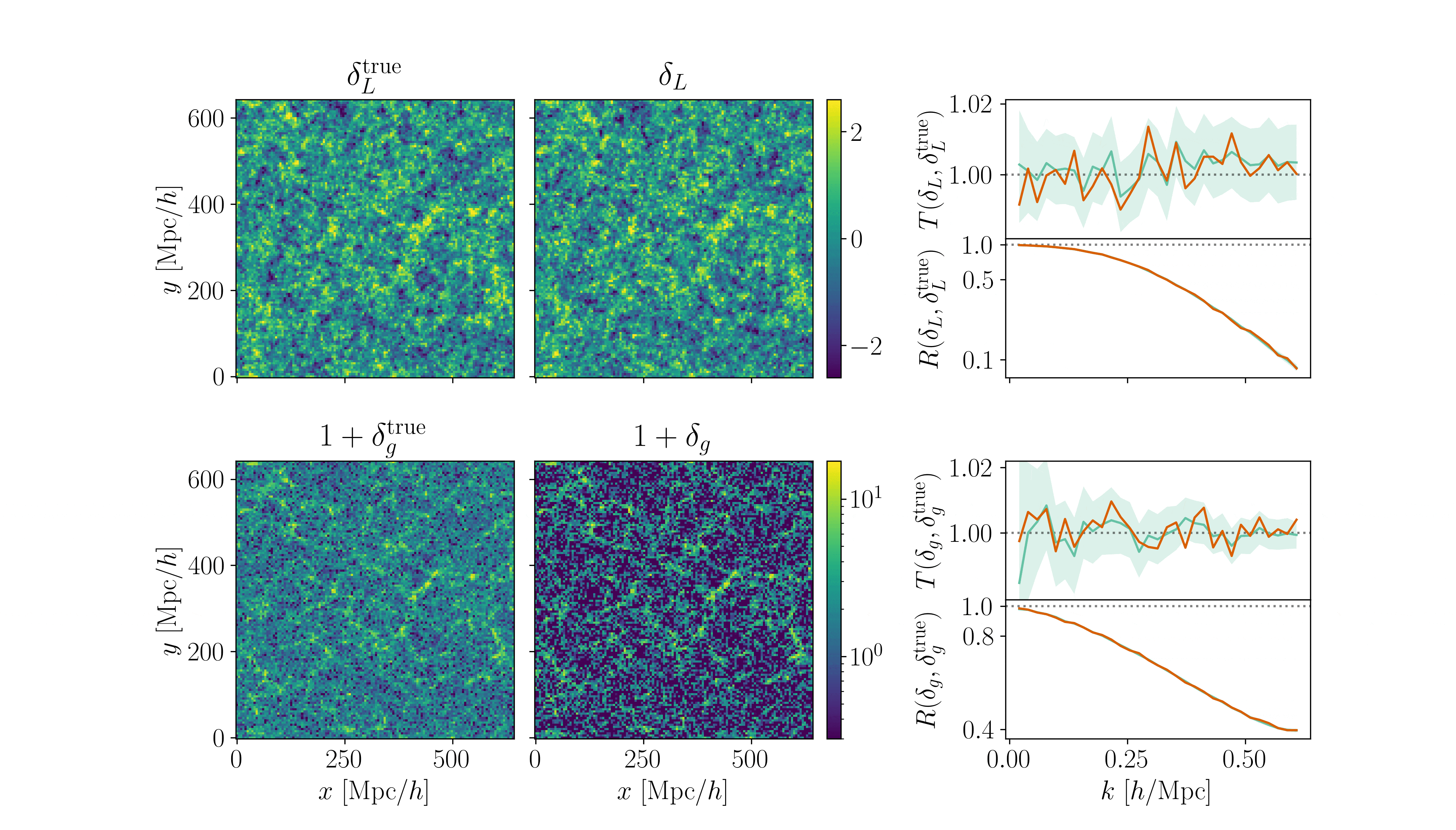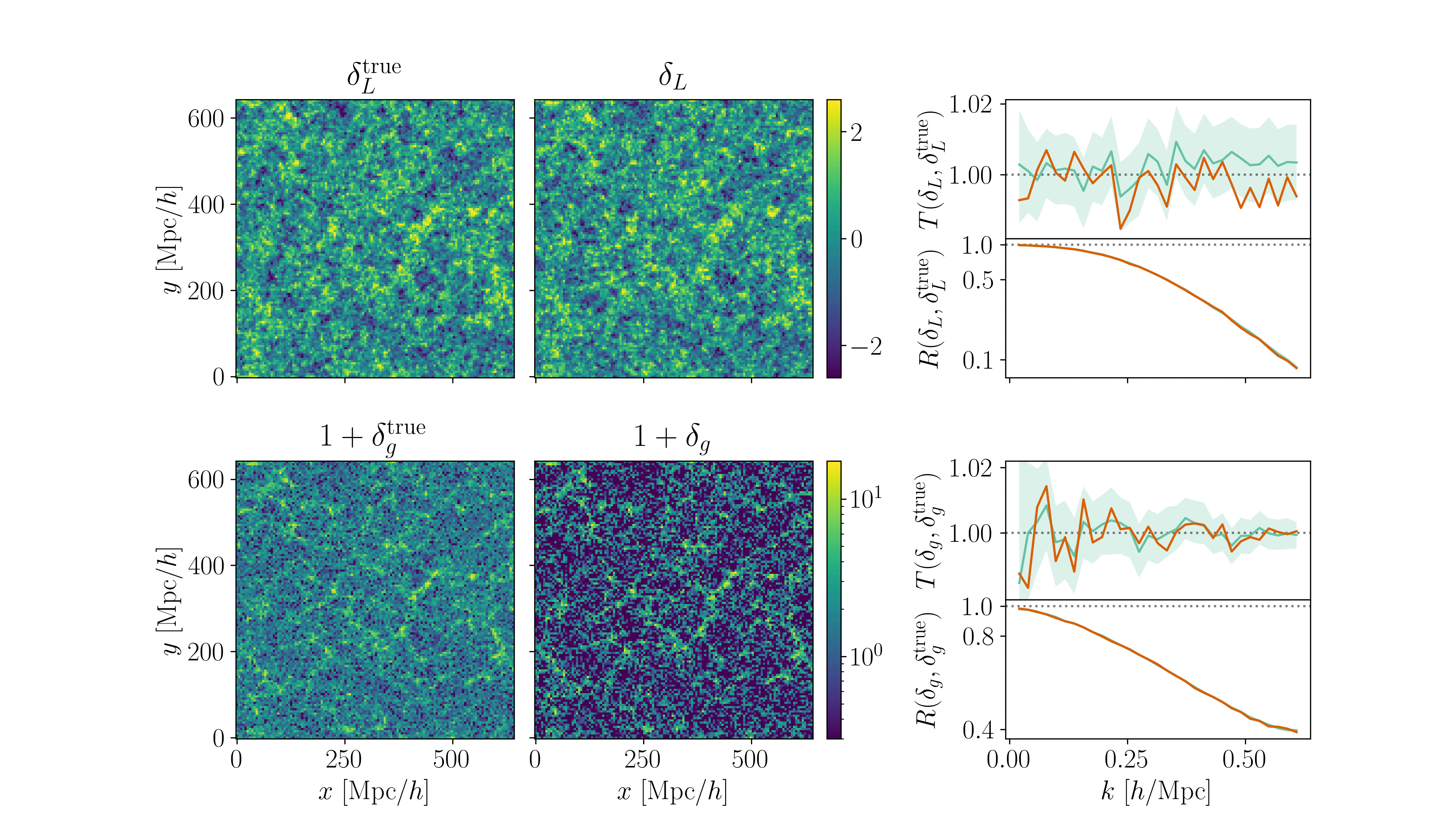
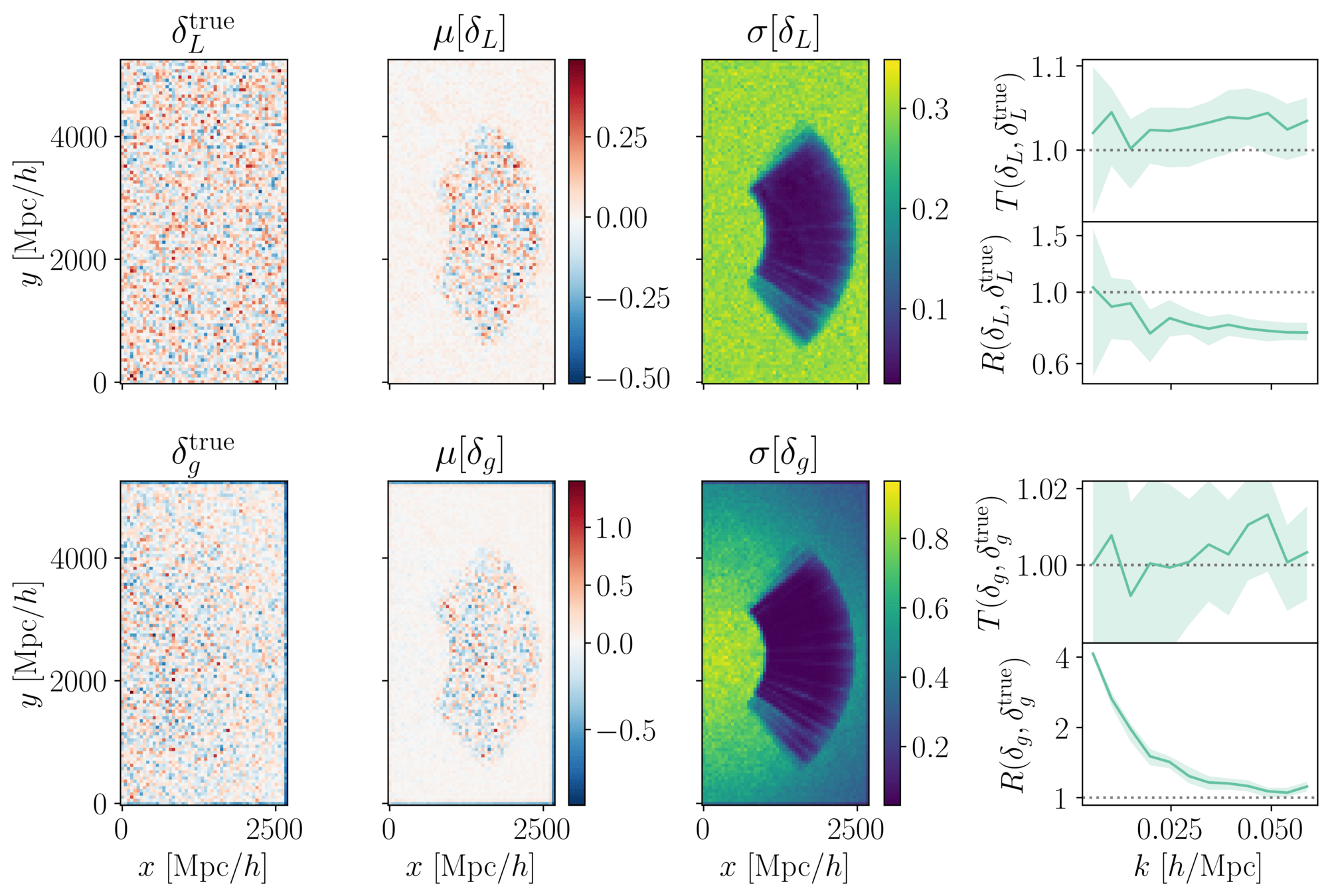
Fitting AbacusSummit+HOD
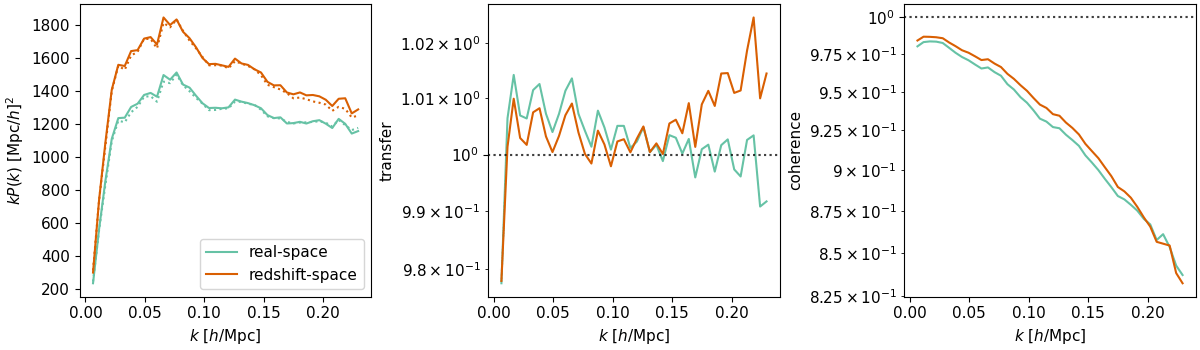
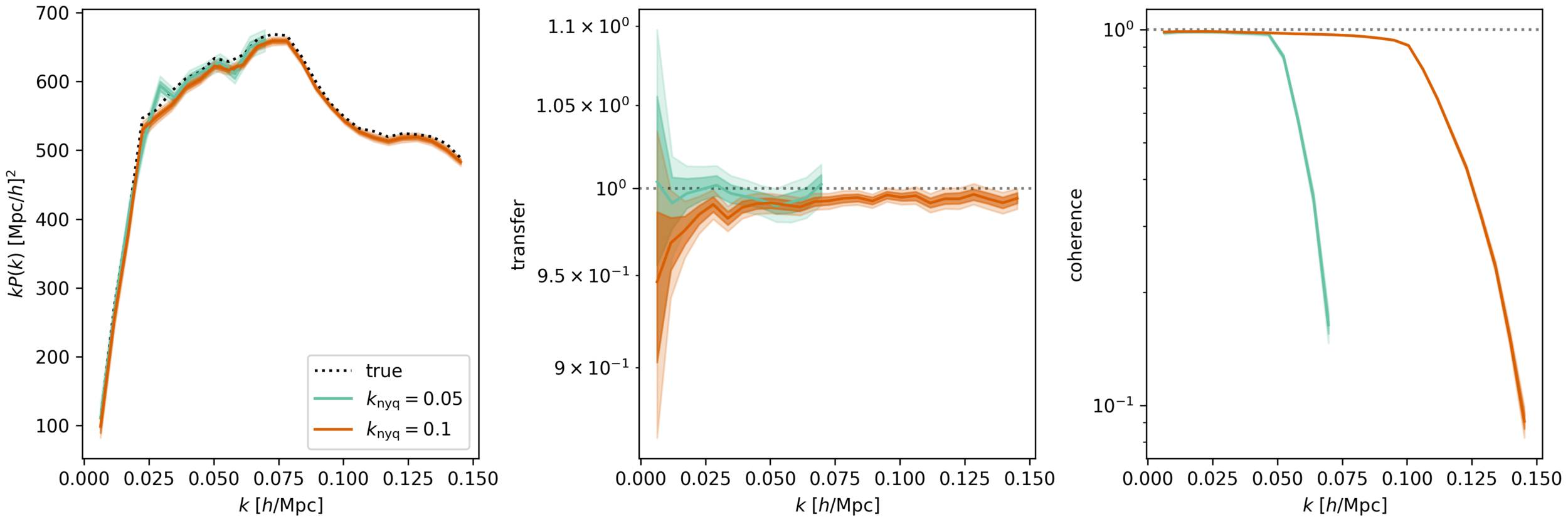
- CDM: fix initial conditions. Match within \(0.5\%\) at field-level for \(k_\mathrm{nyq} < 0.1 h/\mathrm{Mpc} \)
- Tracer (LRG, \(z=0.8\)): fix initial conditions and optimize on EFT parameters
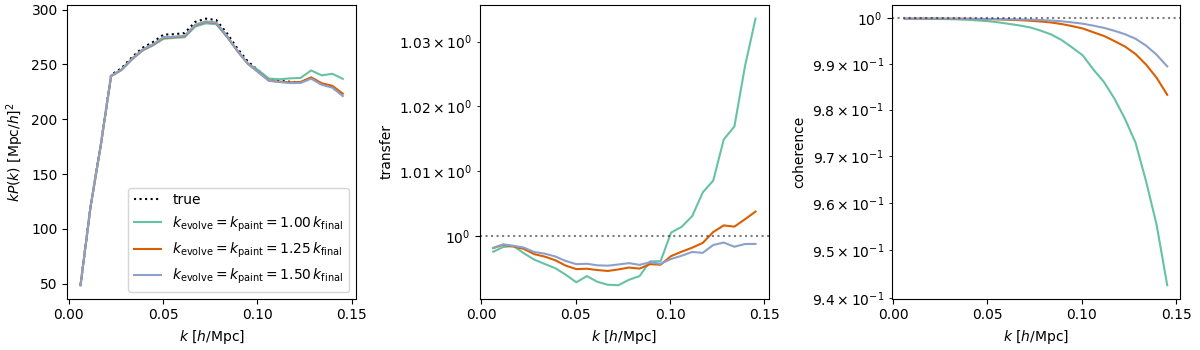
$$\sqrt{P_{\delta} / P_{\delta^\mathrm{true}}}$$ = amplitude info
$$P_{\delta,\delta^\mathrm{true}} / \sqrt{P_{\delta}P_{\delta^\mathrm{true}}}$$ = phase info
Galaxy stochasticity characterization
EFT says \({\color{purple}\sigma_0}(1+{\color{purple}\sigma_\delta}\delta_g^\mathrm{det})\)
Poisson \(\simeq \sigma_0=\sigma_\delta=1\), but fit shows sub-Poisson
For positivity, we take:
\({\color{purple}\sigma_0}\ln(1+e^{1+{\color{purple}\sigma_\delta}\delta_g^\mathrm{det}})\)
Quite Gaussian for \(k_\mathrm{nyq} \leq 0.15 h/ \mathrm{Mpc}\)👍
So \(\delta_g \sim \mathcal N(\delta_g^\mathrm{det},\, {\color{purple}❓})\)
EFT says \({\color{purple}\sigma_0}(1+{\color{purple}\sigma_{2}}k^2 + {\color{purple}\sigma_{\mu,2}}(\mu k)^2)\)
Negligible for currently probed scales.
If not, can be implemented in real domain with sparse matrices.
Galaxy stochasticity = \(\delta_g^\mathrm{true} -\delta_g^\mathrm{det}\), and we take \(\delta_g^\mathrm{det}\) to be EFT best fit.
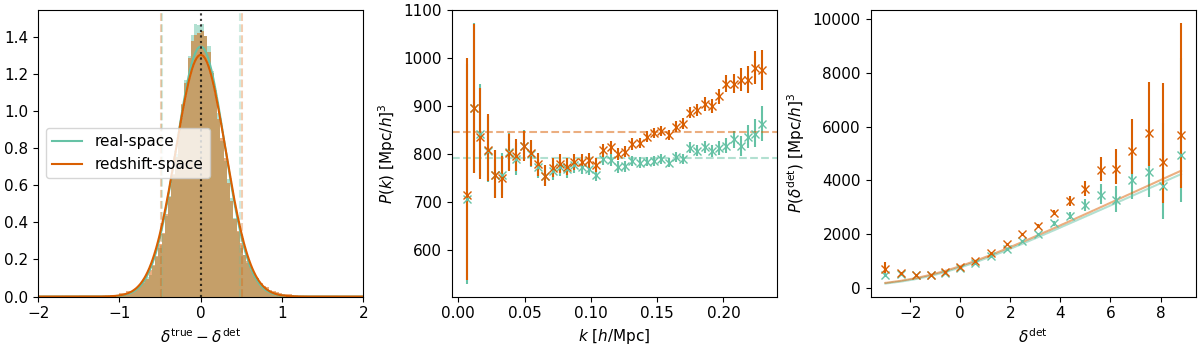
\(\sigma^2(\delta^\mathrm{det})\)
Preliminary FLI results
- CDM:
- Tracer (LRG, \(z=0.8\)):
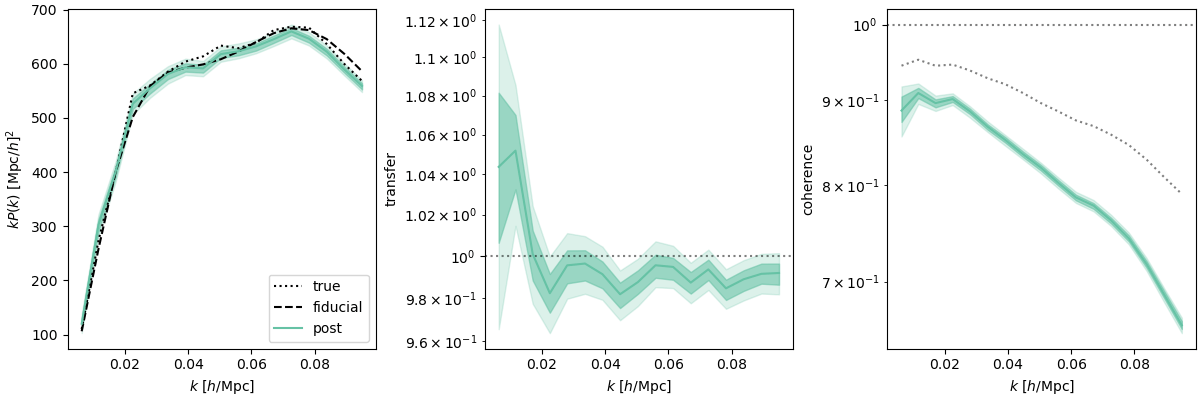
\((2\ \mathrm{Gpc}/h)^3,\, \operatorname{dim}(\delta_L) = 96^3,\,k_\mathrm{nyq} = 0.1 h / \mathrm{Mpc}\)
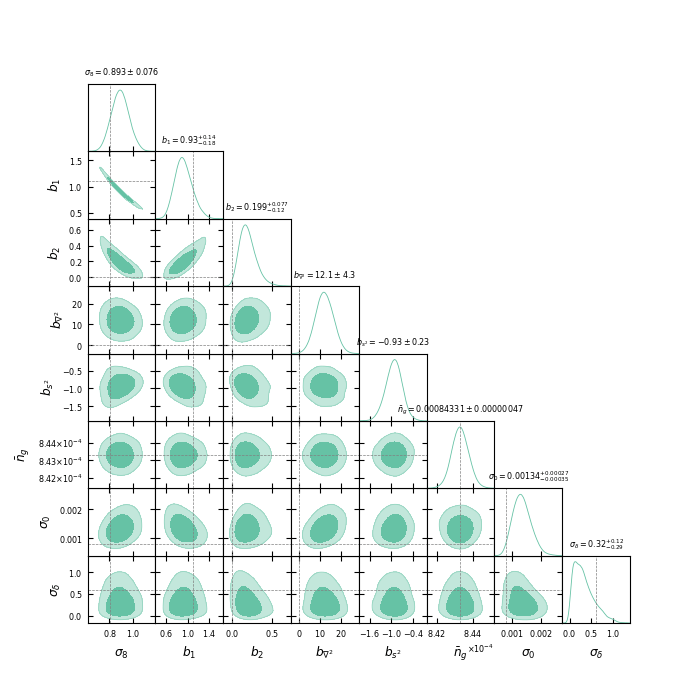
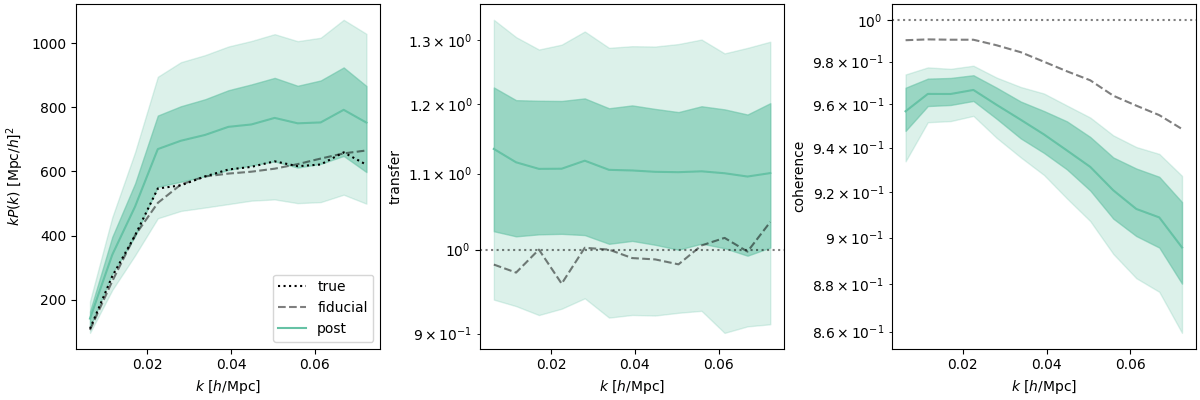
\((2\ \mathrm{Gpc}/h)^3,\, \operatorname{dim}(\delta_L) = 48^3\), \(k_\mathrm{nyq} = 0.05 h / \mathrm{Mpc}\)
PRELIMINARYInfer the initial conditions and \(\sigma_8\)
Preliminary FLI results on PNG
On AbacusSummit + HOD mock (\(f_\mathrm{NL}= 0\))
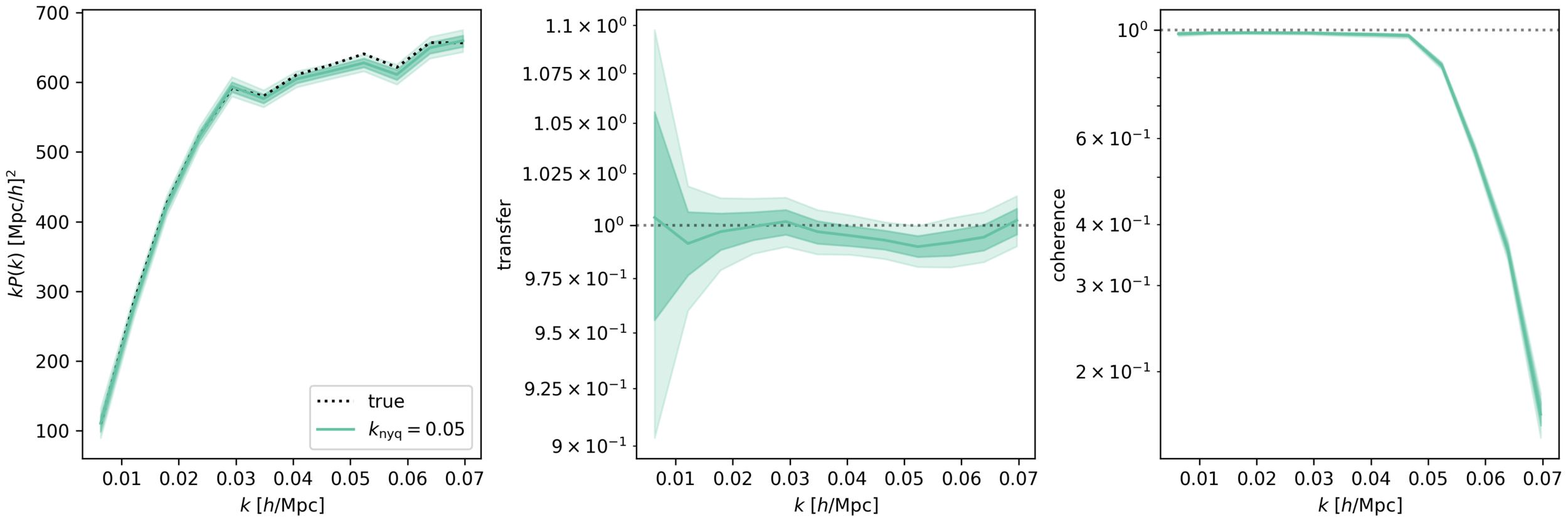
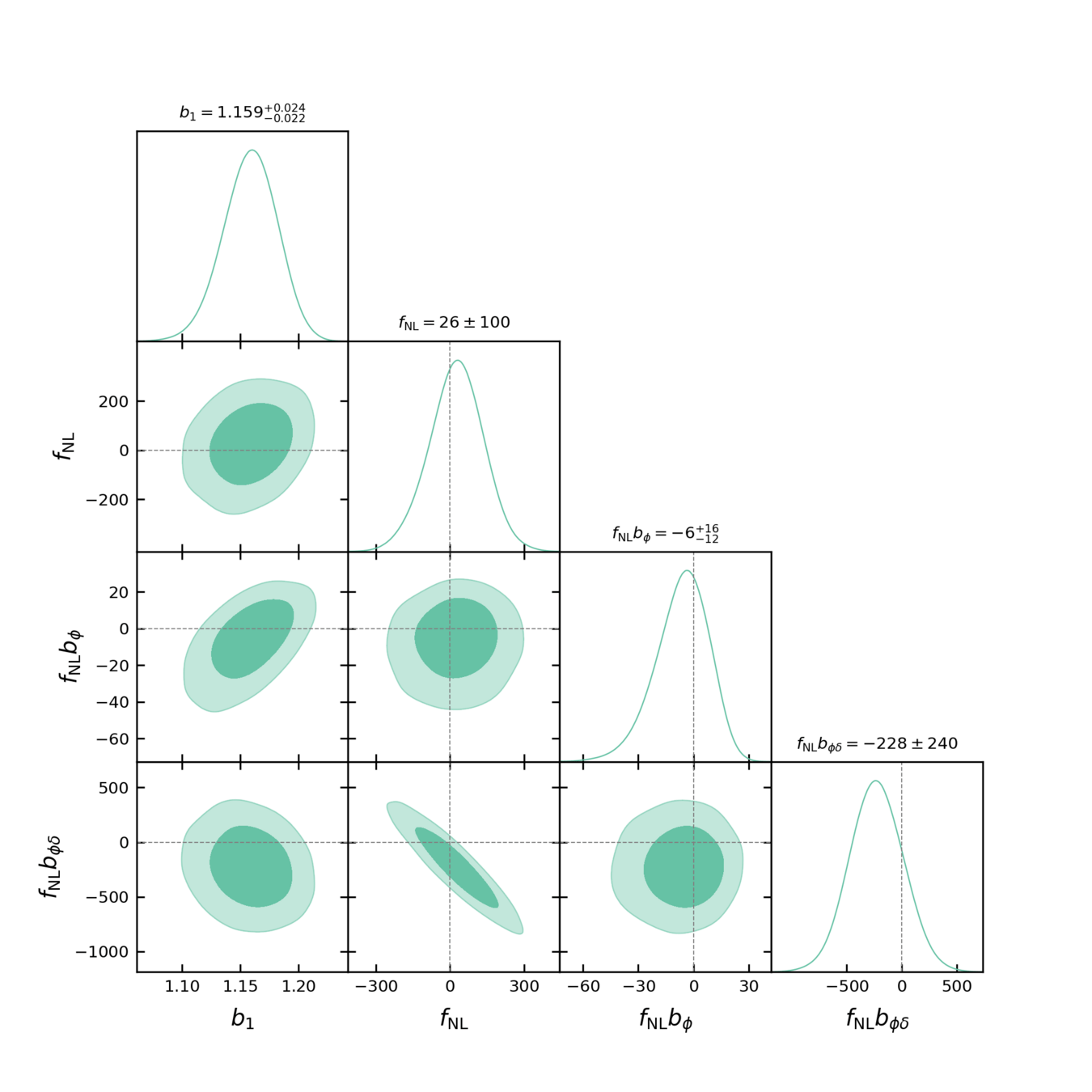
For \(k_\mathrm{nyq} = 0.05\ h/\mathrm{Mpc}\), inference compatible with \(f_\mathrm{NL}= 0\).
TBD: posterior calibration tests
\((2\ \mathrm{Gpc}/h)^3,\, \mathrm{LRG}\, z=0.8\)
PRELIMINARYPreliminary FLI results on PNG
On AbacusSummit + HOD mock (\(f_\mathrm{NL}= 0\))

For \(k_\mathrm{nyq} = 0.1\ h/\mathrm{Mpc}\),
\(f_\mathrm{NL} b_\phi\) compatible, but not \(f_\mathrm{NL} b_{\phi \delta}\) nor \(f_\mathrm{NL}\)
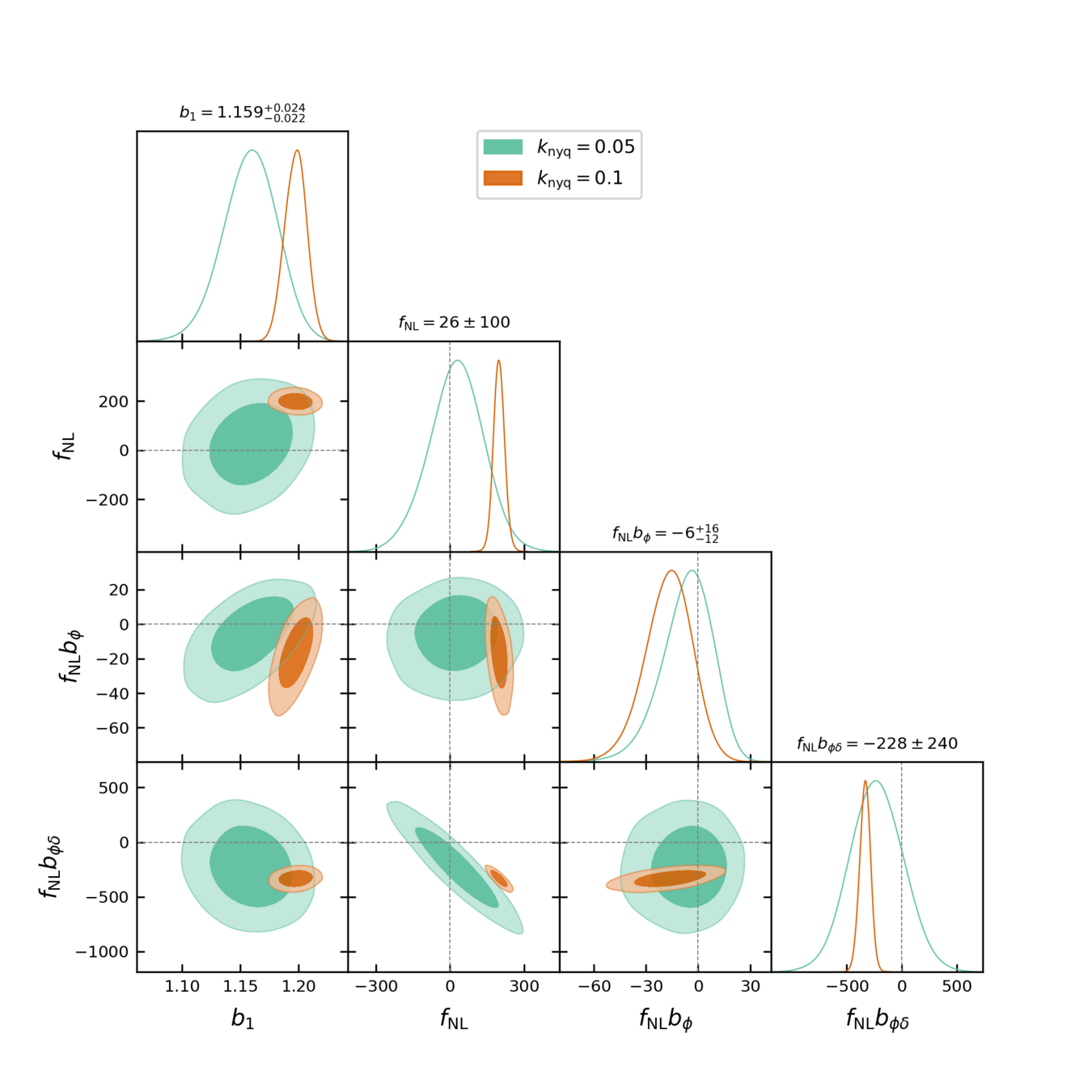

For \(k_\mathrm{nyq} = 0.05\ h/\mathrm{Mpc}\), inference compatible with \(f_\mathrm{NL}= 0\).
TBD: posterior calibration tests
\((2\ \mathrm{Gpc}/h)^3,\, \mathrm{LRG}\, z=0.8\)
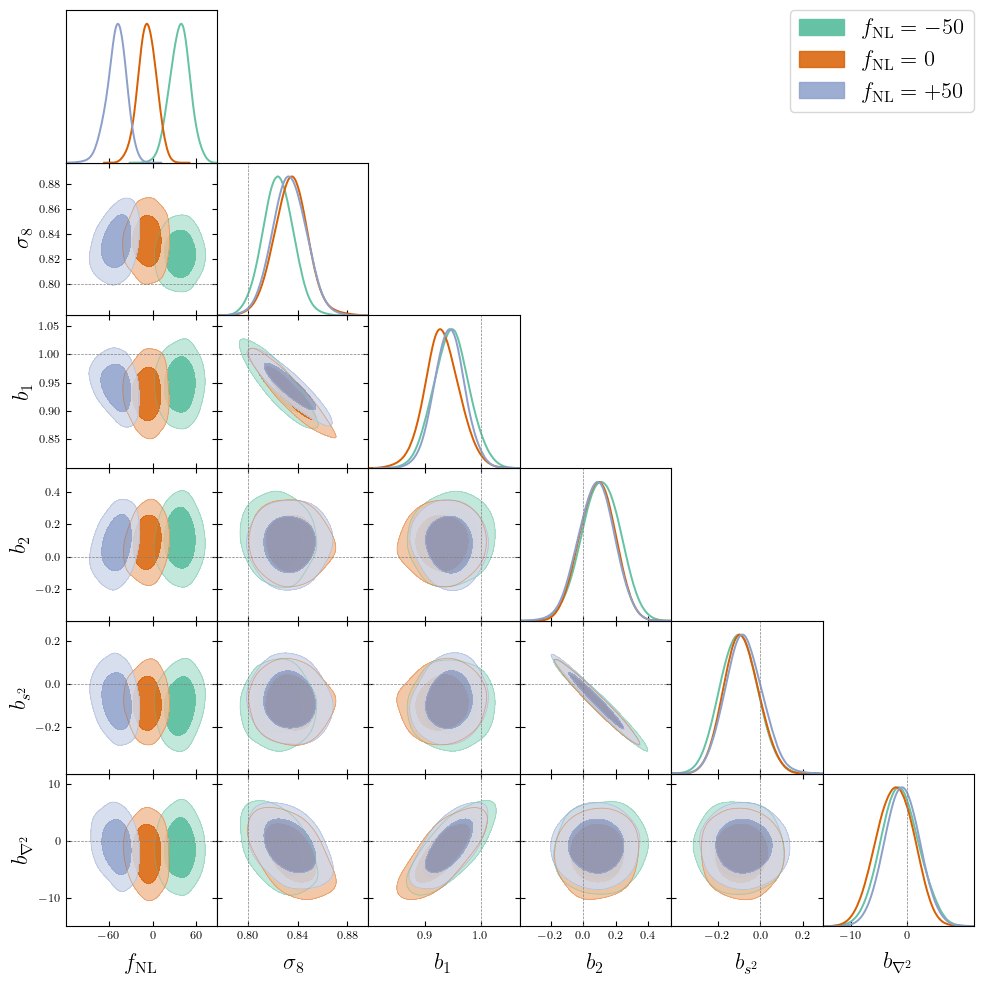
PRELIMINARYPreliminary FLI results on PNG
On \(f_\mathrm{NL}\neq 0\) FastPM + HOD mocks
PRELIMINARY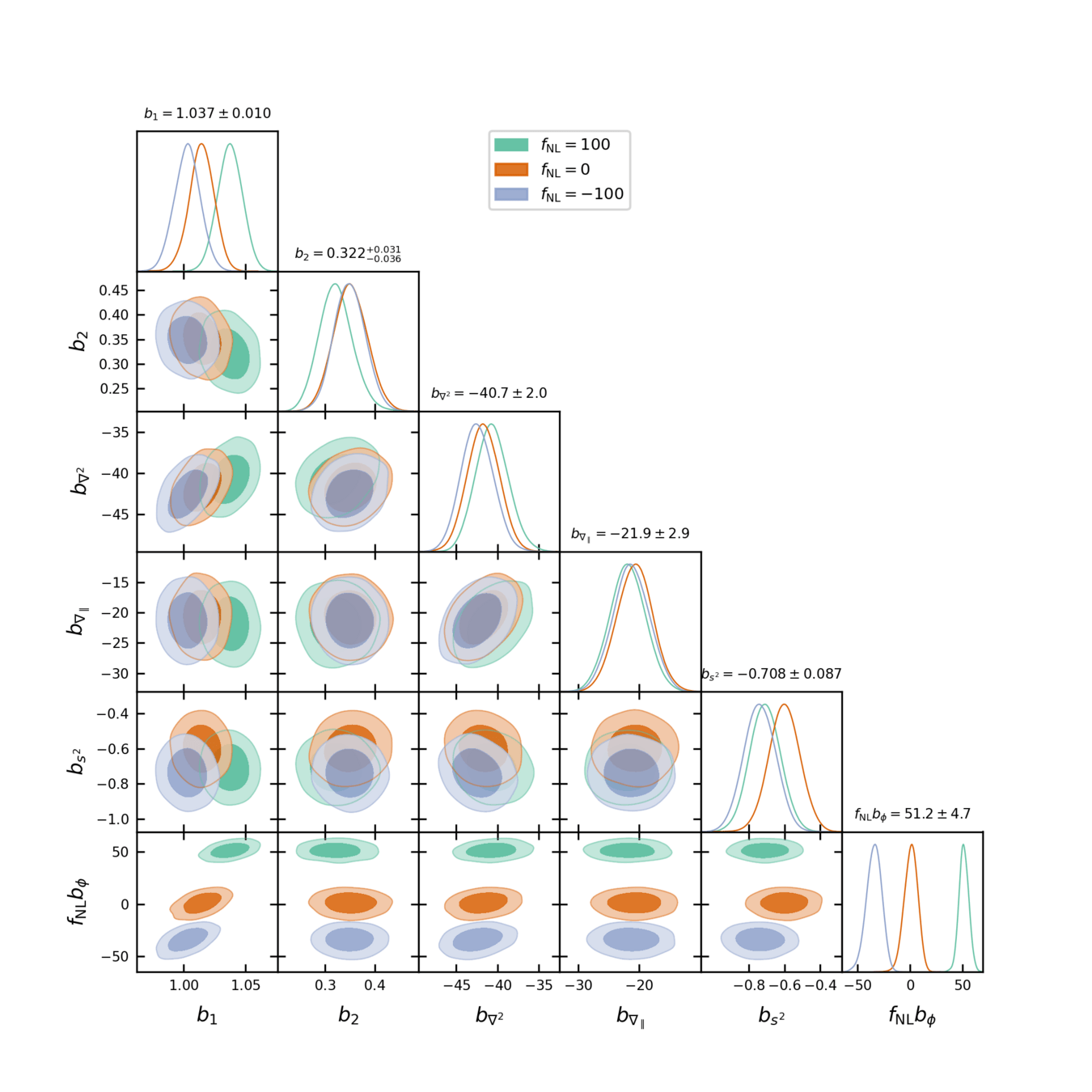
\((2.76\ \mathrm{Gpc}/h)^3,\,k_\mathrm{nyq} = 0.073 h/ \mathrm{Mpc},\\ \mathrm{QSO}\, z=1,\, \operatorname{dim}(\delta_L) = 96^3\)
Probing inflation with FLI
NOW: validation on AbacusSummit (DESI reference sims) and FastPM + HOD mocks
\((2.76\ \mathrm{Gpc}/h)^3,\,k_\mathrm{nyq} = 0.073 h/ \mathrm{Mpc},\\ \mathrm{QSO}\, z=1,\, \operatorname{dim}(\delta_L) = 96^3\)
PNG, ideal first demonstration of FLI:
- Most of signal from easier large scales
- Result very sensitive to systematics, more directly implemented at field-level
- Bonus: fully explicit/explainable

PRELIMINARYNext steps:
- Validation of survey realism on contaminated mocks
- Application to DESI LRGs and QSOs
In prep: Simon+2025
Preliminary FLI results on PNG
On \(f_\mathrm{NL}\neq 0\) FastPM + HOD mocks (courtesy of Edmond)
PRELIMINARY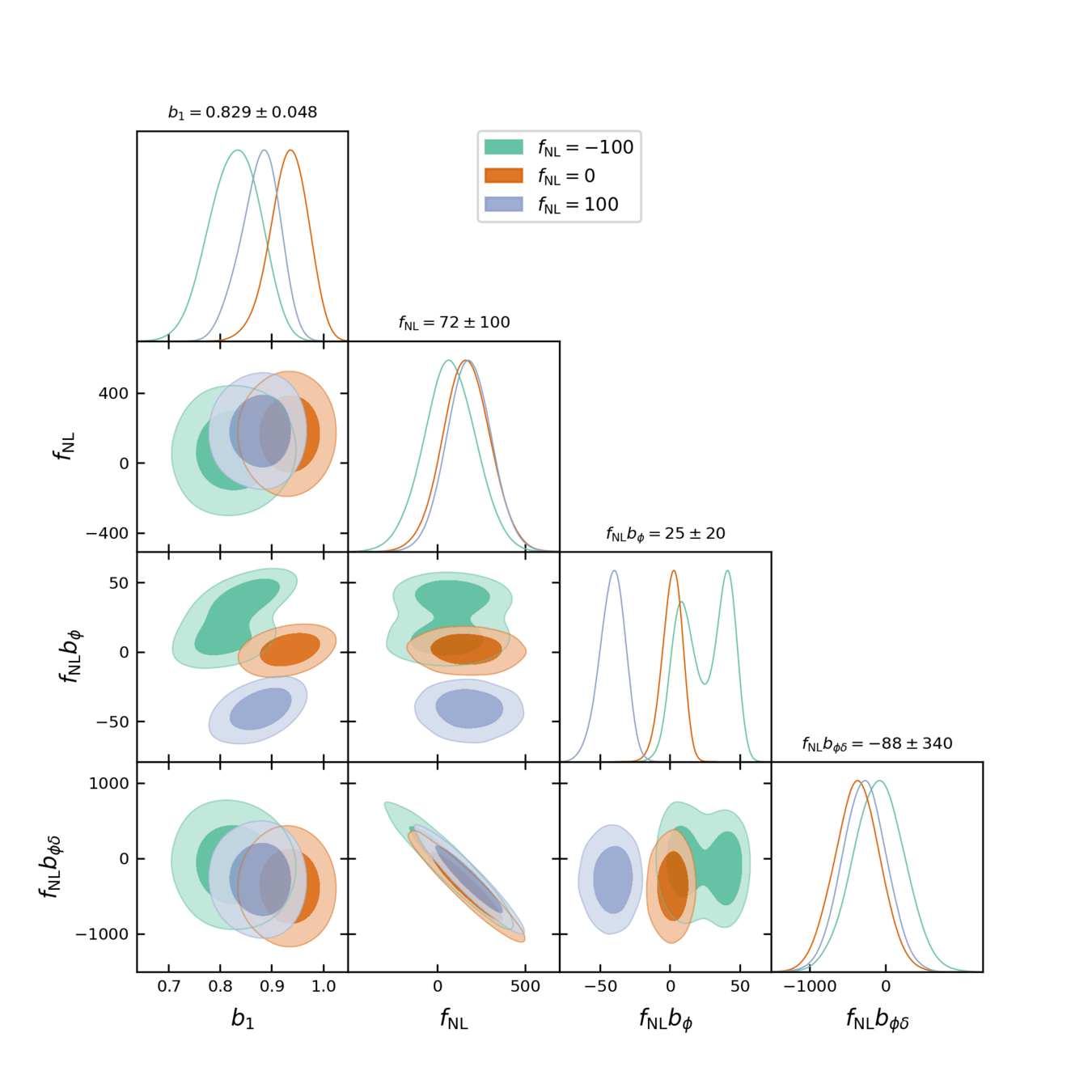
\((2.76\ \mathrm{Gpc}/h)^3,\,k_\mathrm{nyq} = 0.036 h/ \mathrm{Mpc},\\\, \mathrm{QSO}\, z=1,\,\operatorname{dim}(\delta_L) = 48^3\)
Preliminary FLI results on PNG
On \(f_\mathrm{NL}\neq 0\) FastPM + HOD mocks (courtesy of Edmond)
PRELIMINARY\((2.76\ \mathrm{Gpc}/h)^3,\,k_\mathrm{nyq} = 0.073 h/ \mathrm{Mpc},\\ \mathrm{QSO}\, z=1,\, \operatorname{dim}(\delta_L) = 96^3\)
Next steps:
- confirm the calibration at relevant scales on PNG-Unitsims
- light-cone, survey selection, imaging...
validation on contaminated mocks
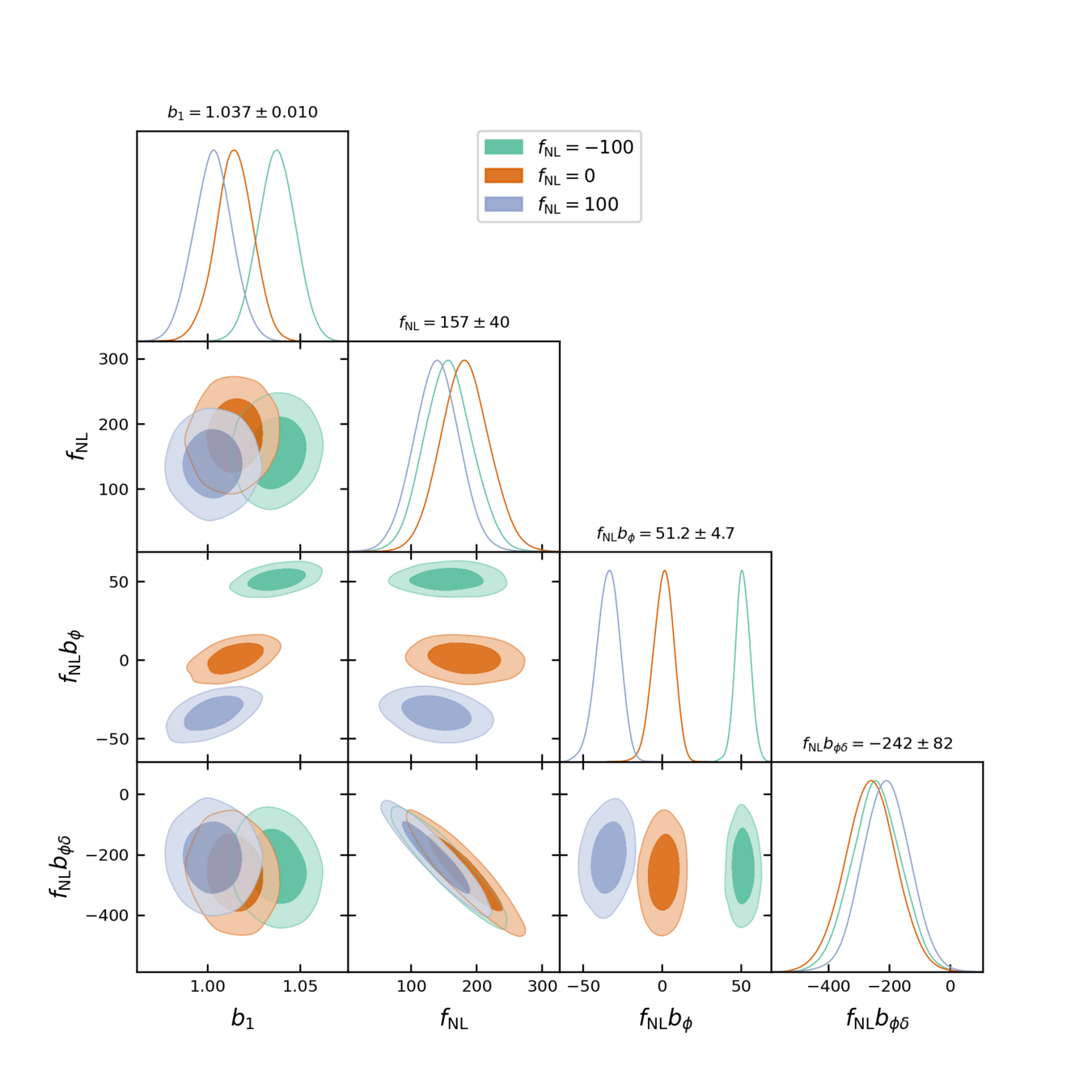
Preliminary FLI results on PNG
On \(f_\mathrm{NL}\neq 0\) FastPM + HOD mocks (courtesy of Edmond)

PRELIMINARY\((2.76\ \mathrm{Gpc}/h)^3,\,k_\mathrm{nyq} = 0.073 h/ \mathrm{Mpc},\\ \mathrm{QSO}\, z=1,\, \operatorname{dim}(\delta_L) = 96^3\)
PRELIMINARY
\((2.76\ \mathrm{Gpc}/h)^3,\,k_\mathrm{nyq} = 0.036 h/ \mathrm{Mpc},\\\, \mathrm{QSO}\, z=1,\,\operatorname{dim}(\delta_L) = 48^3\)
Next steps:
- confirm the calibration at relevant scales on PNG-Unitsims
- light-cone, survey selection, imaging...

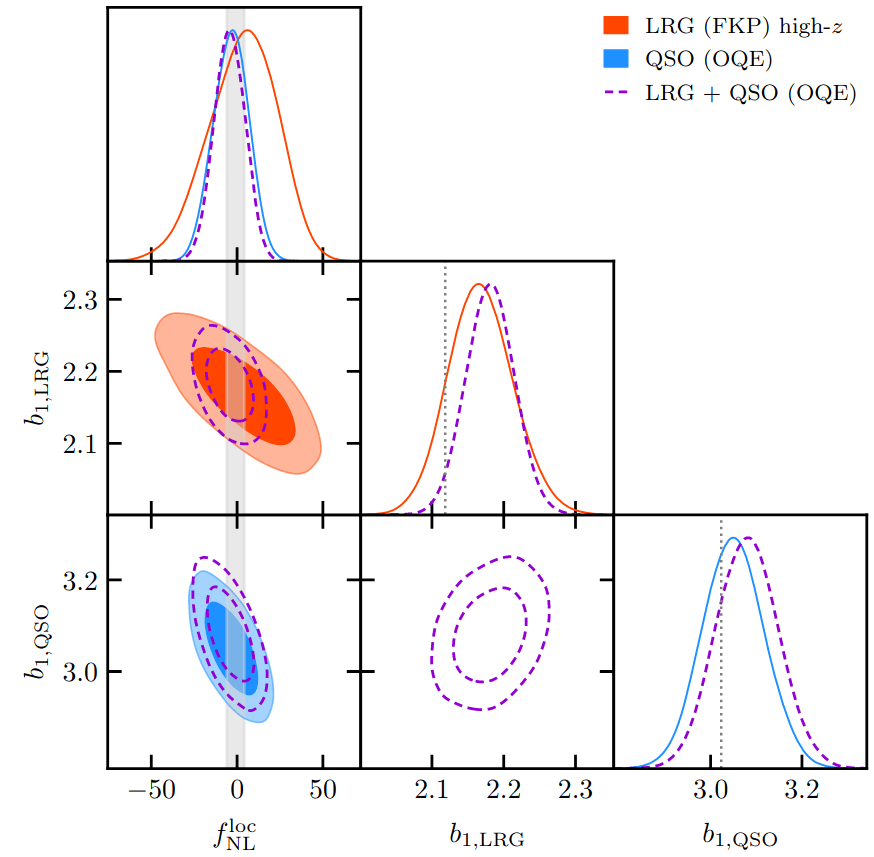
PRELIMINARYPrevious results
on LRG SGC footprint (self-specified)
\(k_\mathrm{max} \approx 0.04\ h/\mathrm{Mpc}\)
\(\sigma[f_\mathrm{NL}] \approx 20\), consistent with power spectrum analysis (Chaussidon+2024)
Roadmap:
- model validation (w/o PNG) on AbacusSummit
- model validation (w/ PNG) on PNG-Unitsims
- Systematics model validation on contaminated mocks
- Application to DESI DR1 LRG and QSO
| Part | Implementation | Validation |
|---|---|---|
| MCMC | ✅️ | ✅️ |
| LSS formation | ✅️ | ✅️ |
| Galaxy bias | ✅️ | ✅️ |
| Galaxy stochasticity | ✅️ | 🗘 |
| Selection | ✅️ | 🗘 |
| Lightcone | ✅️ | |
| Integral Constraint | ✅️ | |
| Imaging |
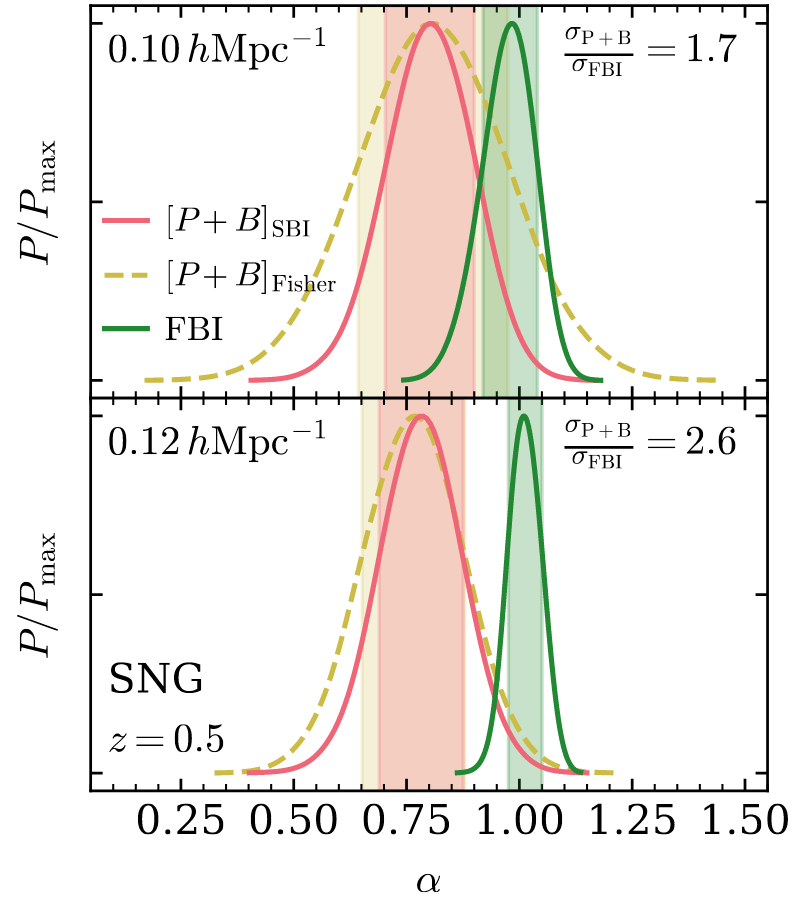
Field-level implementation is
more direct than for P+B analyses
- Lightcone
- Survey selection
- Imaging (linear modeling for LRG and QSO,
more complex for ELG) - Radial Integral Constraint
Toward more survey realism
Less relevant for PNG:
- Fiber assignment (incomplet.+competition+collisions)
- Redshift uncertainty
\(\Delta z\) due to broad QSO bands
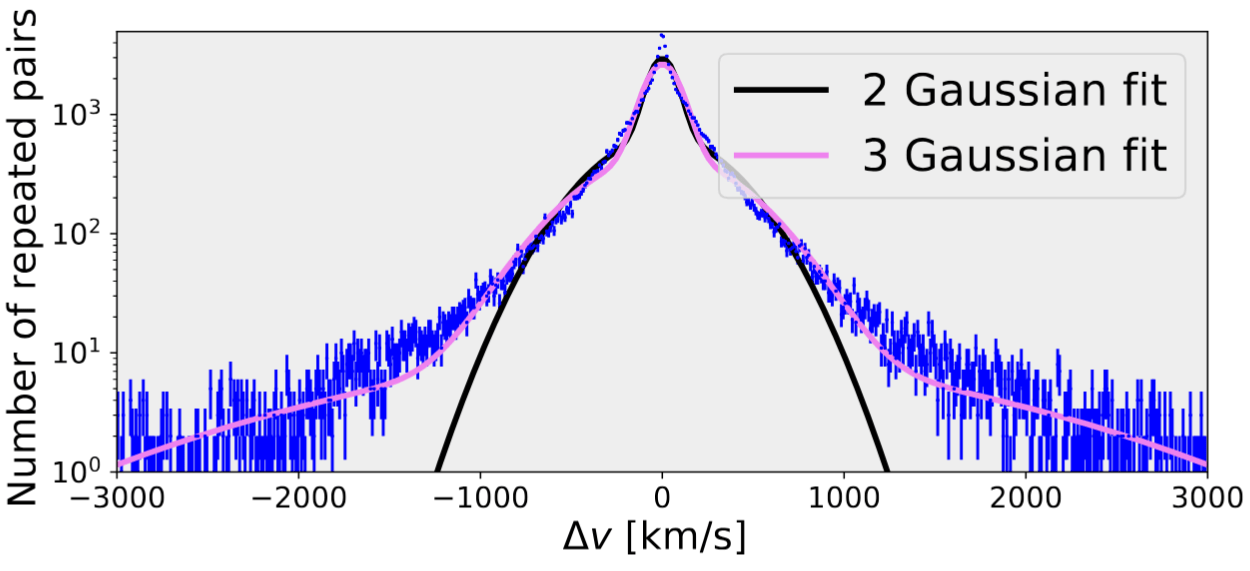
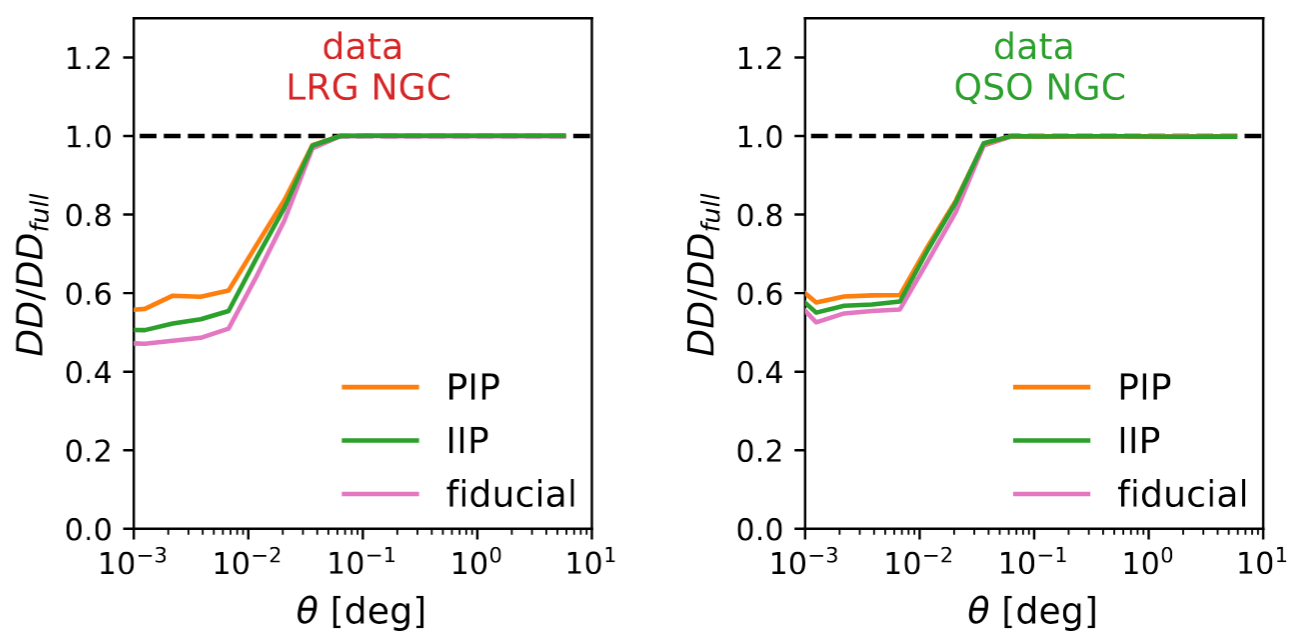
FA damping at small angles
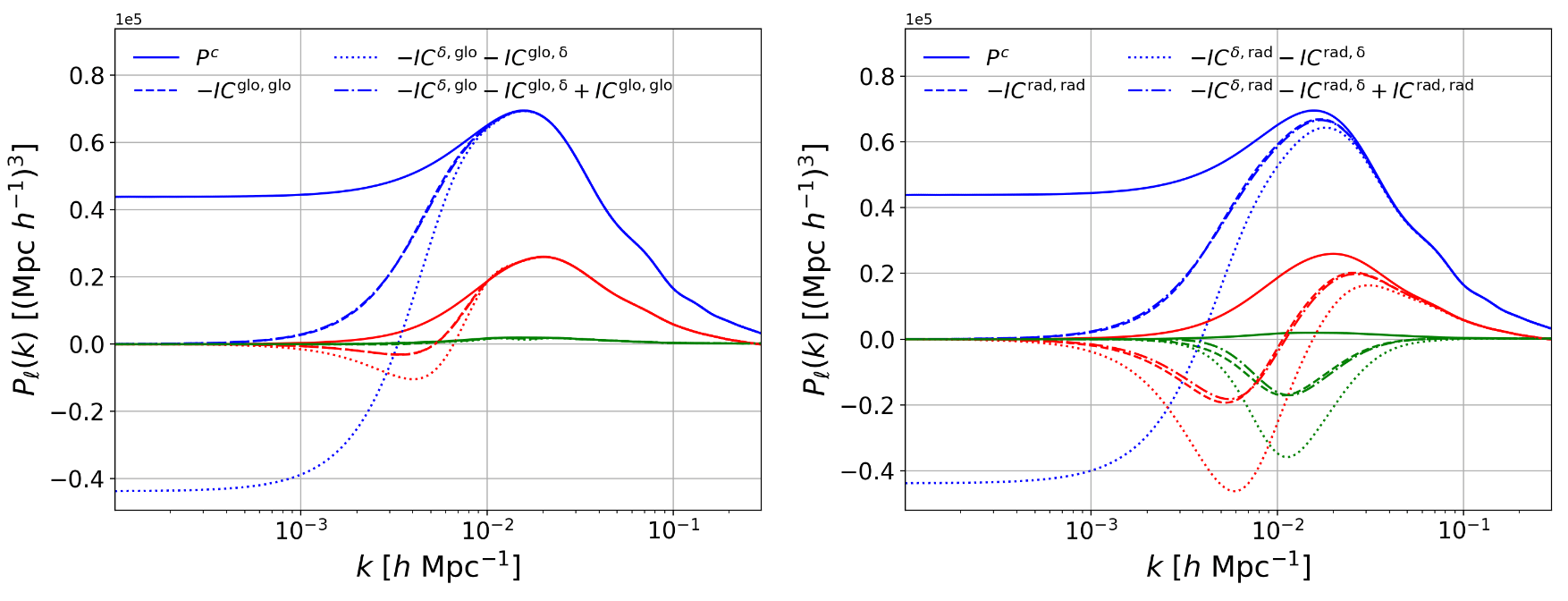
RIC damping on large scales
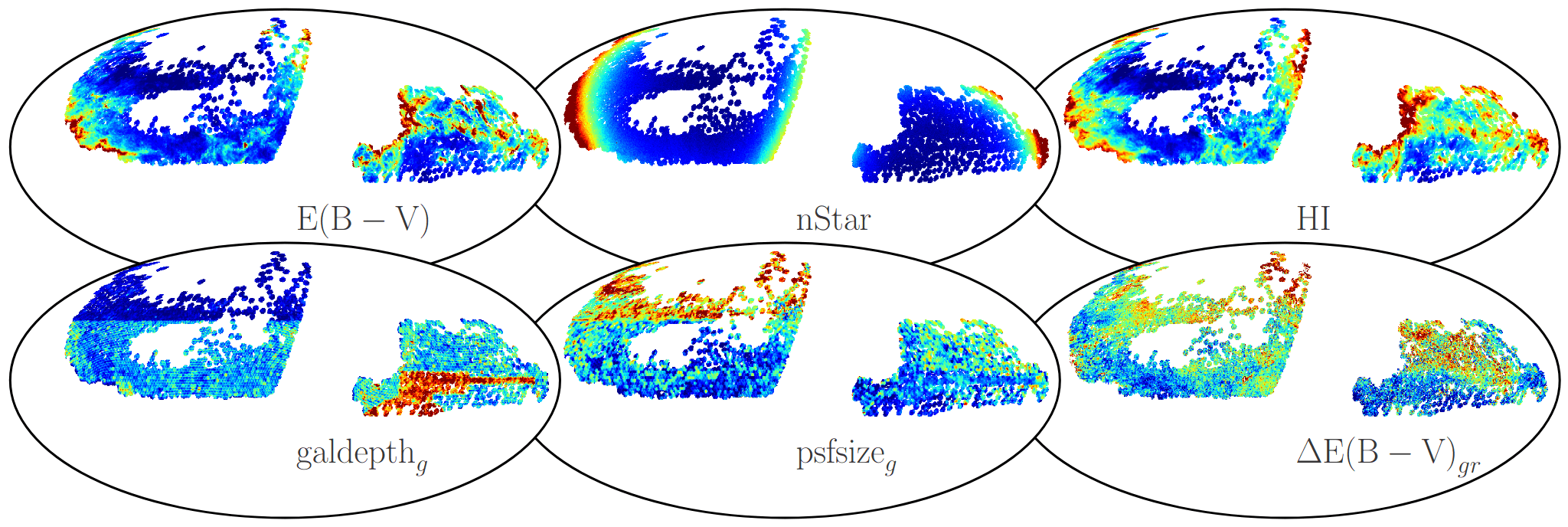
Imaging templates
Field-level implementation is
more direct than for P+B analyses
- Lightcone
- Survey selection
- Imaging (linear modeling for LRG and QSO,
more complex for ELG) - Radial Integral Constraint
Toward more survey realism
Less relevant for PNG:
- Fiber assignment (incomplet.+competition+collisions)
- Redshift uncertainty
\(\Delta z\) due to broad QSO bands


FA damping at small angles

RIC damping on large scales

Imaging templates


PRELIMINARY\(k_\mathrm{max} \approx 0.04\ h/\mathrm{Mpc}\)
FLI on LRG SGC footprint with lightcone, survey selection, and RIC
Perspectives for FLI with PFS and DESI
- Make use of overlap between DESI and PFS tracers
- Approximate sampling methods for fast iterations
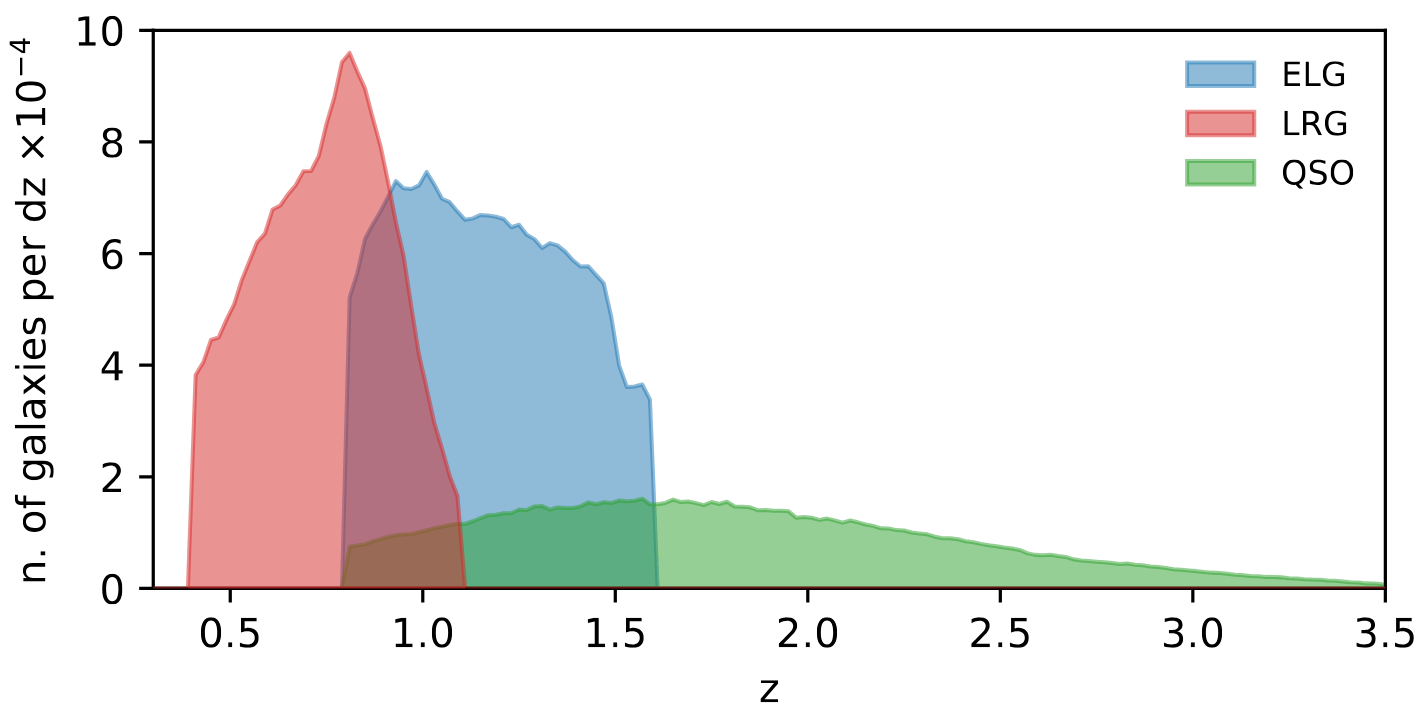
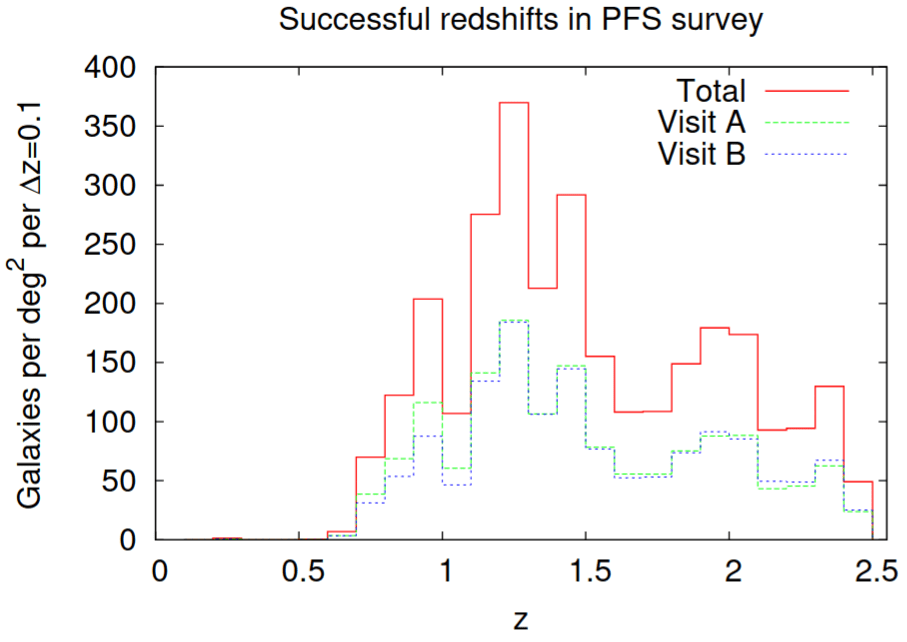



- To probe smaller scales and constrain structure growth, improve and robustify EFT modeling, FoG peculiar velocities, ELG imaging, informed by high-fidelity simulations

Perspectives for FLI with DESI

-
To probe smaller scales, revise EFT likelihood, peculiar velocities, ELGs, FA, and \(\Delta z\)
- Make use of the overlap between DESI tracers
- Extend EFT modeling to Ly\(\alpha\)-forests to probe LSS at higher redshift
- Approximate sampling methods for fast iterations

\(k_\perp\) might be enough, espec. for DR2

FoG+broad QSO bands
\((k\mu)^2\) might not be enough
Perspectives for FLI with DESI

-
To probe smaller scales, revise EFT likelihood, peculiar velocities, ELGs, FA, and \(\Delta z\)
- Make use of the overlap between DESI tracers for cosmic variance cancellation
- Extend EFT modeling to Ly\(\alpha\)-forests to probe LSS at higher redshift
- Approximate sampling methods for fast iterations

\(k_\perp\) might be enough, espec. for DR2

FoG+broad QSO bands
\((k\mu)^2\) might not be enough
Perspectives for FLI with DESI
-
Approximate sampling methods for fast iterations
$$\log p(x,\theta) \approx \log p(x,\theta,\hat z) + \tfrac{d}{2}\log(2\pi) +\tfrac12\log |H_z(x,\theta,\hat z)|$$
Laplace Approx with Hutchinson trace and Chebyshev polynomials for stochastic estimation of the log determinant. Then plug in MCLMC?
- Boltzmann sampling with diffusion model?

Thank you!
Field-level modeling of PNG
$$\begin{align*}w_g&=1+{\color{purple}b_{1}}\,\delta_{\rm L}+{\color{purple}b_{2}}\delta_{\rm L}^{2}+{\color{purple}b_{s^2}}s^{2}+ {\color{purple}b_{\nabla^2}} \nabla^2 \delta _{\rm L}\\&\quad\quad\! + {\color{purple}b_\phi f_{\rm NL}} \phi + {\color{purple} b_{\phi\delta} f_{\rm NL}} \phi \delta_{\rm L}\\\Delta \boldsymbol q_\parallel &= H^{-1} \dot{\boldsymbol q}_\parallel + {\color{purple}b_{\nabla_\parallel}} \nabla_\parallel \delta_\mathrm{L}\end{align*}$$
\(\phi_{\mathrm{NL}}=\phi+{\color{purple}f_{\mathrm{NL}}}\phi^{2}\)
\(\boldsymbol q_\mathrm{LPT} \simeq \boldsymbol q_\mathrm{in} + \Psi_\mathrm{LPT}(\boldsymbol q_\mathrm{in}, z(\boldsymbol q_\mathrm{in}))\)
one-shot 2LPT light-cone
\(n_g^\mathrm{obs}(\boldsymbol q) \approx (1+\delta_g(\boldsymbol q))\, {\color{purple}\bar n_g(\,r)}\, {\color{blue}W(\boldsymbol q)}\, (1+{\color{purple}\beta_i} {\color{green}T^i(\theta)})\)
RIC relax + selection + imag. templates
\(\delta_g \sim \mathcal N(\delta_g^\mathrm{det}, \sigma^2)\) with
\(\sigma(k) = {\color{purple}\sigma_0}(1+{\color{purple}\sigma_2} k^2 + {\color{purple}\sigma_{\mu2}}(k\mu)^2)\)
EFT-based modeling, many scale cuts alleviating discretization effects (see Stadler+2024)
A word on integral constraints


Radial Integral Constraint
\(\delta_g \propto n_g - \braket{n_g}\approx n_g - \bar n_g(r)\)
i.e. impose \(\bar \delta_g(r) = 0\)
Global Integral Constraint
\(\delta_g \propto n_g - \braket{n_g} \approx n_g - \bar n_g\)
i.e. impose \(\bar \delta_g = 0\)
To be answered
-
3 \(f_\mathrm{NL}\) "values" to infer:
- \(f_\mathrm{NL}\) in init field, \(b_\phi f_\mathrm{NL}\) and \(b_{\phi\delta} f_\mathrm{NL}\) in galaxy bias
-
"universality" relations robust at field-level?
\(b_\phi = 2 \delta_c (1 + b_1 - p)\) and \(b_{\phi \delta} = b_\phi - b_1 + \delta_c b_2\)
-
Redshift varying biases? templates?
- \(b_1(z) = a_1 (1+z)^2 + c_1\)? \(b_2(z)\), \(b_s^2(z)\),...?
- Redshift bins? Interpolation?
- Max resolution we can robustly + computationally push to
- \(k_\mathrm{max} \leq 0.14\, h/\mathrm{Mpc}\)?

Where we are
What it looks like
Inferring jointly cosmology, bias parameters, and initial matter field allows full universe history reconstruction


million-dimensional inference:
4h on 1 GPU node vs. days/weeks for other codes
- Different samplers and strategies used for field-level (e.g. Lavaux+2018, Bayer+2023). Additional comparisons required.
- We provide a consistent benchmark for field-level from galaxy surveys. Build upon \(\texttt{NumPyro}\) and \(\texttt{BlackJAX}\).
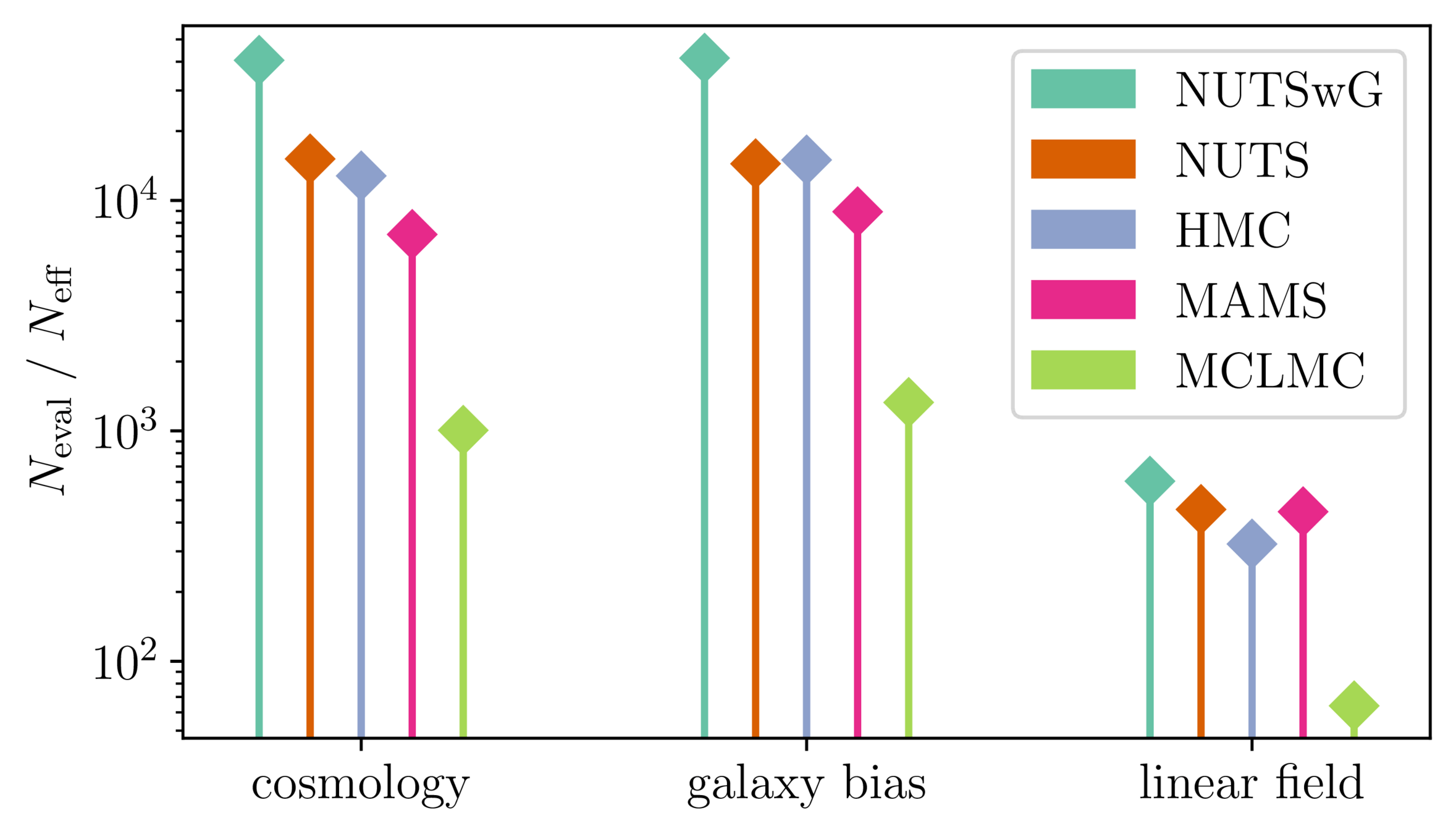
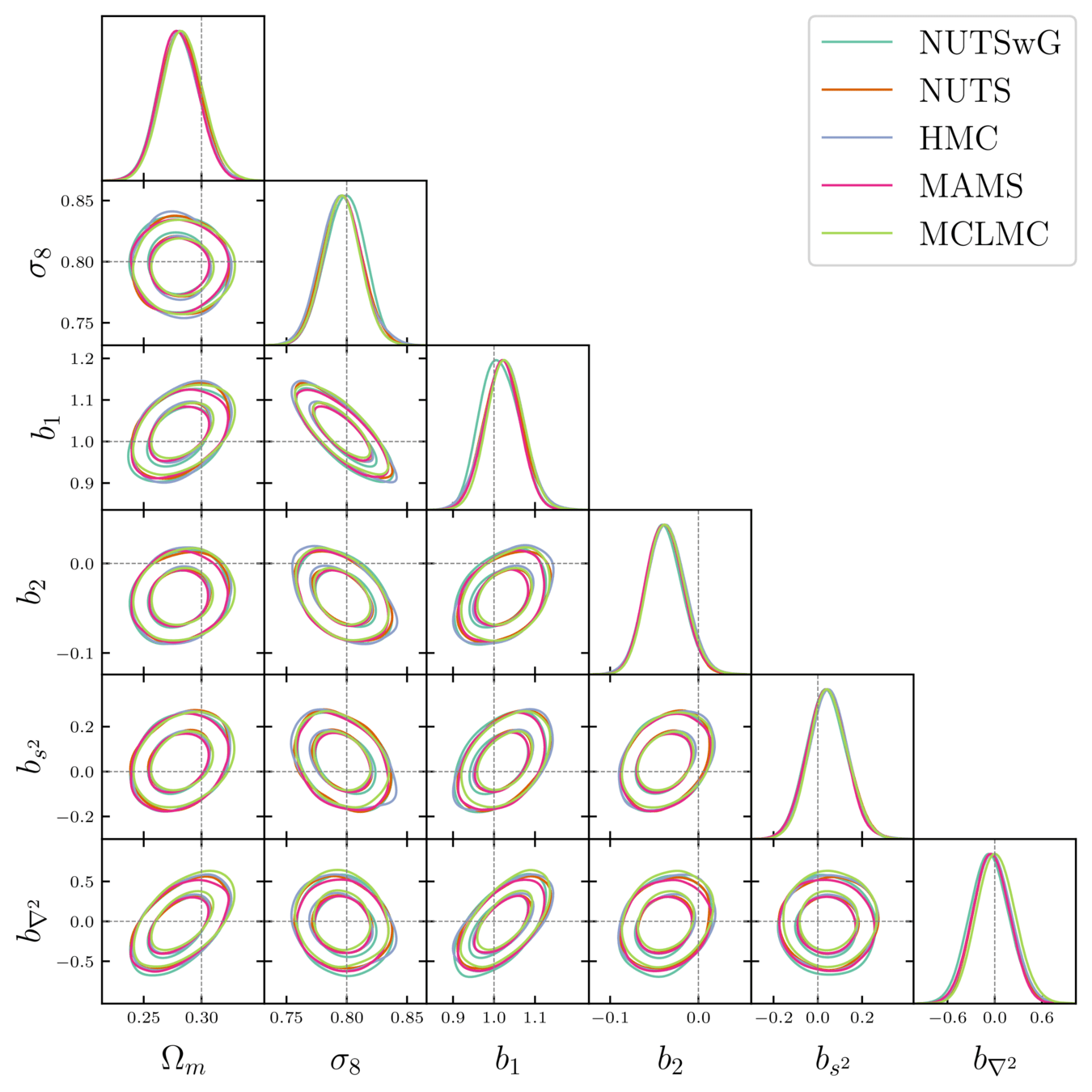
Samplers comparison
= NUTS within Gibbs
= auto-tuned HMC
= adjusted MCHMC
= unadjusted Langevin MCHMC
10 times less evaluations required
Unadjusted microcanonical sampler outperforms any adjusted sampler
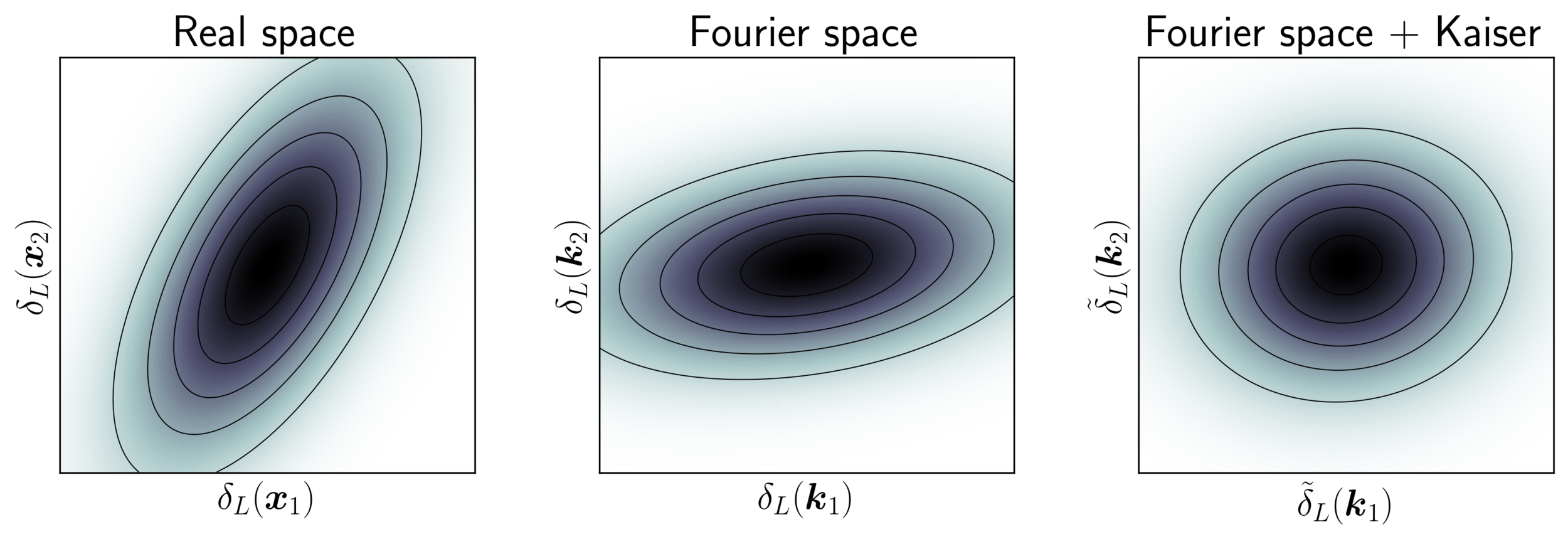
Model preconditioning
- Sampling is easier when target density is isotropic Gaussian
- The model is reparametrized assuming a tractable Kaiser model:
linear growth + linear Eulerian bias + flat sky RSD + Gaussian noise
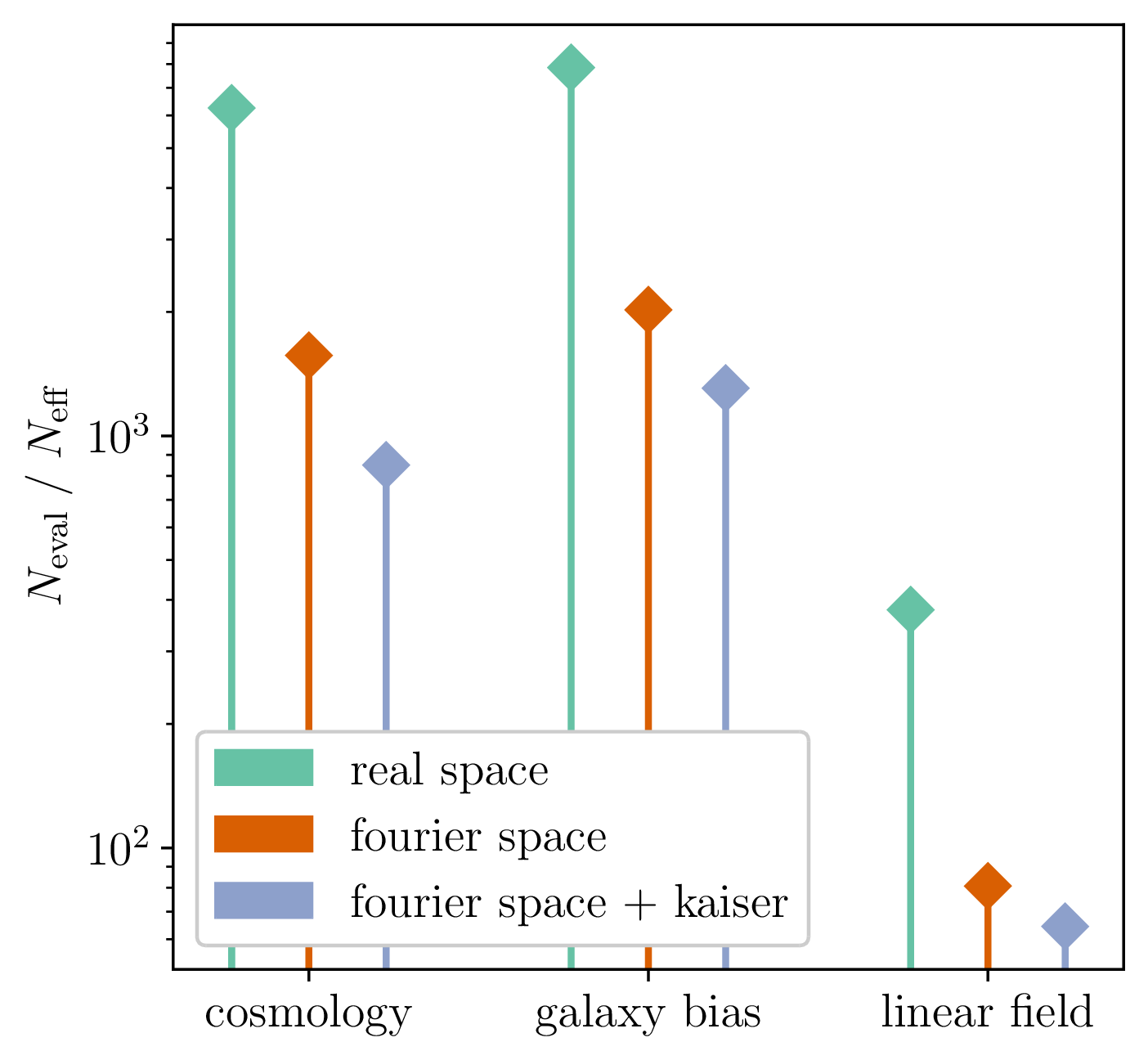
10 times less evaluations required


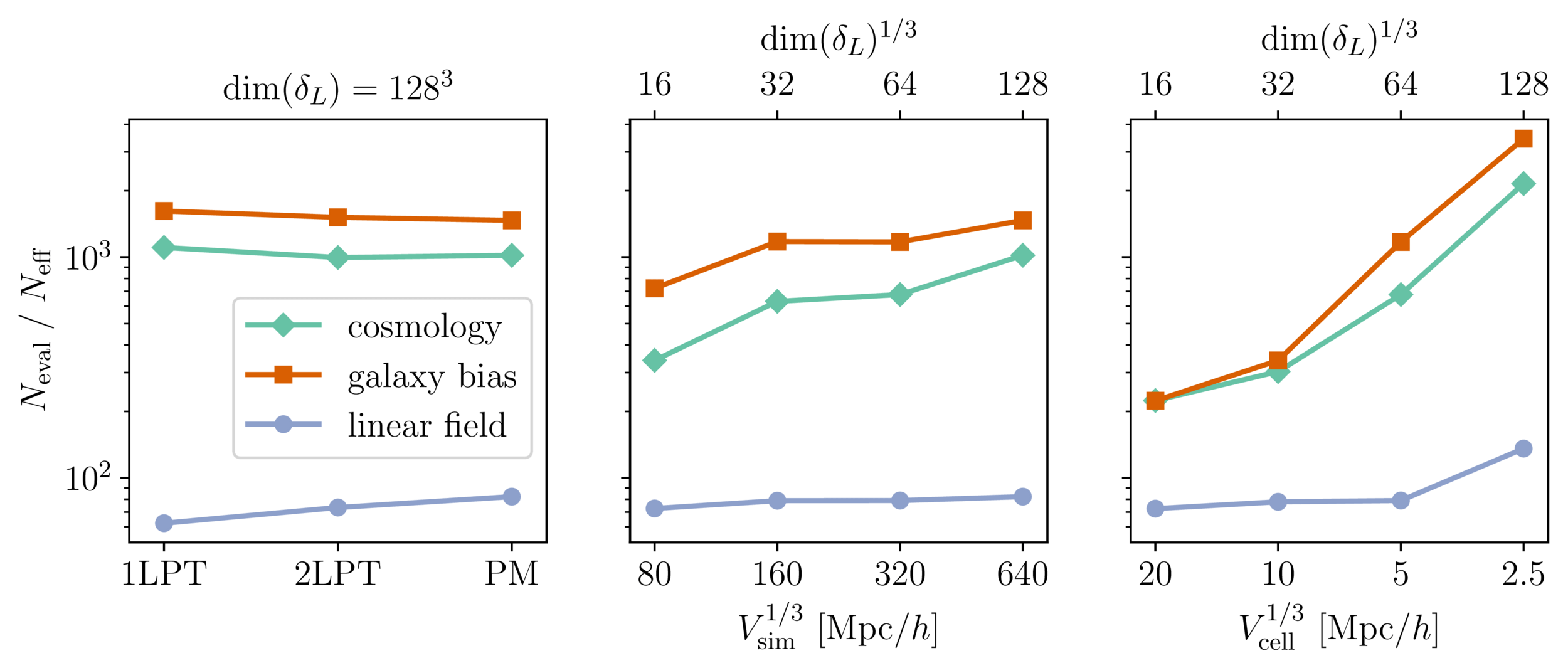
Benchmark results
- Promising for future inferences, going multi-GPU using JaxDecomp
- Code readily available at github.com/hsimonfroy/benchmark-field-level
Mildly dependent with respect to formation model and volume
Probing smaller scales could be harder
MCLMC sampler + field-level preconditioning assuming a linear Kaiser model:
4h on a 8GPU-node for \(128^3\) PM inference
Handling bias in unadjusted MCLMC
- Microcanonical dynamics \(\implies\) energy should not vary
- Numerical integration yields quantifiable errors that can be linked to bias
- Stepsize can be tuned to ensure controlled bias, see Robnik+2024
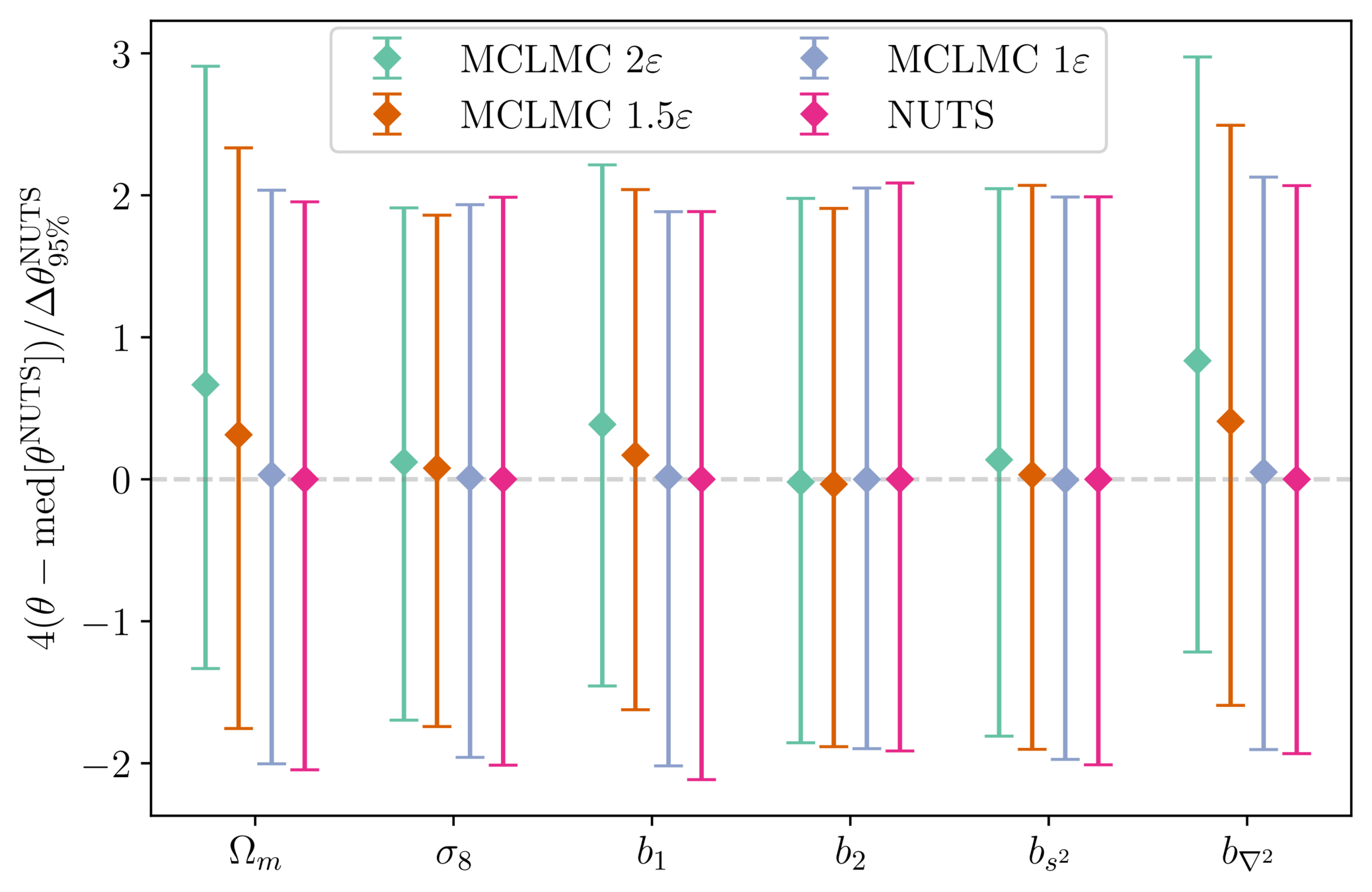
reducing stepsize rapidly brings bias under Monte Carlo error
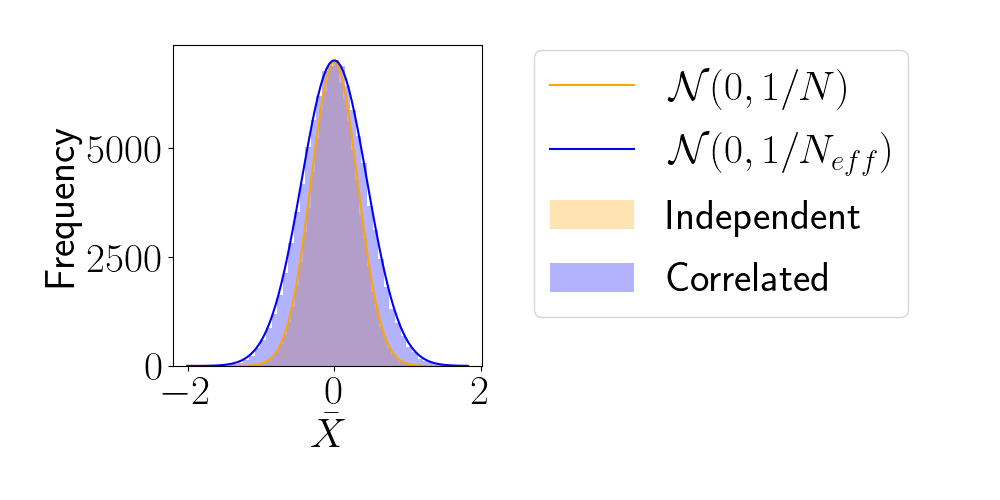
-
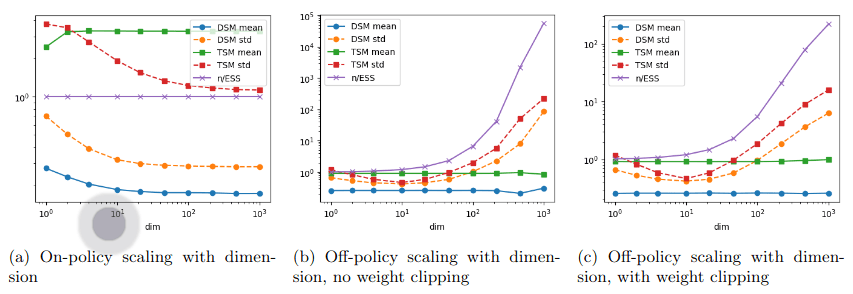
Effective Sample Size (ESS)
- number of i.i.d. samples that yield same statistical power.
- For sample sequence of size \(N\) and autocorrelation \(\rho\) $$N_\textrm{eff} = \frac{N}{1+2 \sum_{t=1}^{+\infty}\rho_t}$$so aim for as less correlated sample as possible.
- Main limiting computational factor is model evaluation (e.g. N-body), so characterize MCMC efficiency by \(N_\text{eval} / N_\text{eff}\)
How to compare samplers?
Tally
- Currently visiting Montréal in Laurence Perreault-Levasseur team
- Talks:
- Optimal cosmo information extraction at Sesto (for Euclid people)
- DESI meeting at Berkeley (for colab)
- CoBALt at Institut Pascal (for inflation theorists)
- Bayesian Deep Learning 3 at APC (for deep learners)
- ED Festival (for particle physicists)
- GDR Cophy 2h tutorial
- Papers:
- stat paper at NeurIPS2024 (from master internship)
- Benchmarking Field-Level in review on JCAP
- PNG measurement at the field level in prep
- Teaching: Bachelor 2 Biostats (20h) and Master 1 Maths (15) courses at UPsaclay
- Formation:
- VSS, Science ethics, Sustainable dev. (Open Science left)
- Euclid summer school

Next steps
- Scientific:
- Validation for PNG inference and application to DESI
- Alternative sampling method for field-level inference
- Going Multi-GPU
- Manuscript:
- Detailed plan at the end of December, first chapter in January
- Looking and applying for postdocs this Autumn,
hence the meetings and visits...


Hugo SIMON
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE



- Field-level Bayesian inference
- High-dimensional sampling
- Differentiable N-body simulations
- Primordial non-Gaussianity from DESI


Hugo SIMON
PhD student at CEA Paris-Saclay, supervised by
Arnaud DE MATTIA and François LANUSSE


- Field-level Bayesian inference
- High-dimensional sampling
- Differentiable N-body simulations
- Primordial non-Gaussianity field-level inference from DESI