The Team

Hugo Hadfield

Queens' College

Eric Wieser

Gonville and Caius College

Prof. Joan Lasenby

Trinity College

Cambridge University Signal Processing and Communications Laboratory

CGA Robotics Motivation

Building algorithms to control robots is inherently geometric

 

Forward Kinematics is typically all about composing and chaining transformations (rotation and translation)

 

Inverse Kinematics requires finding intersections and reflections of geometric primitives (especially circles and spheres)

 

Conformal Geometric Algebra (CGA) combines many geometric primitives, intersections and transformations

Geometric Algebra Recap

Set up a bunch of orthogonal basis vectors, define the geometric product of a basis vector with itself, eg. for 3DGA

e_1e_1 = 1, \, e_2e_2 = 1, \, e_3e_3 = 1

The multiplication of two orthogonal basis vectors anticommutes and we often use a shorthand to write it

e_1e_2 = -e_2e_1 = e_{12}

If we now make two vectors and multiply them with the geometric product we can see what happens

(e_1 + e_2)(e_1 + e_3) = e_1e_1 + e_2e_1 + e_2e_3 + e_1e_3 \\ = 1 - e_{12} + e_{23} + e_{13}
e_1e_1 = 1, \, e_2e_2 = 1, \, e_3e_3 = 1

Geometric Algebra Recap 2.

The result of the geometric product has both terms that are scalars and terms that are the multiplication of two basis vectors

(e_1 + e_2)(e_1 + e_3) = 1 - e_{12} + e_{23} + e_{13}

Let's define an operation, the grade selection operation

\left< 1 - e_{12} + e_{23} + e_{13}\right>_0 = 1
\left< 1 - e_{12} + e_{23} + e_{13}\right>_2 = - e_{12} + e_{23} + e_{13}

If there is nothing of the grade in there, then it gives 0

\left< 1 - e_{12} + e_{23} + e_{13}\right>_1 = 0

Geometric Algebra Recap 3.

The result of the geometric product can be written with grade selection

(e_1 + e_2)(e_1 + e_3) = \left< (e_1 + e_2)(e_1 + e_3) \right>_0 + \left< (e_1 + e_2)(e_1 + e_3) \right>_2\\ = 1 - e_{12} + e_{23} + e_{13}

Inner (dot) product

And this motivates us to define two new products...

Outer (wedge) product

X_a\wedge Y_b = \left< X_a Y_b \right>_{a+b}
X_a\cdot Y_b = \left< X_a Y_b \right>_{|a-b|}

Note: people define various different behaviours of the inner product with scalars

3D to 5D

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } X = \frac{1}{2}x^2\ninf + x + \no

CGA creates two more basis vectors that square to +1 and -1 respectively:


\[ e_1^2 = 1, e_2^2 = 1, e_3^2 = 1, \bf{e_4^2 = 1, e_5^2 = -1} \]
We use the extra basis vectors to construct two null vectors *


n_{\infty} = e_4 + e_5
n_{0} = \frac{1}{2}(e_5 - e_4)

Then use the null vectors to embed our 3D point in 5D

* Note, people use a range of different notations here in papers etc, it doesn't really matter what you use as long as you are consistent!

For more info see references [1,2]

Properties of the mapping

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } X = up(x) = \frac{1}{2}x^2\ninf + x + \no

This is not a random choice!

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } X_1 \cdot X_2 \propto (x_1 - x_2)^2

Dot product between points is proportional to the squared distance between them

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } X^2 = 0

The null vectors correspond to the origin and infinity!

n_0 = up(0)

Check:

Like in graphics programming where we work with 4D homogeneous coordinates, here we go to 5D for more power :)

Representing Primitives

Geometric primitives can be made by wedging points together (see [2,3])

Point

Point pair/line segment

Circle

Infinite line

Sphere

Infinite plane

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } X = up(x) = \frac{1}{2}x^2\ninf + x + \no
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } P = X_1\wedge X_2
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } C = X_1\wedge X_2 \wedge X_3
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } L = X_1\wedge X_2 \wedge \bf{\ninf}
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } S = X_1\wedge X_2 \wedge X_3 \wedge X_4
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \Pi = X_1\wedge X_2 \wedge X_3 \wedge \bf{\ninf}

Representing Primitives 2

Geometric primitives can be made from traditional parameterisations via their dual (see [2,3])

Point pair

line segment

Circle

Infinite line

Infinite plane

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } P = -[(\hat{m} I_3 - (x_c\wedge \hat{m})I_3\ninf)\wedge(X_c - \frac{1}{2}\rho^2\ninf)]I_5
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } C = -[(\hat{m} + (\hat{m}\cdot x_c)\ninf)\wedge(X_c - \frac{1}{2}\rho^2\ninf)]I_5
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } L = -(\hat{m} I_3 - (x\wedge \hat{m})I_3\ninf)I_5
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \Pi = -(\hat{m} + d\ninf)I_5

Sphere

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } S = -(X_c - \frac{1}{2}\rho^2 \ninf)I_5

Primitive Intersections

The meet or vee operator does intersection: \( \vee \)

(see [2,3])

 

The meet (wrt \(I_5\)) is a linear operator, it is distributive and associative

 

Intersections can be chained easily

C = S_1 \vee S_2 \\ P = S_1 \vee S_2 \vee S_3

Transformations

CGA transformations contain all the motors ie. rotation and translation, but they also contain scaling and inversion, (all angle preserving transformations)

 

Rotors can again be represented as the exponentiation of bivectors (Lie algebra -> Lie group mapping)

(see [2,4,5])

 

Can nicely chain and interpolate transformations

 

Almost everything is completely "covariant", ie. you can prove it at the origin and it will hold everywhere

Transformations 2

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } e^{\frac{t\wedge \ninf}{2}} = 1 - \frac{1}{2}t\wedge \ninf\\
e^{\frac{\theta}{2}B} = \cos(\frac{\theta}{2}) + \sin(\frac{\theta}{2})B\\
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } e^{\frac{-\alpha }{2}\ninf\wedge \no} = \cosh(\frac{\alpha}{2}) + \sinh(\frac{\alpha}{2})\ninf\wedge \no

Rotation rotor

Translation rotor

Scaling rotor

All rotors are applied the same way:

Y = RX\tilde{R}

Reflections in CGA

Reflections are done by sandwiching one object inside another

Y = PXP

Introduction to serial robots

Serial robots have a series of joints, one after another

Known as a serial kinematic chain

Most common type of industrial robot

Common Serial Robots

Building Cars

Colaborating with people

Image source: Universal Robots

Image source: Robot Worx

Serial Robot Forward Kinematics 3DGA

Consider a 2-link 3 degree of freedom serial robot arm

Where does the end point go as we change the motor angles?

R_0 = \cos(\theta_0/2) + \sin(\theta_0/2)e_1\wedge e_3
R_1 = \cos(\theta_1/2) + \sin(\theta_1/2)e_1\wedge e_2
R_{\text{base}} = R_0R_1
x = R_{\text{base}}[\rho e_1]\tilde{R}_{\text{base}}
y = x + R_2[-l e_1]\tilde{R_2}
R_2 = R_{\text{base}}[\cos(\theta_2/2) + \sin(\theta_2/2)e_1\wedge e_2]

Get the end point

Construct the base rotors

Get the elbow point

Construct the elbow rotor

\rho
l
y
\theta_0
\theta_1
\theta_2
x

Serial Robot Forward Kinematics CGA

What if we want the full orientation of the endpoint?

Can we construct a rotor from origin to endpoint?

R_0 = \cos(\theta_0/2) + \sin(\theta_0/2)e_1\wedge e_3
R_1 = \cos(\theta_1/2) + \sin(\theta_1/2)e_1\wedge e_2
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } R_\rho = 1 - \frac{1}{2}\rho e_1\wedge \ninf
R_2 = \cos(\theta_2/2) + \sin(\theta_2/2)e_1\wedge e_2
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } R_l = 1 + \frac{1}{2}l e_1\wedge \ninf
R = R_0R_1R_\rho R_2R_l
\newcommand{\no}{n_{0}} Y = R\no\tilde{R}

Construct the base rotors

Construct the first link's translation rotor

Construct the elbow and link 2 translation rotor

The combined rotor is the product of all of them

\rho
l
y
\theta_0
\theta_1
\theta_2
x

Serial Robot Inverse Kinematics

\rho
l
y
\theta_0
\theta_1
\theta_2
\newcommand{\ninf}{n_{\infty}} S_Y = I_5(Y - \frac{1}{2}l^2\ninf)
\newcommand{\ninf}{n_{\infty}} S_{\text{base}} = I_5(n_0 - \frac{1}{2}\rho^2\ninf)
C = S_Y\vee S_{\text{base}}
\newcommand{\ninf}{n_{\infty}} \Pi = n_0\wedge up(e_3)\wedge Y\wedge \ninf
\newcommand{\ninf}{n_{\infty}} P = \Pi\vee C
\newcommand{\ninf}{n_{\infty}} X = \left[1 + \frac{P}{\sqrt{P\tilde{P}}}\right](P\cdot\ninf)
x

(If \(P^2 < 0 \) then y is out of reach)

Construct a sphere at the base, \(n_0\)

Construct a sphere at the endpoint, y

Intersect the spheres to give a circle

Define a vertical plane through the endpoint and base

Intersect the circle and the plane to give a point pair

Choose one of the elbow position solutions

x = -\frac{-\sum_{j=1}^{j=3}(X\cdot e_j)e_j}{X\cdot n_\infty}

Parallel Robots

Parallel robots are composed of multiple kinematic chains

Inverse kinematics typically easy

Forward kinematics hard

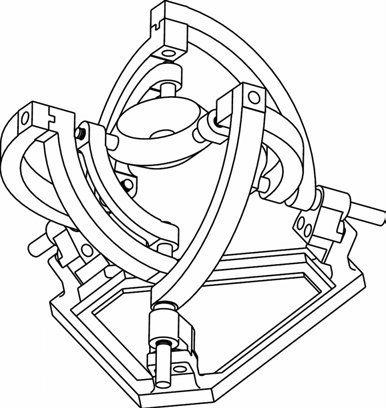
Delta Robot

Agile Eye

Stewart Platform

Image source: aemksystems

Image source: Rapid Prototyping for Robotics [6]

Image source: grabcad

The Agile Eye

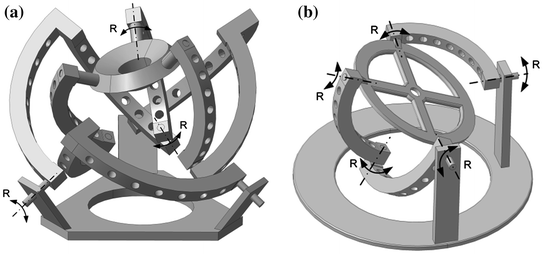
The Agile Eye is a parallel robot originally designed for orienting cameras very quickly

(a) 3DoF Agile Eye

(b) 2DoF Agile Eye

2DoF version can change the orientation of the camera but cannot freely roll about the camera axis

Image source: Parallel Wrists for Enhancing Grasping Performance [7]

Forward Kinematics of 2dof Agile Eye

R_0 = \cos(\theta_0/2) + \sin(\theta_0/2)e_1\wedge e_2
R_1 = \cos(\theta_1/2) + \sin(\theta_1/2)e_1\wedge e_3
x_0 = R_0r_ee_3\tilde{R_0}
x_1 = R_1r_ee_1\tilde{R_1}
\newcommand{\ninf}{n_{\infty}} \Pi_0 = R_0[up(e_1)\wedge up(-e_1)\wedge up(e_2)\wedge \ninf]\tilde{R_0}
\newcommand{\ninf}{n_{\infty}} \Pi_1 = R_1[up(e_3)\wedge up(-e_3)\wedge up(e_2)\wedge \ninf]\tilde{R_1}
\newcommand{\ninf}{n_{\infty}} S = I_5(n_0 - \frac{1}{2}r_e^2\ninf)
\newcommand{\ninf}{n_{\infty}} T = \Pi_1\vee \Pi_0 \vee S
P_c = (1 + \frac{T}{\sqrt{T\tilde{T}}})(T\cdot n_0)
\newcommand{\ninf}{n_{\infty}} m = I_5(T\wedge up(x_0)\wedge \ninf)

Construct the drive rotors

Find the elbow points

Get the point pair on the camera plate

Get the normal to the plate

Inverse Kinematics of 3DoF Agile Eye

The axes of the motors all intersect at a single point, the centre of rotation

We define a rotation rotor R that fully defines the plate position

Each point on the plate defines an additional circle where the elbow could be

The fixed axis of each motor defines a fixed circle on which the elbow must lie

Image source: Dynamic stiffness model of spherical parallel robots [8]

Delta Robots

  • Very fast moving
  • Simple forward and inverse kinematics
  • Cheap and easy to build

History of the Delta Robot

  • Invented by Reymond Clavel at EPFL in 1985
  • Inspired by a visit to a chocolate factory

Image source: EPFL

Model of a Delta Robot

Image source: wikipedia

Image source: Modelling and Control of A Parallel Kinematic Robot [9]

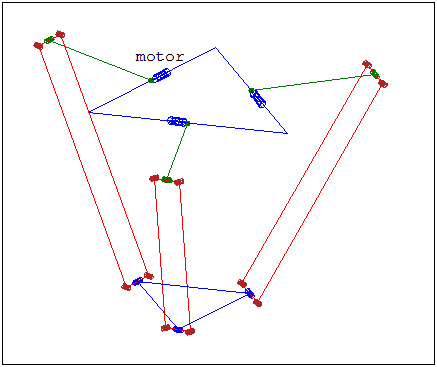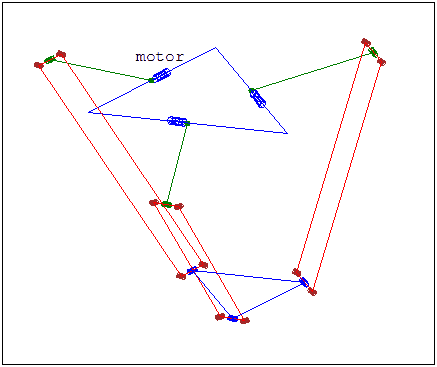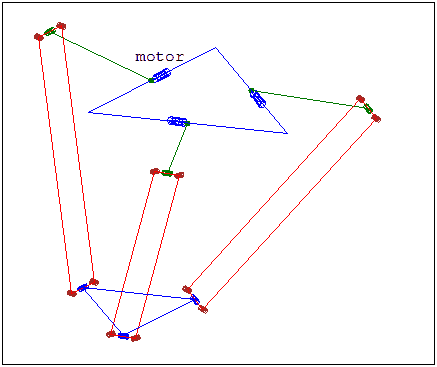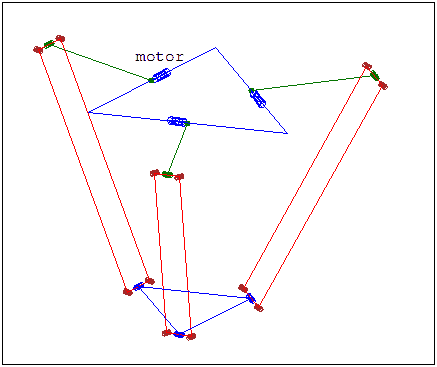
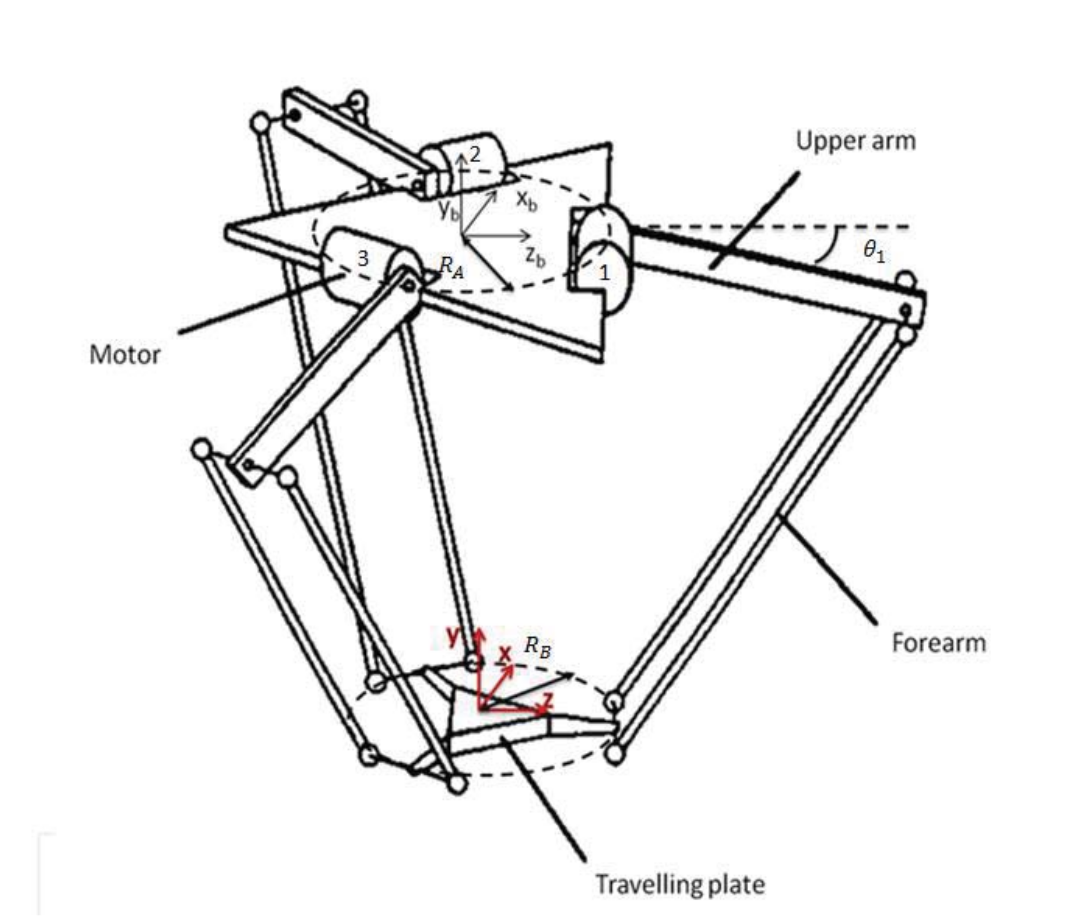
Forward Kinematics

a_i = (r_b - r_e + l\cos(\theta_i))s_i + l\sin(\theta_i)e_3

Get the pseudo-elbow point \(A_i\)

Y = -\tilde{P}(T\cdot n_\infty)P\\ y = \frac{-\sum_{j=1}^{j=3}(Y\cdot e_j)e_j}{Y\cdot n_\infty}
A_i = \frac{1}{2}a_i^2n_\infty + a_i - n_0
\Sigma_i = A_i - \frac{1}{2}\rho^2n_\infty

Construct a sphere about the pseudo-elbow

T = I_5\bigwedge_{i=0}^{i=2}\Sigma_i
P = 1 + \frac{T}{\sqrt{T^2}}

The intersection of the three spheres (one from each limb) correspond to the two possible possitions of the centre of the end plate

r_e
Y
A_i
r_b
l
\rho
\theta

Reachable Volume

Inverse Kinematics

\Sigma_i = \text{up}(y + r_es_i) - \frac{1}{2}\rho^2n_\infty

If \(T_i^2 < 0\) then the target point is unreachable

Construct three possible elbow position circles

Construct three possible elbow position spheres

C_i = \left( \text{up}(r_bs_i) - \frac{1}{2}l^2n_\infty \right)\wedge(I_3s_i\wedge e_3)
z_i = a_i - r_bs_i \\ \theta_i = \operatorname{atan2}({z_i\cdot e_3, z_i\cdot s_i})
T_i = (C_i\wedge\Sigma_i)I_5

Intersect each sphere with its corresponding circle and select one possible intersection solution per limb

A_i = -\tilde{P_i}(T_i\cdot n_\infty)P_i\\

Finally get the motor angles

P_i = \frac{1}{2}(1 + \frac{T_i}{\sqrt{T_i^2}})
a_i = -\frac{\sum_{j=1}^{j=3}(A_i\cdot e_j )e_j}{A_i\cdot n_\infty}
r_e
Y
\Sigma_i
r_b
l
\rho
\theta
C_i

Linear Function to Matrix

Many GA operations are linear and chainable

B = S_3 \vee (P(1 - t\wedge n_\infty)(S_1\vee S_2)(1 + t\wedge n_\infty)P)

Linear functions can be converted to matrices (if you so desire..)

Linearity is great for differentiation!

B = M S_1
\frac{\partial{B}}{\partial \alpha} = M \frac{\partial{S_1}}{\partial \alpha}
\frac{\partial{B}}{\partial \alpha} = S_3 \vee \left( P(1 - t\wedge n_\infty)\left(\frac{\partial{S_1}}{\partial \alpha} \vee S_2\right)(1 + t\wedge n_\infty)P \right)

This turns out to be very useful for robotics

CALCULUS ON THE VERTICAL SLIDES BELOW

Forward Jacobian

  • Move only one motor

  • This fixes two of the spheres, they intersect in a circle
  • We are therefore interested in the differential of the end point of the point pair made from intersection of the circle and the moving sphere
  • First we need to find how the center of the sphere changes as we move theta
\Sigma_i = A_i - \frac{1}{2}\rho^2n_\infty \\
  • How does point pair move with the sphere?
= \frac{\partial \Sigma_i}{\partial \theta_i} = \frac{\partial A_i}{\partial \theta_i} = -(r_b - r_e)l\sin(\theta_i)n_\infty - l\sin(\theta_i)s_i + l\cos(\theta_i)e_3
= \left( \frac{\partial a_i}{ \partial \alpha}\cdot a_i \right)n_\infty + \frac{\partial a_i}{\partial \alpha}
\frac{\partial \Sigma_i}{\partial \alpha} = \frac{\partial A_i}{\partial \alpha} = \frac{1}{2}\frac{\partial a_i^2}{\partial \alpha}n_\infty + \frac{\partial a_i}{\partial \alpha} \\

Forward Jacobian (2)

T = \Sigma_i\wedge C\\ \frac{\partial T }{\partial \theta_i} = \frac{\partial \Sigma }{\partial \theta_i}\wedge C\\

- Now we need to know how the conformal endpoint of the point pair changes

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } P = \frac{1}{2}\left(1 + \frac{T}{\sqrt{T^2}}\right)\\ Y = -\tilde{P}(T\cdot n_\infty)P\\ \pdiff{P}{\theta_i} = \frac{1}{2T^2}\left(\sqrt{T^2}\pdiff{T}{\theta_i} - T\frac{\pdiff{T}{\theta_i}\cdot T}{\sqrt{T^2}}\right)\\ \pdiff{Y}{\theta_i} = -\tilde{\pdiff{P}{\theta_i}}(T\cdot n_\infty)P -\tilde{P}(\pdiff{T}{\theta_i}\cdot n_\infty)P -\tilde{P}(T\cdot n_\infty)\pdiff{P}{\theta_i}

- How does the 3D endpoint change with the conformal endpoint change? (derivative of 'down' function)

Forward Jacobian (3)

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \pdiff{y}{\theta_i} = \frac{ -\sum_{j=1}^{j=3}\left(\pdiff{Y}{\theta_i}\cdot e_{j}\right)e_j (Y\cdot\ninf) + \sum_{j=1}^{j=3}\left(Y\cdot e_{j}\right)e_j (\pdiff{Y}{\theta_i}\cdot\ninf) }{ (Y\cdot\ninf)^2 }
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } y = \frac{-\sum_{j=1}^{j=3}(Y\cdot e_j)e_j}{Y\cdot n_\infty}

- We now have a closed form expression for the derivative of the endpoint wrt. theta and we didn't have to use maple once!

- We can use this for control and optimisation. Consider a cost function:

Forward Jacobian In Use

g(y) = (y-t)^2 \\ \frac{\partial g}{\partial \theta_i} = 2\frac{\partial y}{\partial \theta_i}\cdot(y-t)

- We therefore have a closed form for

and so can do gradient descent

\nabla g

- Given the forward jacobian we can simply invert the 3x3 matrix at each point to get the inverse jacobian

OR

- We can differentiate our inverse kinematic equations..

Inverse Jacobian

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} \Sigma_i &= X_i - \frac{1}{2}\rho^2n_\infty \\ \frac{\partial \Sigma_i}{\partial \alpha} &= \frac{\partial X_i}{\partial \alpha} = \left(\pdiff{x_i}{\alpha}\cdot x_i\right) \ninf + \pdiff{x_i}{\alpha}\\ x_i &= y + r_es_i\\ \frac{\partial x_i}{\partial \alpha} &= \frac{\partial y}{\partial \alpha} \end{aligned}

Starting with \(\Sigma_i \)

Differentiate wrt. a scalar param \( \alpha \)

the sphere centred at the meeting of the 4 bar mechanism and the end platform

- Now we need to know how the elbow positions vary with \alpha

Inverse Jacobian (2)

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} C_i &= \left( B_i - \frac{1}{2}l^2n_\infty \right)\wedge(I_3s_i\wedge e_3)\\ T_i &= (\Sigma_i\wedge C_i)^*\\ \pdiff{T_i}{\alpha} &= (\pdiff{\Sigma_i}{\alpha}\wedge C_i)^* \end{aligned}

- Here \(A_i\) is the conformal elbow position

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} \pdiff{A_i}{\alpha} &= -\tilde{\pdiff{P_i}{\alpha}}(T_i\cdot n_\infty)P_i -\tilde{P_i}(\pdiff{T_i}{\alpha}\cdot n_\infty)P_i -\tilde{P_i}(T_i\cdot n_\infty)\pdiff{P_i}{\alpha}\\ \pdiff{a_i}{\alpha} &= \frac{ -\sum_{j=1}^{j=3}\left(\pdiff{A_i}{\alpha}\cdot e_{j}\right)e_j (A_i\cdot\ninf) + \sum_{j=1}^{j=3}\left(A_i\cdot e_{j}\right)e_j (\pdiff{A_i}{\alpha}\cdot\ninf) }{ (A_i\cdot\ninf)^2 } \end{aligned}

- Finally we need to know how the joints vary with elbow position

Inverse Jacobian (3)

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} z_i &= a_i - r_bs_i \\ \theta_i &= \operatorname{atan2}(z_i\cdot e_3, z_i\cdot s_i)\\ \frac{\partial \theta_i}{\partial \alpha} &= \frac{z_i\cdot s_i}{|z_i\cdot s_i|}\frac{z_i\cdot s_i \frac{\partial z_i}{\partial \alpha}\cdot e_3 - z_i\cdot e_3 \frac{\partial z_i}{\partial \alpha}\cdot s_i}{z_i^2} \end{aligned}

- We are done (Once again no Maple!)

- The inverse jacobian allows us to map velocity of the endpoint to velocity of joints

Inverse Jacobian in Use

g(y) = (y - t)^2 \\ \frac{\partial g}{\partial y} = 2(y-t)\\

- In other words, to minimise cost at maximum rate drive the end point linearly at our target point (obviously)

- With the inverse jacobian we can do exactly that

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} \pdiff{y}{\alpha_j} \propto (2(t-y))\cdot e_j \end{aligned}

Kinematics and dynamics for mechanics

So far we have dealt with geometry of robots, constraints and kinematics of the end effector

 

Now we would like to also deal more generally with statics and dynamics

 

Ideally our setup should be familiar/intuitive to robotics practitioners and researchers to make it easy to use.

Forces as lines

Forces have a line of action, an orientation, and a magnitude

We can therefore naturally encode a force as an infinite line in CGA

\newcommand{\ninf}{n_{\infty}} F = \lambda[\hat{m}I_3 - (p\wedge\hat{m})I_3\ninf]

force magnitude

force direction

3d point through which the line passes

Note we have used the dual construction of the line here, ie. F is a bivector

Conditions for static equilibrium of a rigid body

The conditions for static equilibrium of a body subject to external forces and moments:

 

No net linear force

 

No net moment

 

What does this mean for our CGA force line formulation?

The Sum of CGA Lines 1.

What is the sum of two CGA force lines?

\newcommand{\ninf}{n_{\infty}} F_1 = \lambda_1[\hat{m_1}I_3 - (p_1\wedge\hat{m_1})I_3\ninf]
\newcommand{\ninf}{n_{\infty}} F_2 = \lambda_2[\hat{m_2}I_3 - (p_2\wedge\hat{m_2})I_3\ninf]
\newcommand{\ninf}{n_{\infty}} F_1 + F_2 = (\lambda_1\hat{m_1} + \lambda_2\hat{m_2})I_3 - ( {\bf p} \wedge (\lambda_1\hat{m_1} + \lambda_2\hat{m_2}))I_3\ninf \\+ {\bf h(\lambda_1\hat{m_1} + \lambda_2\hat{m_2})\ninf}

Another force line + something else.. (see [10])

Let's consider a simple case: two force lines in a plane

The Sum of CGA Lines 2.

\newcommand{\ninf}{n_{\infty}} {\bf h(\lambda_1\hat{m_1} + \lambda_2\hat{m_2})\ninf} = 0

So when the force lines meet at a point the sum of lines is just another line, ie:

\newcommand{\ninf}{n_{\infty}} F_1 + F_2 = (\lambda_1\hat{m_1} + \lambda_2\hat{m_2})I_3 - ( {\bf p} \wedge (\lambda_1\hat{m_1} + \lambda_2\hat{m_2}))I_3\ninf

The resultant force line passes through p which is the point at which they intersect. It also points in the direction of, and has magnitude the same as, the vector sum \( \lambda_1\hat{m_1} + \lambda_2\hat{m_2}\):

The Sum of CGA Lines 3.

\newcommand{\ninf}{n_{\infty}} {\bf h(\lambda_1\hat{m_1} + \lambda_2\hat{m_2})\ninf} = 0

So for parallel force lines:

\newcommand{\ninf}{n_{\infty}} F_1 + F_2 = (\lambda_1\hat{m_1} + \lambda_2\hat{m_2})I_3 - ( {\bf p} \wedge (\lambda_1\hat{m_1} + \lambda_2\hat{m_2}))I_3\ninf
\newcommand{\ninf}{n_{\infty}} F_1 + F_2 = {\bf h(\lambda_1\hat{m_1} + \lambda_2\hat{m_2})\ninf}

But for anti-parallel force lines of equal magnitude:

Physically speaking, balanced anti-parallel forces create a pure moment

\newcommand{\ninf}{n_{\infty}} {\bf h(\lambda_1\hat{m_1} + \lambda_2\hat{m_2})\ninf}

is the moment generated by the geometric arrangement of forces

Moment of a force line about a point

OK so we know how to do forces and we have a representation of a moment, but how do we calculate the moment of a line about a point?

\newcommand{\ninf}{n_{\infty}} M = [I_5((F_1I_5)\wedge P)]\wedge \ninf = (F_1\cdot P)\wedge \ninf

For a point P  and dual force line \(F_1\) the moment bivector M is given by:

This again produces a moment bivector of the from: \(  a\wedge n_{\infty} \) , where \(|a|\) is the magnitude of the moment and \(\hat{a}\) is the direction of the moment axis

Wrenches: Forces and moments as screws

Both dual force lines and our bivector moments are screws, and specifically because they carry forces/moments they are known as wrenches (see [12])

\newcommand{\ninf}{n_{\infty}} S = mI_3 - ( p \wedge m)I_3\ninf + h\hat{m}\ninf

If h is 0 then we have a force line

Iif m is 0 magnitude we have a pure moment

The general form of a screw is:

We can add and subtract screws at will and we will still stay on the screw manifold

Static equilibrium, external forces and moments

With both external moments \(M_j \) and forces \(F_i \) our static equilibrium equation is:

\sum_i F_i + \sum_j M_j = 0
\sum_k S_k = 0

We could also think of all the force and moments as screws and so:

But what happens if they don't sum to 0?

Screw momentum and screw velocity

\sum_k S_k = \frac{d\Omega}{dt}

And we can define a screw velocity \(\dot{B}\) such that:

We will define a screw momentum quantity, \(\Omega\),

such that the sum of external wrenches is its time derivative

\dot{R} = \frac{1}{2}R\dot{B}

where \(R\) is the rotor that transforms things from the body frame to the world frame (see [11,14])

Principal Screws of Inertia

e_1
e_2
e_2

Screw momentum and screw velocity are related by screw inertia (see [13])

We can quantify screw inertia by considering how much a wrench would effect the body if it was already moving in one of 6 specific ways, these movements are the Principal Screws of Inertia

What is the response if it is rotating about axis \(e_1\) or  \(e_2\) or \(e_3\)?

What is the response if it is translating along axis \(e_1\) or  \(e_2\) or \(e_3\)?

The screw inertia tensor

\Omega_b = M(\dot{B_b}) = m\sum_{i=1}^{i=3} \left[ (\dot{B_b}\cdot t^i)l_i + \gamma_i(\dot{B_b}\cdot l^i)t_i \right]
M^{-1}(\Omega_b) = \dot{B_b} = \frac{1}{m}\sum_{i=1}^{i=3}\left[ \frac{1}{\gamma_i}(\Omega_b\cdot t^i)l_i + (\Omega_b\cdot l^i)t_i \right]
\newcommand{\no}{n_0} % \begin{align*} l^1 = -e_1I_3\\ l^2 = -e_2I_3\\ l^3 = -e_3I_3\\ t^1 = e_1\wedge \no\\ t^2 = e_2\wedge \no\\ t^3 = e_3\wedge \no % \end{align*}
\newcommand{\ninf}{n_{\infty}} % \begin{align*} l_1 = e_1I_3\\ l_2 = e_2I_3\\ l_3 = e_3I_3\\ t_1 = e_1\wedge \ninf\\ t_2 = e_2\wedge \ninf\\ t_3 = e_3\wedge \ninf % \end{align*}

Principal screws of inertia

The screw inertia tensor \(M\) and its inverse \(M^-1\) map between screw velocity \(\dot{B_b}\) and screw momentum \(\Omega_b\) in the body frame (aligned with the principal axes)

Reciprocal principal screws of inertia

\(m\) is the body's mass

\(\gamma_i\) is the body's second moment of area about each axis

Setting up for simulation

To integrate all our bits and bobs we will use a standard 4'th order Runge-Kutta method (RK4)

To use the RK4 method we need to define our state \(y\) and a function \(f\) that returns the derivative of that state at a given time t and an initial value of \(y\) to start the simulation off at \(t_0\)

\dot{y} = f(t, y), \quad y(t_0) = y_0

Our goal will be to simulate a couple of interesting dynamics phenomena as a test of correctness

The governing equations

y = \begin{bmatrix} R \\ \Omega \end{bmatrix}

The state we track is the rotor \(R\) that transforms from the body frame to the world frame and the screw momentum \(\Omega\) in the world frame

The body is under the influence of a time varying wrench \(W_b\) expressed in the body frame

\dot{y} = \begin{bmatrix} \dot{R} \\ \dot{\Omega} \end{bmatrix} = \begin{bmatrix} \frac{1}{2}R\dot{B} \\ RW_b\tilde{R} \end{bmatrix} = \begin{bmatrix} \frac{1}{2}RM^{-1}(\tilde{R}\Omega R) \\ RW_b\tilde{R} \end{bmatrix}

http://www2.eng.cam.ac.uk/~hemh1/movies.htm#tumblebook

http://www2.eng.cam.ac.uk/~hemh1/gyroscopes/flash.html

Summary

CGA combines primitives, intersections, transformations (+Lie groups, algebras) and easy derivatives (wrt scalars)

 

(C)GA is not some alien language, it is the tools and techniques you already know and love packaged with a common interface

 

CGA is easy to work with and computationally feasable for real time applications (all the demos here are running in the browser!)

Thanks for listening!

If you are interested in getting involved then check out the pygae github group and have a go with the python clifford package for numerical GA

Run some GA code today!

  • Javascript
  • Fully in browser
  • Great for interactive demos like the ones in this slide

ganja.js

Run some GA code today!

  • Python
  • Access to a vast library of scientific toolkits:
    • numpy
    • scipy
    • jupyter
    • ...

clifford

Event Horizon Telescope Collaboration

Run some GA code today!

  • Best of both worlds
  • Run your python computations, visualize in-browser

pyganja

Let's get started

References

  1. Chris Doran and Anthony Lasenby, Geometric Algebra for Physicists (Cambridge: Cambridge University Press, 2003), https://doi.org/10.1017/CBO9780511807497.
  2. Leo Dorst, Daniel Fontijne, and Stephen Mann, Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry, Morgan Kaufmann Series in Computer Graphics (Amsterdam : San Francisco: Elsevier ; Morgan Kaufmann, 2007).
  3. Anthony Lasenby, Joan Lasenby and Rich Wareham (2004) A covariant approach to geometry using geometric algebra. Technical Report. University of Cambridge Department of Engineering, Cambridge, UK.
  4. Rich Wareham and Joan Lasenby, ‘Mesh Vertex Pose and Position Interpolation Using Geometric Algebra’, in Articulated Motion and Deformable Objects, ed. Francisco J. Perales and Robert B. Fisher, Lecture Notes in Computer Science (Springer Berlin Heidelberg, 2008), 122–31.
  5. Lars Tingelstad and Olav Egeland, ‘Motor Parameterization’, Advances in Applied Clifford Algebras 28, no. 2 (May 2018): 34, https://doi.org/10.1007/s00006-018-0850-2.
  6. Imme Ebert-Uphoff et al., ‘Rapid Prototyping for Robotics’, in Cutting Edge Robotics, ed. Vedran Kordic, Aleksandar Lazinica, and Munir Mer (Pro Literatur Verlag, Germany, 2005), https://doi.org/10.5772/4639.
  7. Massimo Callegari et al., ‘Parallel Wrists for Enhancing Grasping Performance’, in Grasping in Robotics, ed. Giuseppe Carbone, vol. 10 (London: Springer London, 2013), 189–219, https://doi.org/10.1007/978-1-4471-4664-3_8.
  8. Alessandro Cammarata et al., ‘Dynamic Stiffness Model of Spherical Parallel Robots’, Journal of Sound and Vibration 384 (December 2016): 312–24, https://doi.org/10.1016/j.jsv.2016.08.014.

  9. Rosquist, K. (2013).Modelling and Control of a Parallel Kinematic Robot. ISRNLUTFD2/TFRT–5929–SE. Master’s Thesis. Department of Automatic Control,LTH, Lund University, Lund, Sweden

  10. H. Hadfield and J. Lasenby, ‘Direct Linear Interpolation of Geometric Objects in Conformal Geometric Algebra’, Advances in Applied Clifford Algebras 29, no. 4 (September 2019): 85, https://doi.org/10.1007/s00006-019-1003-y.

  11. Anthony Lasenby, Robert Lasenby, and Chris Doran, ‘Rigid Body Dynamics and Conformal Geometric Algebra’, in Guide to Geometric Algebra in Practice, ed. Leo Dorst and Joan Lasenby (London: Springer, 2011), 3–24, https://doi.org/10.1007/978-0-85729-811-9_1.

  12. Jaime Gallardo-Alvarado, Kinematic Analysis of Parallel Manipulators by Algebraic Screw Theory (Springer International Publishing, 2016), https://doi.org/10.1007/978-3-319-31126-5.

  13. Tischler, C.R., Downing, D.M., Lucas, S.R., Martins, D.: Rigid-body inertia and screw geometry. In: Proceedings of a symposium commemorating the legacy, works, and life of Sir Robert Stawell Ball upon the 100th anniversary of a treatise on the theory of screws. Cambridge (2000)

  14. Michael Boyle, ‘The Integration of Angular Velocity’, Advances in Applied Clifford Algebras 27, no. 3 (1 September 2017): 2345–74, https://doi.org/10.1007/s00006-017-0793-z.