Modulated NODEs NeurIPS 2024

When I think about ‘dynamics’/‘dynamical systems’ this is what I mean:

spatiotemporal data is everywhere

Human brain

Medicine (Disease Spread)

Science (Fluids, Climate)

Robotics (Video generation)

Stock Markets

Simulate: Dynamical Representations

Neural Wave Machines (Keller, 2023),
Artificial Kuramoto Oscillatory Networks (Miyato, 2024)

Explain: Discover Potential Differential Equations

Symbolic Regression, LLMs(?)

Acceleration: Replace Simulator

Scaling/Generalisation: Remove Dependency on Grid/Mesh

Operator Based Models

PINNs, Neural Fields

Flexible (data driven): Parameterise the vector field as a NN

Neural ODE (~Flow Matching)

Optical Flow

Gaussian Processes

spatiotemporal data is everywhere

scale of problem

Decoding

Network

Encoder/Decoder Architecture

Encoding

Network

Modelling in

Latent Space

Modulated

Neural ODEs

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

Modulated NODEs

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

Key Idea:

length, mass

length of limbs

influence dynamics

influence reconstruction

color of a ball

color of clothes

does setting apart dynamic states from

underlying static factors of variation improve existing model performance?

Modulated NODEs

Key Idea:

does setting apart dynamic states from

underlying static factors of variation improve existing model performance?

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

\mathbf{z}_0

Latent Space

Encoding

Network

Decoding

Network

Forward

Simulation

(ODE)

\mathbf{d}

Dynamics Modulator

Modulator Prediction

Network

\mathbf{s}

Modulator Prediction

Network

Static Modulator

Latent NODE

(Chen et al., 2018)

ours

MoNODE (2023)

Parameters of an ODE

Style of a digit

influence dynamics

influence reconstruction

Modulated NODEs

\mathbf{d} \sim p(\mathbf{d}) ~\quad \textit{// dynamics modulator} \\

\mathbf{s} \sim p(\mathbf{s}) ~~\quad \textit{// static modulator} \\

\mathbf{z}_0 \sim p(\mathbf{z}_0) \quad \textit{// latent ODE state} \\

Generative Model

\mathbf{x}_i \sim p_{\phi}(\mathbf{x}_i \mid \mathbf{z}_i ~;~ \mathbf{s}).

\mathbf{z}_i = \mathbf{z}_0 + \int_{t_0}^{t_i} \mathbf{f}_{\mathbf{\theta}}(\mathbf{z}(\tau);\mathbf{d})~d \tau \\

implicit, point-estimates

ELBO (Chen, 2018)

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

Modulated NODEs

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

A general framework

Latent NODE

(Chen et al., 2018)

Second Order NODE

(Norcliffe et al., 2020)

Latent Second Order NODE

(Yildiz et al., 2019)

Heavy Ball NODE

(Xia et al., 2021)

Modulated NODEs

Define the modulators and evaluate the framework

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

\mathbf{d}

each trajectory a different parametrization

\frac{dx}{dt} = \alpha x - \beta xy

\frac{dy}{dt} = \delta xy - \gamma y

Predator-Prey

Part I. Dynamics Modulator

Part II. Static Modulator

\mathbf{s}

each trajectory a different 'style'

Rotating MNIST

Part III. Both Modulator Variables

CMU Human Mocap

(Wandt et al., 2015)

Modulated NODEs

A general framework

that improves forecasting and generalization (on average by 55.25% (MSE) across all experiments)

Sinusoidal Data

Latent NODE

(Chen et al., 2018)

ours Mo-xNODE

Heavy Ball NODE

(Xia et al., 2021)

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

\mathbf{d}

Part I. Dynamics Modulator

Modulated NODEs

A general framework

that is easier to train

ours: Mo-xNODE

NODE (Chen et al., 2018)

SONODE (Norcliffe et al., 2020)

HBNODE (Xia et al., 2021)

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

Sinusoidal Data

\mathbf{d}

Part I. Dynamics Modulator

Modulated NODEs

A general framework

that disentangles underlying FoVs

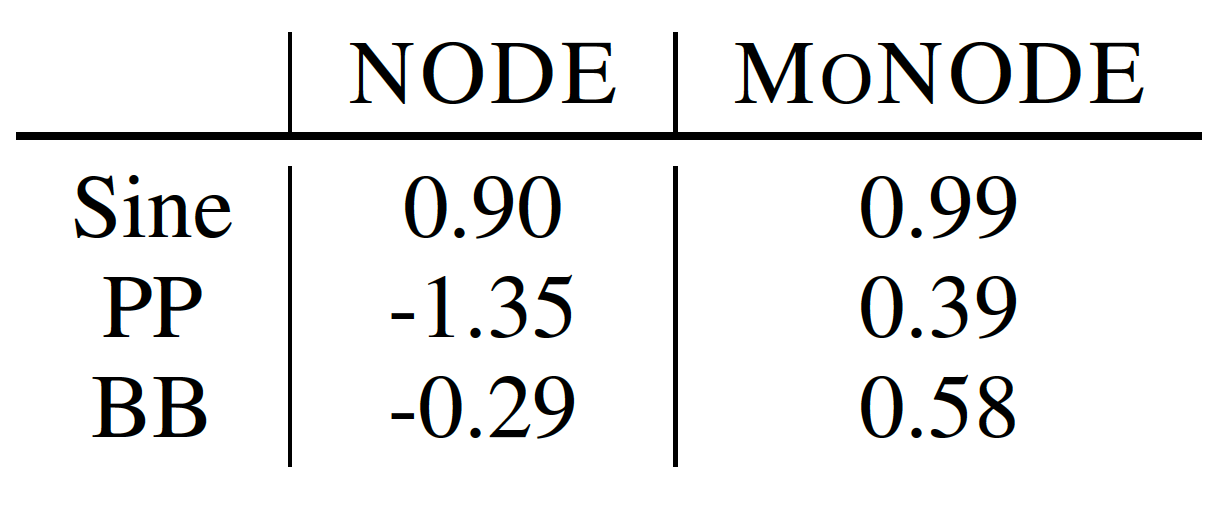
Table 2. R^2 scores to predict the unknown FoV from inferred latents. Higher is better.

\frac{dx}{dt} = \alpha x - \beta xy

\frac{dy}{dt} = \delta xy - \gamma y

dynamics

modulator

PP parameters

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

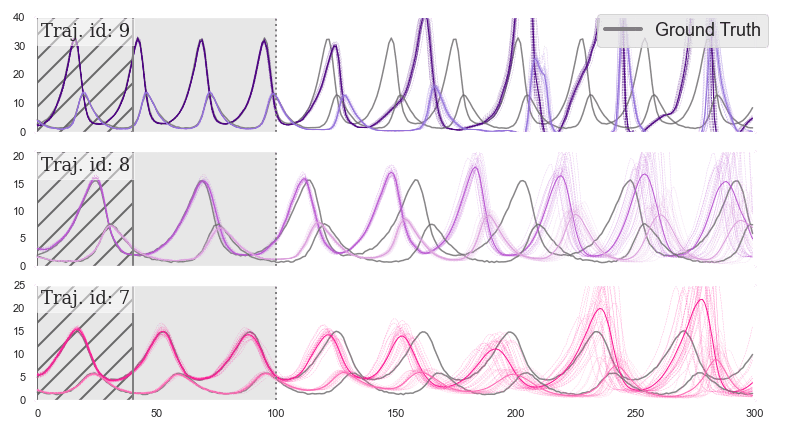
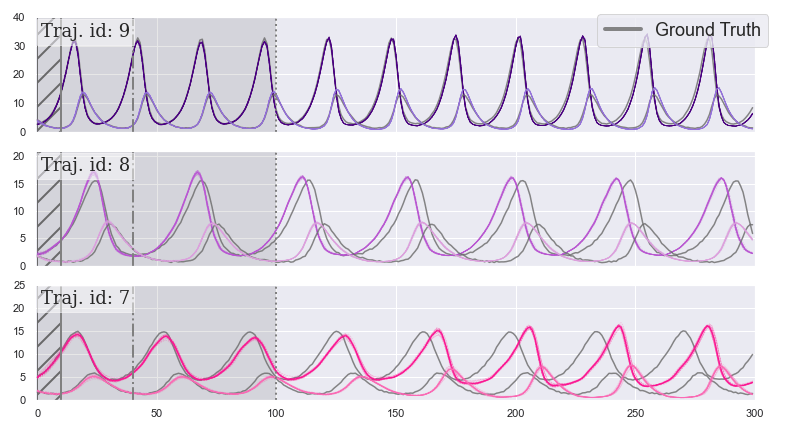
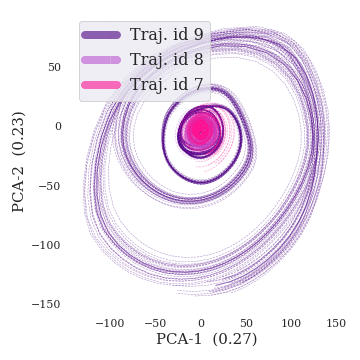
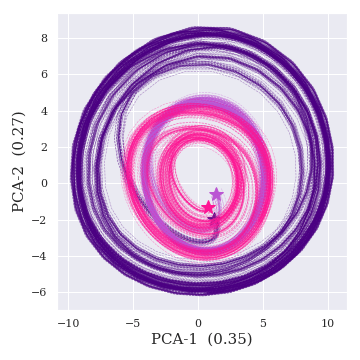
HBNODE

Mo-HBNODE

\mathbf{d}

Part I. Dynamics Modulator

Modulated NODEs

A general framework

that disentangles underlying FoVs

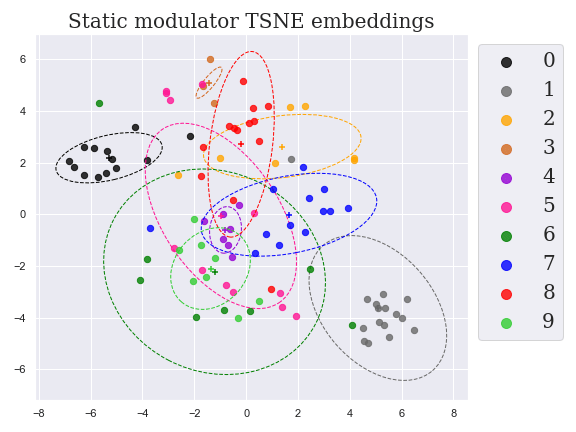
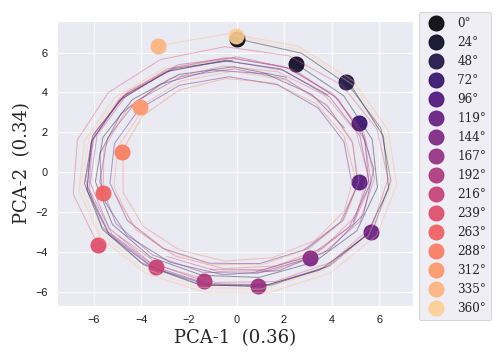
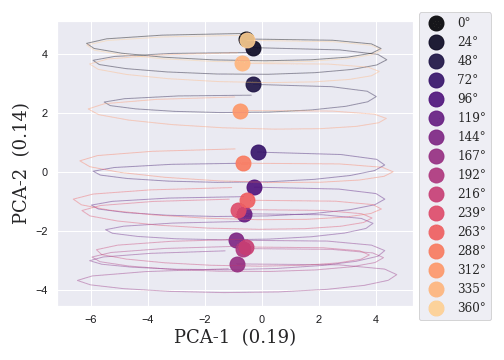
NODE

MoNODE

Part II. Static Modulator

\mathbf{s}

and correspond to their 'descriptive' roles

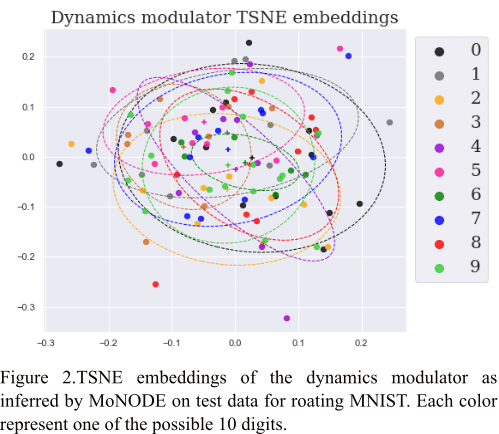
Modulated NODEs

that improves performance

on real world data

Table 3. Test MSE and standard deviation. Lower is better.

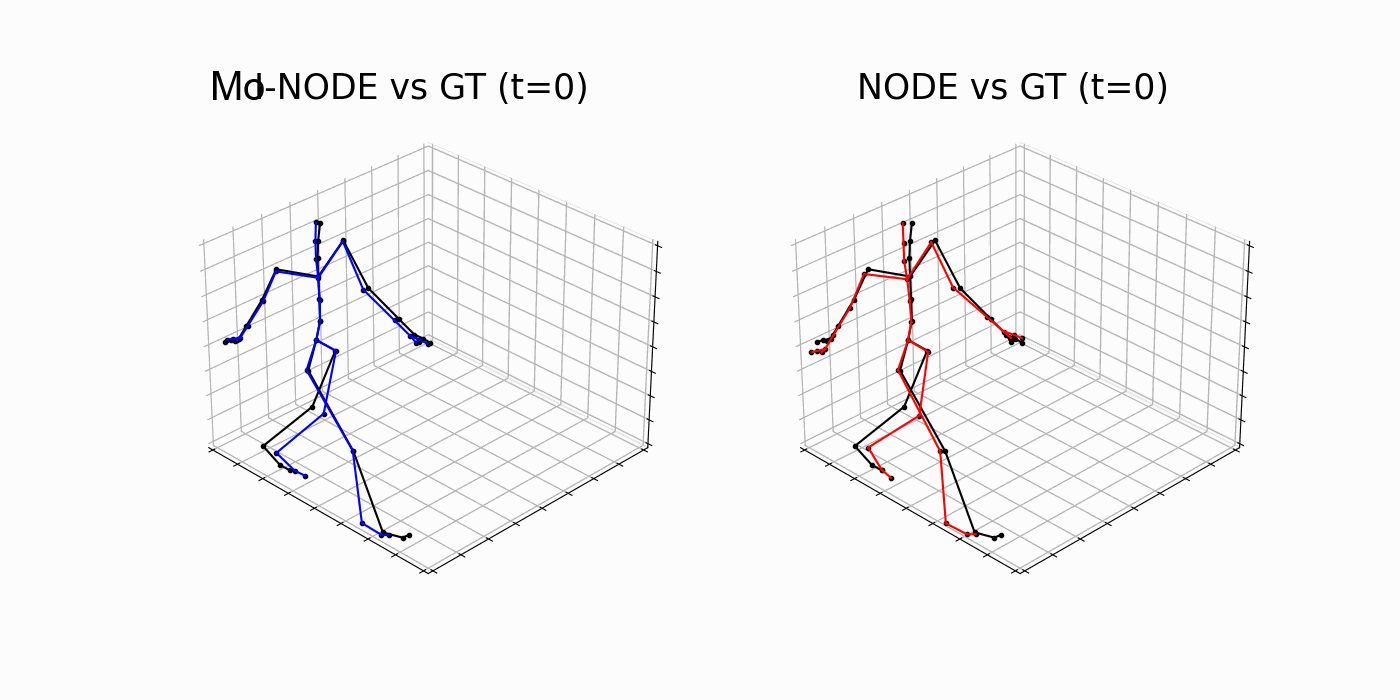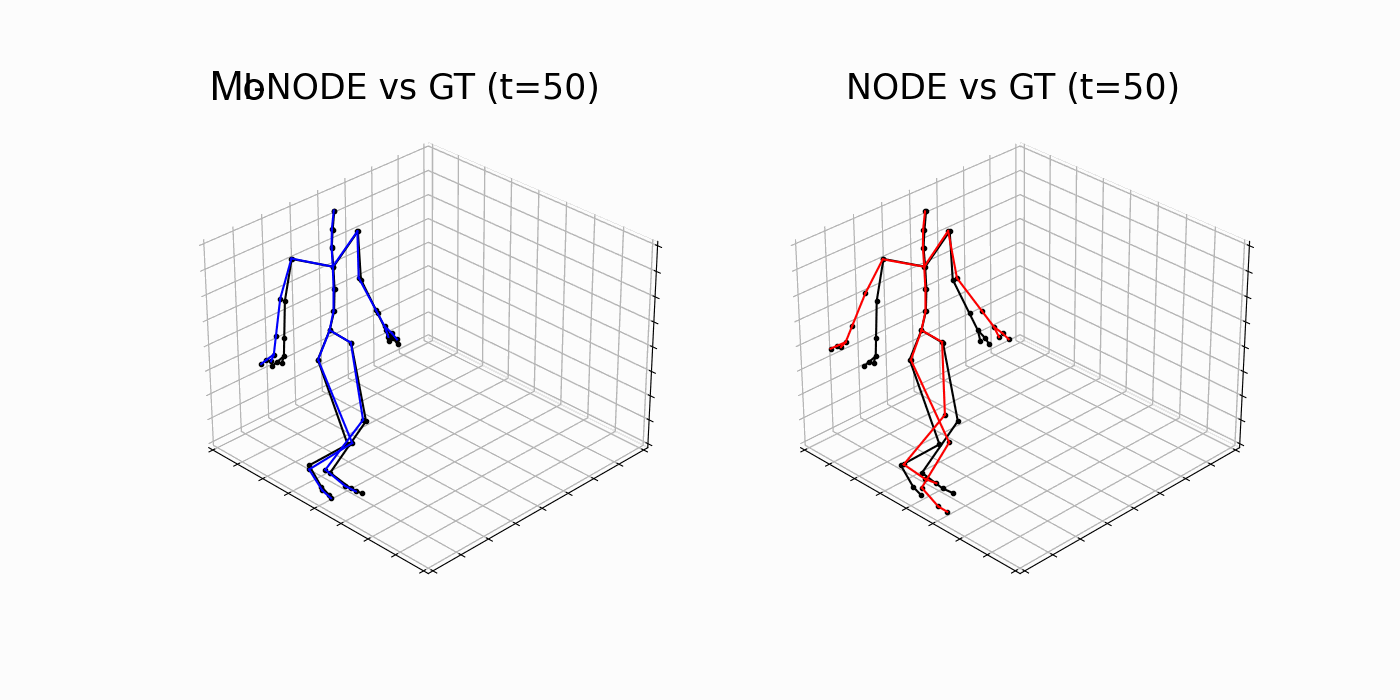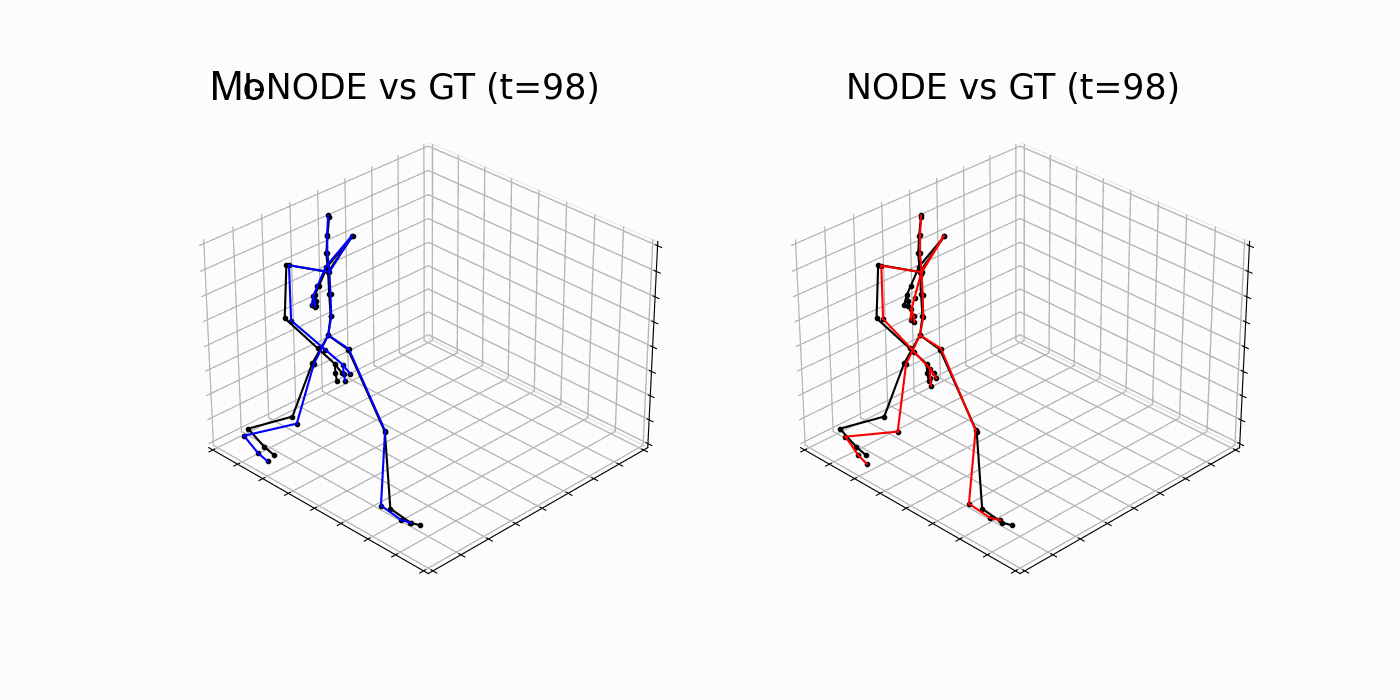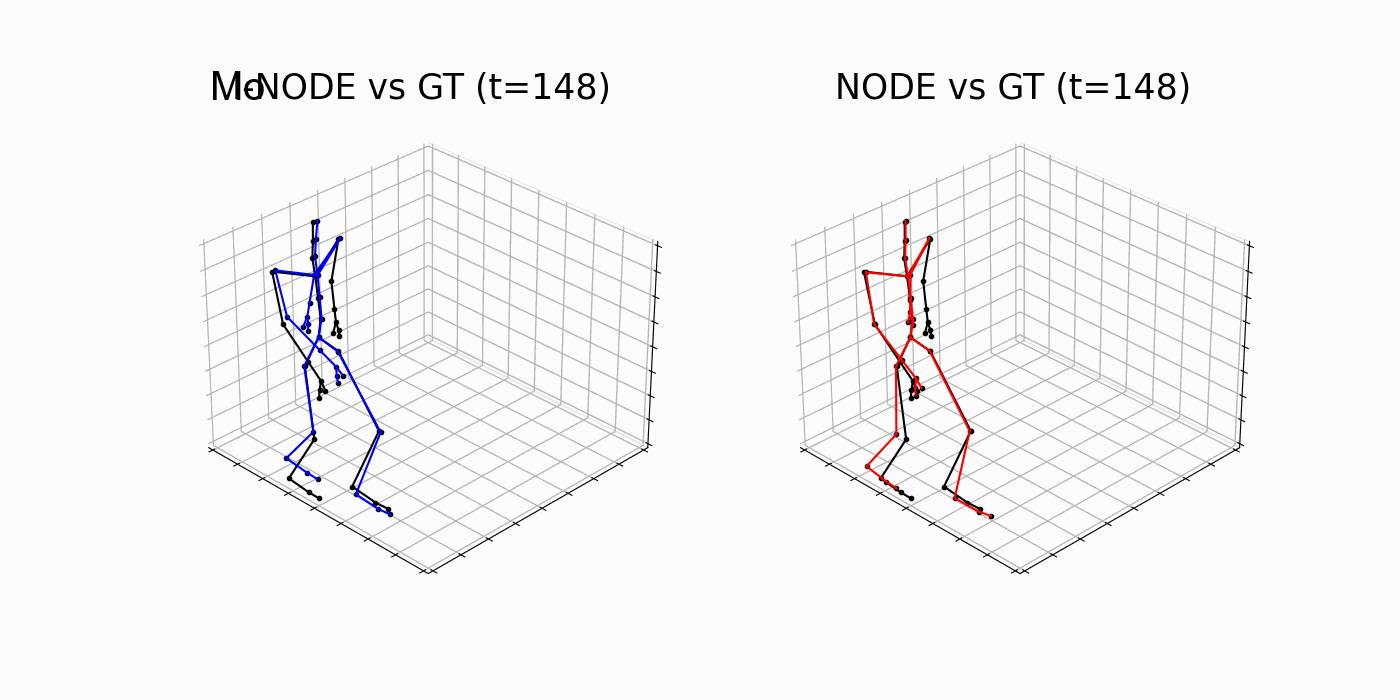
MoNODE

NODE

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

Part III. Both Modulator Variables

Modulated NODEs

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

\mathbf{z}_0

Latent Space

Encoding

Network

Decoding

Network

Forward

Simulation

(ODE)

\mathbf{d}

Dynamics Modulator

Modulator Prediction

Network

\mathbf{s}

Modulator Prediction

Network

Static Modulator

influence dynamics

influence reconstruction

Modeling dynamic's variation through time-invariant modulator variables is beneficial:
results in an ODE state that is consistent with the true dynamics and
modulator variables that correlate with the true unknown factors of variation

key take-away:

Thank you for your attention

I.A. Auzina, Ç. Yıldız, S. Magliacane, M. Bethge and E. Gavves

Modulated NODEs

All experiments and models publicly available at:

https://github.com/IlzeAmandaA/MoNODE