The Physics of Chaos

Ian O'Reilly & Dylan Scully

Deterministic But Chaotic systems

  • Three Orbital Bodies

 

  • Bunimovitch Stadium

 

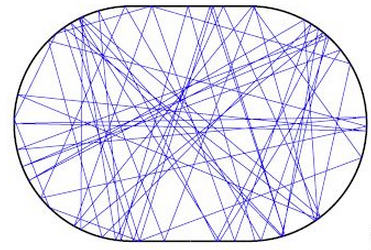
  • Snooker Triangle

 

  • Double Pendulum

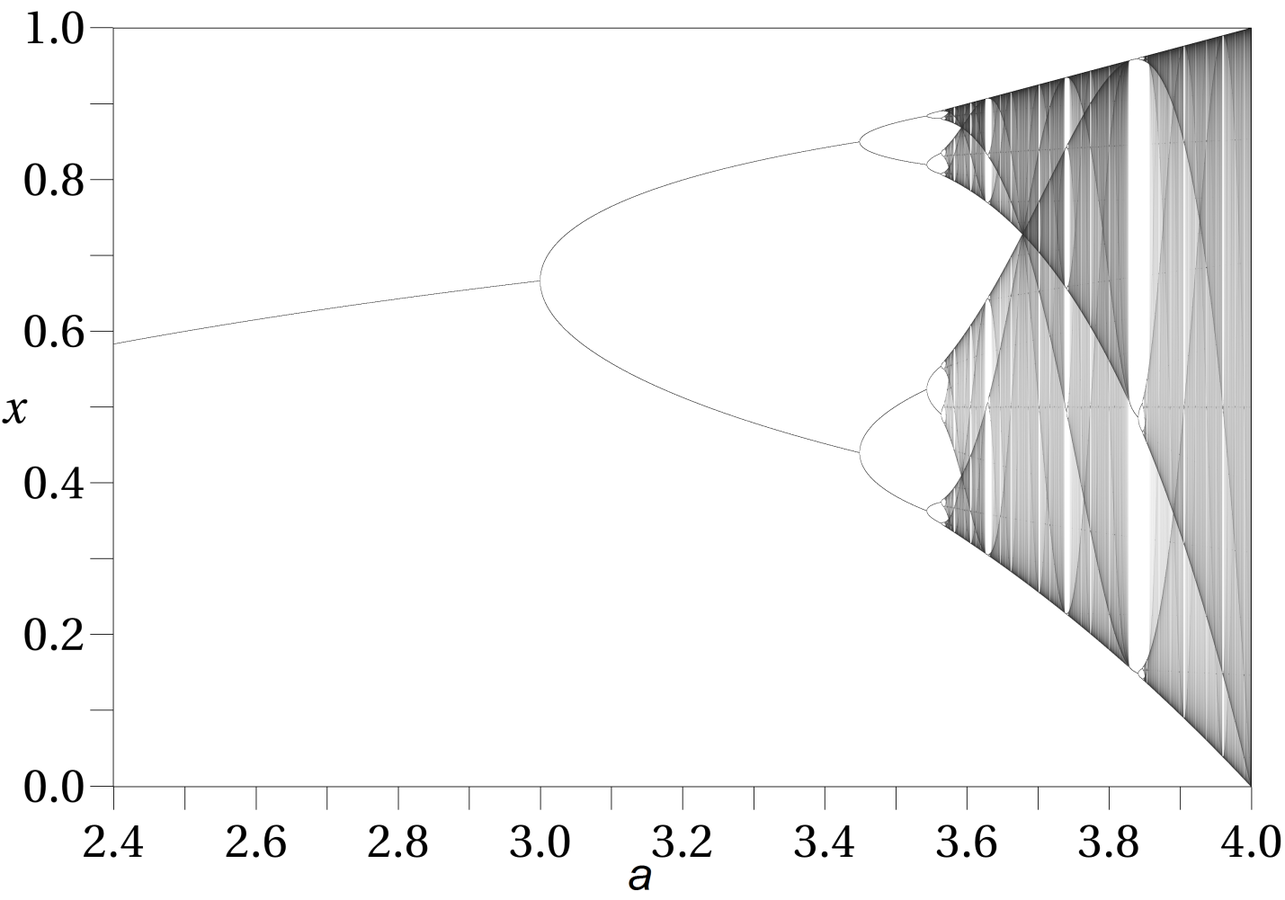
The logistic Map

X_{n+1} = A X_n(1-X_n)
X​n+1​​=AX​n​​(1−X​n​​)

The logistic map

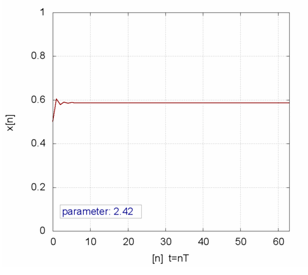
The logistic map

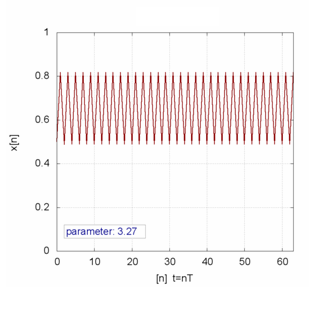
The logistic map

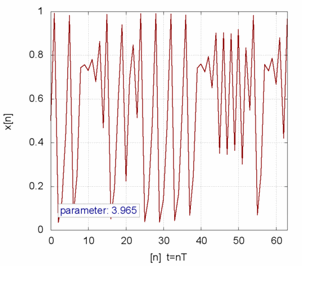
The logistic map

Lorenz: The Godfather of chaos theory

  • Weather prediction
  • Fluid drop models
  • Computer models
  • Data Truncation

Attractors

  • The Lorenz Attractor

 

  • The strange Attractor
dx/dt = P(y-x)
dx/dt=P(y−x)
dy/dt = Rx-y-xz
dy/dt=Rx−y−xz
dz/dt = xy-By
dz/dt=xy−By

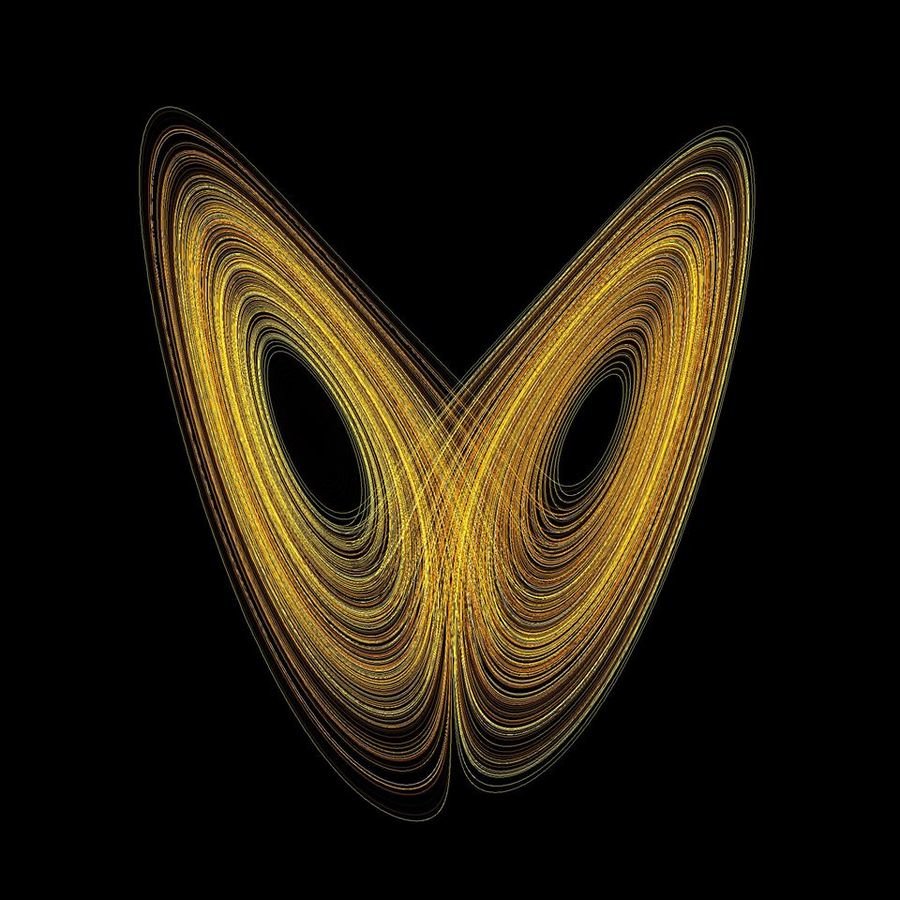
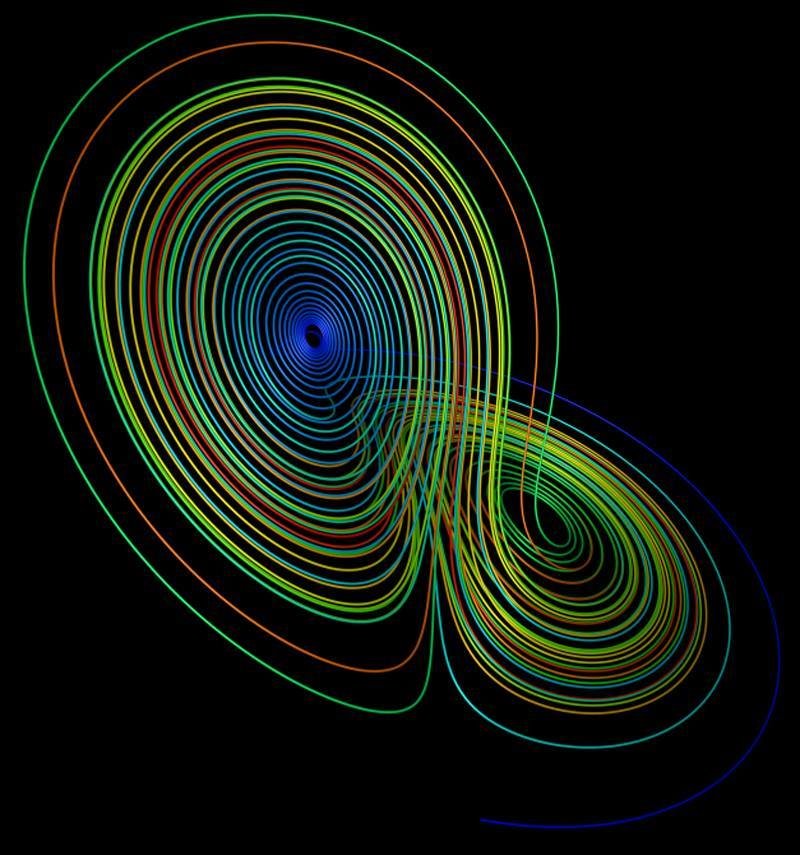
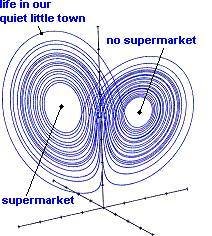
The Butterfly Effect

Does A Butterfly Flapping its wings in Argentina Cause a tornado in Kansas? 

Chaos in Philosphy

  • If The world is fully deterministic, and you had a perfect knowledge of the outcome, you could work backward to find out what was going on at any point in time.  
  • Does a model that is fully deterministic, but highly susceptible to initial conditions describe all of life?
  • Does this chaotic but deterministic model describe the illusion, but ultimate lack of free will? 

"We're better at predicting events at the edge of the galaxy or inside the nucleus of an atom than whether it'll rain on aunties garden party three Sundays from now... we can't even predict the next drip from a dripping tap when it gets irregular. Each drip sets up the conditions for the next, the smallest variation blows the prediction apart, and the weather is unpredictable in the same way, will always be unpredictable."

                             -Tom Stoppard, Arcadia, Act I, Scene 4

Refrences

Baines, P. G. "Lorenz, E.N. 1963: Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences 20, 130-41.1." Progress in Physical Geography 32.4 (2008): 475-80. Web.

May, Robert. "The Best Possible Time to Be Alive -The Logistic Map." It Must Be Beautiful: Great Equations of Modern Science. Ed. Graham Farmelo. London: Granta, 2002. N. pag. Print

Nakanishi, Hisao. "Oscillatory Motion and Chaos." Computational Physics. By Nicholas J. Giordano. Upper Saddle River, NJ: Prentice Hall, 1997. N. pag. Print.

Paladin, Gr., and A. Vulpiani. "Characterization of Strange Attractors as Inhomogeneous Fractals." Lettere Al Nuovo Cimento Series 2 41.3 (1984): 82-86. Web.

Uittenbogaard, Arie. "Chaos Theory for Beginners; An Introduction." Abarim Publications. N.p., n.d. Web. 12 Mar. 2015.

Woolfson, Michael M., and Malcolm S. Woolfson. "39-Chaos and Physical Calculations." Mathematics for Physics. Oxford: Oxford UP, 2007. N. pag. Print.

Made with Slides.com