Measurement of Chronic Mental Stress through Short-Form Video Content
Aadharsh Aadhithya [CB.EN.U4AIE20001]
GUIDES: Dr. Soman K.P, Dr. Sachin Kumar S, Dr. Neethu Mohan
Measurement of Chronic Mental Stress through Short-Form Video Content

Introduction
Introduction
- The WHO has qualified stress as a 'world epidemic' due to its increasingly greater incidence on health.
- High levels of chronic stress have adverse effects on physical and mental health.
- If the stress response system remains active for a prolonged period, this can increase the likelihood of developing several health issues, such as anxiety, depression, and various physical ailments (McEwen, 2007), and add to the global burden of disease (GBD 2019 Mental Disorders Collaborators, 2022).
Introduction
- Measuring stress is crucial for timely intervention due to its impact on health and well-being. It helps in identifying vulnerable individuals and reducing the causes of stress (Cranwell-Ward, 2005).
- Despite its association with chronic diseases, stress is rarely assessed in primary care, highlighting the need for its routine measurement (Wulsin, 2022).
- Stress measurement also allows for the verification of intervention effectiveness and assessment of individual differences in stress reactivity (Sumińska, 2022).
- However, the lack of a precise definition of stress and a reliable measurement method remain significant challenges (Llobe, 2019).
Literature Review
- Adolescents in India face many stressors in their day-to-day lives and thus experience high levels of stress. A cross-sectional study with rural adolescent students in Maharashtra showed high prevalence rates of depression (53.9%), anxiety (59.7%), and stress (43.8%) measured with the Depression, Anxiety, and Stress Scale (DASS-21) and a strong correlation between stress, depression, and anxiety (Shaikh et al., 2018).
- A study with high school students from the south zone of Delhi indicated that stress notably affected adolescents’ mental health, leading to internalizing problems such as anxiety and withdrawal or externalizing problems such as rule-breaking and aggression (Mathew et al., 2015).
- A large-scale qualitative study was conducted with 191 adolescents from Delhi and Goa, where 22 focus group discussions were conducted to identify the most common stressors experienced by Indian adolescents. The study revealed that academic pressure, romantic relationships, negotiating autonomy, and safety/victimization were the most frequently reported stressors.
- The students felt pressured to perform well academically, were stressed due to parental disapproval or failure of romantic relationships, faced restrictions of personal freedom, felt peer pressure to use substances, and experienced safety concerns such as bullying, corporal punishment, and gender discrimination (Parikh et al., 2019).
- Urban adolescents in Mysore were found to face the following main stressors: family pressure, academic stress, peer-related stress, lack of financial security, and gender discrimination (Nagabharana et al., 2021).
- Girls, also face stress related to gender roles and sexual harassment (Parikh, 2019).
Literature Review
- A range of methods exist for measuring stress, including self-reporting scales, physiological and biochemical measures, and questionnaires (Downs, 1990; Reisman, 1997; Derevenco, 2000).
- These methods can assess stress factors, reactions, and relationships with the environment, and are particularly useful in diagnosing occupational stress (Derevenco, 2000).
- However, the diagnosis of stress is complex and subject to experimental error.
Literature Review
Literature Review
-
A range of methods have been developed to identify and quantify stressors. Cohen (1995) provides a comprehensive overview, including check-list and interview measurements of stressful life events, as well as the measurement of stress hormones and immune response.
-
Sharma (2012) focuses on non-invasive and unobtrusive sensors for measuring stress, and computational techniques for stress recognition and classification.
-
Cooper (1983) reviews research on work stressors, such as shift work, job overload, and role conflicts.
-
Aguiló (2015) presents a method to objectively quantify stress levels, based on the identification of stress types and indicators, and the use of psychometric tests and well-documented stressors.
Rationale
- Chronic stress in adolescence is a more pressing problem.
- Studies have shown that chronic stress in adolescence has deteriorating impact on several aspects of them including lowered academic performance, low self-esteem, high demands, poor health, and insufficient sleep. (Schraml, 2012).
- Furthermore, The growing prevalence of stress, anxiety, and depression in adolescents is a concern, with potential impacts on brain development and treatment options (McKain, 2019).
Rationale
- The rise of viewership of short-form video content is an Interesting Phenomenon
- The Adolescent population in Particular is a large consumer of short-form video content, and its almost a second-hand habit to scroll through reels, and liking has become almost an unconscious effort one might take.
Research Gap
- Several studies have studied the negative impacts of short-form video content on the youth population (Muda (2018)).
- Various other studies have looked into the possibility of using short-form video content as an intervention. (Yuting Yang,2023) For example, investigated the effect of a short video-based mental health intervention on depressive symptoms in Chinese adolescents.
- These efforts and studies suggest a strong tie between short-form video content and mental health, But No studies till now have tried to use short-form video content to estimate/quantify one's mental state like stress/ to identify stressors.
- We believe This type of measurement would be highly relevant, and a natural means of measurement for the adolescent population.
Objectives
- Hence our Interdisciplinary study aims to access the following:
Given A sequence of reels/shorts(Short form video Content) , and which reels/shorts a person likes (Liking Pattern), be used as an estimator for chronic stress, and possibly identify the stressors.
Objectives
1) Given A sequence of reels/shorts(Short form video Content), and which reels/shorts a person likes (Liking Pattern), be used as an estimator for chronic stress, and possibly identify the stressors.
2) Can shorts/Reels be used as in Intervention to improve mental mood?
PRIMARY:
SECONDARY:
1) Develop a RAG Based Chatbot for patient information about stress
2) Try different affective modalities as augmented information to improve the outcomes mentioned in the primary objectives
External Collaborators:
- Dr. Kamal Bijilani ( Dean, School of AI, Ampritapuri; Director, Center for AI and Medicine , Amrita Hospital, Faridabad; )
- Dr. Meltem Alkoyak-Yildiz ( Head of Department of Cognitive Sciences and Psychology; Ammachi Labs)
- Dr. Sanjay Pandey ( Head of Neurology and Stroke Medicine, Amrita Hospital, Faridabad )
Methodology
Methodology
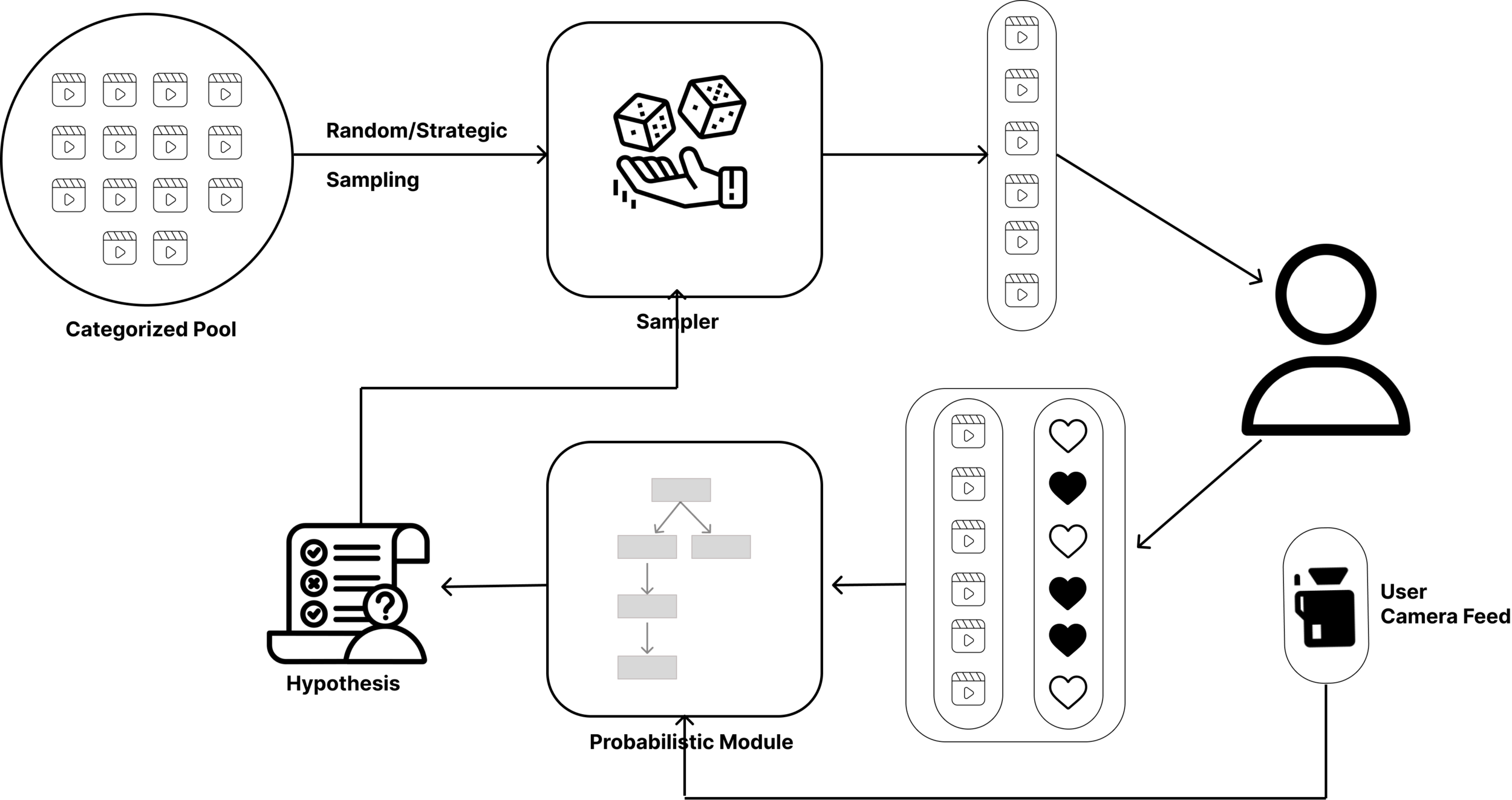
- A scrutinized pool or reels/shorts will be collected and tagged.
- A participant will be shown a sequence of reels, following a sampling strategy from the pool of reels for a stipulated period, like 2 min.
- The like patterns of the participants are analyzed and the system tries to give a score and identify the stressor.
- The scores will be accessed to see if there is data agreement with standardized psycometric tests
Methodology
Methodology
THIS REVIEW

Methodology
Emotion Recognition Through Camera
Methodology
Emotion Recognition Through Camera
0 : Anger ; 1 : Disgust ; 2 : Fear ; 3:Happiness ;4 : Sadness ; 5 : Surprise ;6 : Neutral (593 samples)
Dataset
- CK dataset which has 593 images from 123 individuals
The output of this module shall be input to the probablistic module

Methodology
Emotion Recognition Through Camera
Dataset
Experiments on other dataset will be performed; Waiting for access;
Methodology
Emotion Recognition Through Camera
Dataset
Experiments on other dataset will be performed; Waiting for access;
MuSe-Stress: Multimodal Emotional Stress(MuSe2021) Creators
Methodology
Emotion Recognition Through Camera
Dataset
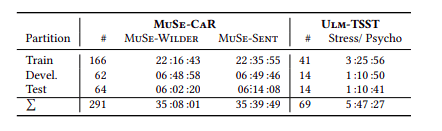
MuSe-Stress: Multimodal Emotional Stress(MuSe2021) Creators
- 69 participants (49 of them female) are aged between 18 and 39 years, providing a total amount of about 6 hours of data.
- Modalities: audio, video,text, Optional(ECG, RESP and BPM signals).
- The dataset has been rated by three annotators continuously for the emotional dimensions of valence and arousal.
Methodology
Emotion Recognition Through Camera
Model
Neural Tangent Kernel-based Kernel Regression
Methodology
Emotion Recognition Through Camera
Model
Neural Tangent Kernel-based Kernel Regression
Methodology
Emotion Recognition Through Camera
Model
Neural Tangent Kernel-based Kernel Regression
Methodology
Emotion Recognition Through Camera
Benchmark

[1] P. Tiwari and S. Veenadhari, "An Efficient Classification Technique For Automatic Identification of Emotions Leading To Stress," 2022 IEEE 6th Conference on Information and Communication Technology (CICT), Gwalior, India, 2022, pp. 1-5, doi: 10.1109/CICT56698.2022.9997823.
Target Outcomes
Target Outcomes
1) Tool/App: A tool or an App that can be deployed anywhere to access the stress levels.
2) Publication: An Interdiciplinary, Journal publication/Draft
Timeline
Timeline
| APP DEV | DATA COLLECTIO | ANALYSIS and System Dev | Results Consolidation | Paper Drafting | |
|---|---|---|---|---|---|
| WEEK 1 | |||||
| WEEK 2 | |||||
| WEEK 3 | |||||
| WEEK 4 | |||||
| WEEK 5 | |||||
| WEEK 6 |











Thank You
APPENDIX - I
What does it mean?
What does it mean?
Set of all points (x,y) that satisfy the relation 3x+4y=12.
What does it mean?
Set of all points (x,y) that satisfy the relation 3x+4y=12.
How many soltions possible?
What does it mean?
Set of all points (x,y) that satisfy the relation 3x+4y=12.
How many soltions possible?
Set of all points (x,y) that satisfy the relation 3x+4y=12.
Set of all points (x,y) that satisfy the relation 3x+4y=12.

Now, From these infinite solutions, give me a solution that is closest to the origin!
The solution lies on the perpendicular line from the origin? r
Now, From these infinite solutions, give me a solution that is closest to the origin!
The solution lies on the perpendicular line from the origin?
But what is the direction perpendicular to that line?
Now, From these infinite solutions, give me a solution that is closest to the origin!
The solution lies on the perpendicular line from the origin?
But what is the direction perpendicular to that line?
4
3
Now, From these infinite solutions, give me a solution that is closest to the origin!
The solution lies on the perpendicular line from the origin?
But what is the direction perpendicular to that line?
4
3
Now, From these infinite solutions, give me a solution that is closest to the origin!
The solution lies on the perpendicular line from the origin?
But what is the direction perpendicular to that line?
4
3
A vector that is perpendicular to [4 3]
Now, From these infinite solutions, give me a solution that is closest to the origin!
The solution lies on the perpendicular line from the origin?
4
3
Then This solution is of the form
Excercise: Find c
Least Norm Solution
Now, From these infinite solutions, give me a solution that is closest to the origin!
Least Norm Solution
This is a plane in 3D
Now, From these infinite solutions, give me a solution that is closest to the origin!
Least Norm Solution
This is a plane in 3D
Infinite solutions are possible. "Least-Norm" Solution is again in a direction perpendicular to this plane
Now, From these infinite solutions, give me a solution that is closest to the origin!
Least Norm Solution
This is a plane in 3D
Infinite solutions are possible. "Least-Norm" Solution is again in a direction perpendicular to this plane
Direction that is perpendicular to the plane is:
Now, From these infinite solutions, give me a solution that is closest to the origin!
This is a plane in 3D
Infinite solutions are possible. "Least-Norm" Solution is again in a direction perpendicular to this plane
Least norm solution is of the form
Now, From these infinite solutions, give me a solution that is closest to the origin!
What does this mean geometrically?
Now, From these infinite solutions, give me a solution that is closest to the origin!
What does this mean geometrically?
Intersection of two planes: is a line
Infinite solutions!
Infinite points. Find point, closest to the origin!
Now, From these infinite solutions, give me a solution that is closest to the origin!
What does this mean geometrically?
Intersection of two planes: is a line
Infinite solutions!
Infinite points. Find point, closest to the origin!
The Point is on a line Orthogonal to the Line of intersection of both the planes.
Now, From these infinite solutions, give me a solution that is closest to the origin!
What does this mean geometrically?
Intersection of two planes: is a line
Infinite solutions!
Infinite points. Find point, closest to the origin!
The Point is on a line Orthogonal to the Line of intersection of both the planes.
But But, There are Skew lines in 3D!
But it should be on the plane perpendicular to the line
Now, From these infinite solutions, give me a solution that is closest to the origin!
What does this mean geometrically?
Intersection of two planes: is a line
Infinite solutions!
Infinite points. Find point, closest to the origin!
But But, There are Skew lines in 3D!
But it should be on the plane perpendicular to the line
Now, From these infinite solutions, give me a solution that is closest to the origin!
What does this mean geometrically?
Intersection of two planes: is a line
Infinite solutions!
Infinite points. Find point, closest to the origin!
But But, There are Skew lines in 3D!
But it should be on the plane perpendicular to the line
Now, From these infinite solutions, give me a solution that is closest to the origin!
Infinite solutions!
LESSON
The least norm solution, always lies in the row space of A
Now, From these infinite solutions, give me a solution that is closest to the origin!
Infinite solutions!
Theorem
The least norm solution, always lies in the row space of A
Representer Theorem
APPENDIX I
The least norm solution lies in the rowspace of A. In other words, it is a linear combination of the rows of A
It is of the form
APPENDIX - II
Pseudoinverse
Column Space
LNS
Row Space
Right Null Space
A is 8x8, with rank 4
Pseudoinverse
Column Space
LNS
Row Space
Right Null Space
A is 8x8, with rank 4
Pseudoinverse
Pseudoinverse
Column Space
LNS
Pseudoinverse
Column Space
LNS
Column Space
LNS
B In Col Space
B Not In Col Space
Pseudoinverse
Column Space
LNS
Column Space
LNS
B In Col Space
B Not In Col Space
Pseudoinverse
Column Space
LNS
Column Space
LNS
B In Col Space
B Not In Col Space
Pseudoinverse