Digital Manufacturing Assignment-2

Introduction to Digital Manufacturing

Aadharsh Aadhithya - CB.EN.U4AIE20001
Anirudh Edpuganti - CB.EN.U4AIE20005

Madhav Kishor - CB.EN.U4AIE20033

Onteddu Chaitanya Reddy - CB.EN.U4AIE20045
Pillalamarri Akshaya - CB.EN.U4AIE20049

Team-1

Introduction to Digital Manufacturing

Question 1

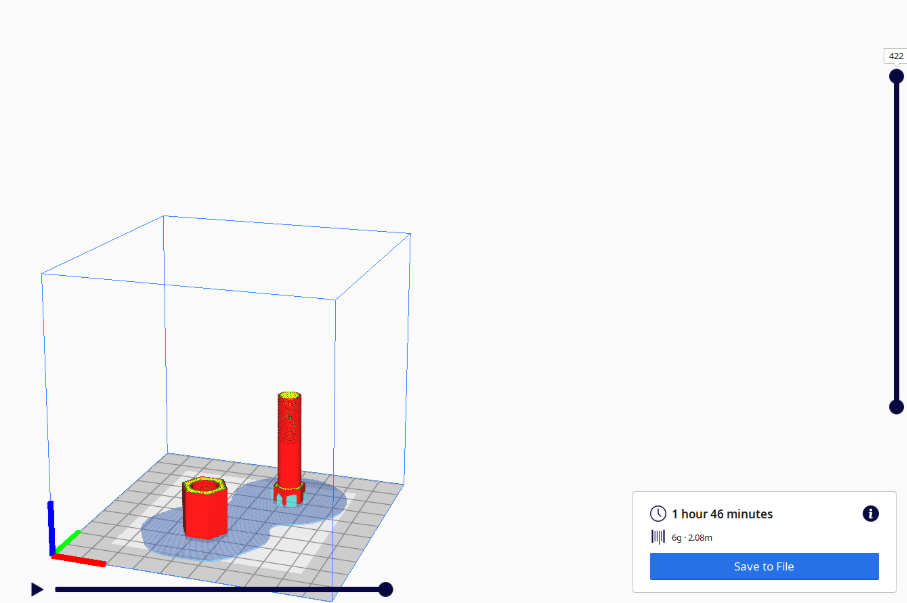
Bolts are mechanical fastners having a hexagonal head and a cylindrical shaft groovedhelically using a profile named the thread profile. Nuts on the other hand have complimentary helical grooves on their inner surfaces

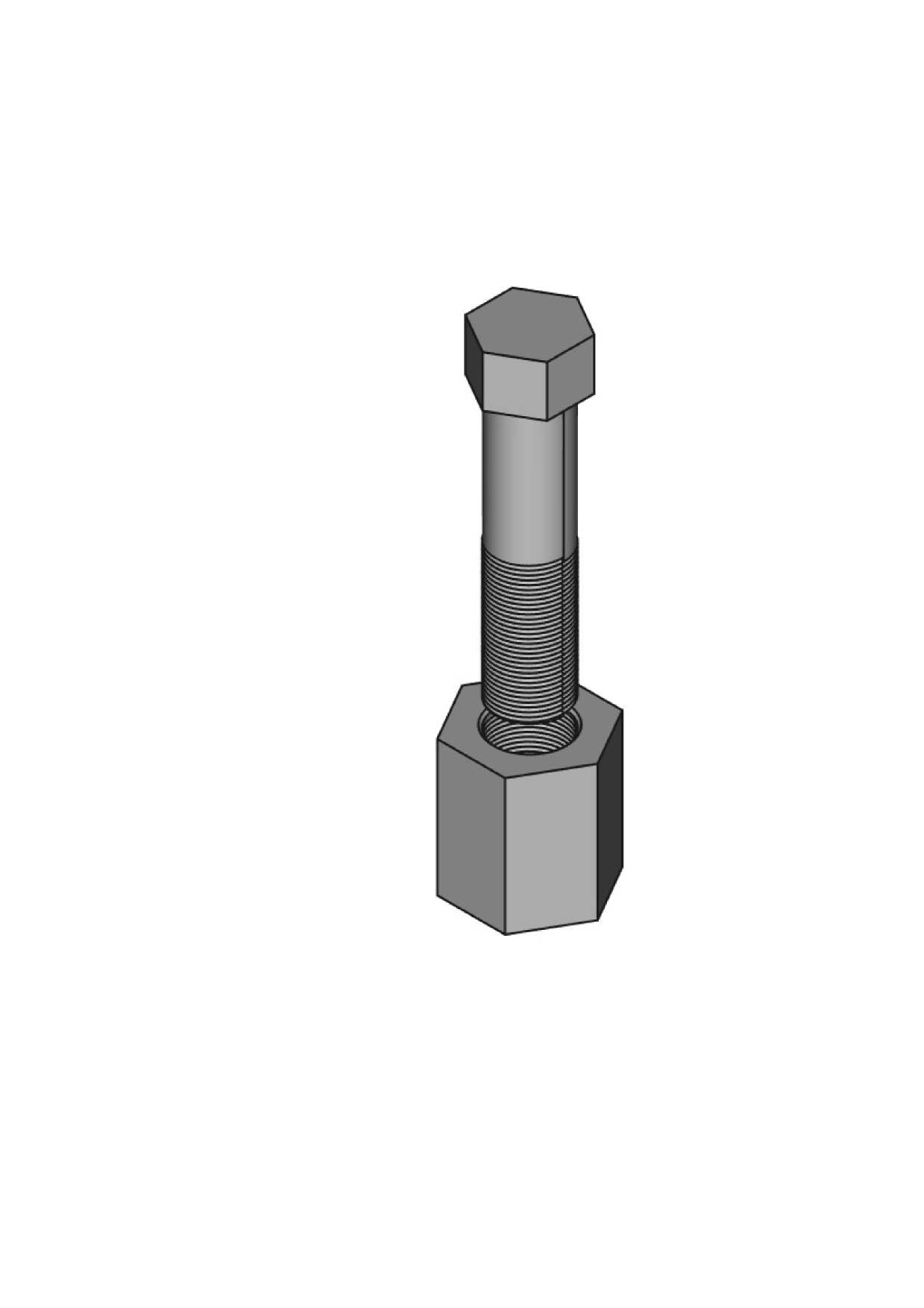
Slicing

Introduction to Digital Manufacturing

Question 2

Model and slice two gears perfectly meshing with each other as given below.

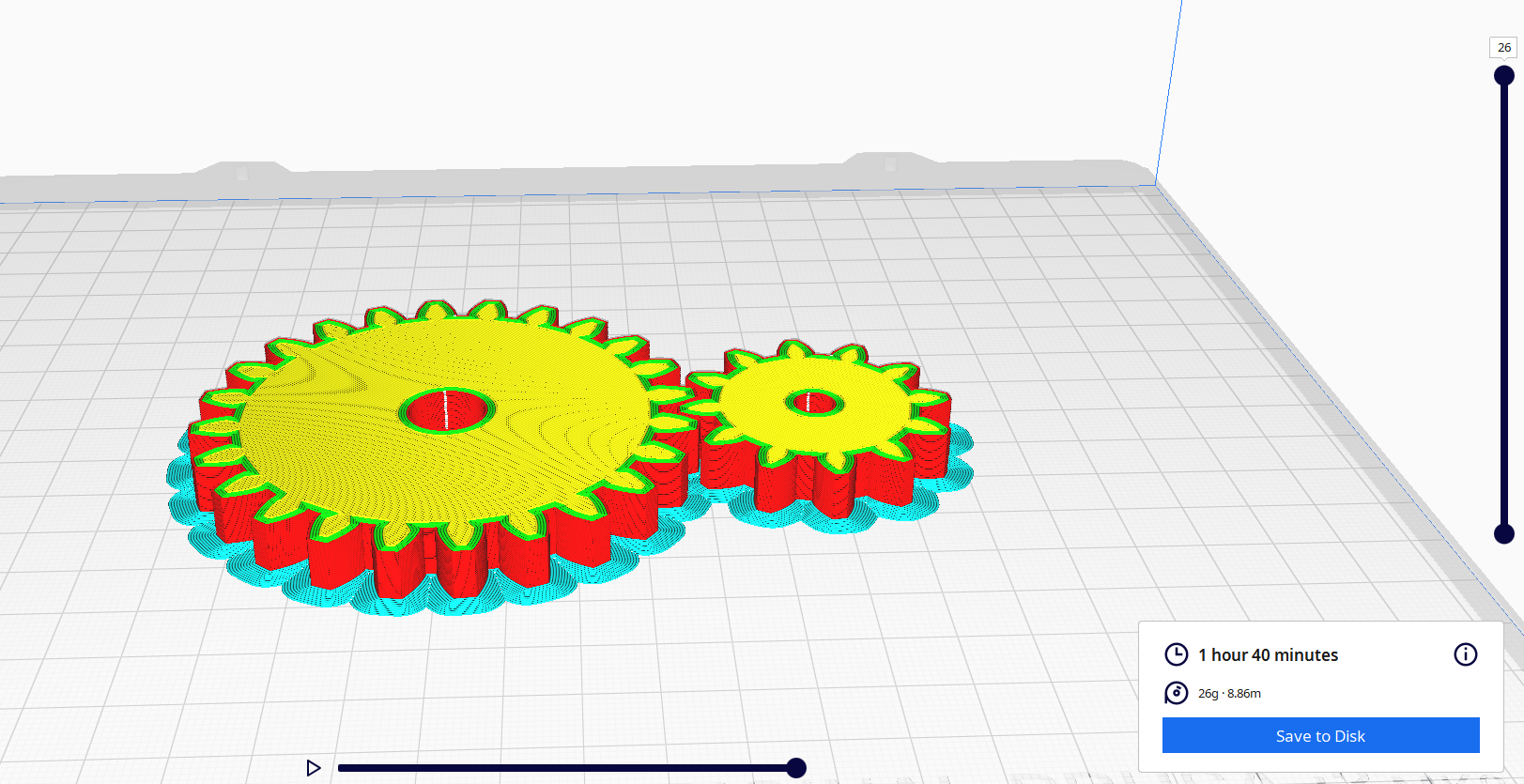
Slicing

Introduction to Digital Manufacturing

Design a Roly-Poly toy. Strategise the modeling and slicing off a rolly poly toy that can be 3D printed. The team should be able to justify that the final 3D printed toy would behave similarly to to the roly-poly tows available in the market

Question 3

Introduction to Digital Manufacturing

\}

\textit{L}

Introduction to Digital Manufacturing

\}

\textit{L}

\}

\textit{U}

Introduction to Digital Manufacturing

\}

\textit{L}

\}

\textit{U}

z

C_L \rightarrow (0,0,c_l)

C_L

Introduction to Digital Manufacturing

\}

\textit{L}

\}

\textit{U}

z

C_L \rightarrow (0,0,c_l)

C_L

C_U \rightarrow (0,0,h_l+c_u)

h_1

C_U

Introduction to Digital Manufacturing

\}

\textit{L}

\}

\textit{U}

z

C_L \rightarrow (0,0,c_l)

C_L

C_U \rightarrow (0,0,h_l+c_u)

h_1

C_U

C_L , C_U = \frac{\int r dm}{\int dm}

Introduction to Digital Manufacturing

\}

\textit{L}

\}

\textit{U}

z

C_L \rightarrow (0,0,c_l)

C_L

C_U \rightarrow (0,0,h_l+c_u)

h_1

C_U

C_L , C_U = \frac{\int r dm}{\int dm}

Depends on the Geometry and Distribution of mass about these axes

Introduction to Digital Manufacturing

\}

\textit{L}

\}

\textit{U}

z

C_L \rightarrow (0,0,c_l)

C_L

C_U \rightarrow (0,0,h_l+c_u)

h_1

C_U

C_L , C_U = \frac{\int r dm}{\int dm}

Suppose the Body is Symmetric about z axis , then Center of mass has no component perpendicular to z axis

Introduction to Digital Manufacturing

\}

\textit{L}

\}

\textit{U}

z

C_L \rightarrow (0,0,c_l)

C_L

C_U \rightarrow (0,0,h_l+c_u)

h_1

C_U

C_L , C_U = \frac{\int r dm}{\int dm}

Suppose the Body is Symmetric about z axis , then Center of mass has no component perpendicular to z axis

Center of Mass is along z axis (0,0,z)

Introduction to Digital Manufacturing

z

C_L \rightarrow (0,0,c_l)

C_L

C_U \rightarrow (0,0,h_l+c_u)

h_1

C_U

C_L , C_U = \frac{\int r dm}{\int dm}

z

C_L

h_1

C_U

\theta

Introduction to Digital Manufacturing

z

C_L

h_1

C_U

\theta

z = ax^2 + by^2

Let us Focus on the lower part

Suppose the Lower Part is a Paraboloid

Project the Paraboloid onto z-x plane, and we will get the figure shown beside

z = ax^2

Introduction to Digital Manufacturing

z

C

h_1

\theta

C = \frac{M_L C_L + M_U C_U}{M_L + M_U}

Introduction to Digital Manufacturing

z

C

h_1

\theta

C = \frac{M_L C_L + M_U C_U}{M_L + M_U}

B

A(x_0,z_0)

x

z - z_0 = 1\frac{1}{2ax_0}(x-x_0)

F

(M_L + M_u)g

Introduction to Digital Manufacturing

z

C

h_1

\theta

C = \frac{M_L C_L + M_U C_U}{M_L + M_U}

B

A(x_0,z_0)

x

z - z_0 = 1\frac{1}{2ax_0}(x-x_0)

F

(M_L + M_u)g

z = -\frac{1}{2ax_0} (x) + \frac{1}{2a} + ax_0^2

Introduction to Digital Manufacturing

z

C

h_1

\theta

C = \frac{M_L C_L + M_U C_U}{M_L + M_U}

B

A(x_0,z_0)

x

z - z_0 = 1\frac{1}{2ax_0}(x-x_0)

F

(M_L + M_u)g

z = -\frac{1}{2ax_0} (x) + \frac{1}{2a} + ax_0^2

x=0

B ~ (0, \frac{1}{2a}+ax_0^2)

Introduction to Digital Manufacturing

z

C

h_1

\theta

B

A(x_0,z_0)

x

F

(M_L + M_u)g

(0, \frac{1}{2a}+ax_0^2)

c>\frac{1}{2a}+ax_0^2

Introduction to Digital Manufacturing

z

C

h_1

\theta

B

A(x_0,z_0)

x

F

(M_L + M_u)g

(0, \frac{1}{2a}+ax_0^2)

c>\frac{1}{2a}+ax_0^2

z

C

h_1

\theta

B

A(x_0,z_0)

x

F

(M_L + M_u)g

(0, \frac{1}{2a}+ax_0^2)

c<\frac{1}{2a}+ax_0^2

Introduction to Digital Manufacturing

z

C

h_1

\theta

B

A(x_0,z_0)

x

F

(M_L + M_u)g

(0, \frac{1}{2a}+ax_0^2)

c<\frac{1}{2a}+ax_0^2

Further, This can be Generalised to any geometry

For the Roly-Poly Toy to be in "Stable-Equlibrium", Its Center of Mass should be as low as possible

Further, For an extensive study, it is possible to model the equilibrium of the toy using second-order differential equations with constant coeffitients

\frac{5R}{8}

\frac{h}{4}

C_z = \frac{M_L C_L + M_U C_U}{M_L+M_U}

C_L = \frac{5R}{8}

C_U = \frac{h}{4}

if \, \, \frac{M_L}{ M_U} = 1

\frac{1}{2} ( \frac{5R}{8} + (\frac{h}{4} + R) ) < R

h < \frac{3R}{2}

(h,r) \rightarrow (15mm,5mm)

Slicing