19AIE201
Introduction to Robotics
IRB 140
19AIE201
Introduction to Robotics
Aadharsh Aadhithya - CB.EN.U4AIE20001
Anirudh Edpuganti - CB.EN.U4AIE20005
Madhav Kishor - CB.EN.U4AIE20033
Onteddu Chaitanya Reddy - CB.EN.U4AIE20045
Pillalamarri Akshaya - CB.EN.U4AIE20049
Team-1
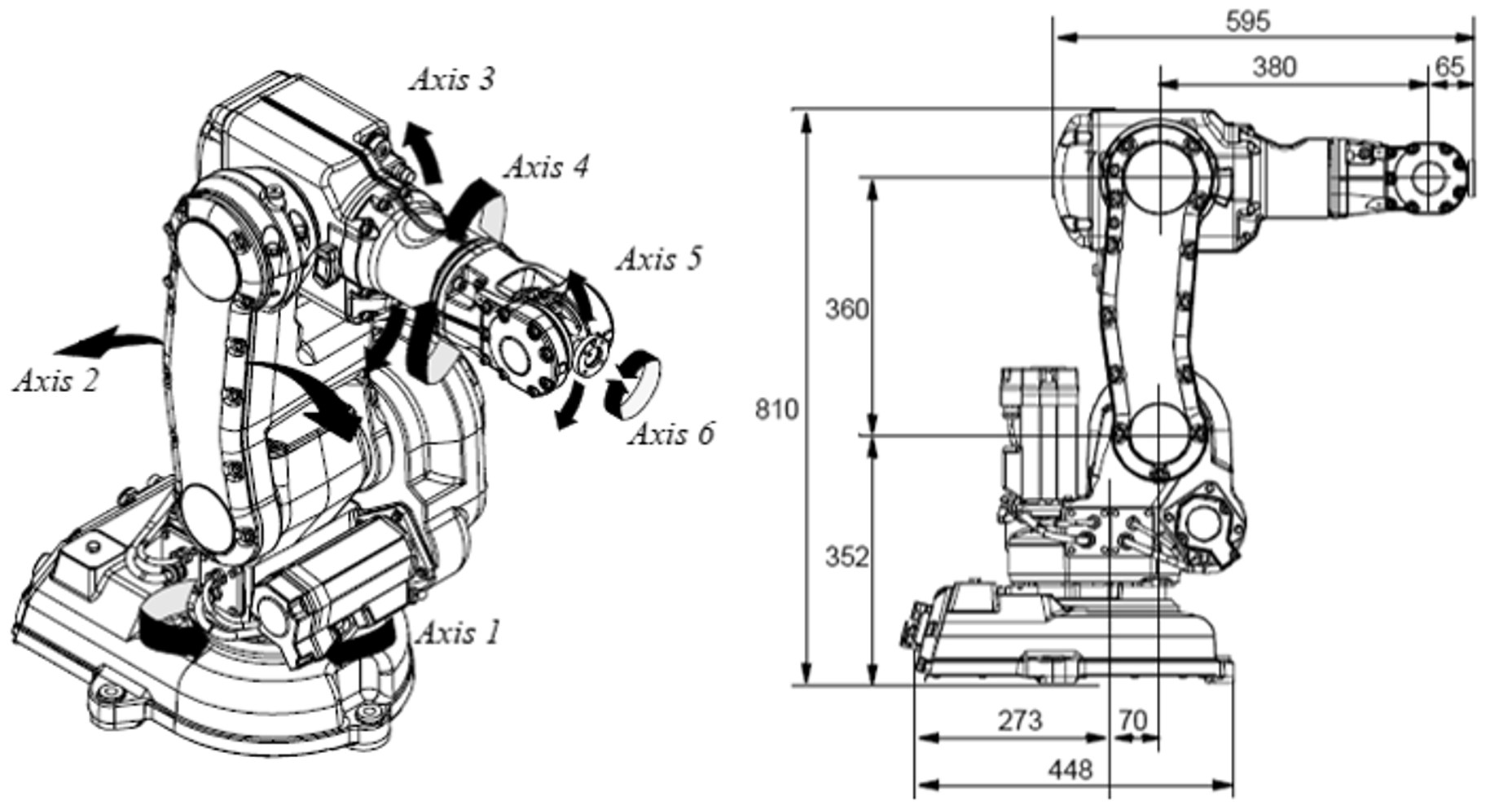
IRB 140

Text
" Small, powerful, and fast 6-axes robot. Compact and very powerful. The IRB 140 six axes multipurpose industrial robot handles a payload of 6 kg with a reach of 810 mm (to axis 5) It can be floor mounted, inverted or wall mounted at any angle. The robust design with fully integrated cables adds to the overall flexibility and the collision detection function ensures the robot is reliable and safe."

Link Twist
Z

Link Length
Z

Joint Angle
X

Link offset
X

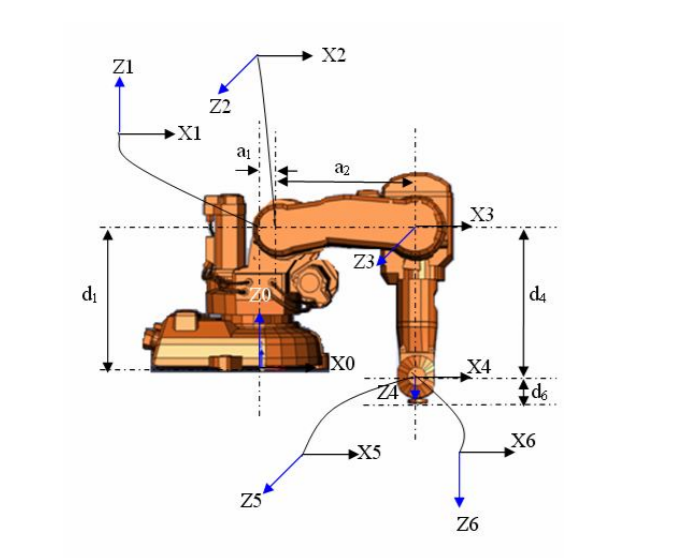
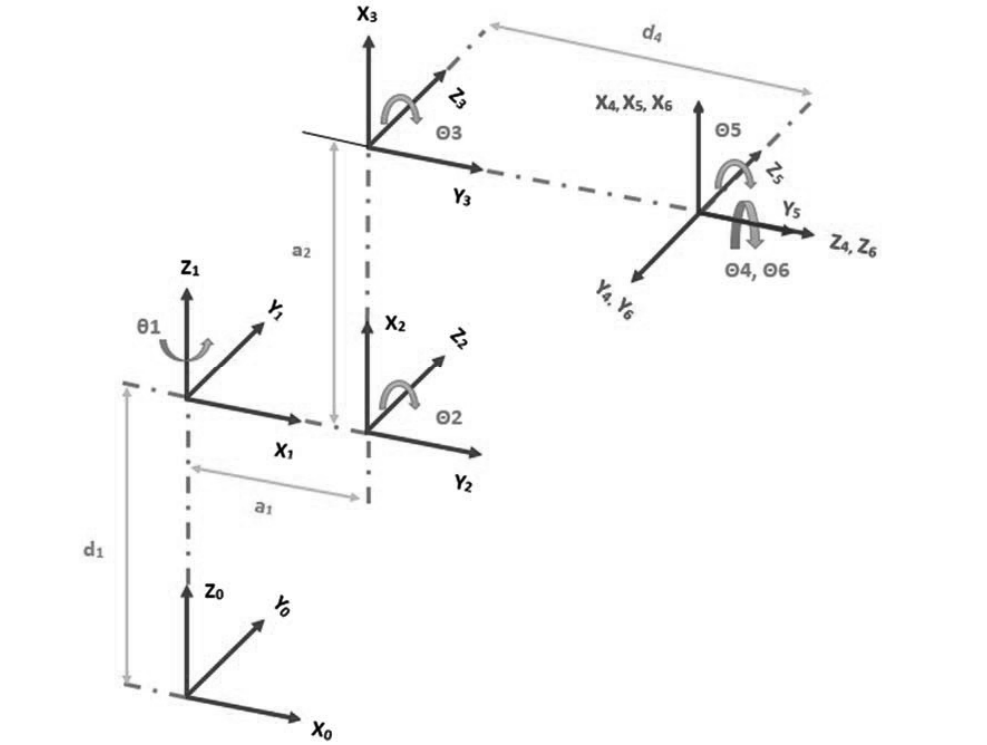
MDH Parameters
| 0 | 0 | 0.352 | |
| -90 | 0.070 | 0 | |
| 0 | 0.360 | 0 | |
| -90 | 0 | 0.380 | |
| 90 | 0 | 0 | |
| -90 | 0 | 0 |
Forward Kinematics
MDH Parameters - Given
MDH Parameters - Given
Inverse Kinematics
MDH Parameters - Given
MDH Parameters - Given
How to solve this??
Before that, lets see an application based on IK
Before that, lets see an application based on IK
Pantograph
19AIE201
Introduction to Robotics
Closed form solution
Closed Form Solution
Closed Form Solution
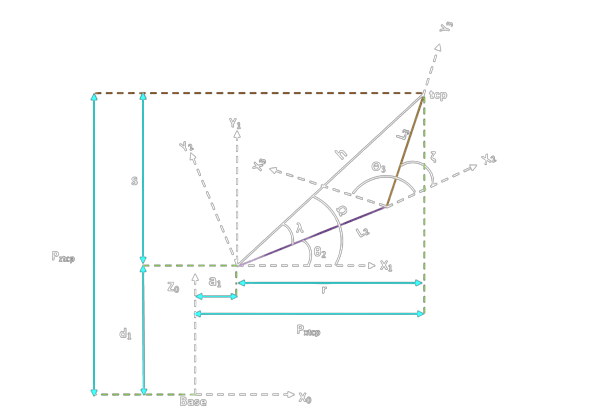
Closed Form Solution

Closed Form Solution

19AIE201
Introduction to Robotics
Newton-Raphson method
Newton-Raphson method
Newton-Raphson method
Newton-Raphson method
Newton-Raphson method
Jacobian Matrix
19AIE201
Introduction to Robotics
Trajectory Planning
Trajectory Planning
Tracking the change in position, velocity and acceleration of joints w.r.t the time.
Trajectory Planning
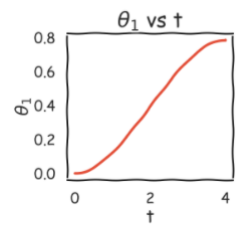
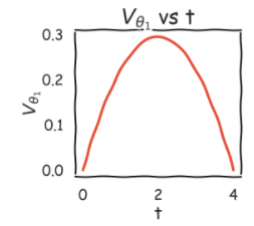
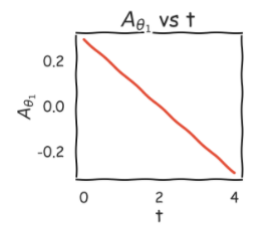
Trajectory Planning
Polynomial Function
Trajectory Planning
Polynomial Function
Trajectory Planning
Polynomial Function
Trajectory Planning
Polynomial Function
Trajectory Planning
Constraints
Trajectory Planning
Constraints
Trajectory Planning
Constraints
Trajectory Planning
Constraints
Trajectory Planning
Constraints
Trajectory Planning
Using these constraints...
Trajectory Planning
Using these constraints...
Trajectory Planning
In these equations...
Trajectory Planning
We get this
19AIE201
Introduction to Robotics
Jacobian
Jacobian
Jacobian
Jacobian
Thank you sir