2024年粒子天体物理重点实验室系列学术报告|8月19日上午10:00 @高能所
Enhancing Gravitational Wave Astronomy with Artificial Intelligence
He Wang (王赫)
hewang@ucas.ac.cn
International Centre for Theoretical Physics Asia-Pacific (ICTP-AP), UCAS
Taiji Laboratory for Gravitational Wave Universe (Beijing/Hangzhou), UCAS
On behalf of the LIGO-VIRGO-KAGRA collaborations



Enhancing Gravitational Wave Astronomy with Artificial Intelligence
He Wang (王赫)
hewang@ucas.ac.cn
International Centre for Theoretical Physics Asia-Pacific (ICTP-AP), UCAS
Taiji Laboratory for Gravitational Wave Universe (Beijing/Hangzhou), UCAS
On behalf of the LIGO-VIRGO-KAGRA collaborations




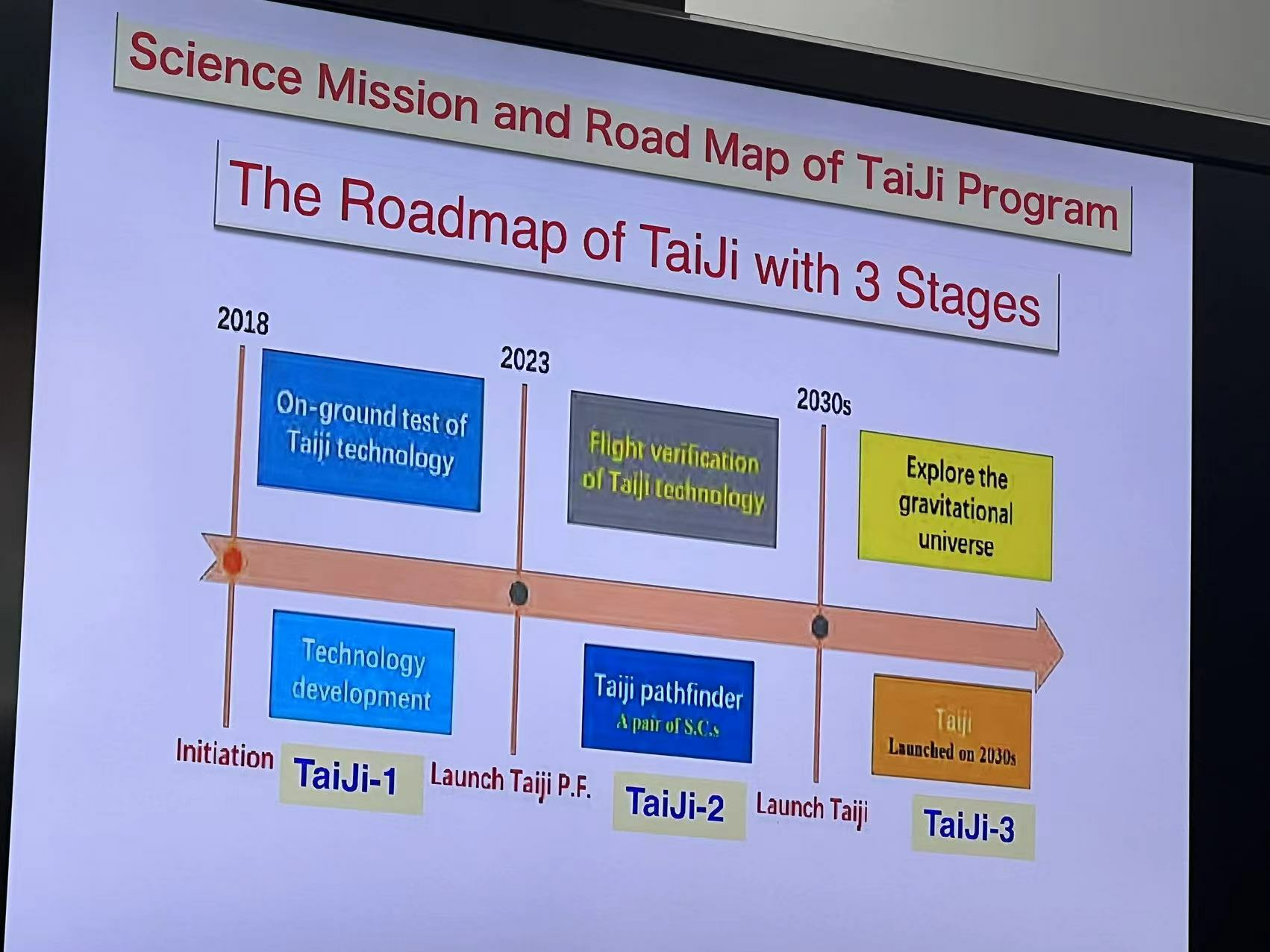
Taiji
Tianqin
https://twitter.com/chipro/status/1768388213008445837?s=46&t=JmDXWgIucgr_FlsBFTvuRQ
DINGO+SEOBNRv4EHM找了3个ebbh
Evidence for eccentricity in the population of binary black holes observed by LIGO-Virgo-KAGRA
https://dcc.ligo.org/LIGO-G2400750

BEFORE
AFTER

LIGO-G2300554
Content


- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- (Space-based GW Detection)

-
In 1916, A. Einstein proposed the GR and predicted the existence of GW.
-
Gravitational waves (GW) are a strong field effect in the GR.
-
2015: the first experimental detection of GW from the merger of two black holes was achieved.
-
2017: the first multi-messenger detection of a BNS signal was achieved, marking the beginning of multi-messenger astronomy.
-
2017: the Nobel Prize in Physics was awarded for the detection of GW.
-
As of now: more than 90 gravitational wave events have been discovered.
-
O4, which began on May 24th 2023, is currently in progress.
-


Gravitational waves generated by binary black holes system
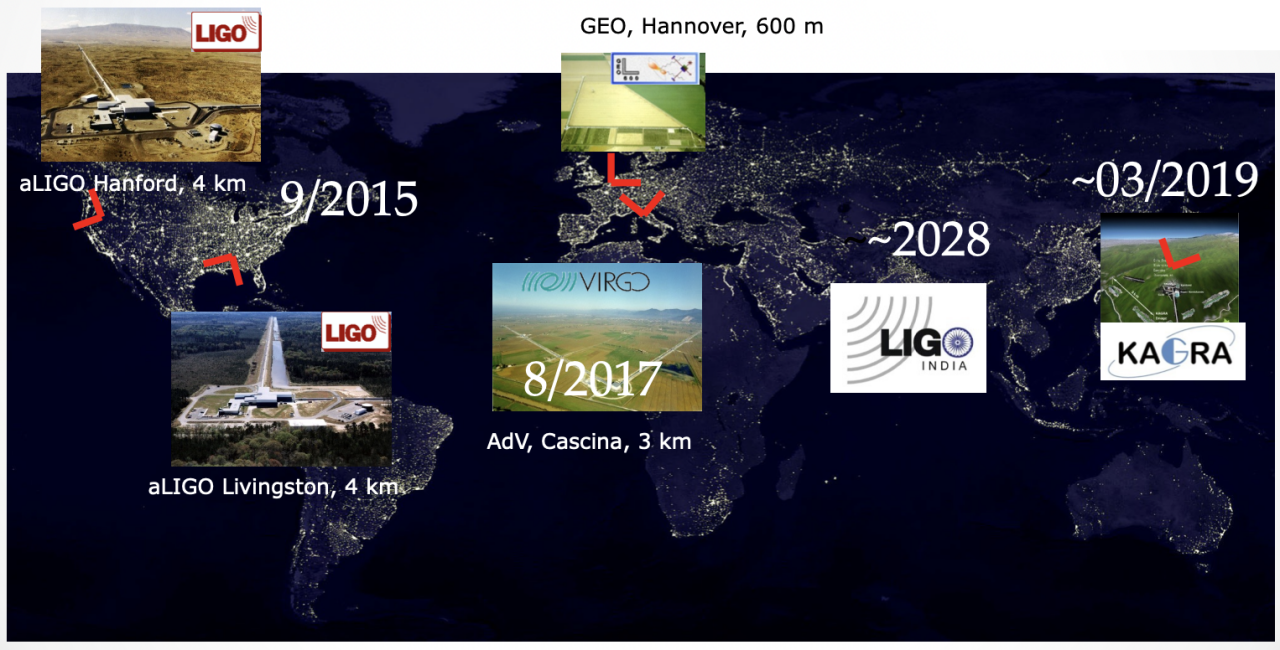
GW detector
LIGO-VIRGO-KAGRA network
2017 Nobel Prize in Physics
Gravitational Wave Astronomy
-
引力波探测打开了探索宇宙的新窗口
-
不同波源,频率跨越 20 个数量级,不同探测器
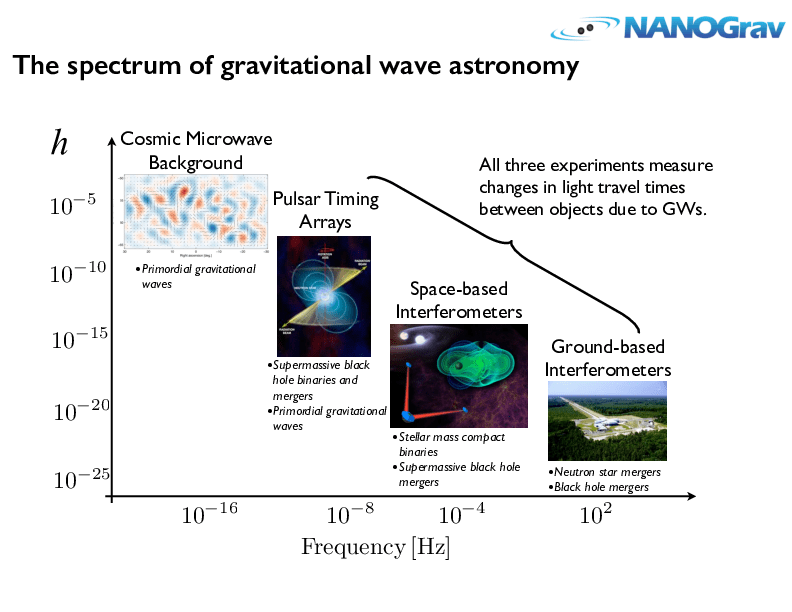
-
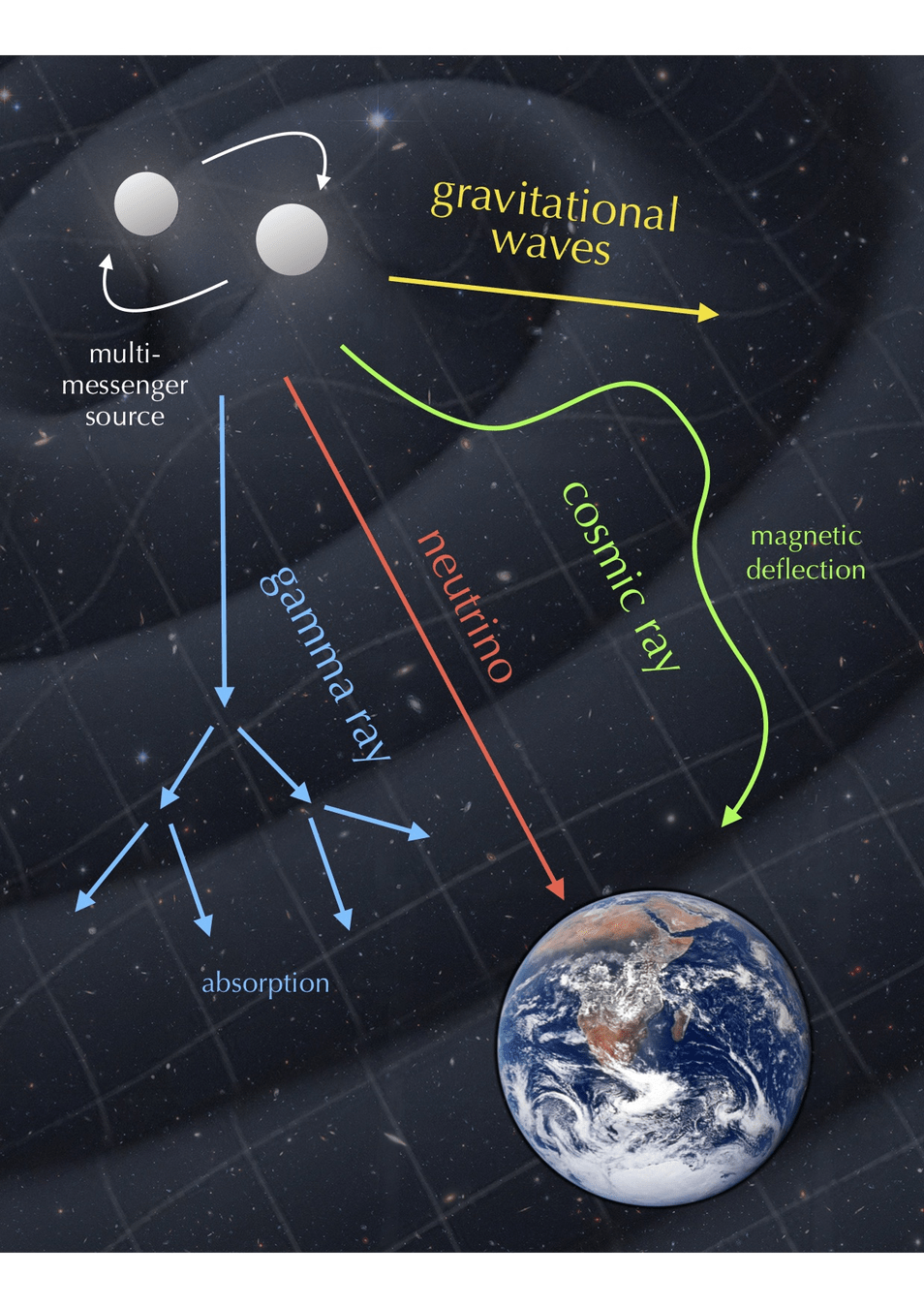
多信使天文学

Gravitational Wave Astronomy

-
Fundamental Physics
- Existence of gravitational waves
- To put constraints on the properties of gravitons
-
Astrophysics
- Refine our understanding of stellar evolution
- and the behavior of matter under extreme conditions.
-
Cosmology
- The measurement of the Hubble constant
- Dark energy
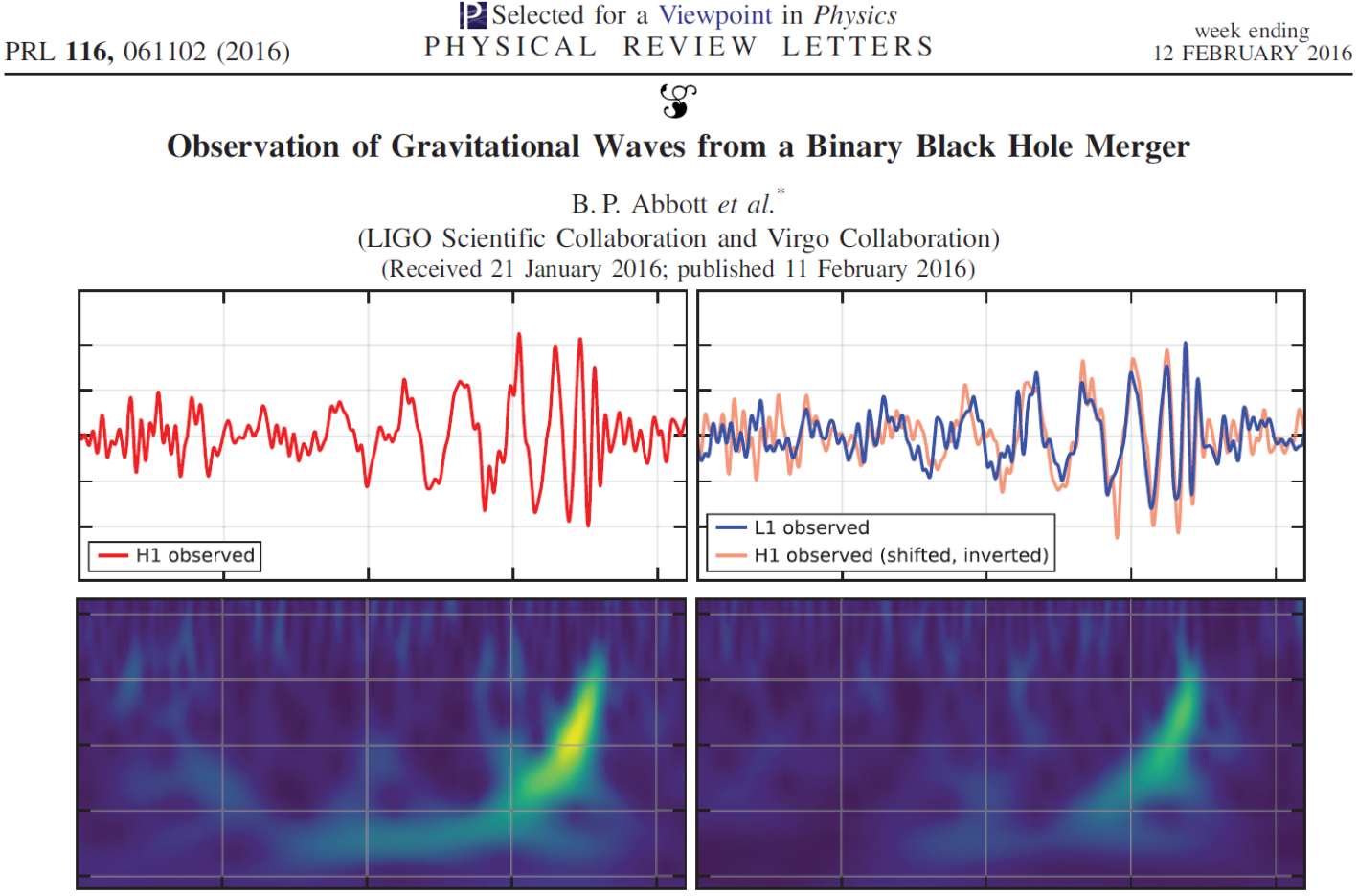
The first GW event of GW150914
- Detecting gravitational waves require a mix of FIVE key ingredients:
- good detector technology
- good waveform predictions
- good data analysis methodology and technology
- coincident observations in several independent detectors
- coincident observations in electromagnetic astronomy
—— Bernard F. Schutz
DOI: 10.1063/1.1629411
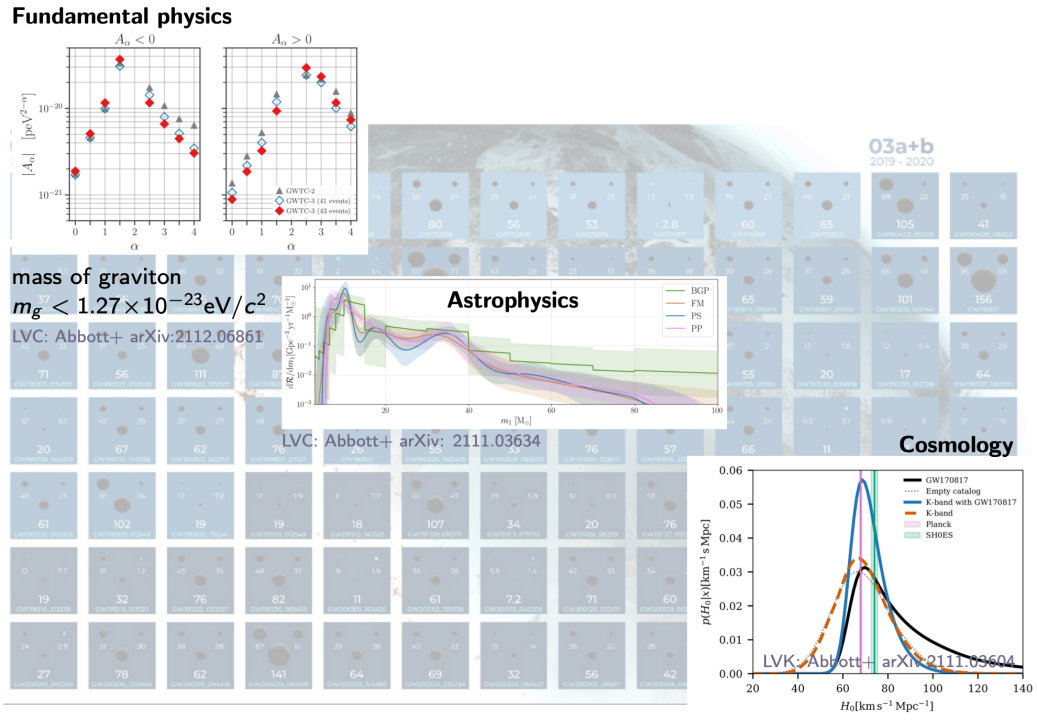
GWTC-3
Gravitational Wave Astronomy

-
Fundamental Physics
- Existence of gravitational waves
- To put constraints on the properties of gravitons
-
Astrophysics
- Refine our understanding of stellar evolution
- and the behavior of matter under extreme conditions.
-
Cosmology
- The measurement of the Hubble constant
- Dark energy
- Detecting gravitational waves require a mix of FIVE key ingredients:
- good detector technology
- good waveform predictions
- good data analysis methodology and technology
- coincident observations in several independent detectors
- coincident observations in electromagnetic astronomy
—— Bernard F. Schutz
DOI: 10.1063/1.1629411

GWTC-3
Gravitational Wave Astronomy
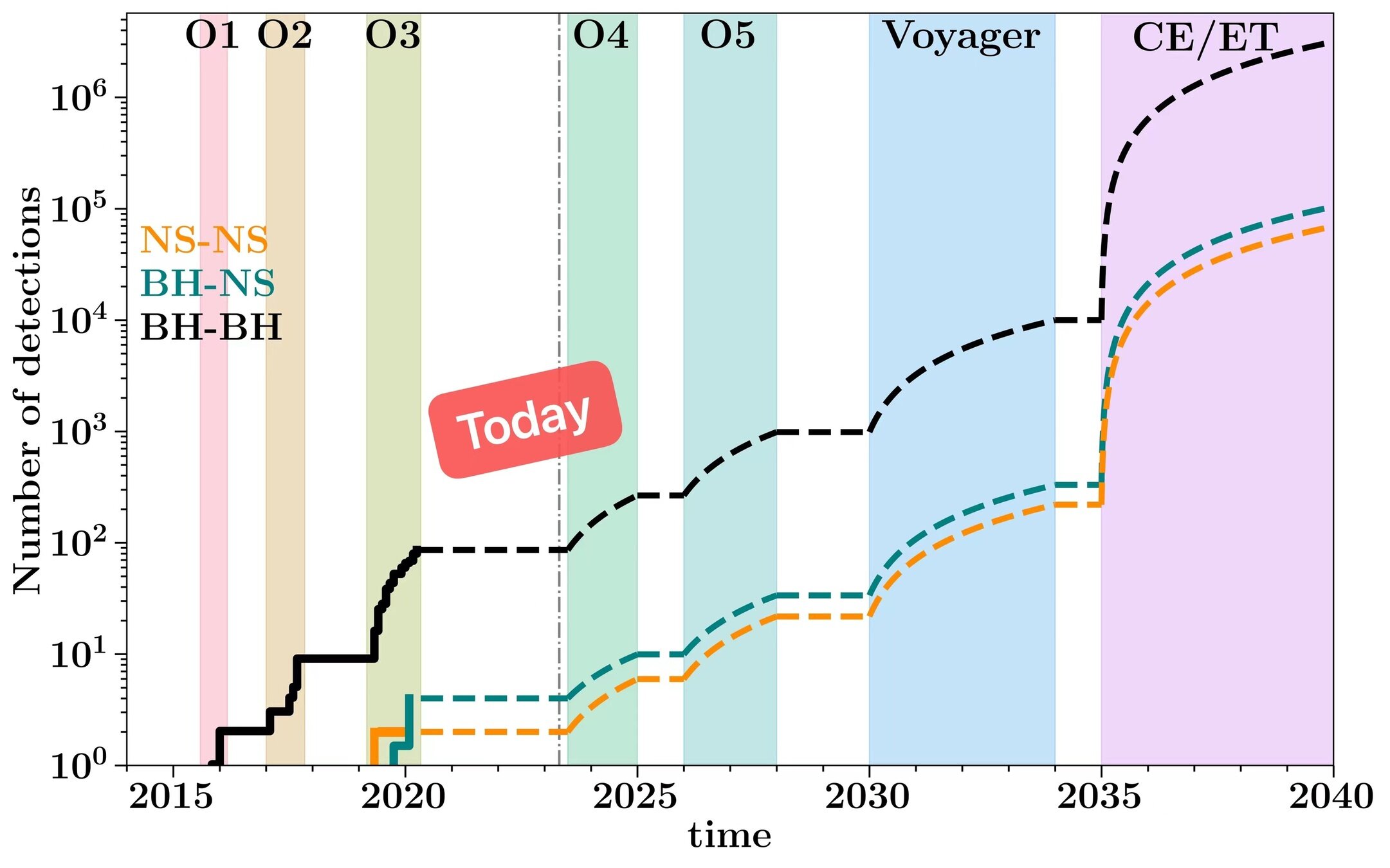
©Floor Broekgaarden (repo)

Technical Challenges: Data Processing for GW
GW Data characteristics
-
Noise: non-Gaussian and non-stationary
-
Signal:
-
(Earth-based) A low signal-to-noise ratio (SNR) which is typically about 1/100 of the noise amplitude (-60 dB).
-
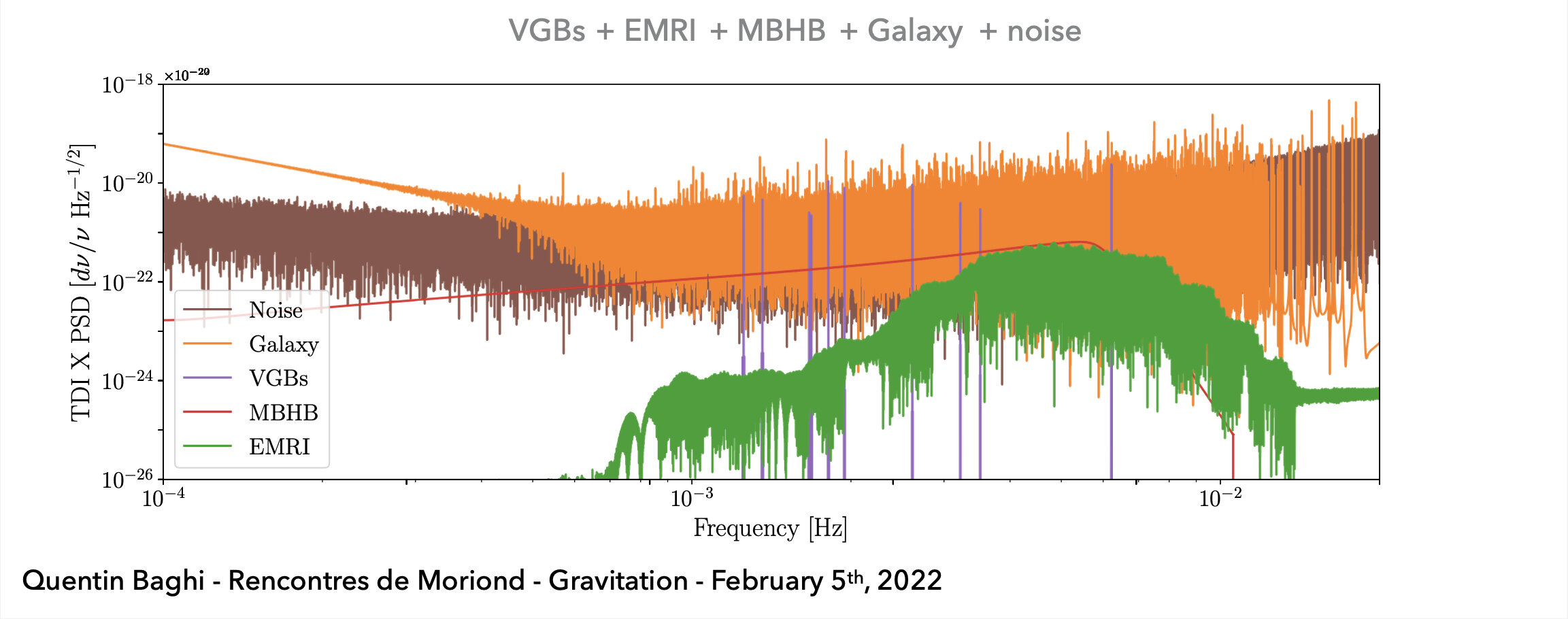
(Space-based) A superposition of all GW signals (e.g.: \(10^4\) of GBs, \(10\sim10^2\) of SMBHs, and \(10\sim10^3\) of EMRIs, etc.) received during the mission's observational run.
-
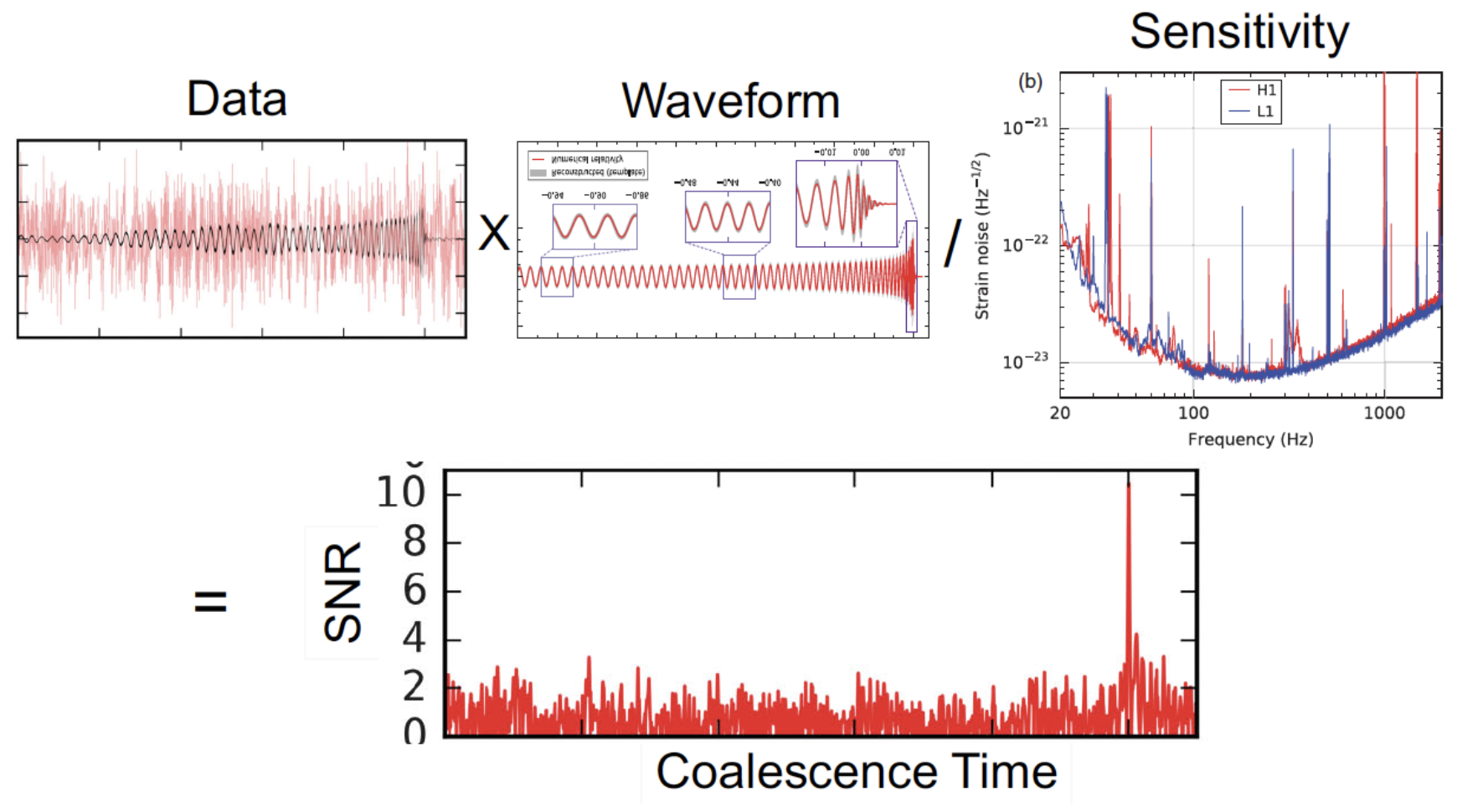
Matched filtering techniques (匹配滤波方法)
-
In Gaussian and stationary noise environments, the optimal linear algorithm for extracting weak signals
- Works by correlating a known signal model \(h(t)\) (template) with the data.
- Starting with data: \(d(t) = h(t) + n(t)\).
- Defining the matched-filtering SNR \(\rho(t)\):
\(\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2 \) , where \(\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df \) ,
\(\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df \), \(S_n(f)\) is noise power spectral density (one-sided).
Text

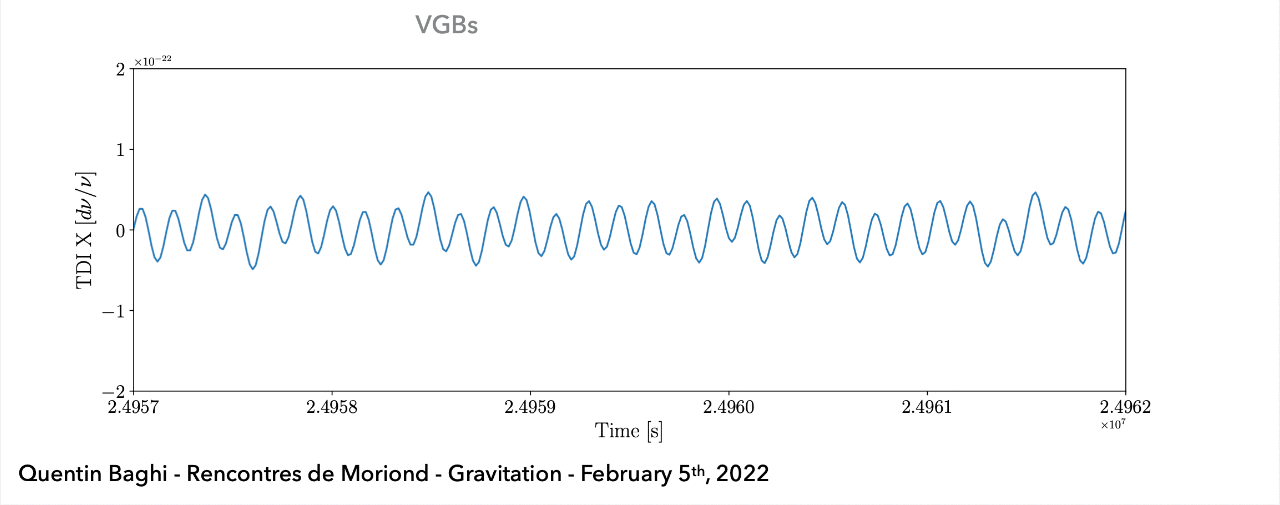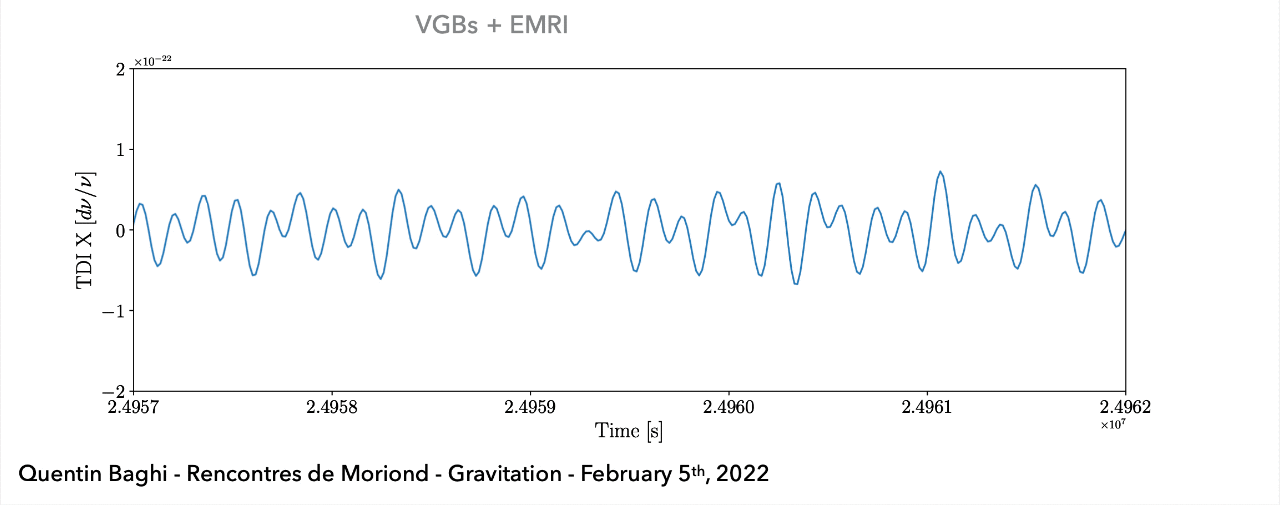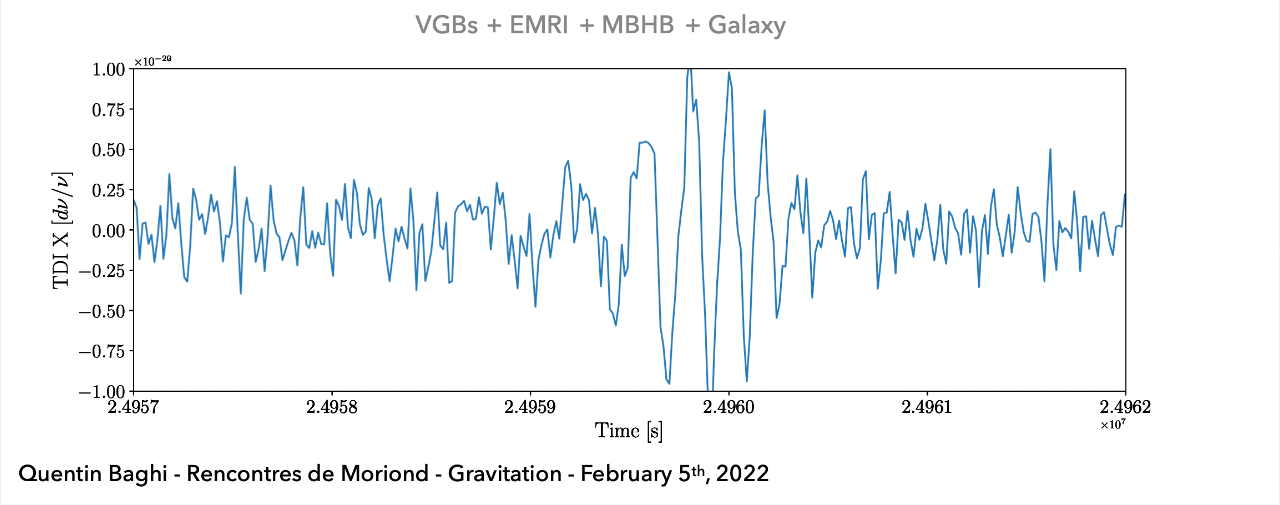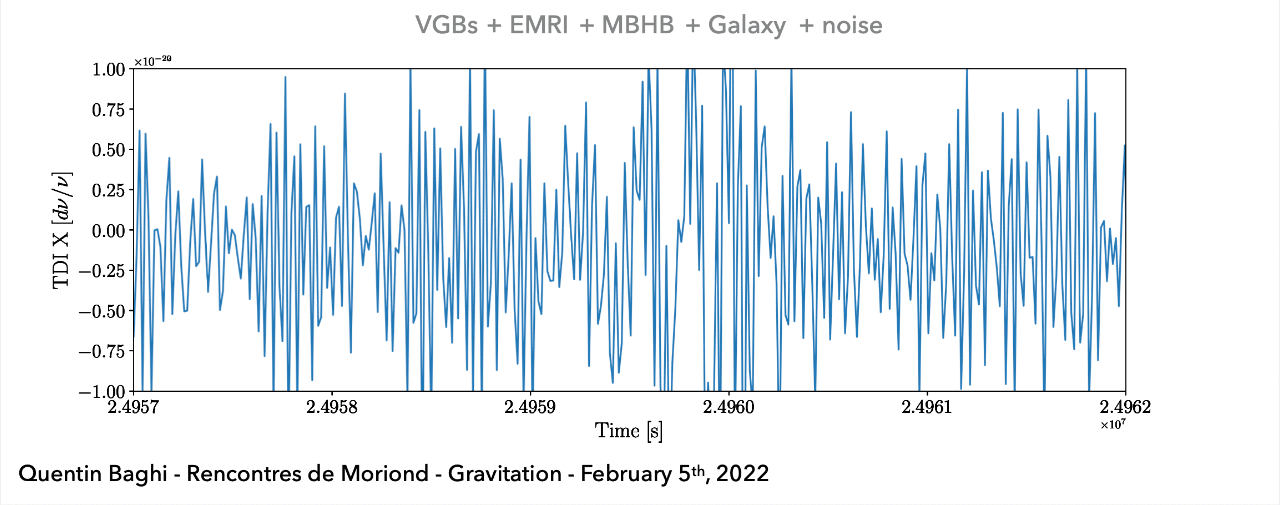
LIGO-VIRGO-KAGRA
LISA / Taiji project

Text
-
Frequentist hypothesis testing and likelihood princple:
-
make some assumptions about signal and noise hypothesis
-
write down the likelihood function for a signal in noise
-
find the parameters that maximise it
-
define a corresponding detection statistic
\(\rightarrow\) recover the MF
-
-
Bayesian hypothesis testing:
- start from the same likelihood
- define a prior over signal parameters
- marginalise over them to arrive at a Bayes factor
- Often the dirty secret: just treat this as a Frequentist detection statistic
\(\rightarrow\) recover the MF (for certain prior choices)

目录

- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- (Space-based GW Detection)

科学智能:AI for Science
-
2016年,AlphaGo 第一版发表在了 Nature 杂志上
-
2021年,AI预测蛋白质结构登上 Science、Nature 年度技术突破,潜力无穷
-
2022年,DeepMind团队通过游戏训练AI发现矩阵乘法算法问题
-
《达摩院2022十大科技趋势》将 AI for Science 列为重要趋势
-
“人工智能成为科学家的新生产工具,催生科研新范式”
-
-
2023年,DeepMind发布AI工具GNoME (Nature),成功预测220万种晶体结构
-
AI for Science:为科学带来了模型与数据双驱动的新的研究范式
-
AI + 数学、AI + 化学、AI + 医药、AI + 量子、AI + 物理、AI + 天文 ...
-




AlphaGo 围棋机器人

AlphaTensor 发现矩阵算法

AlphaFold 蛋白质结构预测

验证数学猜想
Text

Pioneering works utilizing CNN
- The most common and direct approach, from Computer Vision (CV) to GW signal processing: pixel point \(\Rightarrow\) sampling point.
- Convolutional neural networks (CNN) can achieve comparable performance to Matched Filtering and surpass them in terms of execution speed (with GPU support) under Gaussian stationary noise.
AI for Science \(\rightarrow\) AI for GW Astronomy
- Artificial Intelligence (AI) has great potential to revolutionize gravitational wave astronomy by improving data analysis, modeling, and detector development.
- Representation and supervised learning crucially extract features from GW signals, autonomously identifying informative features and leveraging labeled data for accuracy.
Text
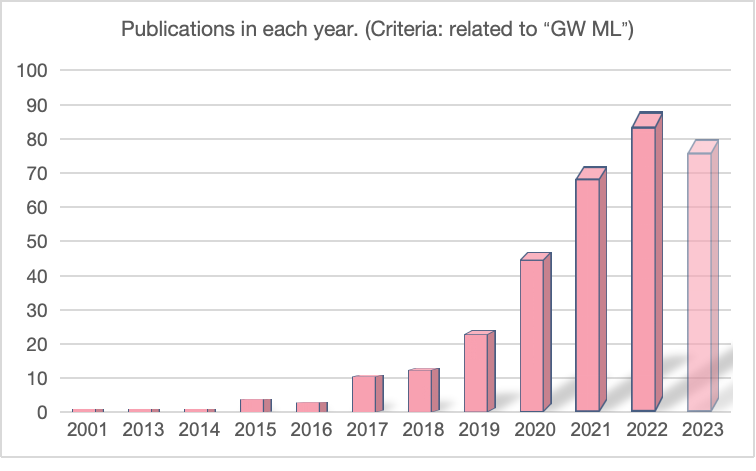
Exported: Oct, 2023 (in preparation)
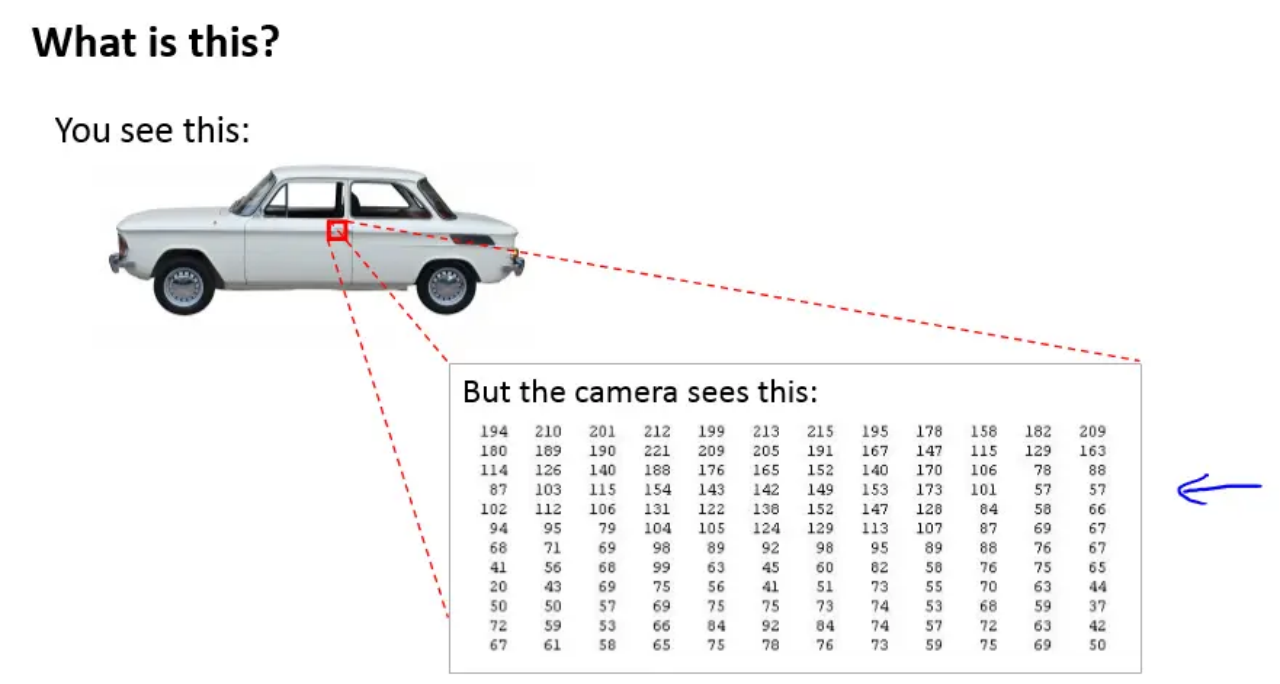

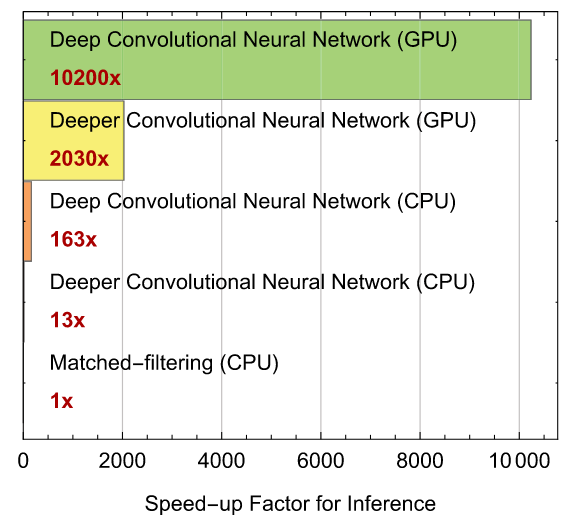
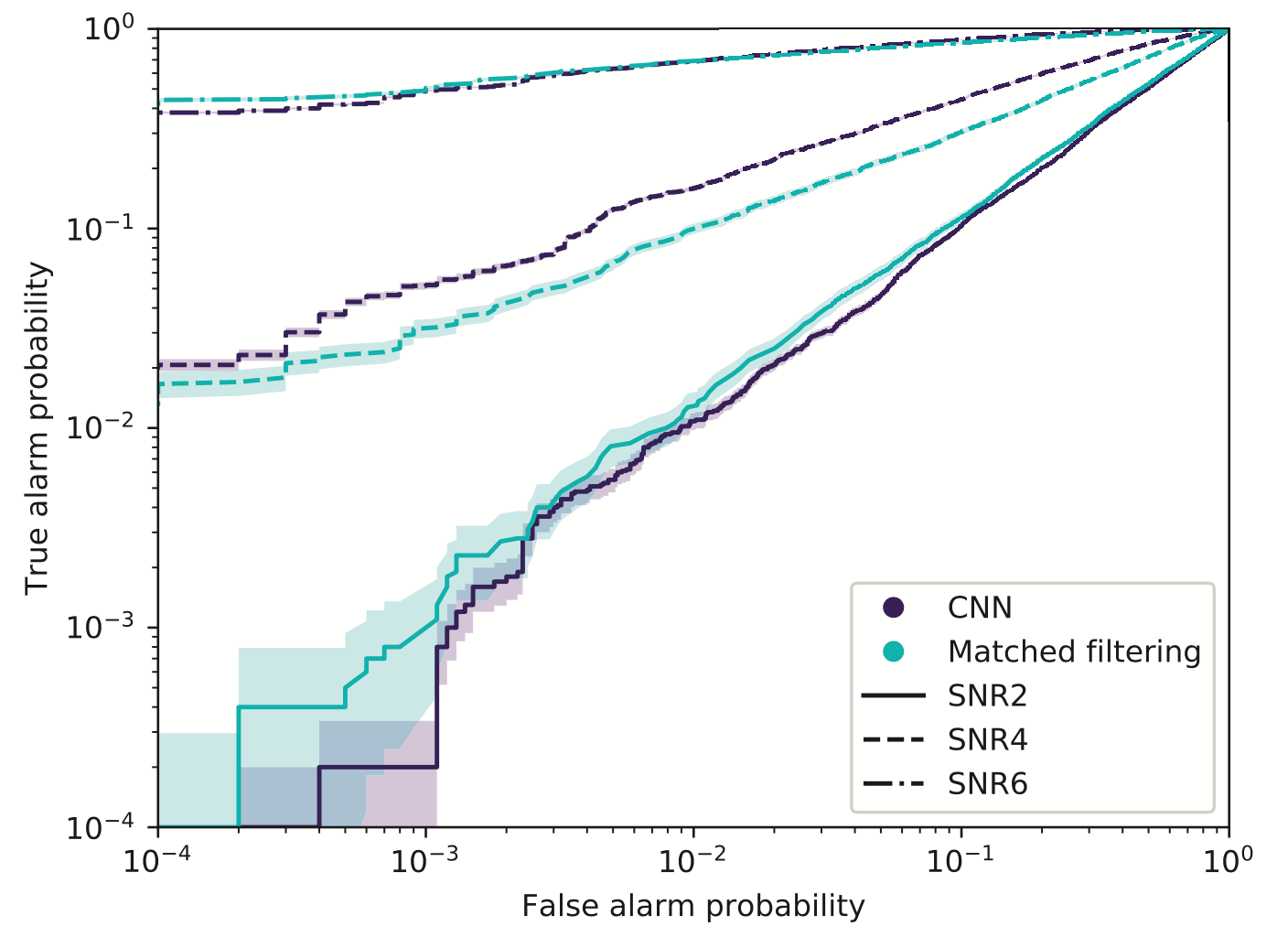
PRL, 2018, 120(14): 141103.
PRD, 2018, 97(4): 044039.
引力波数据处理:人工智能技术应用
Content




- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- (Space-based GW Detection)

GW search · Pipeline
Text

Introduction to Speed and Efficiency
- Machine Learning (ML) offers unparalleled speed in GW detection.
- The increasing sensitivity to noise and the growing number of GW events demand faster analysis capabilities.
The Need for Integration (an AI pipeline!)
- Numerous AI algorithms exist for signal detection (see more: https://wiki.ligo.org/MLA/ML_at_LIGO_and_VIRGO), highlighting the need for a streamlined pipeline.
- However, none are operational in O4 due to infrastructure challenges and the lack of standardized sensitivity measures against non-stationary noise.
Case study: Pipeline
- The Aframe online pipeline (arXiv:2403.18661) represents a significant step forward.
- Utilizes GPU acceleration for signal preprocessing, model inference, and real-time false alarm rate calculation.
Text
Text

Aframe
S.S. Chaudhary, et al. arXiv:2308.04545
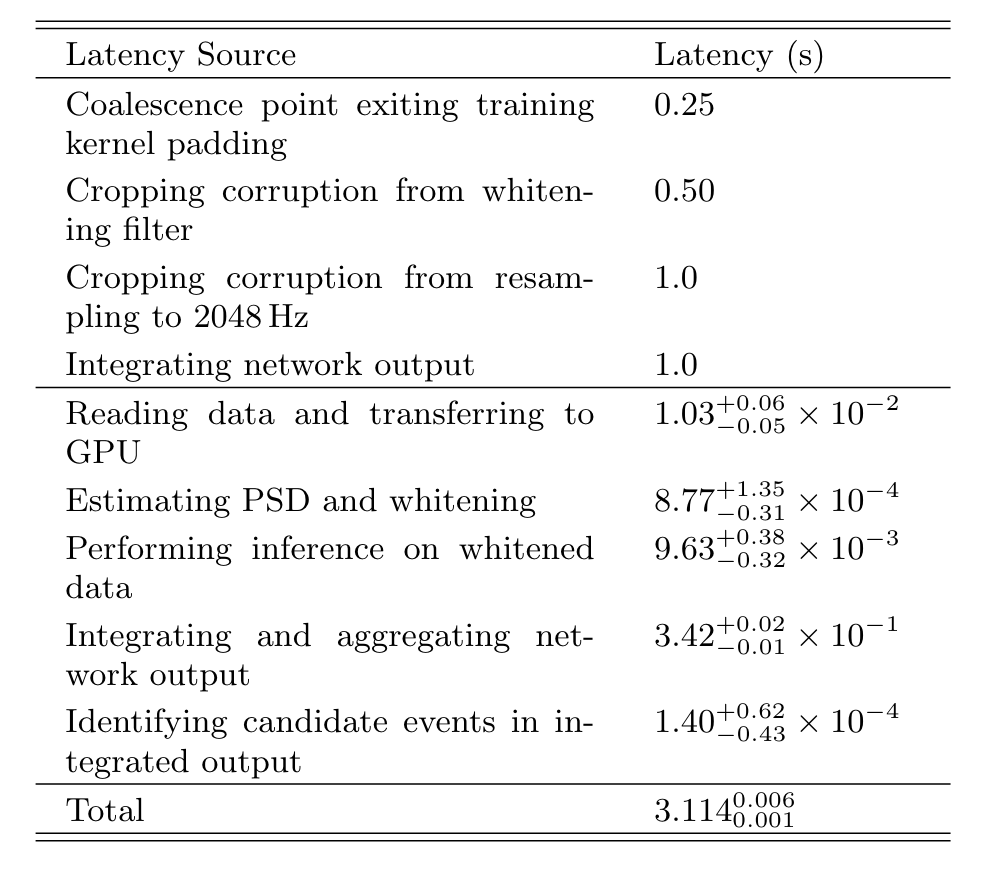
GW search · Pipeline
Text

Challenges and Future Directions
- A comprehensive online pipeline should consider various signal types, including BNS and NSBH, and all detectors, including Virgo and KAGRA.
- Beyond false alarm rates, additional real-time information is crucial for a holistic analysis.
Case study: Pipeline
- The Aframe online pipeline (arXiv:2403.18661) represents a significant step forward.
- Despite its advancements, it primarily focuses on BBH signals, with decreased performance on longer signals like BNS, a point also highlighted in MLGWSC1(PRD, 2209.11146).
Text
Aframe
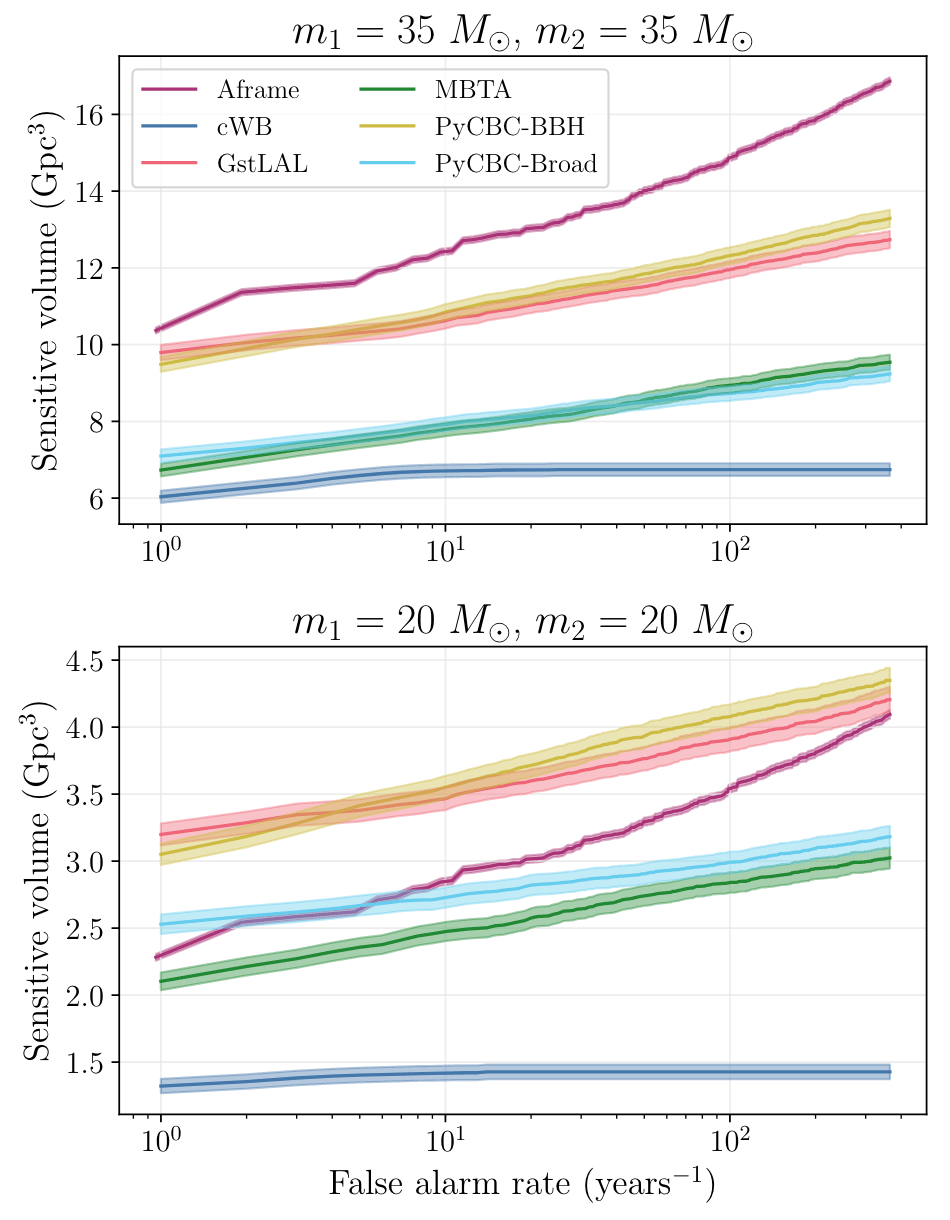


OpenLVEM, June 08, 2023. Low Latency UPDATE.

Matched-filtering Convolutional Neural Network (MFCNN)
Text
- GW templates can be utilized as recognizable features for signal detection.
- It is feasible to generalize both matched-filtering and neural networks.
- Linear filters (i.e., matched-filtering) in signal processing can be reformulated as neural layers (i.e., CNNs).
MLGWSC-1
-
The majority of AI algorithms used for testing are highly sensitive to non-Gaussian real noise backgrounds, resulting in high false positive rates.
(MFCNN group) H.W., et al. PRD (2023)

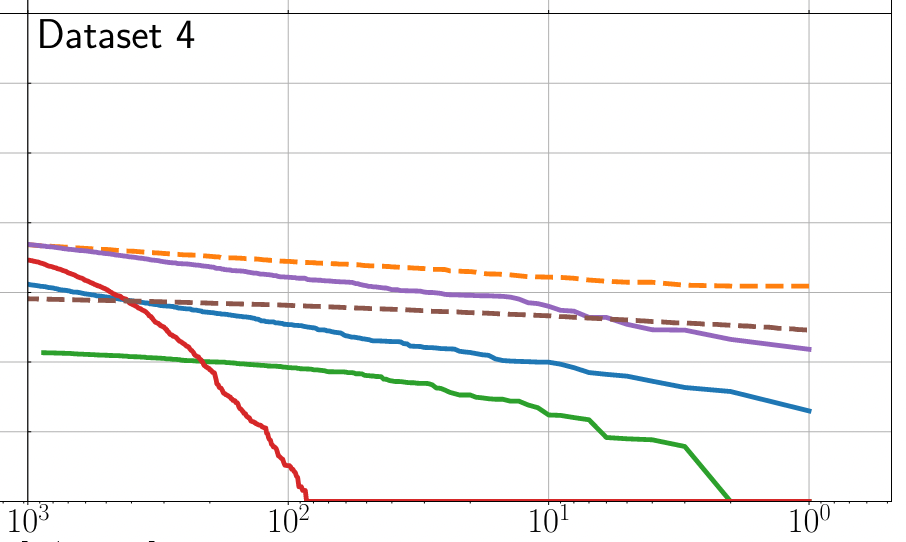
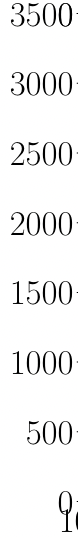
Text
CL.M., W.W., H.W., et al. PRD (2022)
Ensemble learning
-
Leverages statistical approaches to utilize more information for making informed decisions by combining multiple models.
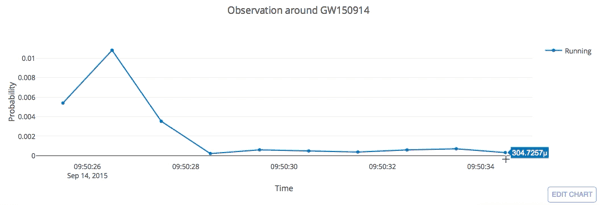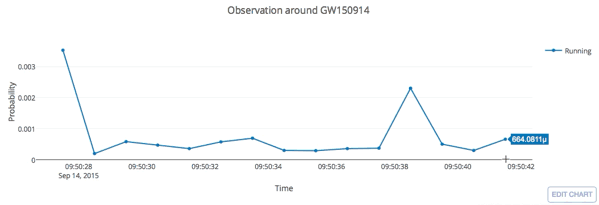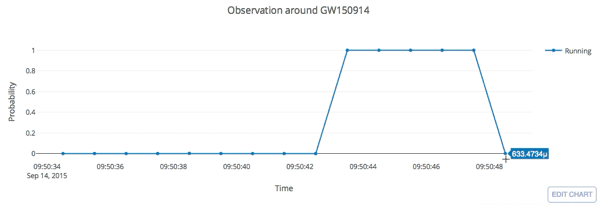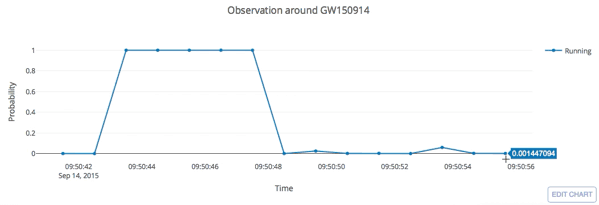
Real-time GW searches for GW150914
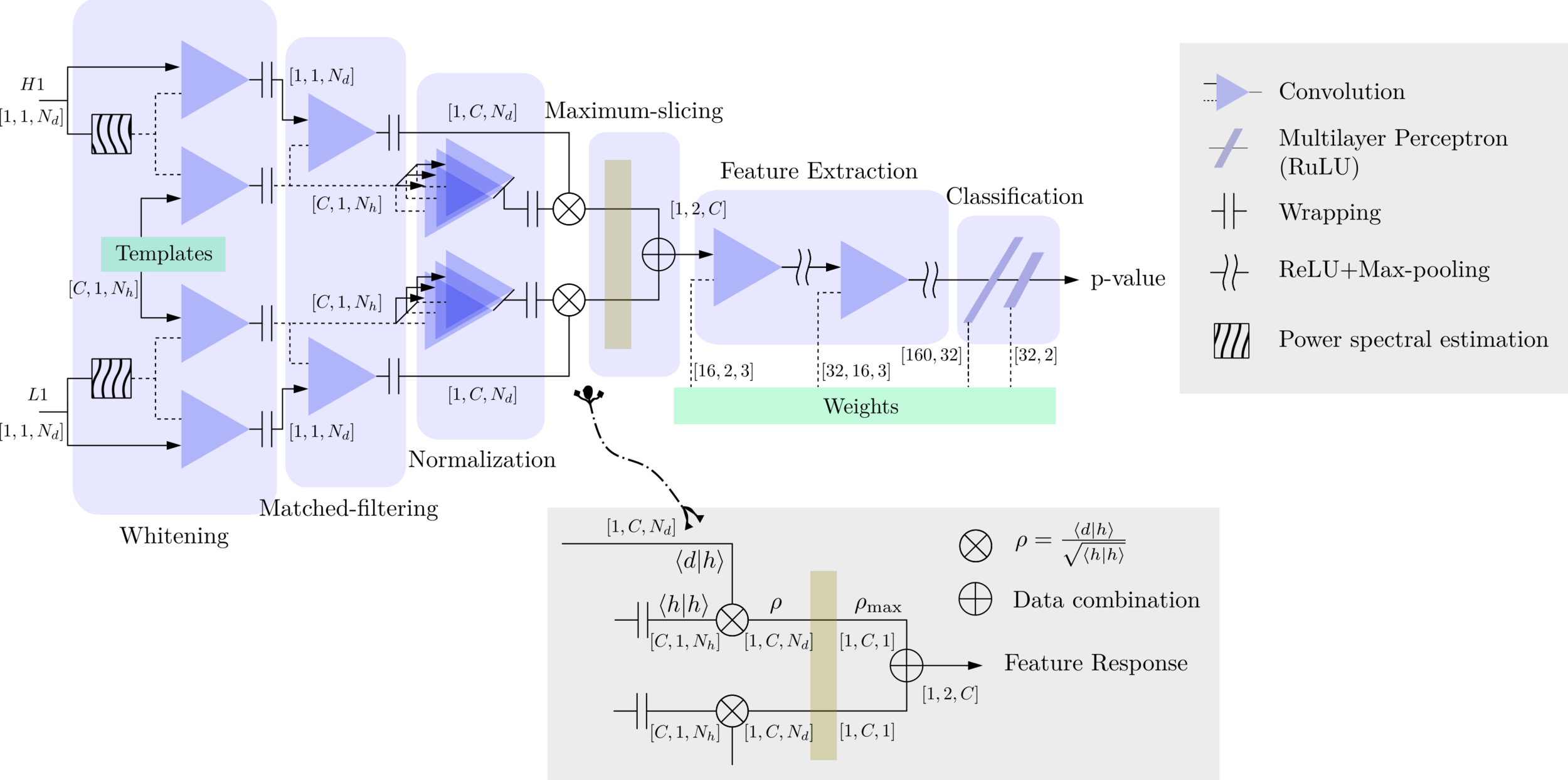
H.W., et al. PRD (2020)
Text
Expanding the dimension of the output
- is to call more information to make decisions in improving AI models.
Text
CL.M., W.W., H.W., et al. PRD (2023)
GW search · Pipeline
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.


Real-time GW searches for GW150914
He Wang, et al. PRD 101, 10 (2020): 104003
He Wang, et al. MLST. 5, 1 (2024): 015046.
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.


He Wang, et al. PRD 101, 10 (2020): 104003
He Wang, et al. MLST. 5, 1 (2024): 015046.


Real-time GW searches for GW150914
GW search · Pipeline

数据增益 -> GWToolkit (缺一个好看的高吞吐性能图和loss/acc性能图)+ Data Protal (缺一个可视化和性能表现CKAN?)
Pipeline -> MFCNN + WaveFormer(缺雪藏event的corner图); bGR(缺结果图)
信号探测(缺各种文章中的探测统计量图像)-> 引出新的理论缺失: machine learning GW statistics
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.
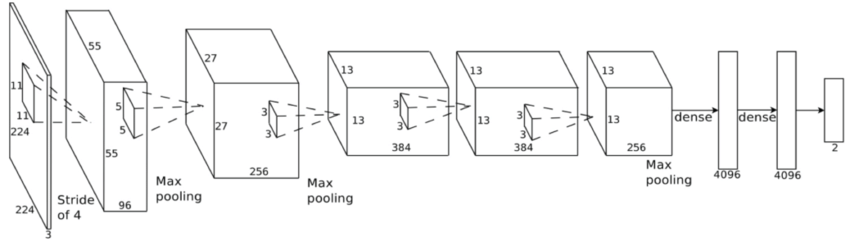
Feature extraction
Convolutional Neural Network (ConvNet or CNN)
Classification
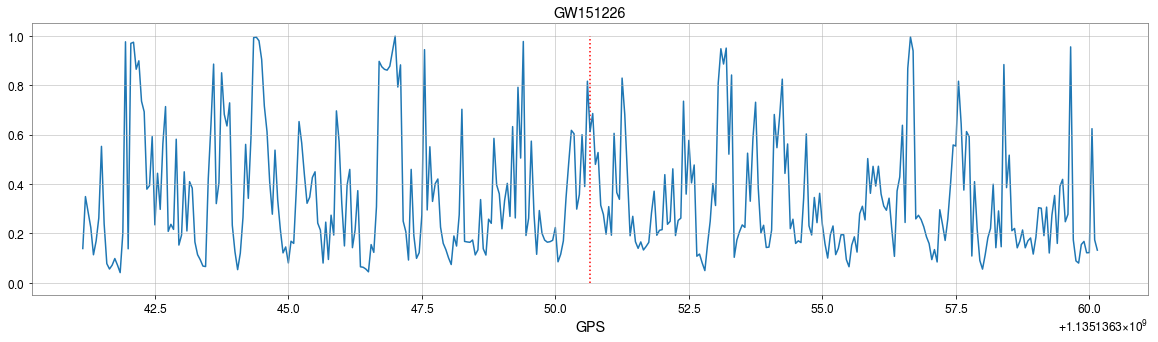

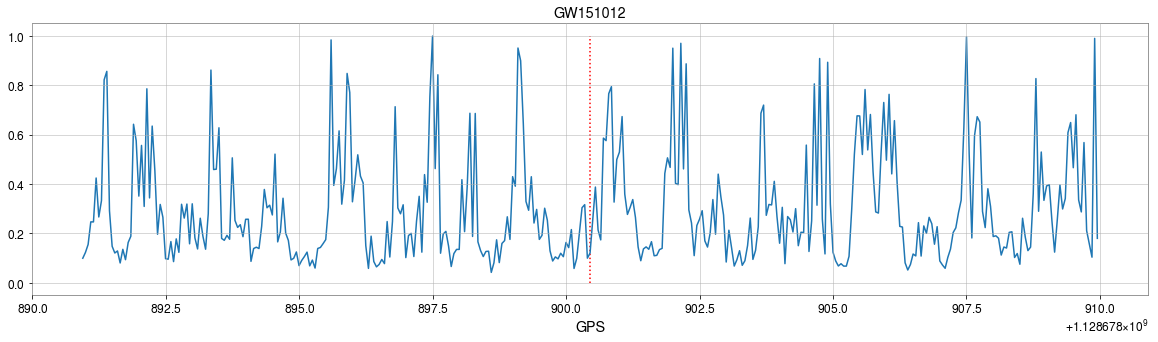
GW150914
GW151226
GW151012
- CNNs always works pretty good on stimulated noises.
- However, when on real noises from LIGO, this approach does not work that well.
- It's too sensitive against the background + hard to find GW events)
>> Is it matched-filtering ?
>> Wait, It can be matched-filtering!
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.

He Wang, et al. PRD 101, 10 (2020): 104003
GW150914
GW151226
GW151012
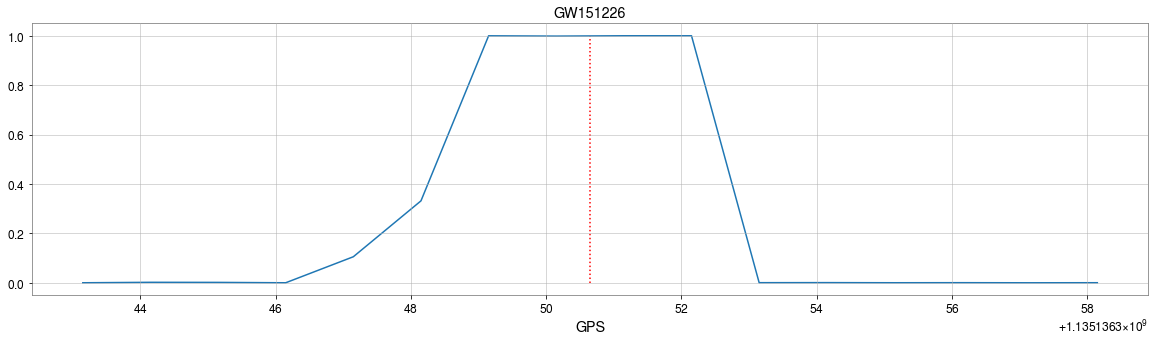
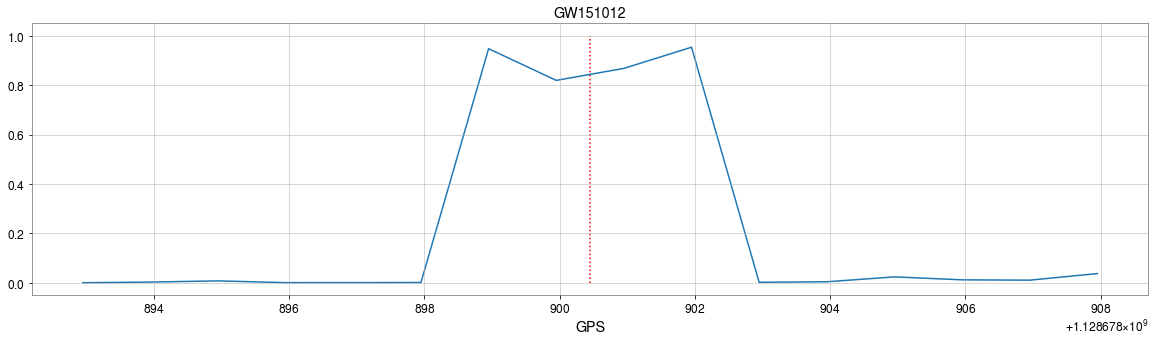
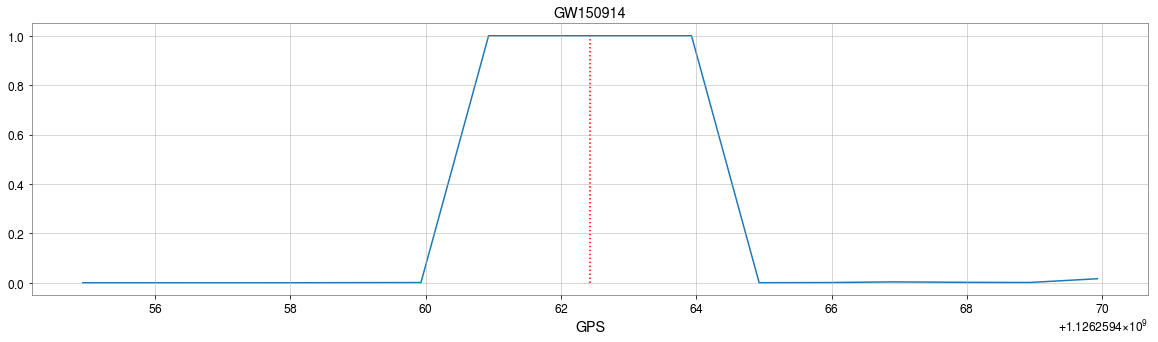
MFCNN MFCNN MFCNNMatched-filtering (cross-correlation with the templates) can be regarded as a convolutional layer with a set of predefined kernels.
- In practice, we use matched filters as an essential component of feature extraction in the first part of the CNN for GW detection.

Real-time GW searches for GW150914
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.

He Wang, et al. PRD 101, 10 (2020): 104003
- Transform matched-filtering method from frequency domain to time domain.
- The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):
Frequency domain
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.

He Wang, et al. PRD 101, 10 (2020): 104003
- Transform matched-filtering method from frequency domain to time domain.
- The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):
Frequency domain
Time domain
(normalizing)
(matched-filtering)
\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)
(whitening)
where
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.

He Wang, et al. PRD 101, 10 (2020): 104003
- Transform matched-filtering method from frequency domain to time domain.
- The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):
Frequency domain
Time domain
(normalizing)
(matched-filtering)
\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)
(whitening)
where
Deep Learning Framework
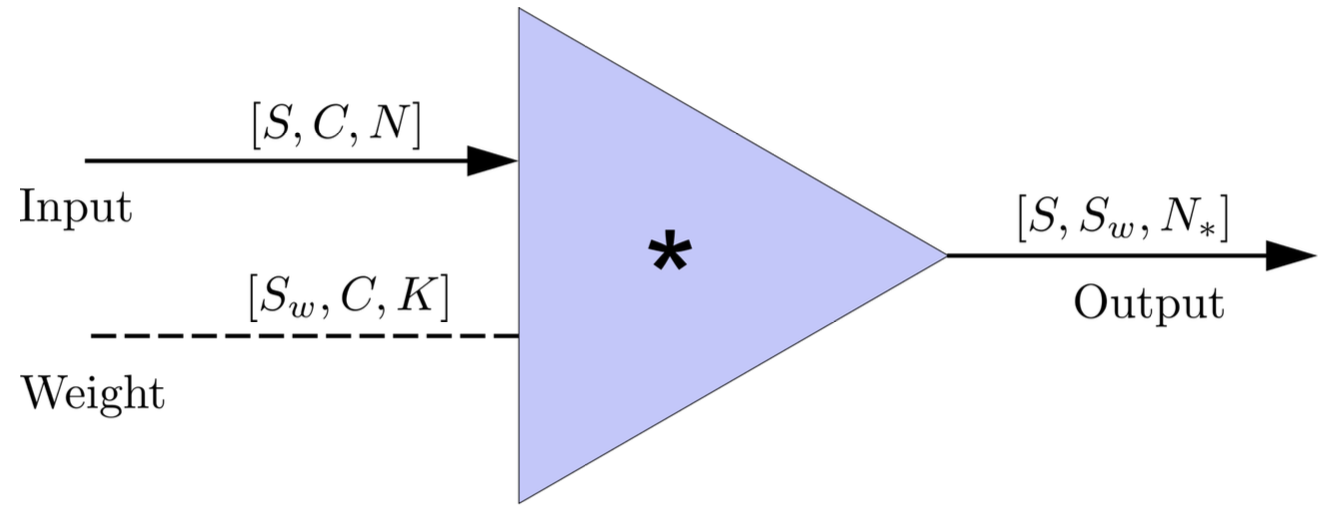
- In the 1-D convolution (\(*\)) on Apache MXNet, given input data with shape [batch size, channel, length] :
FYI: \(N_\ast = \lfloor(N-K+2P)/S\rfloor+1\)
(A schematic illustration for a unit of convolution layer)
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.

He Wang, et al. PRD 101, 10 (2020): 104003
- Transform matched-filtering method from frequency domain to time domain.
- The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):
Frequency domain
Time domain
(normalizing)
(matched-filtering)
\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)
(whitening)
where
Deep Learning Framework
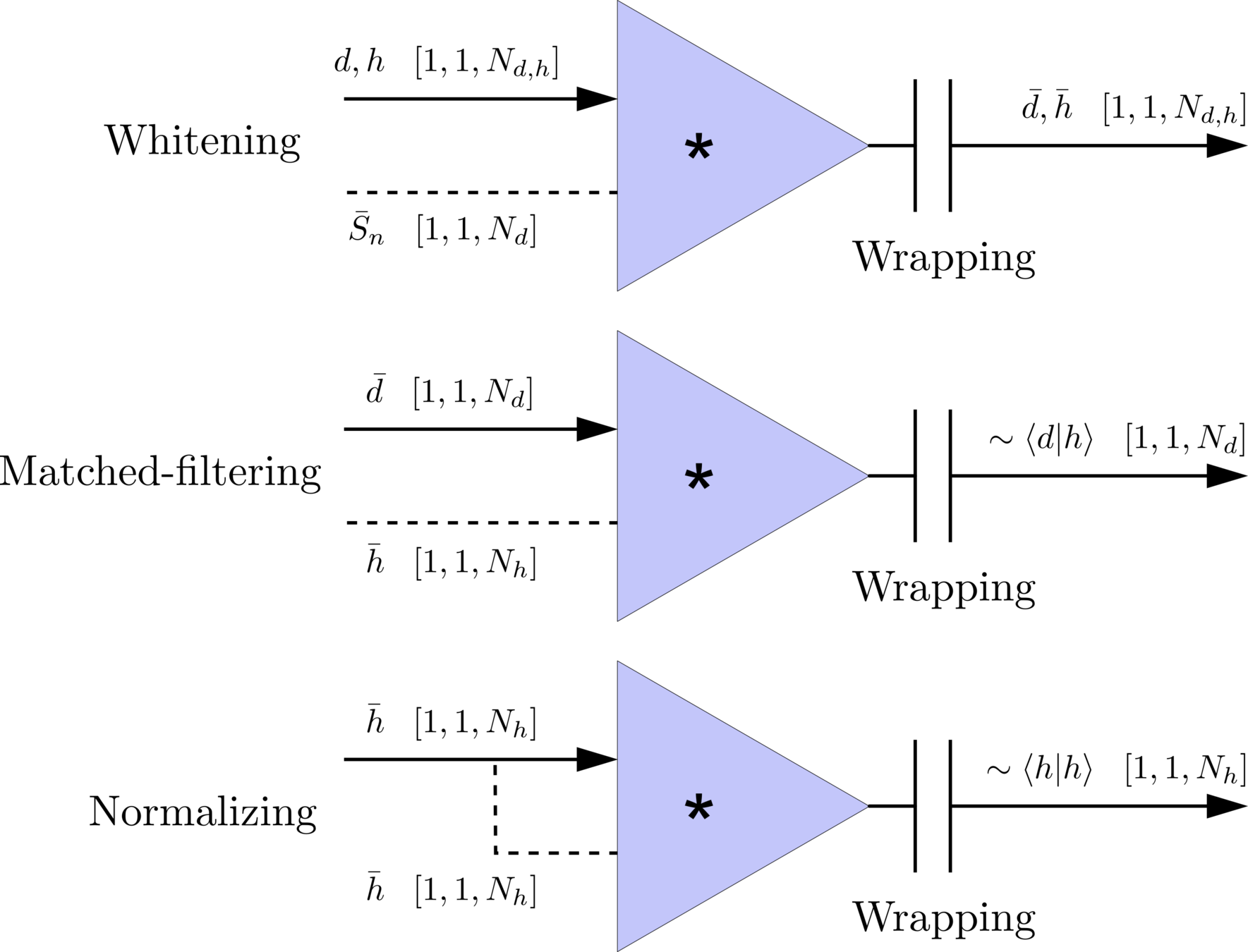


GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.

He Wang, et al. PRD 101, 10 (2020): 104003
Time domain
(normalizing)
(matched-filtering)
\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)
(whitening)
where
Deep Learning Framework



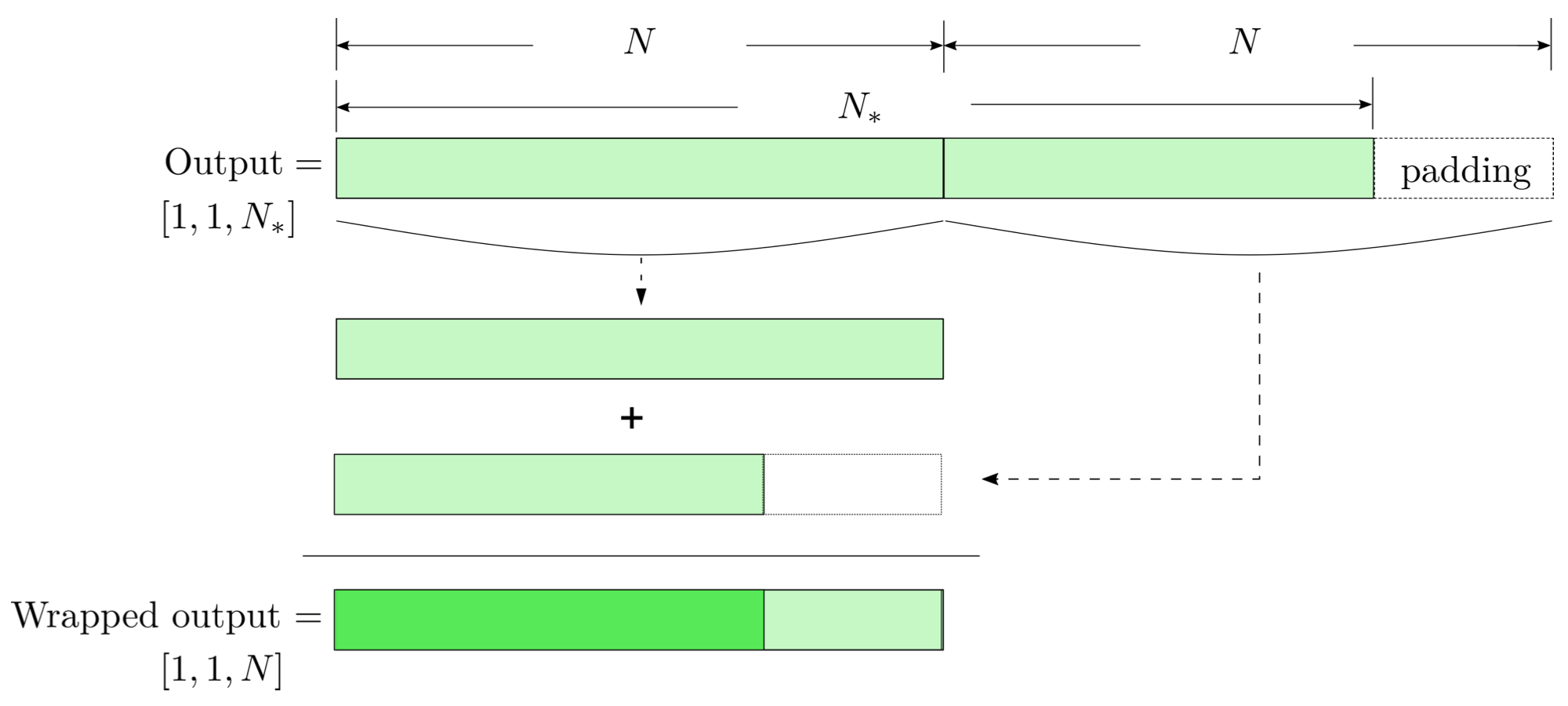
modulo-N circular convolution
GW search · Pipeline
Text

Beyond Speed: Generalization and Discovery in GW Detection
- Our primary goal is not speed but the model's ability to generalize and discover new GW signals, including those beyond the reach of matched filtering techniques and General Relativity (GR).
- Leveraging our experience in signal modeling (MFCNN) and noise modeling (WaveFormer), we are gradually building an offline pipeline capable of searching for signals in complete GW observation data and calculating FARs.

He Wang, et al. PRD 101, 10 (2020): 104003
import mxnet as mx
from mxnet import nd, gluon
from loguru import logger
def MFCNN(fs, T, C, ctx, template_block, margin, learning_rate=0.003):
logger.success('Loading MFCNN network!')
net = gluon.nn.Sequential()
with net.name_scope():
net.add(MatchedFilteringLayer(mod=fs*T, fs=fs,
template_H1=template_block[:,:1],
template_L1=template_block[:,-1:]))
net.add(CutHybridLayer(margin = margin))
net.add(Conv2D(channels=16, kernel_size=(1, 3), activation='relu'))
net.add(MaxPool2D(pool_size=(1, 4), strides=2))
net.add(Conv2D(channels=32, kernel_size=(1, 3), activation='relu'))
net.add(MaxPool2D(pool_size=(1, 4), strides=2))
net.add(Flatten())
net.add(Dense(32))
net.add(Activation('relu'))
net.add(Dense(2))
# Initialize parameters of all layers
net.initialize(mx.init.Xavier(magnitude=2.24), ctx=ctx, force_reinit=True)
return netThe available codes: https://gist.github.com/iphysresearch/a00009c1eede565090dbd29b18ae982c

1 sec duration
35 templates used
Content

- GW Astronomy
- AI for Science · GW Data Analysis
-
GW search · Pipeline
- Data Denoising for Signal Detection
- Parameter estimation · Scientific discovery
- Key Takeaways
- (Space-based GW Detection)




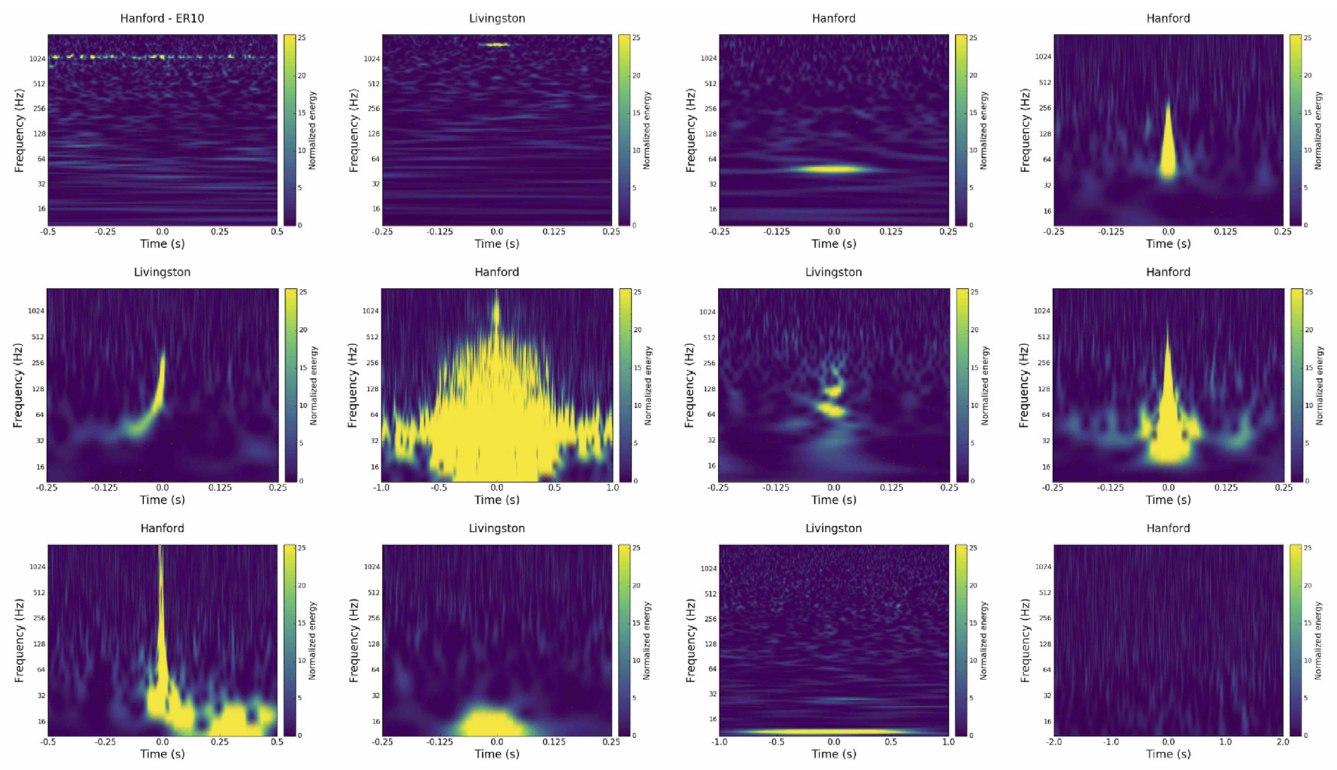
1400Ripples Air Compressor Blip
Extremely Loud Helix Koi Fish
Various types of Glitch
Background

-
The improvement of data quality is a very complex issue, with data from over 20,000 sensor channels determining the quality of the gravitational wave science data channel.
-
Reducing non-Gaussian short-duration pulse interference (Glitches) in gravitational wave data will help reduce the false alarm rate of gravitational wave signals.
-
Removing Glitches from gravitational wave detection data is a multi-classification problem.
- Traditional machine learning algorithms Powell J, et al. CQG, 2015
- Deep learning algorithms Zevin, M, et al. C
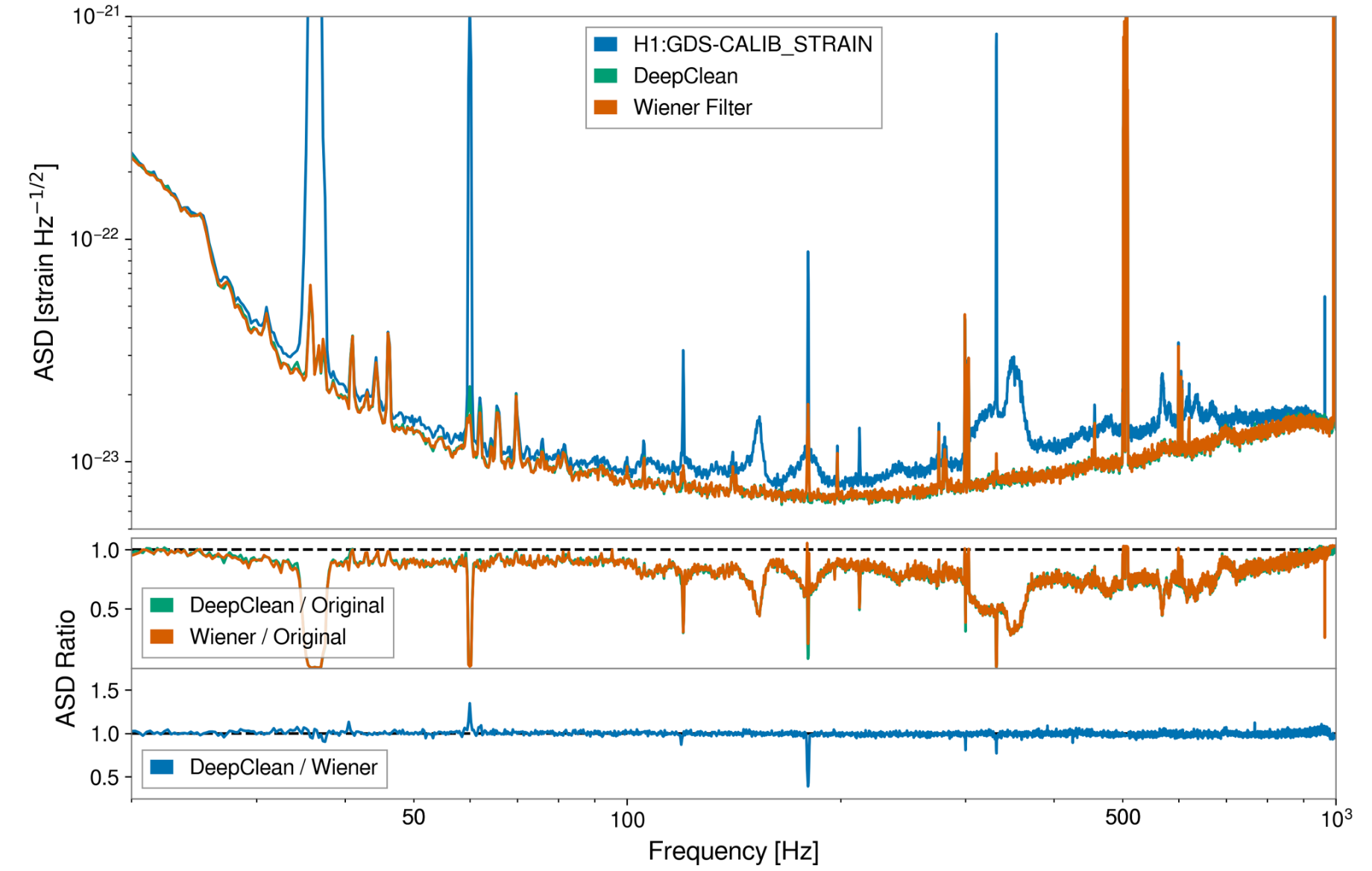
Ormiston R, et al. PRR, 2020
-
DeepClean: One-dimensional Convolutional Neural Network which takes a specified set of witness channels and subsequently outputs the predicted noise in strain.
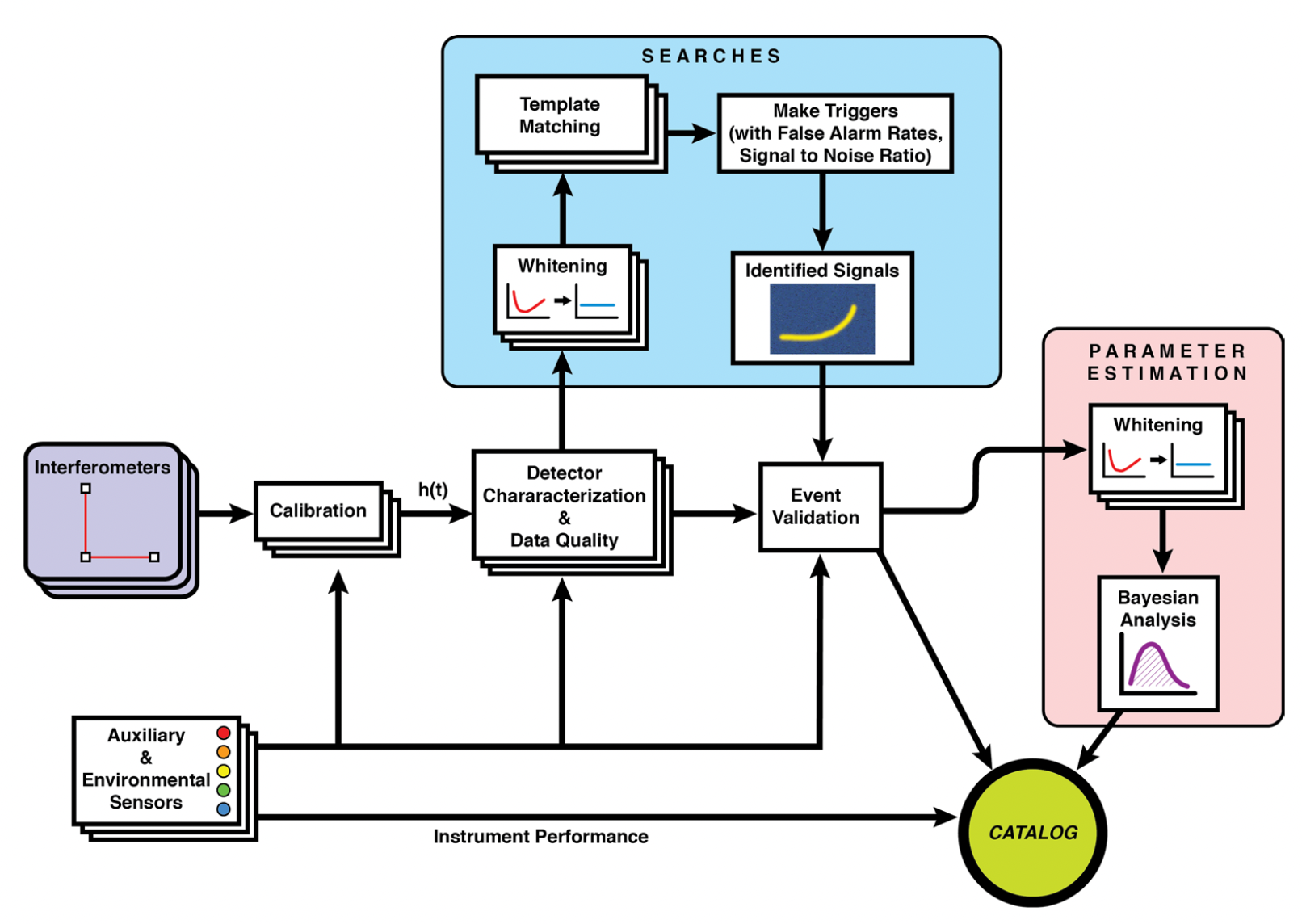
IGWN data processing
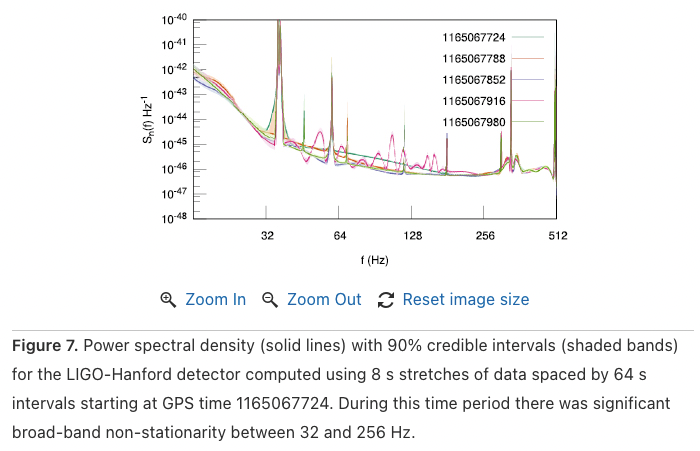
Non-stationary
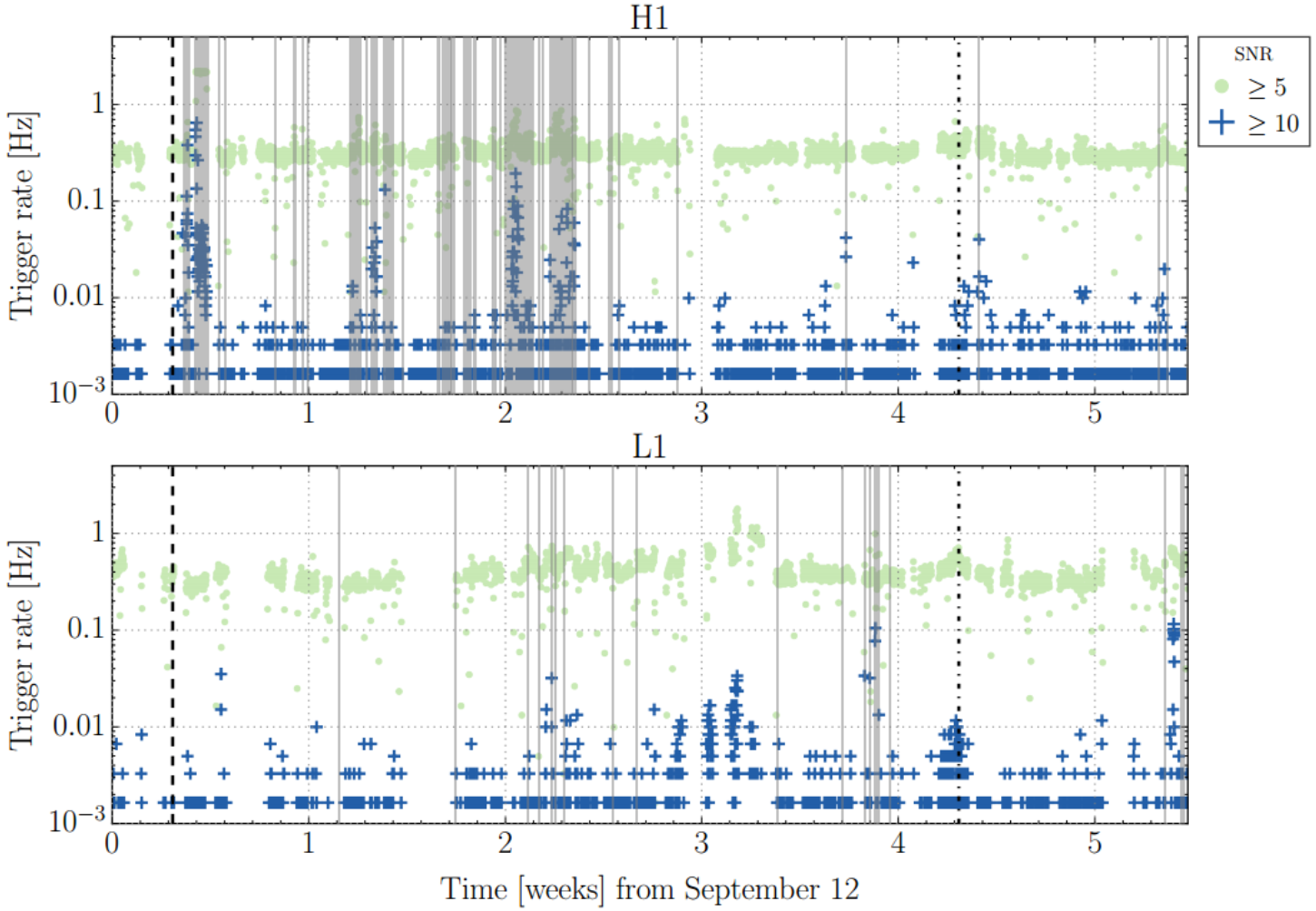
Non-Gaussianity
Background
Related Works
Model Structure
Precessing & Train
Effect on Noise
Effect on BBH signals
Credit: Marco Cavaglià

Network Architecture

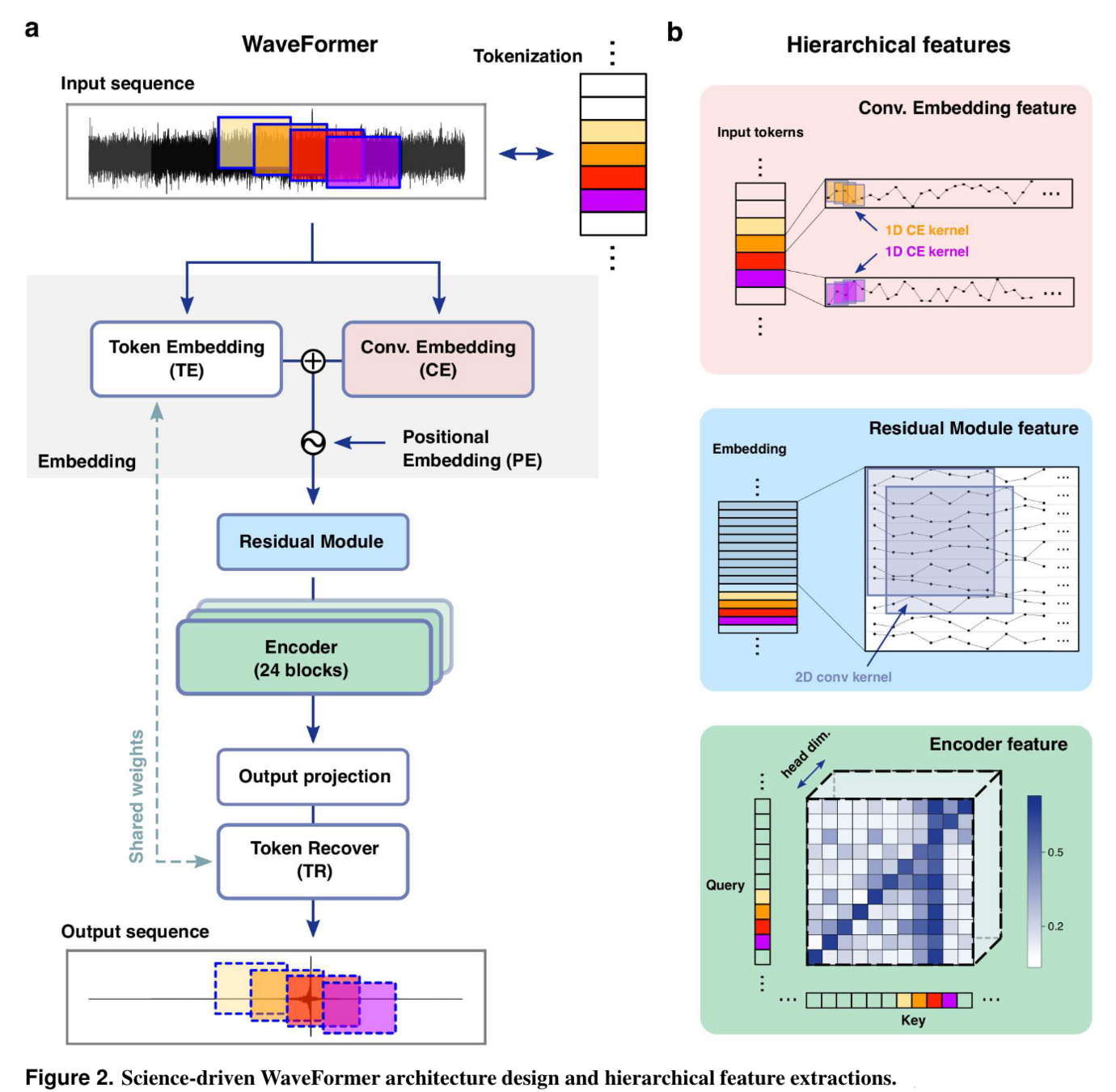
- The WaveFormer, a billion-scale transformer-based model, excels in suppressing realistic noise and recovering injections or GW events, thereby significantly improving data quality.
- In its application, it treats each overlapping time-domain data subsequence as an individual token, akin to tokenization in natural language processing (NLP).
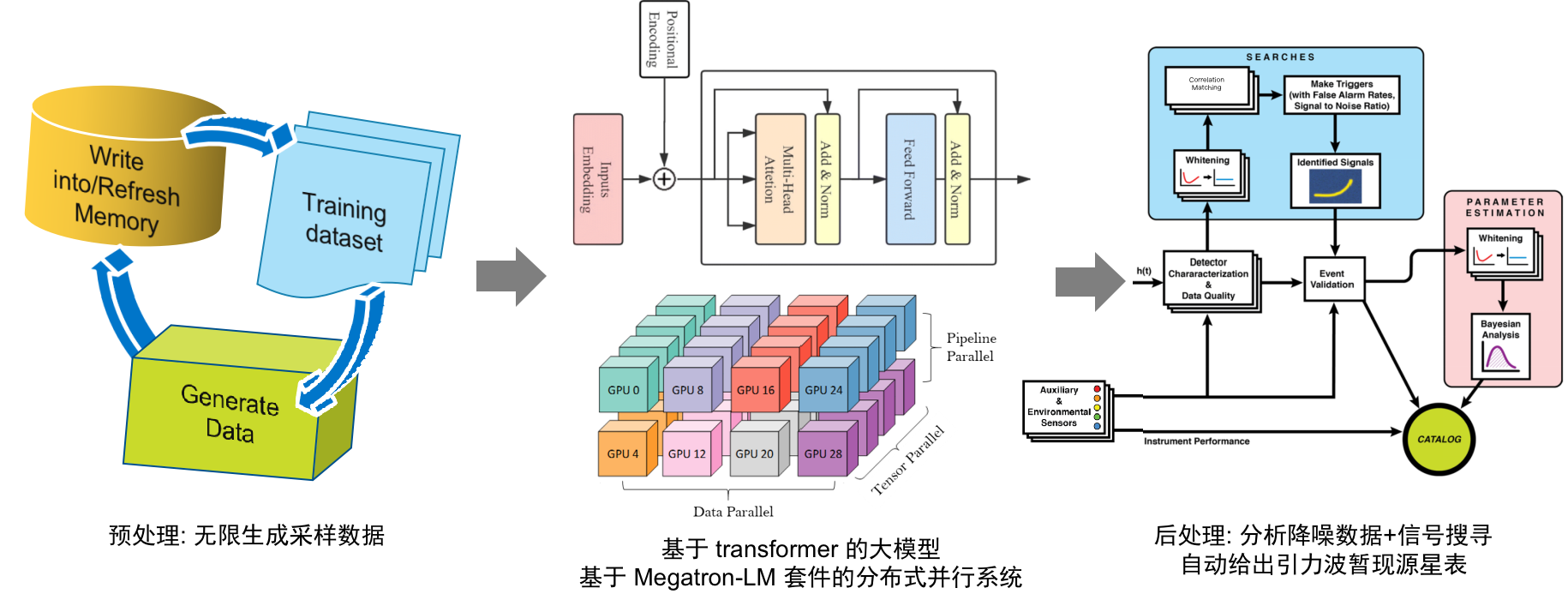




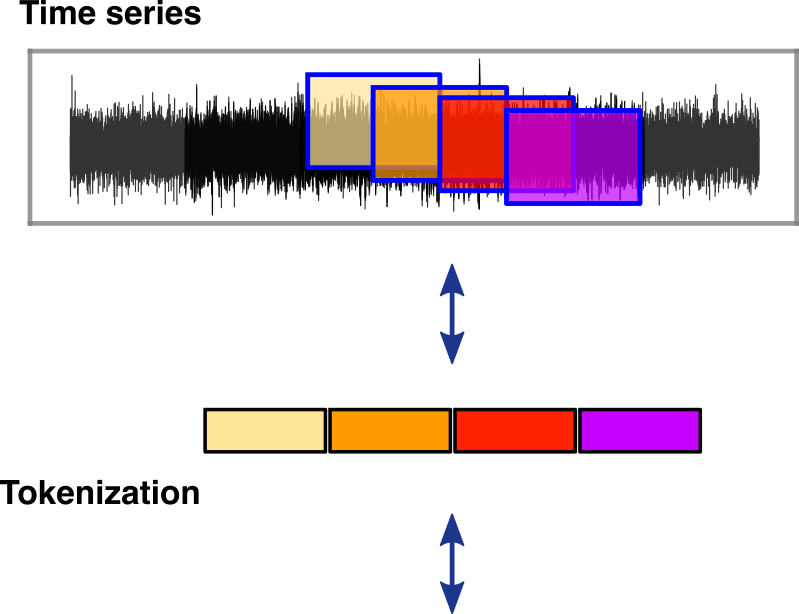
["This", "is", "a", "sample"]
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046





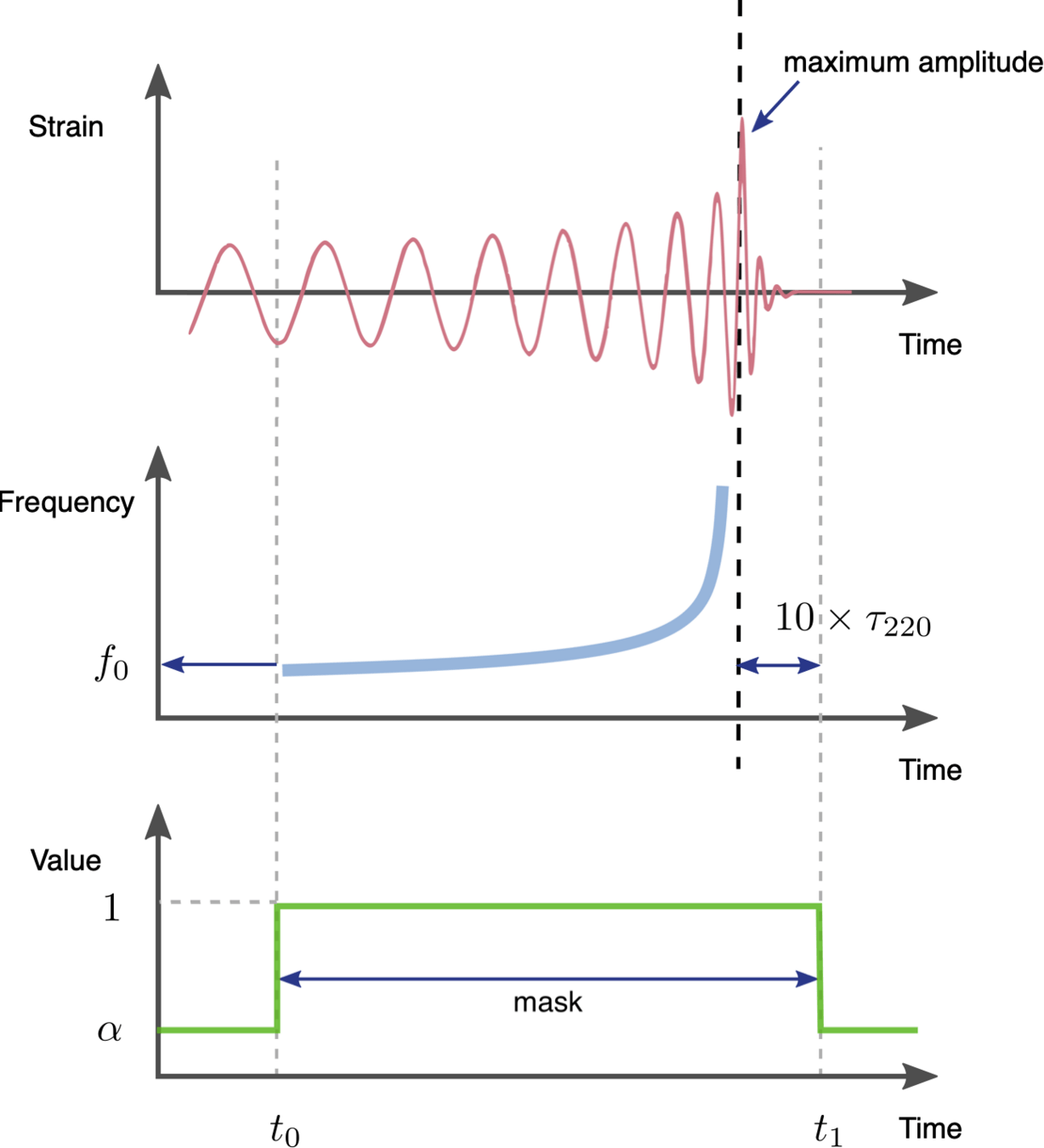
Data Preprocessing and Training Strategy

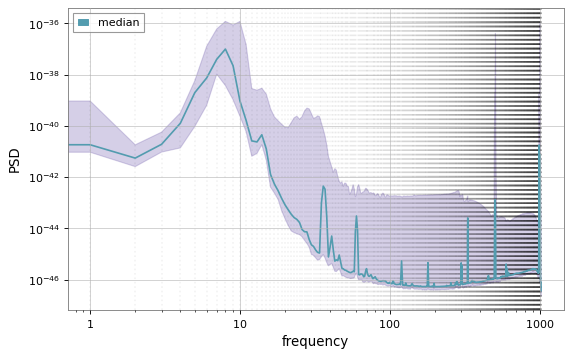
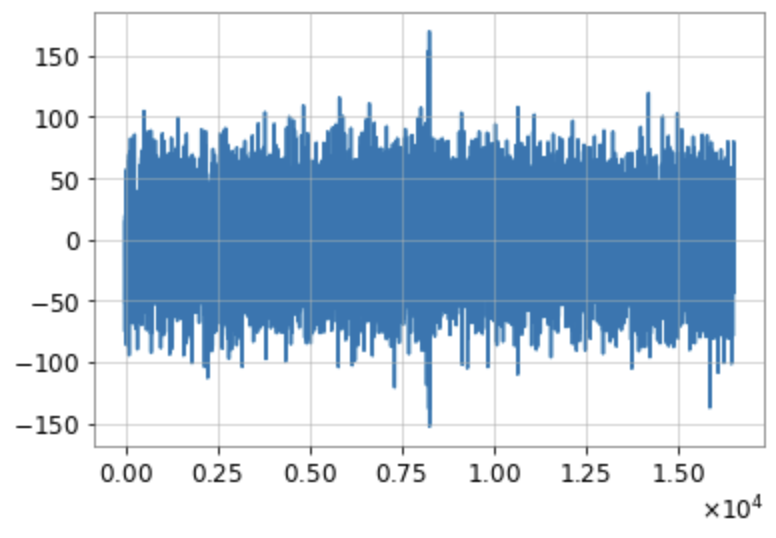
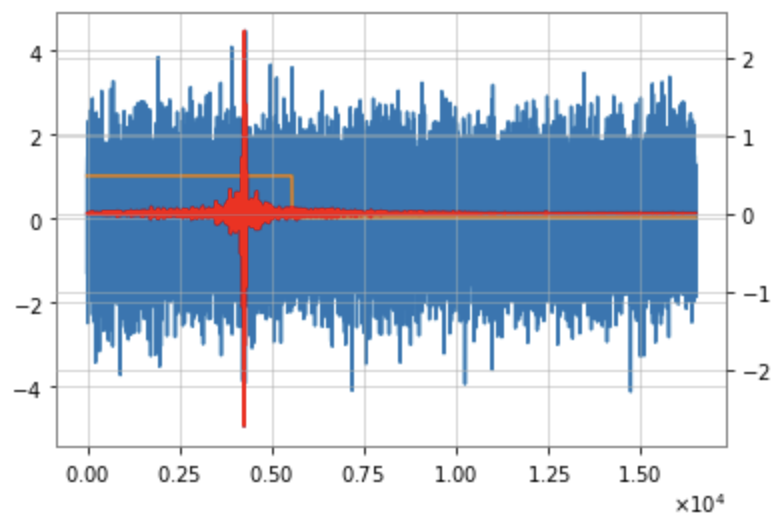
Strain
Whiten
Normalized
∼\(10^{−19}\)
∼\(10^{2}\)
∼\(10^{0}\)
32 s
32 s
merger
\(t_c\) (around GW150914)
(Cal network SNR)
Band-pass: [20, 2048] Hz
Patching (tokenized) with size 0.125 s and overlap 50%
[1, 128, 256]
(Standard normalization)
dynamic masking
[1, 16512]
[1, 128, 256]
(PSD\(_i\) from noise)
Band-pass: [20, 2048] Hz
WaveFormer
MSE-Loss\(_i\)
\(std\)
[1, 128, 256]
Noise\(_i\):
Signal\(_i\):
Input\(_i\):
Label\(_i\):
Output\(_i\):
8.0625 s
8.0625 s
Given �=ℎ+�d=h+n, we can normalize �d as follows:
-
Implementations:
- PSD sampling from real noise.
- input size: 8.0625 sec
- fs = 2048Hz
- Band-pass: 20~2048Hz
- Masked loss
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
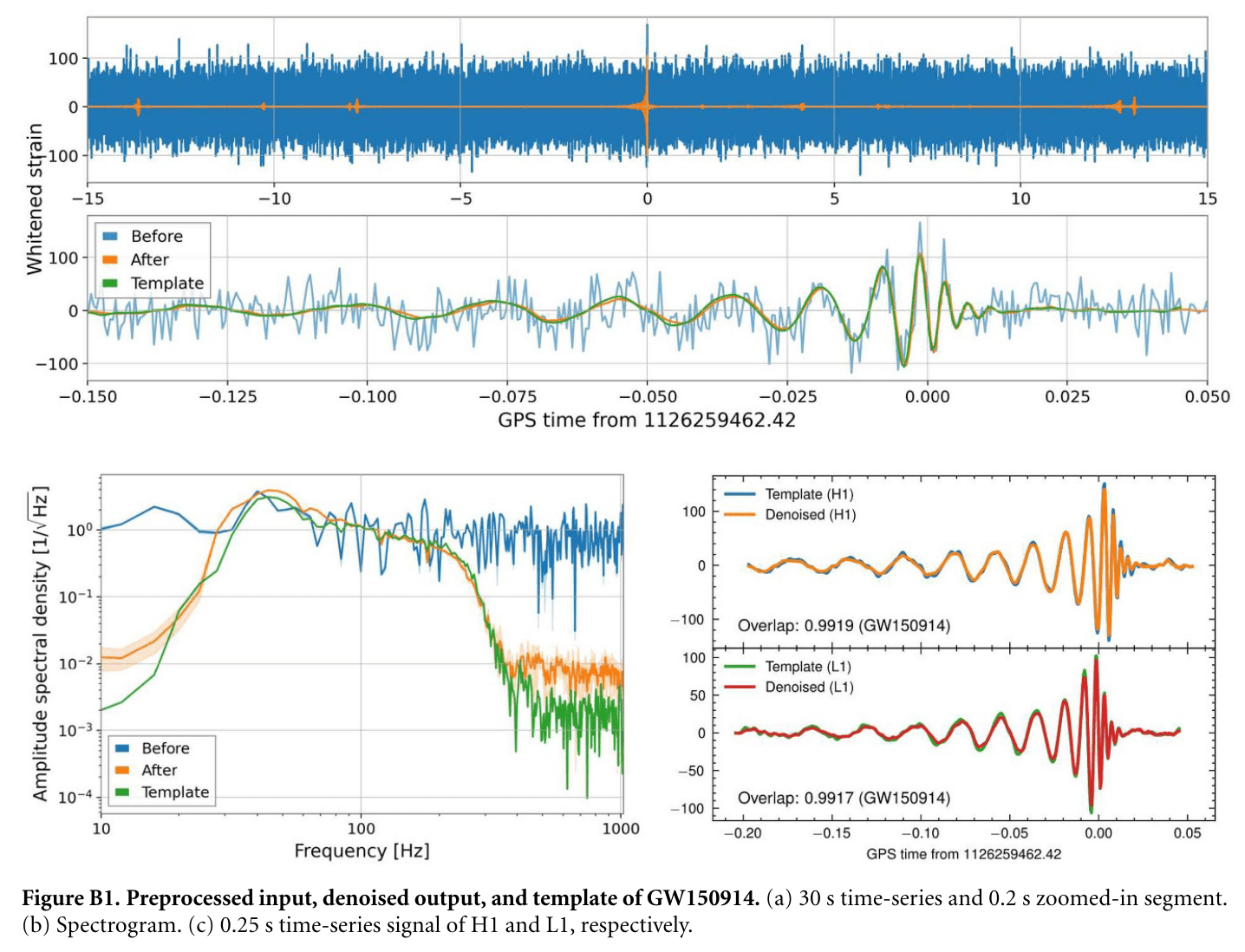
Effect on Realistic Noise

- Noise level percentile amplitude is significantly reduced, by approximately two orders.
- Further ASD analysis shows that WaveFormer effectively eliminates both narrowband and broadband spectral information, substantially lowering frequency contributions.
- Using the Gravity Spy database for glitches with SNR > 10 and confidence > 0.95, results show significant suppression of glitches in real advanced LIGO-Virgo noise.
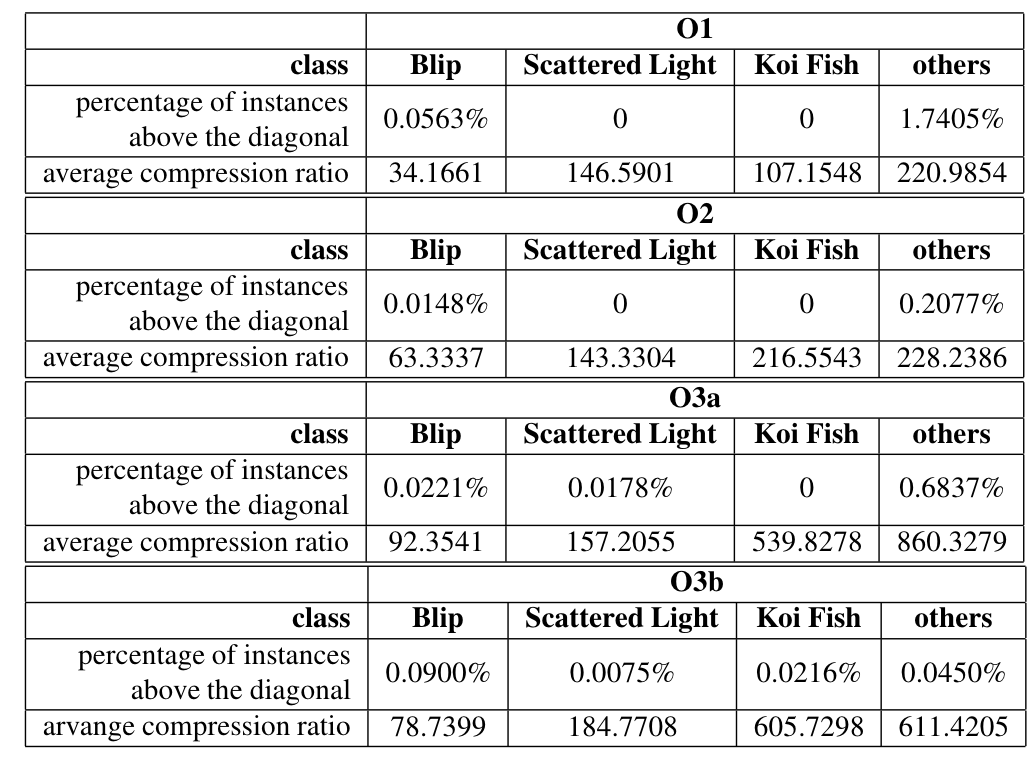
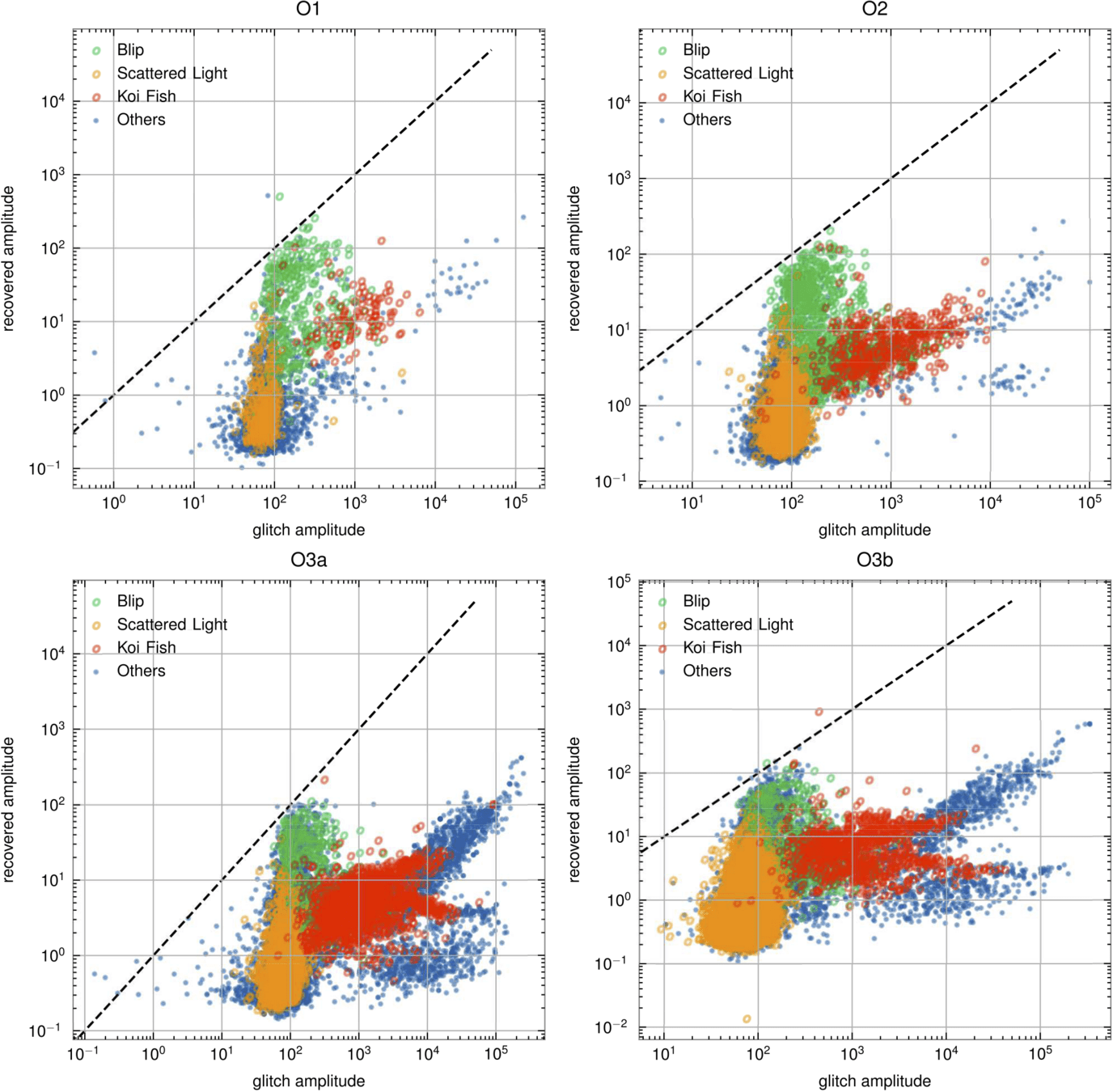
(Bottom panels: results of glitches)
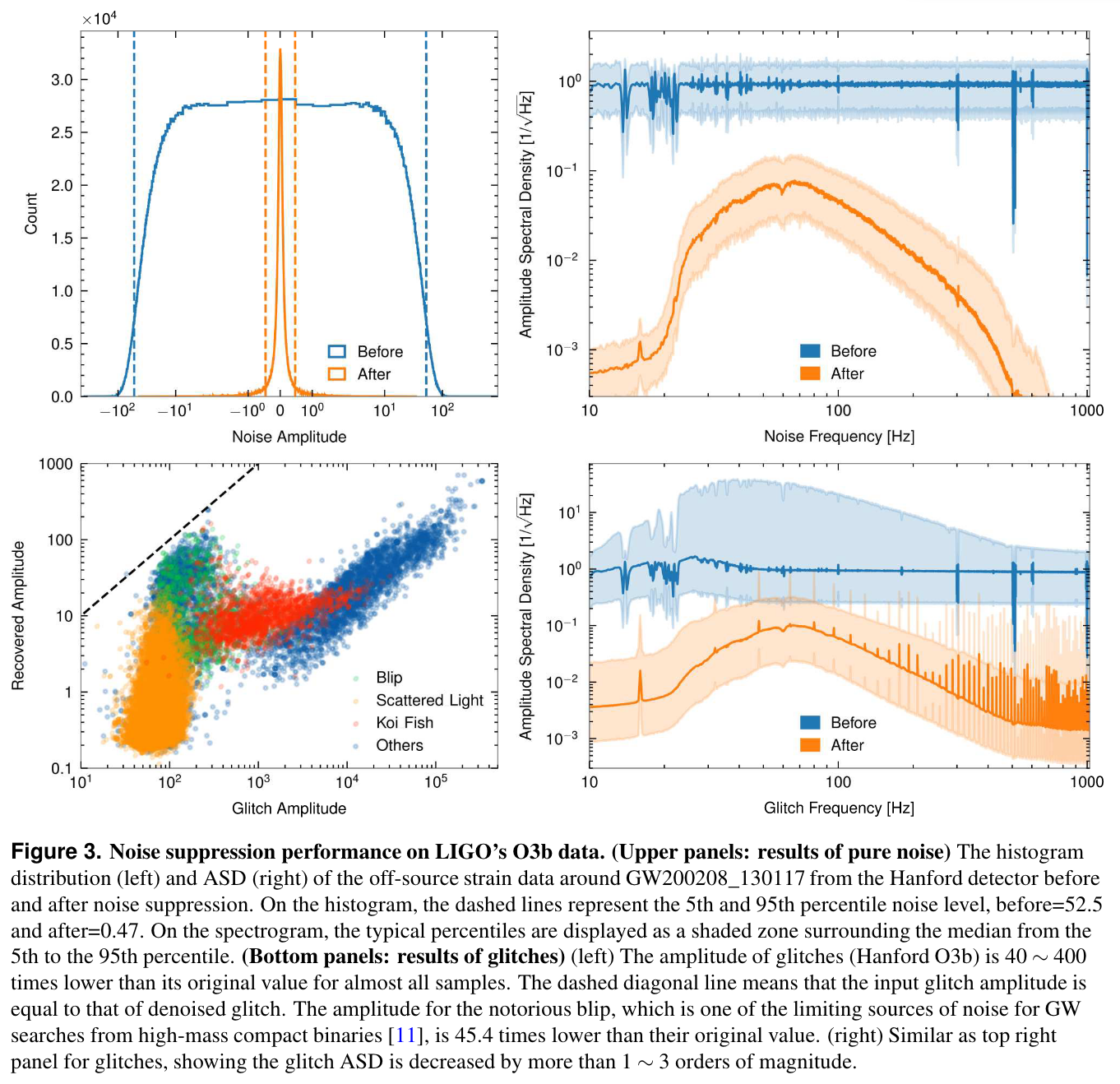

(Upper panels: results of pure noise)
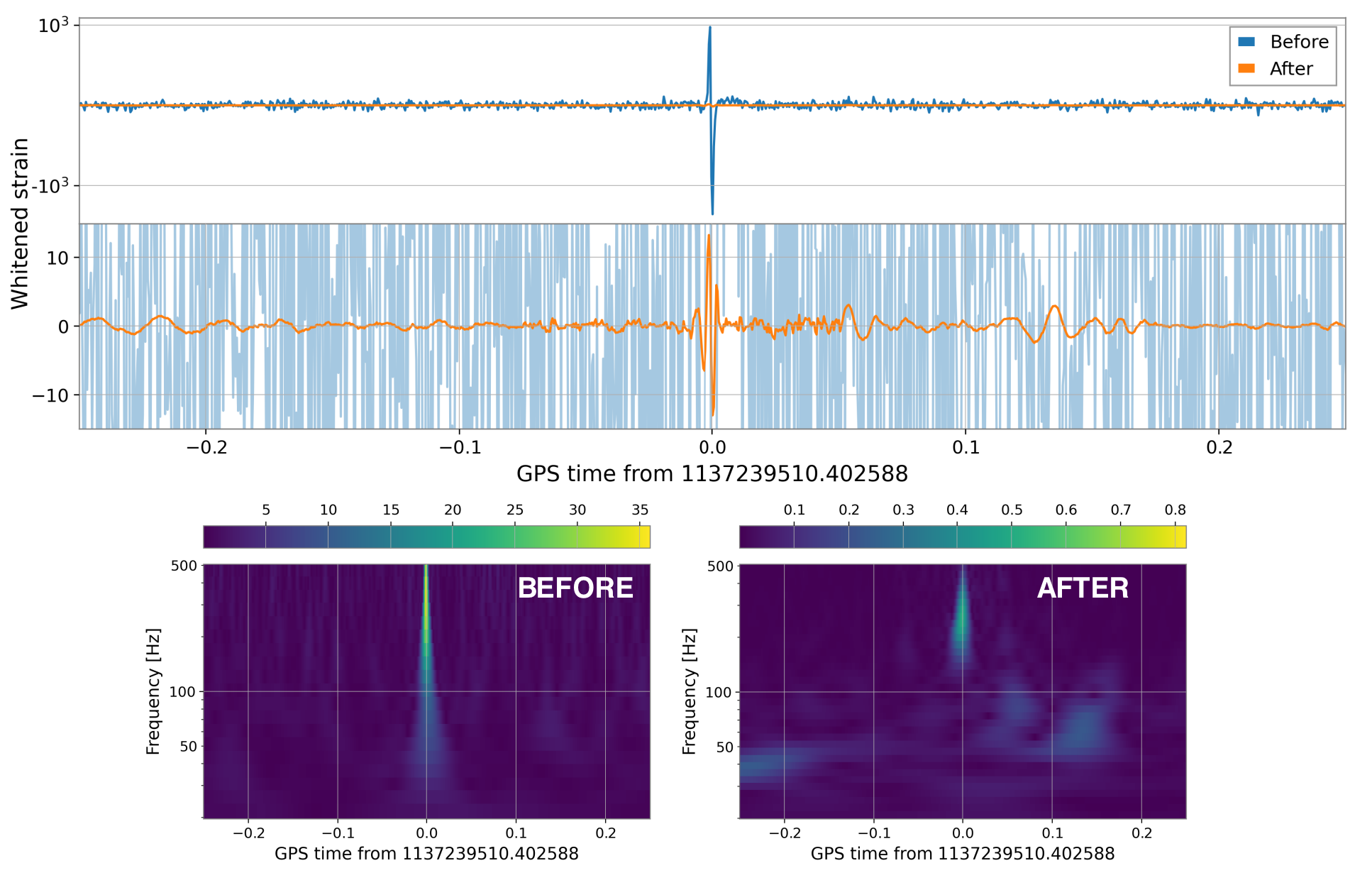
Time-series and spectrogram example of blip.

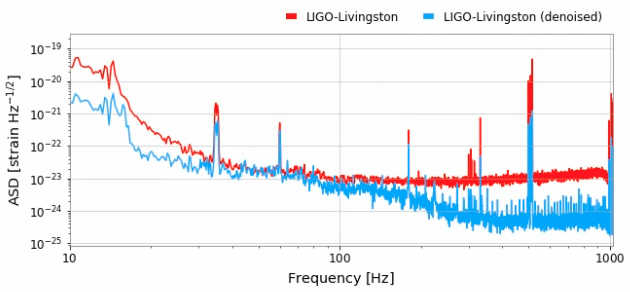
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046

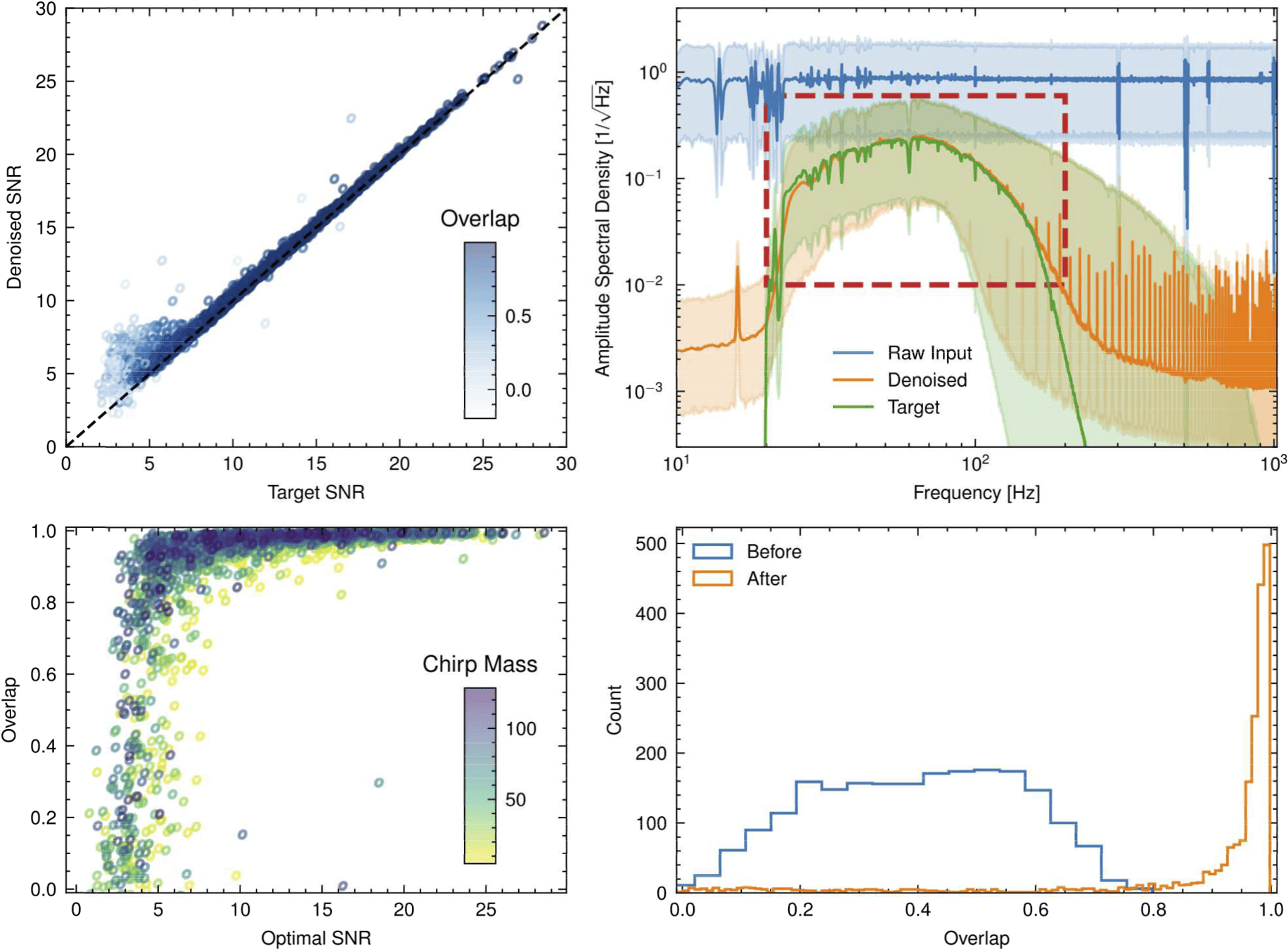
Recovery of Binary Black Holes

- Overlap and matched-filtering signal-to-noise are calculated to represent phase and amplitude recovery performance.
- Among the intermediate frequency range (20–200 Hz) that covers rich BBH signal information, the ASD distribution of denoised waveform is evidently consistent with that of target signal.
(Upper panels: Signal amplitude recovery performance

(Bottom panels: Signal phase recovery performance)
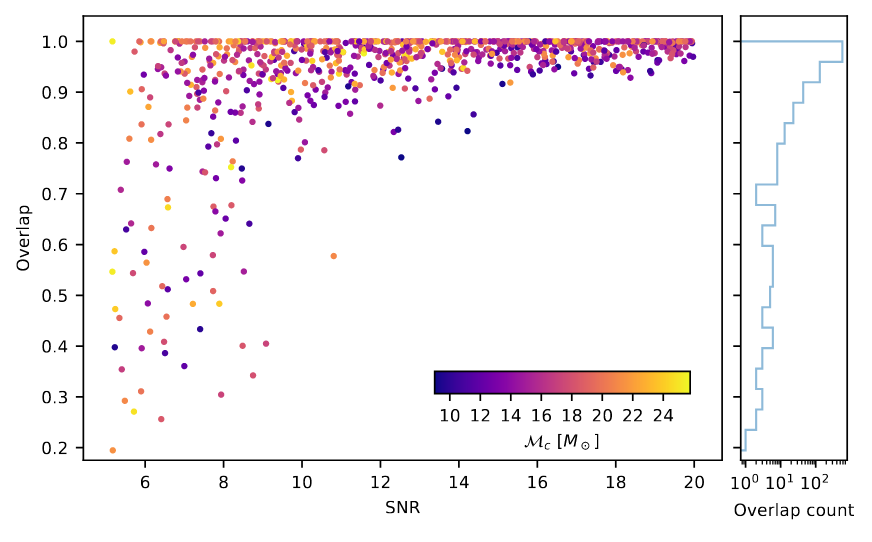
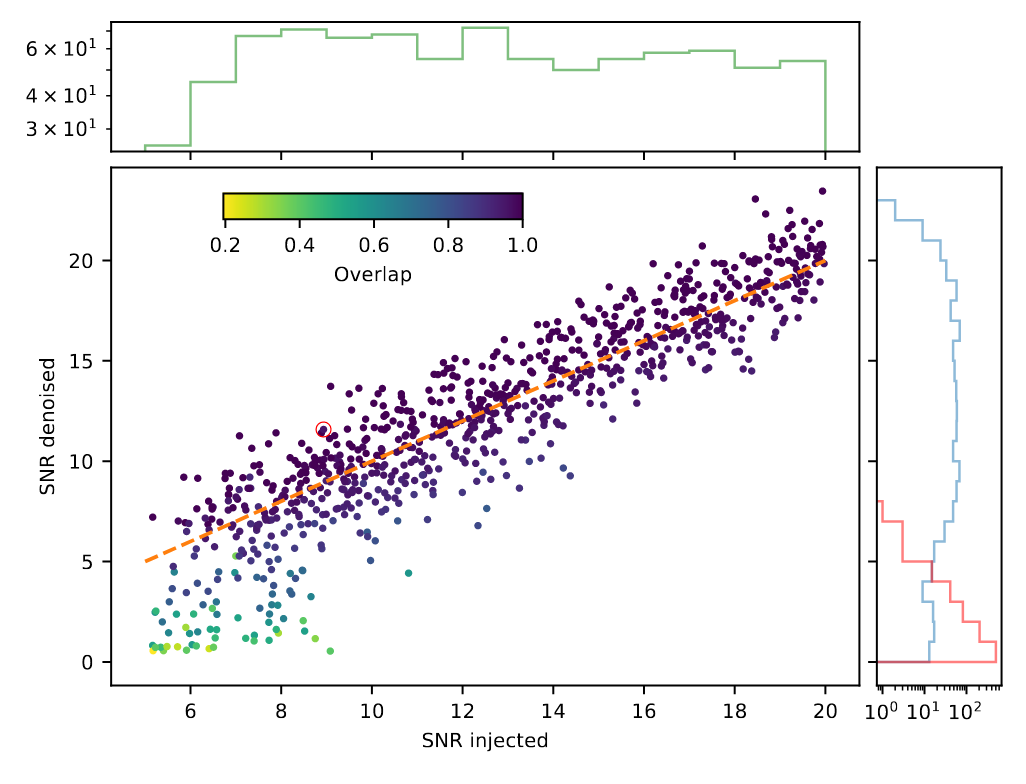
Bacon P. et al. arXiv: 2205.13513
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
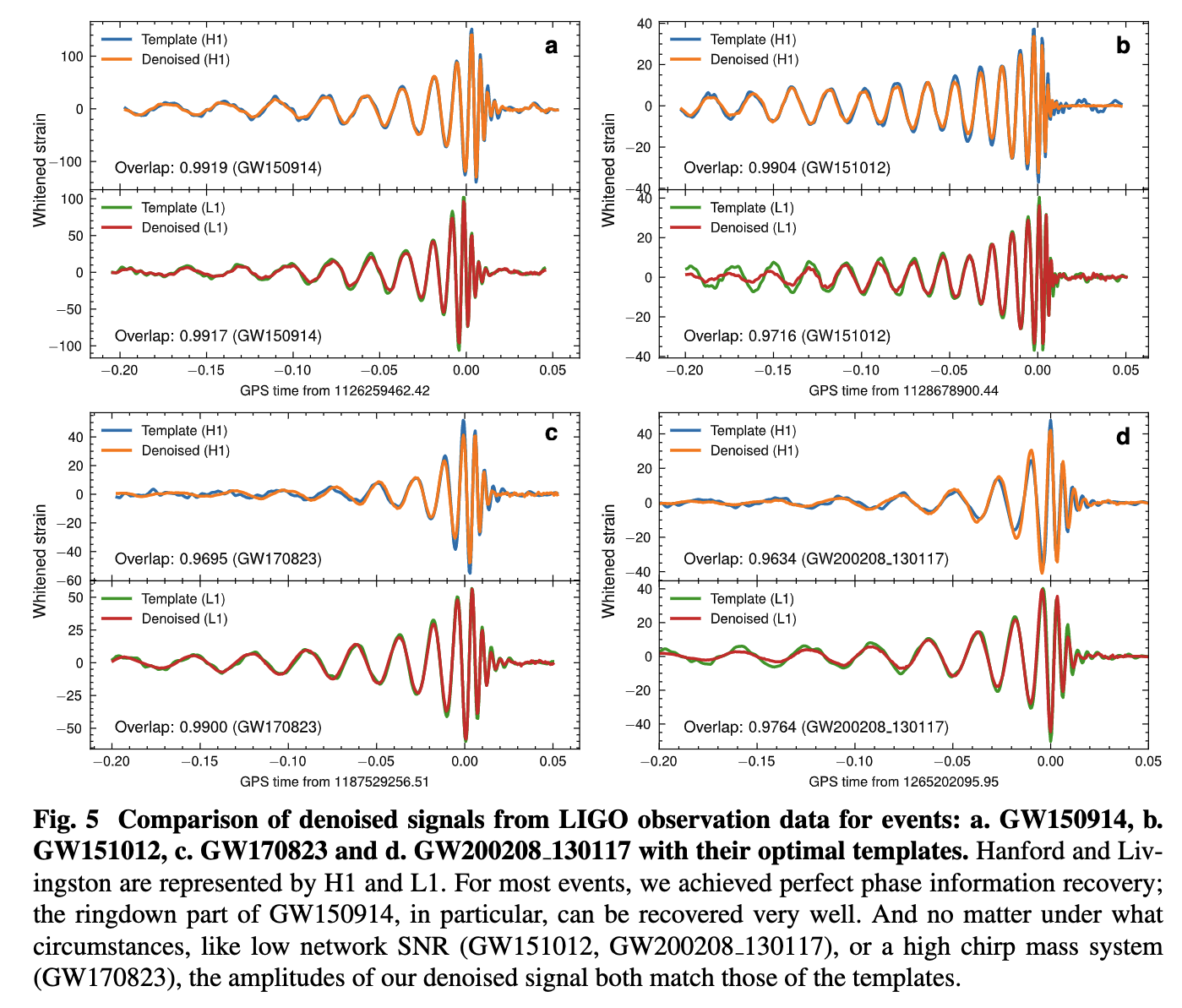
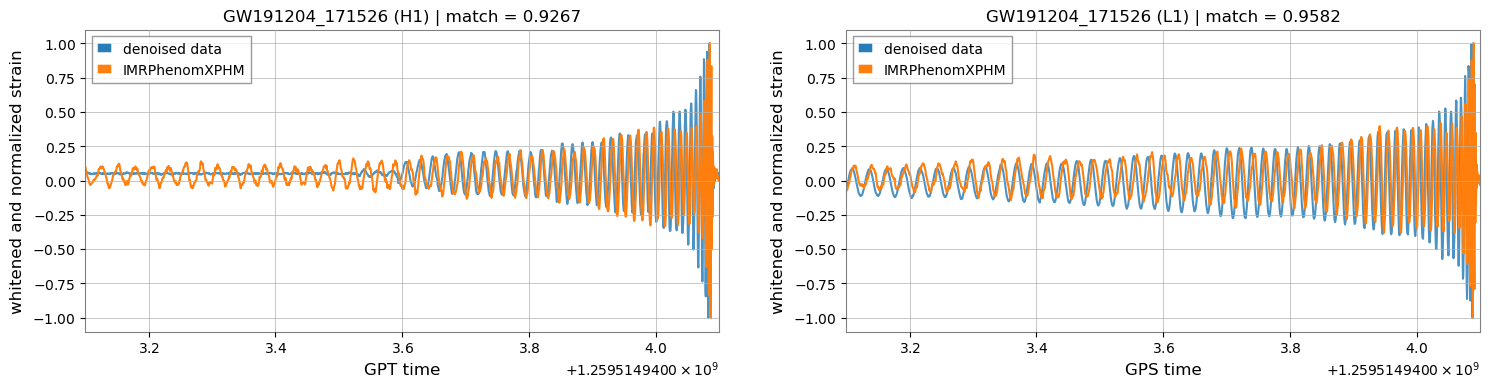

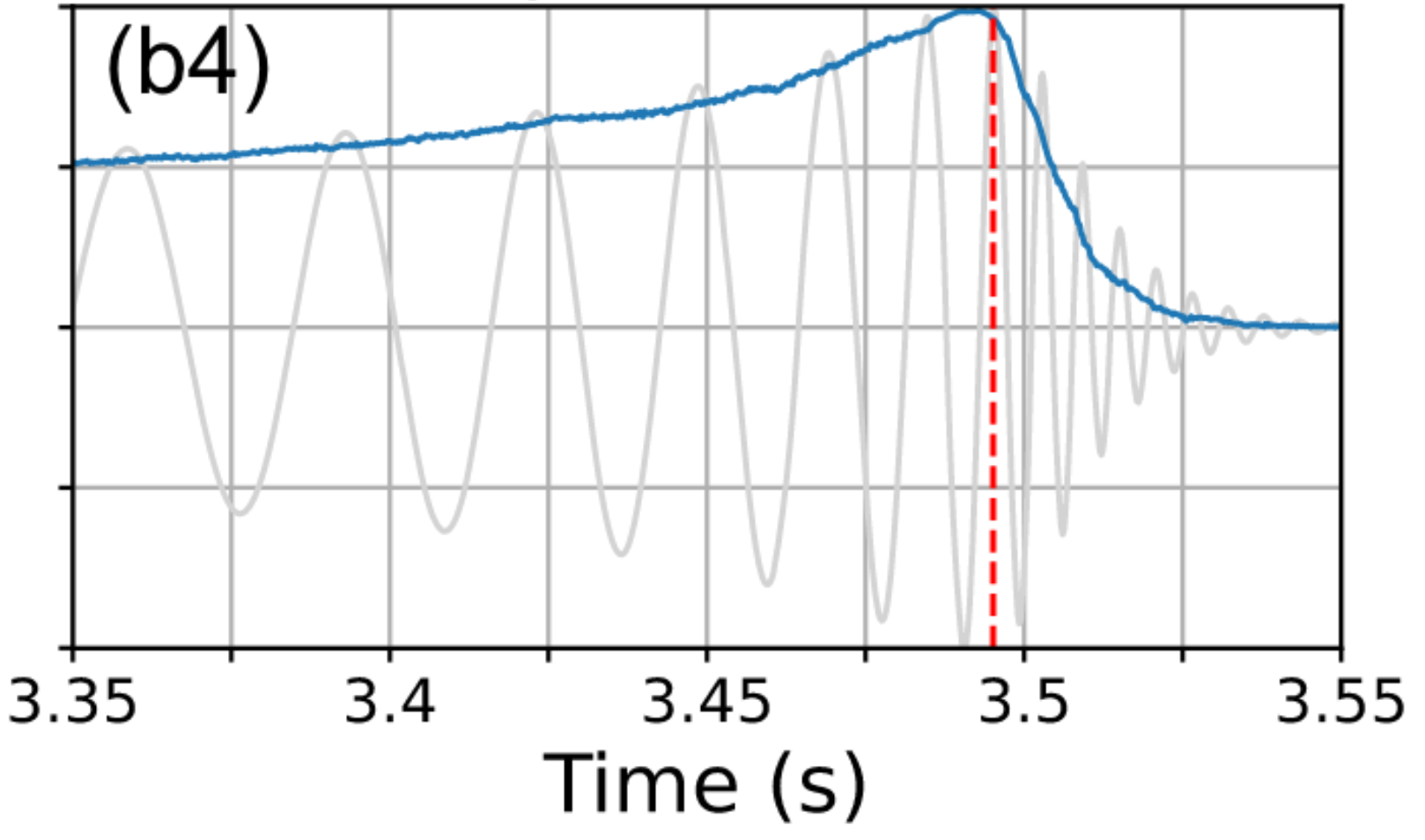
- These results show that our denoising algorithm outperformed others by capturing the characteristic chirping morphology of BBH evolution, and can denoise signals in realistic detection scenarios without affecting signal characteristics such as phase and amplitude.
- For the event GW191204_171526, classified as either an NSBH or a low-mass BBH candidate in GWTC-3, the overlap with IMRPhenomXPHM achieved 0.93 and 0.95 on H1 and L1, respectively, which are marked improvements over those achieved by BayesWave and cWB (with overlaps between 0.82–0.86).
GW191204_171526
Recovery of Binary Black Holes
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
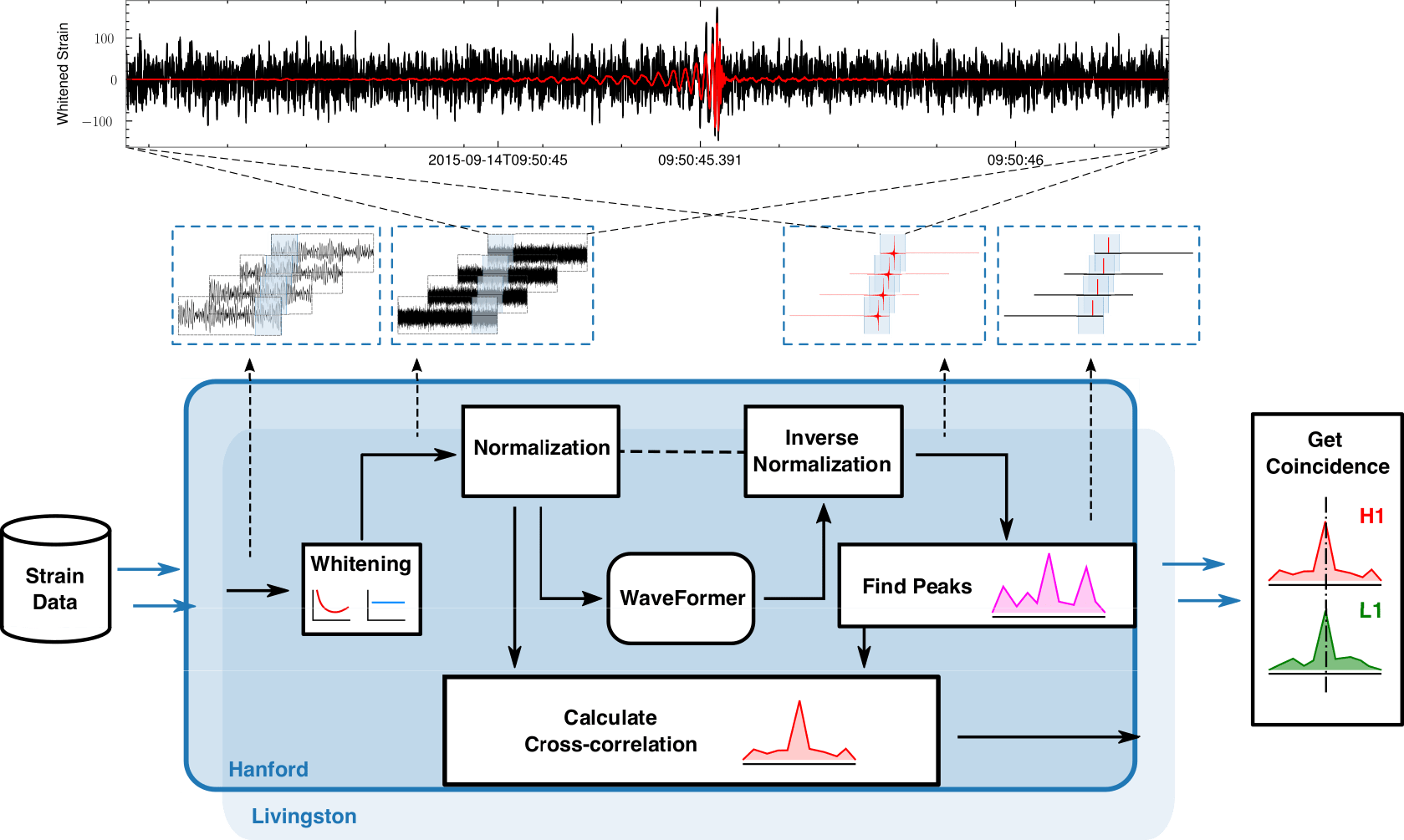
Search Strategy Overview

-
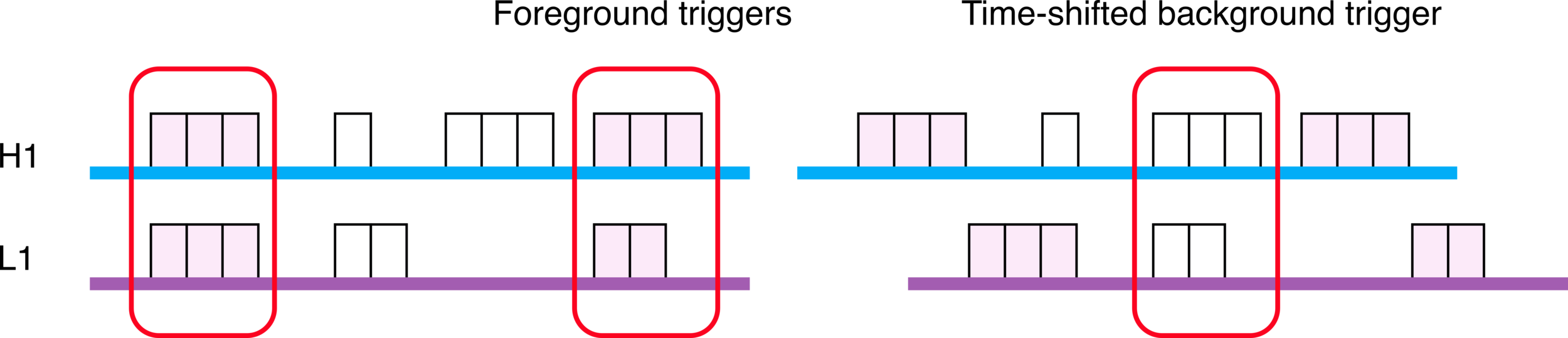
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
-
An search algorithm for GW require that: [cite: 2010.07244]
-
the same signal is seen in the detectors; (the same signal is seen by time-shifting in single detector)
-
the same waveform must be present both detectors;
-
and the signal’s time of arrival must be consistent with the GW travel time between the observatories.
-
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
Search Strategy Overview

-
Firstly, we obtain the denoised output by utilizing Waveformer.
Then, triggers are defined and identified by three steps including:-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
By constraining triggers that exist on both two detectors, we get VALID triggers. (consist 3~4 segments)
-
Calculate the cross-correlation of the to-be-evaluated trigger across channels or within a single channel, between its noisy and corresponding denoised segments, as well as between denoised segments themselves.
-
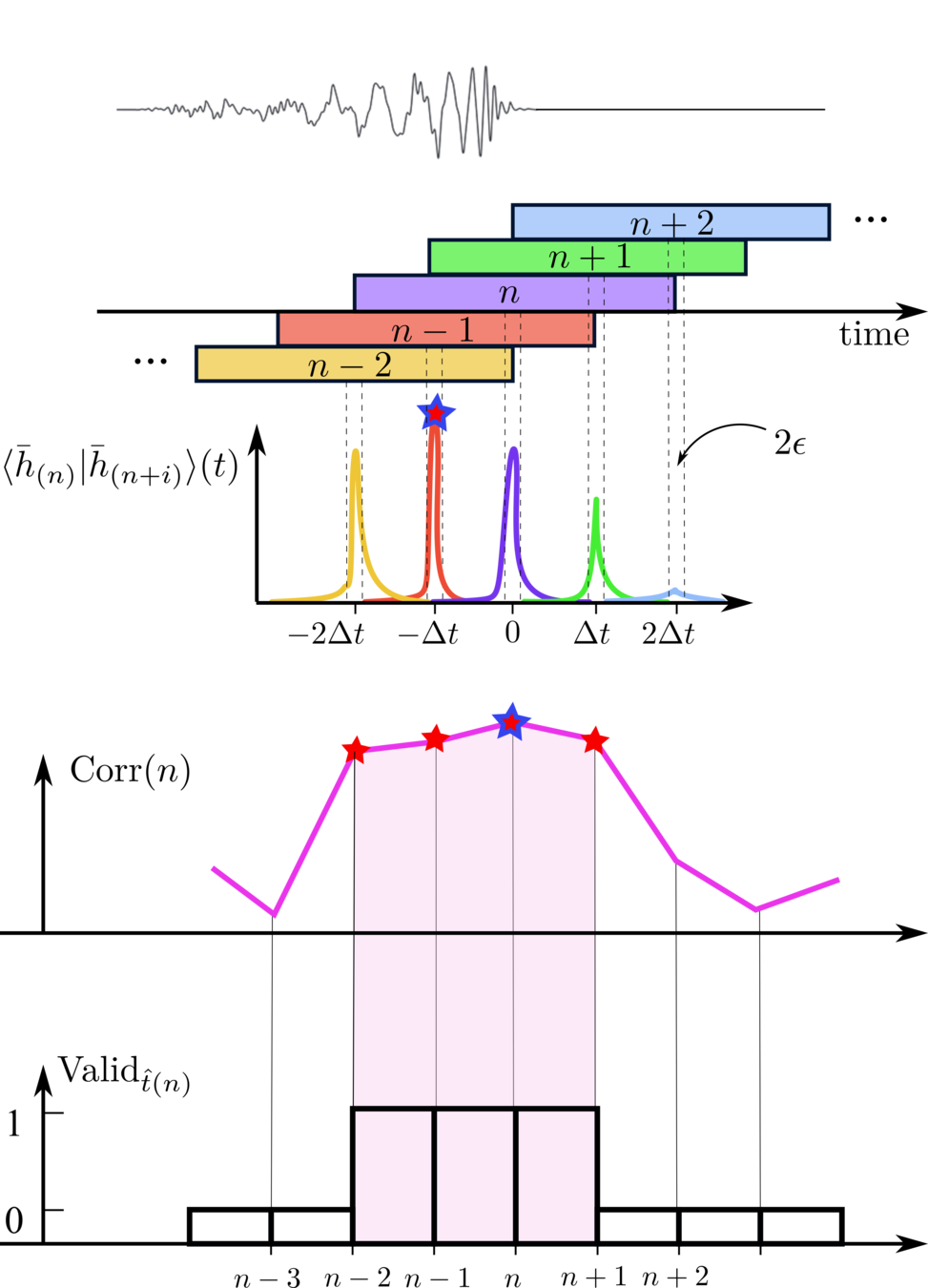
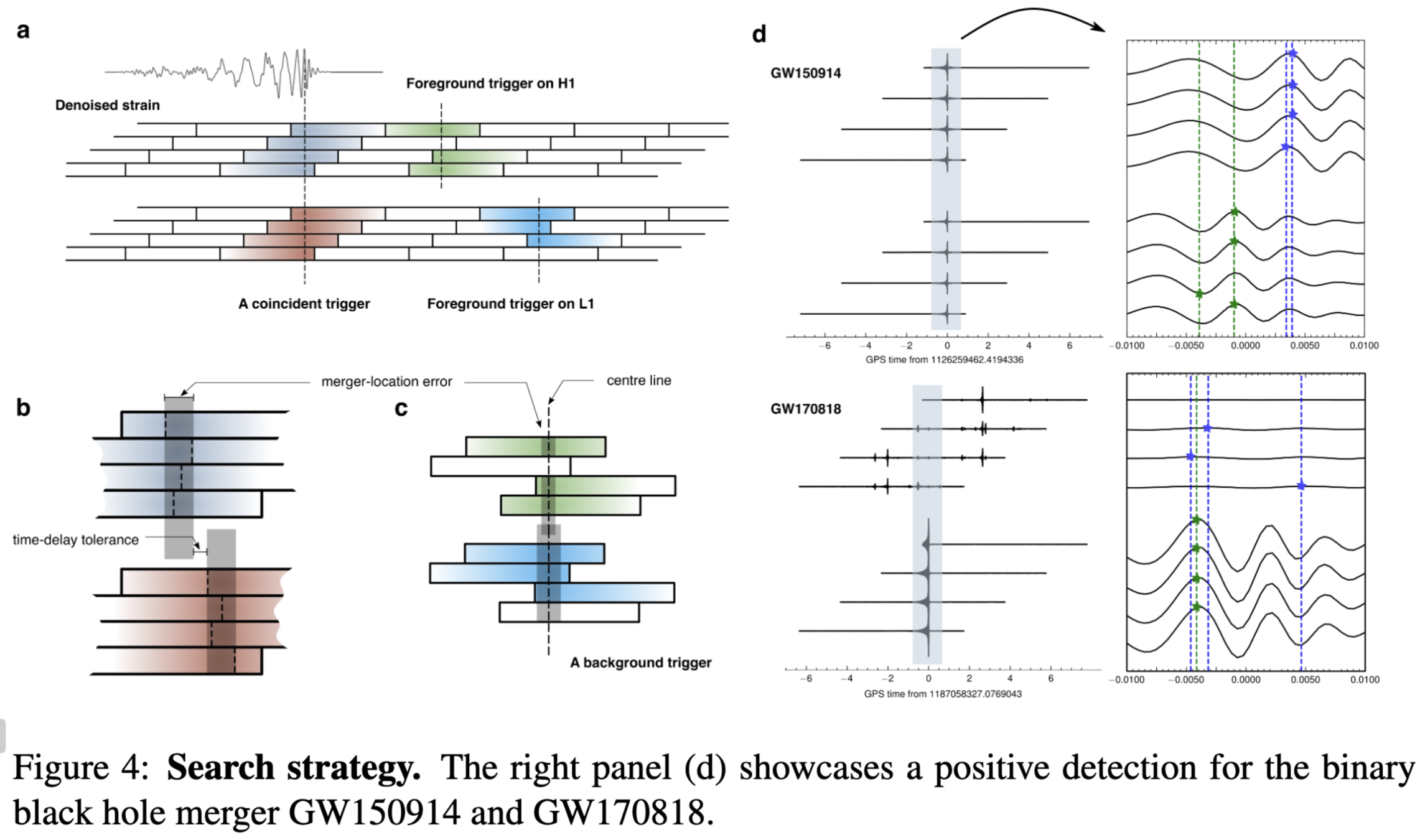
noisy input segments

denoised output segments
\(\bar{H}\)
\(\bar{L}\)
\({H}\)
\({L}\)
AI

He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
Search Strategy Overview


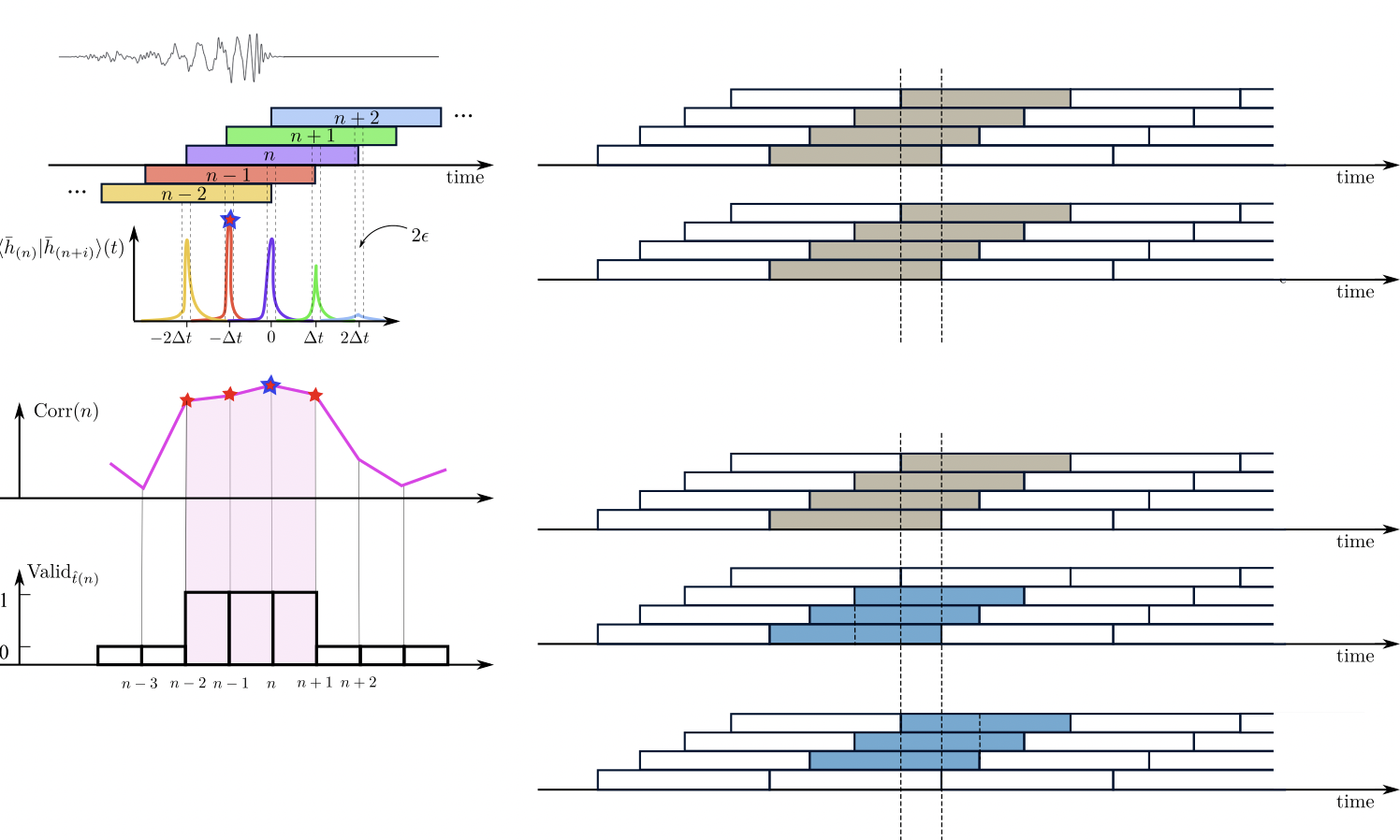
-
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
By constraining triggers that exist on both two detectors, we get VALID triggers. (consist 3~4 segments)
-
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
Search Strategy Overview


-
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
By constraining triggers that exist on both two detectors, we get VALID triggers. (consist 3~4 segments)
-
Calculate the correlation of the to-be-evaluated trigger across channels or within a single channel, between its noisy and corresponding denoised segments, as well as between denoised segments themselves.
-



noisy input segments

denoised output segments
\(\bar{H}\)
\(\bar{L}\)
\({H}\)
\({L}\)
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
Inverse FAR calculation

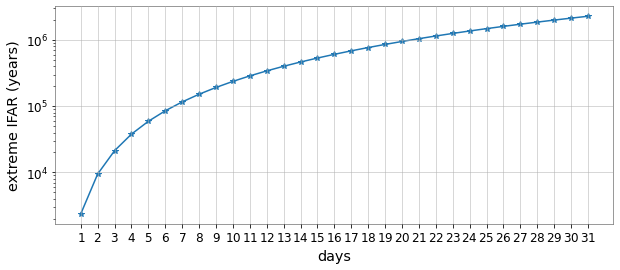

-
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
By constraining triggers that exist on both two detectors, we get VALID triggers. (consist 3~4 segments)
-
Calculate the correlation of the to-be-evaluated trigger across channels or within a single channel, between its noisy and corresponding denoised segments, as well as between denoised segments themselves.
-
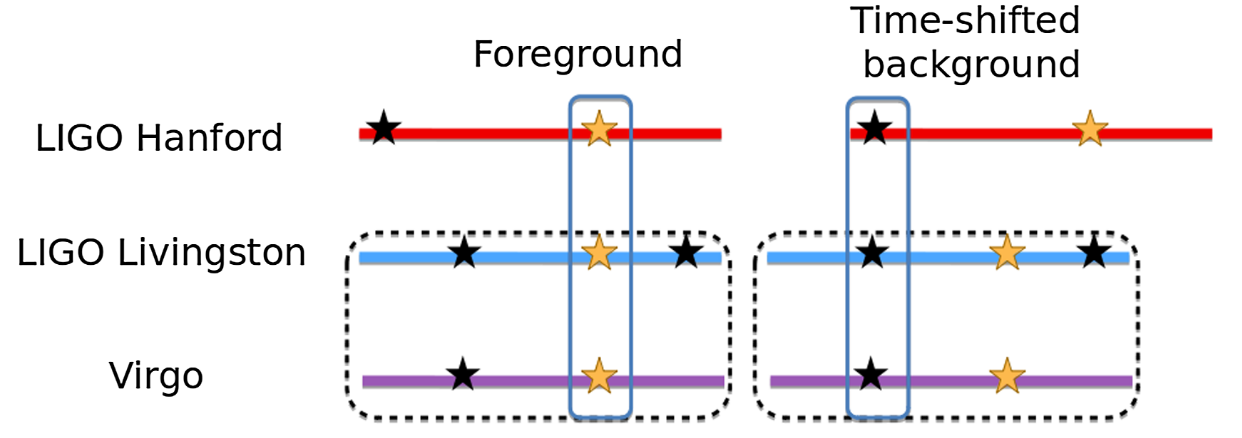
- Through time shift, background analysis is done on other triggers around the target trigger. (time-shift interval 0.1 sec)
- Finally, by counting the number of false alarm trigger pairs, we obtain the IFAR value of the target trigger, which represents the reported or candidate BBH event in this experiment.
OURs
(PyCBC) Davies, et al. PRD 2020
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
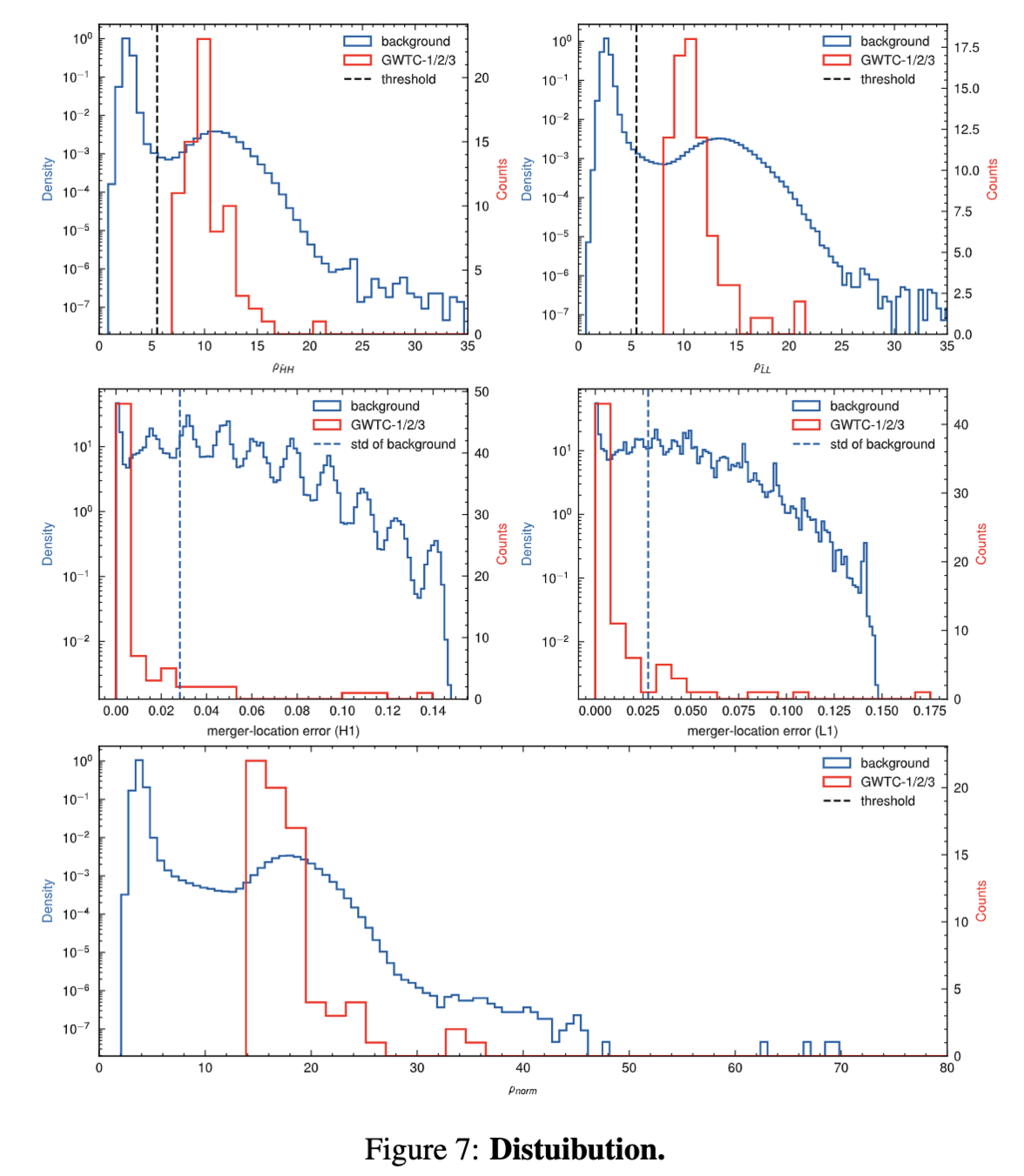
Significance Estimates

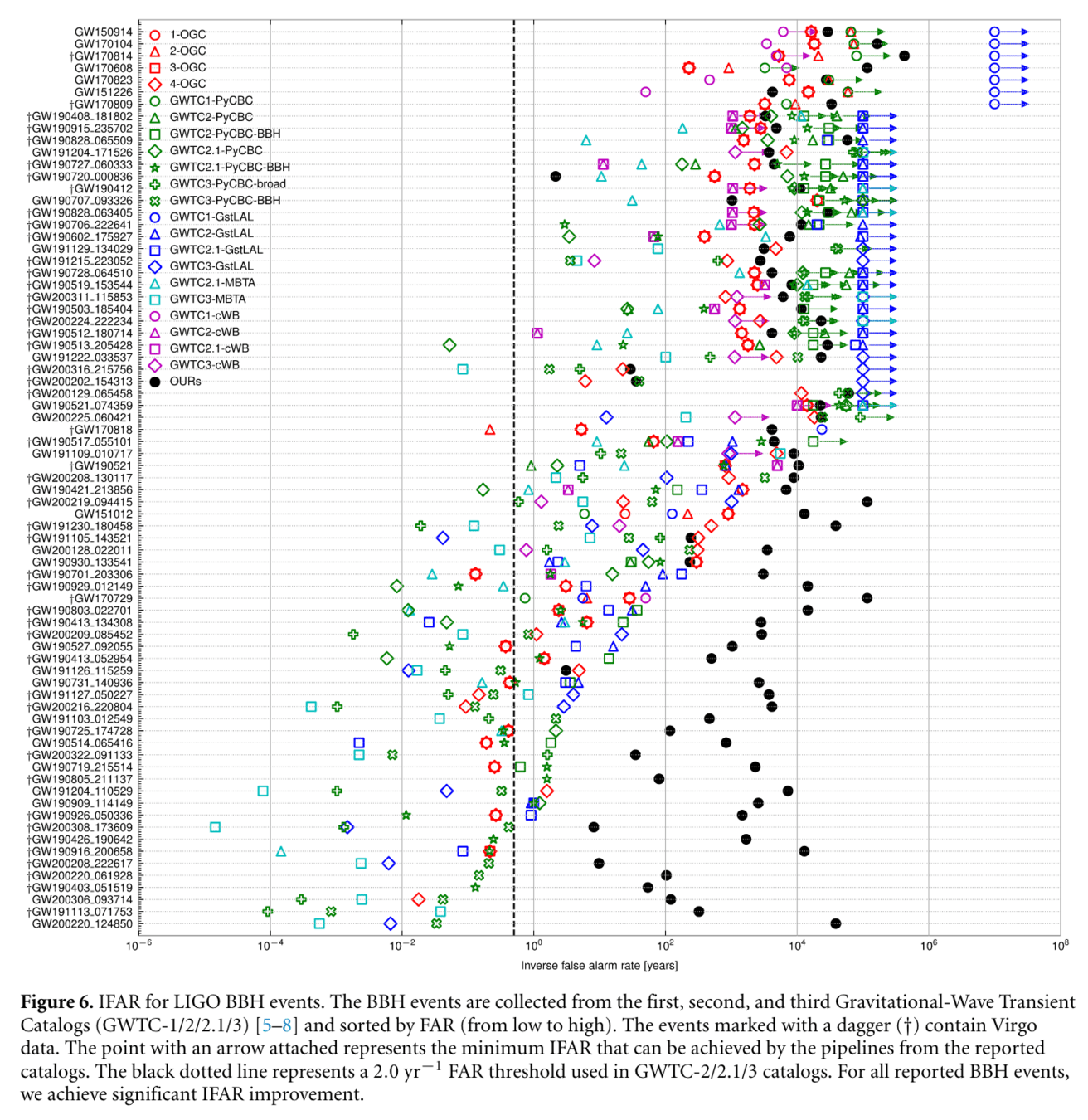
-
Assessed denoising workflow performance by comparing with GWTC-1, GWTC-2, GWTC2.1, and GWTC-3 catalogs and associated data releases.
-
Noted significant divergence in IFAR distribution between our results and those from GWTC and OGC catalogs.
-
Achieved significant IFAR improvement across all 75 reported BBH events, indicating effective suppression of loud terrestrial noise.
-
Example: For low SNR (\(10.8_{-0.4}^{+0.3}\)) event GW200208_130117, obtained an IFAR of 8916 years, surpassing maximum IFAR of <4000 years in other catalogs.
-
-
Variability in IFAR improvement linked to the original data's noise nature, including its non-Gaussian, non-stationary characteristics, and different signal recognition strategies by pipelines.
-
IFAR performance significantly depends on the reduction of non-Gaussian noise near each event.
-
Events with substantial IFAR improvement had misleading non-Gaussian noise effectively eliminated.
-
Events where IFAR underperforms retained non-Gaussian characteristics, possibly due to WaveFormer's inherent systematic errors.
-
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
- Developed an AI-based workflow with WaveFormer, combining convolutional neural network and transformer for effective GW noise suppression and hierarchical feature extraction across a wide frequency range.
- Achieved significant noise suppression and signal recovery performance improvements, including state-of-the-art results on real observational data and BBH events, leading to dramatic data quality improvement and significant IFAR enhancement on 75 reported BBH events.

Text
-
Challenges in Model Interpretability
- The black-box nature of AI models complicates interpretability, challenging the comparison of AI-generated detection statistics with traditional matched filtering chi-square distributions.
- Convincing the scientific community of the pipeline's validity and the statistical significance of new discoveries remains difficult despite the model's ability to identify potential gravitational wave signals.
OURs
LVK. PRD (2016). arXiv:1602.03839
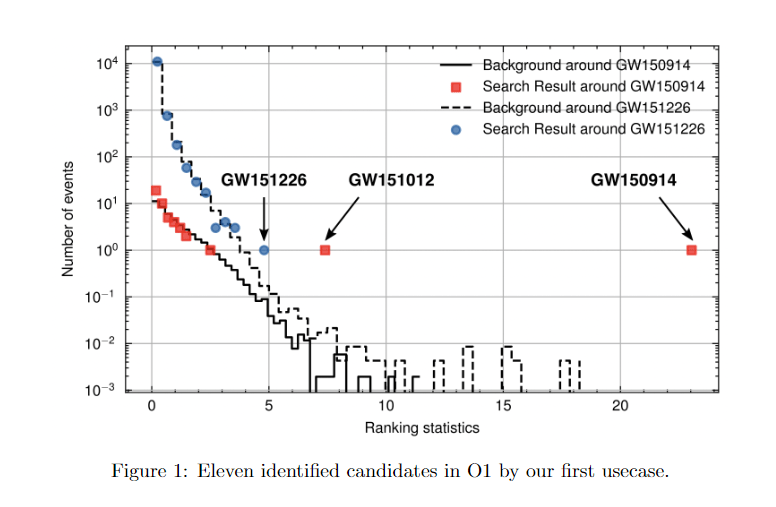
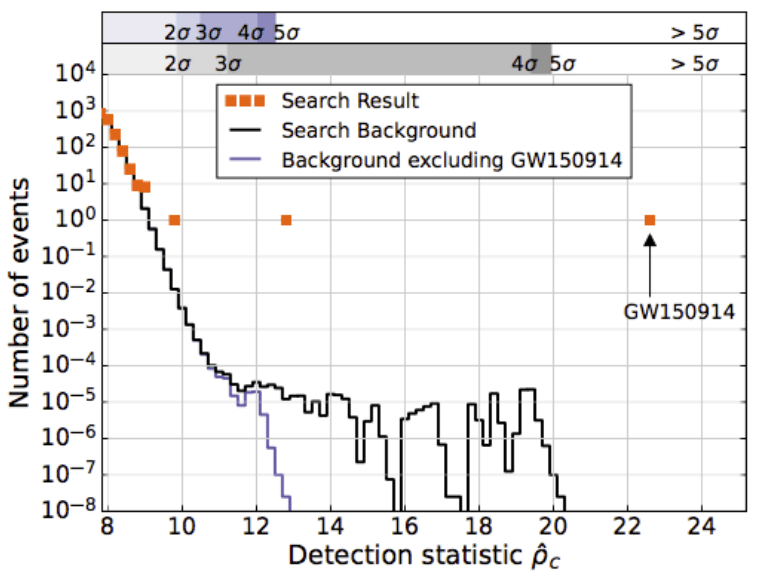
GW151226
GW151012
GW search · Pipeline

He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
GW search · Pipeline

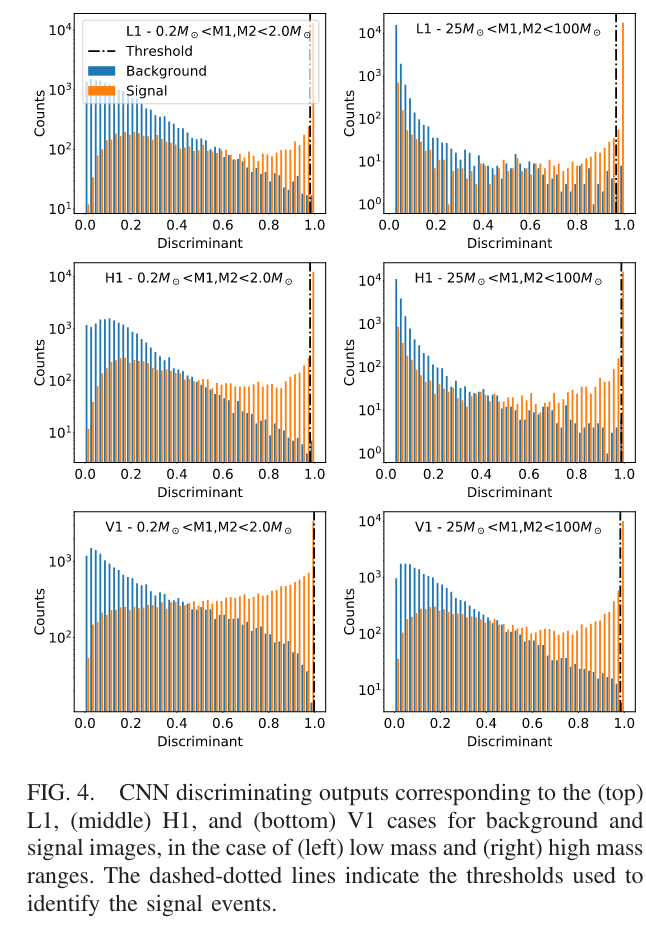
Menéndez-Vázquez A, et al. PRD 2021
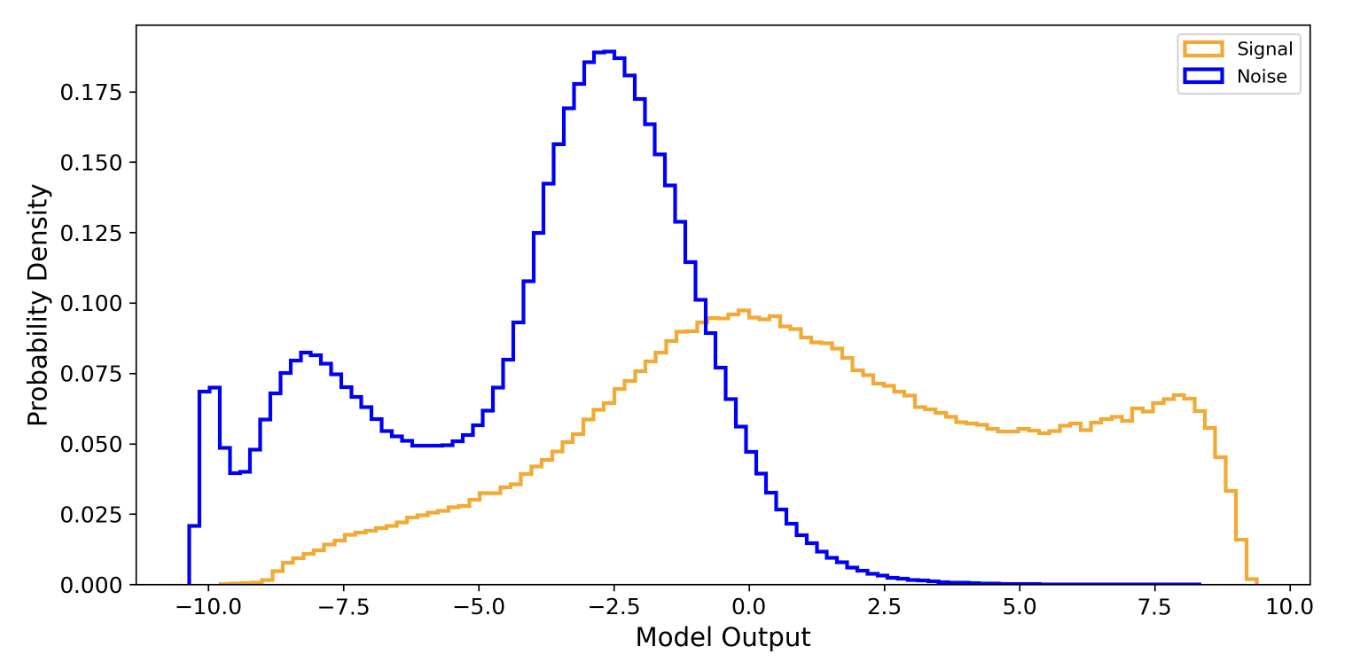
Alfaidi & Messerger. arXiv:2402.04589
The negative log-likelihood cost function always strongly penalizes the most active incorrect prediction. And the correctly classified examples will contribute little to the overall training cost."
—— I. Goodfellow, Y. Bengio, A. Courville. Deep Learning. 2016. (book)

noise
noise + signal
OURs
LVK. PRD (2016). arXiv:1602.03839


GW151226
GW151012
Text
-
Challenges in Model Interpretability
- The black-box nature of AI models complicates interpretability, challenging the comparison of AI-generated detection statistics with traditional matched filtering chi-square distributions.
- Convincing the scientific community of the pipeline's validity and the statistical significance of new discoveries remains difficult despite the model's ability to identify potential gravitational wave signals.
GW search · Pipeline

Exploring Beyond General Relativity
- Much of the discussion on model generalization has been within the GR framework. Our collaboration with 东北大学 on beyond General Relativity (bGR) aims to demonstrate AI's potential advantages in detecting signals that surpass GR's limitations.
Text
Harsh Narola, et al. “Beyond General Relativity: Designing a Template-Based Search for Exotic Gravitational Wave Signals.” PRD 107, 2 (2023): 024017.
Yu-Xin Wang, et al. "Draft in Progress"
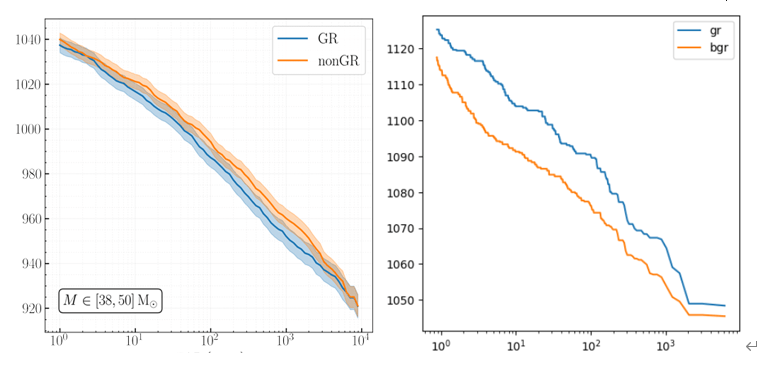
iFAR [years]
iFAR [years]
Sensitivity dfistance [Mpc]
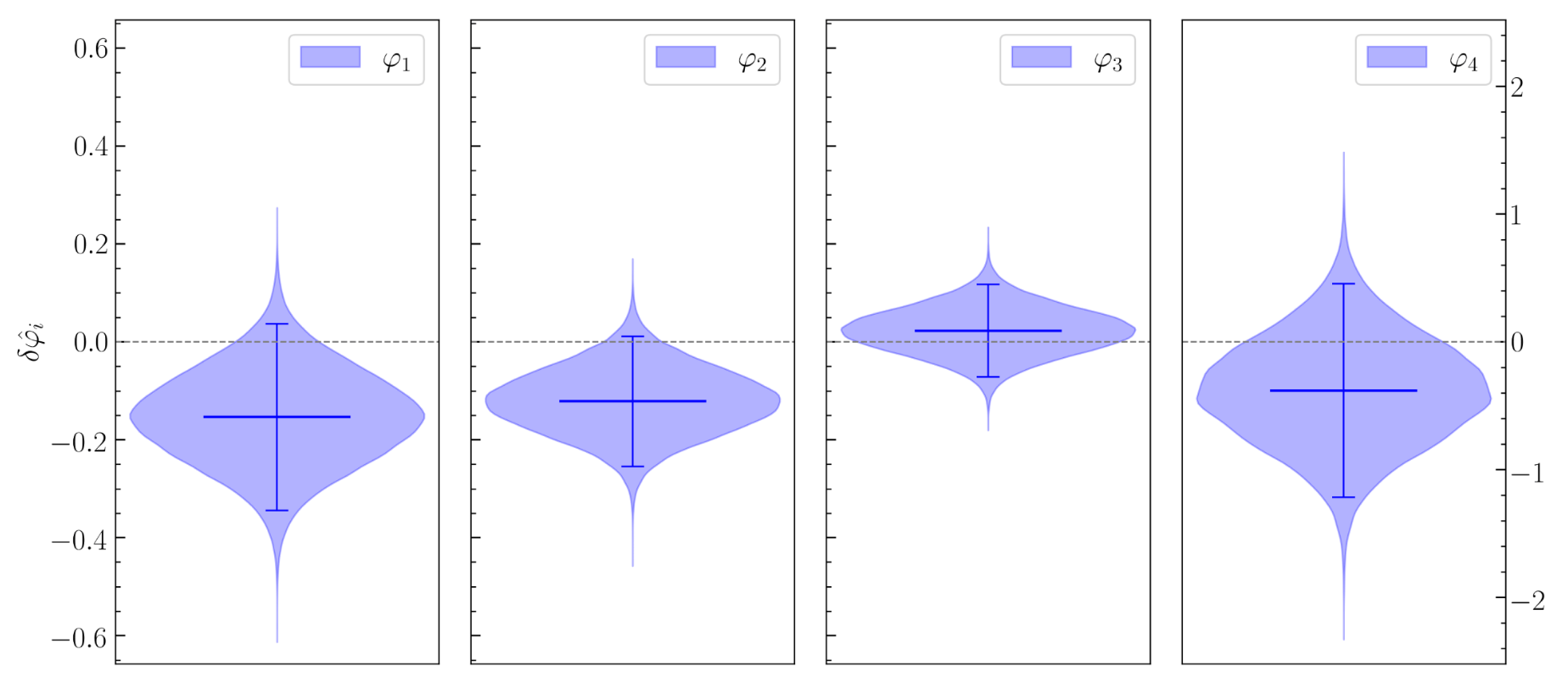
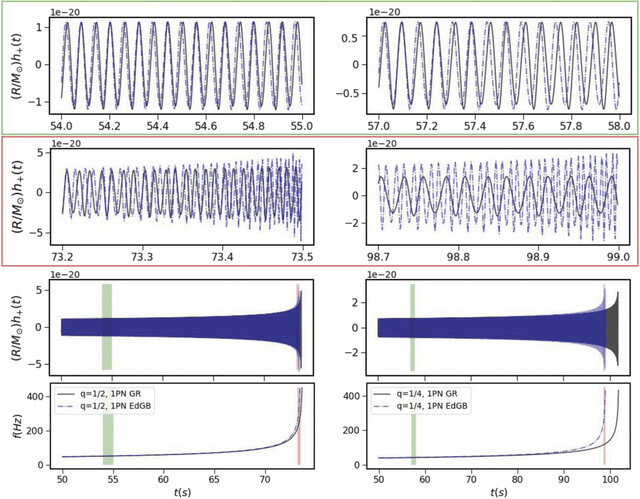
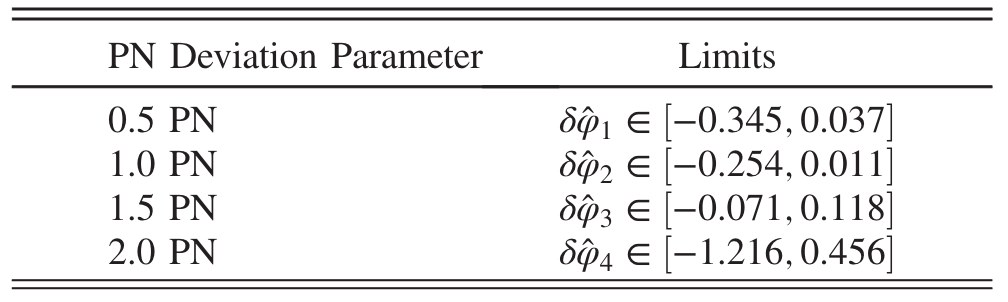
B. P. Abbott et al. (LIGO-Virgo), PRD 100, 104036 (2019).
Content



- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- (Space-based GW Detection)

Parameter estimation · Scientific discovery

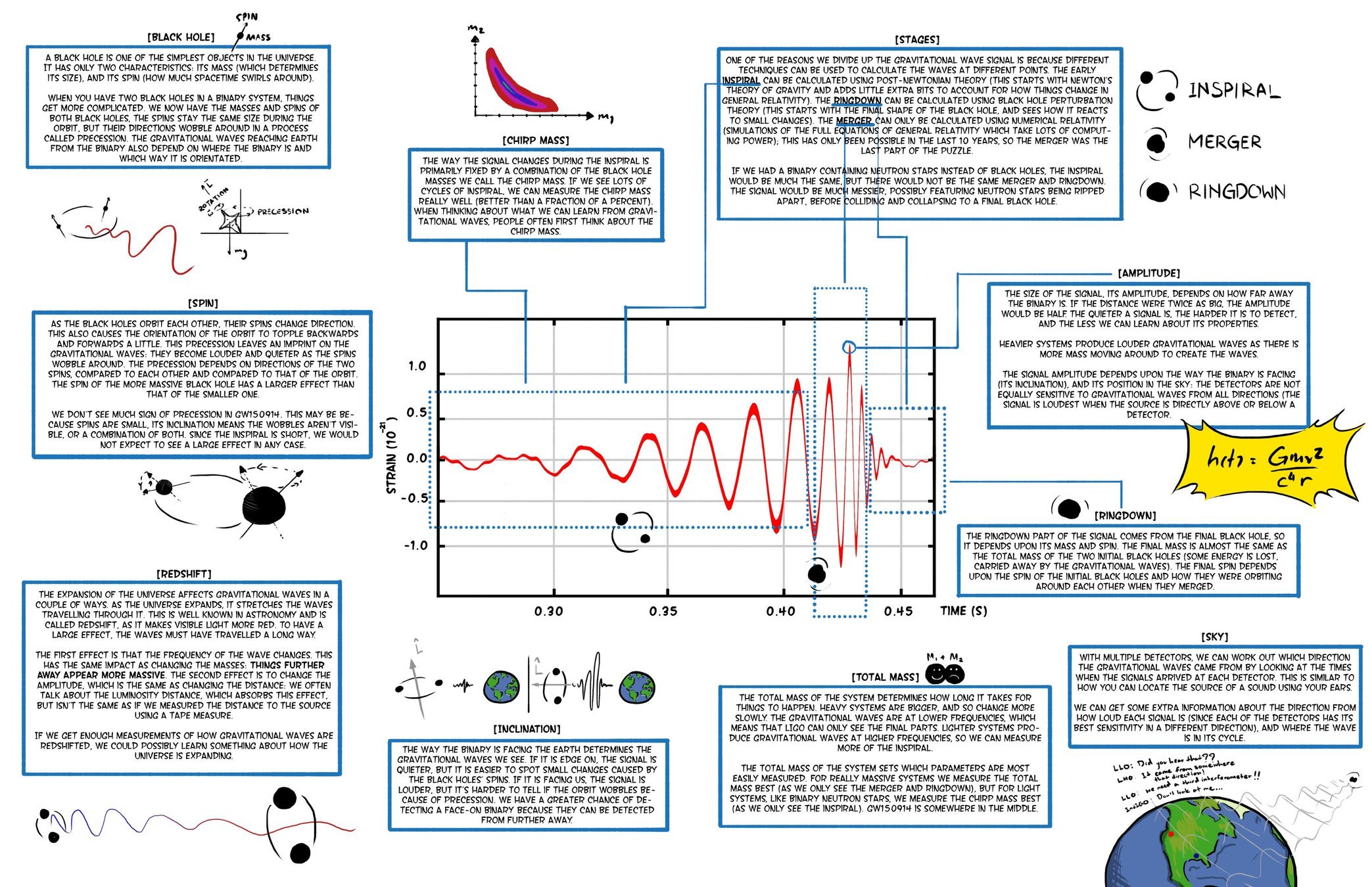
Credit: LIGO Magazine.
-
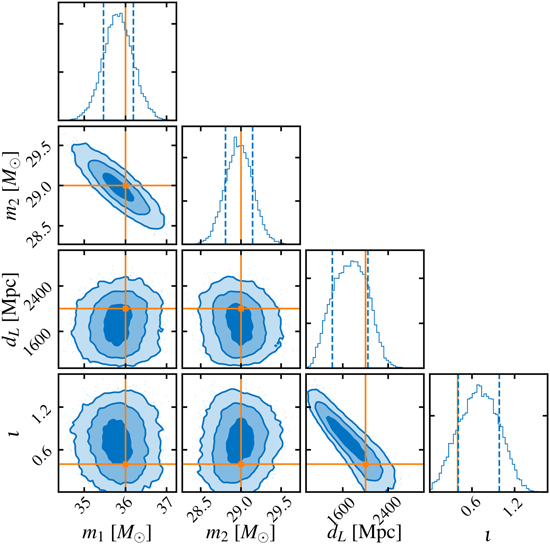
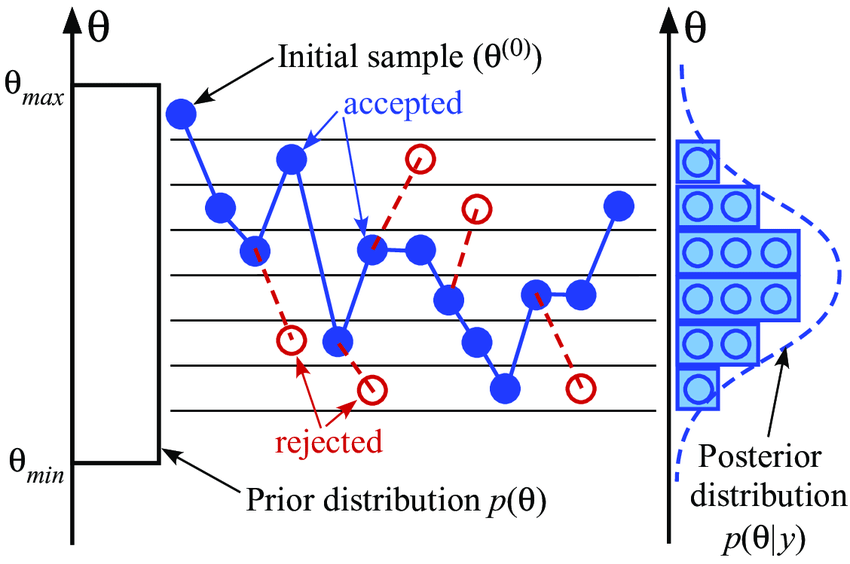
Traditional parameter estimation (PE) techniques rely on Bayesian analysis methods (posteriors + evidence)
- Computing the full 15-dimensional posterior distribution estimate is very time-consuming:
- Calculating likelihood function
- Template generation time-consuming
- Machine learning algorithms are expected to speed up!
AI for Gravitational Wave: Parameter Estimation





Bayesian statistics


Data quality improvement
Credit: Marco Cavaglià
LIGO-Virgo data processing
GW searches
Astrophsical interpretation of GW sources
AI for Gravitational Wave: Parameter Estimation
- A complete 15-dimensional posterior probability distribution, taking about 1 s (<< \(10^4\) s).
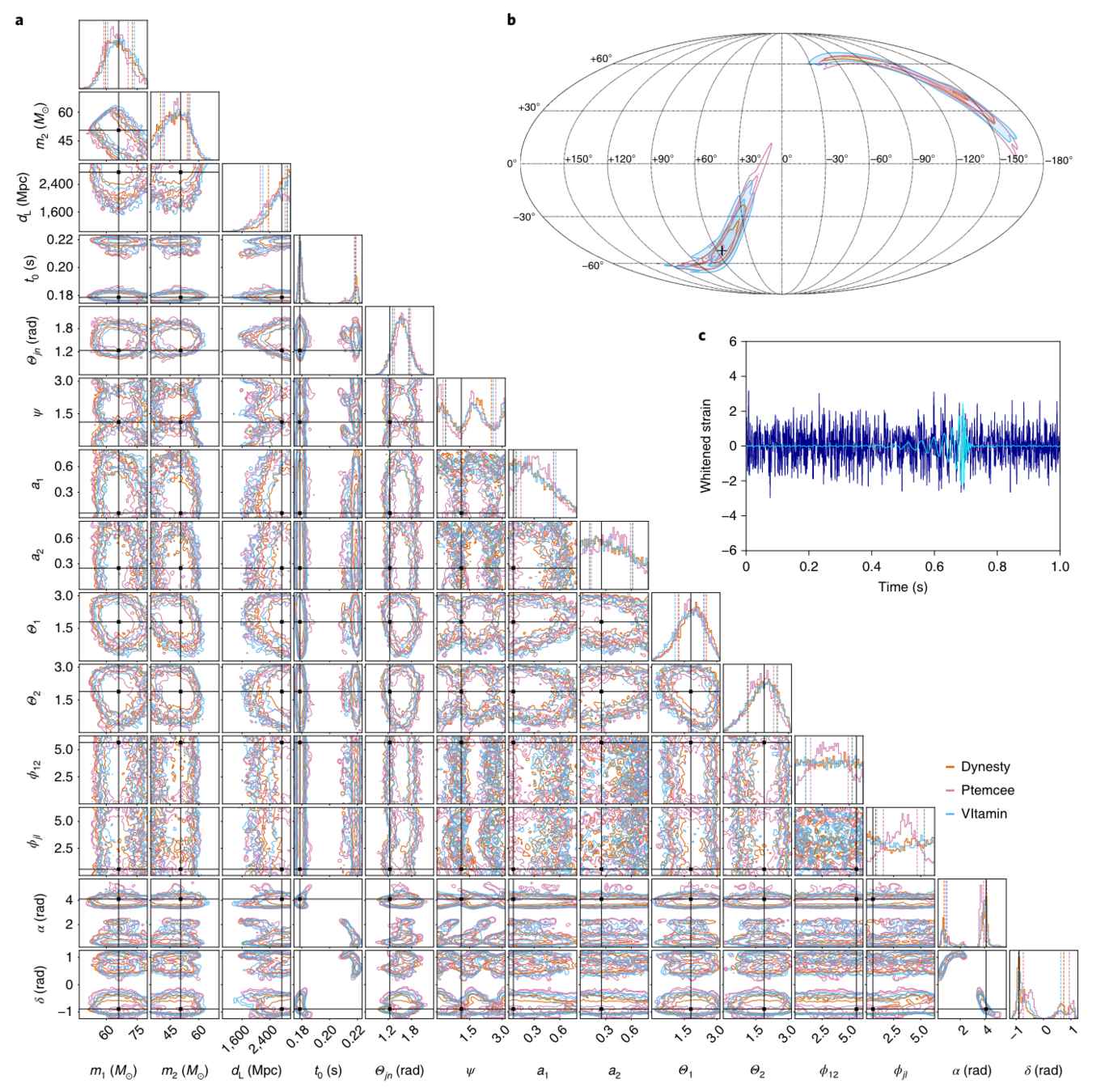
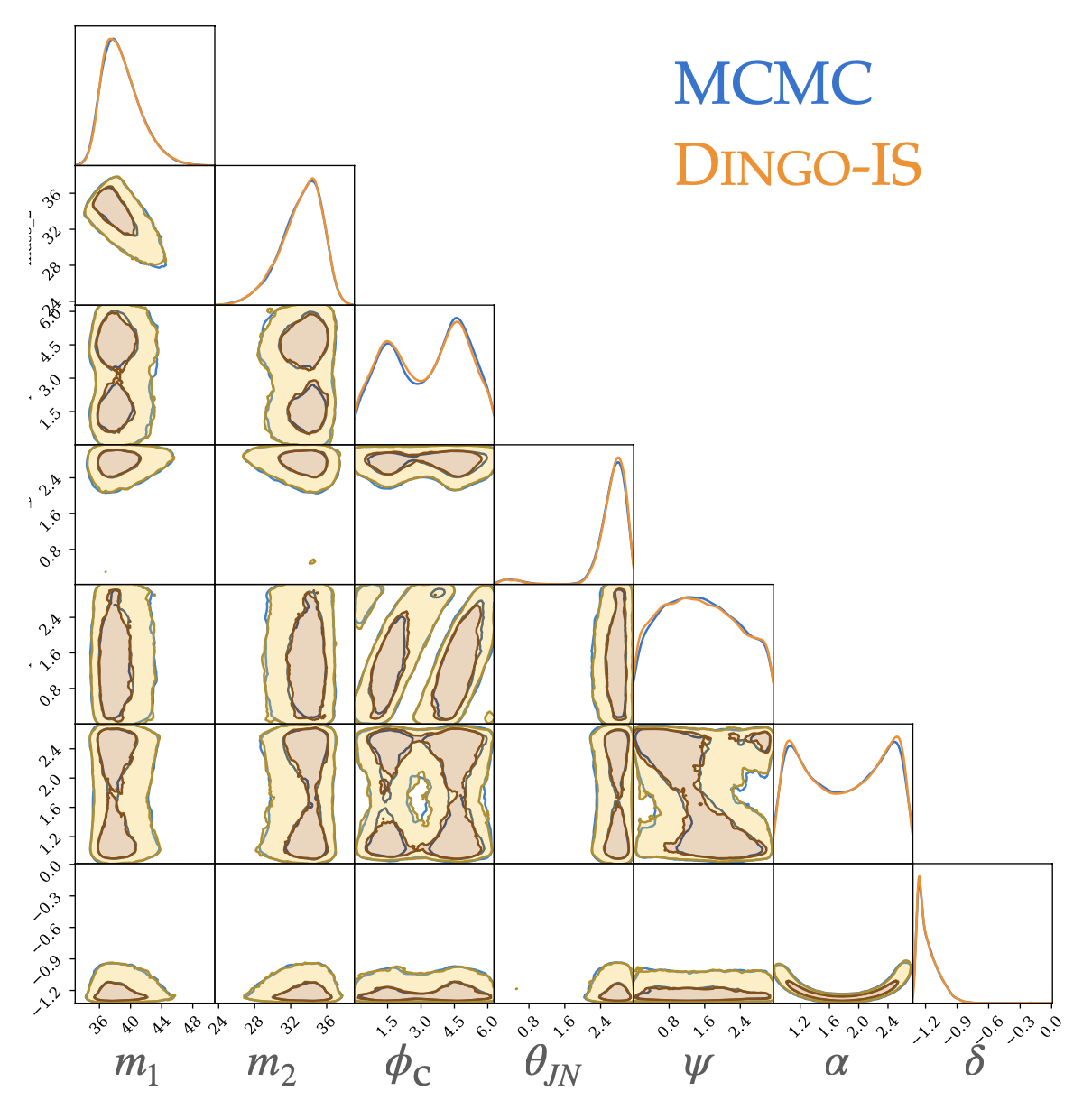
- Prior Sampling: 50,000 Posterior samples in approximately 8 Seconds.
- Capable of calculating evidence
- Processing time: (using 64 CPU cores)
- less than 1 hour with IMRPhenomXPHM,
- approximately 10 hours with SEOBNRv4PHM
PRL 127, 24 (2021) 241103.
PRL 130, 17 (2023) 171403.
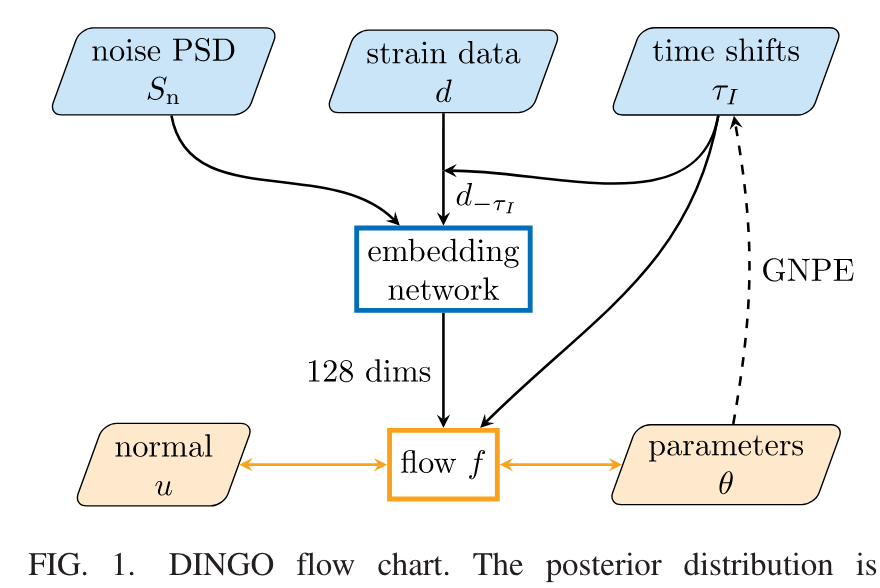
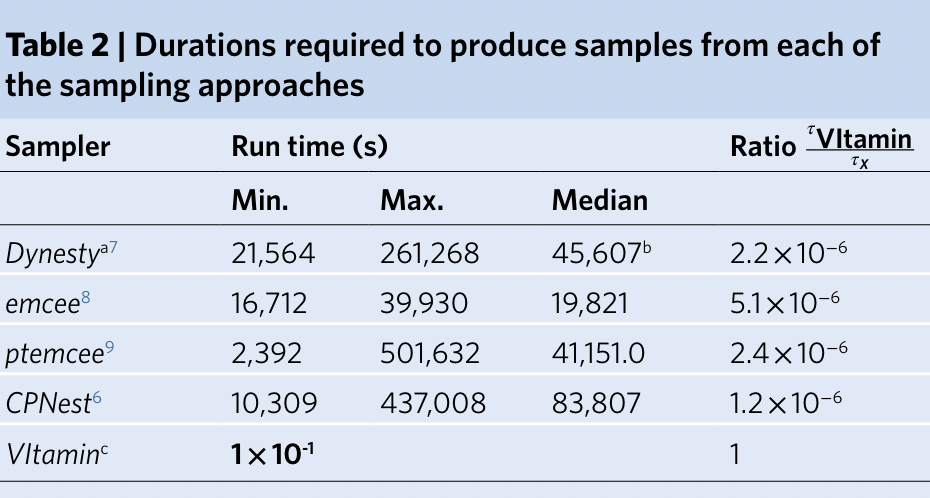
Nature Physics 18, 1 (2022) 112–17
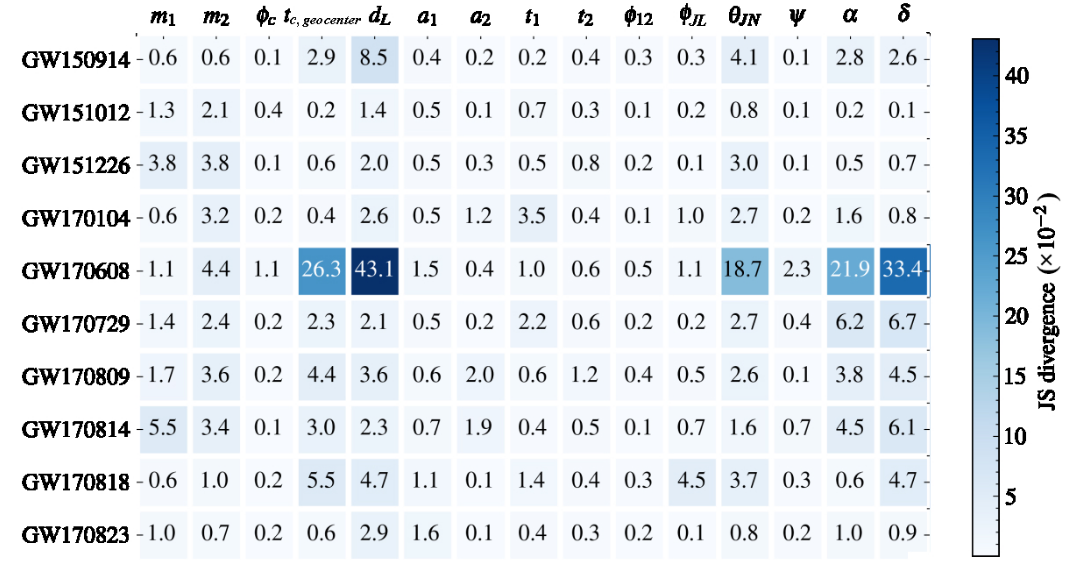
Big Data Mining and Analytics 5, 1 (2021) 53–63.
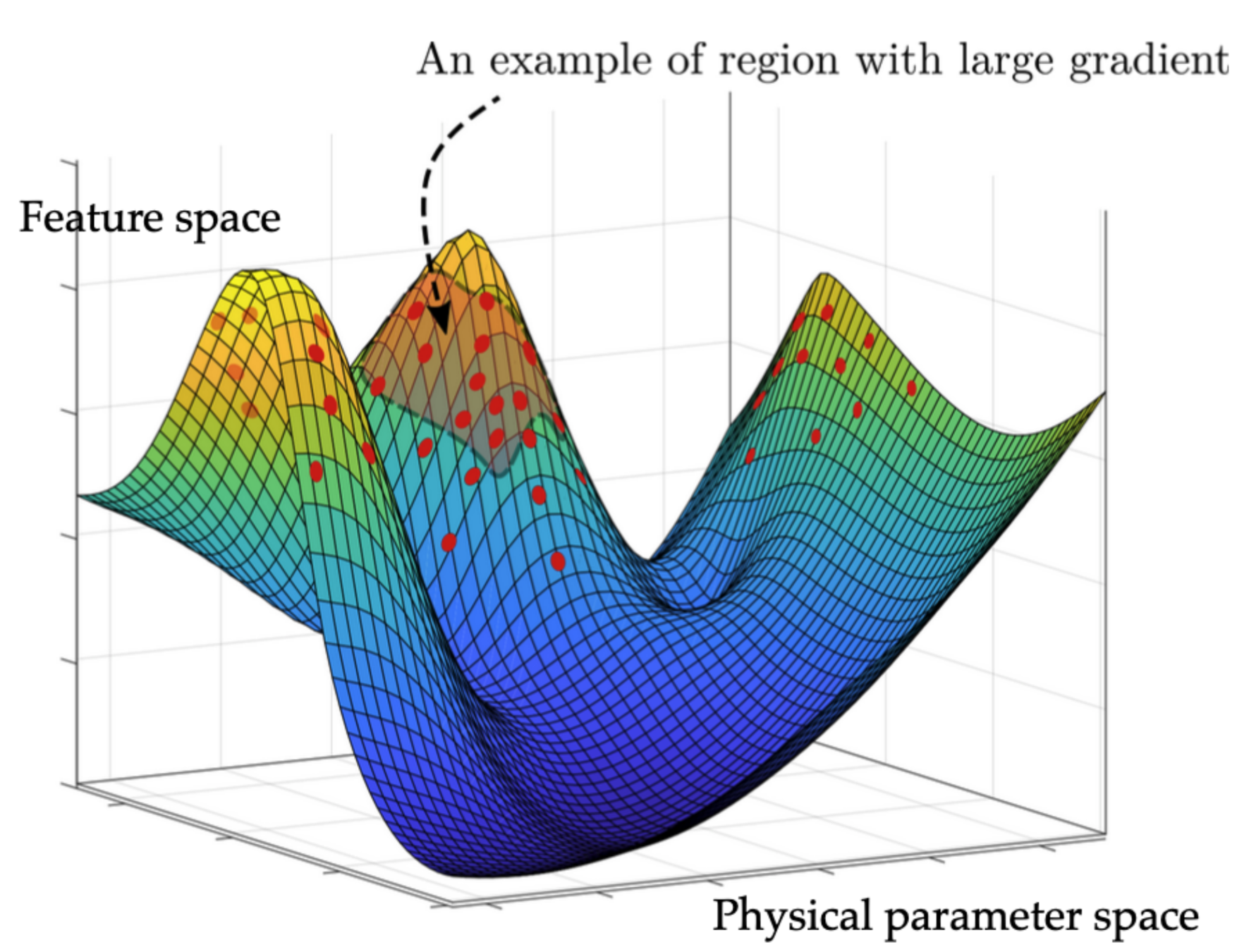
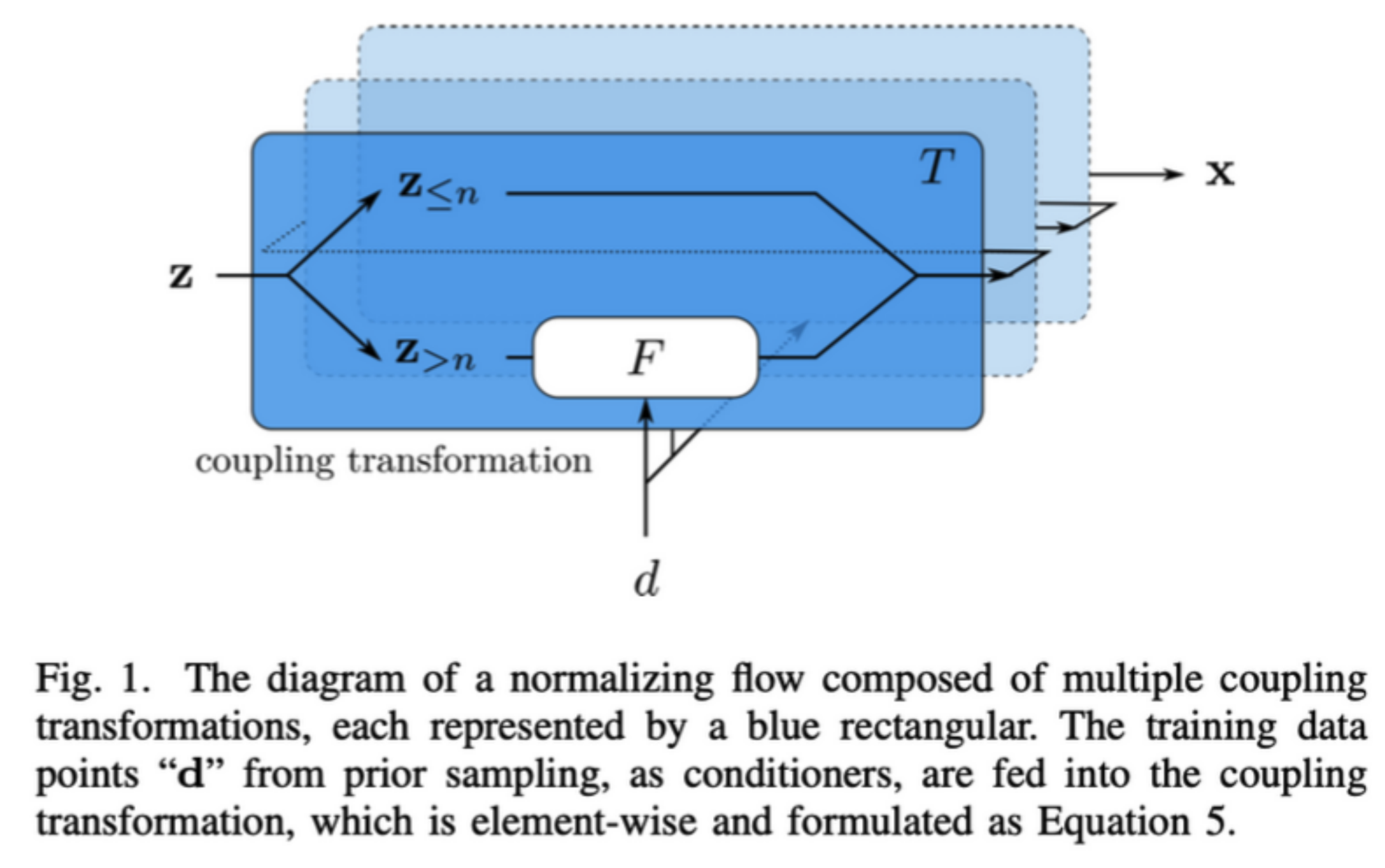
A diagram of prior sampling between feature space and physical parameter space

(Based on 1912.02762)

【【机器学习】白板推导系列(三十三) ~ 流模型(Flow based Model)】
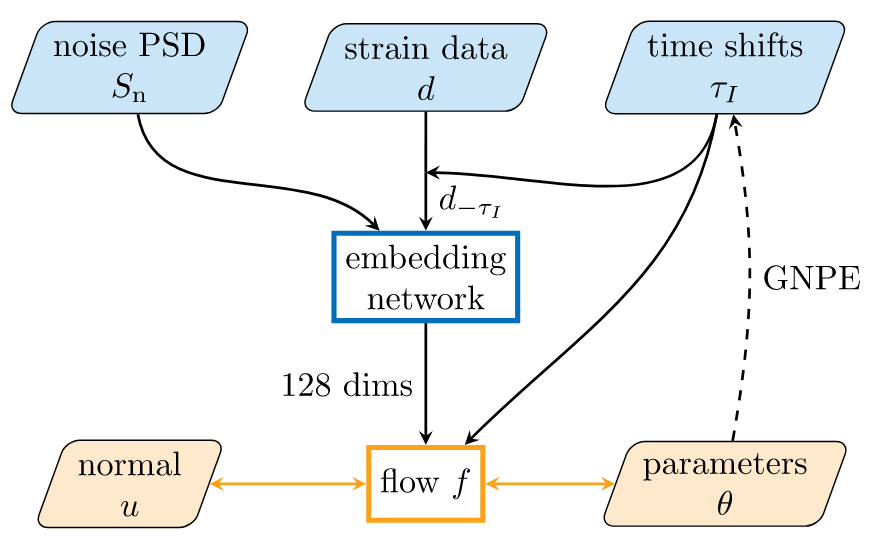
Normalizing Flow Model (1/4)
The main idea of flow-based modeling is to express \(\mathbf{y}\in\mathbb{R}^D\) as a transformation \(T\) of a real vector \(\mathbf{z}\in\mathbb{R}^D\) sampled from \(p_{\mathrm{z}}(\mathbf{z})\):
Note: The invertible and differentiable transformation \(T\) and the base distribution \(p_{\mathrm{z}}(\mathbf{z})\) can have parameters \(\{\boldsymbol{\phi}, \boldsymbol{\psi}\}\) of their own, i.e. \( T_{\phi} \) and \(p_{\mathrm{z},\boldsymbol{\psi}}(\mathbf{z})\).
Change of Variables:
Equivalently,
The Jacobia \(J_{T}(\mathbf{u})\) is the \(D \times D\) matrix of all partial derivatives of \(T\) given by:
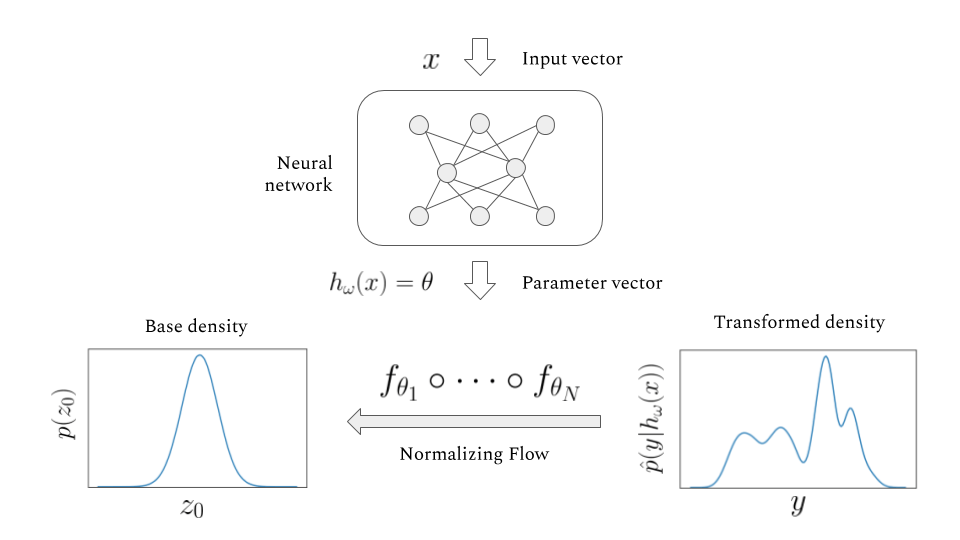

base density
target density

(Based on 1912.02762)
Normalizing Flow Model (2/4)
- Data: target data \(\mathbf{y}\in\mathbb{R}^{15}\) (with condition data \(\mathbf{x}\)).
- Task:
- Fitting a flow-based model \(p_{\mathrm{y}}(\mathbf{y} ; \boldsymbol{\theta})\) to a target distribution \(p_{\mathrm{y}}^{*}(\mathbf{y})\)
- by minimizing KL divergence with respect to the model’s parameters \(\boldsymbol{\theta}=\{\boldsymbol{\phi}, \boldsymbol{\psi}\}\),
- where \(\boldsymbol{\phi}\) are the parameters of \(T\) and \(\boldsymbol{\psi}\) are the parameters of \(p_{\mathrm{z}}(\mathbf{z})=\mathcal{N}(0,\mathbb{I})\).
- Loss function:
- Assuming we have a set of samples \(\left\{\mathbf{y}_{n}\right\}_{n=1}^{N}\sim p_{\mathrm{y}}^{*}(\mathbf{y})\),
Minimizing the above Monte Carlo approximation of the KL divergence is equivalent to fitting the flow-based model to the samples \(\left\{\mathbf{y}_{n}\right\}_{n=1}^{N}\) by maximum likelihood estimation.


base density
target density
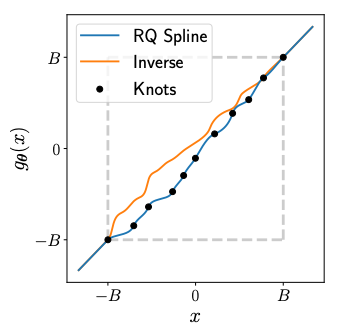
Rational Quadratic Neural Spline Flows
(RQ-NSF)

Train
nflow
Normalizing Flow Model (3/4)

归一化流模型示意图
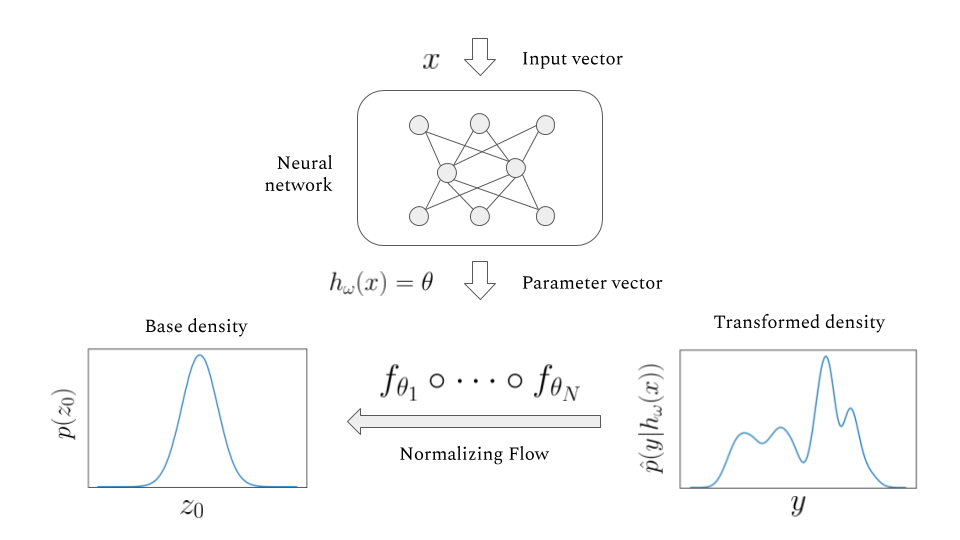

Test
nflow
Train
nflow
Normalizing Flow Model (4/4)
DINGO 要特别快,要足够准
(缺DINGO技术相关的前沿动态)
Enrico 只要够快就足够了,可以做引力检验
(调研所有和最新的AI+引力检验文章)
(缺PyGWB的引入、数据描述、结果)-> 同样遇到如何做statistics的问题
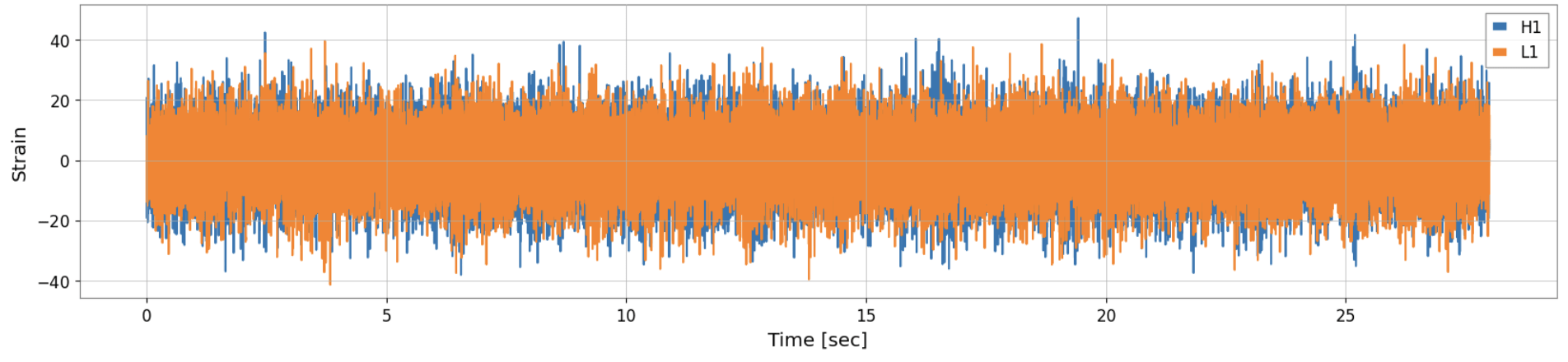
pure signals of SGWB
pure noise
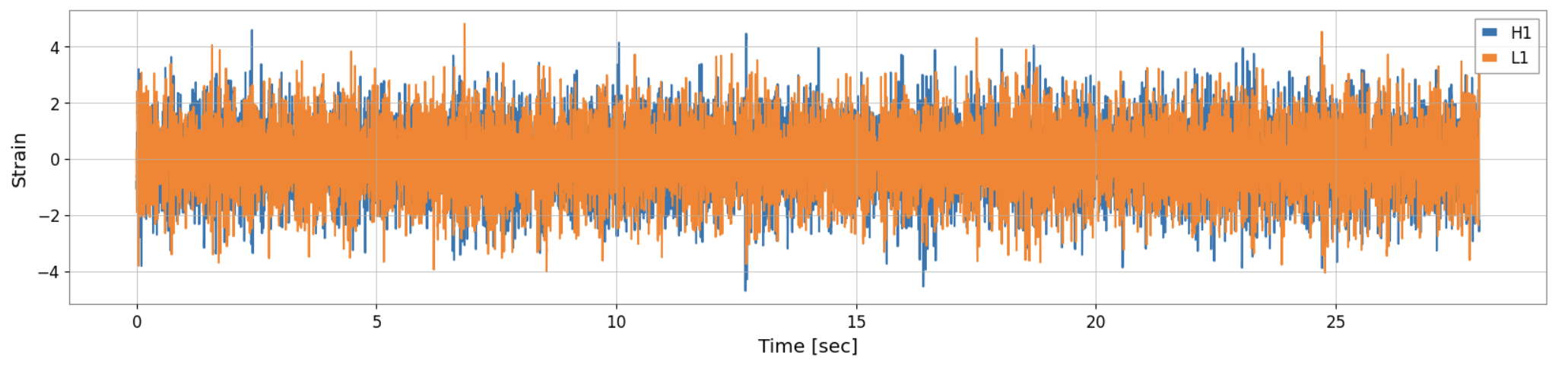
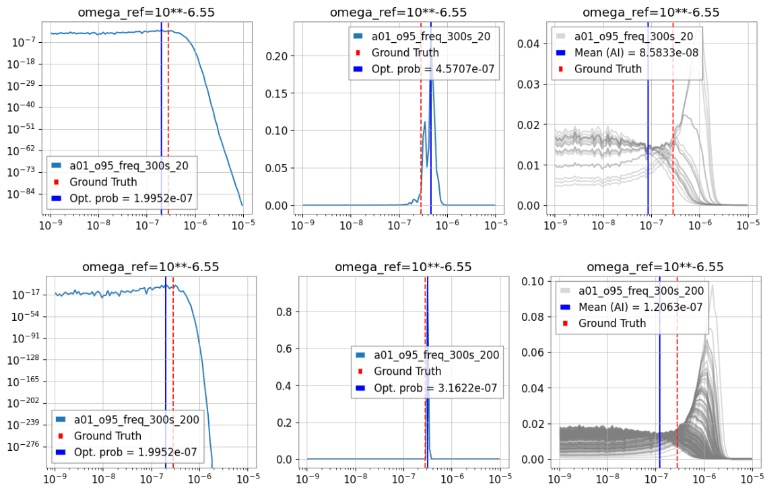
-
Bayesian inference, the Holy Grail of gravitational-wave data analysis,
enables astrophysical interpretation and scientific discoveries.
Simulation-Based Inference (SBI)
- SBI \(\Rightarrow\) Fast and precise parameter estimation.
- SBI \(\Rightarrow\) TGR / Cosmology / PTA ...

Text

PRL 127, 24 (2021) 241103.
PRL 130, 17 (2023) 171403.
Real-time gravitational wave science with neural posterior estimation
Sampling with prior knowledge for high-dimensional gravitational wave data analysis
He Wang, et al. Big Data Min. Anal. (2021)
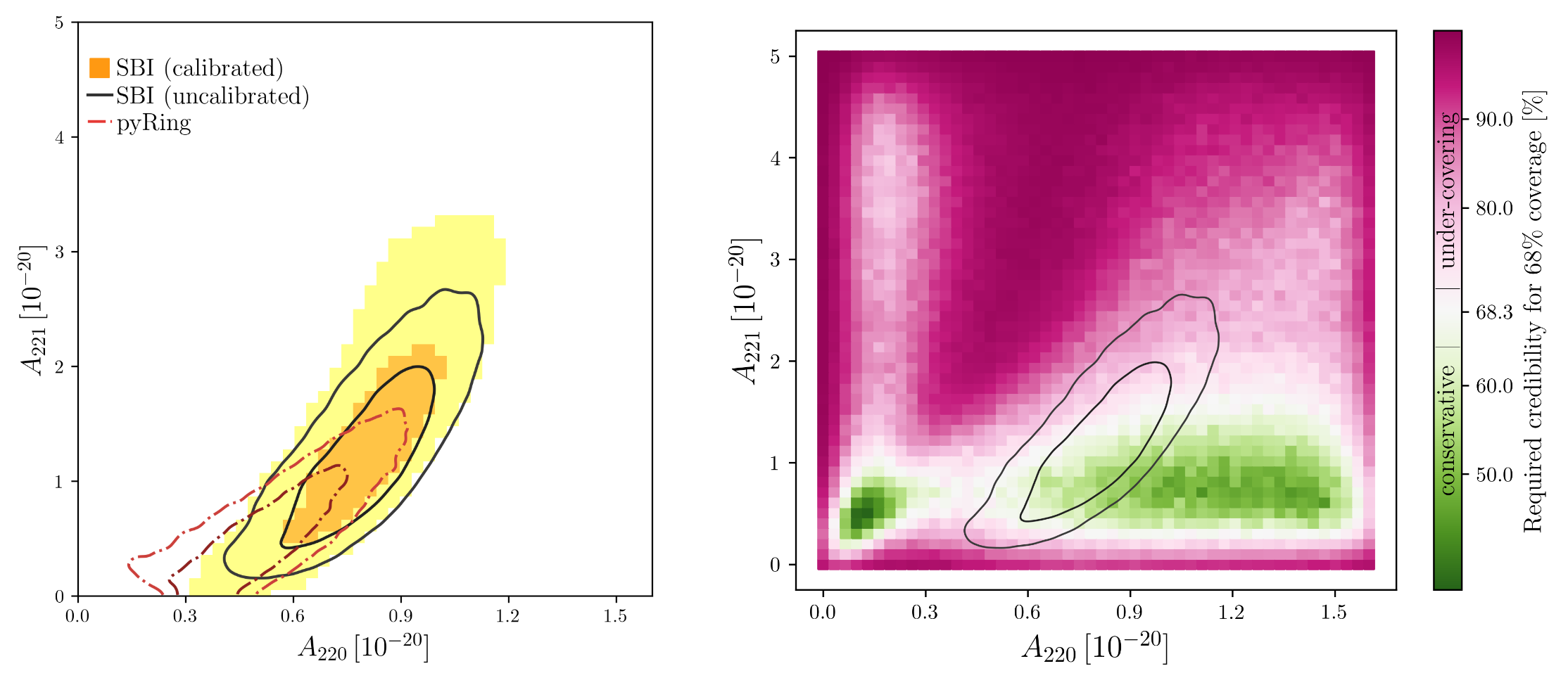
PRD 108, 4 (2023): 044029.
Neural Posterior Estimation with Guaranteed Exact Coverage: The Ringdown of GW150914
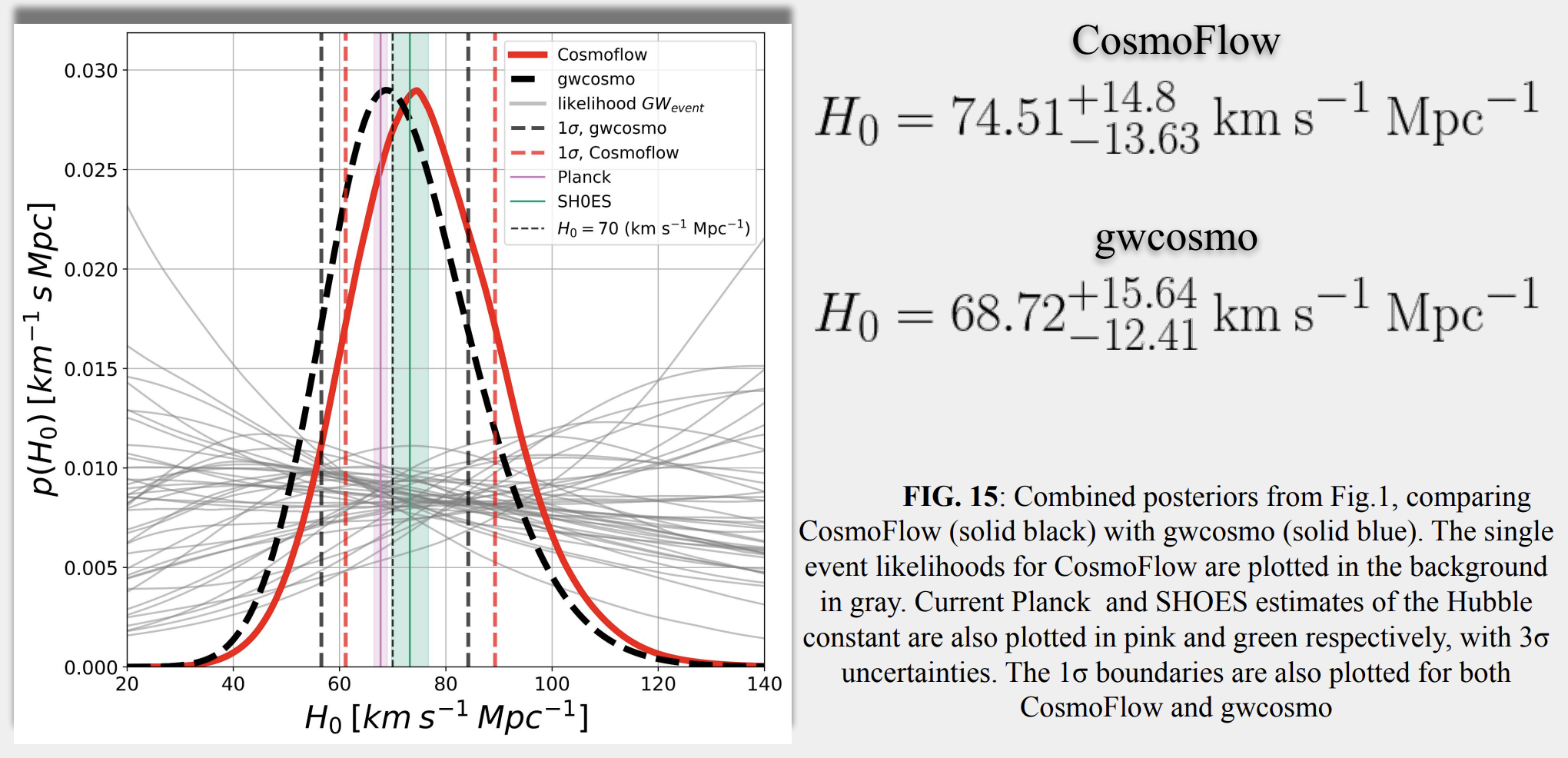
arXiv:2310.13405, LIGO-P2300306
Cosmological Inference using Gravitational Waves and Normalising Flows
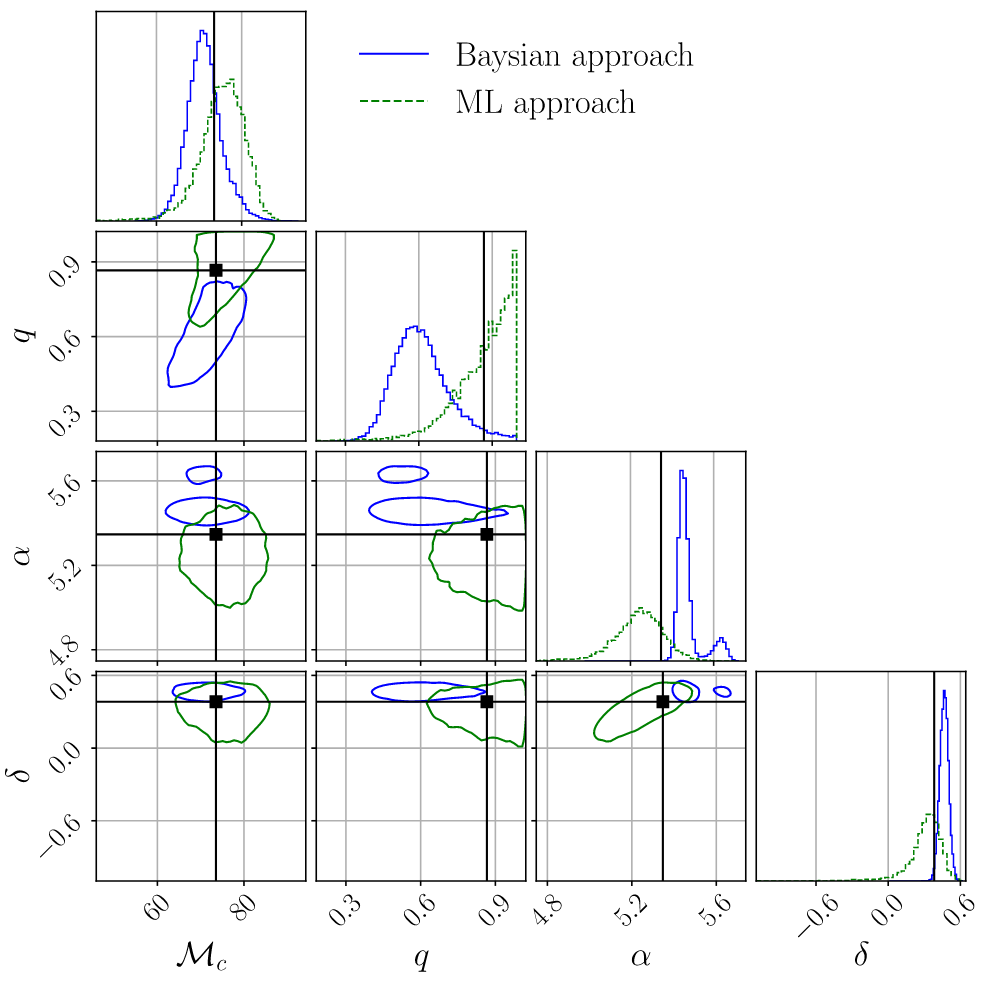
Normalizing Flows as an Avenue to Studying Overlapping Gravitational Wave Signals
Parameter Estimation · Scientific Discovery
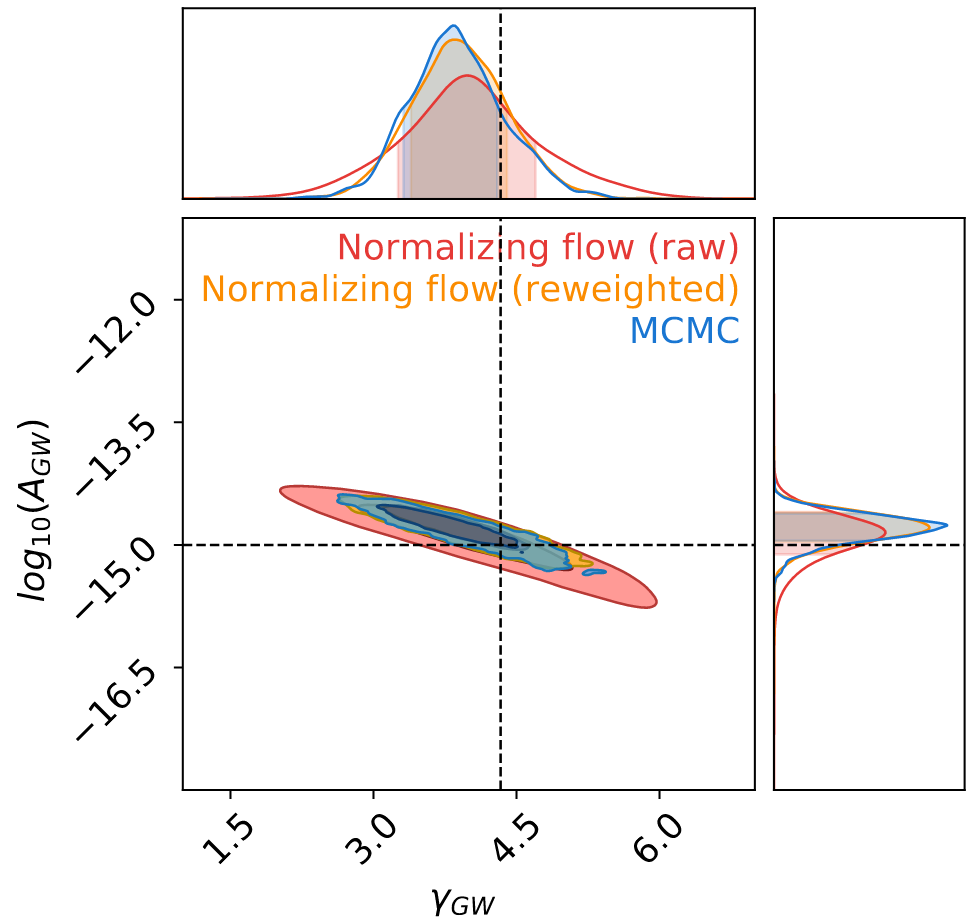
arXiv:2310.12209
Fast Parameter Inference on Pulsar Timing Arrays with Normalizing Flows
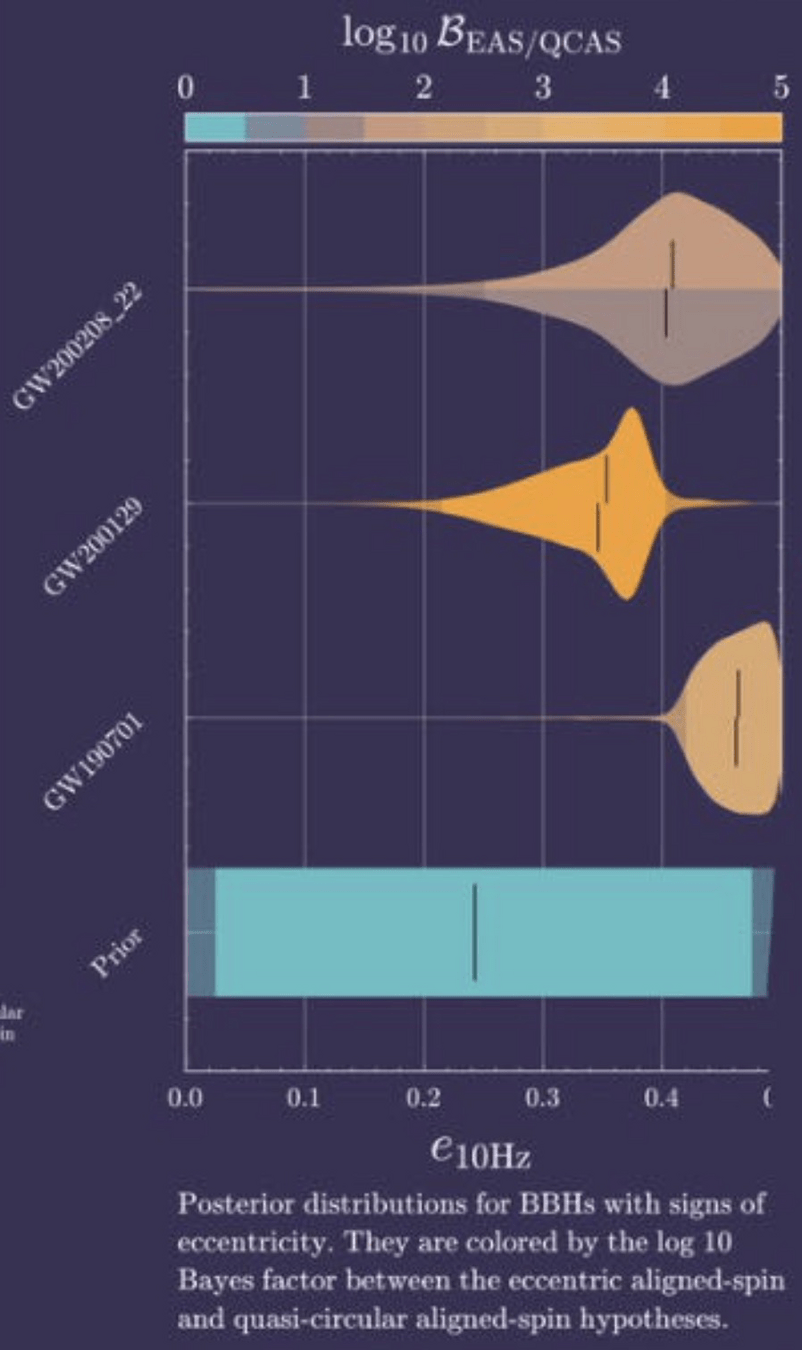
arXiv:2404.14286
Exact coverage first!
Paradigm
New
discovery
first!


PRD 108, 4 (2023): 044029.

Text
Appreciating the Ringdown Overtone Test of GW150914
- A notable work involves ringdown overtone testing, which, acknowledging the difficulty in achieving DINGO-like precision for complex waveforms, leverages the speed advantage of AI.
- By simulating the signal and \(10^3\) realizations of LIGO noise for each pixel, it accomplishes what is impossible for MCMC methods, prioritizing speed over precision in a strategic trade-off.
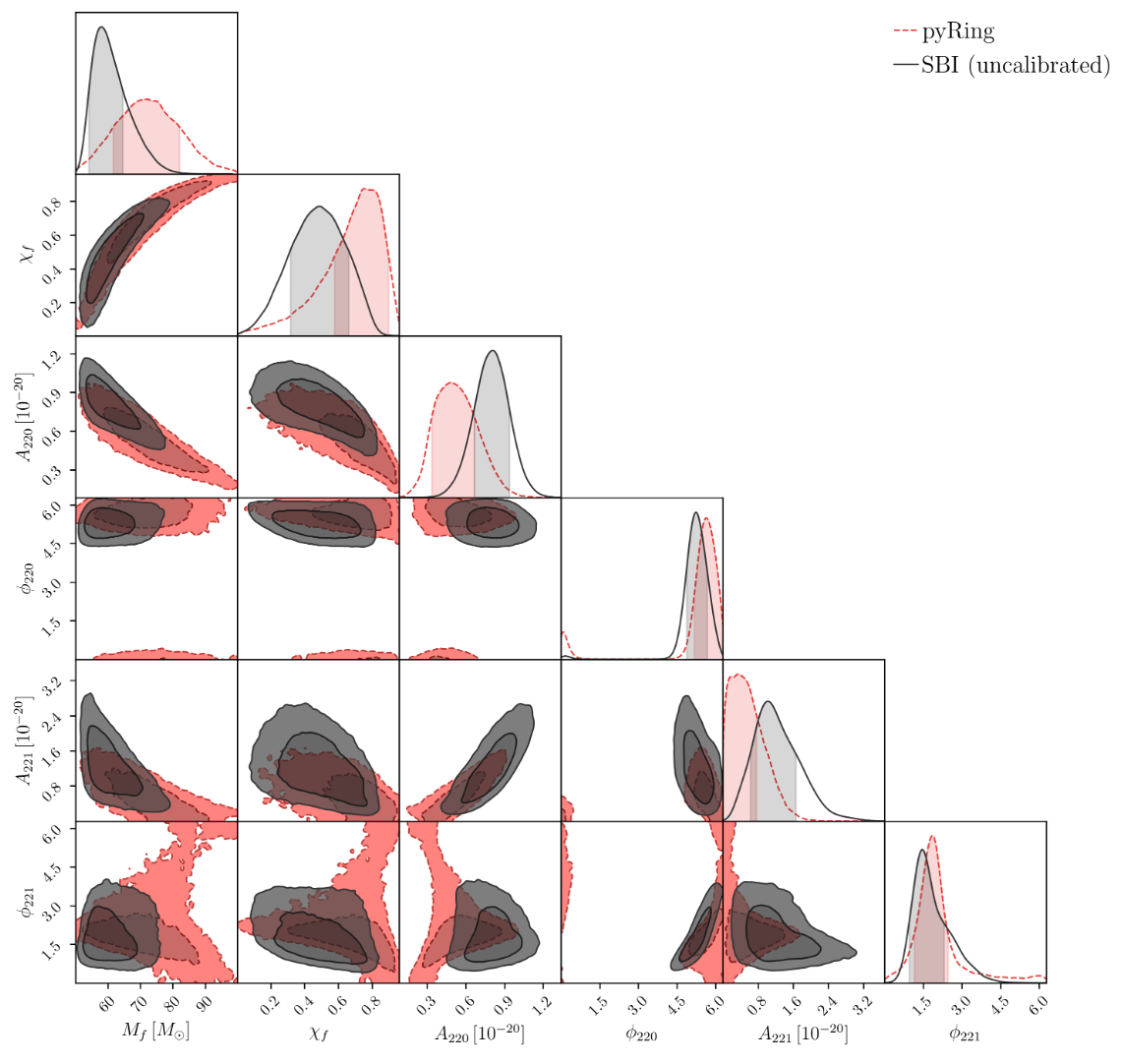

Parameter Estimation · Scientific Discovery





arXiv:2404.14286
-
進撃のnflow model in GW inference area.
-
2002.07656: 5D toy model [1] (PRD)
-
2008.03312: 15D binary black hole inference [1] (MLST)
-
2106.12594: Amortized inference and group-equivariant neural posterior estimation [2] (PRL)
-
2111.13139: Group-equivariant neural posterior estimation [2]
-
2210.05686: Importance sampling [2] (PRL)
-
2211.08801: Noise forecasting [2] (PRD)
-
2305.17161: FMPE
-
2404.14286: eccentricity of BBHs
-
-
https://github.com/dingo-gw/dingo (2023.03)
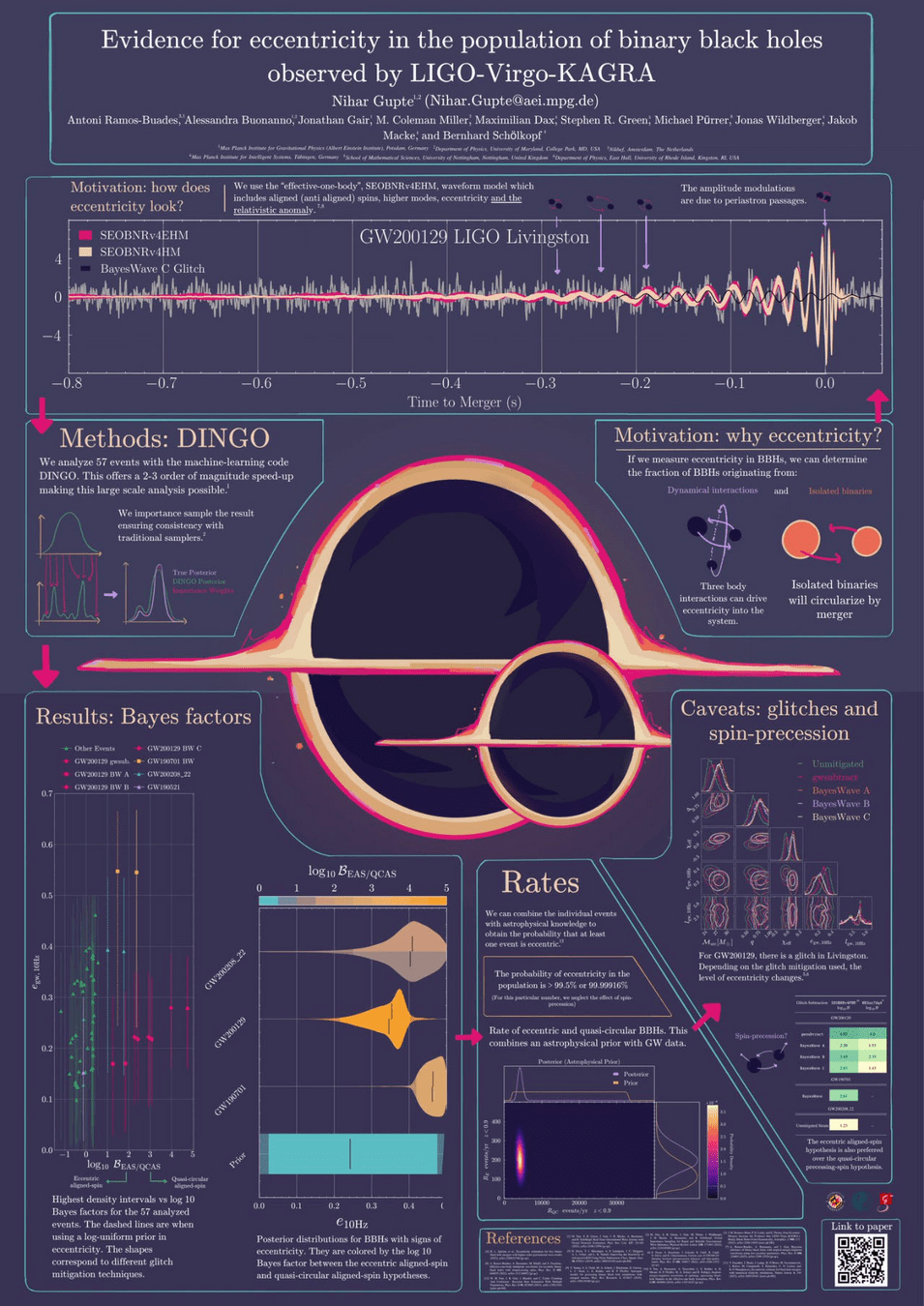
Parameter Estimation · Scientific Discovery

Parameter estimation · Scientific discovery
Text
Exploring Stochastic Gravitational Wave Background with AI
- Utilizing AI for parameter estimation in the stochastic gravitational wave background (SGWB) presents a fascinating blend of rich theoretical content and the potential for optimizing current data processing methods.
- While still preliminary and ongoing, our work shows promising results for high SNR SGWB scenarios, where AI-based posterior probabilities are notably more precise and narrower compared to traditional cross-correlation methods used in PyGWB.
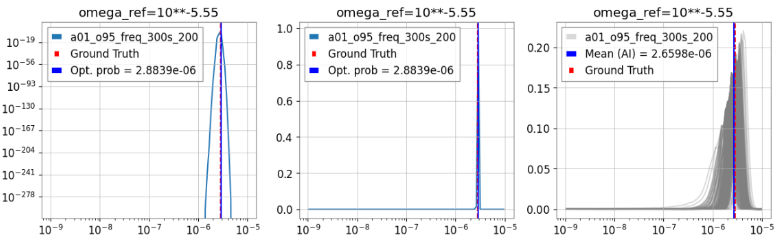

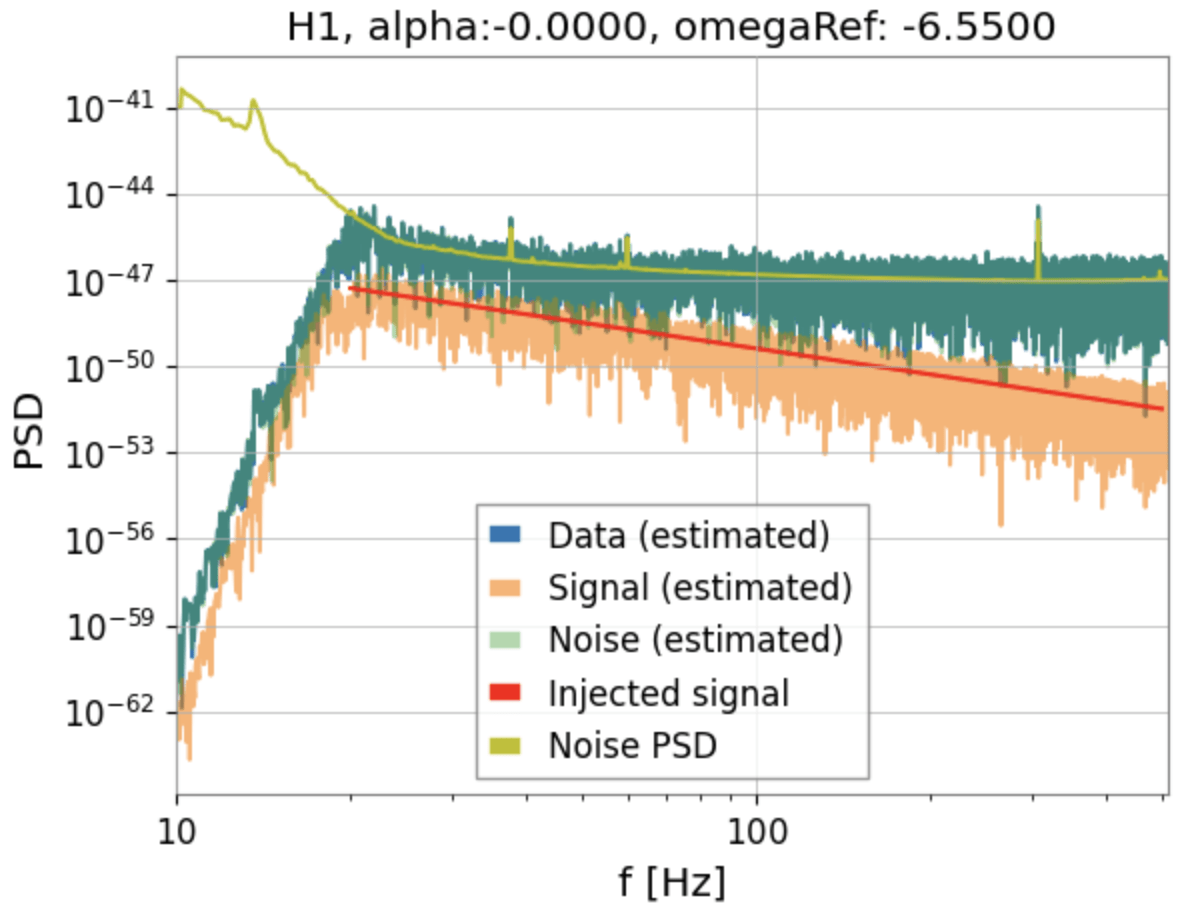
Our result (preliminary)

Parameter estimation · Scientific discovery
Text
Exploring Stochastic Gravitational Wave Background with AI
- Performance saturation is observed between SNR levels of \(10^{-6}\) to \(10^{-7}\), indicating a plateau in model effectiveness in low SNR conditions.
- Unlike PyGWB, which can accumulate cross-correlation data from SGWB to further constrain the power spectrum, AI model outputs do not readily provide statistically meaningful information for aggregation. Multiplying posterior probabilities from multiple segments leads to ambiguous, and potentially biased, results due to the lack of statistically significant fluctuations across different posterior distributions.
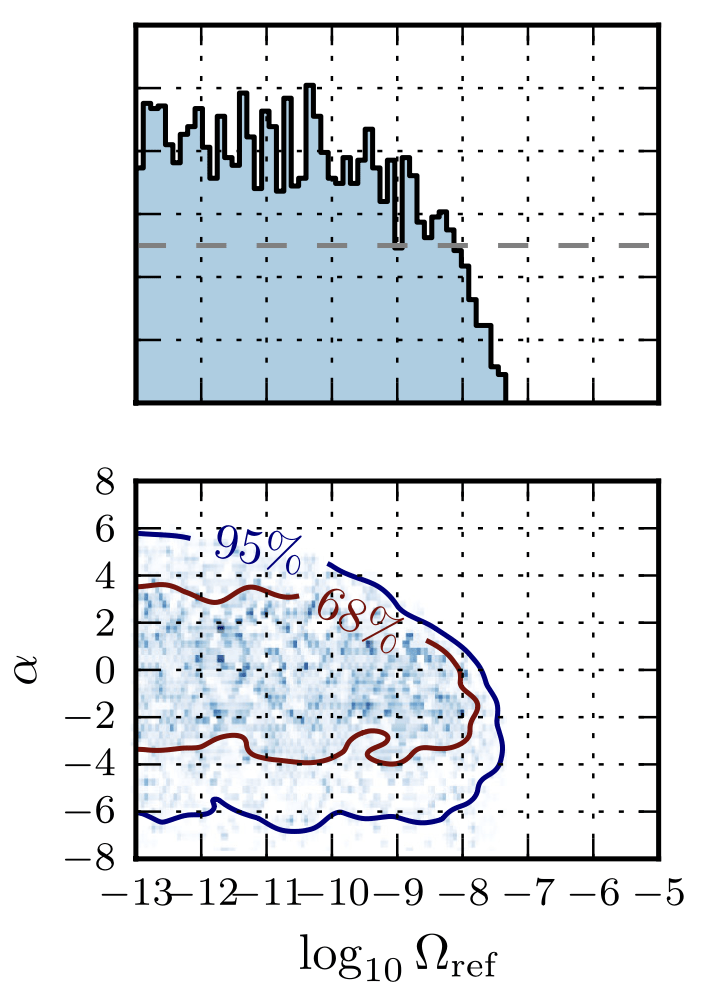
Abbott R, et al. PRD 104, 2 (2021): 022004.
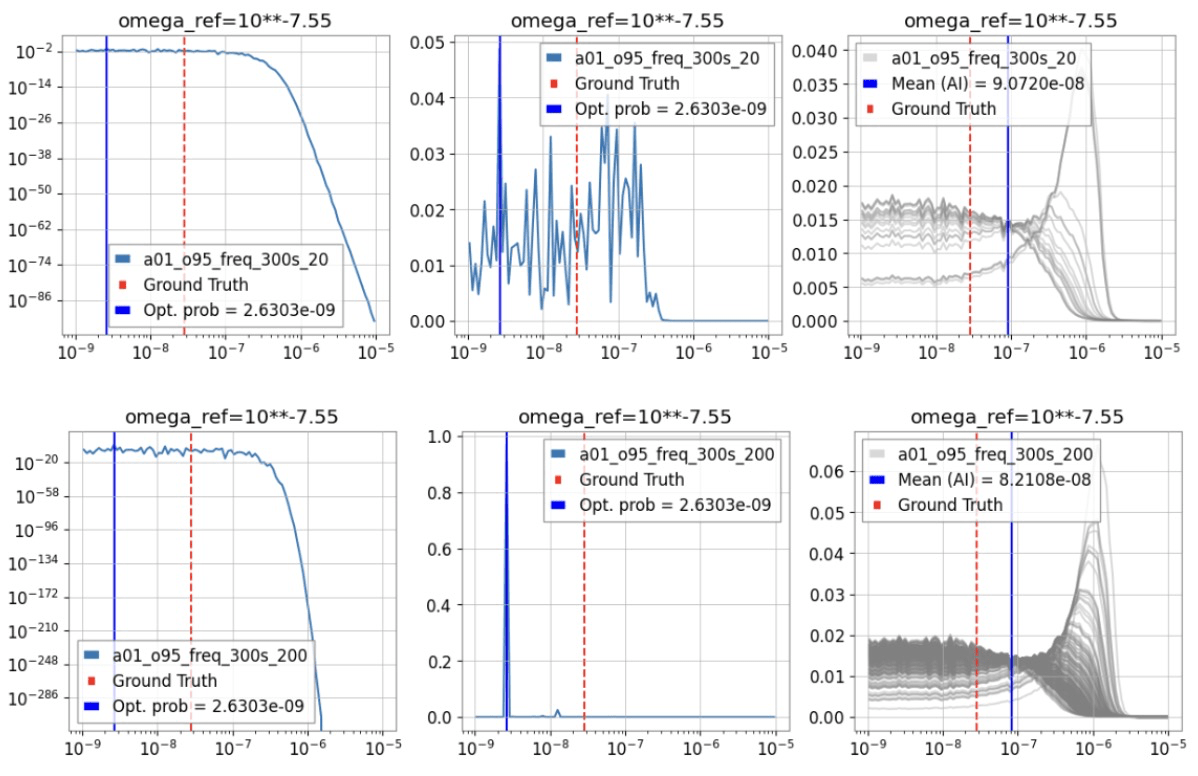
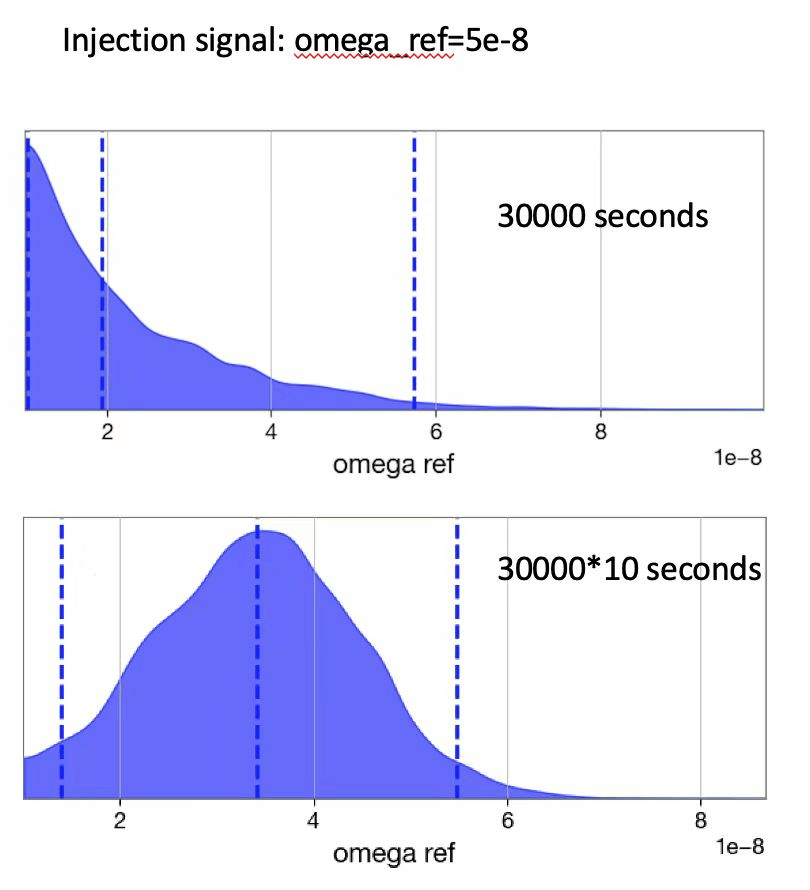
PyGWB result
Our result (preliminary)

AI Predicting the Universe: Opportunities and Challenges
-
Exploring the importance of understanding how AI models make predictions in scientific research.
- The critical role of generative models (生成模型是关键)
- Quantifying uncertainty: a key aspect (不确定性量化问题)
- Fostering controllable and reliable models (模型的可控可信问题)
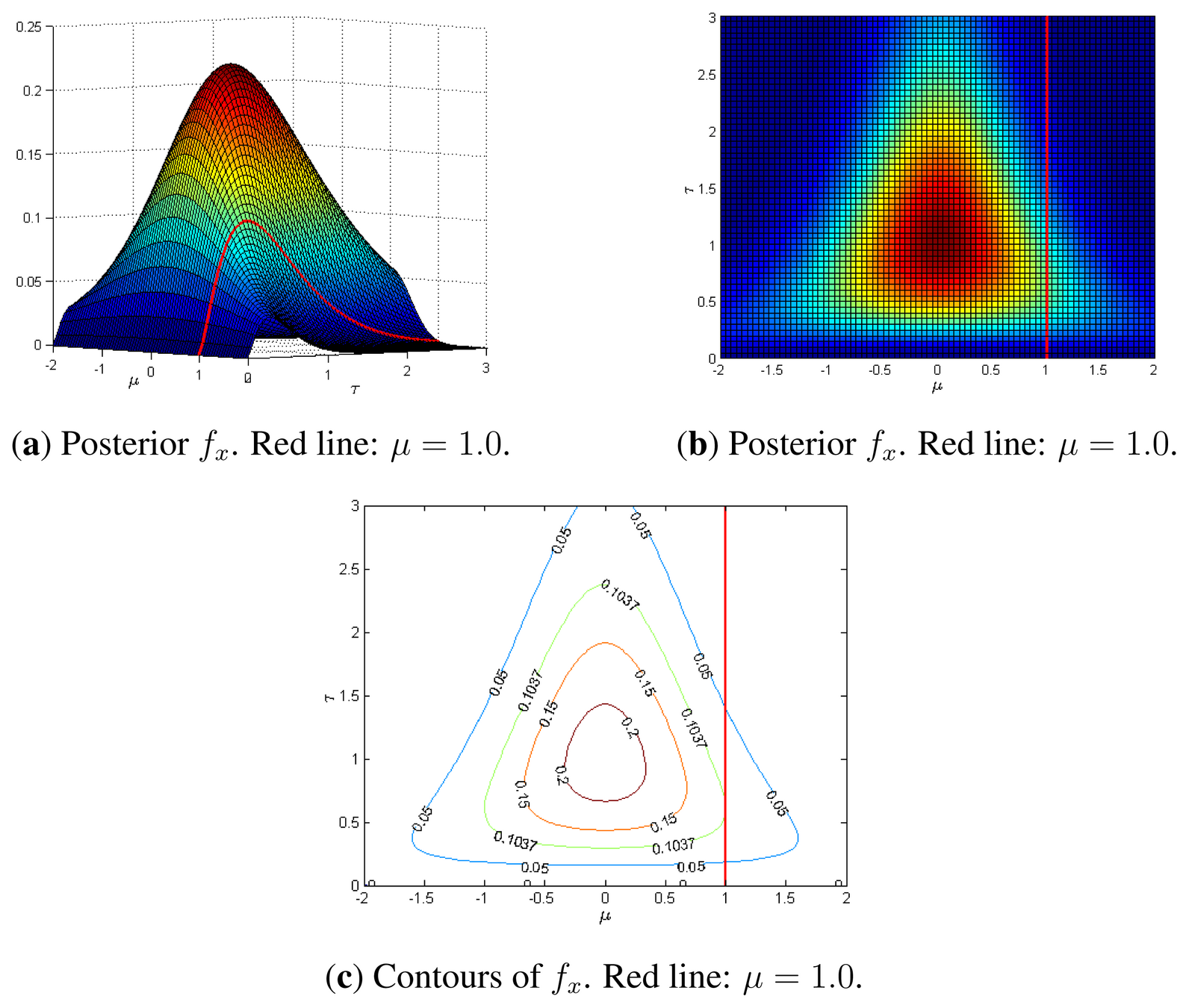

AI or Bayes

Text-to-image
"A running dog"
- The most common and direct approach, from Artificial Intelligence Generated Content (AIGC) to GW statistical inference: pixel point \(\Rightarrow\) inferred parameter.

AI Predicting the Universe: Opportunities and Challenges
-
Exploring the importance of understanding how AI models make predictions in scientific research.
- The critical role of generative models (生成模型是关键)
- Quantifying uncertainty: a key aspect (不确定性量化问题)
- Fostering controllable and reliable models (模型的可控可信问题)



AI or Bayes

Text-to-image
"A corgi running on the street"
A picture is worth a thousand words.
A fraction of a thousand words.
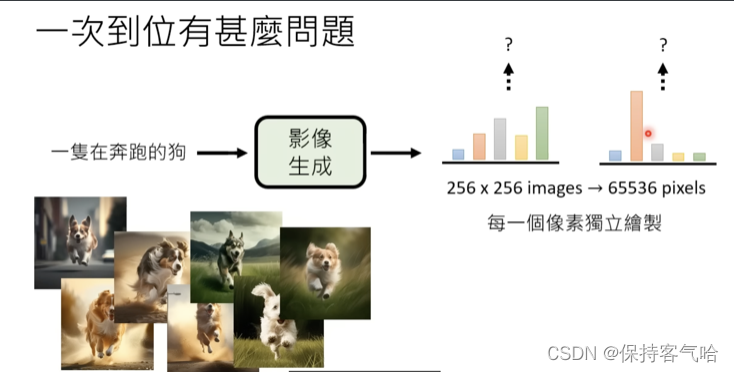
Credit: 李宏毅
"A running dog"
- The most common and direct approach, from Artificial Intelligence Generated Content (AIGC) to GW statistical inference: pixel point \(\Rightarrow\) inferred parameter.
Content


- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- (Space-based GW Detection)

Key Takeaways
Text
AI vs Classical Methods
- In strict sense, at present AI methods have not yet become the perfect alternative to traditional methods (like MF, MCMC, etc.).
- There is a pressing need for the theoretical refinement of ML applications in GW statistics, aiming to bridge current gaps and enhance model reliability.
-
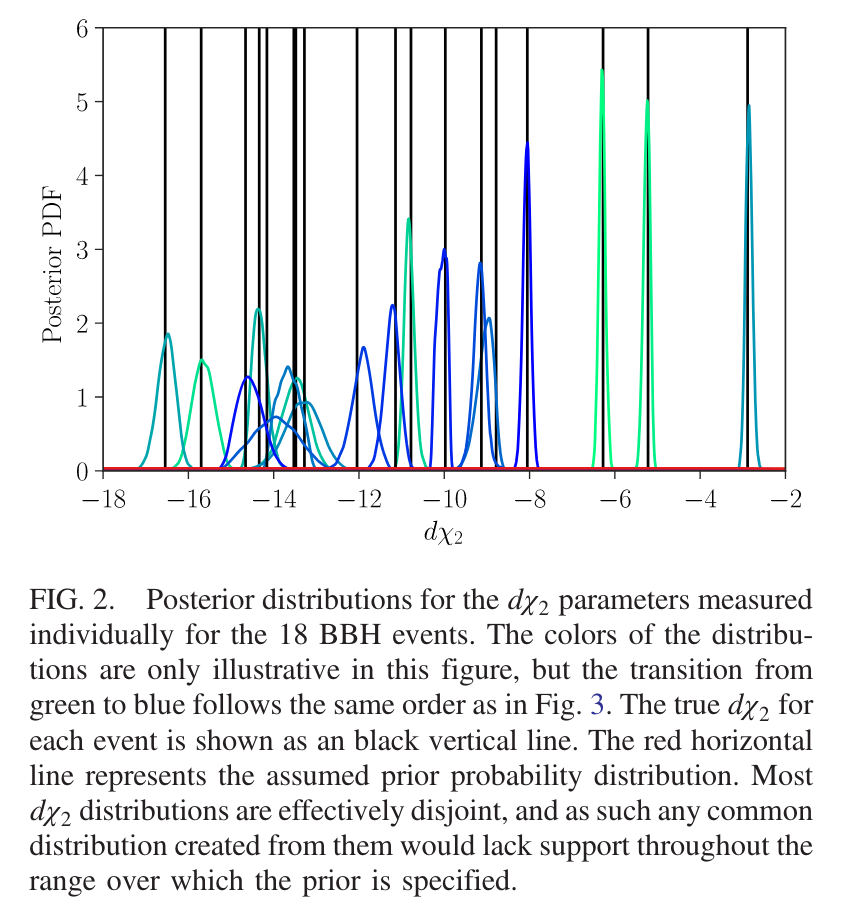
How can we address the issue of strong or unacceptable biases that occur when outputs from AI models are used jointly or in combination to measure properties of a population, sub-population, or ensemble?
(also addressed by 2405.18095)


Alfaidi & Messerger. arXiv:2402.04589

Our result (preliminary)

Menéndez-Vázquez A, et al. PRD 2021

PyGWB result
He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046

Key Takeaways
Text



Statistics
Statistics



AI vs Classical Methods
- In strict sense, at present AI methods have not yet become the perfect alternative to traditional methods (like MF, MCMC, etc.).
- There is a pressing need for the theoretical refinement of ML applications in GW statistics, aiming to bridge current gaps and enhance model reliability.
-
How can we address the issue of strong or unacceptable biases that occur when outputs from AI models are used jointly or in combination to measure properties of a population, sub-population, or ensemble?
(also addressed by 2405.18095)
- How can we construct a gravitational wave statistical theory based on machine learning methods to achieve robust theoretical guarantees for detection statistics and statistical inference?
- \(\rightarrow\) Is the goal to achieve results that are entirely consistent with the statistical properties of traditional methods, or
- \(\rightarrow\) to quantify and calibrate any results provided by AI within the statistical theory framework?


Key Takeaways
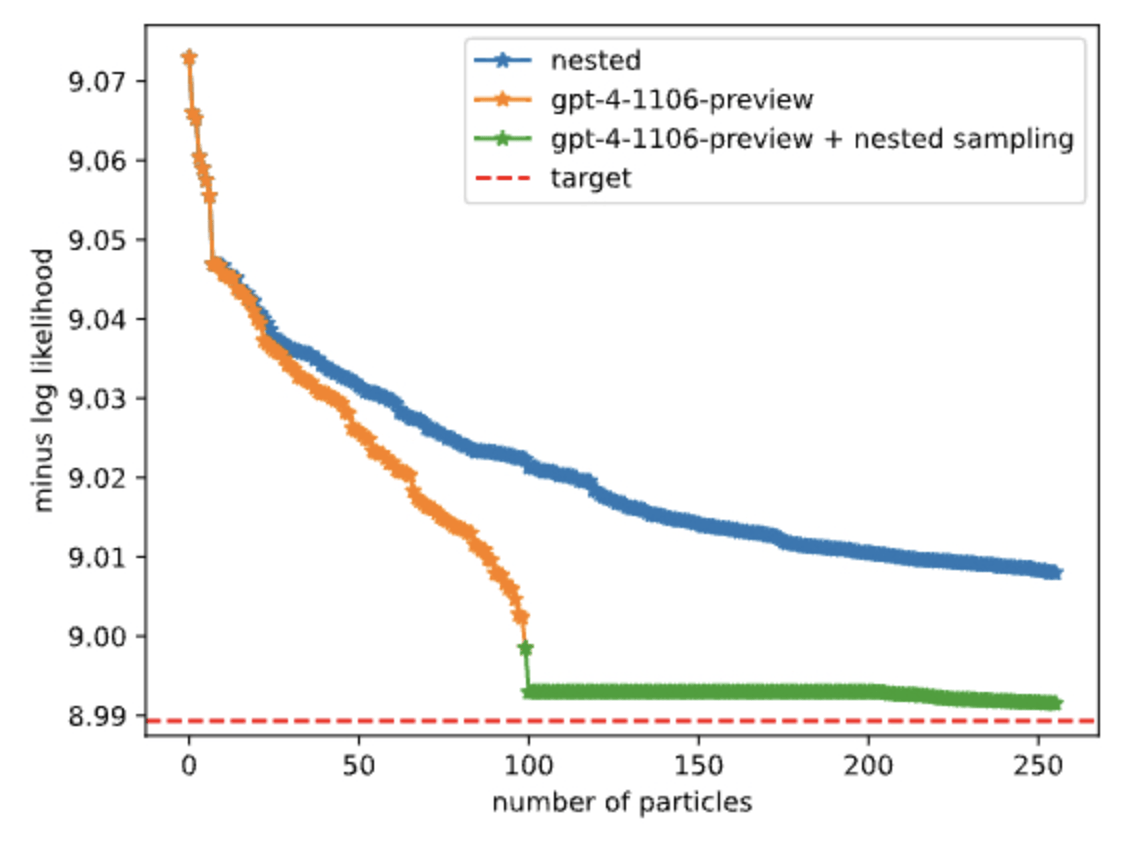
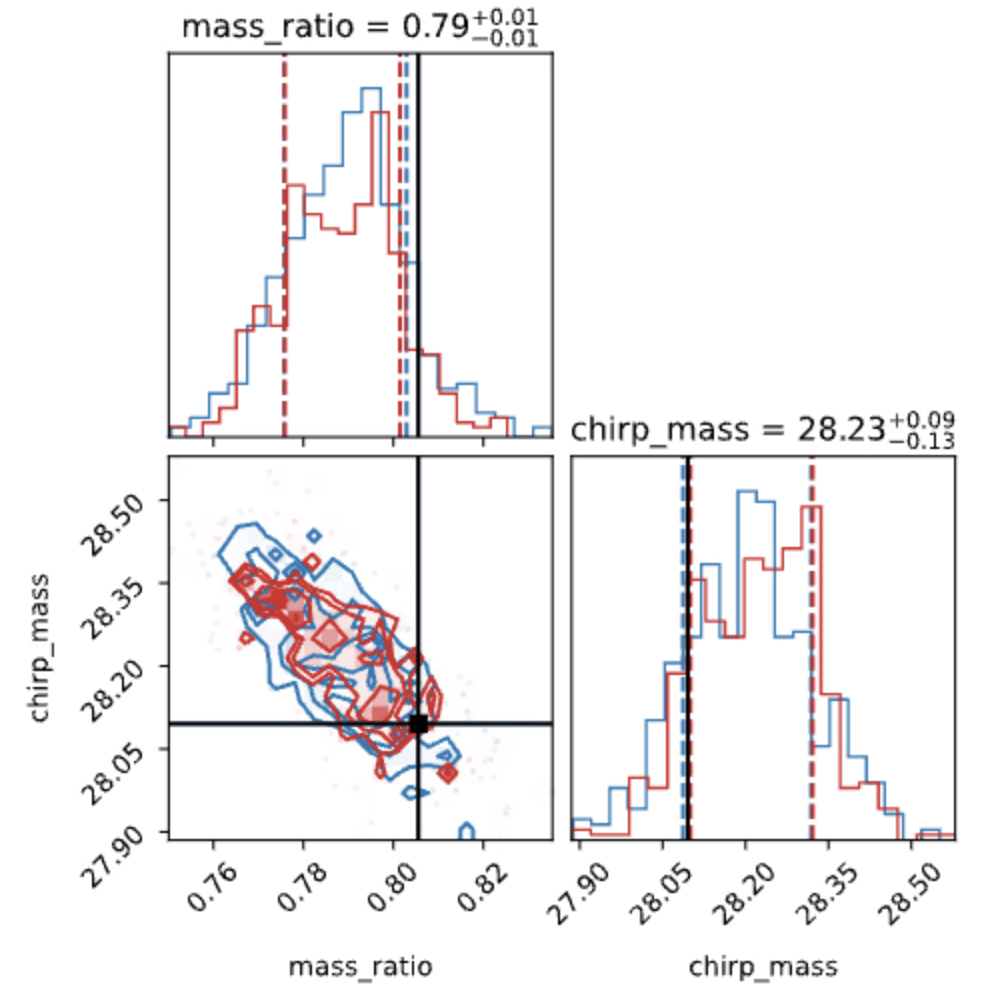
Text
On-going
- Agentic Reasoning for Inference
Text
Insights
- AI is not just a tool; it is a revolutionary pathway for scientific discoveries.
- Theoretical Advancements in ML for GW Statistics
- There is a pressing need for the theoretical refinement of ML applications in GW statistics, aiming to bridge current gaps and enhance model reliability.
- Improve the interpretability of AI models, as it is essential for enhanced and trustworthy discoveries.


Statistics






Statistics
for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This silde: https://slides.com/iphysresearch/2024july_lzu



Key Takeaways


Nature Physics 18, 1 (2022): 9–11
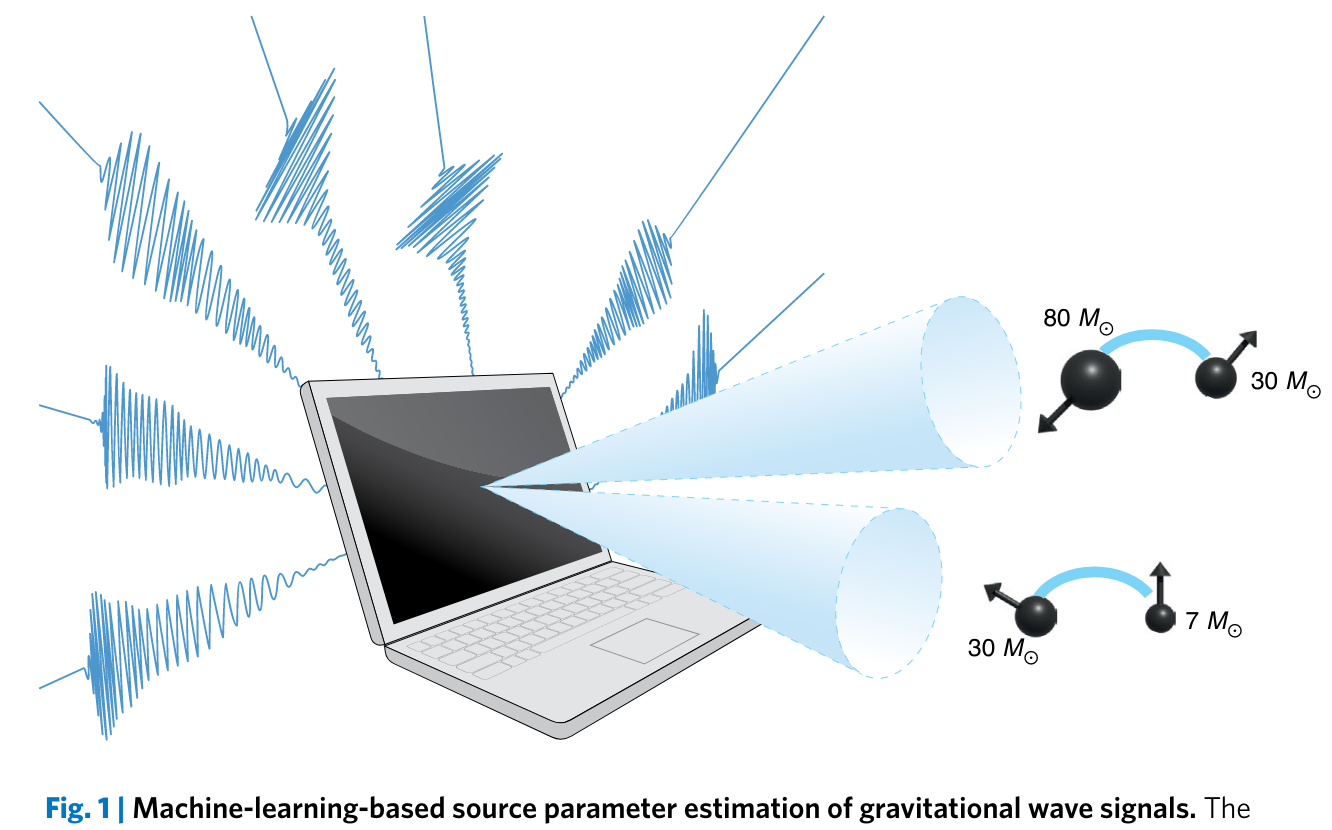
Text
On-going
- Agentic Reasoning for Inference
Text
Insights
- AI is not just a tool; it is a revolutionary pathway for scientific discoveries.
- Theoretical Advancements in ML for GW Statistics
- There is a pressing need for the theoretical refinement of ML applications in GW statistics, aiming to bridge current gaps and enhance model reliability.
- Improve the interpretability of AI models, as it is essential for enhanced and trustworthy discoveries.


for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')For further reference or to cite the work presented today,
please cite this silde: https://slides.com/iphysresearch/2024mar_bnuz


https://twitter.com/chipro/status/1768388213008445837?s=46&t=JmDXWgIucgr_FlsBFTvuRQ
如何把大模型这个概念在合适的地方讲出来?(开头?最后?)
高维、多模态的inference挑战(是整个引力波相关的科学研究的技术难点)
PTMCMC 的算法描述图
Multi-agent 的概念图,及其相关结果的对比图
Parameter estimation · Scientific discovery

Text
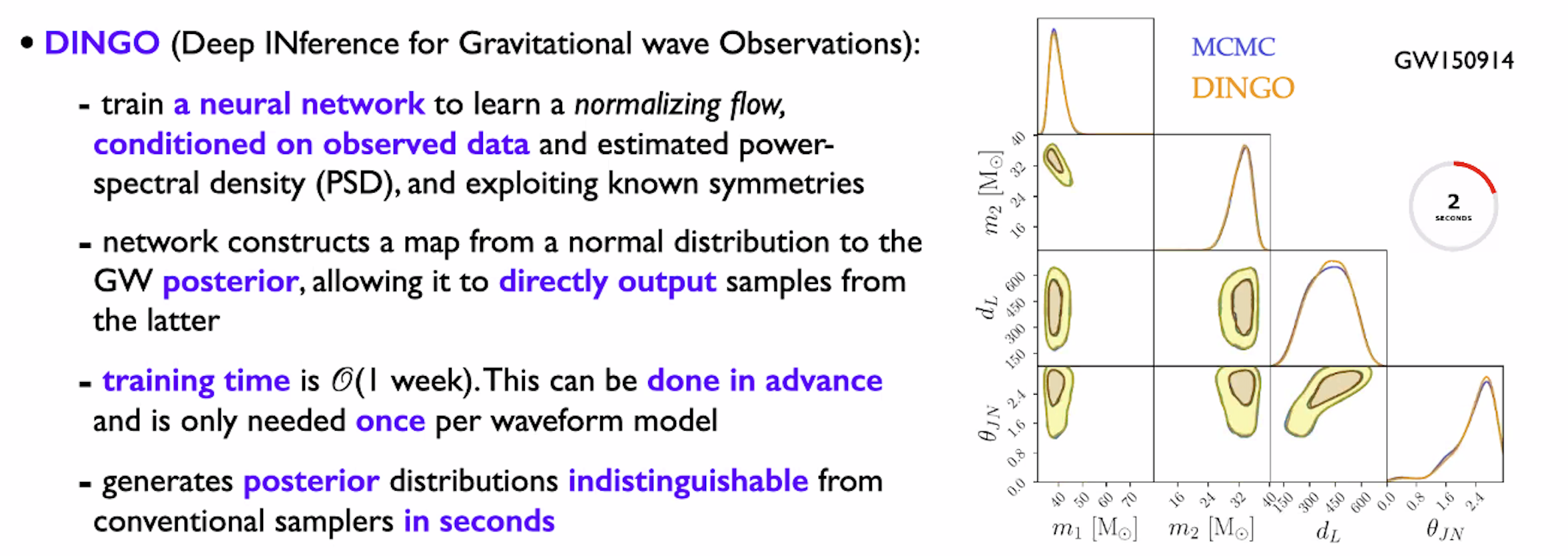
DINGO: A Leap Forward
- DINGO and related works represent the cutting edge in this field within the LIGO frequency band.
- Tested on 42 BBH events from GWTC-3
- Being deployed for O4, with the potential to become a new gravitational wave signal search pipeline
- Capable of calculating evidence
- Processing time: (using 64 CPU cores)
- less than 1 hour with IMRPhenomXPHM,
- approximately 10 hours with SEOBNRv4PHM
- Evidence for eccentricity in the population of BBH observed by LVK. (LIGO-G2400750, 2024 Mar)
-
進撃のnflow model in GW inference area.
-
2002.07656: 5D toy model [1] (PRD)
-
2008.03312: 15D binary black hole inference [1] (MLST)
-
2106.12594: Amortized inference and group-equivariant neural posterior estimation [2] (PRL)
-
2111.13139: Group-equivariant neural posterior estimation [2]
-
2210.05686: Importance sampling [2] (PRL)
-
2211.08801: Noise forecasting [2] (PRD)
-
[1]. https://github.com/stephengreen/lfi-gw (published @2020)
[2]. https://github.com/dingo-gw/dingo (published @2023.03)


目录

- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- Space-based GW Detection

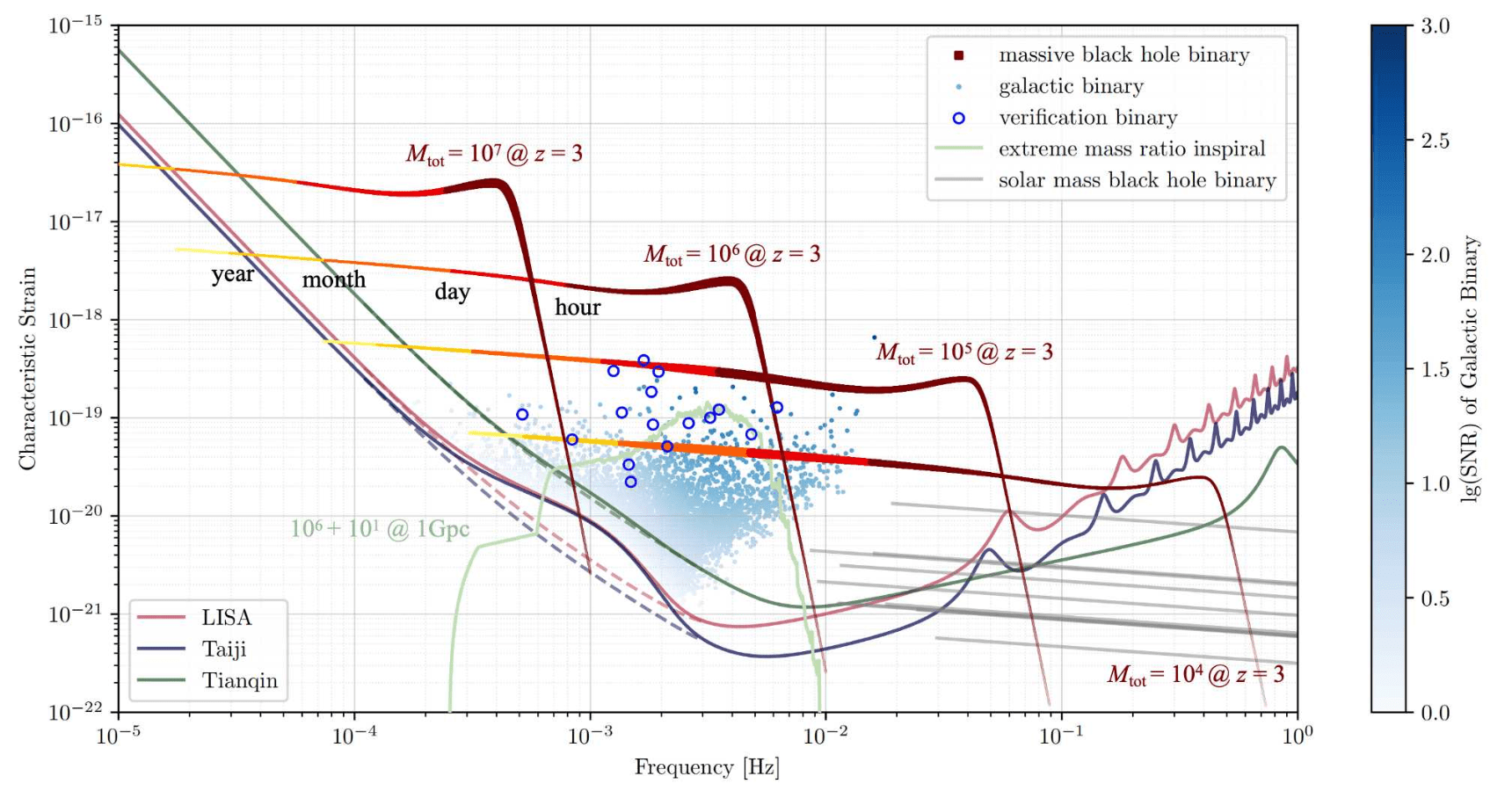
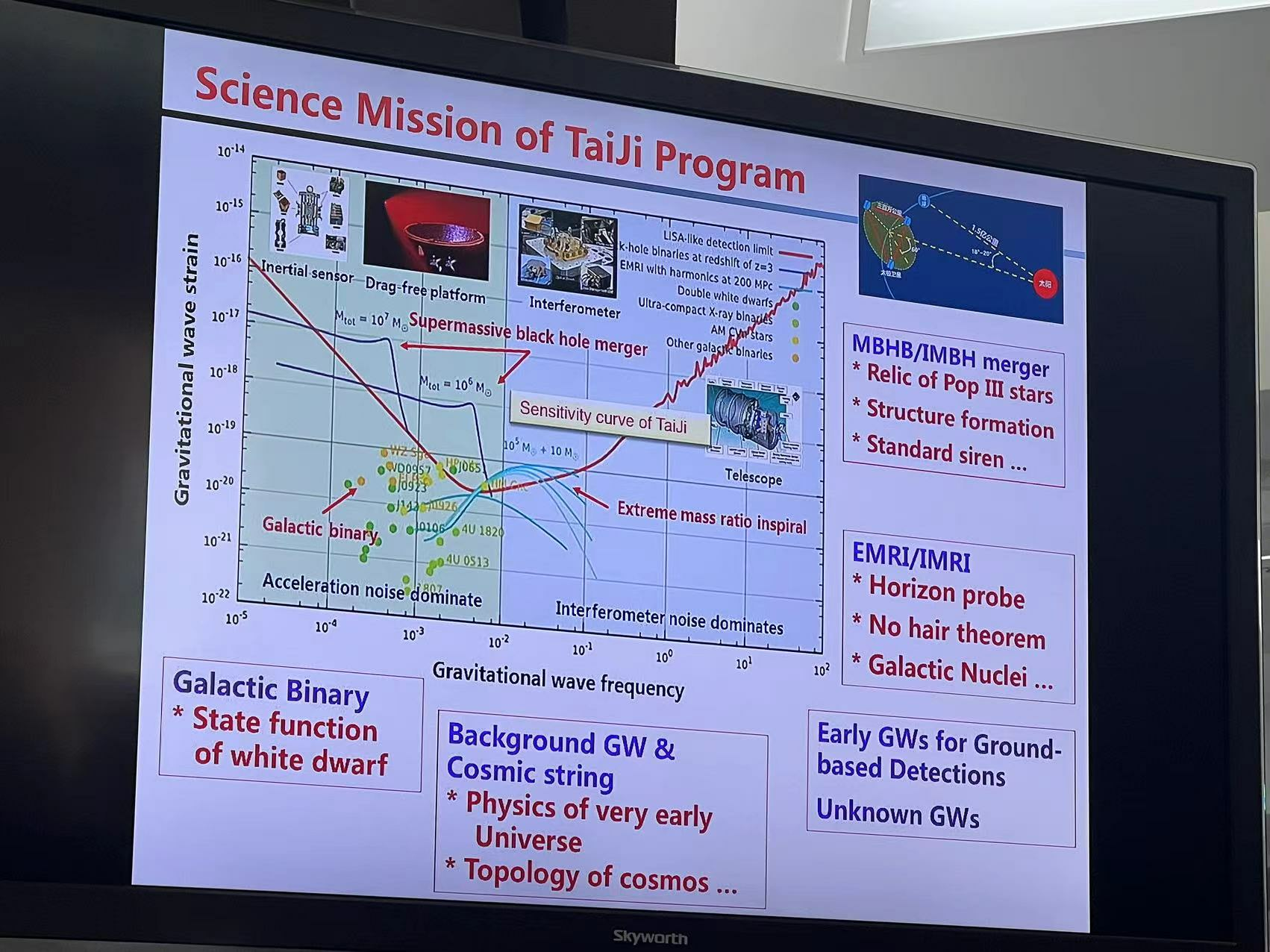
Gravitational waves and sources:
- Galactic Binary (GB) [\(\mathcal{O}(10^4) \text{ in } \mathcal{O}(10^7)\)]
- Massive Black Hole Binary (MBHB) [\(\mathcal{O}(2)\sim\mathcal{O}(10^2)\)]
- Extreme Mass-Ratio Inspiral (EMRI) [\(\mathcal{O}(10)\sim\mathcal{O}(10^3)\)]
- Stellar-mass Black Hole Binary (SBHB)
- Stochastic Gravitational Wave Background (SGWB)
- Unmodelled sources (eg: Burst...)
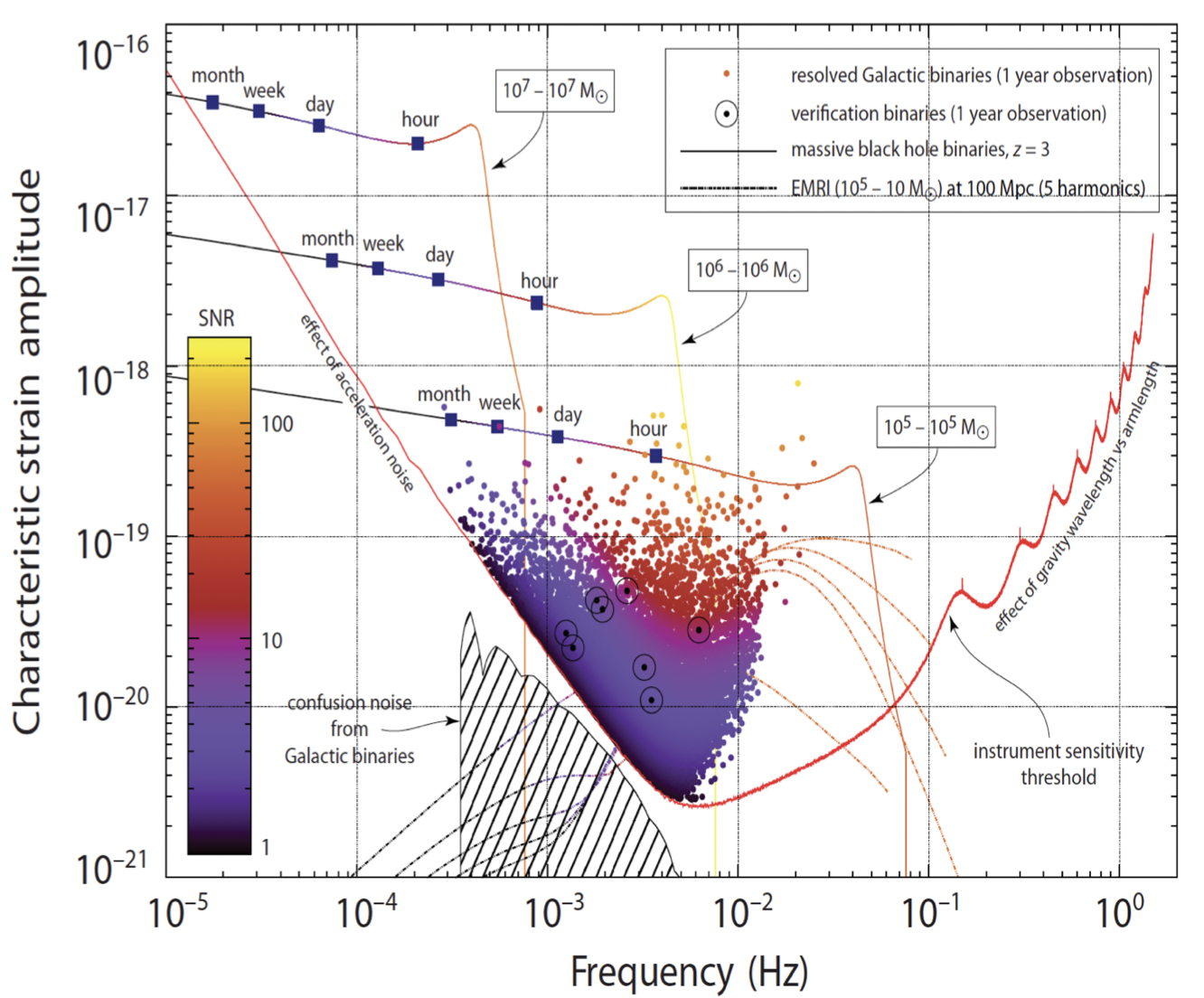
Credit: ESA, K. Holley-Bockelmann


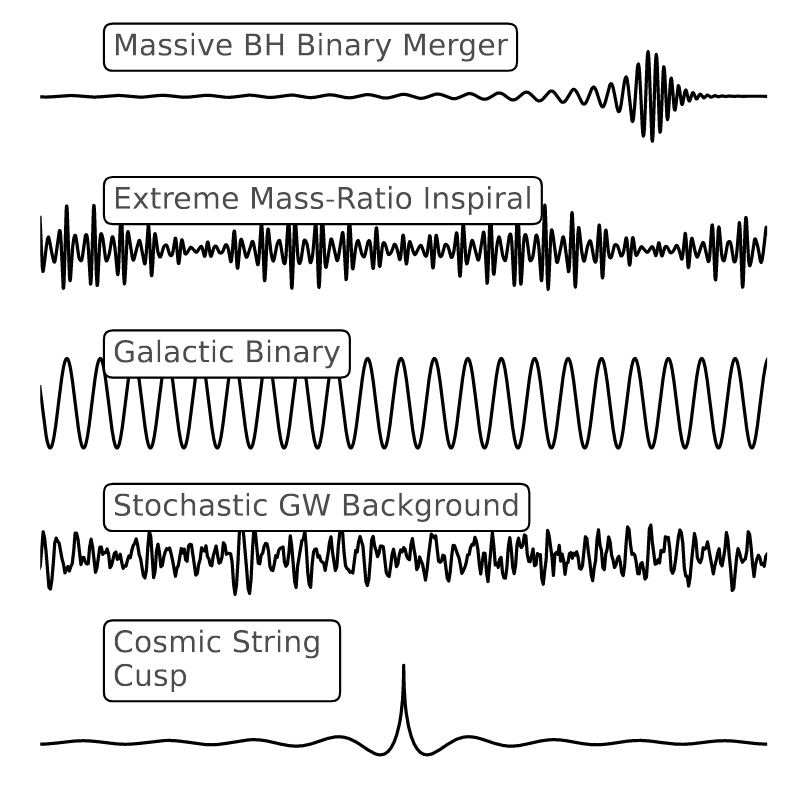
(Sec.8.3.1 The Red Book)
The analysis of scientific data from space-based GW detection differs significantly from ground-based detection:
- A superposition of overlapping signals ( \(\neq\) isolated event)
- Observations of more waveform periods over different time scales ( \(\neq\) short-duration signals)
- Signal-dominated detection ( \(\neq\) noise-dominated)
- Reliance on more complex techniques for noise assessment
( \(\neq\) regular acquisition of signal-free data)
Space-borne GW Detection: Background
空间引力波探测科学数据处理的挑战与人工智能技术的应用
王赫, 杜明辉, 徐鹏, 周宇峰
2024年, 第54卷, 第7期, 270403

Space-borne GW Detection: Background



Analyses cannot treat sources independently and sequentially work through a list of candidate detections.
- The data analyses depend on the simultaneous fitting of complete astrophysical, cosmological, and instrument models to the observed data.
- The need for this so-called “global fit” was identified as the primary challenge to the data analysis early in the space-borne mission formulation.
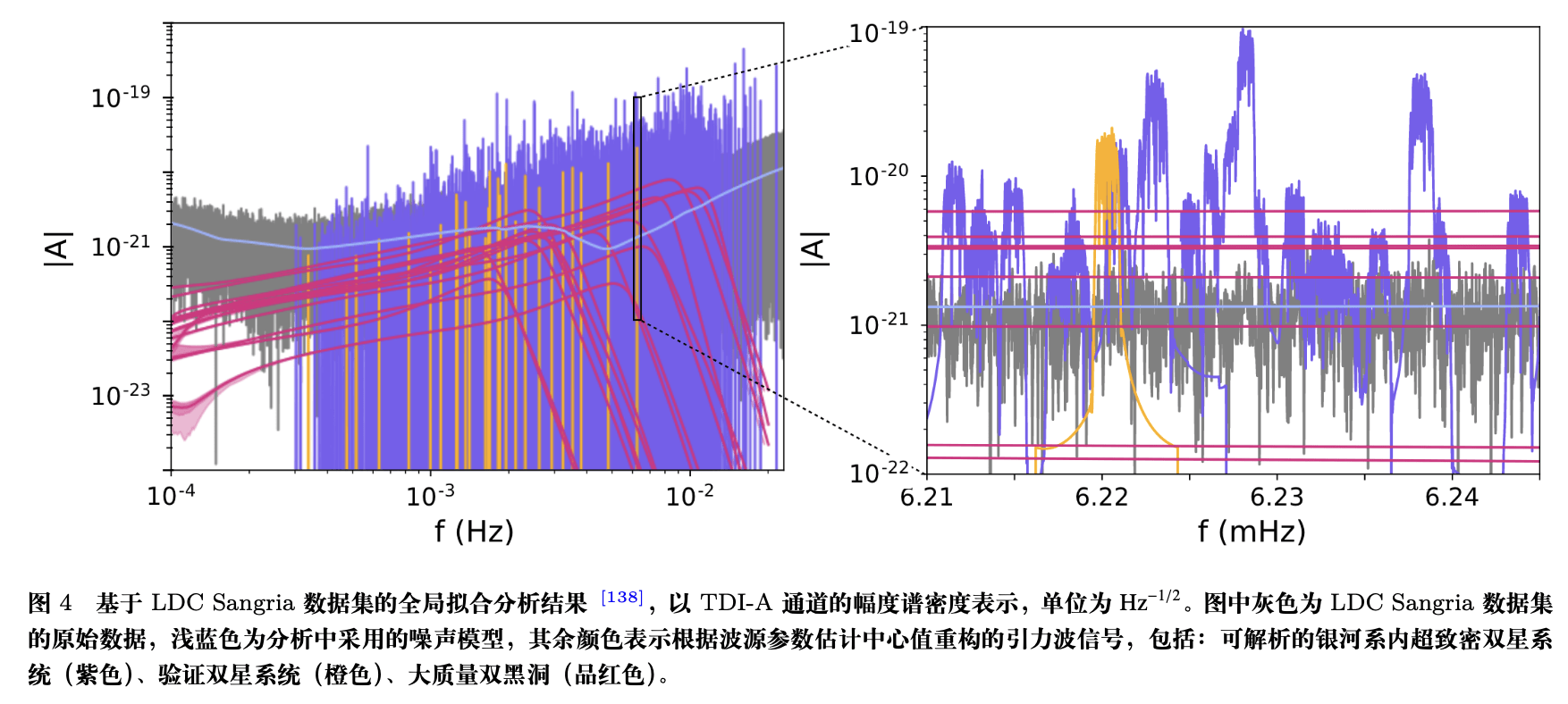
(Sec.8.6 The Red Book)
Global Fit
- The idea of the global fit method is to comprehensively model all astrophysical and instrumental features present in the space-borne gravitational wave data.
Technical challenges:
- High dimensional
- Highly correlated
- Multimodality
- Trans-dimensional
Text
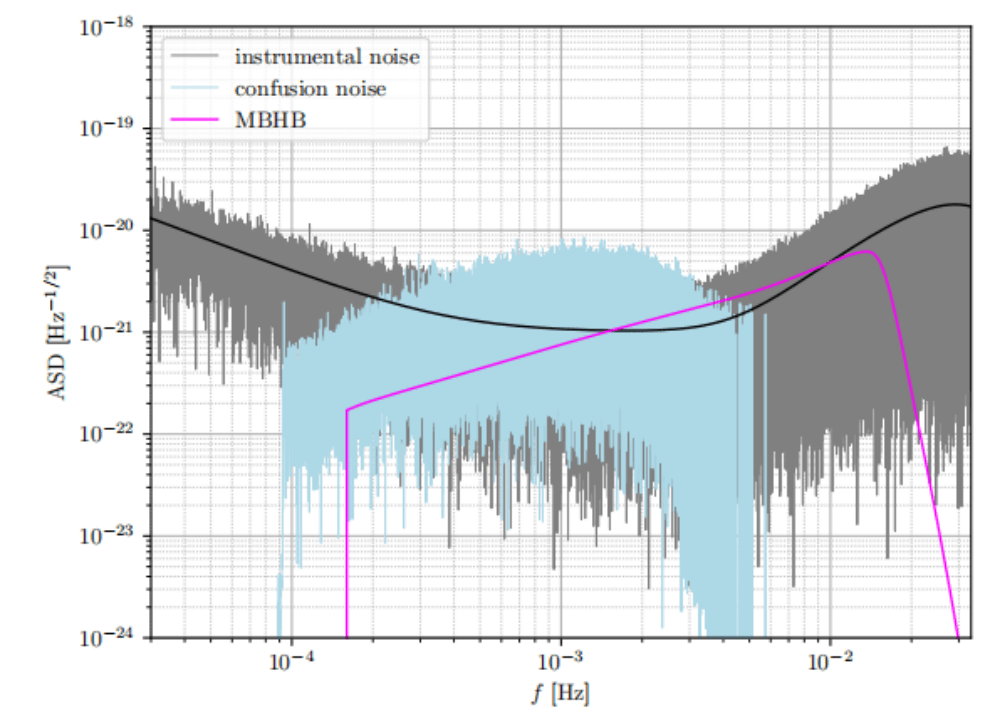
Rapid PE for Space-borne GW Detection

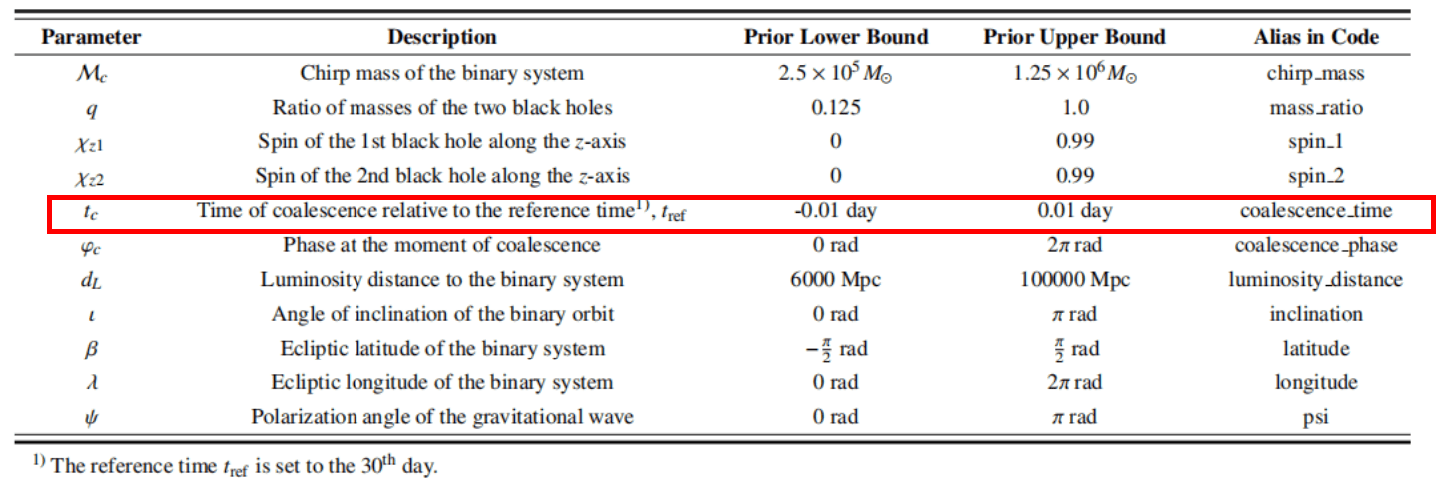
M. Du, B. Liang, HW, P. Xu, Z. Luo, Y. Wu. SCPMA 67, 230412 (2024).
-
Global vs. Individual Analysis: While global-fit techniques effectively manage the dense overlapping of signals in space-based GW data, individual pipelines are crucial for detecting unique events.
-
Role of Individual Pipelines: These pipelines act as a pre-processing step, focusing on particular types of sources and diving deeper into the data. They refine the analysis by working on the latest best-fit residuals from the global fit.
-
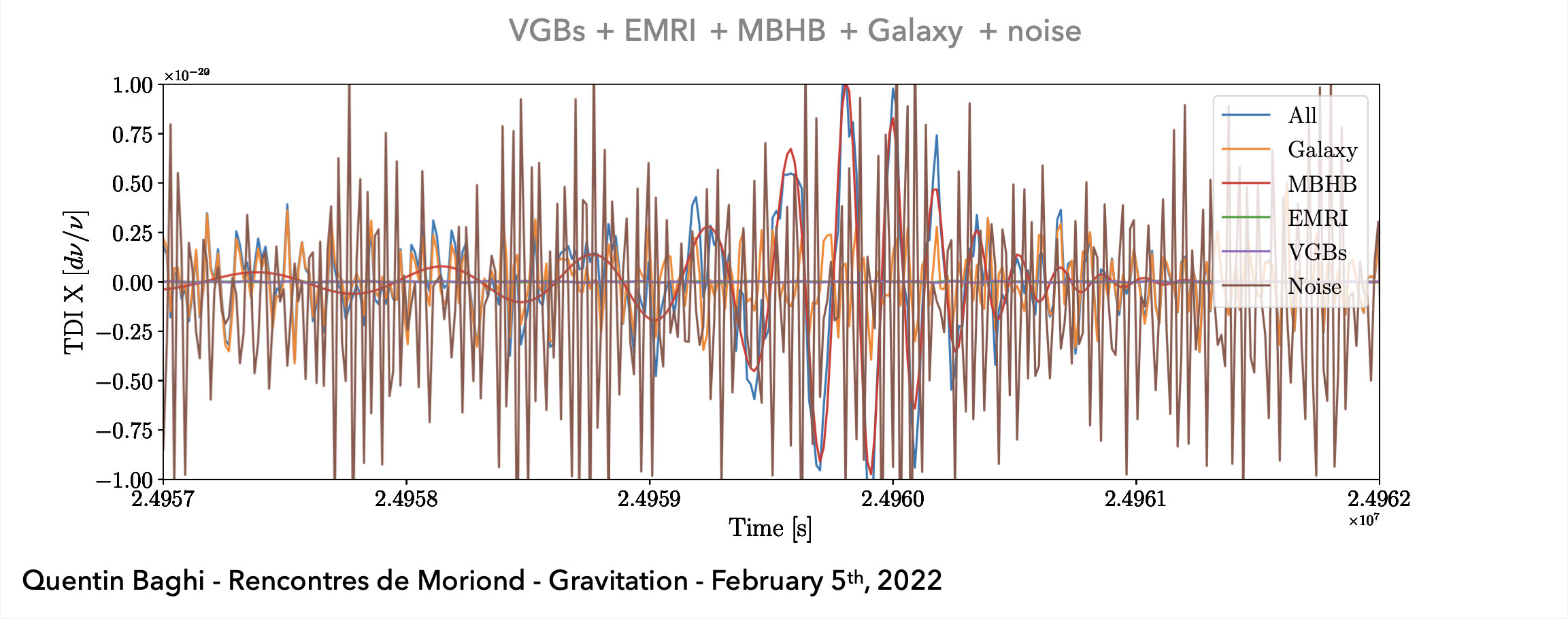
Case Study - MBHB Mergers: Mergers of MBHBs often exhibit high SNR between \(10^2\) to \(10^3\), appearing as distinct peaks in data time series.

-
Data curation
-
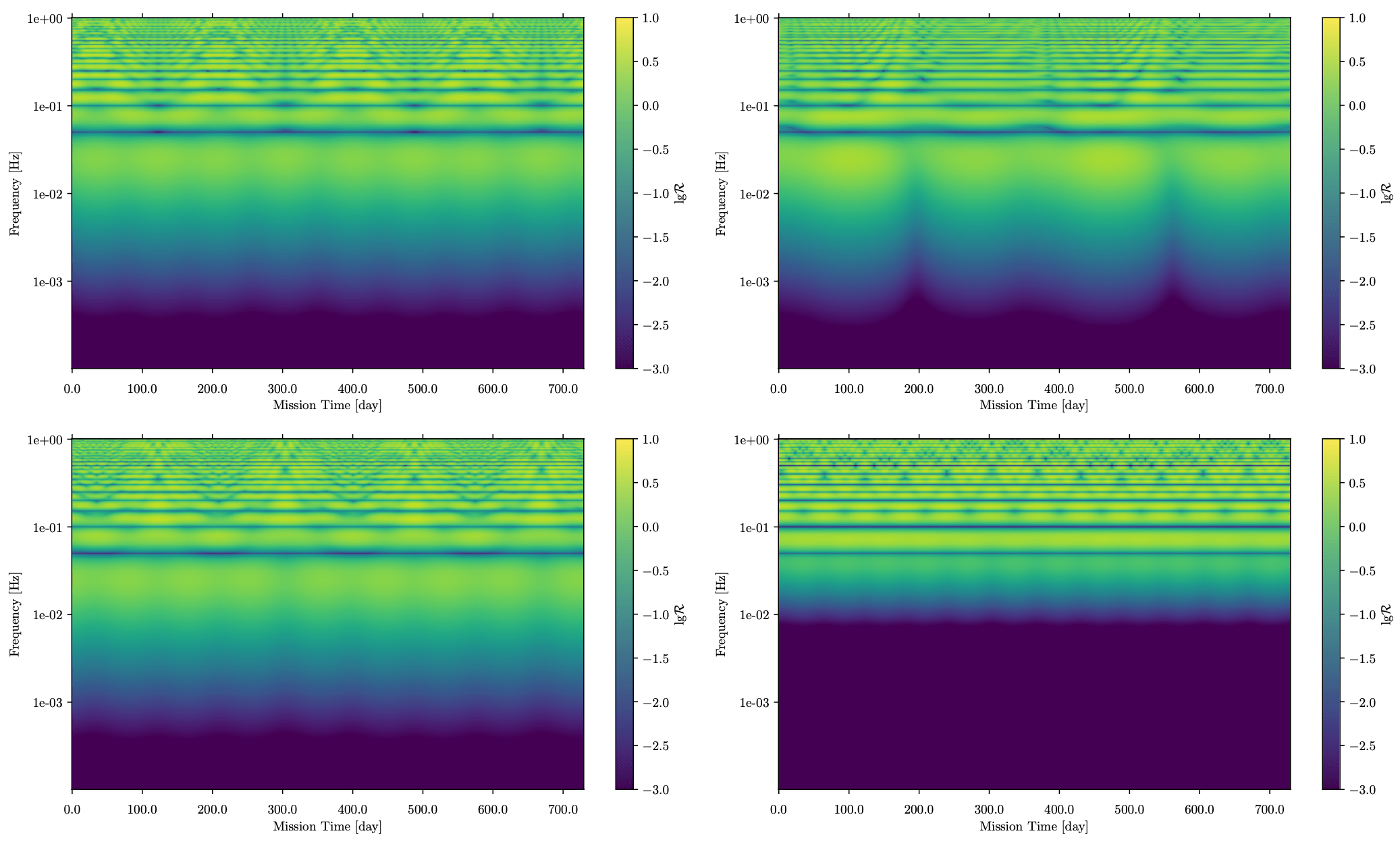
Model: frequency domain; PhenomD; TDI-A/E response
-
Input: 1 day length; 15Hz; shape=(2, 3, 2877)
-
Noise: Gaussian stationary from the noise PSD (for training/test) + GB confusion noise (for test)
-
Project: Taiji program
-
M. Du, B. Liang, HW, P. Xu, Z. Luo, Y. Wu. SCPMA 67, 230412 (2024).
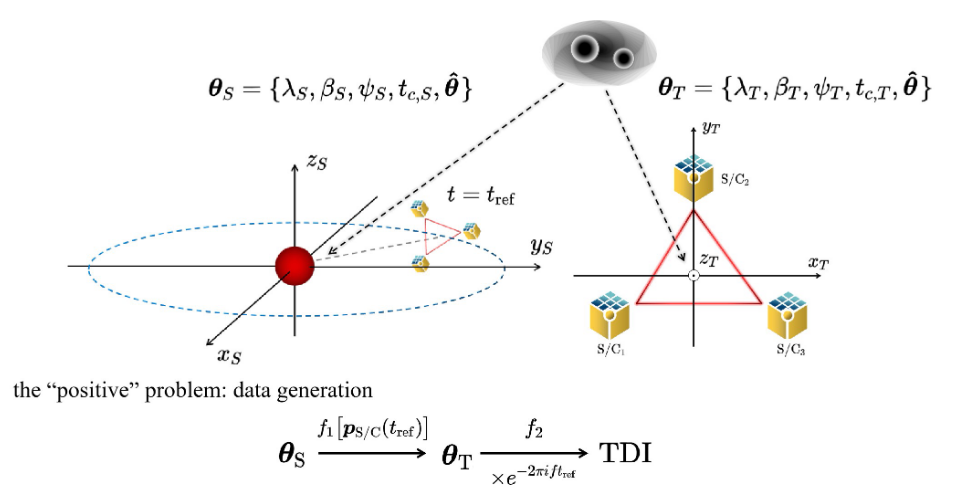
Customization for the Taiji scenario: A scalable approach

-
The top section of the illustration shows the solar system barycenter (SSB) and Taiji frames, with two black dashed arrows symbolizing not two separate GW signals, but rather indicating how the sky location and arrival time of the same GW signal take different values in these two frames.
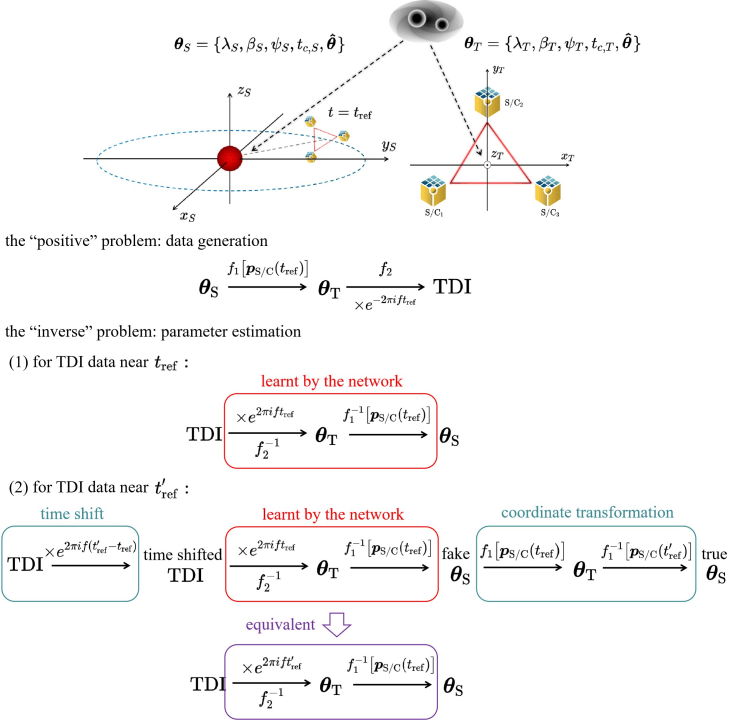

-
The “positive” problem translates the SSB-frame parameters to their Taiji-frame counterparts via a time-dependent mapping \(f_1\), then to the TDI outputs through a time-independent mapping \(f_2\), and an exponential term.
TDI-A
-
These steps can be schematically summarized as:
where \(\mathcal{T}_\alpha^{A, E}(f)\) is often referred to as the transfer function.
M. Du, B. Liang, HW, P. Xu, Z. Luo, Y. Wu. SCPMA 67, 230412 (2024).
Customization for the Taiji scenario: A scalable approach



-
Consequently, even if the network has only learned the time-dependent relationship between \(\boldsymbol{\theta}_S\) and the TDI response at a specific tref (the 30th day in our case), with the aid of coordinate transformation, it has essentially learned the time-invariant mapping \(f_2\), and can be then generalized to make parameter estimation at any other reference time.
-
It is worth noting that our method relies on analytical orbits and
the time-independence of the coordinate transformation \(f_2\).
-
The top section of the illustration shows the solar system barycenter (SSB) and Taiji frames, with two black dashed arrows symbolizing not two separate GW signals, but rather indicating how the sky location and arrival time of the same GW signal take different values in these two frames.
-
The “positive” problem translates the SSB-frame parameters to their Taiji-frame counterparts via a time-dependent mapping \(f_1\), then to the TDI outputs through a time-independent mapping \(f_2\), and an exponential term.
1 year length
can infer at any other reference time
trained on the 30th day only
M. Du, B. Liang, HW*, P. Xu, Z. Luo, Y. Wu*. SCPMA 67, 230412 (2024).
Unbiased estimation and confidence validation

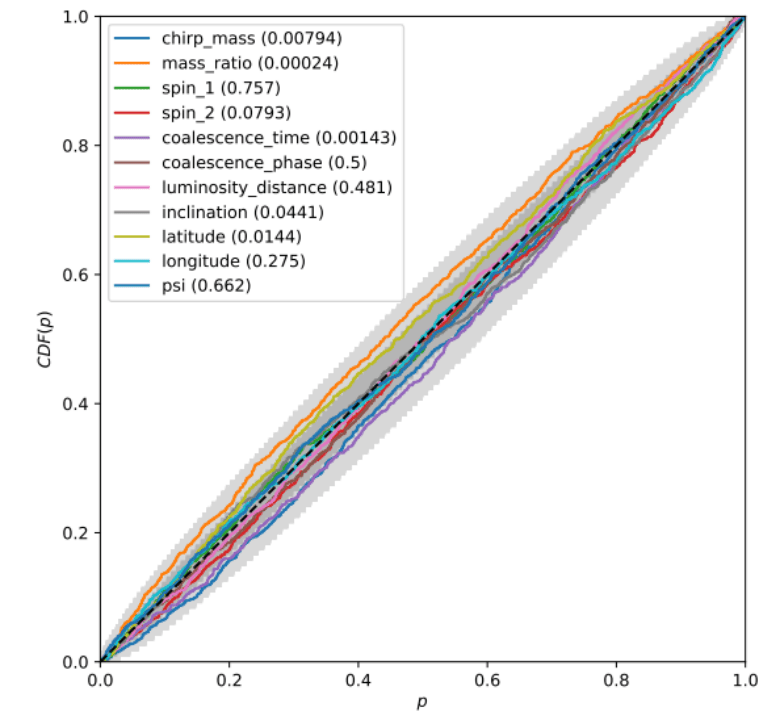
-
Methodology: Utilization of the Kolmogorov-Smirnov (KS) test to compare one-dimensional distributions generated by our algorithms, ensuring the accuracy of parameter estimation.
-
Empirical Validation: Conducted extensive testing on simulated signals, injecting 1000 waveforms from the prior with added confusion noise and varying reference times between 1 and 365 days.
-
Results: The tests assessed the frequency at which true parameters fell within certain confidence levels, confirming that our credible intervals are well-calibrated and reflect true confidence in the signal parameters.

Computational performance
-
10000 posterior samples in 2.7 sec
- The remarkable speed of our method, which outpaces traditional techniques by several orders of magnitude, establishes it as an invaluable tool for preprocessing in global fitting.

M. Du, B. Liang, HW, P. Xu, Z. Luo, Y. Wu. SCPMA 67, 230412 (2024).
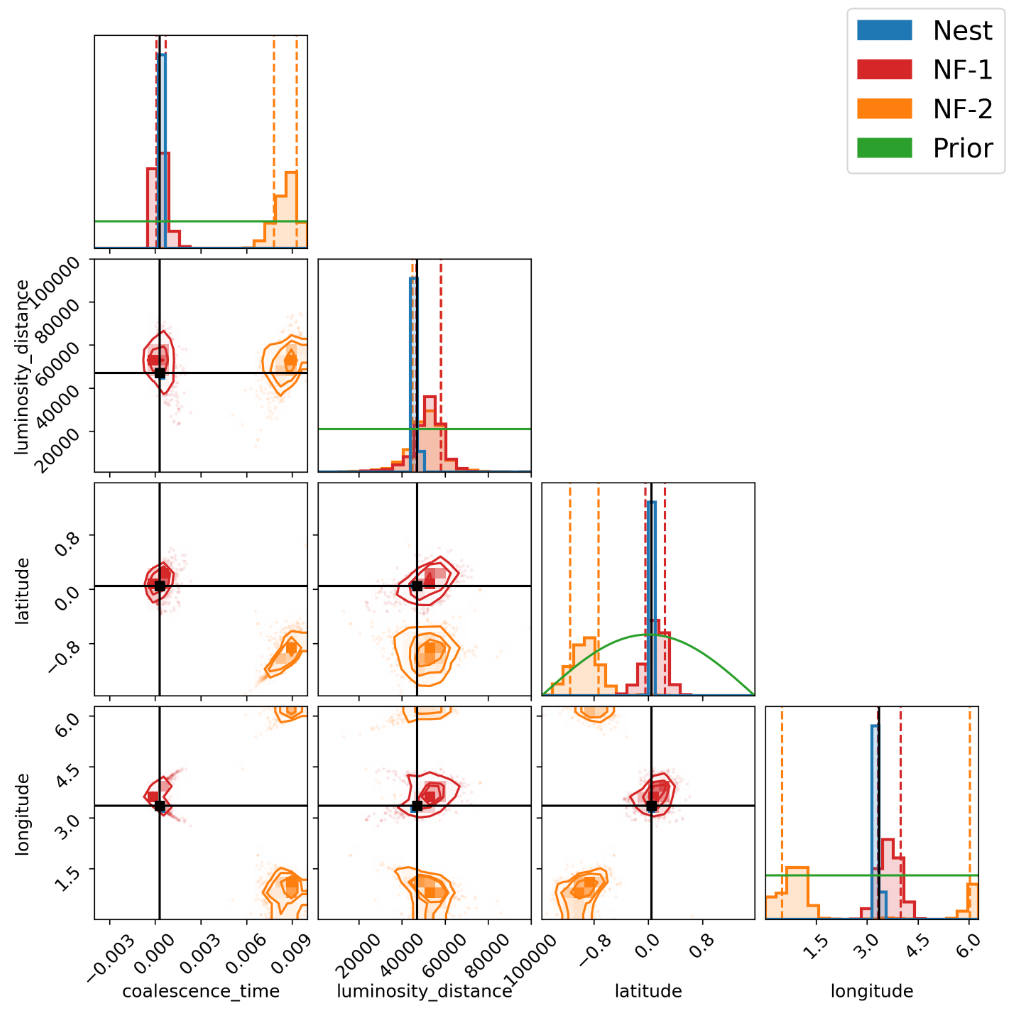
Multimodality in extrinsic parameters

-
Overview of Findings: Nested sampling results indicate minimal expected multimodality in ecliptic coordinates. However, distinct peaks identified in the time of coalescence (\(t_c\)), labeled as NF-1 (dominant) and NF-2 (subdominant), highlight unique multimodal behavior.
- Impact on PE: The presence of these peaks affects the posterior distributions of extrinsic parameters, potentially leading to inaccuracies in \(t_c\) and subsequent parameters due to phase term associations and inherent degeneracies.
- Model Performance: Despite the multimodality, the best-fit values from the NF model closely align with true values within the \(1\sigma\) range for most parameters, and at least \(2\sigma\) for others.
- Comparative Analysis: The ML pipeline tends to produce broader posteriors compared to the Bayesian nested sampling approach.
(NF = Normalizing Flow model)
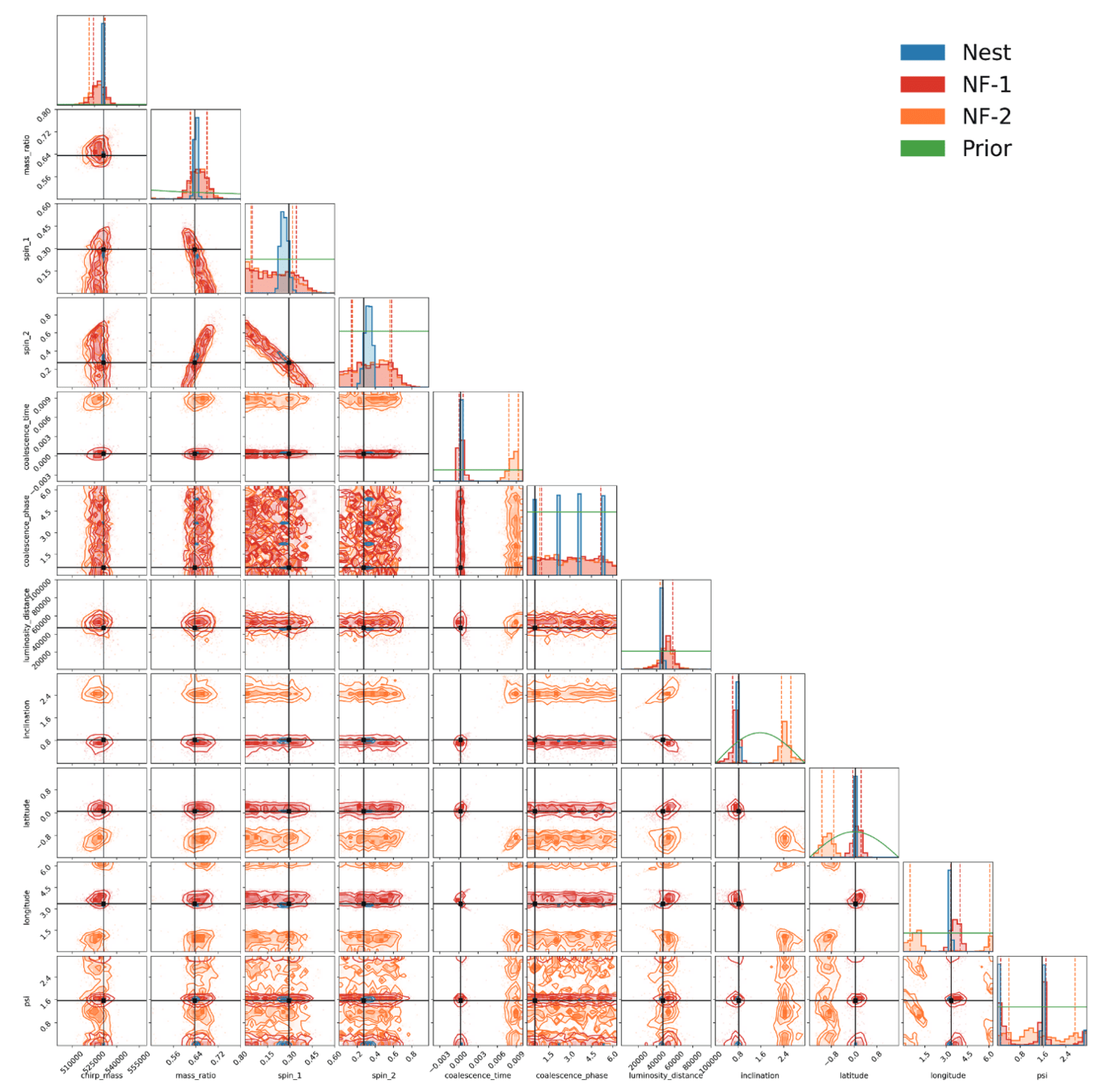
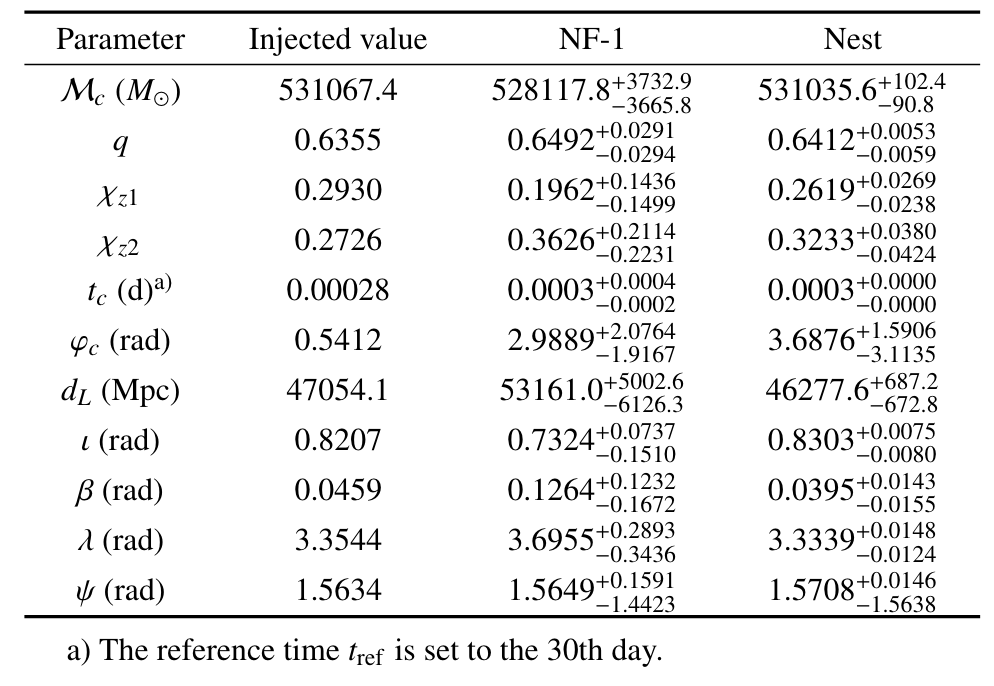

M. Du, B. Liang, HW, P. Xu, Z. Luo, Y. Wu. SCPMA 67, 230412 (2024).
目录

- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- Space-based GW Detection
- Ongoing & Future Plan

Ongoing & Future Plan

Earth-based GW detection (\(\sim10^2\)Hz)
- A Python Toolbox for Gravitational Wave Astronomy: GWToolkit
- This toolbox is powered by Ray/JAX and supports both CPU and GPU. It is designed specifically for machine learning applications.
- Gravitational-Wave Observatory Open Source Data Portal
(基于引力波探测开源数据的共享数据门户) - Can AI identify new GW events from LIGO data?
- Could this be a GW signal beyond General Relativity (GR)?
-
How can we address the issue of strong or unacceptable biases that occur when outputs from AI models are used jointly or in combination to measure properties of a population, sub-population, or ensemble?
(also addressed by 2405.18095)
Text


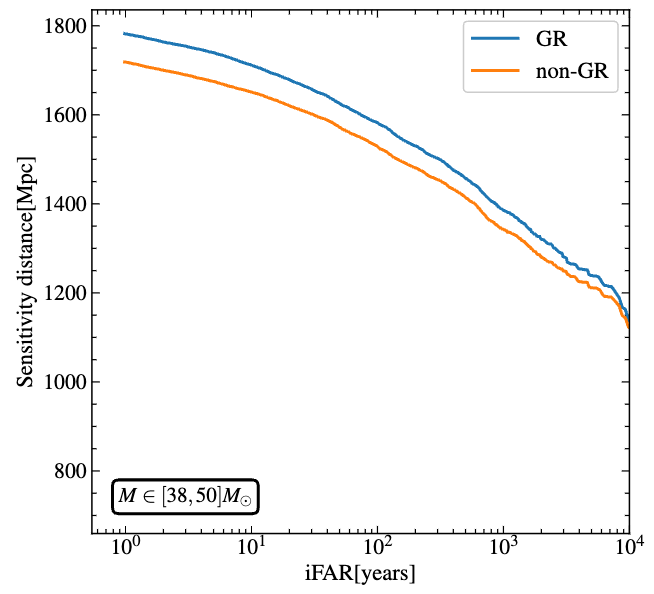
Space-based GW detection (\(\sim10^{-3}\)Hz)
- “Global fit” challenge
- How can we achieve and accelerate the Bayesian inference through algorithmic innovations?
- Flow-based proposal?
- Transdimensional Nested Sampling?
- How can we leverage powerful LLM-based methods to accomplish this?
- How can we achieve and accelerate the Bayesian inference through algorithmic innovations?
Text


中国科学院计算机网络信息中心“东方”超级计算系统 (全国产CPU/GPGPU)






for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')Ongoing and Future Plan

Earth-based GW detection
- A Python Toolbox for Gravitational Wave Astronomy: GWToolkit
- This toolbox is powered by Ray/JAX and supports both CPU and GPU. It is designed specifically for machine learning applications.
- Can AI identify new GW events from LIGO data?
- Could this be a GW signal beyond General Relativity (GR)?
- How can we address the issue of strong or unacceptable biases that occur when outputs from AI models are used jointly or in combination to measure properties of a population, sub-population, or ensemble?
(also addressed by 2405.18095)
Text



Space-based GW detection
- “Global fit” challenge
- How can we achieve and accelerate the Bayesian inference through algorithmic innovations?
- Flow-based proposal?
- Transdimensional Nested Sampling?
- How can we leverage powerful LLM-based methods to accomplish this?
- How can we achieve and accelerate the Bayesian inference through algorithmic innovations?
Text




This silde: https://slides.com/iphysresearch/2024Aug_ihep
Bouns


Text
Calibration Analysis on Denoised / Residual Data
-
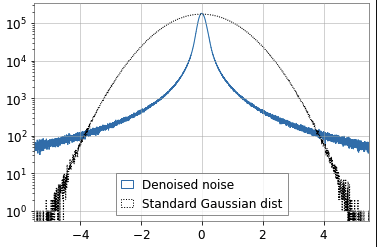
Denoised data
- Non-Gaussian and non-stationary.
- The SNR is evidently high, but it cannot be utilized for parameter estimation. Because:
- Background noise is also non-Gaussian.
- Assessing the unbiasedness of the posterior distribution will be very challenging.
- Is it possible to calibrate or validate the denoised data simultaneously while training the denoiser?
-
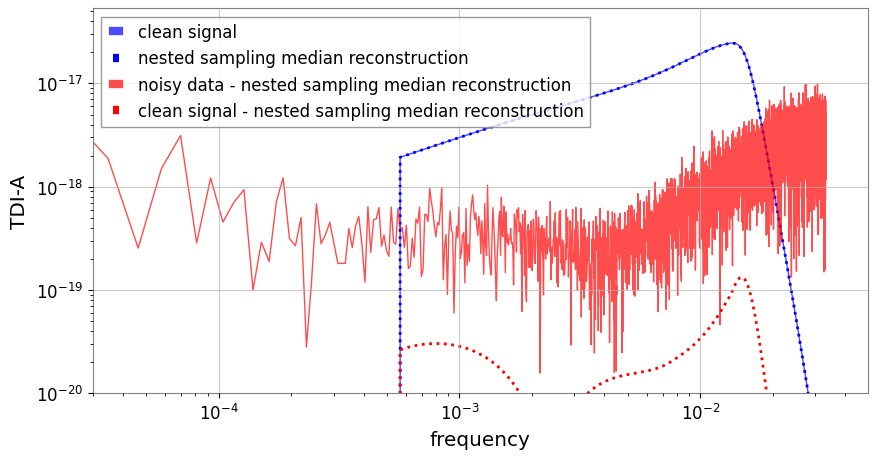
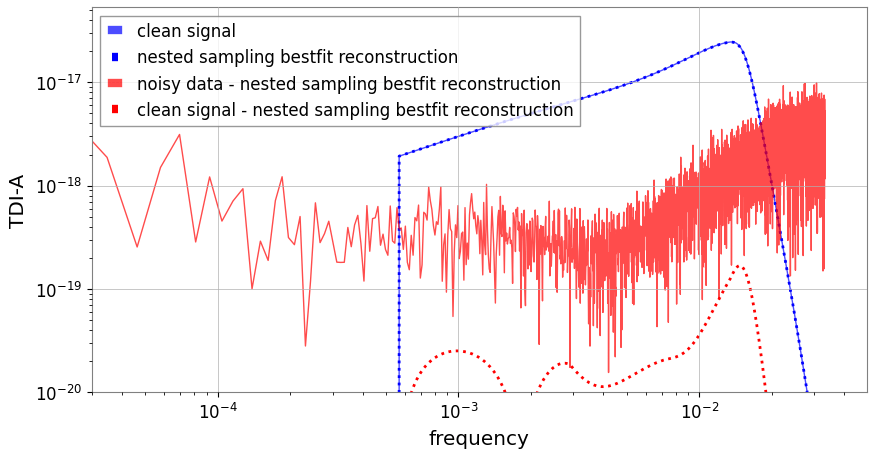
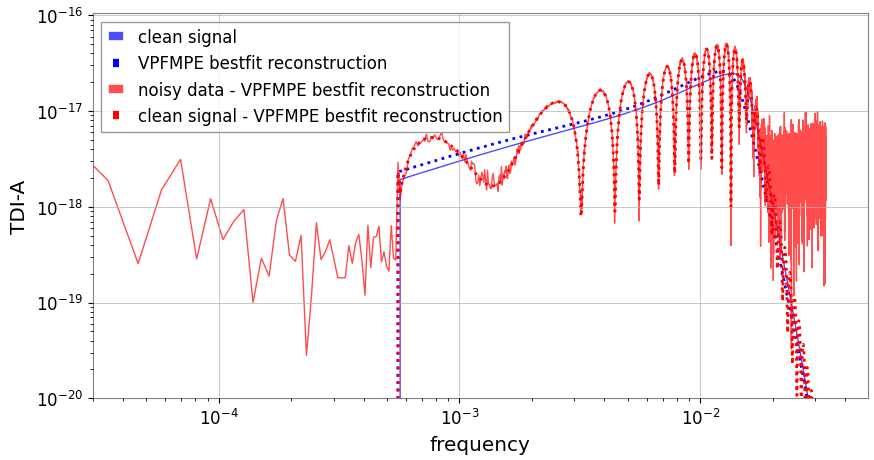
Residual Data (“Global-fit” challenge for LISA)
- Iteratively using exact waveforms is not practical in terms of timeliness, while using approximate waveforms inevitably introduces systematic errors in the residual data during each iteration.
- Is it possible to calibrate the residual data simultaneously during each iteration of the statistical inference?

He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046
M. Du, B. Liang, HW*, P. Xu, Z. Luo, Y. Wu*. SCPMA 67, 230412 (2024).
Key Takeaways & Look Forwards

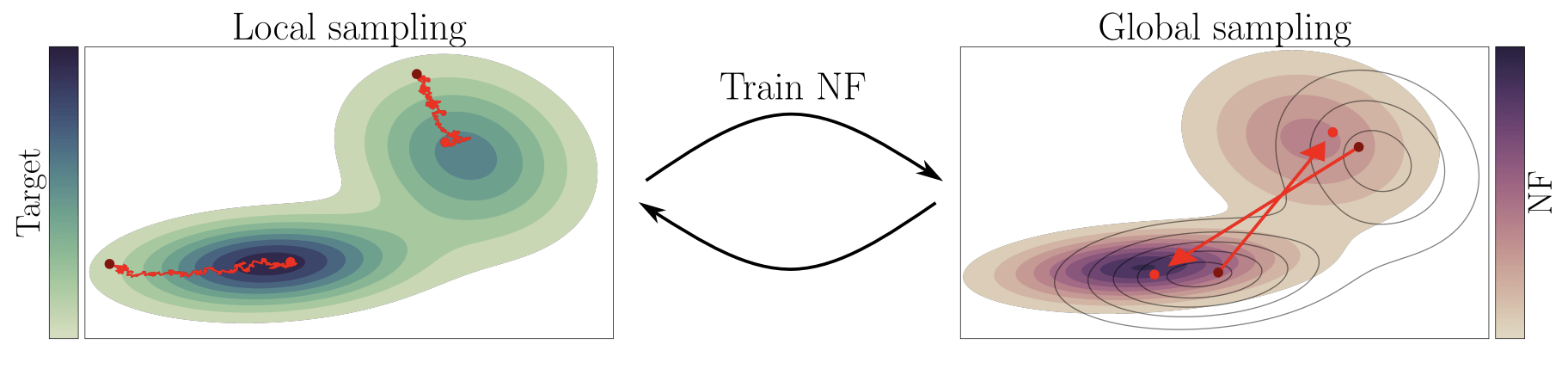
Ongoing and Future Projects
Neural density estimation
- Density fit for posterior distributions
- use the old posterior to form a proposal for the extended data.
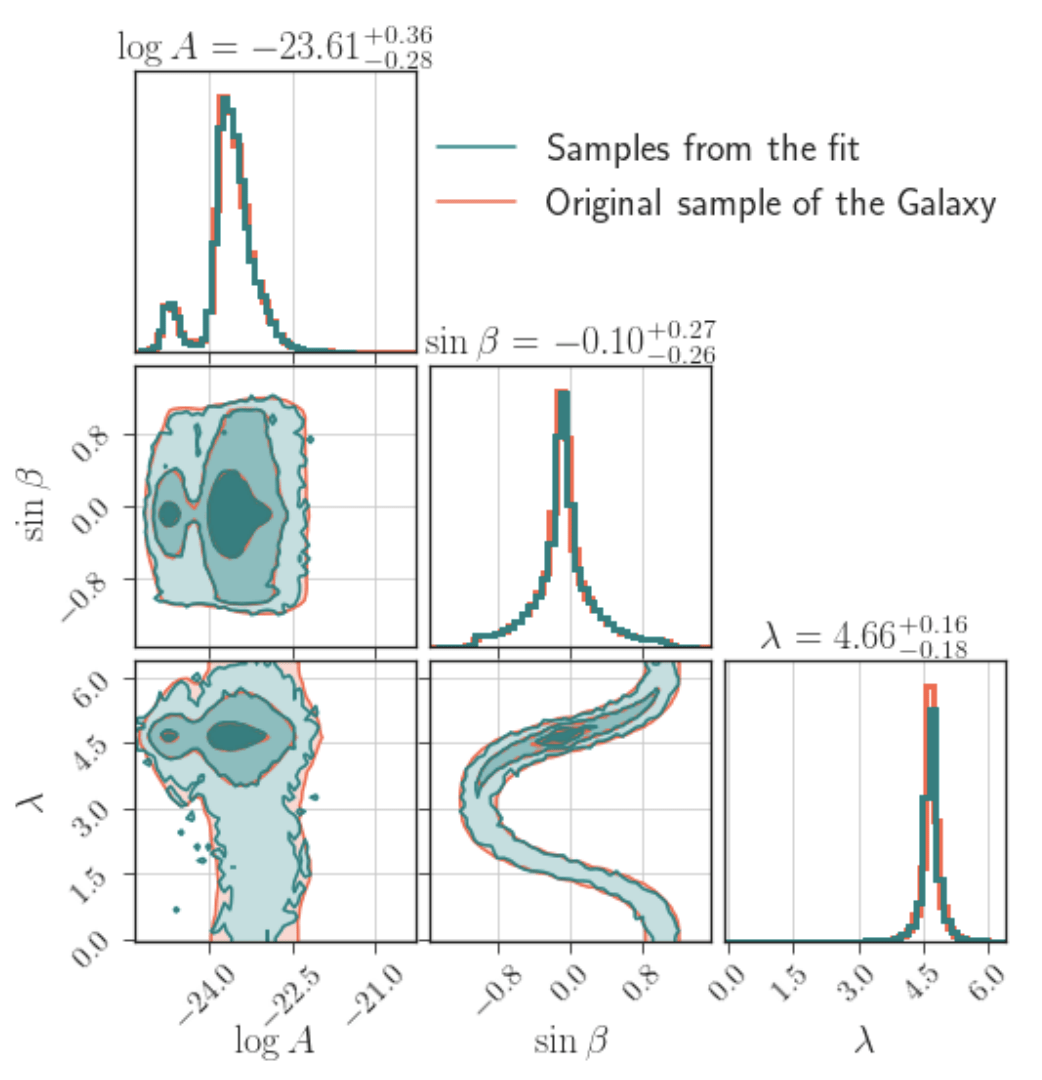
- Density fit for the Galaxy
- fitt a Galaxy model for joint distribution for \((A, \beta, \lambda)\).
- ...
Text


Ref:
- Ashton, G, and C Talbot. MNRAS 507, no. 2 (2021): 2037–51.
- Korsakova, N, et al. (2402.13701)
- Wouters, T, et al. (2404.11397)
Ongoing and Future Projects
Neural density estimation
- Density fit for posterior distributions
- use the old posterior to form a proposal for the extended data.
- Density fit for the Galaxy
- fitt a Galaxy model for joint distribution for \((A, \beta, \lambda)\).
- ...
Text

nflow

目录

- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
- Space-based GW Detection
- Ongoing & Future Plan
- 引力波数据分析之知识框架(GWDA Knowledge Framework)

Key Takeaways

“国际理论物理中心(亚太地区)” 经联合国教科文组织第38届大会审议通过。由中国科学院、基金委和国际理论物理中心共同建设,是进行基础科学前沿与相关交叉科学领域高水平科研、教育和培训的非营利性组织,是联合国教科文组织基础科学方面的在国内的第一个二类中心。







空间引力波探测计划
引力波天文学 & 引力波多信使天文学
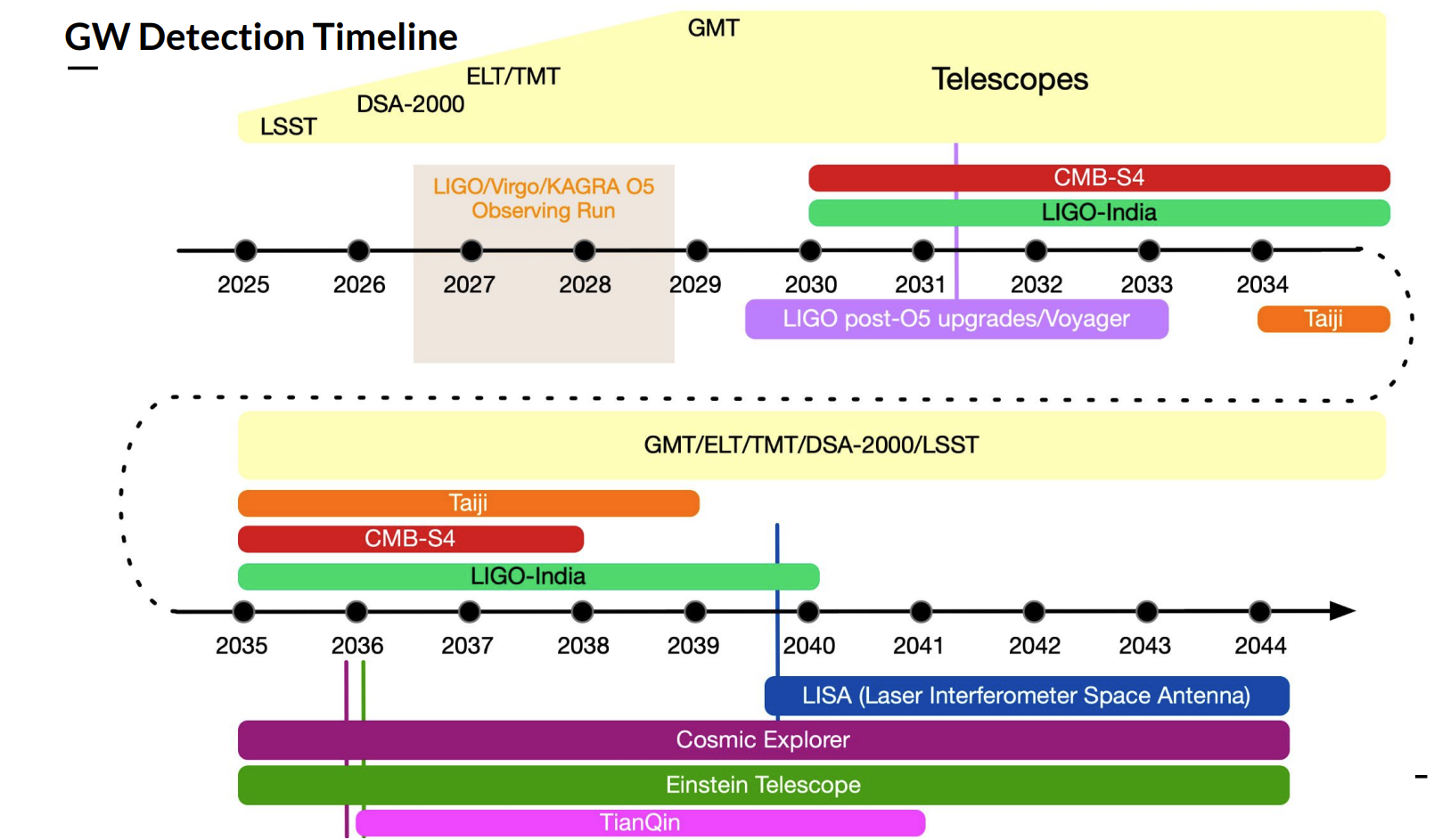
- 目前,国内外正在计划进行各种引力波探测项目,包括利用宇宙微波背景辐射的B模极化的CMB-S4、LiteBIRD、BICEP3/Keck Array、AliCPT;利用脉冲星定时阵列的NANOGrav、EPTA、PPTA、CPTA;利用空间引力波星间激光干涉仪的LISA、太极计划、天琴计划等;以及用于地面引力波干涉仪的ET、BBO。最近,NANOGrav、EPTA和CPTA共同宣布了存在纳赫兹级随机引力波背景的强有力证据。
Chinese Journal of Space Science, 2023, 43(4): 589-599.
LIGO-G2300554

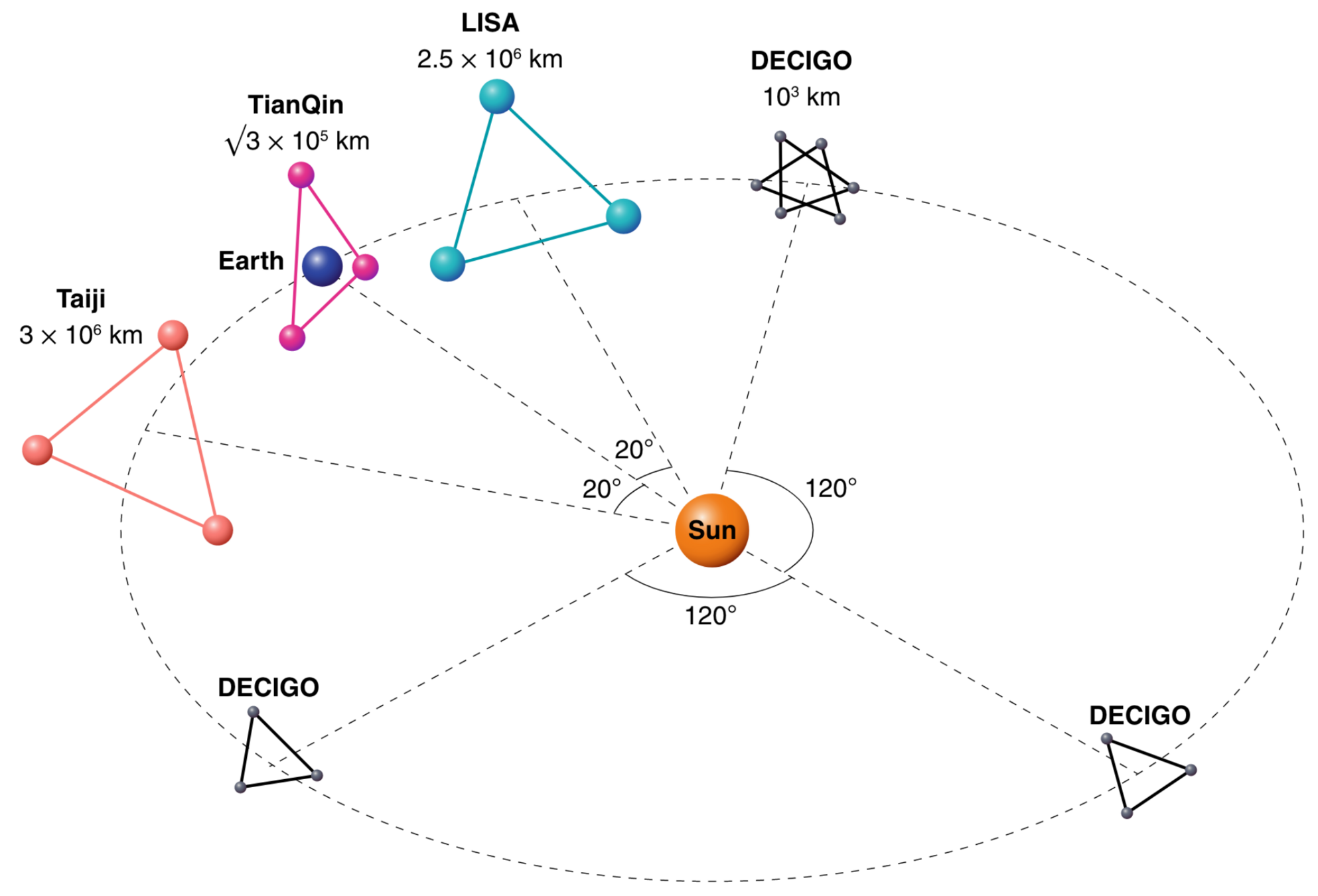
Nat. Astron. 2021, 5(9): 881-889.
Text


空基引力波探测科学数据的分析与地基相比差距很大:
- 大量的混叠波源 ( \(\neq\) 孤立事件)
- 在不同时间尺度上观测到更大的波形周期 ( \(\neq\) 短时信号)
- 信号主导的探测 ( \(\neq\) 噪声主导)
- 依赖更复杂的技术评估噪声 ( \(\neq\) 定期获取无信号数据)
空间引力波观测频段内含有大量的波源和多种波源类型:
- \(10^4\) 可探测的银河系内致密双星绕转 (UCB, VGB)
- \(10\sim10^2\) 超大质量黑洞双星合并 (SMBH)
- \(10\sim10^3\) 极端质量比黑洞双星绕转 (EMRI)
- 恒星级质量黑洞双星的绕转 (SOBH)
- 随机引力波背景 (SGWB)
- 未建模的波源事件 (Burst...)

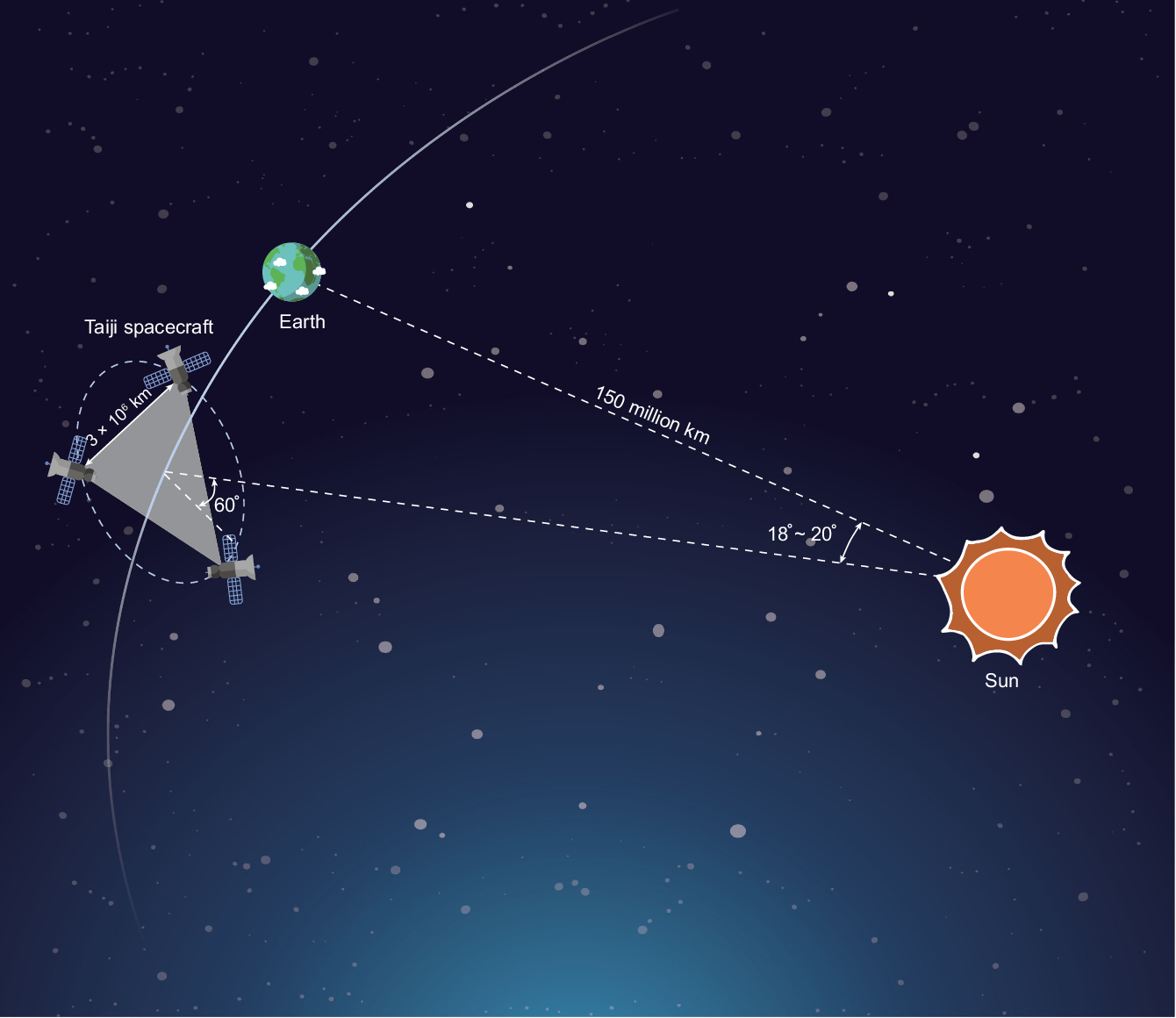
空间太极计划
- 空间引力波探测主要有以下 4 类波源:
-
恒星级质量的致密双星 (黑洞、中子星、白矮星以及它们的两两组合) 的旋近
-
双白矮星的并合、超大质量双黑洞的并合
-
极端质量比旋进 (通常是一个恒星级致密天体绕着一个超大质量黑洞的旋进)
-
宇宙中可能存在的中等质量双黑洞以及前面这些源的信号叠加形成的引力波背景
-

Credit: ESA, K. Holley-Bockelmann
Text
Text

空间引力波探测的典型波源与全局拟合问题

天琴计划

空基引力波探测科学数据的分析与地基相比差距很大:
- 大量的混叠波源 ( \(\neq\) 孤立事件)
- 在不同时间尺度上观测到更大的波形周期 ( \(\neq\) 短时信号)
- 信号主导的探测 ( \(\neq\) 噪声主导)
- 依赖更复杂的技术评估噪声 ( \(\neq\) 定期获取无信号数据)
空间引力波观测频段内含有大量的波源和多种波源类型:
- \(10^4\) 可探测的银河系内致密双星绕转 (UCB, VGB)
- \(10\sim10^2\) 超大质量黑洞双星合并 (SMBH)
- \(10\sim10^3\) 极端质量比黑洞双星绕转 (EMRI)
- 恒星级质量黑洞双星的绕转 (SOBH)
- 随机引力波背景 (SGWB)
- 未建模的波源事件 (Burst...)
Text
Text
空间引力波探测科学数据处理:典型波源


天琴计划

Credit: ESA, K. Holley-Bockelmann

Credit: Minghui Du

空间太极计划


(Sec.8.3.1 Red Book)


空间引力波探测获得的是什么样的 (科学) 数据?
- 来自几十个激光干涉仪的分数频率偏差 (相对多普勒频移)
- 预计天线重新定位 (9天) 和激光重新锁定 (几周) 会导致短时间 (<小时) 的间隔,而类似LPF的意外长时间间隔 (∼天) 经常被考虑在内,总占空比约80-90%。 (日心轨道)
- 主要受激光噪声的影响
- 经过预处理后,得到3个时间延迟干涉 (TDI) 数据流 (X, Y, Z)
- ...


Text
Analyses cannot treat sources independently and sequentially work through a list of candidate detections.
空间引力波探测科学数据处理:数据挑战



空间引力波探测获得的是什么样的 (科学) 数据?
- 来自几十个激光干涉仪的分数频率偏差 (相对多普勒频移)
- 预计天线重新定位 (9天) 和激光重新锁定 (几周) 会导致短时间 (<小时) 的间隔,而类似LPF的意外长时间间隔 (∼天) 经常被考虑在内,总占空比约80-90%。 (日心轨道)
- 主要受激光噪声的影响
- 经过预处理后,得到3个时间延迟干涉 (TDI) 数据流 (X, Y, Z)
- ...
其他重要的科学数据处理的技术挑战:
-
随机噪声(Stochastic noise)
-
仪器瞬变(glitches)
-
频谱线(Spectral lines)
-
数据间断(Data gaps)
-
非平稳性(Non-stationarities)
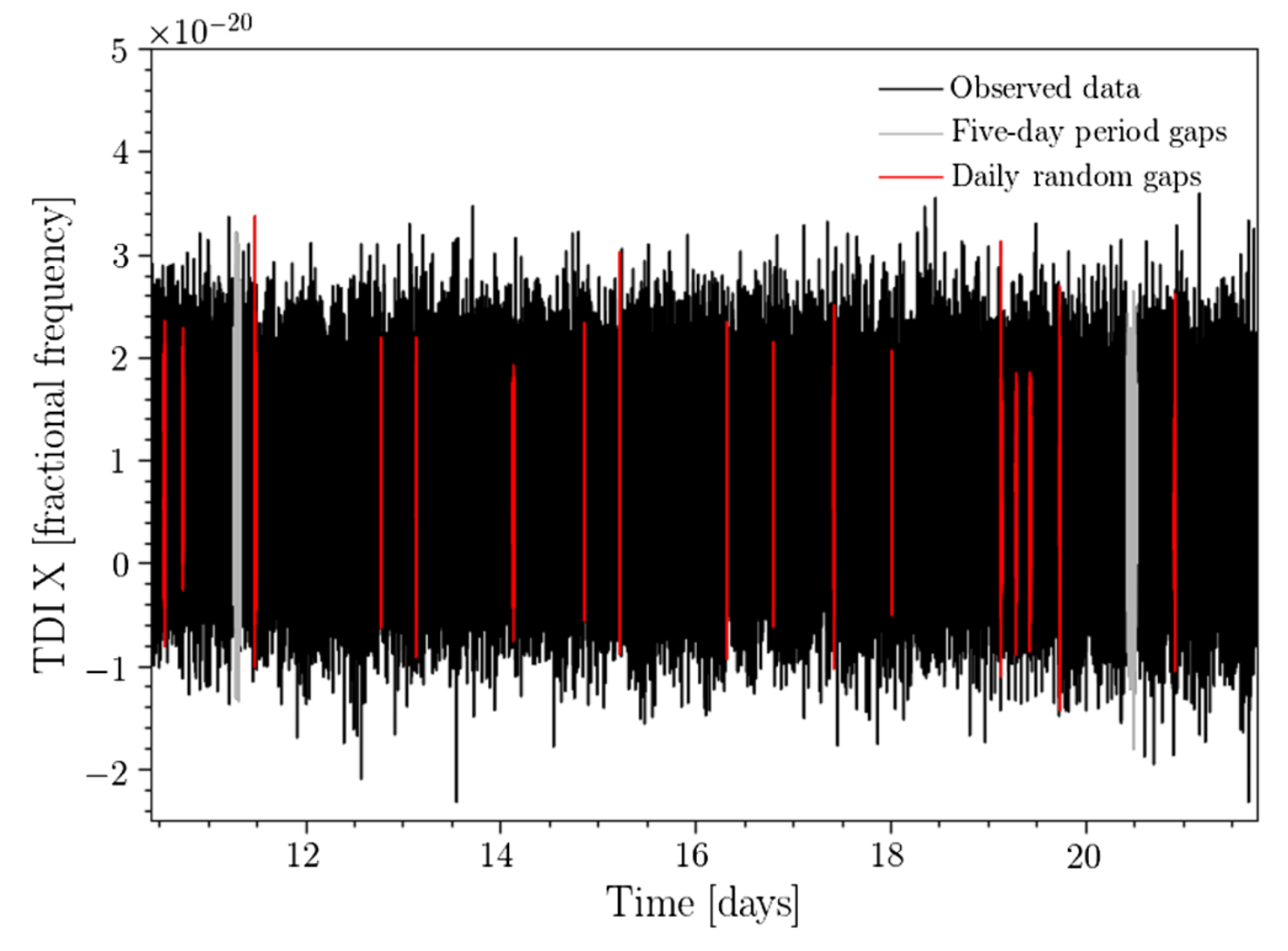
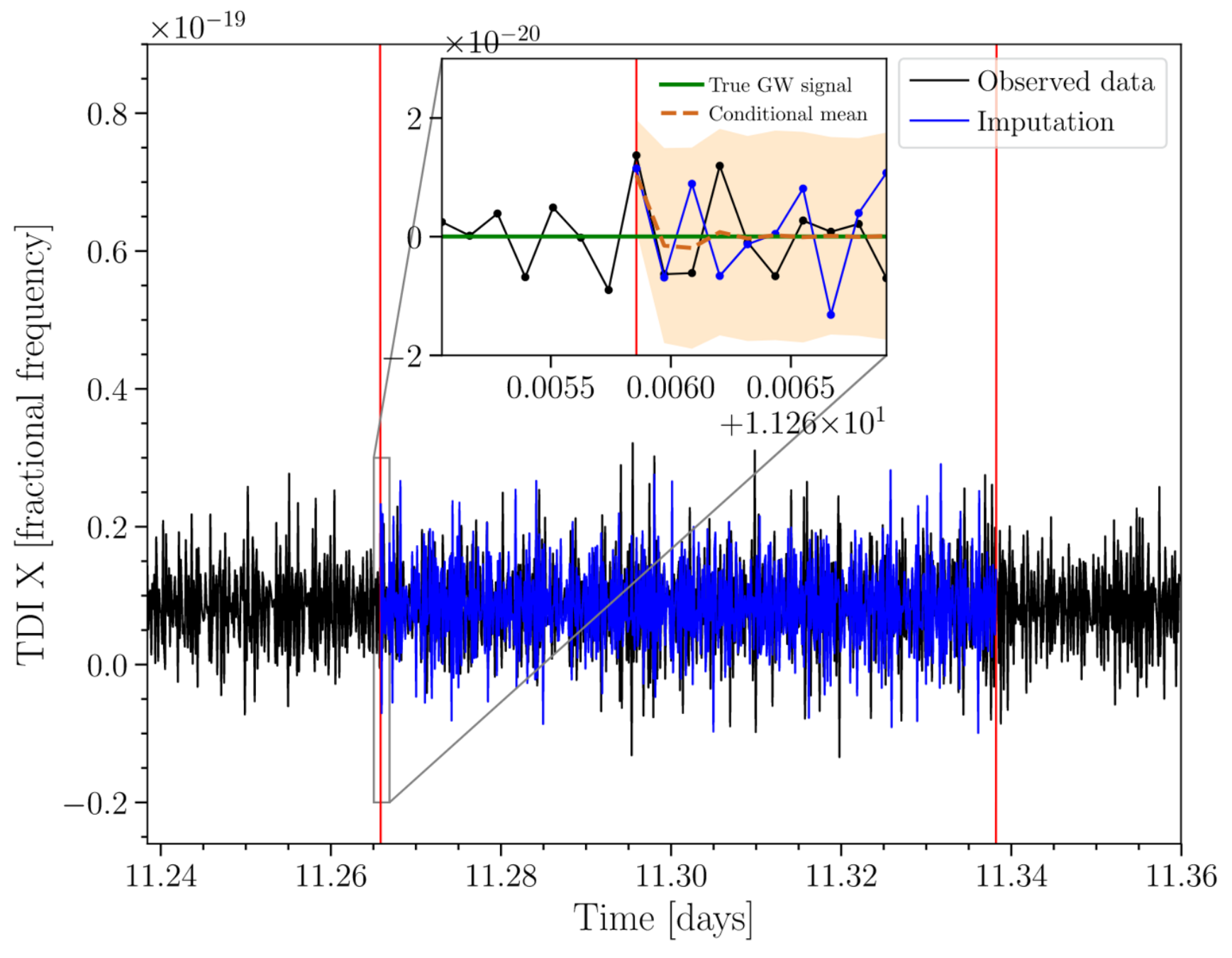
Baghi et al., Phys. Rev. D (2019)


Text
Text

空间引力波探测的典型波源与全局拟合问题
Analyses cannot treat sources independently and sequentially work through a list of candidate detections.

Mock Data Challenges
Text
空间引力波探测科学数据处理:数据挑战

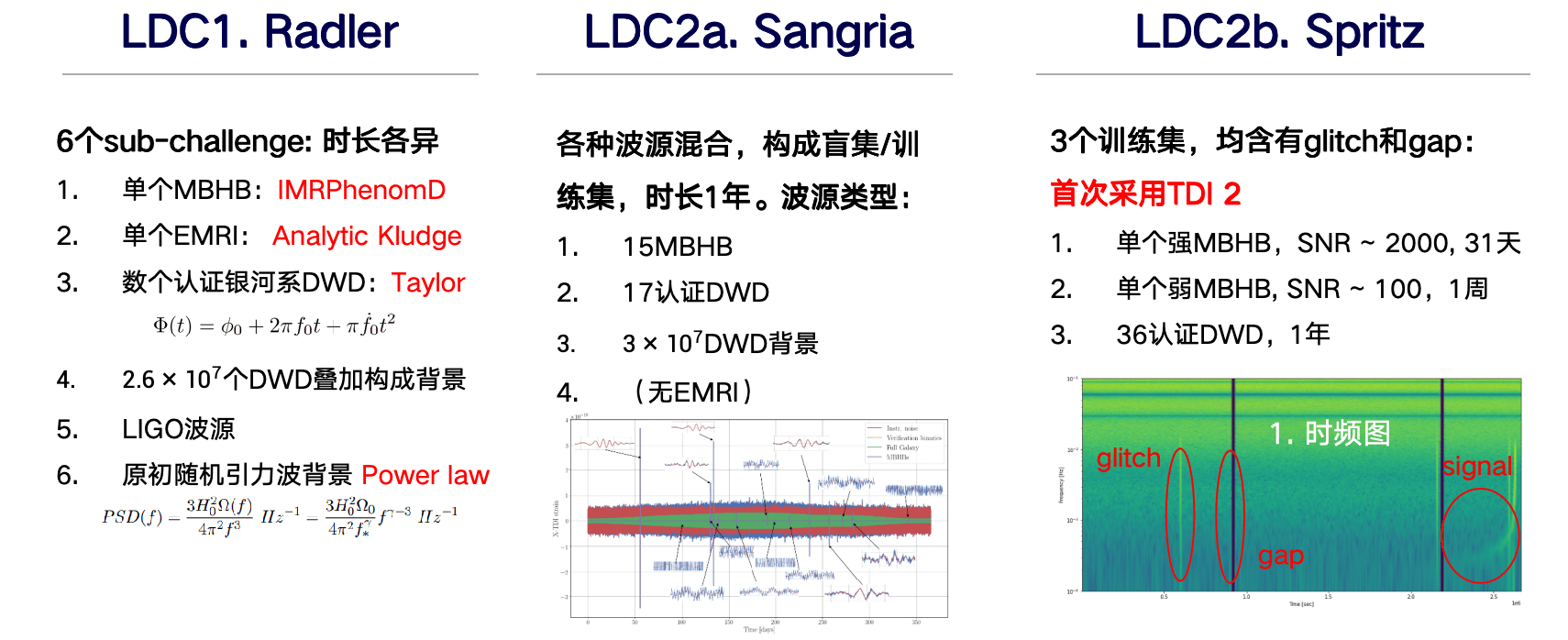
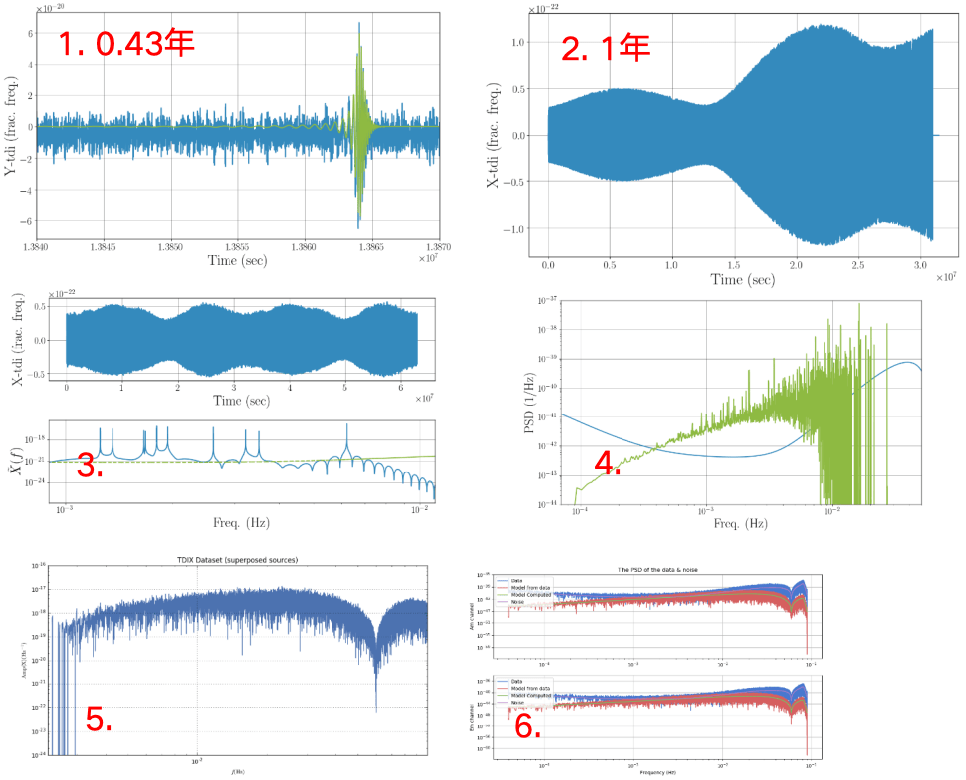


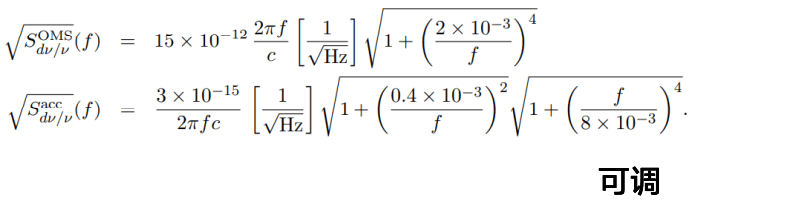

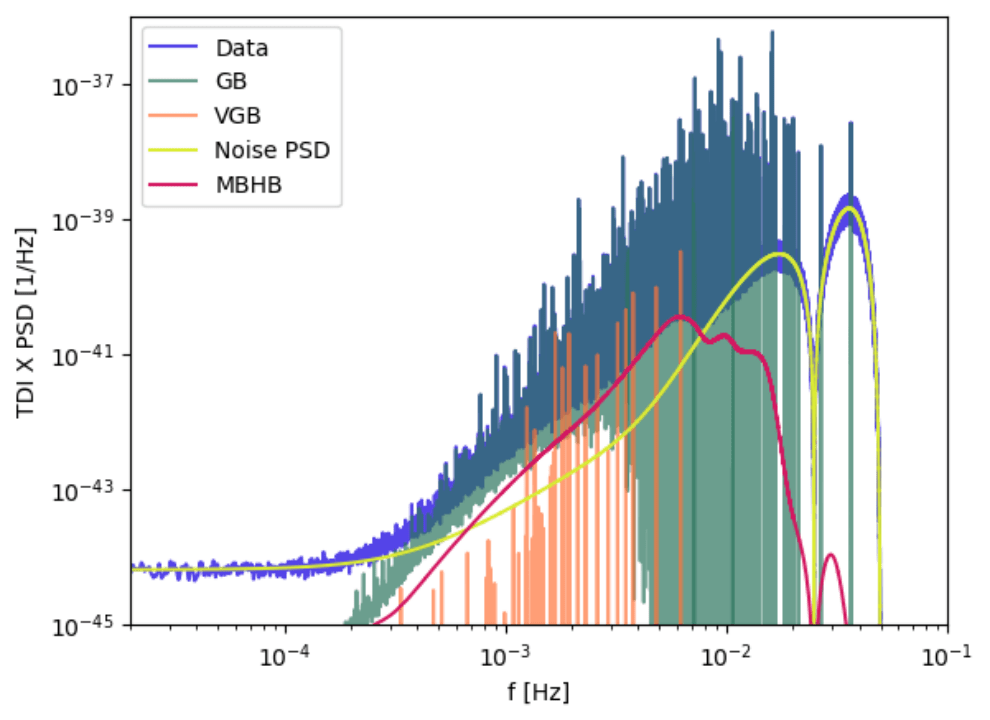
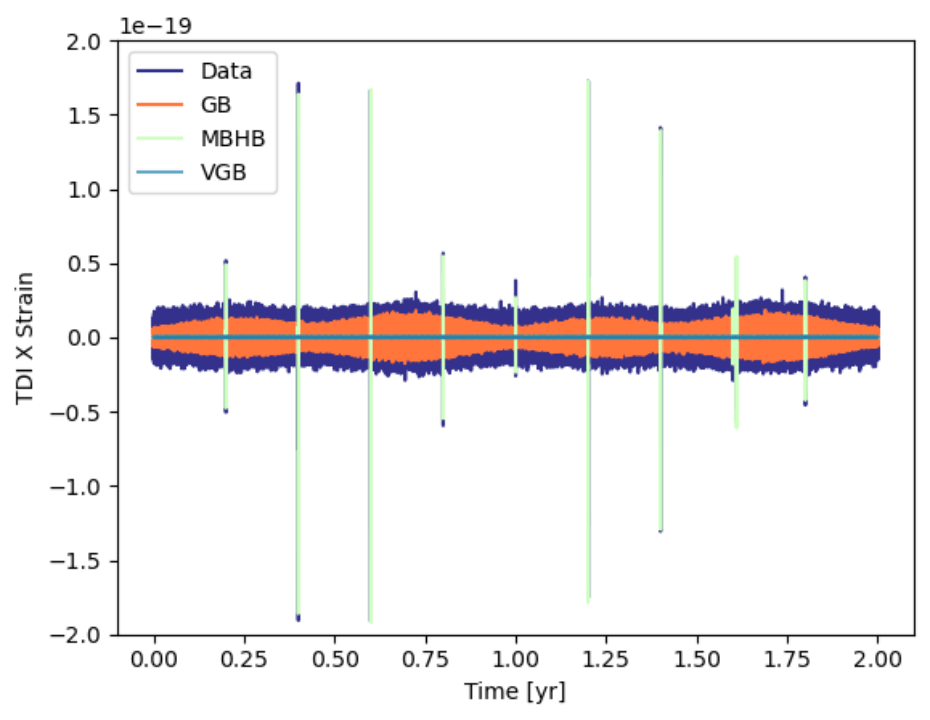


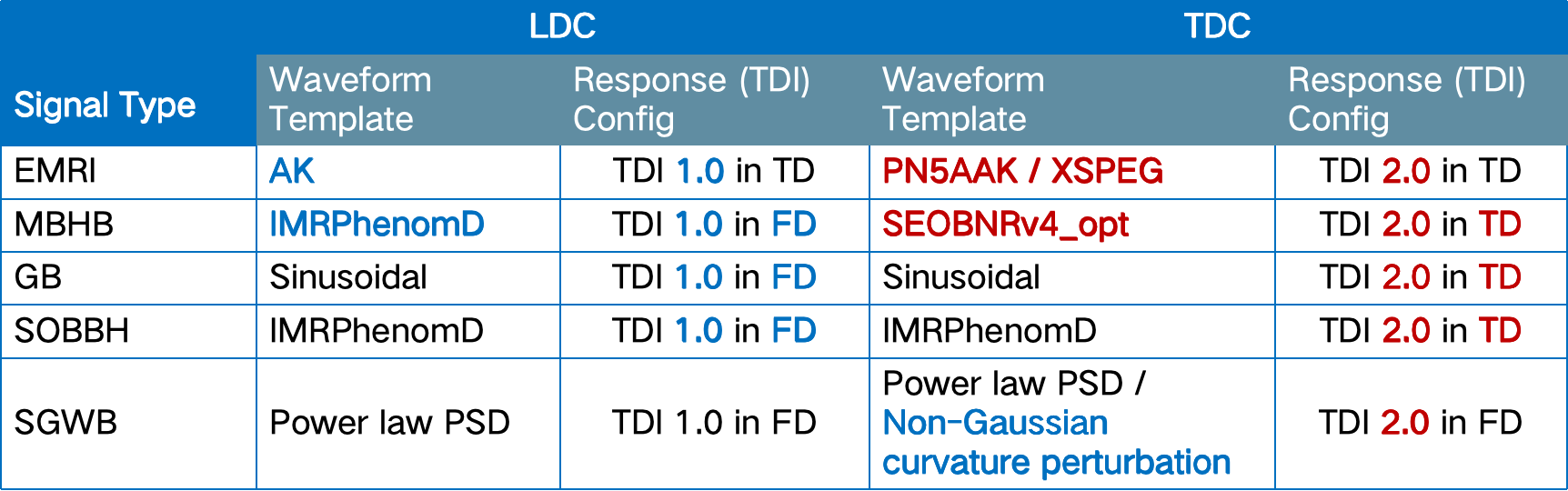
波源模板
- 与地面不同,完备的空间引力波探测模板需要涵盖更广泛的波源参数范围和更复杂的波源运动特性。
- 以 MBHB 为代表的波源信噪比通常较高(可达 \(O(10^3)\) 以上), 对模板的精度要求也相应提高。
- 一些模板(SEOBNRE、SEOBNRPHM、 IMRPhenomXPHM等)加入了如高阶模、离心率、进动等特性,不仅有助于精细刻画波源的运动和演变,也有助于打破参数之间的简并关系,提高参数的估计精度。
- EMRI 双星的质量比约\(10^3 − 10^6\),波形复杂度极高,预期会观测到\(10^4 −10^5\)个周期 (可观测时间长)。
- EMRI模板的核心挑战是数值相对论基准波形的不足?
- 空间引力波探测对其模板的精度和效率要求较高,兼顾精度和效率的方法仍在探索之中(AK、AAK、NK等)。
- 传播路径中考虑引力透镜效应。(5年任务周期内\(\leq4\)个)
Text
空间引力波探测科学数据处理:1. 信号建模与计算
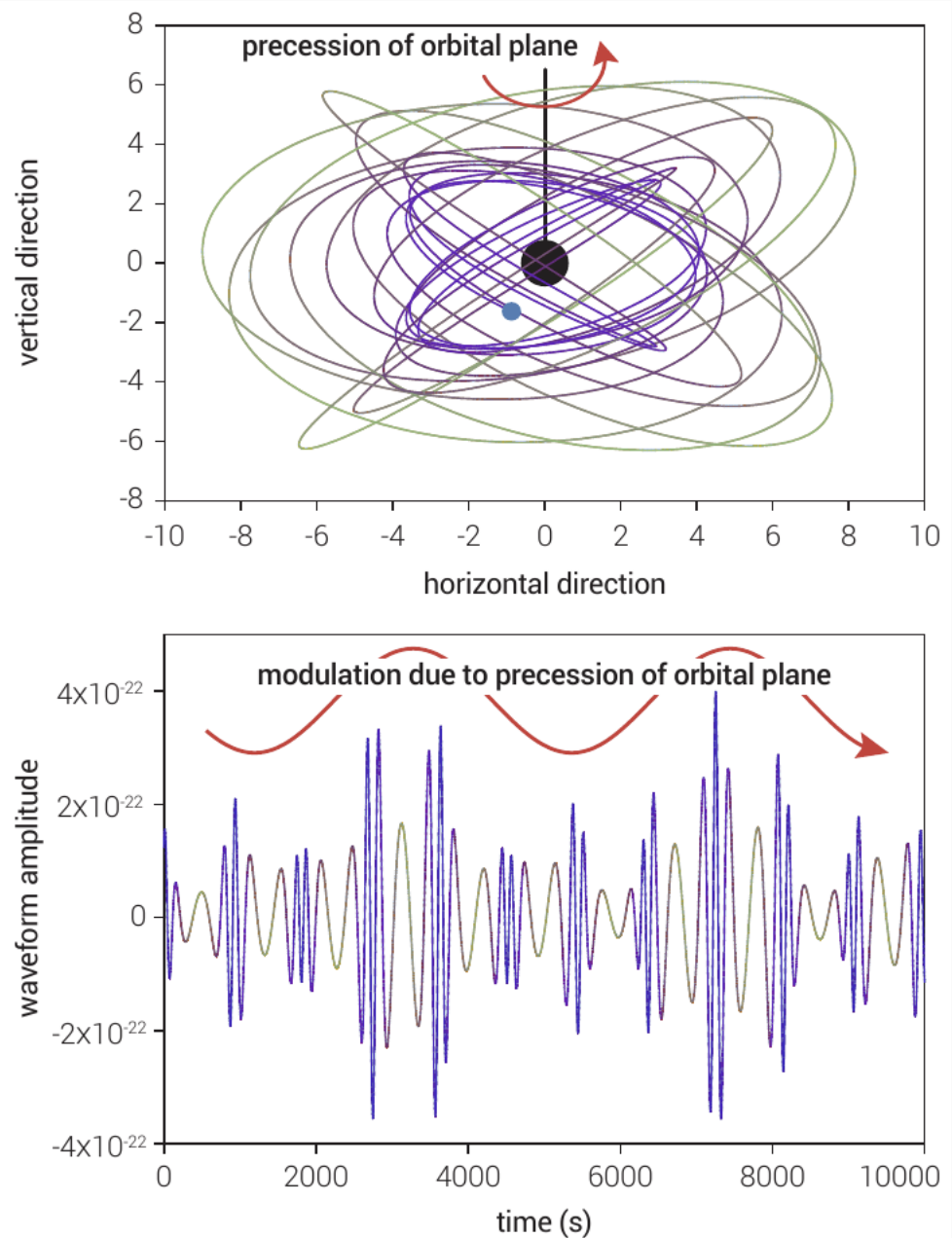

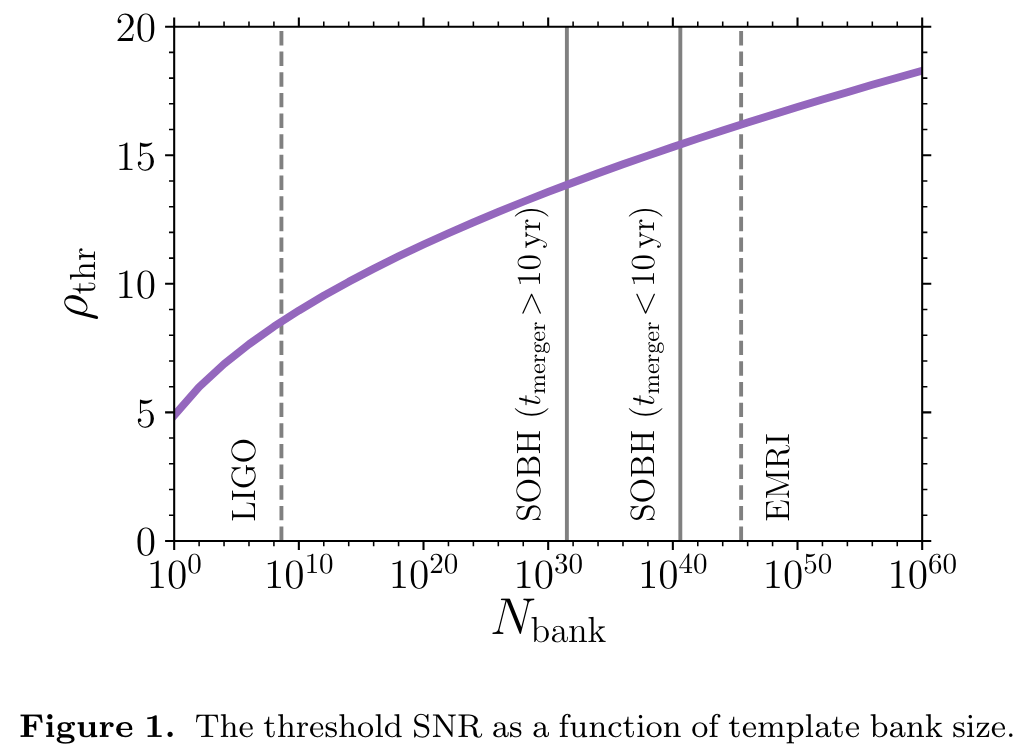
MNRAS 488, L94–L98 (2019)
EMRI 波形模板需求量 40 个数量级以上

Marsat et al. PRD 103, 8 (2021)
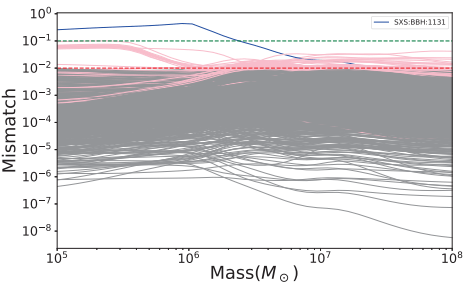
Our results indicate that the existing numerical relativity waveforms are as accurate as 99% with respect to space-based detectors including LISA, Taiji and Tianqin. Such accuracy level is comparable to the one with respect to LIGO.
(ZW, JJZ, ZJC, arXiv:2401.15331)
Bayes' theorem:
探测器响应
- 空间引力波探测响应计算的复杂性:
- 轨道的调制效应:空间引力波探测目标信号的可观测时间可达数月甚至数年,与探测器轨道运动的时间尺度相近。
- TDI 通道的组合:臂长不等、臂长随时间变化以及第二代 TDI 方案有待研究。
Text
空间引力波探测科学数据处理:1. 信号建模与计算
在时域中计算的挑战性在于,在每个采样点处都需要计算波形和响应,如果考虑到不同的 TDI 组合方式,则计算的时间复杂度将进一步增大。频域中的 TDI 响应形式,可简单概况为:
其中 \(\alpha \in\{+, \times\}\),如果要考虑高阶模的贡献,则 \(\alpha=\ell m\) 。\(t_\alpha(f)\) 描述了时间与引力波瞬时频率的关系,可通过
计算, 其中 \(\Psi_\alpha\) 表示 \(\alpha\) 模式频域波形的相位。 \(\mathcal{T}\) 对时间的依赖关系反映了探测器轨道运动对信号的调制效应,如右图所示。调制效应为响应的建模和计算增加了复杂性,但同时也有助于在参数估计中解除外禀参数之间的简并,提升对波源的定位精度。
Bayes' theorem:

TDI-A
TDI-A
TDI-E
TDI-T
Credit: Minghui Du
数据噪声
- 引力波数据分析通常假设噪声是高斯稳态的,数据是连续的,而在实际探测中,噪声的非稳态性、非高斯性及各种可能的数据异常,如环境或设备因素导致的 glitch、数据间断等,都可能导致引力波事件的误警、 漏警或参数估计偏差。
Text
空间引力波探测科学数据处理:2. 噪声与数据异常
Addressing Instrumental Imperfections
-
数据间断(Data gaps)
-
瞬态噪声事件(glitches)
-
频谱线(Spectral lines)
-
非平稳性(Non-stationarities)
-
不完美校准(imperfect calibration)
Text
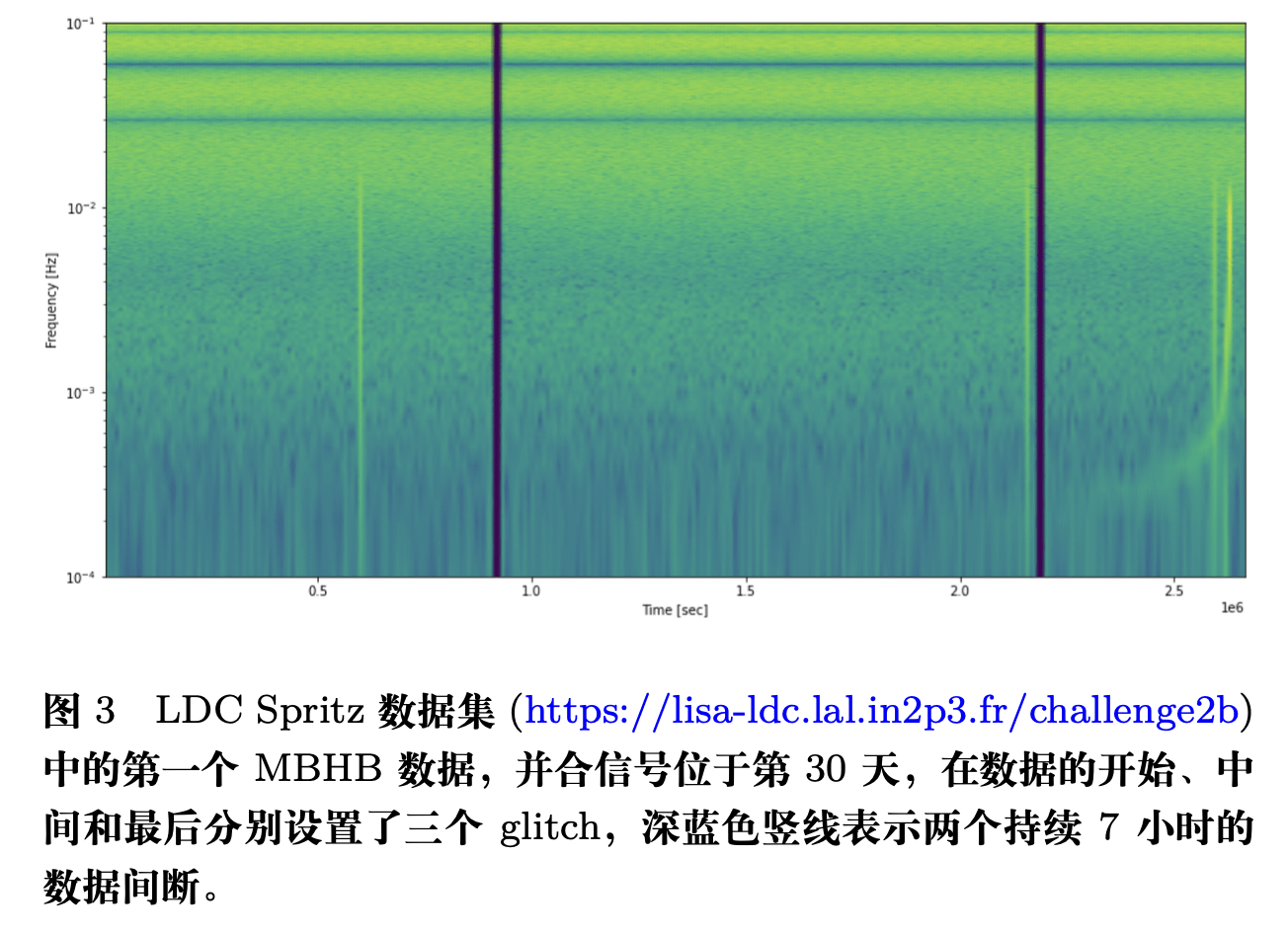
(Sec.8.3.3 Red Book)

Sasli et al., Phys. Rev. D (2023)

Baghi et al., Phys. Rev. D (2019)
似然函数建模
- 针对 glitch 导致的非高斯性,可以考虑用 student-t 分布、 广义双曲分布、高阶 Edge worth 展开等方式为似然函数建模。
Text
Bayes' theorem:
搜索技术
- 空间引力波探测信号搜索流水线开发的重点是天体物理波源,特别是最明亮的 MBHB 和数量最多的 UCB:
-
PyCBC-INFERENCE
- MBHB
-
BILBY
- MBHB
-
Strub et al. PRD 2022/2023
-
UCB
-
GPU-based
-
-
Eryn
- UCB
-
...
-
PyCBC-INFERENCE
Text
空间引力波探测科学数据处理:3. 参数反演
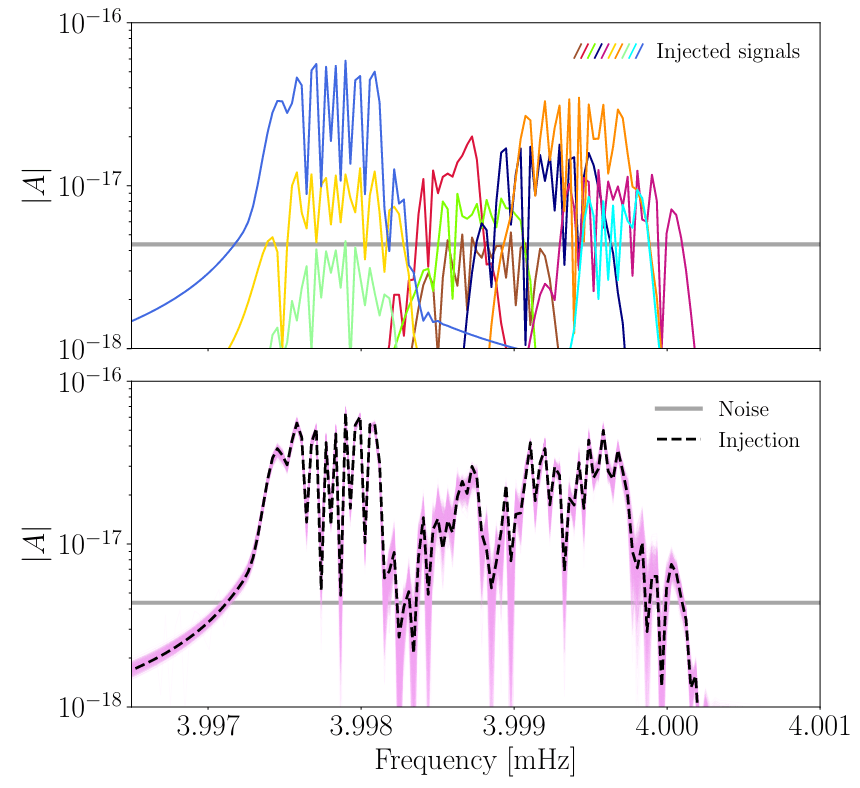
Karnesis et al. 2303.02164.
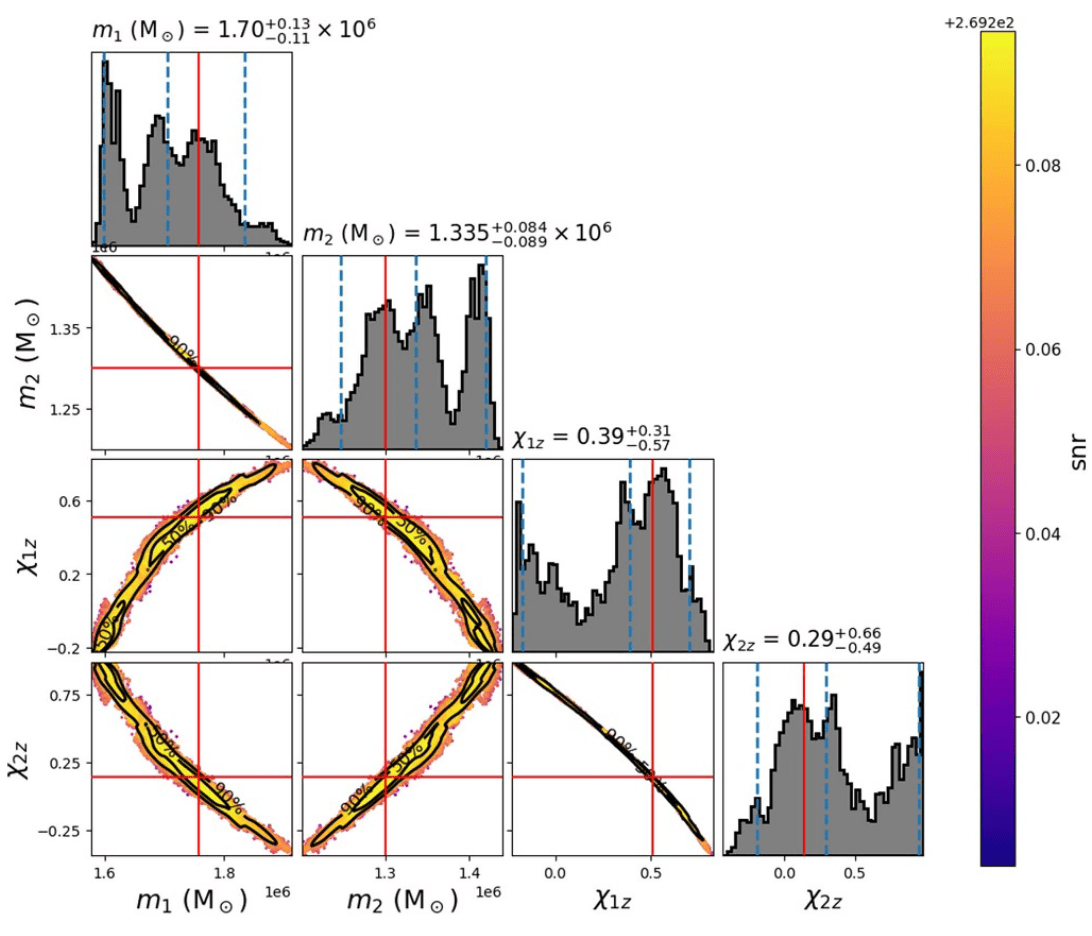
Hoy & Nuttall. 2312.13039.
Weaving et al. CQG 41, (2023)
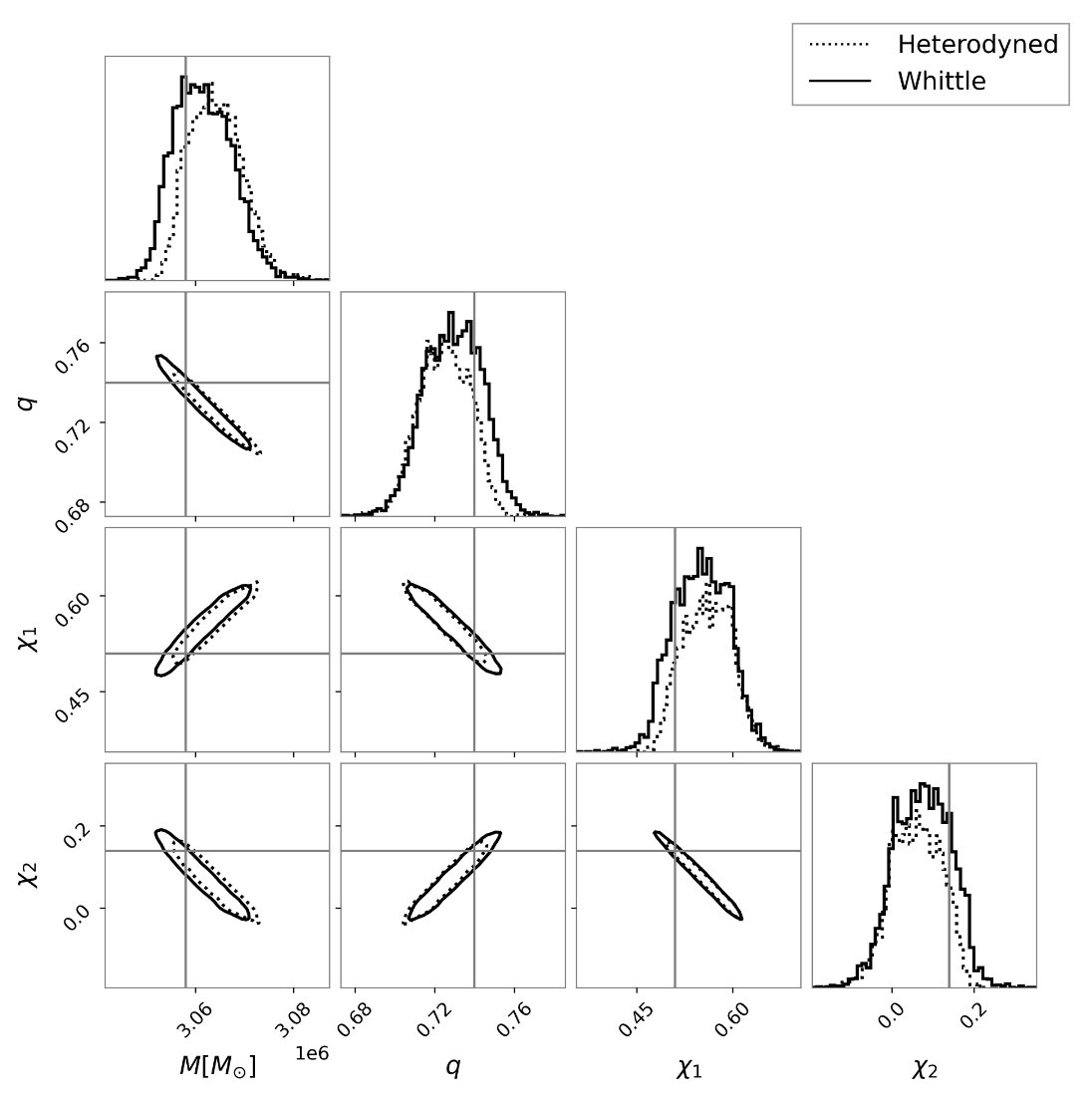
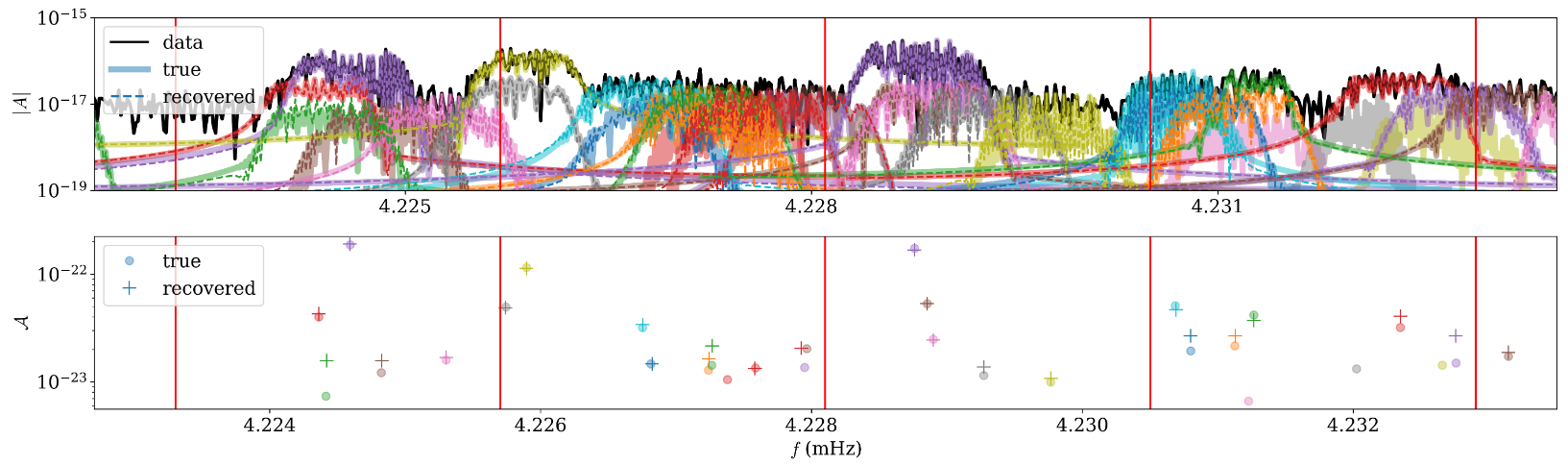
Strub et al., PRD. arXiv:2307.03763
Bayes' theorem:
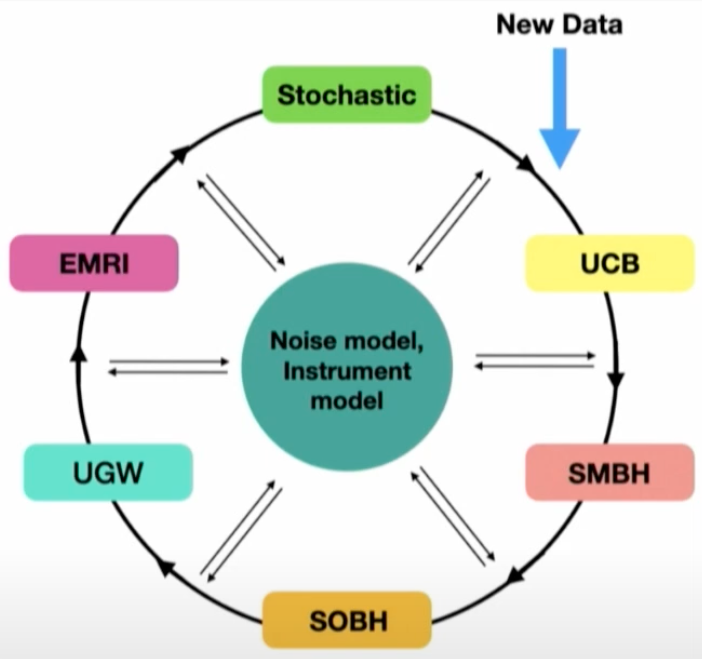
Nat. Astron. 2022, 6(12): 1356-1363.
Nat. Astron. 2022, 6(12): 1334-1338.
背景与挑战
- 空间引力波探测需识别尽可能多的引力波信号源
- 数据中引力波信号相互混叠,影响波源参数反演
- 单独识别单个源或某类特定源类型效率低下
- 波源在任务生命周期内持续存在,增加识别难度
全局拟合方法 (Global-fit method)
- 对所有源/噪声的参数同时做引力波信号全局搜索和波源参数反演
- 随着更多数据的接收,不断更新全局搜索和参数反演的数据
实践应用步骤
- 全局搜索结合其他波源的数据分析流水线
- 在全局搜索后处理最新最佳拟合残差
- 识别到的源反馈至未来的全局搜索方案,以实现持续优化
潜在局限性
- 收敛速度受限
- 受限于未知的波源数目
- \(\mathcal{O}(10^5)\) 高维参数空间
- 波形模板仿真等
全局拟合
Global-fit
Text
Text
Text
Text
空间引力波探测科学数据处理:全局拟合
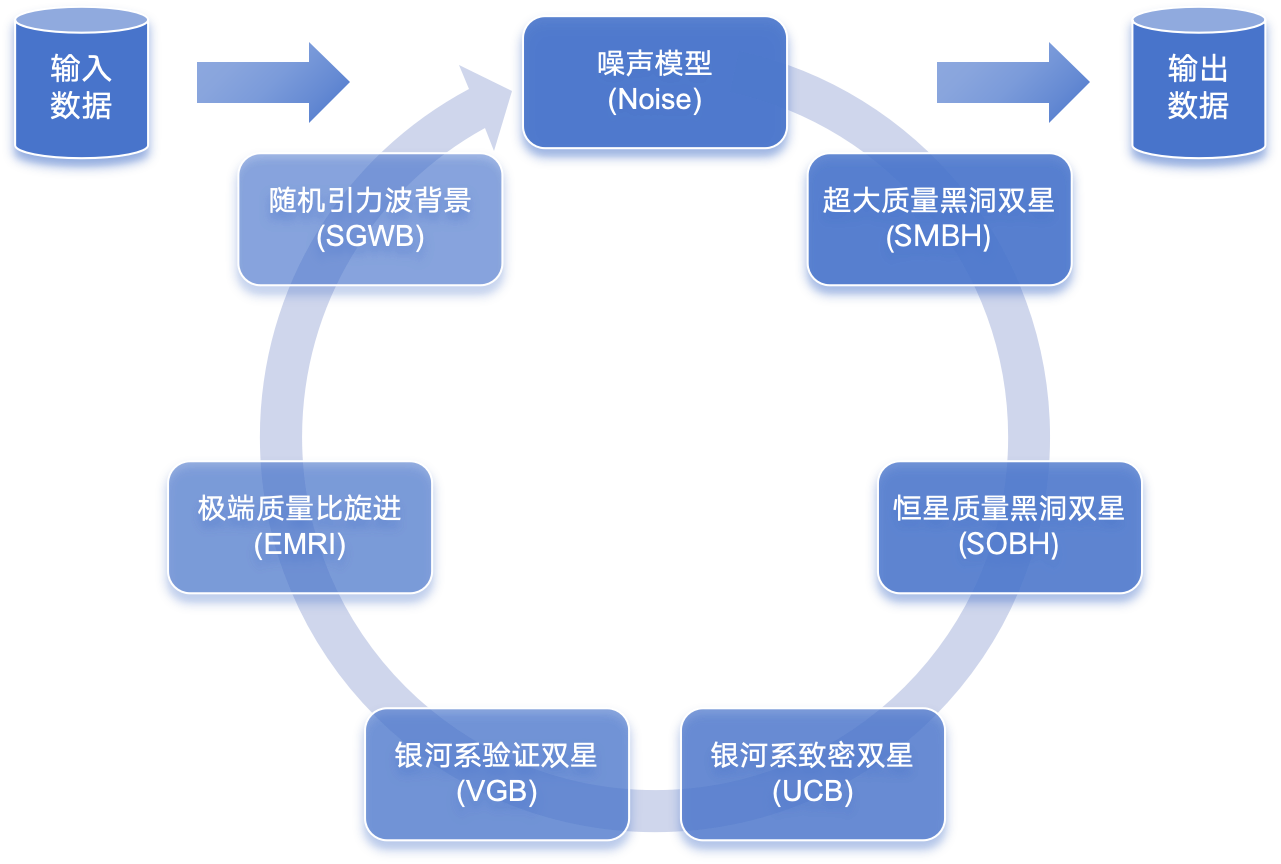
全局拟合
- 全局拟合方法(global fit)思想在于对空间引力波数据中存在的所有天体物理和仪器特征同时进行综合建模。
- 这种方法不仅仅关注单一波源的信号,而是尝试捕捉数据中所有波源的综合影响,对整个数据集进行全面分析,以识别和建模所有潜在的信号和噪声源。
Text
空间引力波探测科学数据处理:3. 参数反演
| Pipeline | Targets | Programing Language (sampling method) | Comments |
|---|---|---|---|
|
GLASS (Littenberg&Cornish 2023) |
Noise, UCB, VGB, MBHB |
C / Python (TPMCMC / RJMCMC) | noise_mcmc+gb_mcmc+vb_mcmc+global_fit |
| Eryn | UCB | Python (TPMCMC / RJMCMC) | No code for UCB case |
| PyCBC-INFERENCE | MBHB | Python (?) | Unavailable |
| Bilby in Space / tBilby | MBHB / ? | ? / Python? (RJMCMC) | Unavailable |
| Strub et al. | UCB | ? (GP) | Unavailable / GPU-based |
| Zhang et al. (LZU) | UCB | ? (PSO) | MLP |
Bayes' theorem:

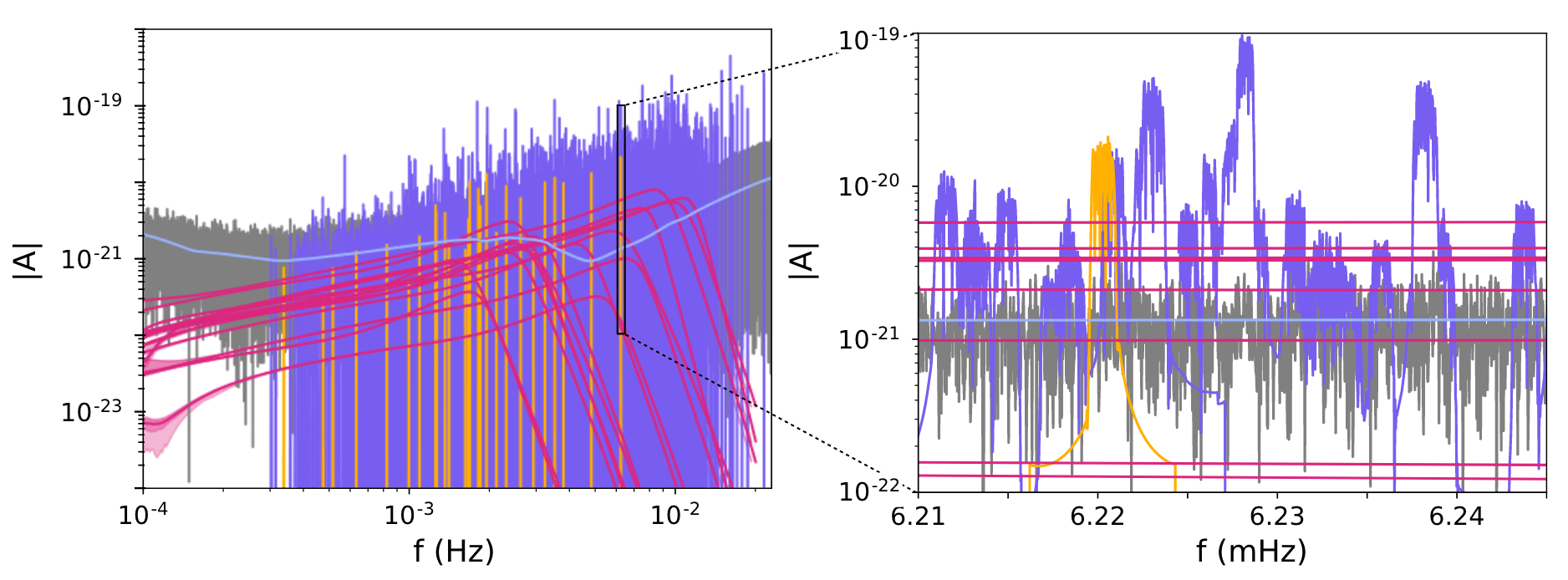
Nat. Astron. 2022, 6(12): 1334-1338.
Nat. Astron. 2022, 6(12): 1356-1363.
(Sec.8.6 Red Book)

超高维度的波源参数空间特性 (编码波形)
- 随着星座的轨道运动,引力波信号会随时间发生变化 (链路相关)。
- 星座对特定波源的探测敏感性也会随时间而改变。
- 我们如何在波形的模式识别中融入星座的轨道运动信息?
科学数据的动态性 (编码数据)
- 面对科学数据的固有复杂性——尤其是数据的高维度——我们应如何应对?
资源优化挑战 (CPU vs GPU)
- 总 CPU 需求 (以 CPU 小时计)是 20-30M,其中每年需要进行3次迭代,每次迭代需要2个管道。用转换系数 10 来估计 GPU 的需求,可估算出所有波源类型的 GPU 卡需求可达 \(10^3\) 以上。(异步调度+并行计算)
- 如何在最小化等待时间和最大化计算
节点效率的过程中,进行资源分配和
优化策略。 - 高频UCB迭代并行计算耗时
- ...
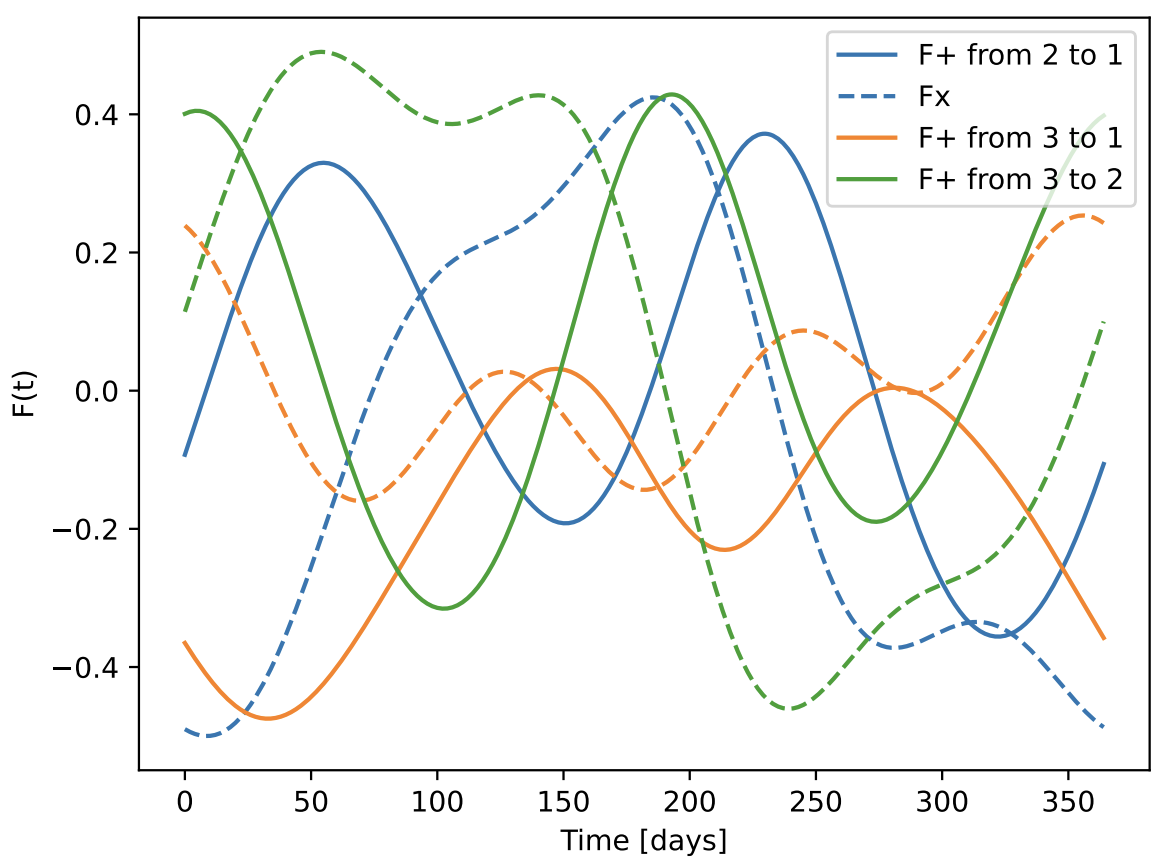
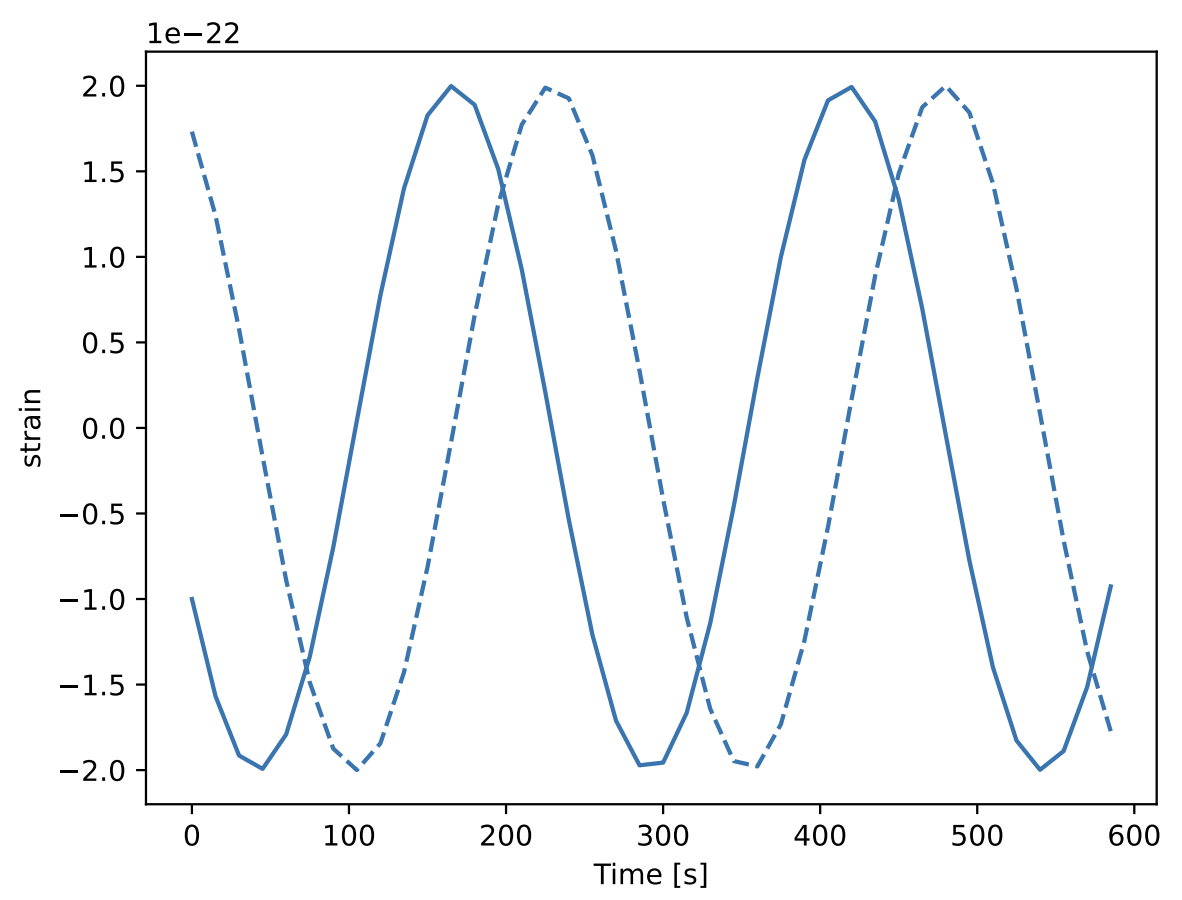
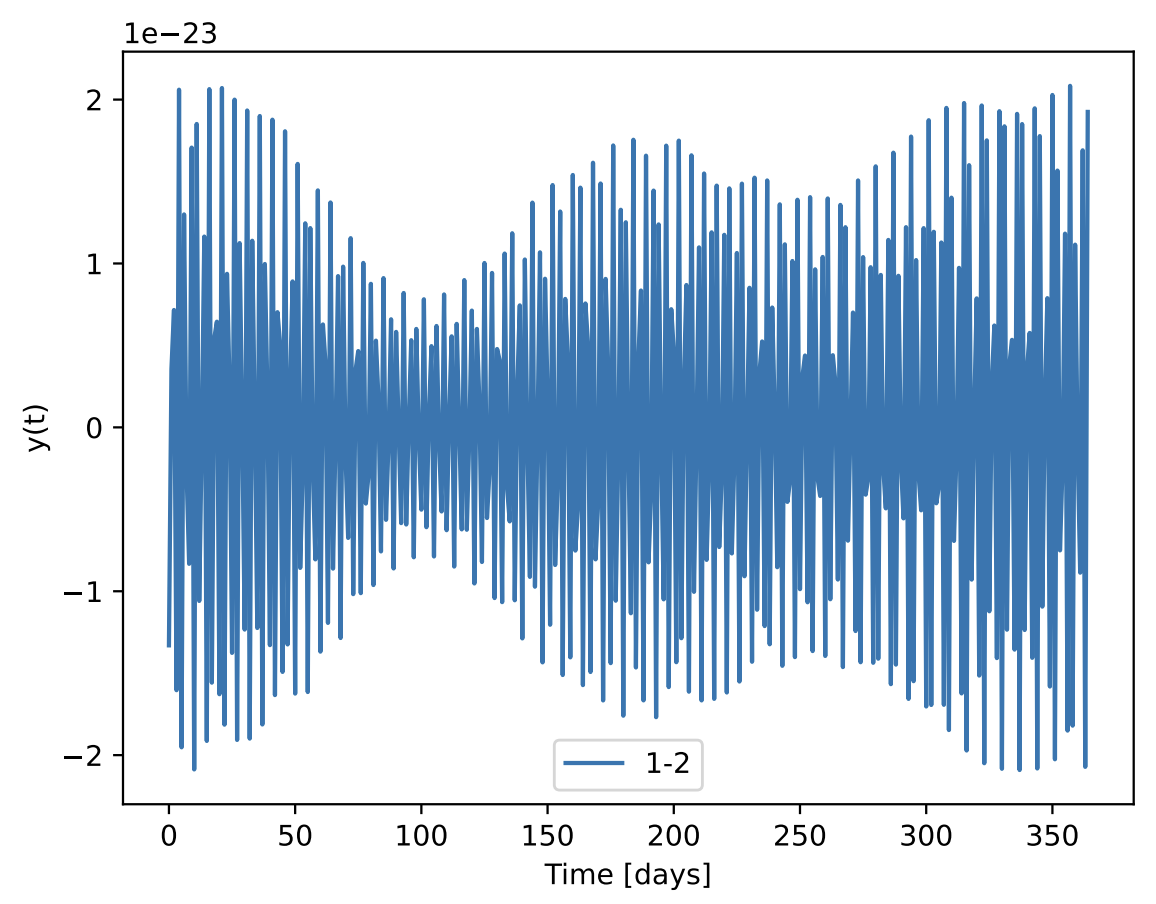
F(t) over 1 year
h(t) over 10 min
y(t) over 1 year
Text
Text
Text
多类型的大量波源混叠问题
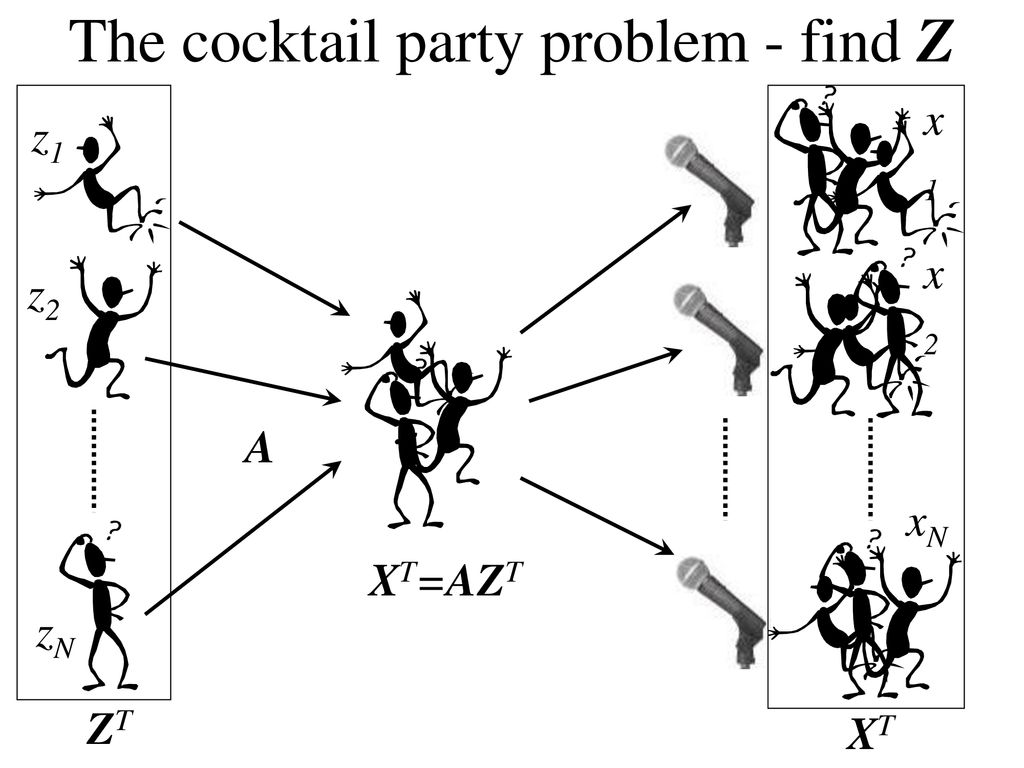
空间引力波探测科学数据处理技术难题
2
Actually, there are more ...
- 非模板引力波信号(背景)的探测与重构
- ...
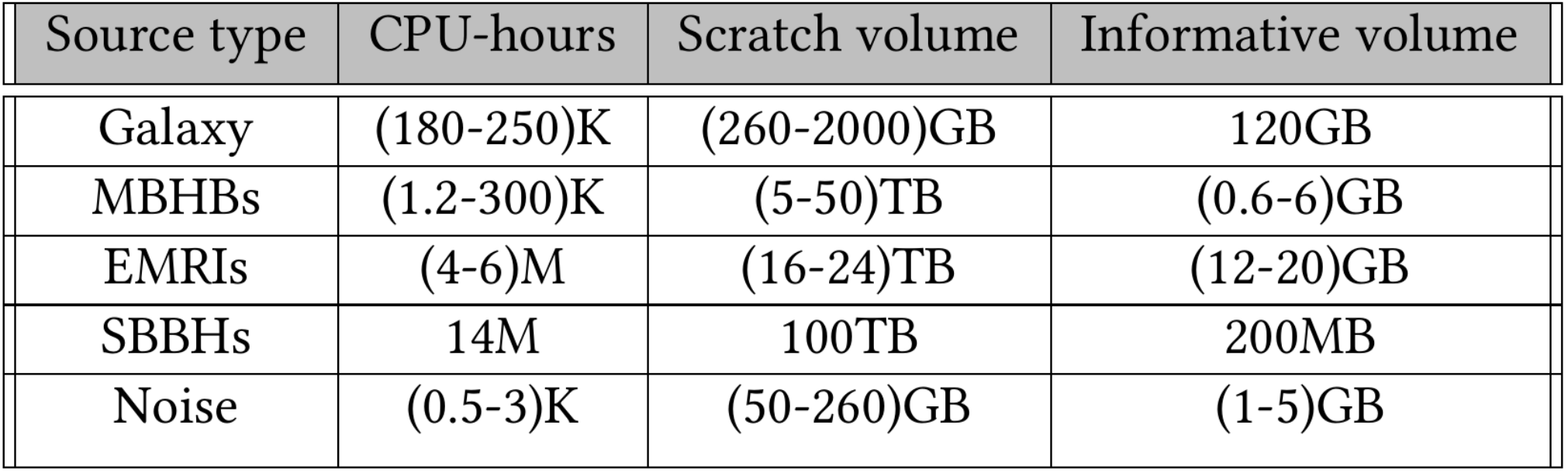
Credit: Maude Le Jeune (2021)
MCMC采样的高效性和收敛性
- 改进Proposal 以有效采样高维+多模+变维的参数空间
- 提高接受率 以确保MC链的高效收敛
Text
-
AI could help ?!
- nflow-assisted? (2402.13701)
-
multi-agentic reasoning


超高维度的波源参数空间特性 (编码波形)
- 随着星座的轨道运动,引力波信号会随时间发生变化 (链路相关)。
- 星座对特定波源的探测敏感性也会随时间而改变。
- 我们如何在波形的模式识别中融入星座的轨道运动信息?
科学数据的动态性 (编码数据)
- 面对科学数据的固有复杂性——尤其是数据的高维度——我们应如何应对?
资源优化挑战 (CPU vs GPU)
- 总 CPU 需求 (以 CPU 小时计)是 20-30M,其中每年需要进行3次迭代,每次迭代需要2个管道。用转换系数 10 来估计 GPU 的需求,可估算出所有波源类型的 GPU 卡需求可达 \(10^3\) 以上。(异步调度+并行计算)
- 如何在最小化等待时间和最大化计算
节点效率的过程中,进行资源分配和
优化策略。 - 高频UCB迭代并行计算耗时
- ...



F(t) over 1 year
h(t) over 10 min
y(t) over 1 year
Text
Text
Text
多类型的大量波源混叠问题

空间引力波探测科学数据处理技术难题
2
Actually, there are more ...
- 非模板引力波信号(背景)的探测与重构
- ...

Credit: Maude Le Jeune (2021)
MCMC采样的高效性和收敛性
- 改进Proposal 以有效采样高维+多模+变维的参数空间
- 提高接受率 以确保MC链的高效收敛
Text
-
AI could help ?!
- nflow-assisted? (2402.13701)
-
multi-agentic reasoning


for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This silde: https://slides.com/iphysresearch/2024may_neu

Nat. Astron. 2022, 6(12): 1356-1363.
Nat. Astron. 2022, 6(12): 1334-1338.
背景与挑战
- 空间引力波探测需识别尽可能多的引力波信号源
- 数据中引力波信号相互混叠,影响波源参数反演
- 单独识别单个源或某类特定源类型效率低下
- 波源在任务生命周期内持续存在,增加识别难度
全局拟合方法 (Global-fit method)
- 对所有源/噪声的参数同时做引力波信号全局搜索和波源参数反演
- 随着更多数据的接收,不断更新全局搜索和参数反演的数据
实践应用步骤
- 全局搜索结合其他波源的数据分析流水线
- 在全局搜索后处理最新最佳拟合残差
- 识别到的源反馈至未来的全局搜索方案,以实现持续优化
局限性
- 收敛速度慢
- 受限于未知的波源数目
- \(\mathcal{O}(10^5)\) 高维参数空间
- 波形模板仿真等
全局拟合
Global-fit

Text
Text
Text
Text

Strub et al., PRD. arXiv:2307.03763

空间引力波探测的典型波源与全局拟合问题

研究现状
-
GLASS (The global LISA analysis software suite)
- Modeling: noise, UCB, VGB, MBHB
- Blind search
-
PyCBC-INFERENCE
- MBHB
-
BILBY
- MBHB
-
Strub et al. PRD 2023
-
UCB
-
GPU-based
-
-
Eryn
- UCB
-
...
空间引力波探测的典型波源与全局拟合问题

Text

Karnesis et al. 2303.02164.

Hoy & Nuttall. 2312.13039.
Weaving et al. CQG 41, (2023)

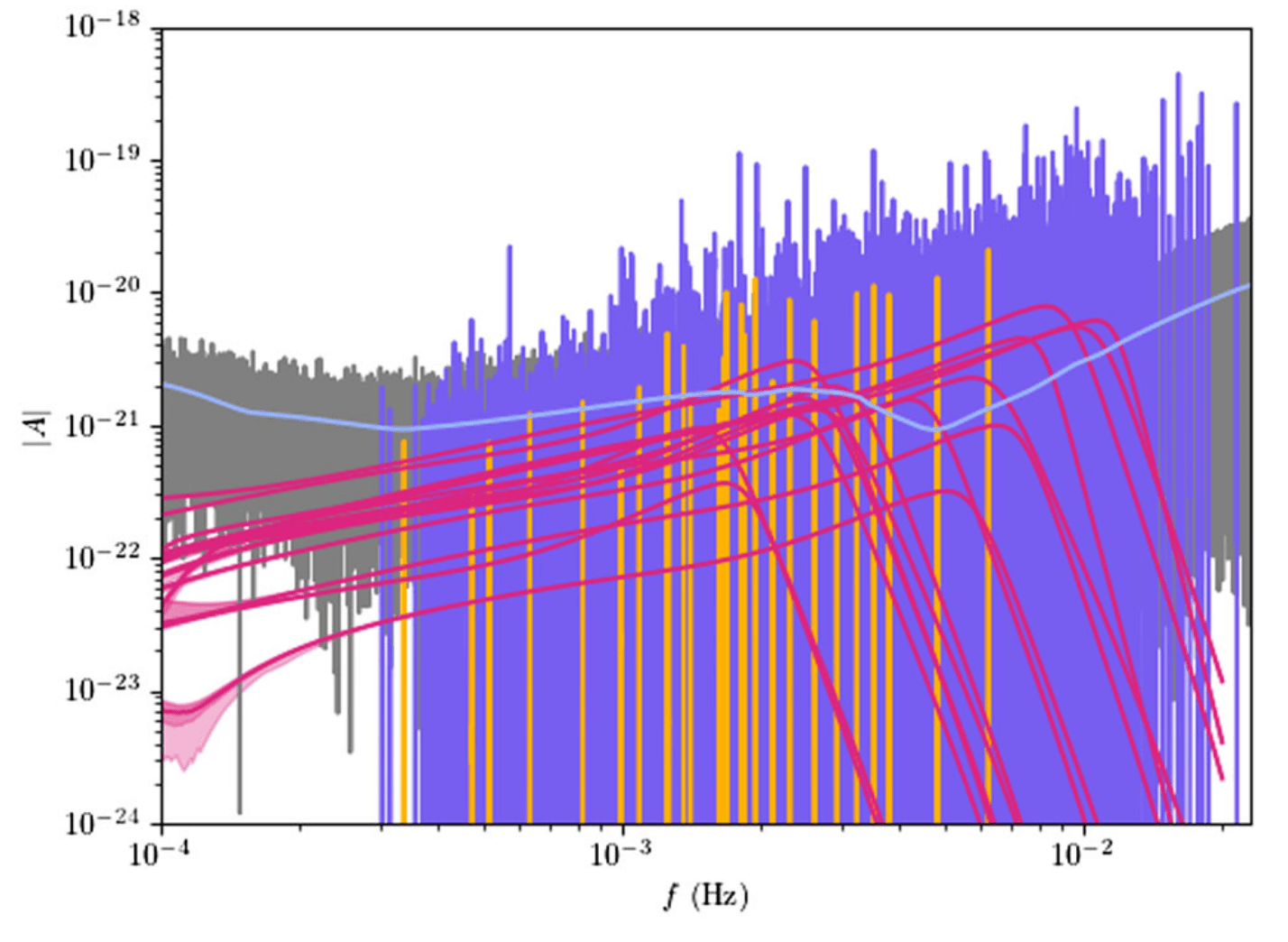
Littenberg & Cornish, Phys. Rev. D (2023)
技术痛点/局限性
- 似然函数:计算耗时/先验知识依赖
- 优化收敛:高频UCB迭代并行计算耗时
- 高性能硬件:CPU+GPU异构并行计算
- ...
Text

- 空间引力波探测:全局拟合问题
- 科学智能:引力波数据处理
- 空间引力波探测科学数据处理:人工智能技术
目录



科学智能:AI for Science
-
2016年,AlphaGo 第一版发表在了 Nature 杂志上
-
2021年,AI预测蛋白质结构登上 Science、Nature 年度技术突破,潜力无穷
-
2022年,DeepMind团队通过游戏训练AI发现矩阵乘法算法问题
-
《达摩院2022十大科技趋势》将 AI for Science 列为重要趋势
-
“人工智能成为科学家的新生产工具,催生科研新范式”
-
-
2023年,DeepMind发布AI工具GNoME (Nature),成功预测220万种晶体结构
-
AI for Science:为科学带来了模型与数据双驱动的新的研究范式
-
AI + 数学、AI + 化学、AI + 医药、AI + 量子、AI + 物理、AI + 天文 ...
-





AlphaGo 围棋机器人

AlphaTensor 发现矩阵算法

AlphaFold 蛋白质结构预测

验证数学猜想


基于 CNN 的开创性研究工作
- 从计算机视觉 (CV) 到GW信号处理的最常见和直接的方法:像素点\(\Rightarrow\)采样点。
-
卷积神经网络 (CNN) 可以用来搜寻双黑洞并合系统所产生的引力波信号
-
灵敏度:与匹配滤波方法可比拟
-
执行速度:远胜过匹配滤波方法 (有GPU加持)
-


Text

PRL, 2018, 120(14): 141103.

PRD, 2018, 97(4): 044039.
AI for Science \(\rightarrow\) AI for GW Astronomy
- Artificial Intelligence (AI) has great potential to revolutionize gravitational wave astronomy by improving data analysis, modeling, and detector development.
- Representation and supervised learning crucially extract features from GW signals, autonomously identifying informative features and leveraging labeled data for accuracy.

Exported: Oct, 2023 (in preparation)
Text

引力波数据处理:人工智能技术应用

引力波数据处理:人工智能技术应用
Matched-filtering Convolutional Neural Network (MFCNN)
Text
- GW templates can be utilized as recognizable features for signal detection.
- It is feasible to generalize both matched-filtering and neural networks.
- Linear filters (i.e., matched-filtering) in signal processing can be reformulated as neural layers (i.e., CNNs).
MLGWSC-1
-
The majority of AI algorithms used for testing are highly sensitive to non-Gaussian real noise backgrounds, resulting in high false positive rates.
(MFCNN group) H.W., et al. PRD (2023)



Text

CL.M., W.W., H.W., et al. PRD (2022)
Ensemble learning
-
Leverages statistical approaches to utilize more information for making informed decisions by combining multiple models.

Real-time GW searches for GW150914

H.W., et al. PRD (2020)
Text
Expanding the dimension of the output
- is to call more information to make decisions in improving AI models.
Text

CL.M., W.W., H.W., et al. PRD (2023)


目录

- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery
- Key Takeaways
-
Space-based GW Detection
- AI-powered

空间引力波探测科学数据处理:人工智能技术

- 极端质量比黑洞双星的绕旋 (EMRI) 是空间引力波探测的重要信号源。
- 由于相对论效应的影响,波形复杂度极高,预期会观测到 \(10^4 \sim 10^5\) 周期。
- 深度学习技术的应用:波形建模
- 利用GPU加速EMRI波形的模式识别分析,为毫赫兹空间引力波数据分析提供了强大的计算工具和新的可能性,显著提升了数据处理的效率和精度


Text
\(h(\theta):=\sum_i \alpha_i(\theta) e_i \equiv \alpha(\theta) \text {, }\)
where \(\alpha\in\mathbb{C}^{241}\) and reduced basis \(\{e_i\}\) with \(\left\langle e_i \mid e_j\right\rangle=\delta_{i j}\).
深度学习算法的学习目标:
\((\mathcal{M}_c, \eta)\in\Theta\subset\mathbb{R}^2\)
\((\alpha_r, \alpha_i) \in\mathbb{R}^{482} \)
Neural
Network
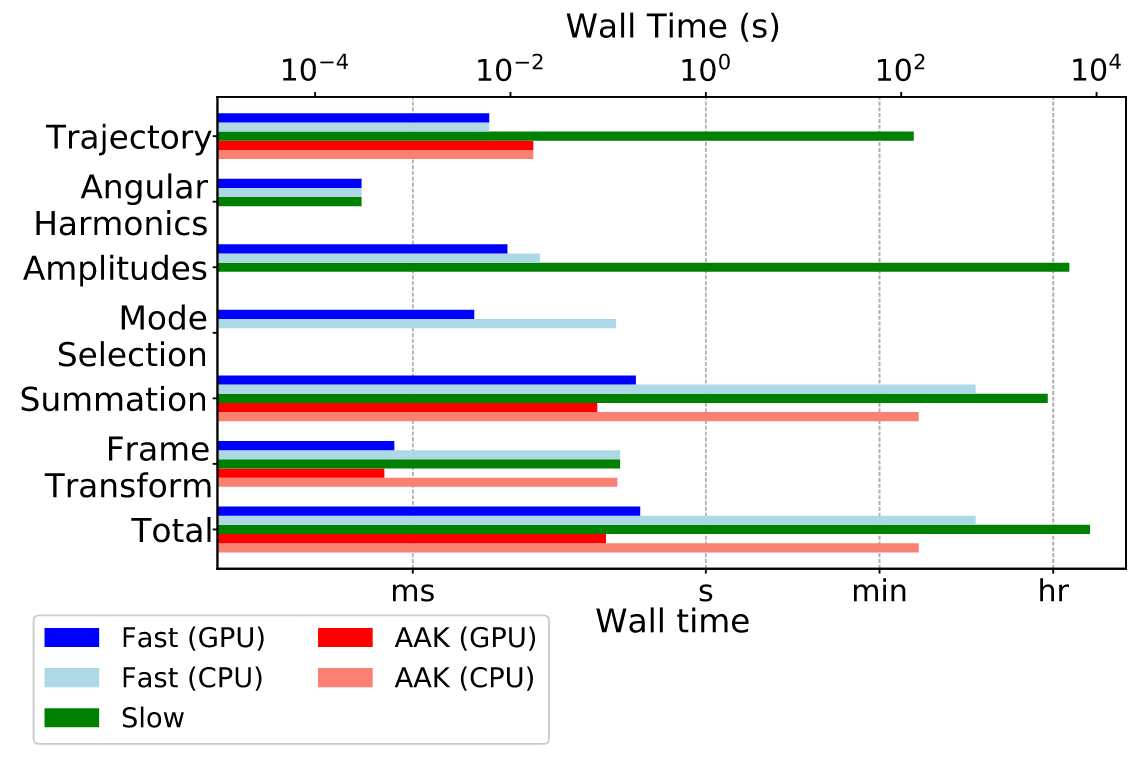
AAK - FastEMRIWaveforms (FEW)
Katz et al., Phys. Rev. D (2021)
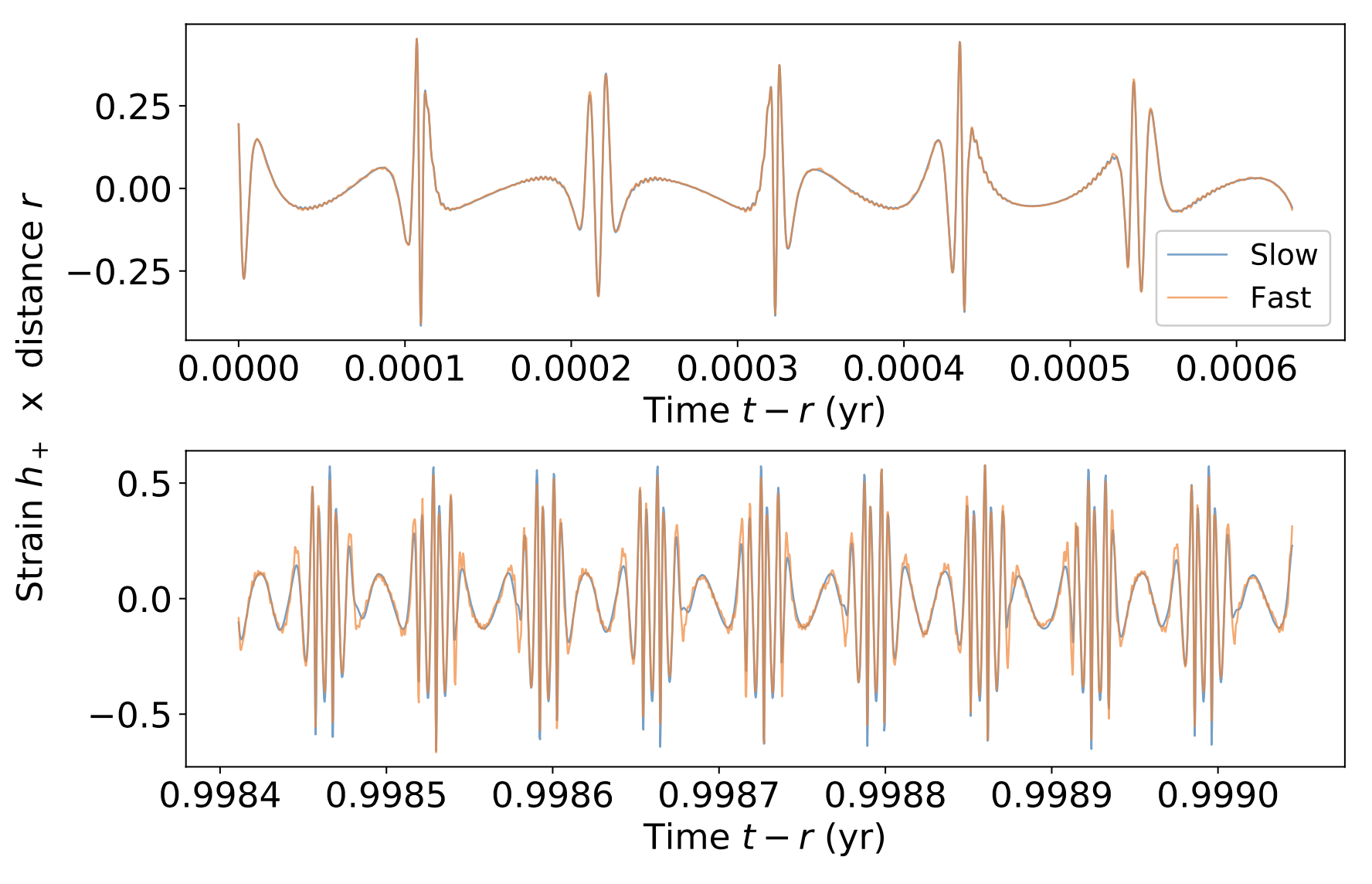
Chua et al., Phys. Rev. Lett., (2021)
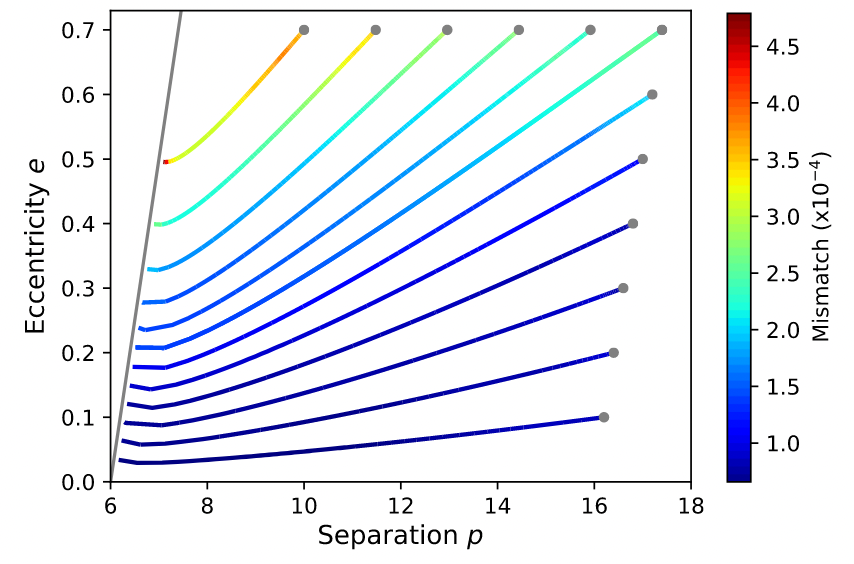
~1s (快 ≳\(10^4\) 倍)

MNRAS 488, L94–L98 (2019)
EMRI 波形模板需求量 40 个数量级以上
Text

- 极端质量比黑洞双星的绕旋 (EMRI) 是空间引力波探测的重要信号源。
- 传统的匹配滤波方法需求巨量的高精度波形模板 (\(约10^{40}\)) ,计算上不切实际。
- 深度学习技术的应用:信号探测
- 通过基于人工智能模型的 EMRIs 波形的原理验证研究,能够在约 10 毫秒的时间内实现波形信号的有效探测。


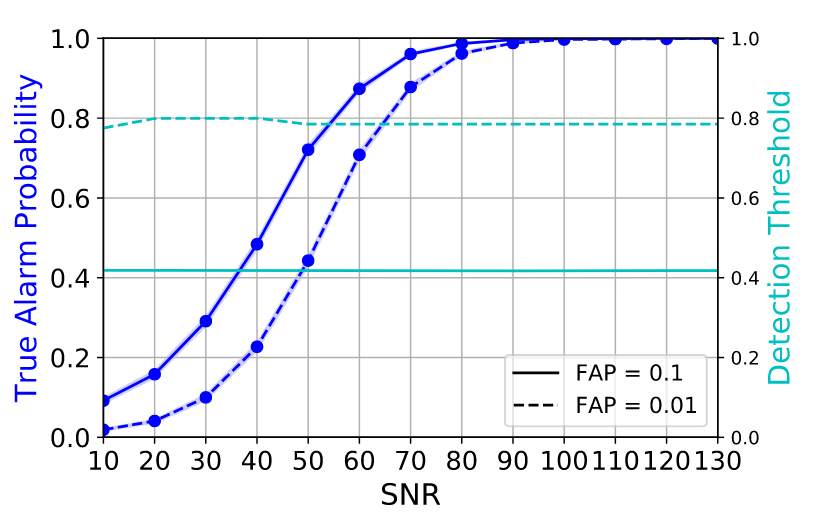
张雪婷, C. Messenger, N. Korsakova,
ML Chan, 胡一鸣, 张建东, Phys. Rev. D (2022)
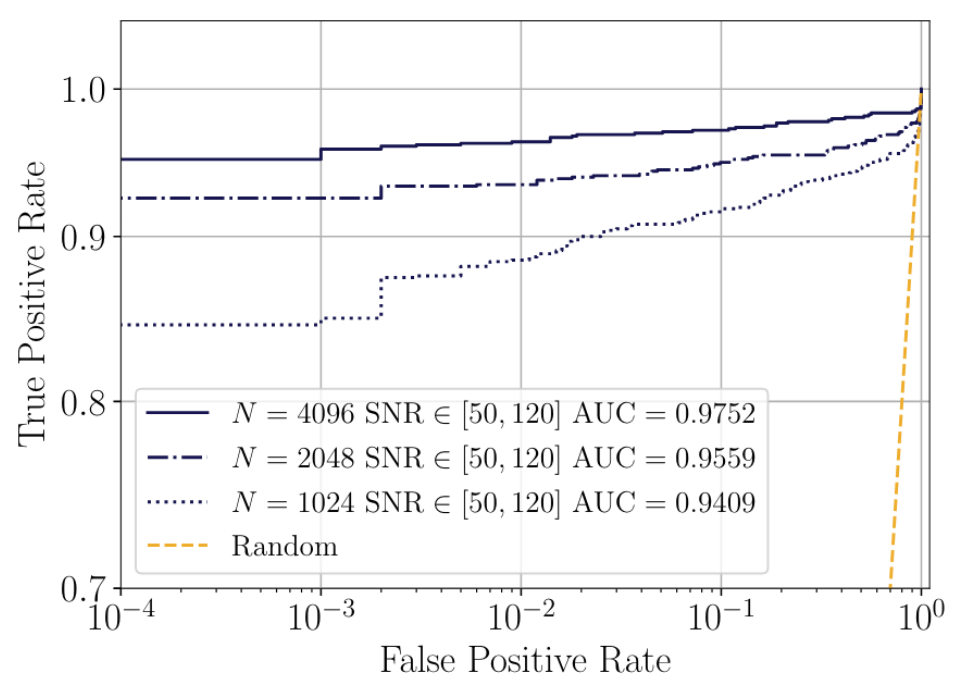
赵天宇, 周阅, 施锐俊, 曹周键, 任智祥, arXiv:2308.16422

恽倩芸, 韩文标, 郭意扬, 王赫, 杜明辉, arXiv:2309.06694
Text

| Zhang et al. PRD (2022) |
Zhao et al. (2308.16422) |
Yun et al. (2309.06694) |
|
|---|---|---|---|
| TDI | - | TDI-1.5 | TDI-2.0 |
| Duration | 3 months | 1 year | 0.5 year |
| Waveform Family (train) | AK | AAK | AAK |
| Waveform Family (test) | AK / AAK | AK / AAK | AAK |
| GW Project | TianQin | LISA | Taiji |
| Acceleration Noise [fm/sqrt(Hz)] | 1 | 3 | 3 |
| OMS Noise [pm/sqrt(Hz)] | 1 | 15 | 8 |
| Base Model | CNN | CNN | CNN |
| Input Feature domain | time | frequency | time-frequency |
| sampling rate | 1/30 Hz | 1/15 Hz | 1/10 Hz |
Text
空间引力波探测科学数据处理:人工智能技术

- 极端质量比黑洞双星的绕旋 (EMRI) 是空间引力波探测的重要信号源。
- 传统的匹配滤波方法需求巨量的高精度波形模板 (\(约10^{40}\)) ,计算上不切实际。
- 深度学习技术的应用:信号探测/参数反演
- 通过基于人工智能模型的 EMRIs 波形的原理验证研究,能够在约 10 毫秒的时间内实现波形信号的有效探测,以及对波源参数的反演。


Text

| Yun et al. (2311.18640) |
|---|
| TDI-2.0 |
| 0.5 year |
| AAK |
| AAK / EOB |
| Taiji |
| 3 |
| 8 |
| Unet / VGG |
| time-frequency |
| 1/10 Hz |

| Zhang et al. PRD (2022) |
Zhao et al. (2308.16422) |
Yun et al. (2309.06694) |
|
|---|---|---|---|
| TDI | - | TDI-1.5 | TDI-2.0 |
| Duration | 3 months | 1 year | 0.5 year |
| Waveform Family (train) | AK | AAK | AAK |
| Waveform Family (test) | AK / AAK | AK / AAK | AAK |
| GW Project | TianQin | LISA | Taiji |
| Acceleration Noise [fm/sqrt(Hz)] | 1 | 3 | 3 |
| OMS Noise [pm/sqrt(Hz)] | 1 | 15 | 8 |
| Base Model | CNN | CNN | CNN |
| Input Feature domain | time | frequency | time-frequency |
| sampling rate | 1/30 Hz | 1/15 Hz | 1/10 Hz |
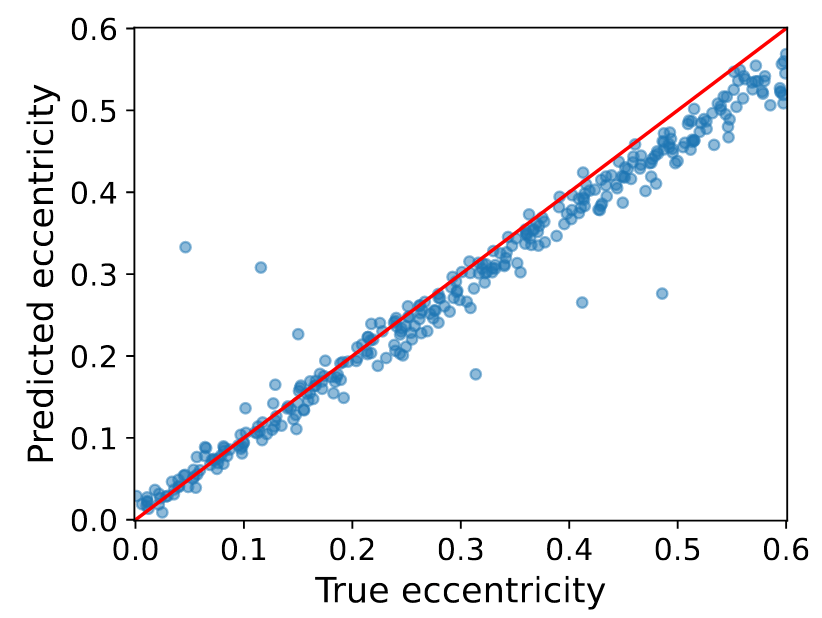
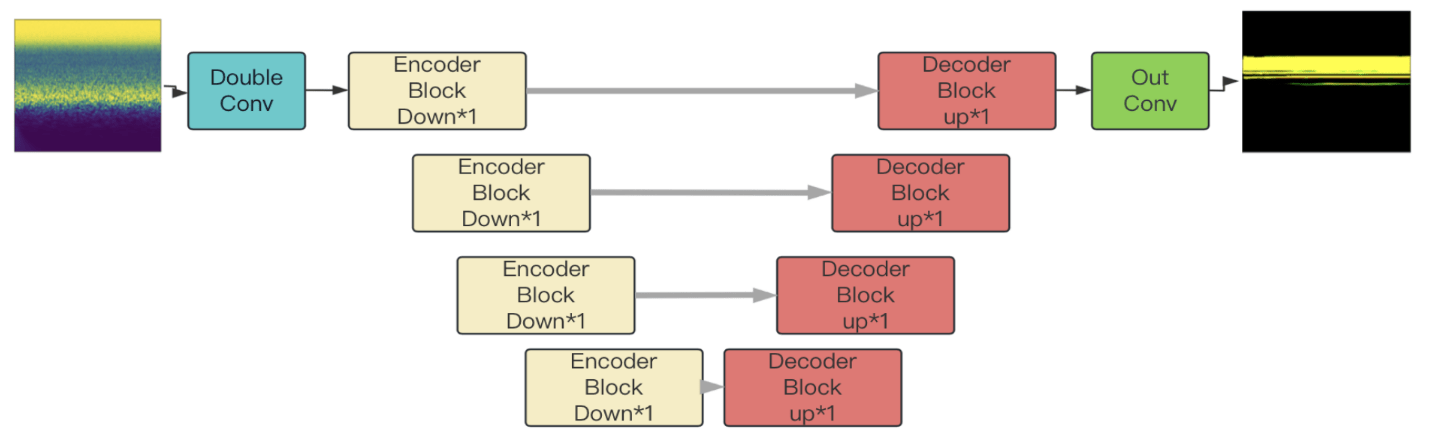
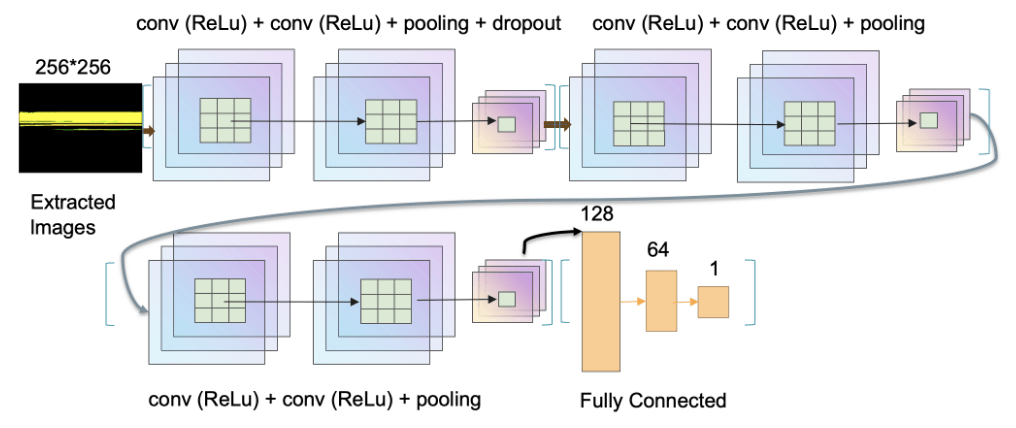
空间引力波探测科学数据处理:人工智能技术
Text

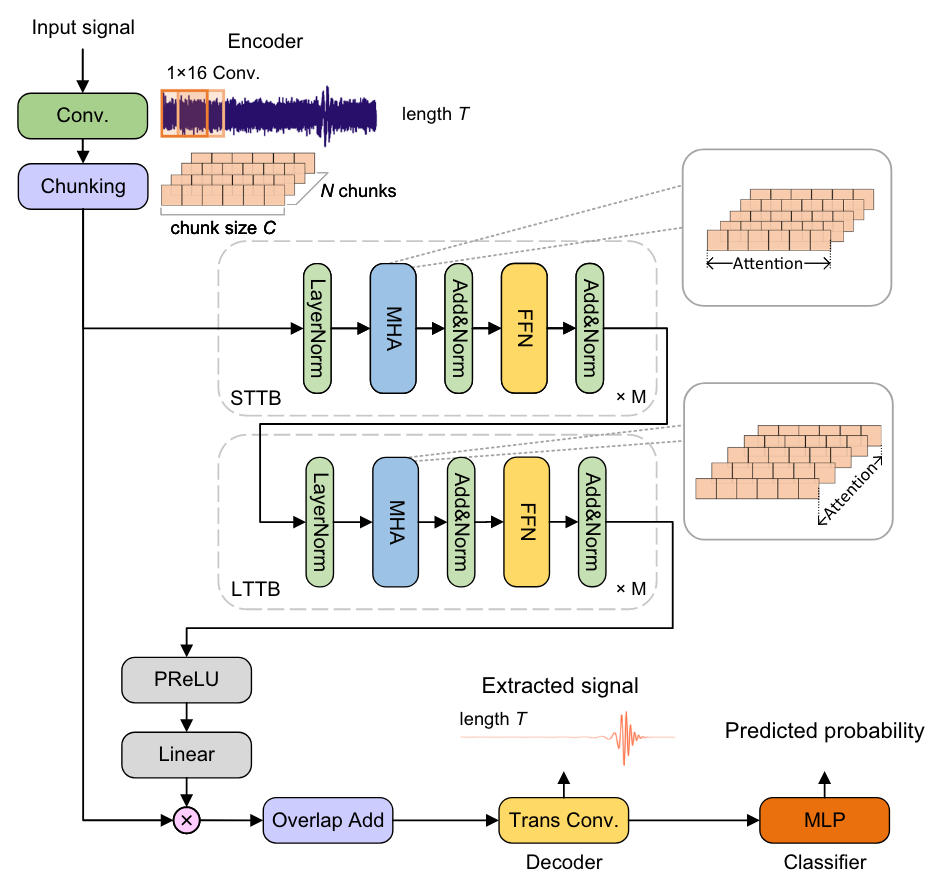
- 超大质量黑洞双星 (MBHB) 的并合是空间引力波可以探测到的最强瞬态信号源,对于低红移源,信噪比 (SNR) 可超过1000。
- 预期质量范围是 \(10^4\sim10^7\) 太阳质量,可观测到晚期的双星绕旋、并合和振荡衰减阶段,事件率约为每年几个到几百个。
- 深度学习技术的应用:信号探测
- 通过基于人工智能模型的原理验证研究,可实现多种波源波形信号的实时探测。
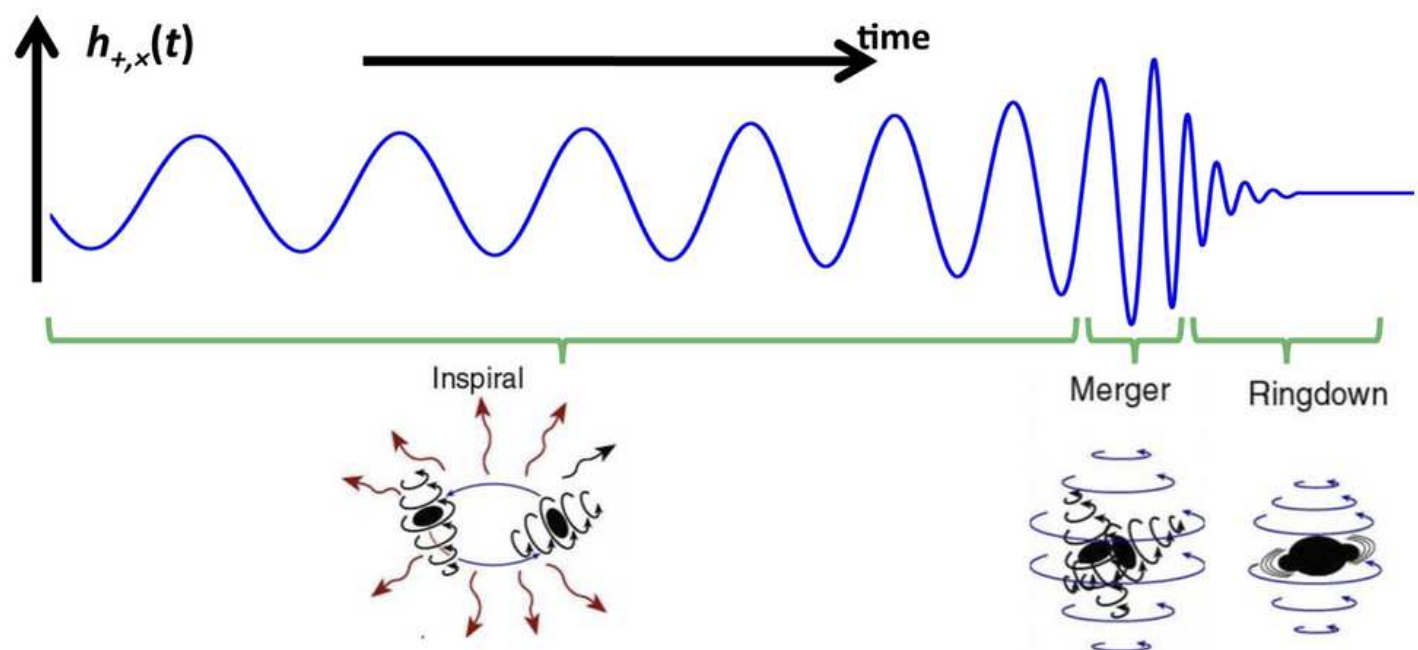

赵天宇*, Ruoxi Lyu*, 王赫, 曹周键, 任智祥, Commun. Phys., (2023)
"One Model to Rule Them All":EMRI / MBHB / GBs / SGWB 的信号提取
王赫, 吴仕超, 曹周键, 刘骁麟, 朱建阳,
Phys. Rev. D, (2020)

阮文洪*, 王赫*, 刘畅, 郭宗宽,
Phys. Lett. B, (2023)
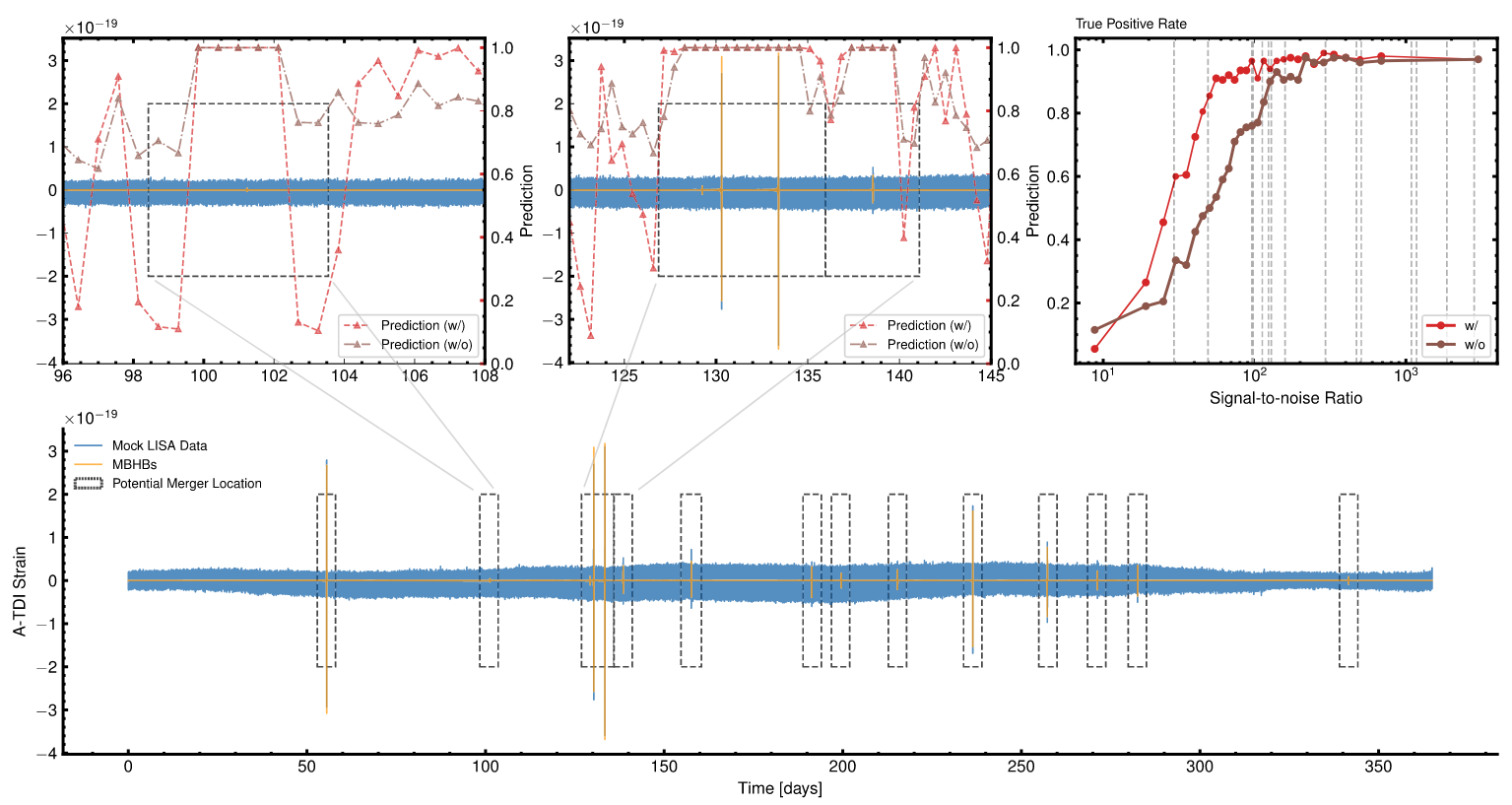
LDC 一年数据上对 MBHB (+GBs) 信号的信号探测
Text

空间引力波探测科学数据处理:人工智能技术
Text

杜明辉*, 梁博*, 王赫†, 徐鹏, 罗子人, 吴岳良†, accepted by SCPMA, arXiv:2308.05510

- 超大质量黑洞双星 (MBHB) 的并合是空间引力波可以探测到的最强瞬态信号源,对于低红移源,信噪比 (SNR) 可超过1000。
- 预期质量范围是 \(10^4\sim10^7\) 太阳质量,可观测到晚期的双星绕旋、并合和振荡衰减阶段,事件率约为每年几个到几百个。
- 深度学习技术的应用:参数反演
- 人工智能算法可实现混叠 MBHB 信号的全波源参数反演,比传统估计后验分布算法的采样效率高 3 个数量级。
阮文洪, 王赫, 刘畅, 郭宗宽,
Universe (2023)
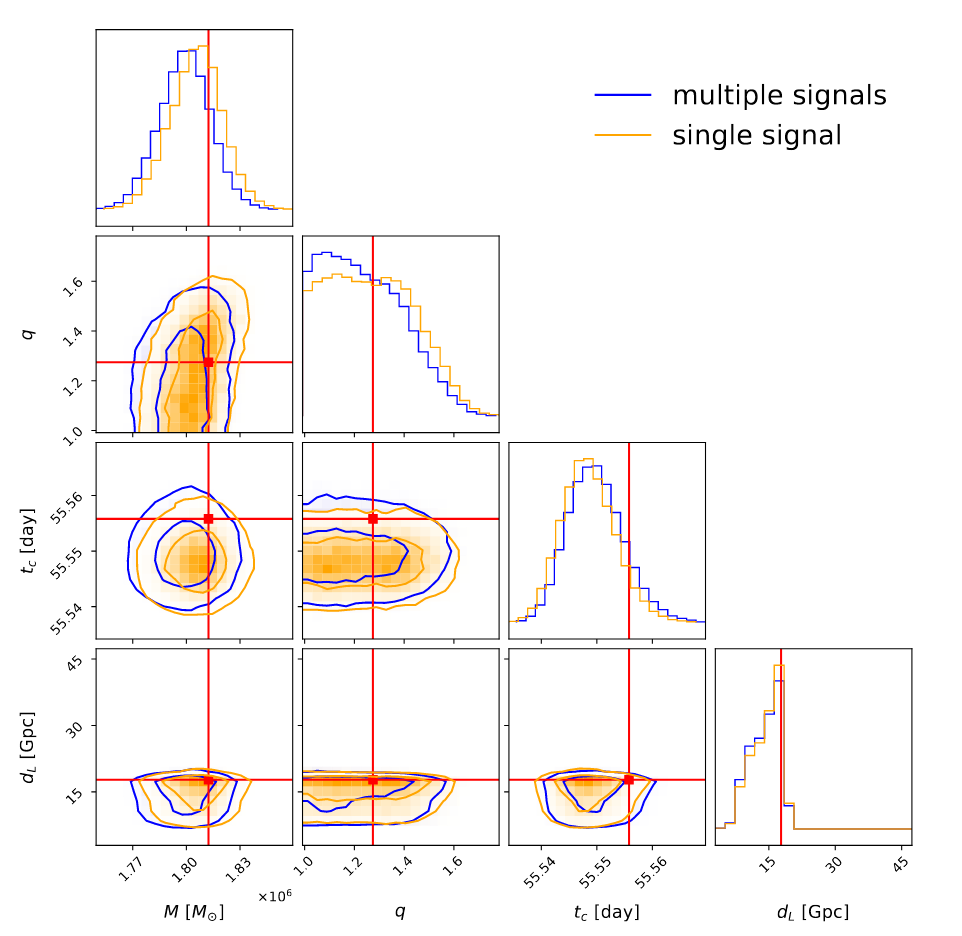



Text

亮点:
- 可以实现完整参数维度的快速参数反演
- 在AI推断结果中发现额外的多模态
- 利用投影对称性解放模型的泛化性
空间引力波探测科学数据处理:人工智能技术
Text
Text

杜明辉*, 梁博*, 王赫†, 徐鹏, 罗子人, 吴岳良†, accepted by SCPMA, arXiv:2308.05510

- 超大质量黑洞双星 (MBHB) 的并合是空间引力波可以探测到的最强瞬态信号源,对于低红移源,信噪比 (SNR) 可超过1000。
- 预期质量范围是 \(10^4\sim10^7\) 太阳质量,可观测到晚期的双星绕旋、并合和振荡衰减阶段,事件率约为每年几个到几百个。
- 深度学习技术的应用:参数反演
- 人工智能算法可实现混叠 MBHB 信号的全波源参数反演,比传统估计后验分布算法的采样效率高 3 个数量级。
阮文洪, 王赫, 刘畅, 郭宗宽,
Universe (2023)




Text


亮点:
- 可以实现完整参数维度的快速参数反演
- 在AI推断结果中发现额外的多模态
- 利用投影对称性解放模型的泛化性
空间引力波探测科学数据处理:人工智能技术
Text
Text

for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This silde: https://slides.com/iphysresearch/2024may_neu
- 超大质量黑洞双星 (MBHB) 的并合是空间引力波可以探测到的最强瞬态信号源,对于低红移源,信噪比 (SNR) 可超过1000。
- 预期质量范围是 \(10^4\sim10^7\) 太阳质量,可观测到晚期的双星绕旋、并合和振荡衰减阶段,事件率约为每年几个到几百个。
- 深度学习技术的应用:参数反演
- 人工智能算法可实现混叠 MBHB 信号的全波源参数反演,比传统估计后验分布算法的采样效率高 3 个数量级。

Text

空间引力波探测科学数据处理:人工智能技术

归一化流模型示意图


亮点:
- 可以实现完整参数维度的快速参数反演
- 在AI推断结果中发现额外的多模态
- 利用投影对称性解放模型的泛化性
Text
Text

空间引力波探测科学数据处理的技术难题
超高维度的波源参数空间特性 (编码波形)
- 随着星座的轨道运动,引力波信号会随时间发生变化 (链路相关)。
- 星座对特定波源的探测敏感性也会随时间而改变。
- 我们如何在波形的模式识别中融入星座的轨道运动信息?
科学数据的动态性 (编码数据)
- 面对科学数据的固有复杂性——尤其是数据的高维度——我们应如何应对?
计算资源的需求与利用 (CPU vs GPU)
- 总 CPU 需求 (以 CPU 小时计)是 20-30M,其中每年需要进行3次迭代,每次迭代需要2个管道。
- 用转换系数 10 来估计 GPU 的需求,可估算出所有波源类型的 GPU 卡需求可达 \(10^3\) 以上。



F(t) over 1 year
h(t) over 10 min
y(t) over 1 year

Credit: Maude Le Jeune (2021)
Text
Text
Text
2
Actually, there are more ...

- 非模板引力波信号(背景)的探测与重构
- ...
多类型的大量波源混叠问题


for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This slide: https://slides.com/iphysresearch/2024jan_bnu
空间引力波探测科学数据处理的技术难题
超高维度的波源参数空间特性 (编码波形)
- 随着星座的轨道运动,引力波信号会随时间发生变化 (链路相关)。
- 星座对特定波源的探测敏感性也会随时间而改变。
- 我们如何在波形的模式识别中融入星座的轨道运动信息?
科学数据的动态性 (编码数据)
- 面对科学数据的固有复杂性——尤其是数据的高维度——我们应如何应对?
计算资源的需求与利用 (CPU vs GPU)
- 总 CPU 需求 (以 CPU 小时计)是 20-30M,其中每年需要进行3次迭代,每次迭代需要2个管道。
- 用转换系数 10 来估计 GPU 的需求,可估算出所有波源类型的 GPU 卡需求可达 \(10^3\) 以上。



F(t) over 1 year
h(t) over 10 min
y(t) over 1 year

Credit: Maude Le Jeune (2021)
Text
Text
Text
2
Actually, there are more ...

- 非模板引力波信号(背景)的探测与重构
- ...
多类型的大量波源混叠问题


空间引力波探测科学数据处理:人工智能技术
-
波形建模
- 极端质量比黑洞双星的绕旋 (EMRIs) 是空间引力波探测的重要信号源
- 传统的匹配滤波方法由于需要大量高精度波形模板而在计算上不切实际
- 深度学习技术的应用:
- 利用GPU加速EMRI波形的模式识别分析,为毫赫兹空间引力波数据分析提供了强大的计算工具和新的可能性,显著提升了数据处理的效率和精度
EMRI 波形模板需求量 40 个数量级以上

MNRAS 488, L94–L98 (2019)
Chua et al., Phys. Rev. Lett., (2021)

~1s (快 ≳\(10^4\) 倍)
\(h(\theta):=\sum_i \alpha_i(\theta) e_i \equiv \alpha(\theta) \text {, }\)
where \(\alpha\in\mathbb{C}^{241}\) and reduced basis \(\{e_i\}\) with \(\left\langle e_i \mid e_j\right\rangle=\delta_{i j}\).
深度学习算法的学习目标
\((\mathcal{M}_c, \eta)\in\Theta\subset\mathbb{R}^2\)
\((\alpha_r, \alpha_i) \in\mathbb{R}^{482} \)
Neural
Network
Chua et al., PRL 122, 21 (2019): 211101.
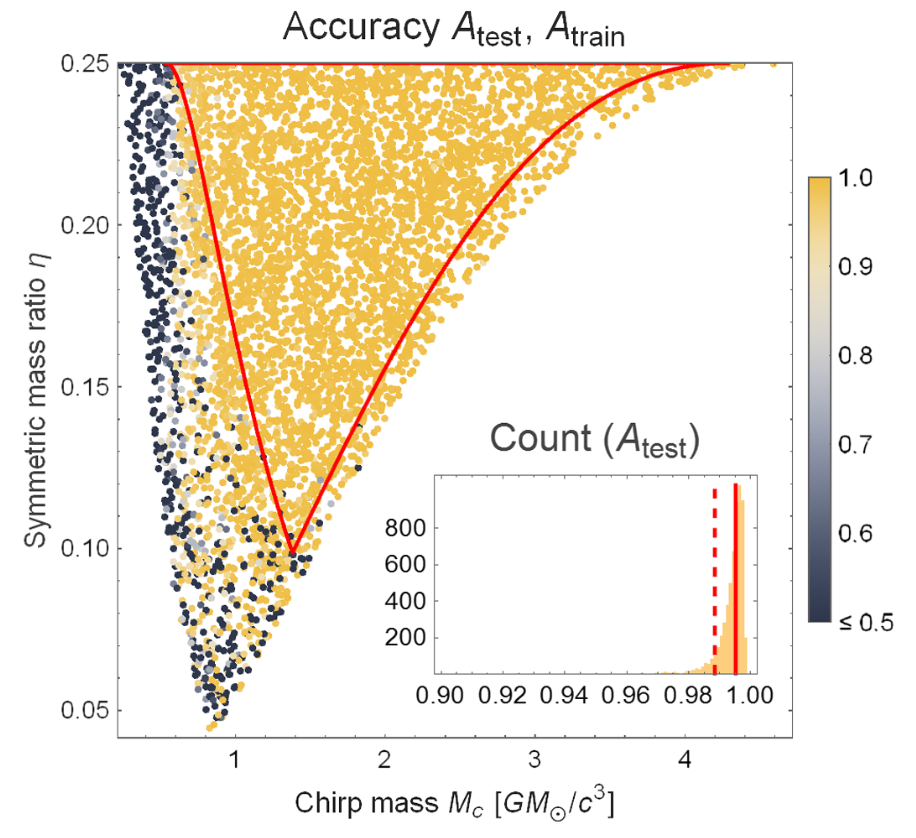
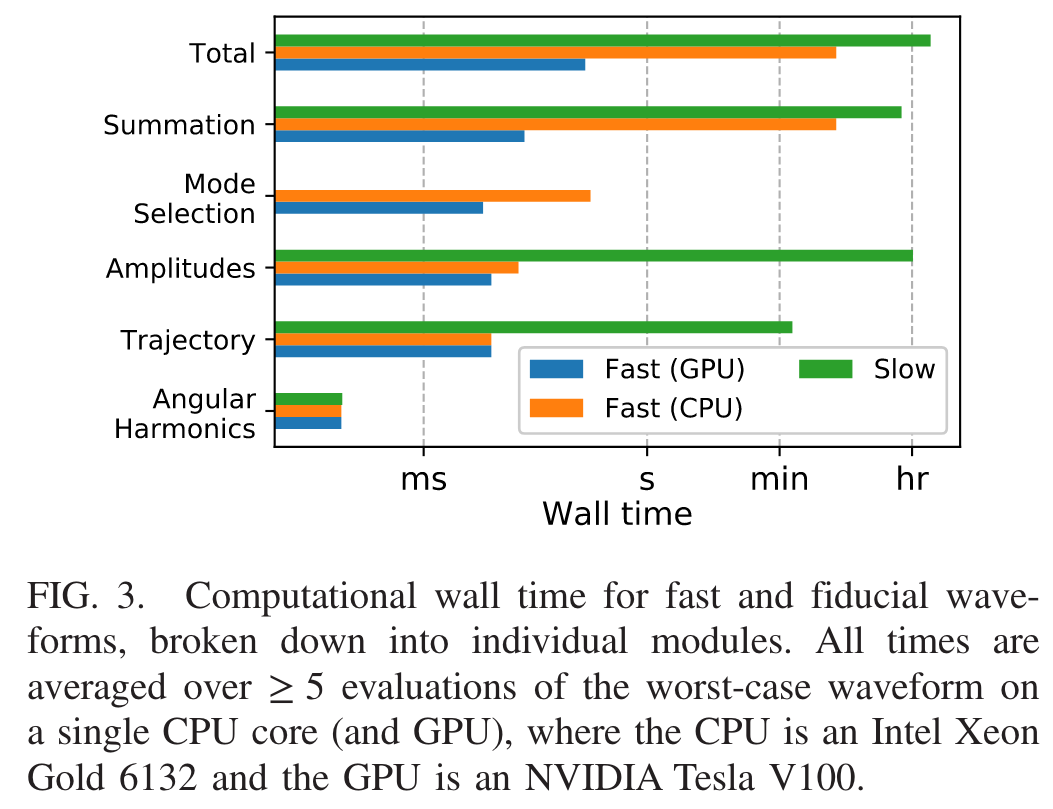
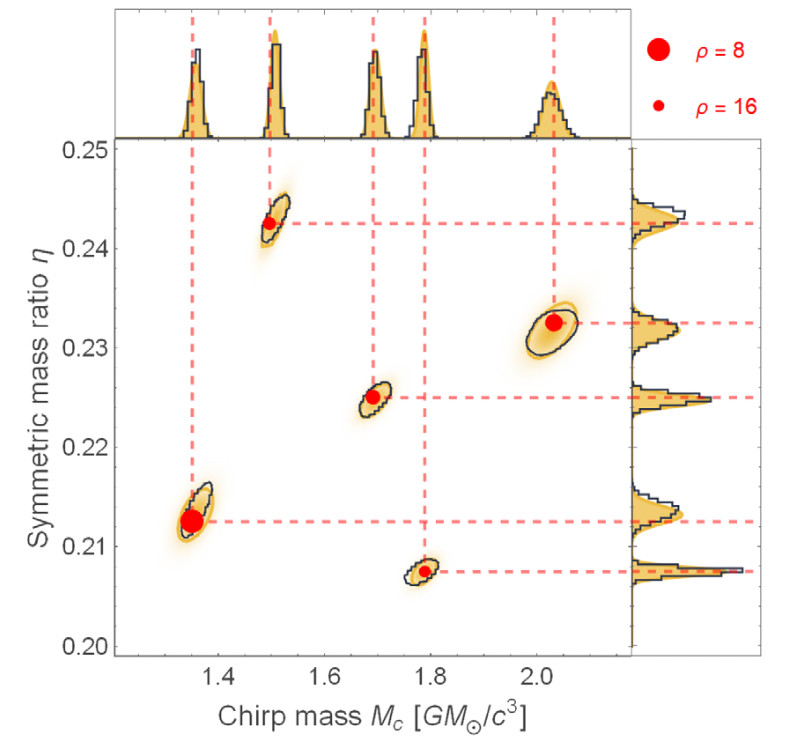
Chua & Vallisneri. PRL 124, 4 (2020): 041102.

Katz et al., PRD 104, 6 (2021): 064047.
AKK - FastEMRIWaveforms (FEW) package
Katz et al., Phys. Rev. D (2021)


- 波形建模
-
信号探测
- EMRI
空间引力波探测科学数据处理:人工智能技术
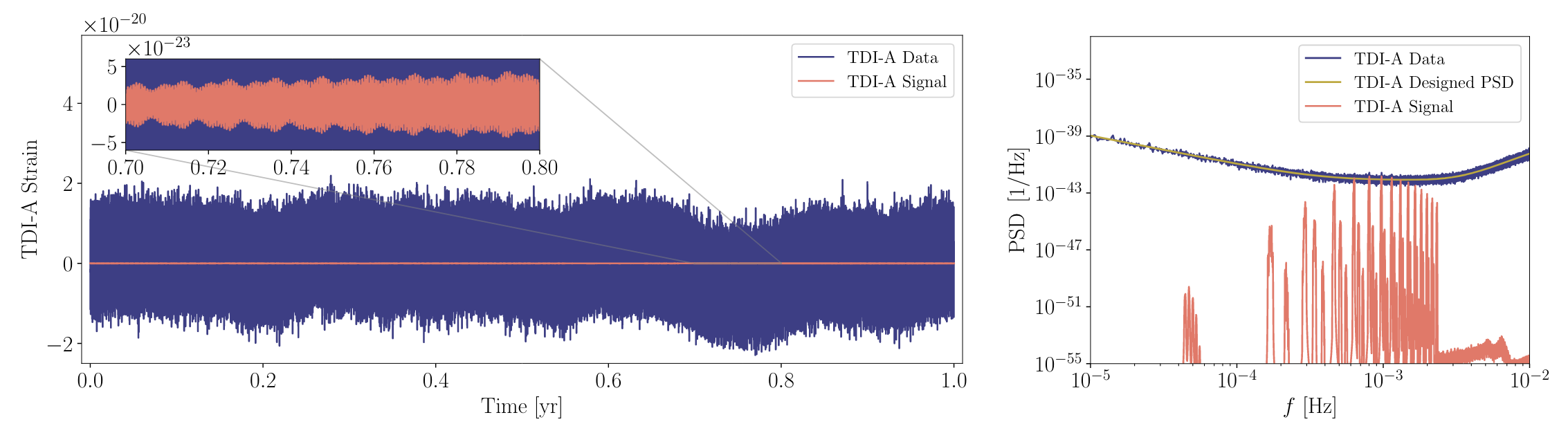
时长 1 年且含有信噪比 70的EMRI时域数据


目录


- 空间引力波探测:全局拟合问题
- 科学智能:引力波数据处理
- 空间引力波探测科学数据处理:人工智能技术
- AI for 科学发现:机遇与挑战 (bonus)
-
Bayesian inference, the Holy Grail of gravitational-wave data analysis,
enables astrophysical interpretation and scientific discoveries.
Simulation-Based Inference (SBI)
- SBI \(\Rightarrow\) Fast and precise parameter estimation.
- SBI \(\Rightarrow\) Test of General Relativity (TGR) / Cosmology / PTA ...


AI Predicting the Universe: Opportunities and Challenges
Text

PRL 127, 24 (2021) 241103.
PRL 130, 17 (2023) 171403.

Real-time gravitational wave science with neural posterior estimation
Sampling with prior knowledge for high-dimensional gravitational wave data analysis
H.W., et al. Big Data Min. Anal. (2021)

PRD 108, 4 (2023): 044029.
Neural Posterior Estimation with Guaranteed Exact Coverage: The Ringdown of GW150914

arXiv:2310.12209
Fast Parameter Inference on Pulsar Timing Arrays with Normalizing Flows

arXiv:2310.13405, LIGO-P2300306
Cosmological Inference using Gravitational Waves and Normalising Flows
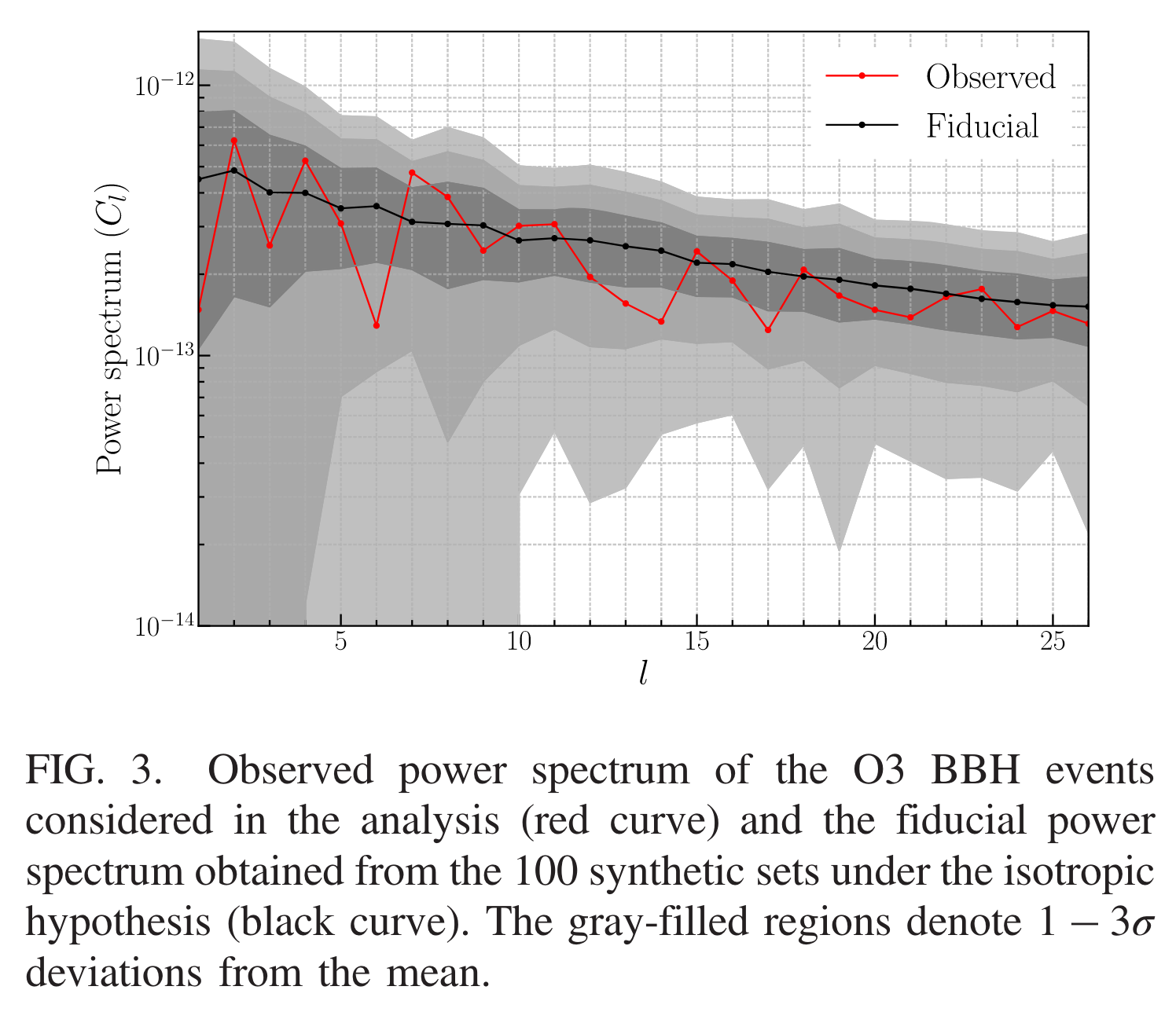
PRL 131, 17 (2023): 171403.
Angular Power Spectrum of Gravitational-Wave Transient Sources as a Probe of the Large-Scale Structure


Key Takeaways
On-going
- About Data: We are developing a software toolkit called GWToolkit that integrates gravitational wave signal processing and generic asynchronous data pipeline capabilities.
- About Models: Let's continue to leverage representation learning and explore the use of GPT-like language models for scientific discovery.
Insights
- AI is not just a tool; it is a revolutionary pathway for scientific discoveries.
- The future is filled with technical challenges, even when it comes to using AI, including:
- Super high-dimensional parameter inference
- Super high-dimensional of GW data strains
- "Gravitational Wave Astrostatistics" has the potential to become a new field of knowledge.
- Improve the interpretability of AI models, as it is essential for enhanced and trustworthy discoveries.
Text
Text
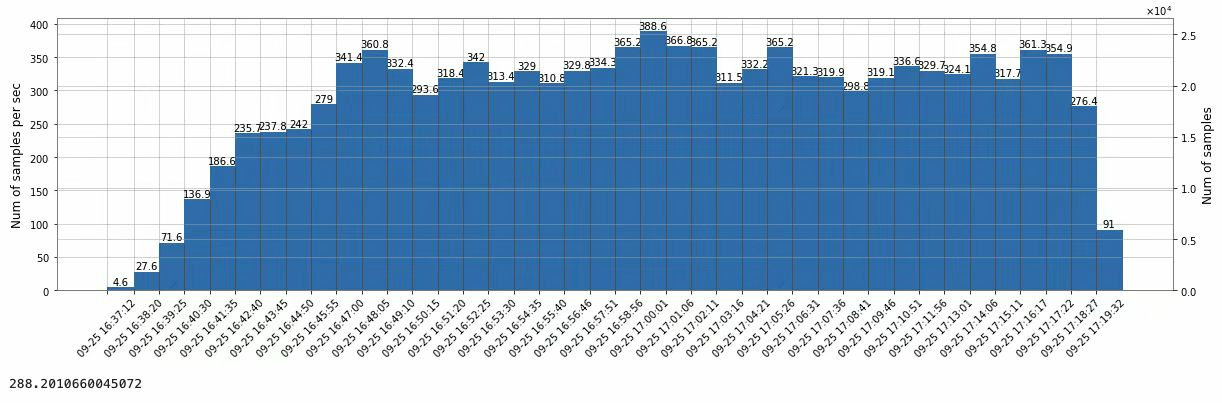
Dynamic training samples in memory.

Nature Physics 18, 1 (2022): 9–11


Key Takeaways
On-going
- About Data: We are developing a software toolkit called GWToolkit that integrates gravitational wave signal processing and generic asynchronous data pipeline capabilities.
- About models: Let's continue to leverage representation learning and explore the use of GPT-like language models for scientific discovery.
Insights
- AI is not just a tool; it is a revolutionary pathway for scientific discoveries.
- The future is filled with technical challenges, even when it comes to using AI, including:
- Super high-dimensional parameter inference
- Super high-dimensional of GW data strains
- "Gravitational Wave Astrostatistics" has the potential to become a new field of knowledge.
- Improve the interpretability of AI models, as it is essential for enhanced and trustworthy discoveries.
Text
Text

Dynamic training samples in memory.

Nature Physics 18, 1 (2022): 9–11
for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This slide: https://slides.com/iphysresearch/2024jan_bnu
空间引力波探测的典型波源与全局拟合问题
GW sources and the global-fit problem
其他科学数据处理挑战:Glitches, gaps, non-stationarities
-
机器学习技术的原理验证研究
-
波形建模:(review: 2101.11608, 2203.08434)
-
EMRI
- Chua, Alvin J. K., Michael L. Katz, Niels Warburton, and Scott A. Hughes. “Rapid Generation of Fully Relativistic Extreme-Mass-Ratio-Inspiral Waveform Templates for LISA Data Analysis.” Physical Review Letters 126, no. 5 (February 2021): 051102. https://doi.org/10.1103/PhysRevLett.126.051102.
- Katz, Michael L., Alvin J. K. Chua, Lorenzo Speri, Niels Warburton, and Scott A. Hughes. “Fast Extreme-Mass-Ratio-Inspiral Waveforms: New Tools for Millihertz Gravitational-Wave Data Analysis.” Physical Review D 104, no. 6 (September 17, 2021): 064047. https://doi.org/10.1103/PhysRevD.104.064047
-
EMRI
-
参数估计:
- MBHB Chua AJK and Vallisneri M. PRL 2021; 2307.14844; 2308.05510
-
信号探测:
- EMRI Zhang XT, Messenger C, et al. PRD 2022; 2308.16422; 2309.06694;
- MBHB Ruan WH, Wang H, Liu C, Guo ZK. arXiv:2111.14546
- EMRI+MBHB+GBs+SGWB Zhao TY, Lyu R, Ren ZX, Wang H, Cao ZJ. arXiv: 2207.07414
-
数据降噪:
- GBs Zhang XH, Zhao SD, Mohanty SD, Liu YX. PRD 2022
-
波形建模:(review: 2101.11608, 2203.08434)
空间引力波探测科学数据处理的技术挑战(超高维参数空间(内禀),非稳态,计算资源)
科学数据处理的深度学习技术应用:现状
- 波形建模(EMRI)
- 信号探测(EMRI, MBHB, ...)
- 参数估计(MBHB)
科学数据处理的深度学习技术应用:现状
- EMRI
- 波形建模
- 信号探测
- MBHB
- 信号探测
- 参数估计
-
In 1916, A. Einstein proposed the GR and predicted the existence of GW.
-
Gravitational waves (GW) are a strong field effect in the GR.
-
2015: the first experimental detection of GW from the merger of two black holes was achieved.
-
2017: the first multi-messenger detection of a BNS signal was achieved, marking the beginning of multi-messenger astronomy.
-
2017: the Nobel Prize in Physics was awarded for the detection of GW.
-
As of now: more than 90 gravitational wave events have been discovered.
-
O4, which began on May 24th 2023, is currently in progress.
-




双星并合系统产生的引力波波源
引力波振幅的测量
地面引力波探测器网络
2017 年诺贝尔物理学奖
Gravitational Wave Astronomy
Gravitational Wave Astronomy
-
Fundamental Physics
- Existence of gravitational waves
- To put constraints on the properties of gravitons
-
Astrophysics
- Refine our understanding of stellar evolution
- and the behavior of matter under extreme conditions.
-
Cosmology
- The measurement of the Hubble constant
- Dark energy

©Floor Broekgaarden (repo)

GWTC-3
- Detecting gravitational waves require a mix of FIVE key ingredients:
- good detector technology
- good waveform predictions
- good data analysis methodology and technology
- coincident observations in several independent detectors
- coincident observations in electromagnetic astronomy
—— Bernard F. Schutz
DOI:10.1063/1.1629411
- AI for Science \(\rightarrow\) AI for GW
- Artificial Intelligence (AI) has great potential to revolutionize gravitational wave astronomy by improving data analysis, modeling, and detector development.




AI for Gravitational Wave
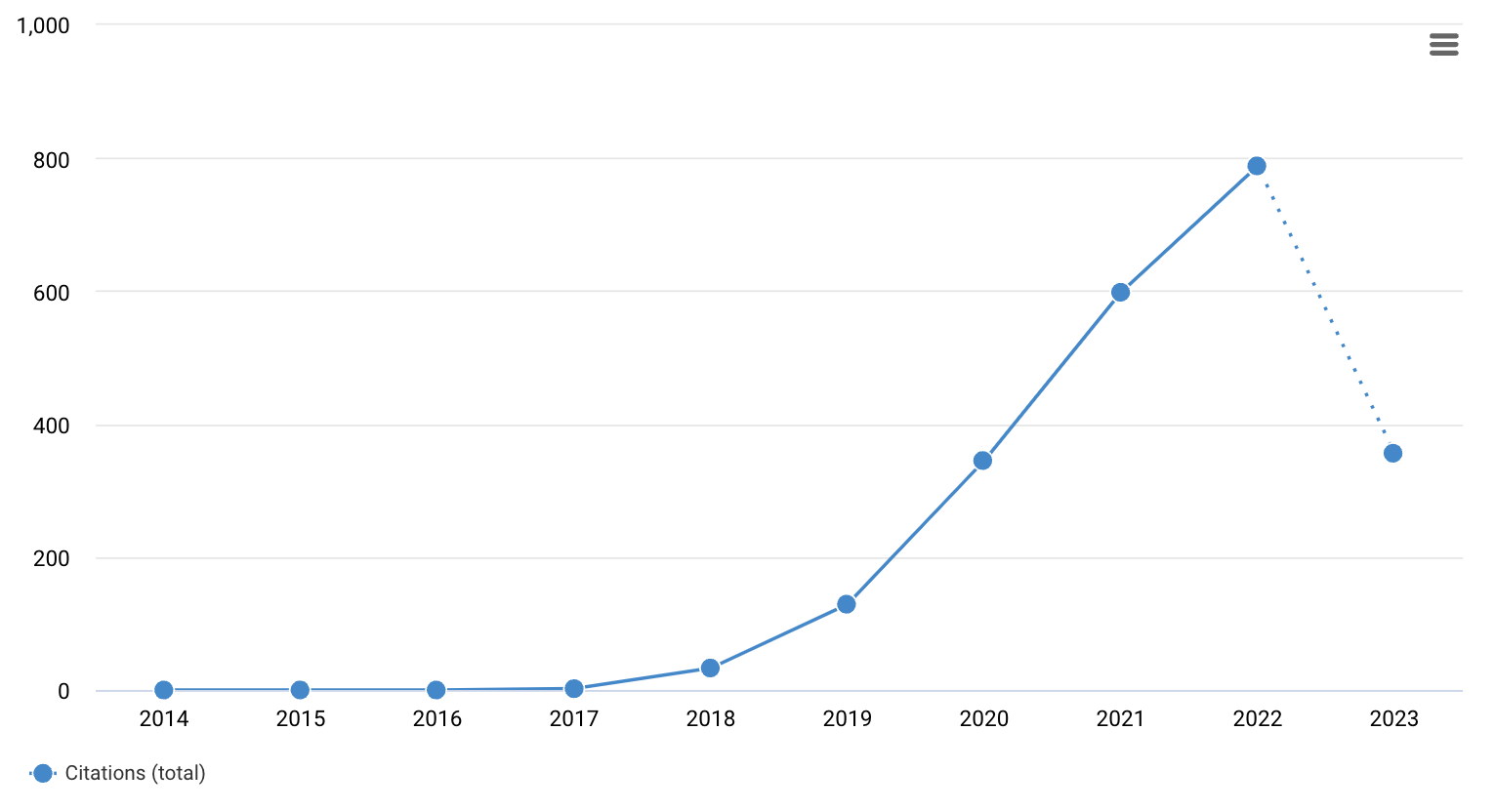
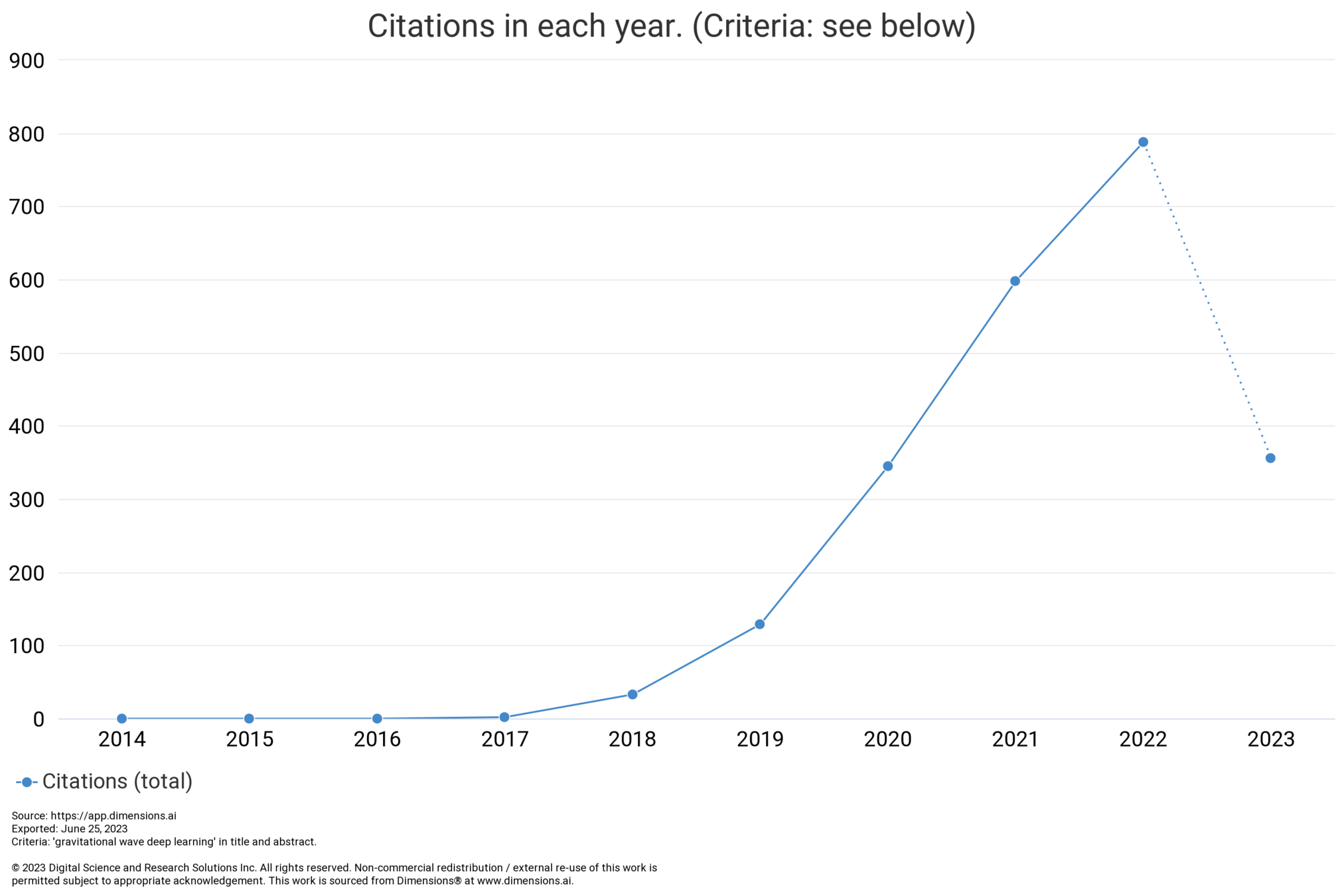

AI for Gravitational Wave
-
GW Data characteristics:
-
Noise: non-Gaussian and non-stationary
-
Signal: A low signal-to-noise ratio (SNR) which is typically about 1/100 of the noise amplitude (-60 dB)
-


Data quality improvement
Credit: Marco Cavaglià
LIGO-Virgo data processing
GW searches
Astrophsical interpretation of GW sources
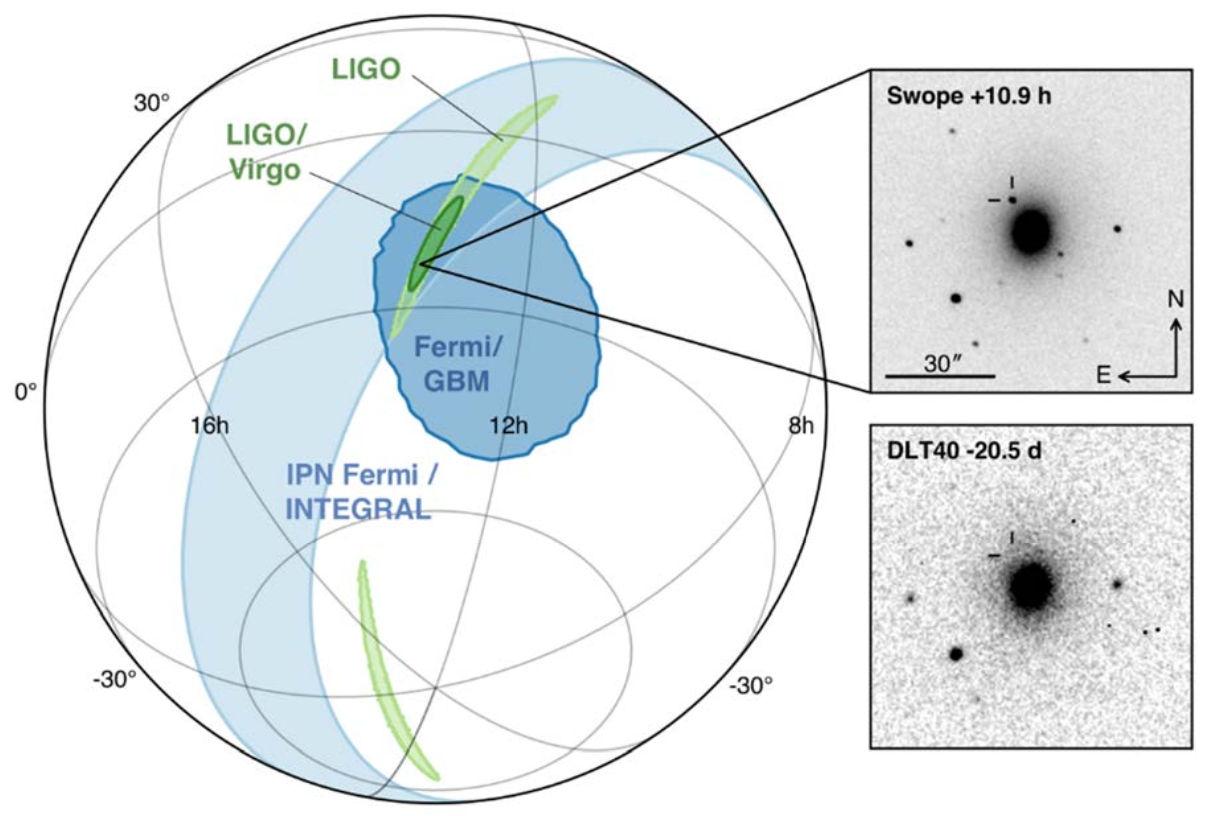
AI for Gravitational Wave: Searches
Matched-filtering Convolutional Neural Network (MFCNN)

GW150914 的实时信号搜寻
-
The majority of machine learning algorithms used for testing are highly sensitive to non-Gaussian real noise backgrounds, resulting in high false positive rates.

LIGO-Virgo data processing

PRD 107, 6 (2023) 063029
-
Ensemble learning leverages statistical approaches to utilize more information for making informed decisions by combining multiple models.

PRD 101, 10 (2020) 104003.

PRD 105, 8 (2022) 083013



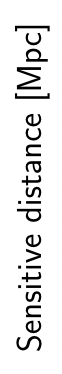
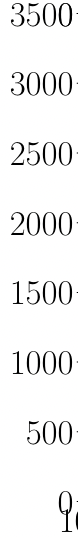
PRD 107, 2 (2023): 023021.
-
Expanding the dimension of the output is to call more information to make decisions in improving AI models.
AI for Gravitational Wave: Parameter Estimation



Bayesian statistics
-
Traditional parameter estimation (PE) techniques rely on Bayesian analysis methods (posteriors + evidence)
- Computing the full 15-dimensional posterior distribution estimate is very time-consuming:
- Calculating likelihood function
- Template generation time-consuming
- Machine learning algorithms are expected to speed up!

Data quality improvement
Credit: Marco Cavaglià
LIGO-Virgo data processing
GW searches
Astrophsical interpretation of GW sources
AI for Gravitational Wave: Parameter Estimation
- A complete 15-dimensional posterior probability distribution, taking about 1 s (<< \(10^4\) s).

LIGO-Virgo data processing

Nature Physics 18, 1 (2022) 112–17
- Prior Sampling: 50,000 Posterior samples in approximately 8 Seconds.


Big Data Mining and Analytics 5, 1 (2021) 53–63.
- Capable of calculating evidence
- Processing time: (using 64 CPU cores)
- less than 1 hour with IMRPhenomXPHM,
- approximately 10 hours with SEOBNRv4PHM


PRL 127, 24 (2021) 241103.
PRL 130, 17 (2023) 171403.
-
Billion-scale transformer-based model (WaveFormer)
- Suppression on realistic noise, and
- Recovery of injections / GW events
arXiv:2212.14283

Data quality improvement
Credit: Marco Cavaglià
LIGO-Virgo data processing
GW searches
Astrophsical interpretation of GW sources
AI for Gravitational Wave: Data Quality Improvement
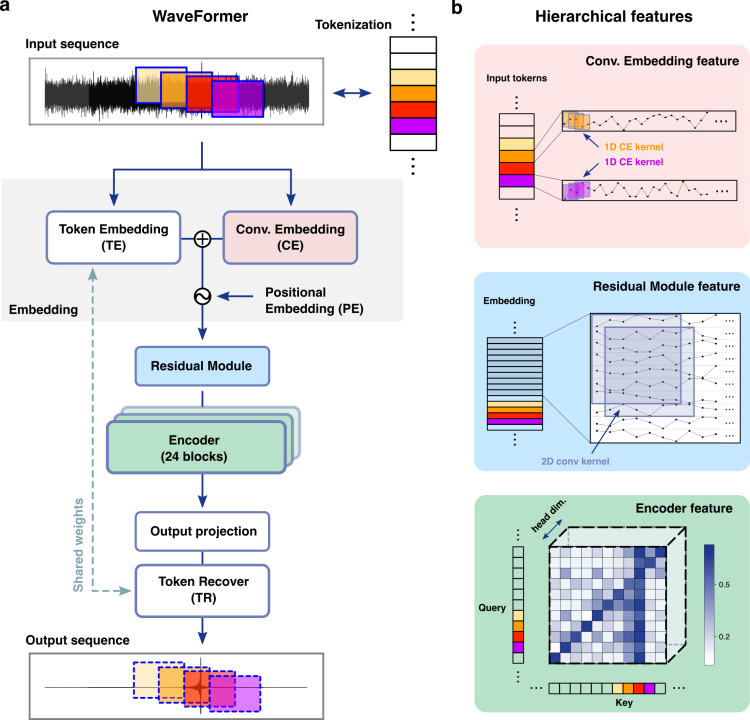
- Billion-scale transformer-based model (WaveFormer)
- Suppression on realistic noise, and
- Recovery of injections / GW events
arXiv:2212.14283
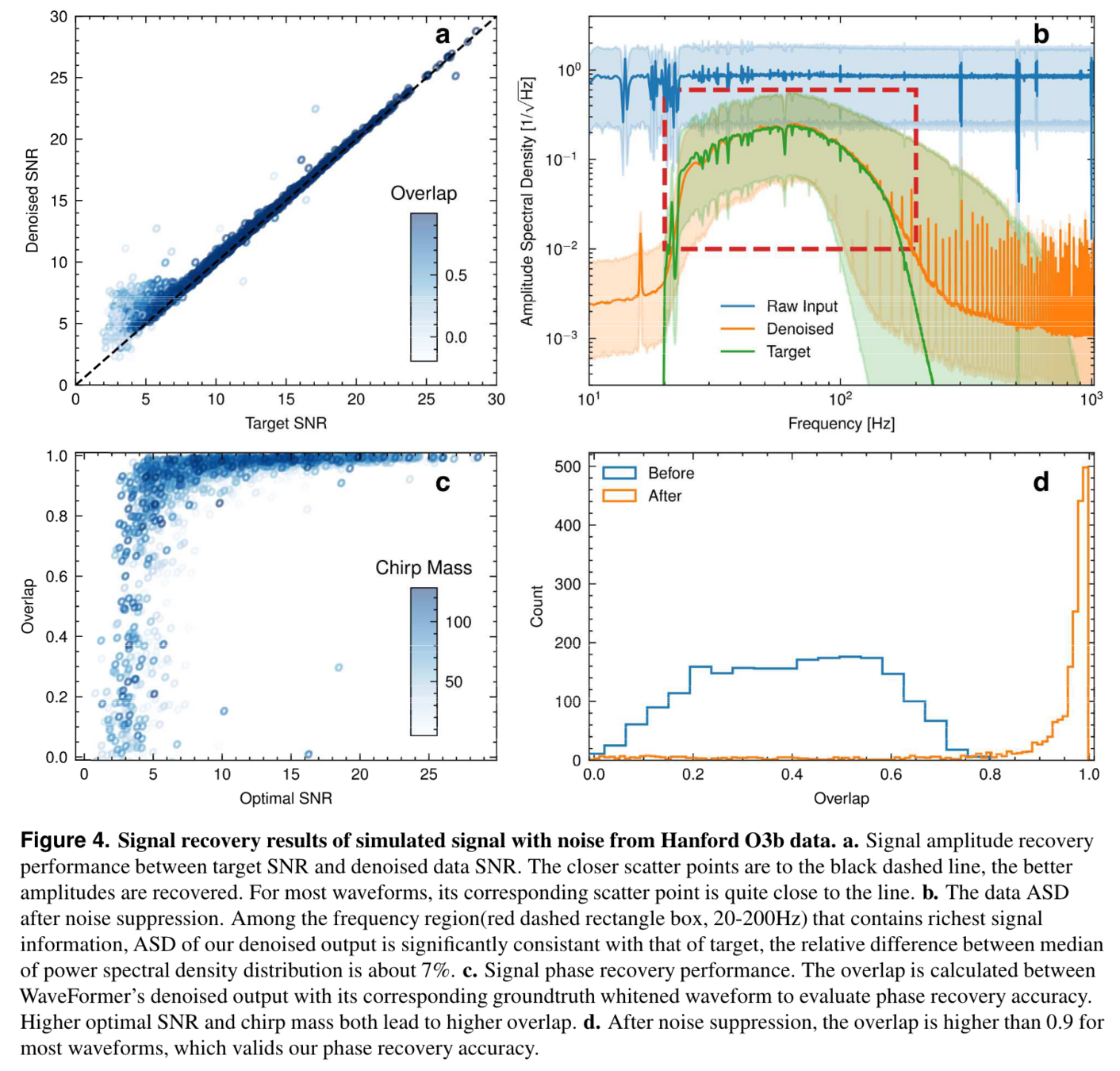
AI for Gravitational Wave: Data Quality Improvement


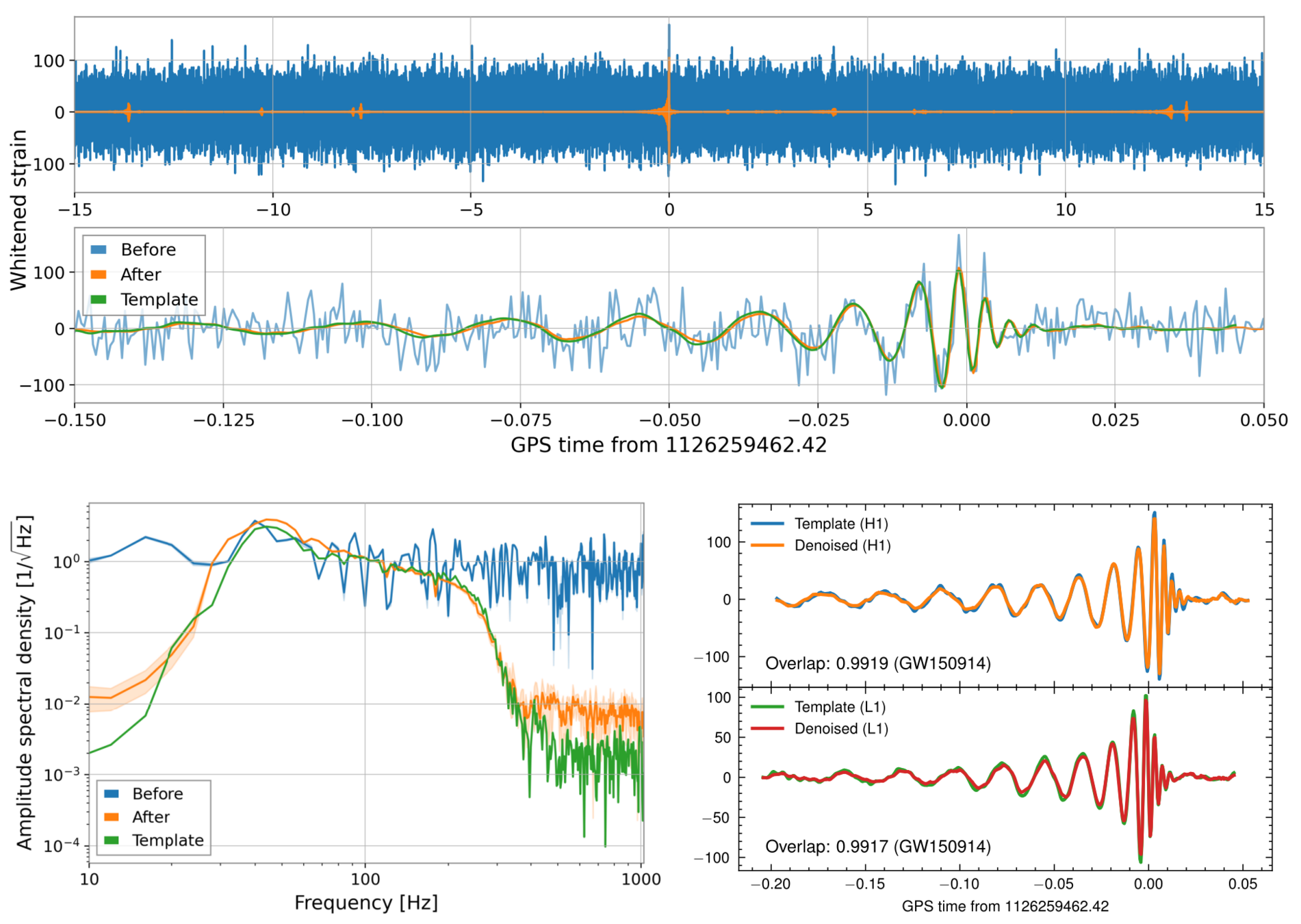

LIGO-Virgo data processing
- Billion-scale transformer-based model (WaveFormer)
- Suppression on realistic noise, and
- Recovery of injections / GW events
arXiv:2212.14283
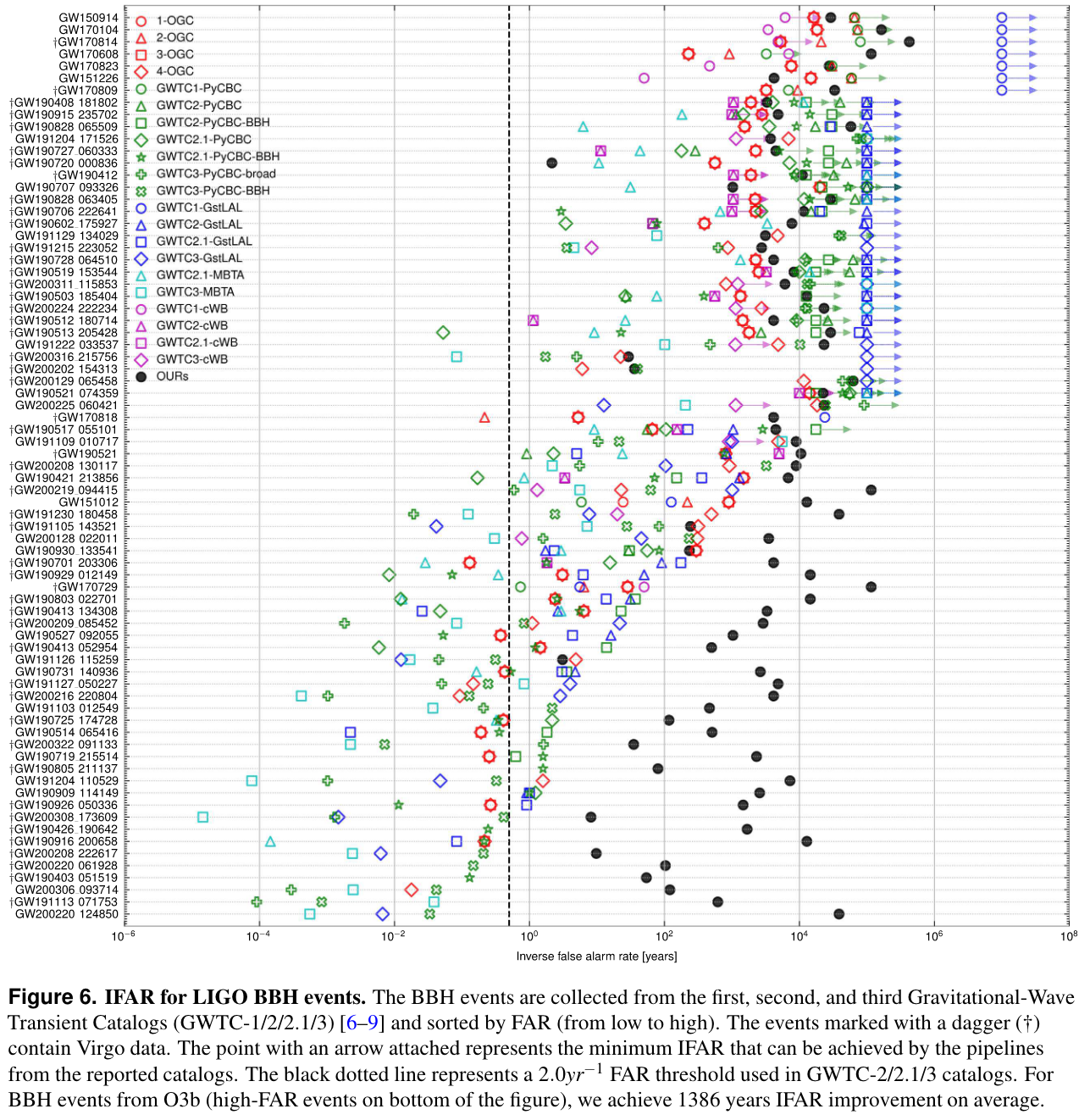
AI for Gravitational Wave: Data Quality Improvement


LIGO-Virgo data processing

Taiji
Space-based Gravitational Wave Data Analysis
- 空间引力波探测主要有以下 4 类波源:
-
恒星级质量的致密双星 (黑洞、中子星、白矮星以及它们的两两组合) 的旋近
-
双白矮星的并合、超大质量双黑洞的并合
-
极端质量比旋进 (通常是一个恒星级致密天体绕着一个超大质量黑洞的旋进)
-
宇宙中可能存在的中等质量双黑洞以及前面这些源的信号叠加形成的引力波背景
-

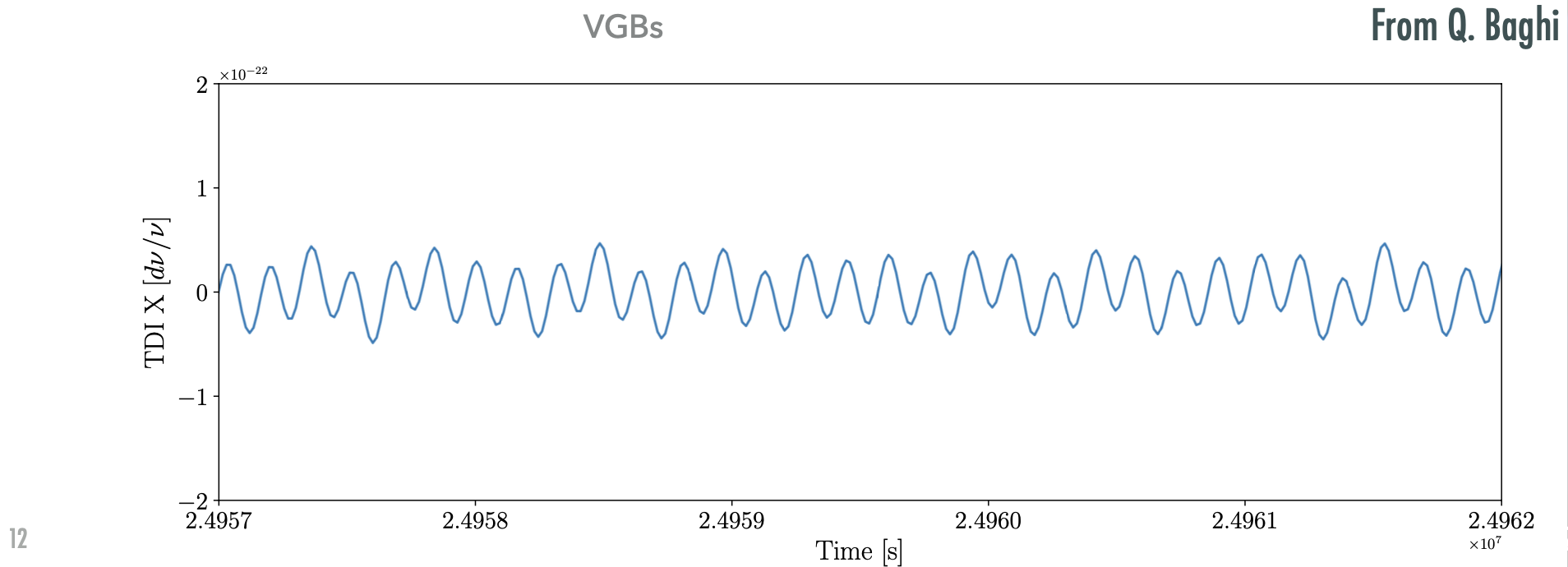
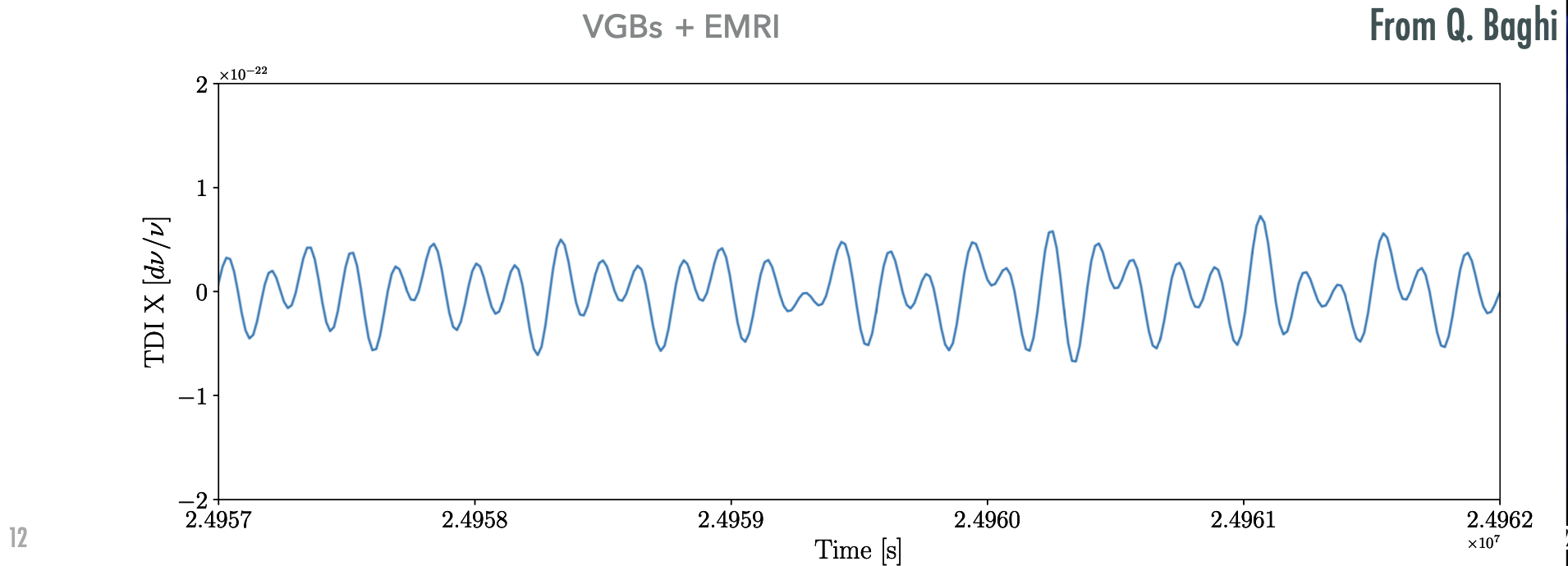
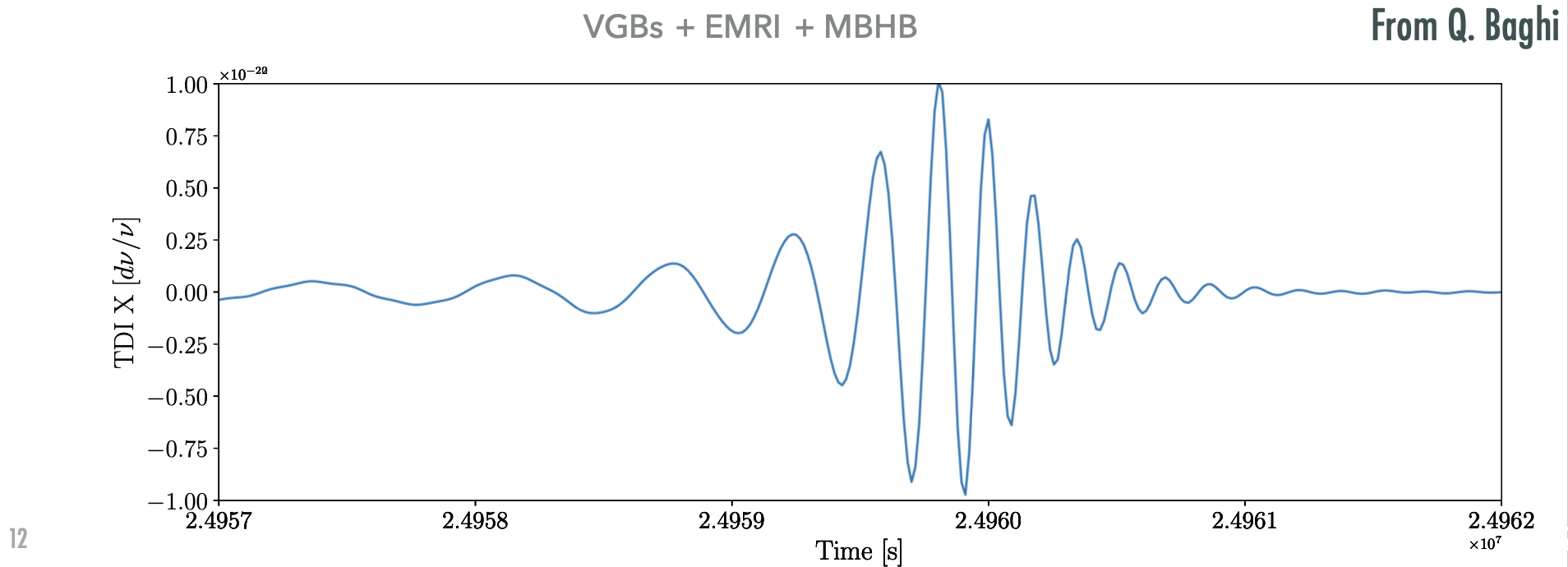
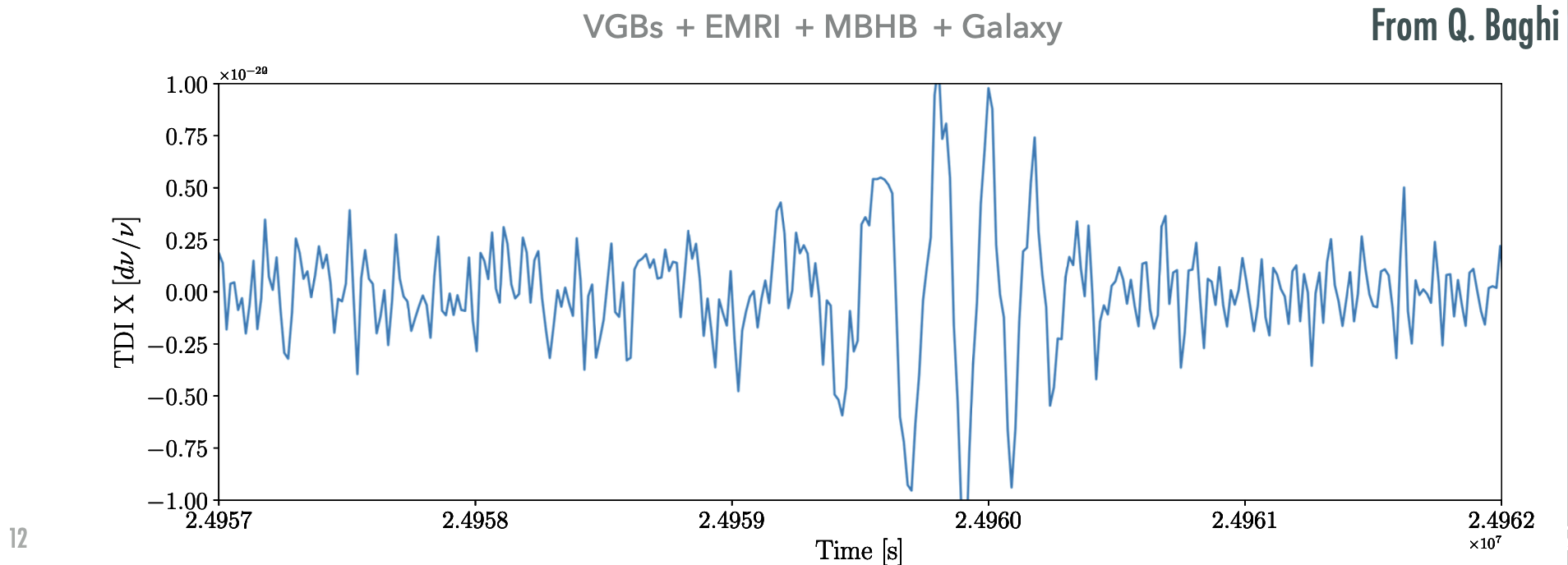
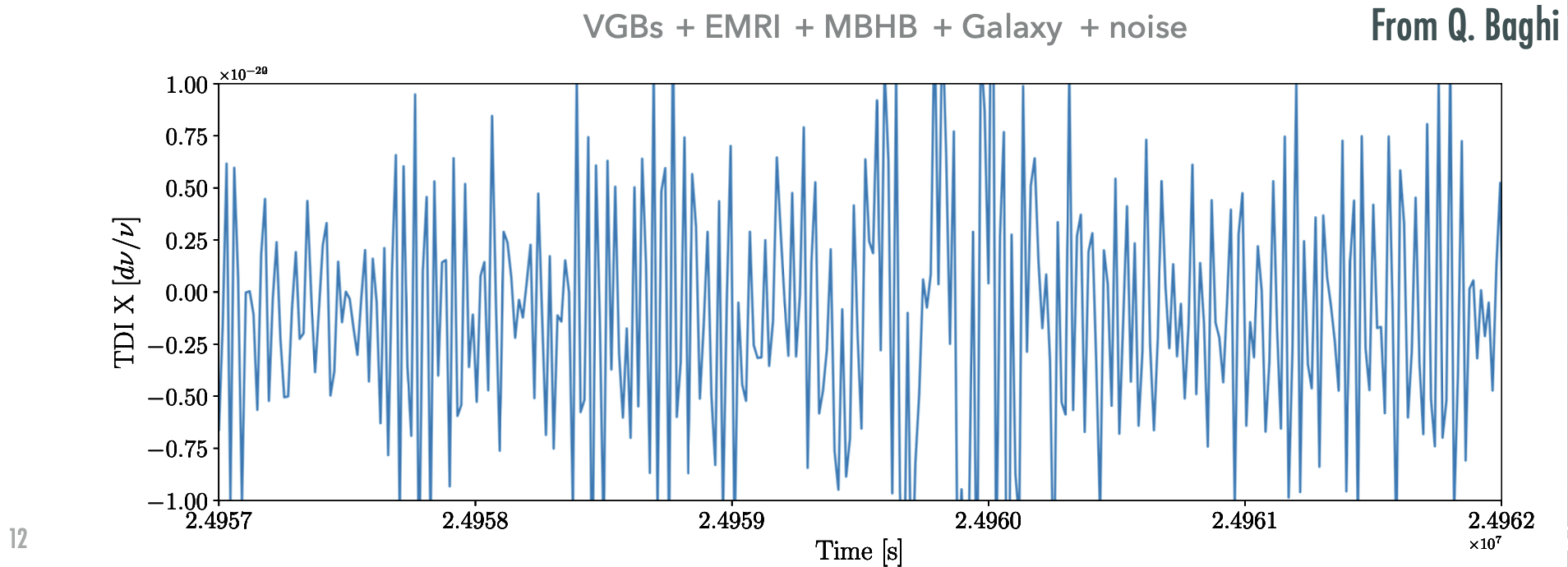
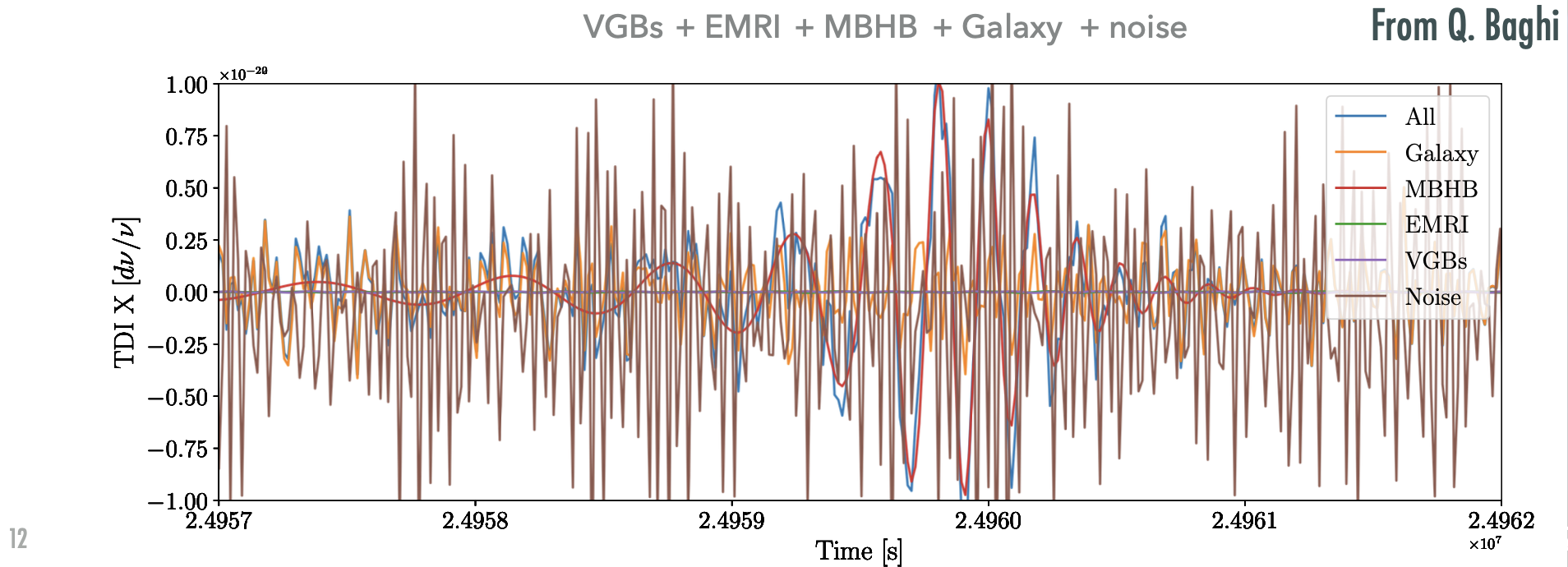
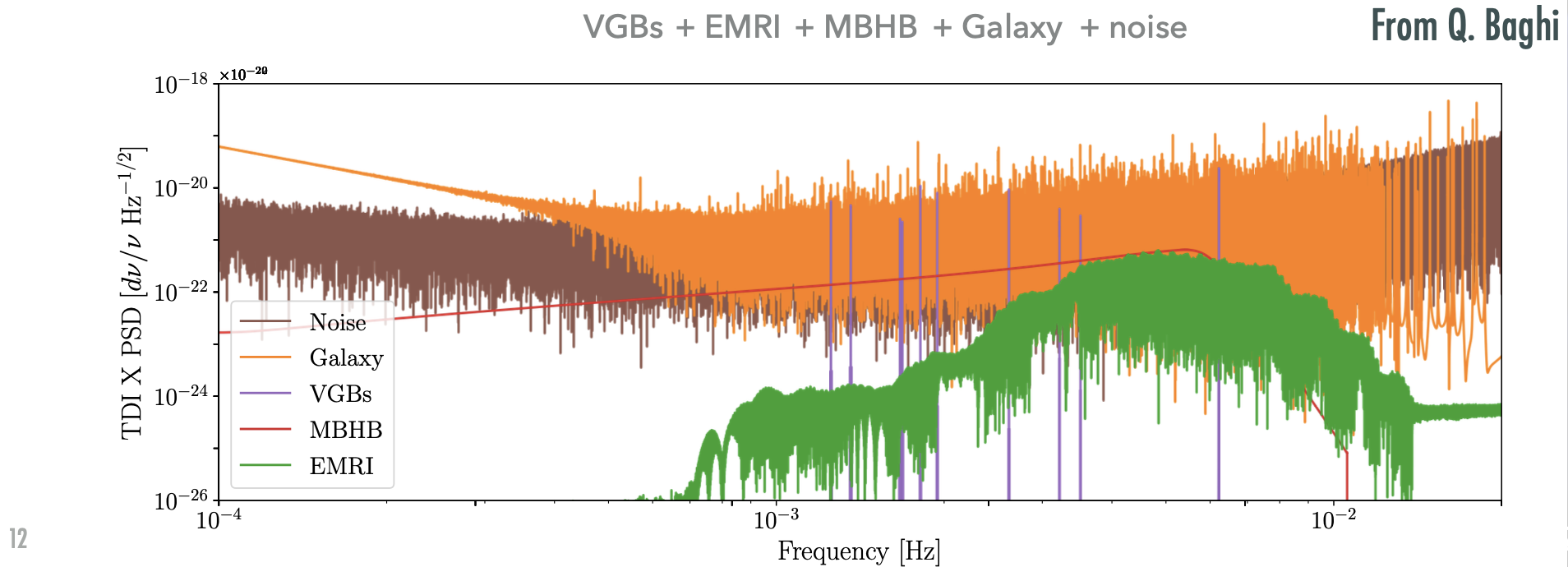
LIGO-G2300554


Credit: ESA, K. Holley-Bockelmann
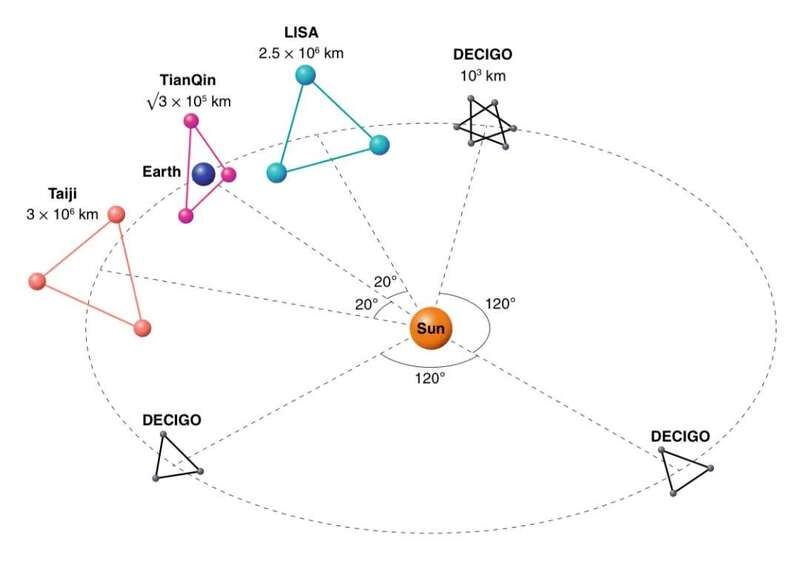
Space-based Gravitational Wave Data Analysis
- Global-fit approach + AI-powered approach
- Searches: Discriminative model
- Inference: Generative model
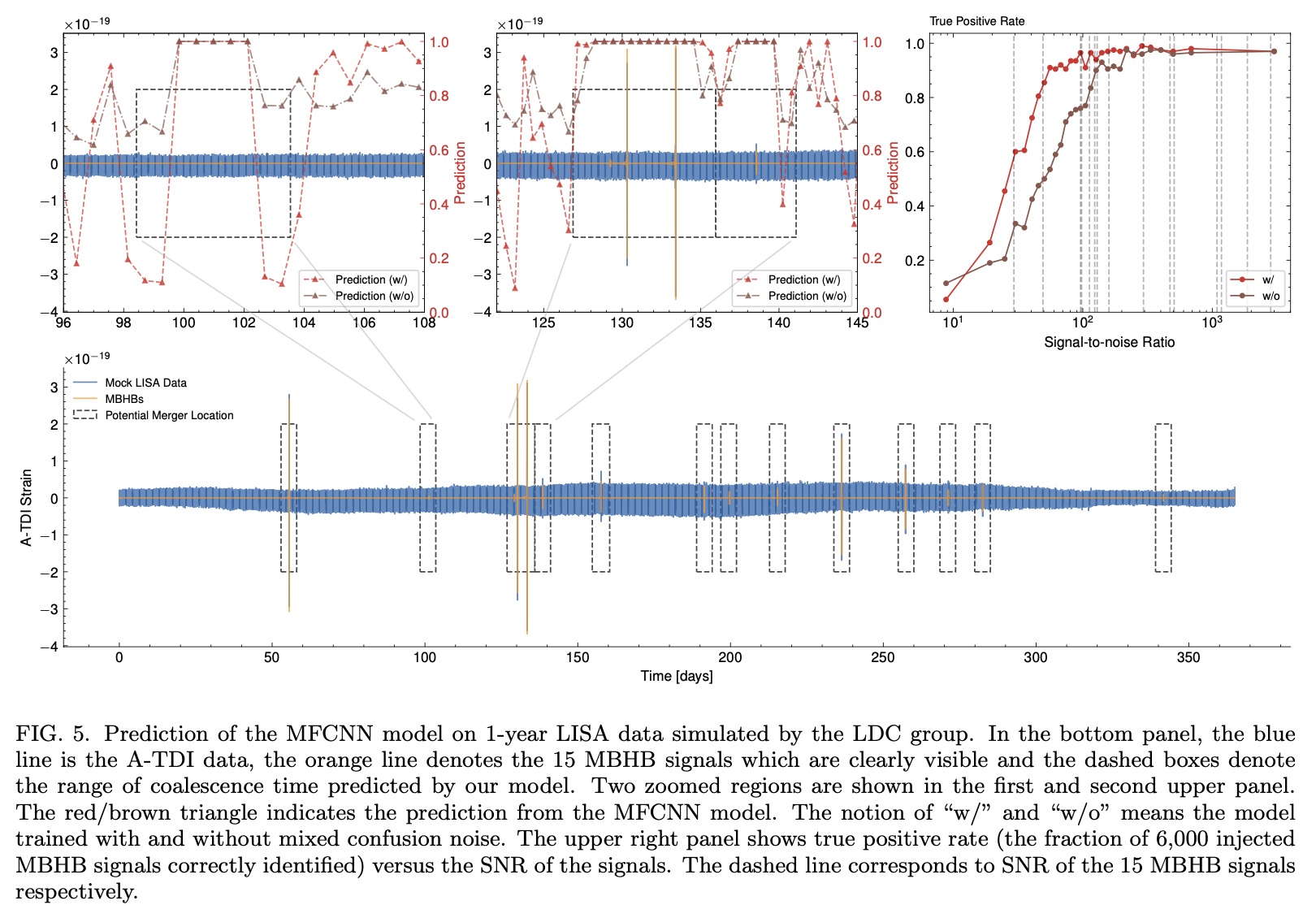
PLB 841 (2023) 137904.
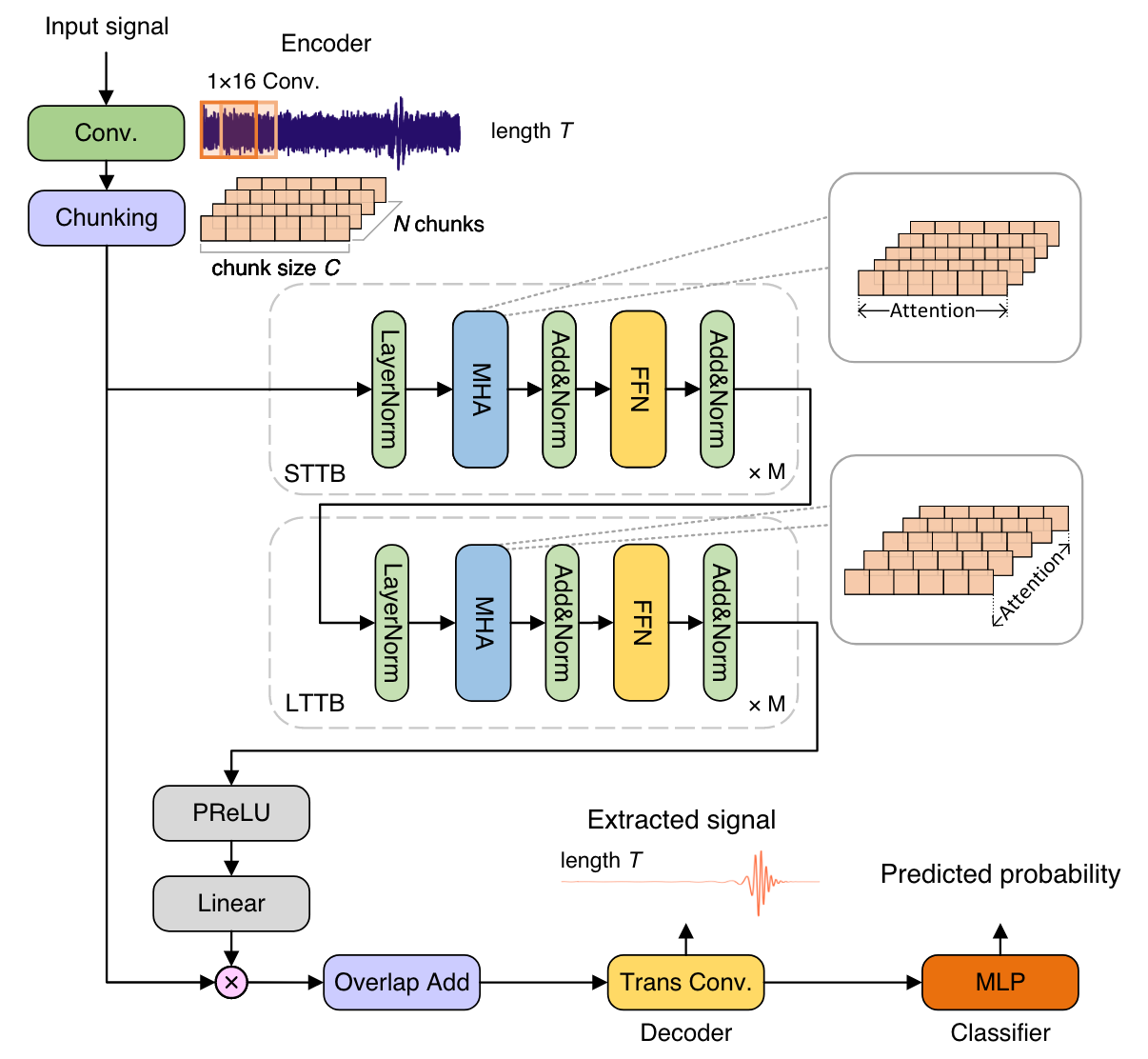
Communications Physics, 2023, 6(1): 212.


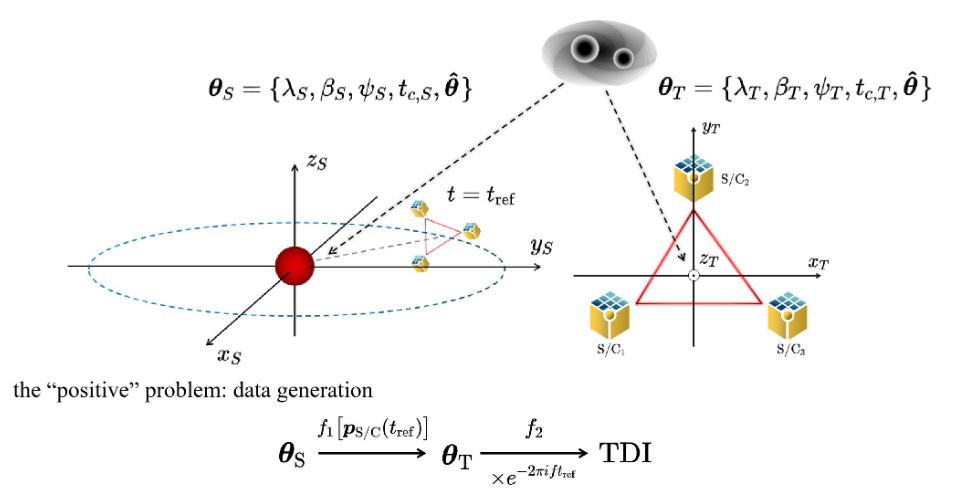
arXiv:2308.05510
Universe, 2023, 9(9): 407.

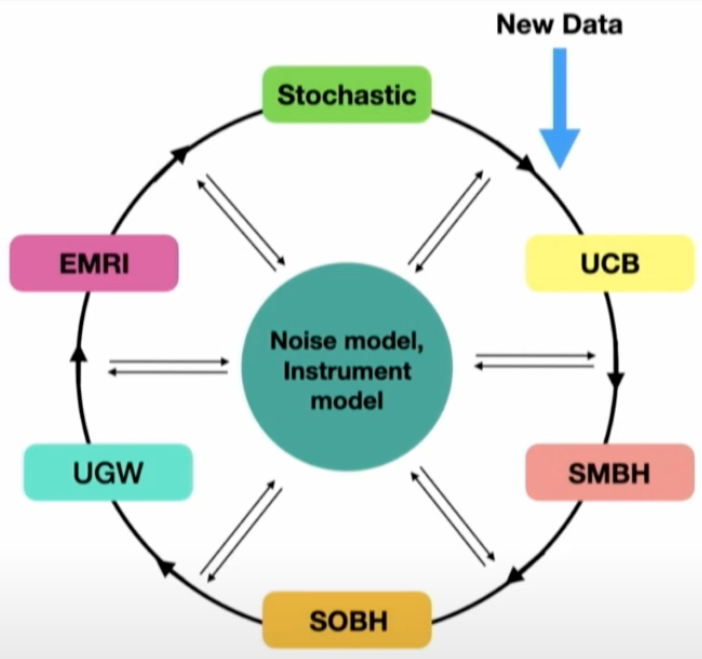
Schematic view of the global fit approach.
-
AI serves as a valuable tool in gravitational wave astronomy:
(Big data & Computational Complexity)- Enhancing data analysis,
- Noise reduction, and
- Parameter estimation.
- It streamlines the research process and allows scientists to focus on the most relevant information.
-
Beyond a Tool: AI transcends its role as a mere tool by enabling scientific discovery in GW astronomy.
- Characterization of GW signals involves
- Exploring beyond the scope of GR ,
- Enabling real-time inference
- "Curse of Dimensionality" in inference
- Overlapping signal (In progress)
- Hierarchical Bayesian Analysis (In progress)
- Test of GR
- Tighter parameter constraints of variance
- Guaranteed exact coverage
- ...
- Characterization of GW signals involves
Challenge in GW Data Analysis: Lessons and Future
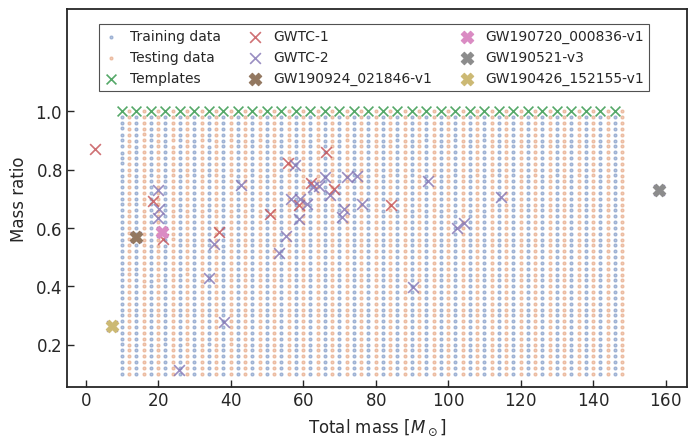
GW170817
GW190412
GW190814
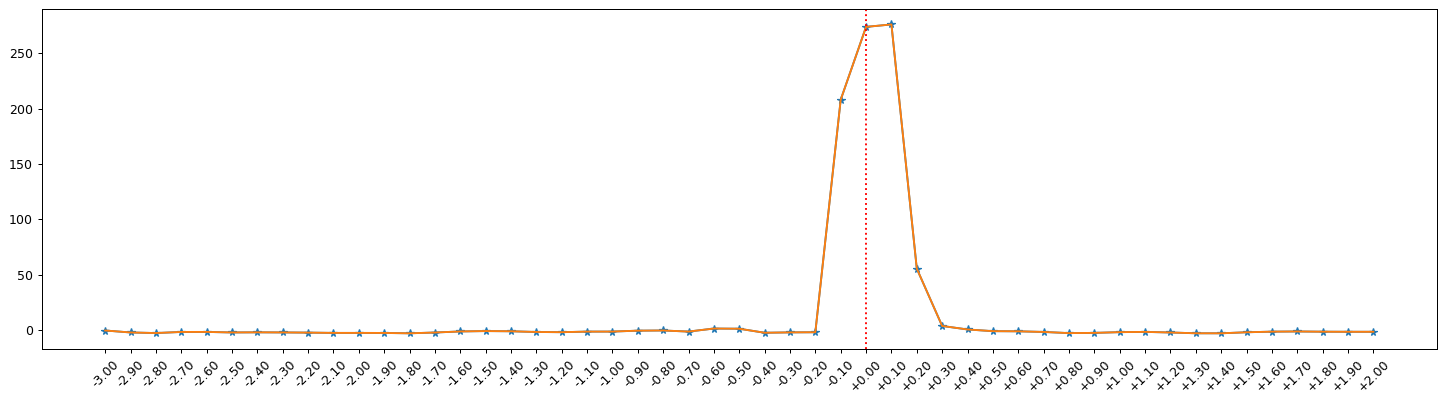
Bayes factor (MCMC)
PRD 101, 10 (2020) 104003.
(In preparation)
Challenge in GW Data Analysis: Lessons and Future
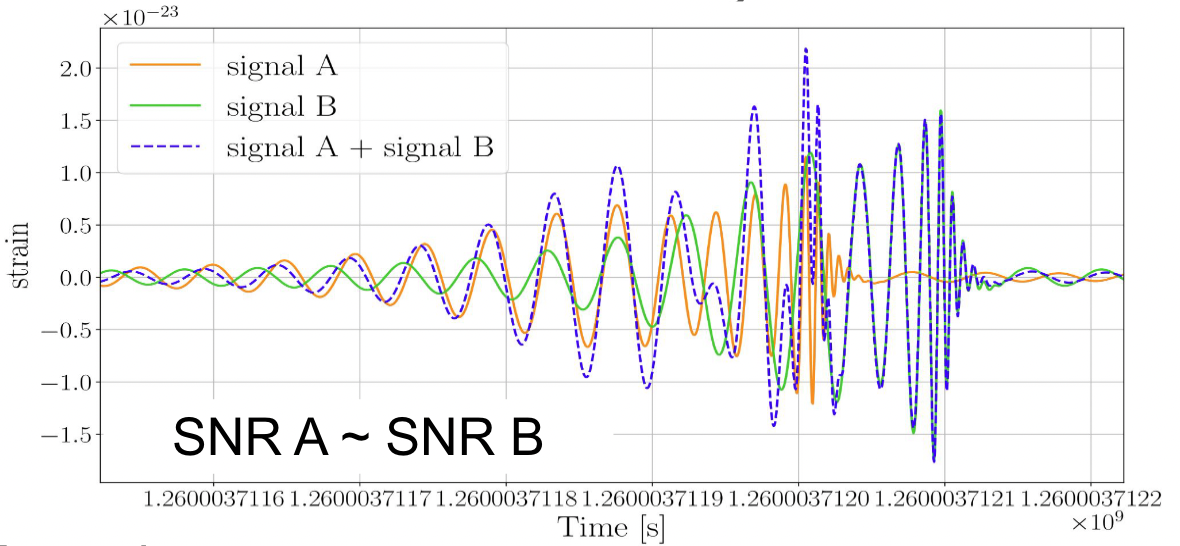
-
AI serves as a valuable tool in gravitational wave astronomy:
(Big data & Computational Complexity)- Enhancing data analysis,
- Noise reduction, and
- Parameter estimation.
- It streamlines the research process and allows scientists to focus on the most relevant information.
-
Beyond a Tool: AI transcends its role as a mere tool by enabling scientific discovery in GW astronomy.
- Characterization of GW signals involves
- Exploring beyond the scope of GR ,
- Enabling real-time inference
- "Curse of Dimensionality" in inference
- Overlapping signal (In progress)
- Hierarchical Bayesian Analysis (In progress)
- Test of GR
- Tighter parameter constraints of variance
- Guaranteed exact coverage
- ...
- Characterization of GW signals involves
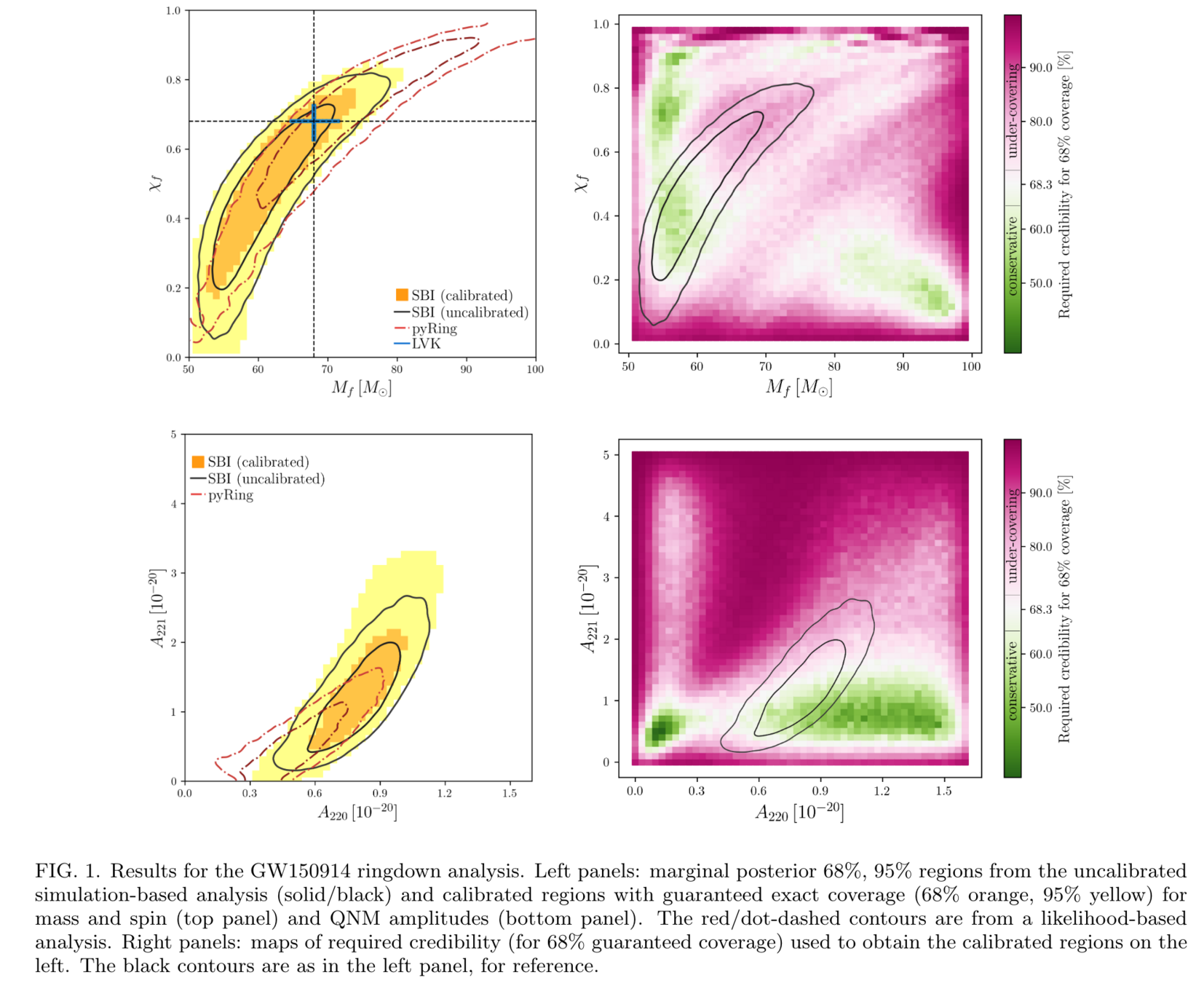
arXiv:2305.18528
Challenge in GW Data Analysis: Lessons and Future
-
AI serves as a valuable tool in gravitational wave astronomy:
(Big data & Computational Complexity)- Enhancing data analysis,
- Noise reduction, and
- Parameter estimation.
- It streamlines the research process and allows scientists to focus on the most relevant information.
-
Beyond a Tool: AI transcends its role as a mere tool by enabling scientific discovery in GW astronomy.
- Characterization of GW signals involves
- Exploring beyond the scope of GR ,
- Enabling real-time inference
- "Curse of Dimensionality" in inference
- Overlapping signal (In progress)
- Hierarchical Bayesian Analysis (In progress)
- Test of GR
- Tighter parameter constraints of variance
- Guaranteed exact coverage
- ...
- Characterization of GW signals involves
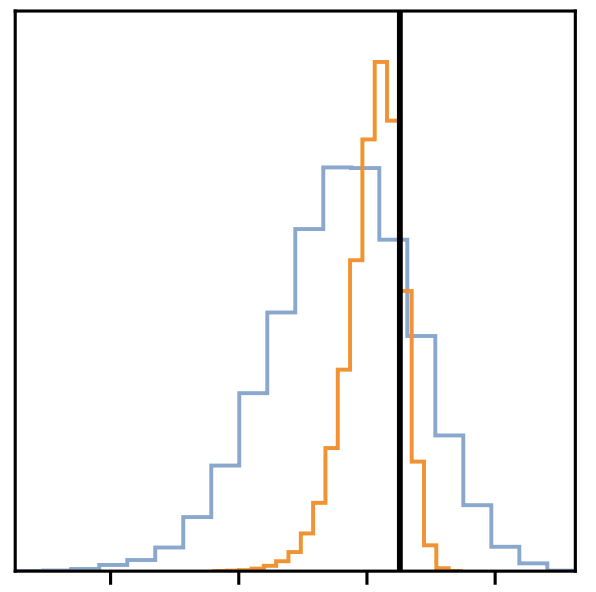
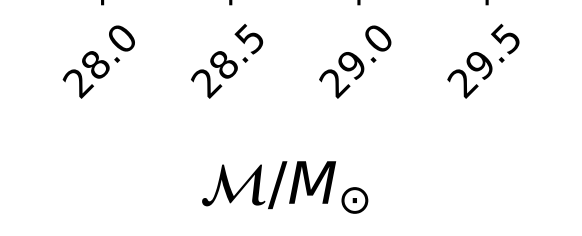

ICML2023
AI for Science: GW Astronomy
- Using Large Language Models (LLMs) for scientific discovery.
- The need for a scientific infrastructure for AI in Science.






- 以国家天文科学数据中心在线服务平台为基础,开发适用于引力波天文学研究的引力波探测开源数据门户 (2023-2025)。
- 开发一套集成引力波数据处理与通用异步计算功能的软件工具包:GWToolkit
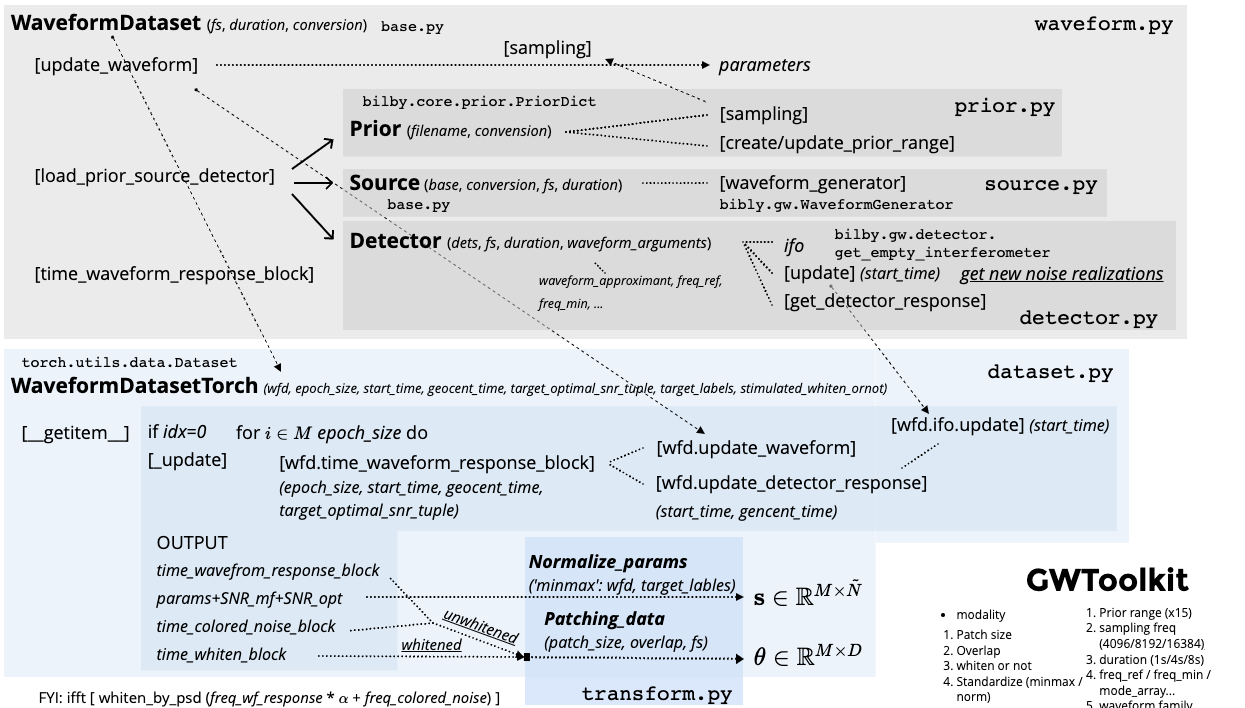



AI for Science: GW Astronomy
-
Exploring the importance of understanding how AI models make predictions in scientific research.
- The critical role of generative models (生成模型是关键)
- Quantifying uncertainty: a key aspect (不确定性量化问题)
- Fostering controllable and reliable models (模型的可控可信问题)



Bayes
AI
Credit: 李宏毅


Text-to-image


AI for Science: GW Astronomy
-
Exploring the importance of understanding how AI models make predictions in scientific research.
- The critical role of generative models (生成模型是关键)
- Quantifying uncertainty: a key aspect (不确定性量化问题)
- Fostering controllable and reliable models (模型的可控可信问题)


Bayes
AI
Credit: 李宏毅
Text-to-image


Key Takeaways
- Gravitational-wave astronomy turns to AI:
- A thriving and highly competitive research field on the international stage.
- Is AI just a tool? Certainly not! It's a revolutionary pathway for scientific discoveries:
- Enabling new discoveries and insights into the universe.
- Addressing Challenges in AI for GW astronomy: essential for enhanced discoveries
- LLM
- Scientific infrastructure
- Interpretability
for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This slide: https://slides.com/iphysresearch/2023ml_astromoy

Smith, Rory. Nature Physics 18, 1 (2022): 9–11
Key Takeaways

“国际理论物理中心(亚太地区)” 经联合国教科文组织第38届大会审议通过。由中国科学院、基金委和国际理论物理中心共同建设,是进行基础科学前沿与相关交叉科学领域高水平科研、教育和培训的非营利性组织,是联合国教科文组织基础科学方面的在国内的第一个二类中心。








Outlook
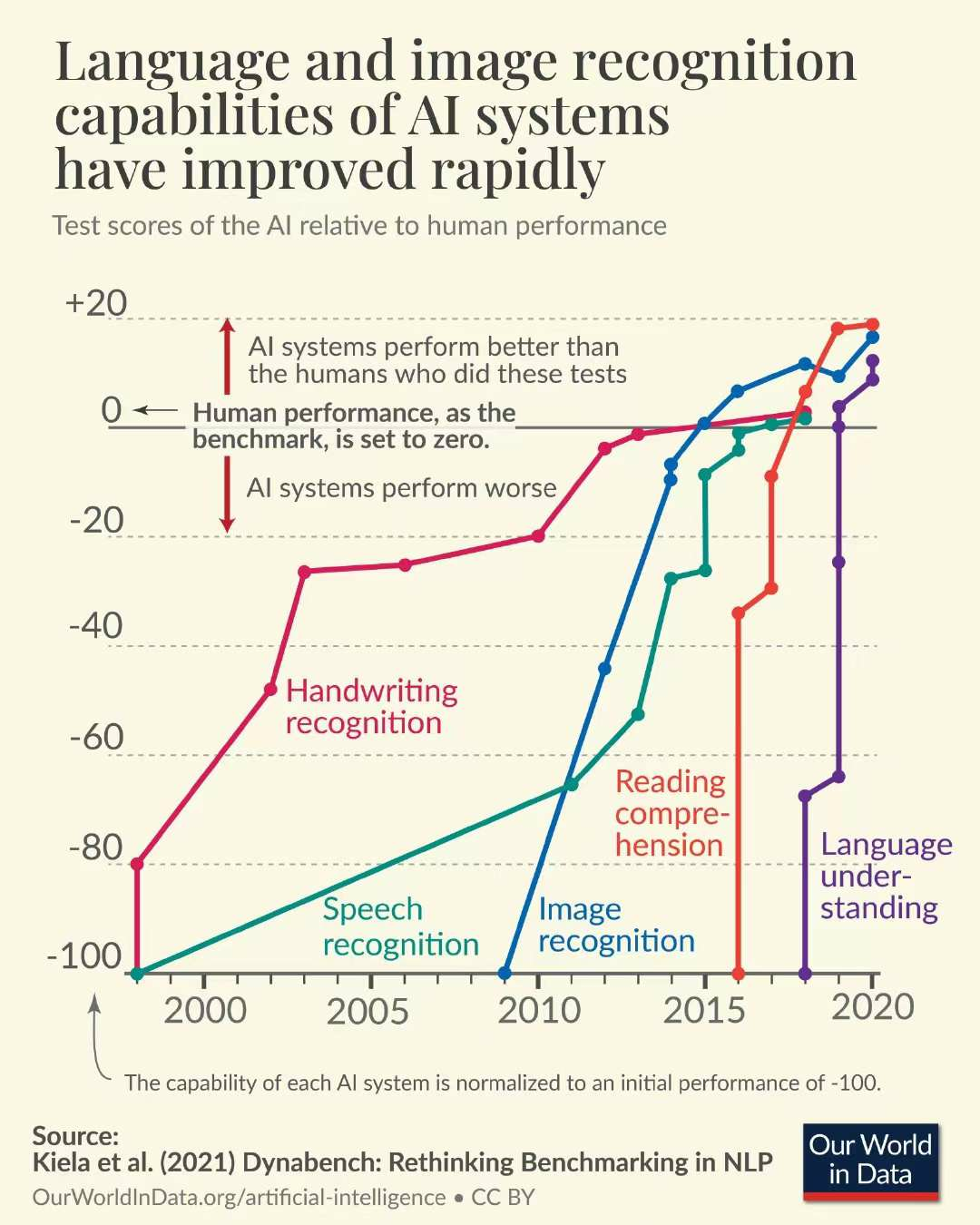
- 值得关注的 AI 技术:
- Large Language Model (LLM)
- AI generated content (AIGC)

WaveFormer
Transformer: 750x / 2yrs
AI for Science



-
2016年,AlphaGo 第一版发表在了 Nature 杂志上
-
2021年,AI预测蛋白质结构登上 Science、Nature 年度技术突破,潜力无穷
-
2022年,DeepMind团队通过游戏训练AI发现矩阵乘法算法问题
-
《达摩院2022十大科技趋势》将 AI for Science 列为重要趋势
-
“人工智能成为科学家的新生产工具,催生科研新范式”
-
-
AI for Science:为科学带来了模型与数据双驱动的新的研究范式
-
AI + 数学、AI + 化学、AI + 医药、AI + 物理、AI + 天文 ...
-
AlphaGo 围棋机器人
AlphaTensor 发现矩阵算法
AlphaFold 蛋白质结构预测
AI for Science