2024年6月5日, 10:10-10:40 | 北京农学院体育馆218
引力波探测与人工智能:现状与未来
王赫 (He Wang)
hewang@ucas.ac.cn
中国科学院大学 · 国际理论物理中心(亚太地区)
中国科学院大学 · 引力波宇宙太极实验室(北京/杭州)
On behalf of the LIGO-VIRGO-KAGRA collaborations




Taiji
Tianqin
https://twitter.com/chipro/status/1768388213008445837?s=46&t=JmDXWgIucgr_FlsBFTvuRQ
DINGO+SEOBNRv4EHM找了3个ebbh
Evidence for eccentricity in the population of binary black holes observed by LIGO-Virgo-KAGRA
https://dcc.ligo.org/LIGO-G2400750

BEFORE
AFTER

LIGO-G2300554
Content


- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery

-
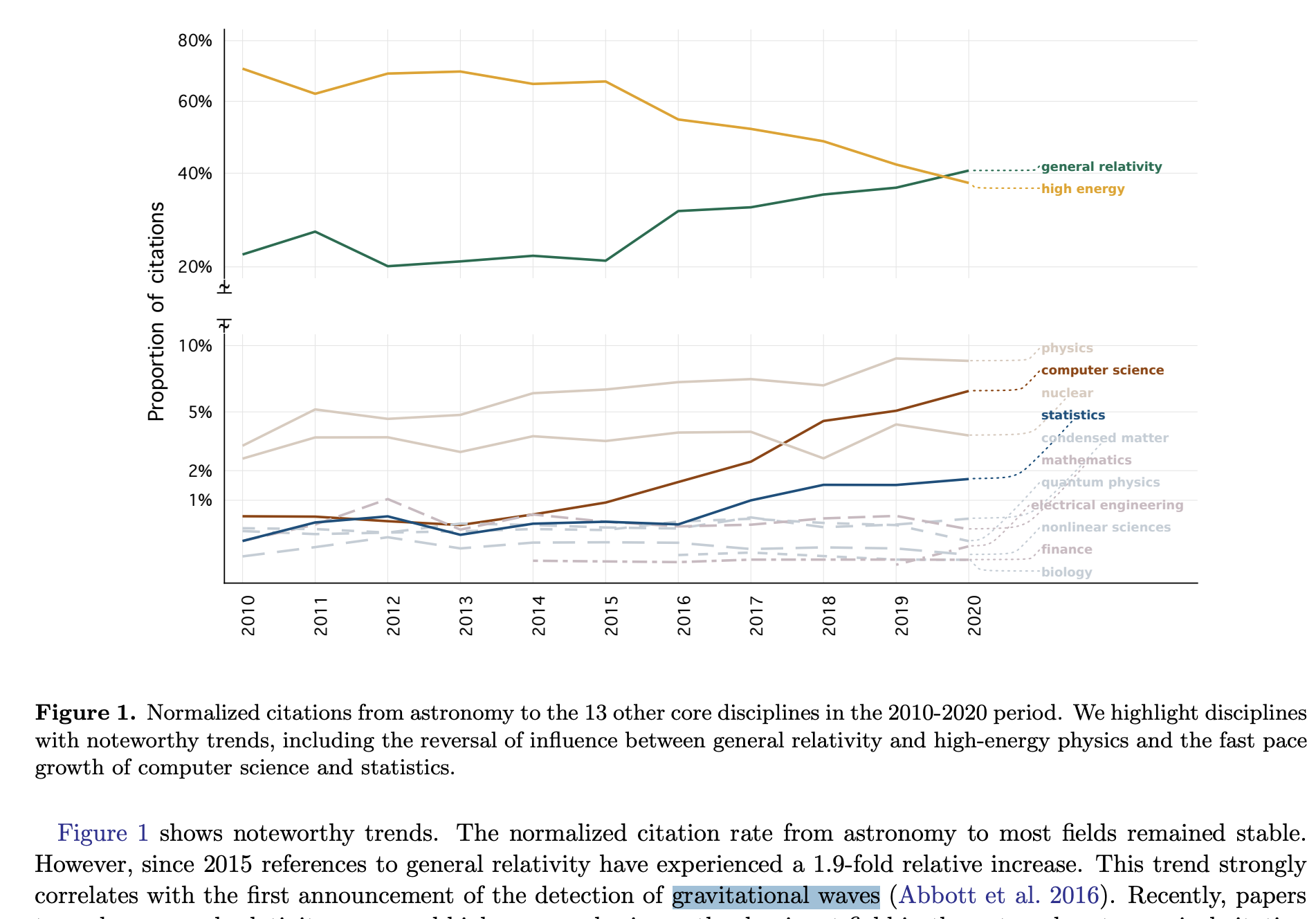
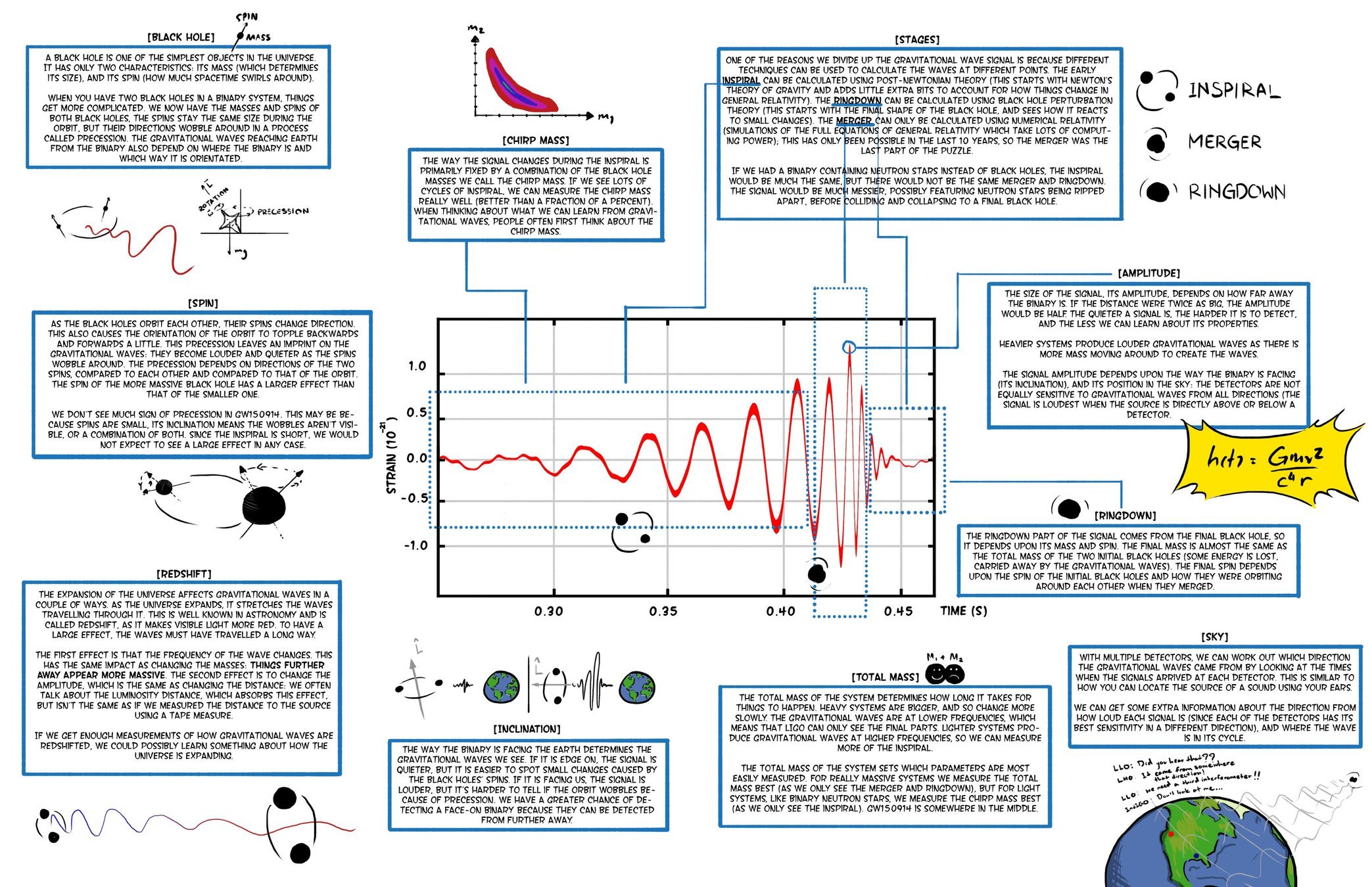
In 1916, A. Einstein proposed the GR and predicted the existence of GW.
-
Gravitational waves (GW) are a strong field effect in the GR.
-
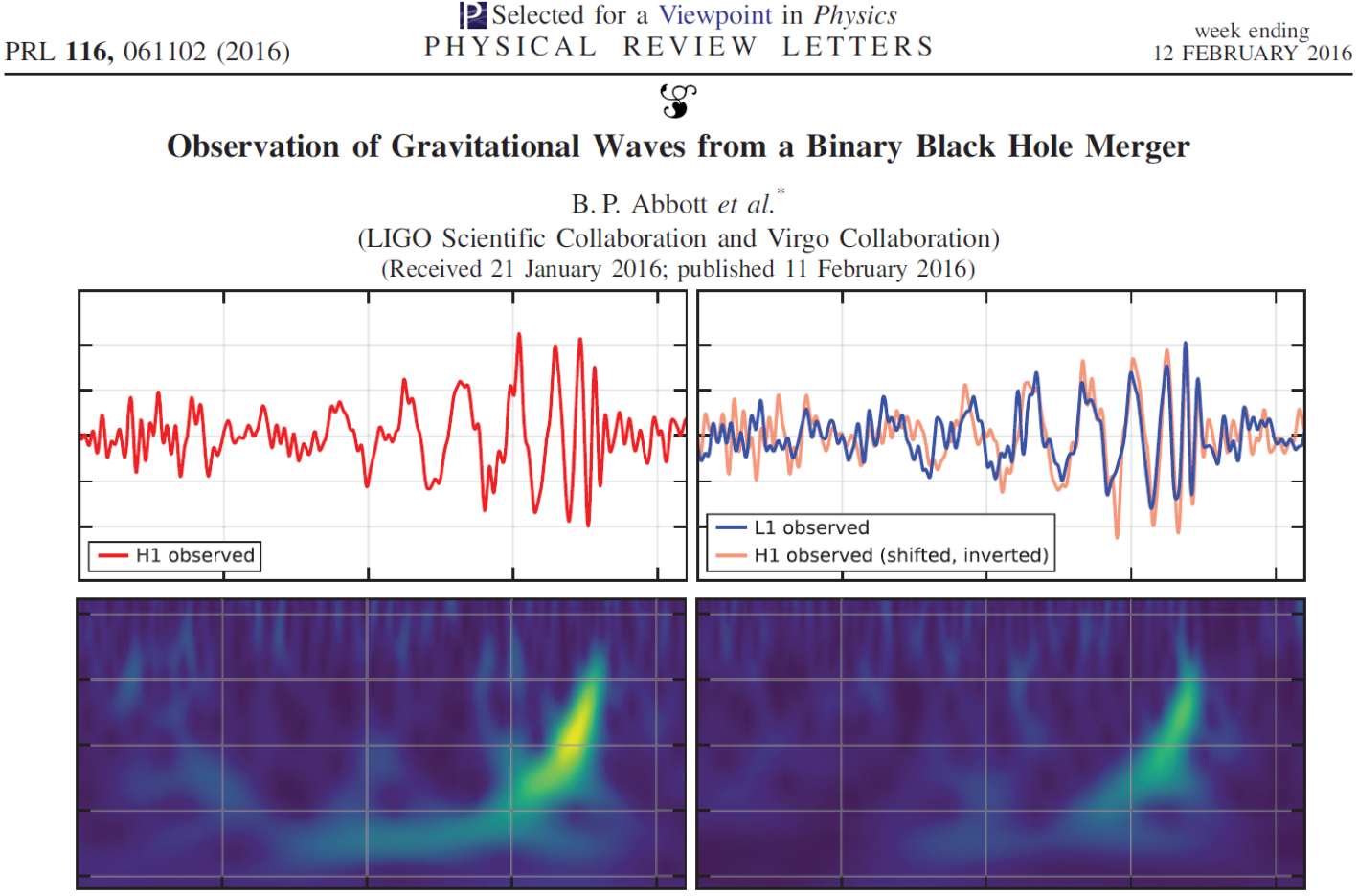
2015: the first experimental detection of GW from the merger of two black holes was achieved.
-
2017: the first multi-messenger detection of a BNS signal was achieved, marking the beginning of multi-messenger astronomy.
-
2017: the Nobel Prize in Physics was awarded for the detection of GW.
-
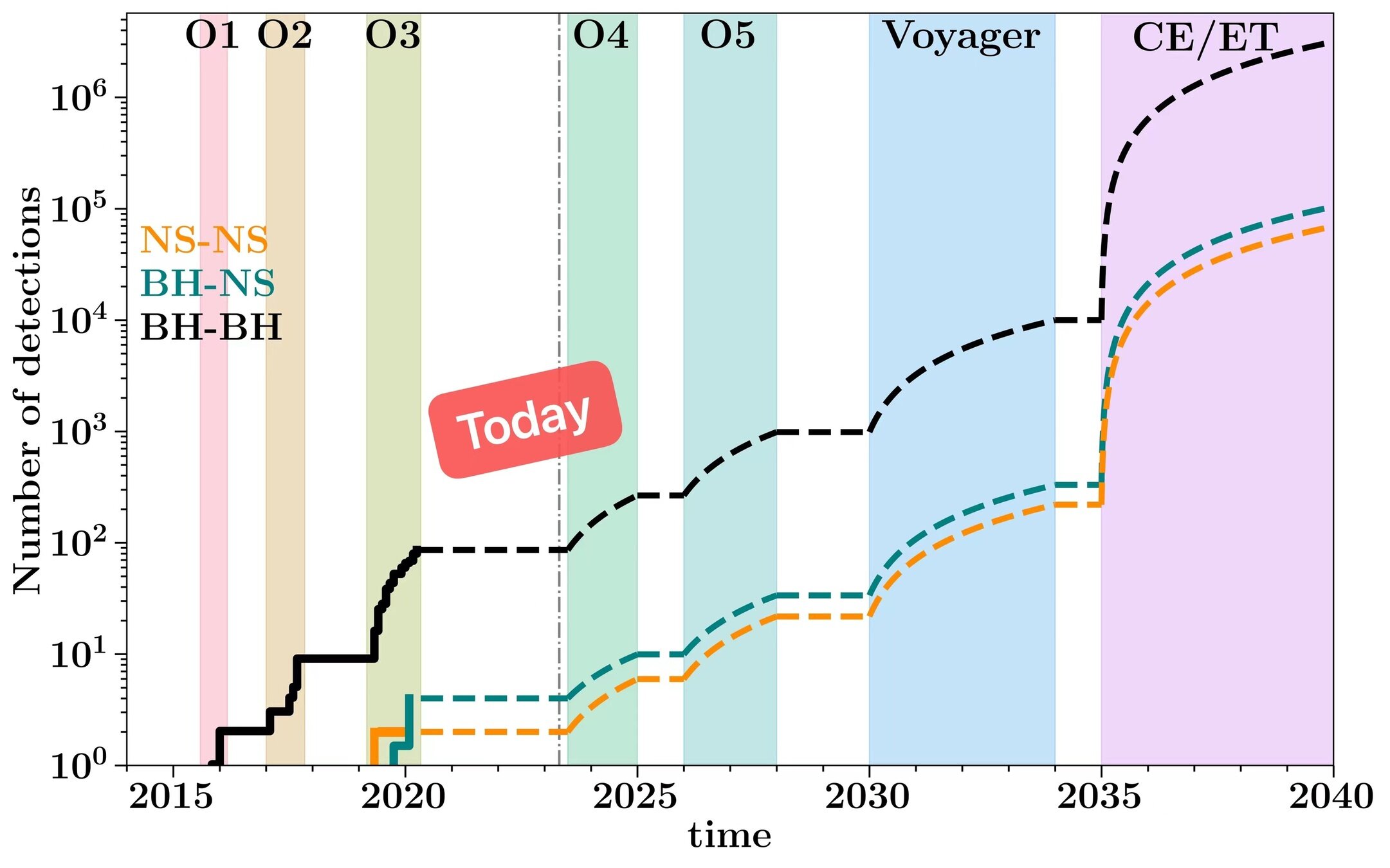
As of now: more than 90 gravitational wave events have been discovered.
-
O4, which began on May 24th 2023, is currently in progress.
-

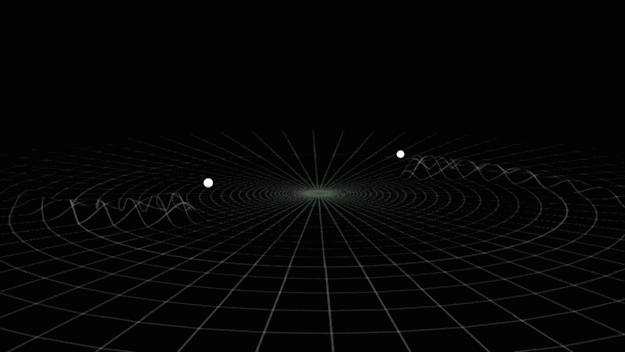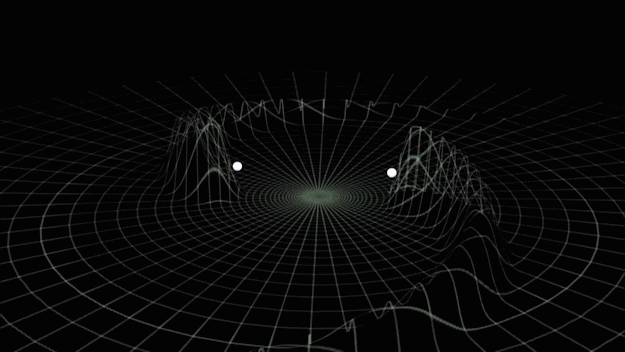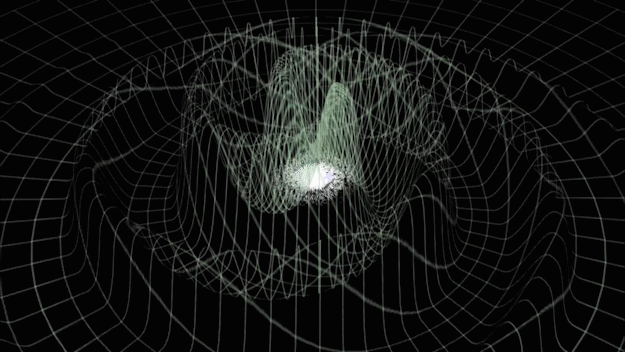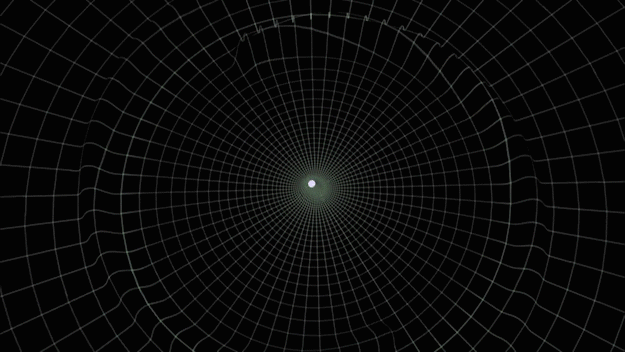

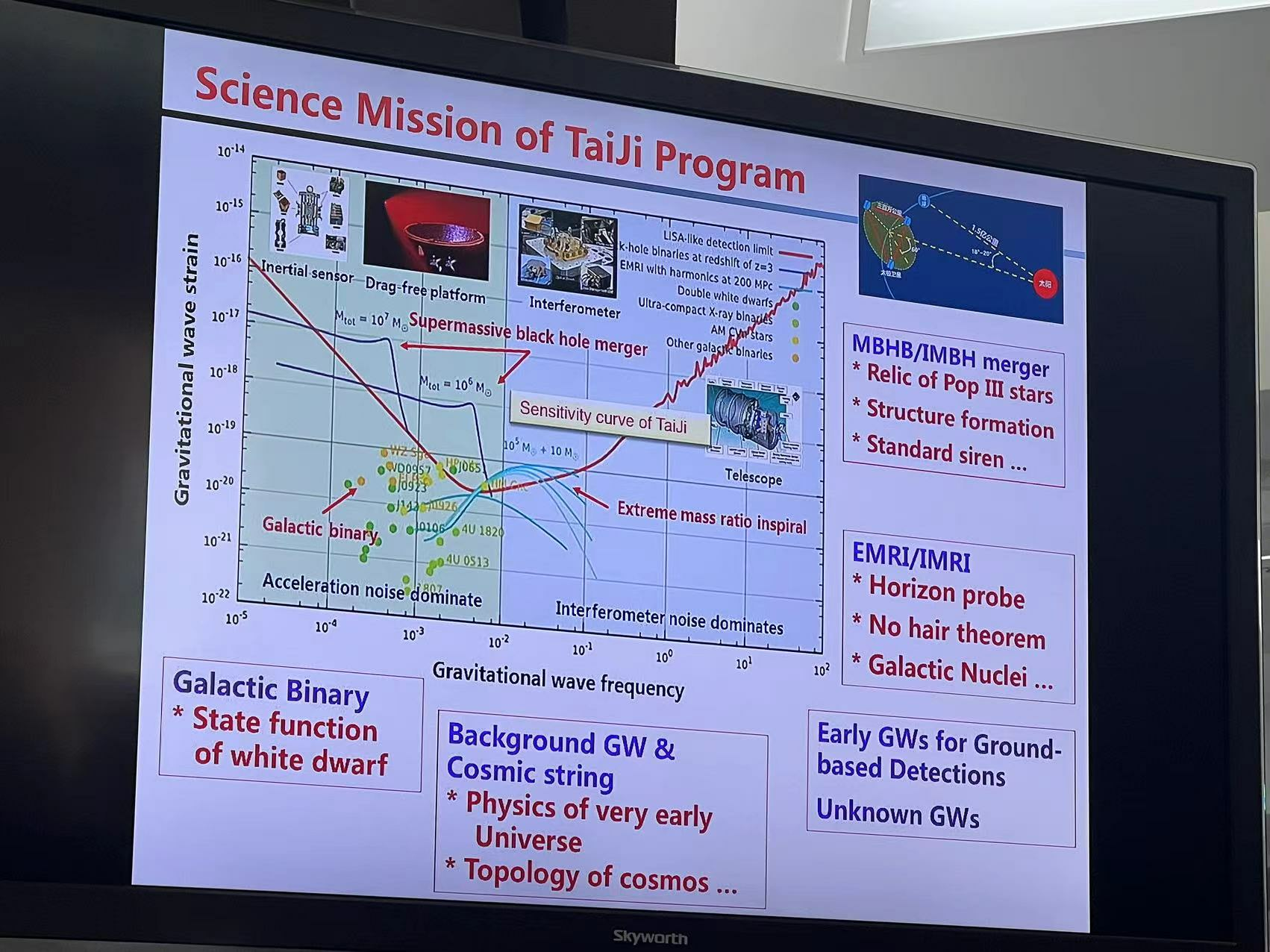
Gravitational waves generated by binary black holes system
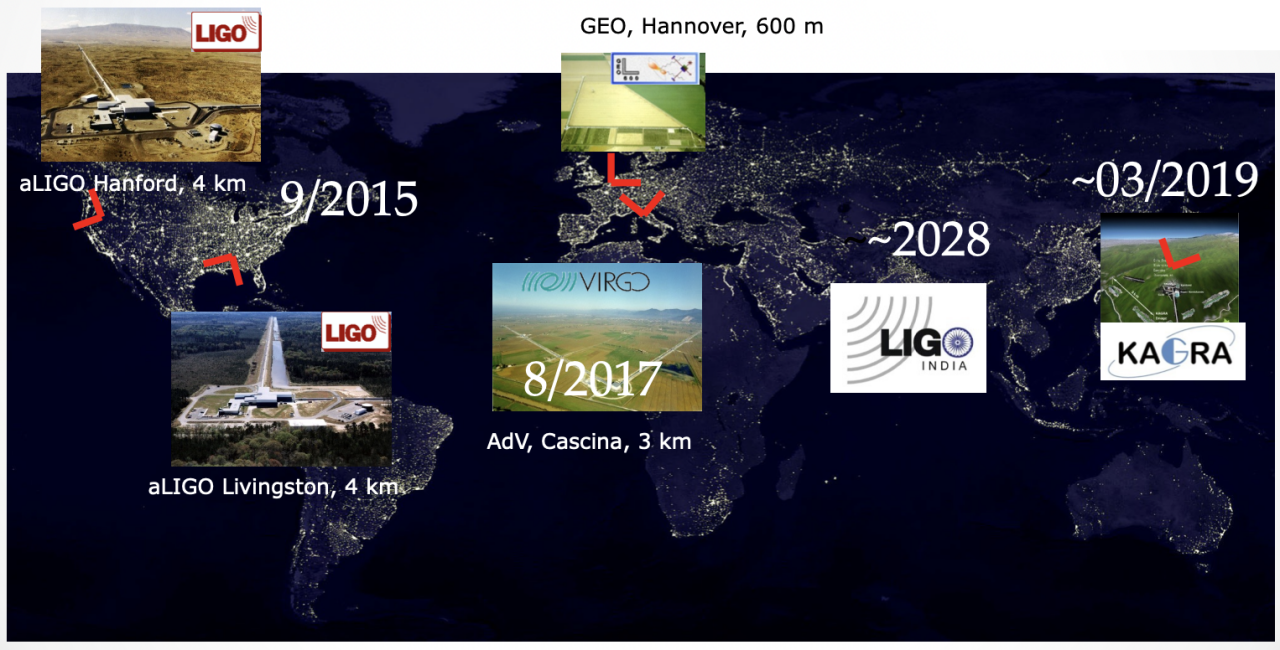
GW detector
LIGO-VIRGO-KAGRA network
2017 Nobel Prize in Physics
Gravitational Wave Astronomy
-
引力波探测打开了探索宇宙的新窗口
-
不同波源,频率跨越 20 个数量级,不同探测器
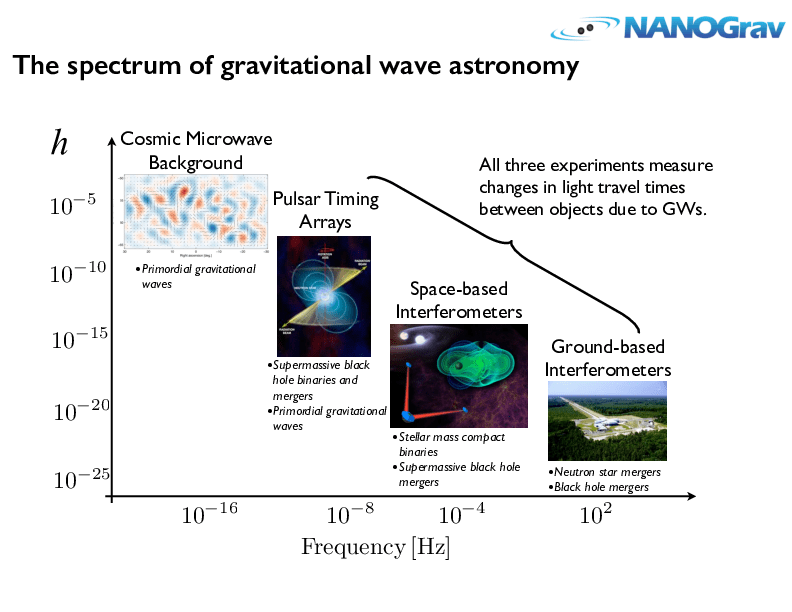
-
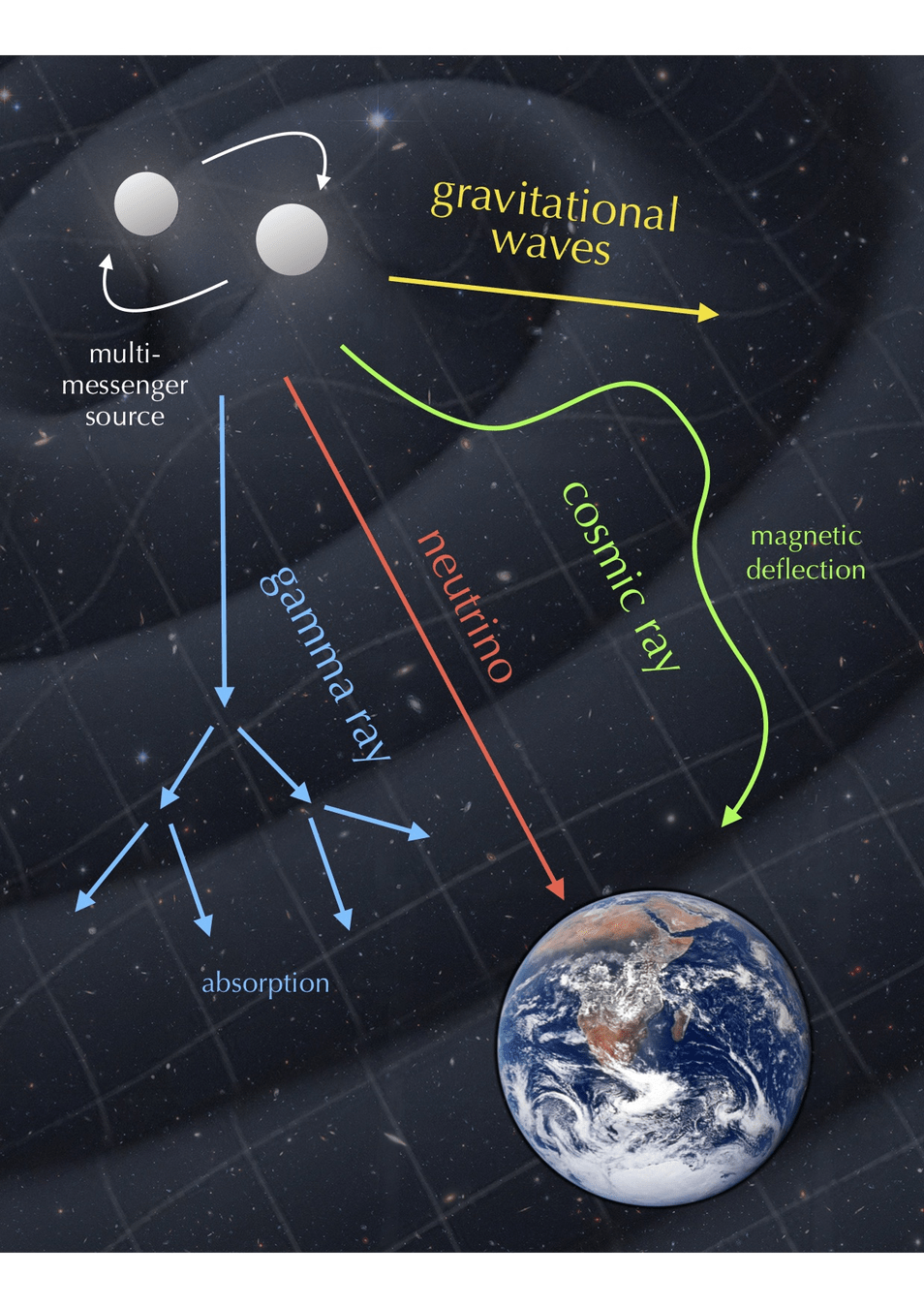
多信使天文学
Gravitational Wave Astronomy


-
Fundamental Physics
- Existence of gravitational waves
- To put constraints on the properties of gravitons
-
Astrophysics
- Refine our understanding of stellar evolution
- and the behavior of matter under extreme conditions.
-
Cosmology
- The measurement of the Hubble constant
- Dark energy
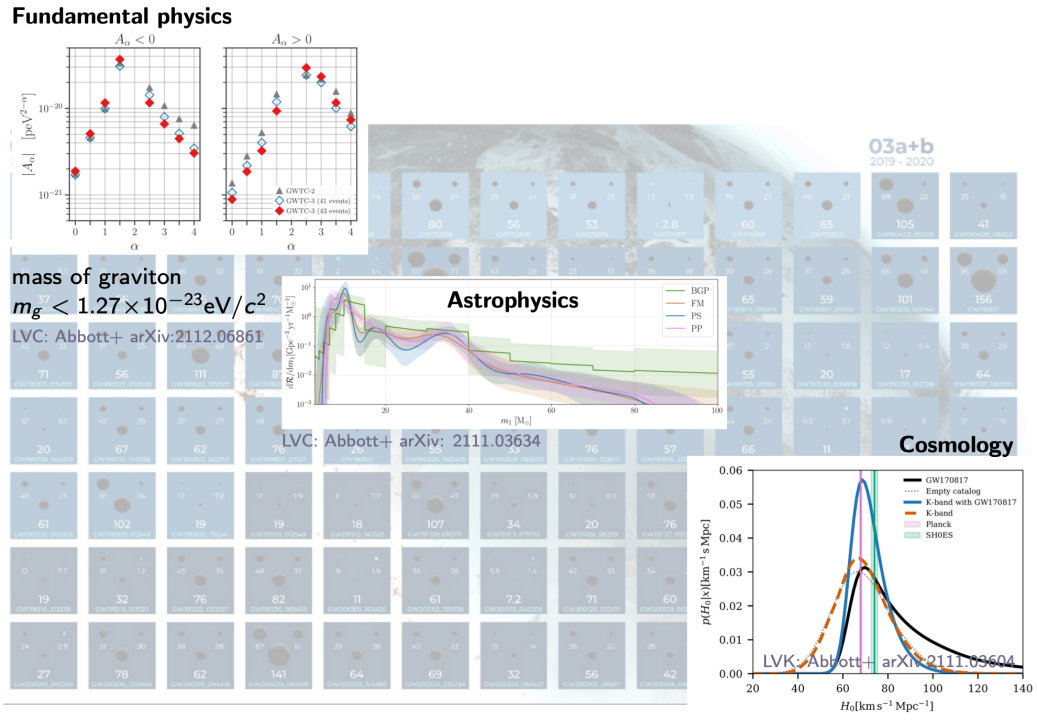
GWTC-3
Gravitational Wave Astronomy
-
The current clouds over fundamental physics:
- 量子力学与广义相对论的统一
- 星系旋转曲线(暗物质)、宇宙加速膨胀(暗能量)
- 哈勃常数H0
- 中微子震荡和质量问题
- ...

-
伯纳德·舒尔茨曾列出成功观测引力波的五条关键要素:
- 良好的探测器技术
- 良好的波形模板
- 良好的数据分析方法和技术
- 多个独立探测器间的一致性观测
- 引力波天文学和电磁波天文学的一致性观测
DOI:10.1063/1.1629411

©Floor Broekgaarden (repo)
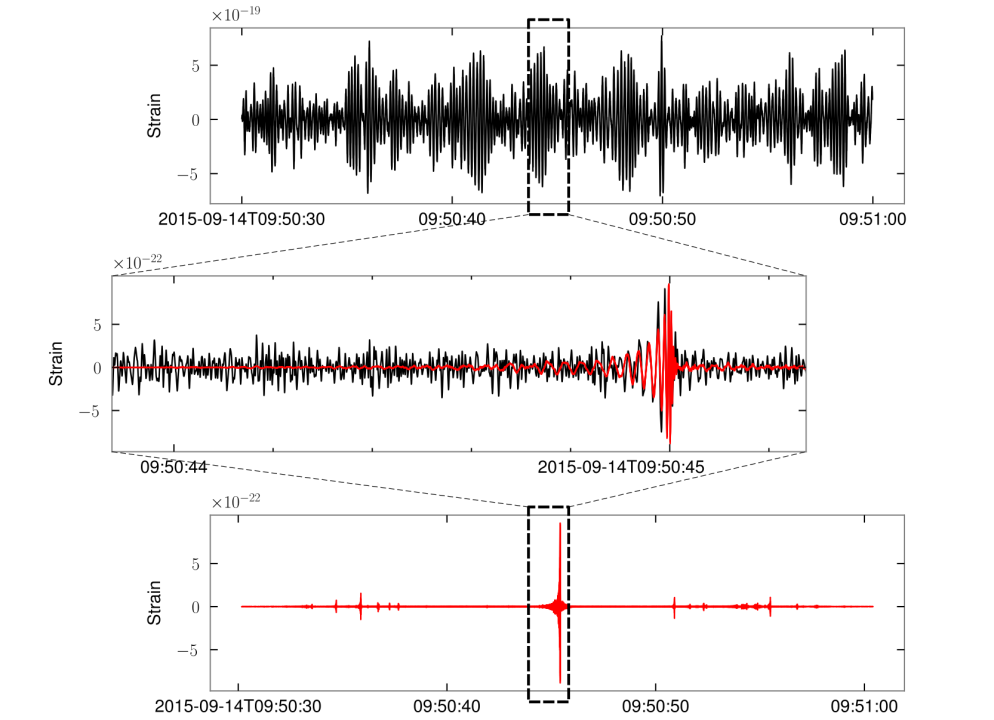
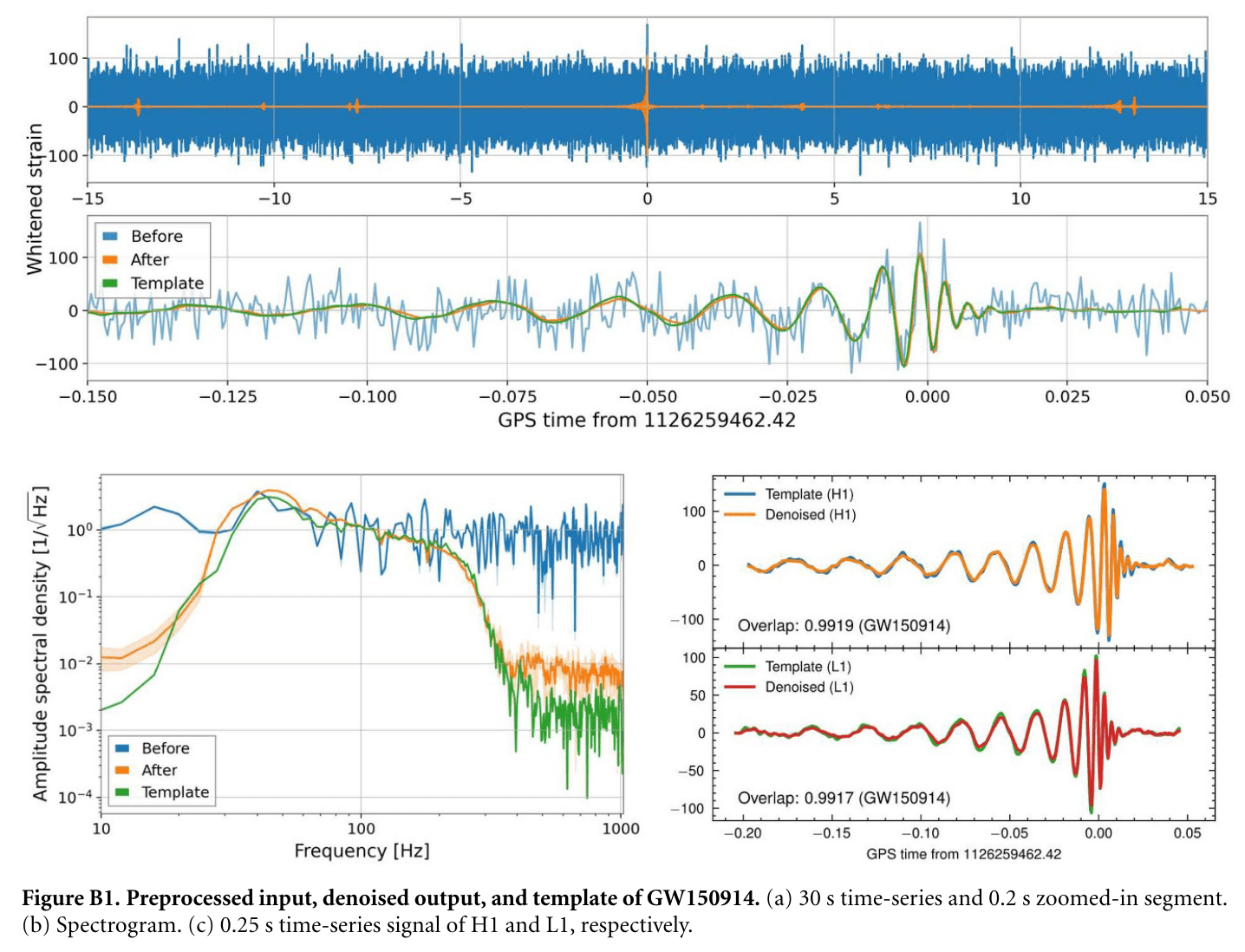
The first GW event of GW150914
引力波天文学与数据处理
引力波天文学与数据处理
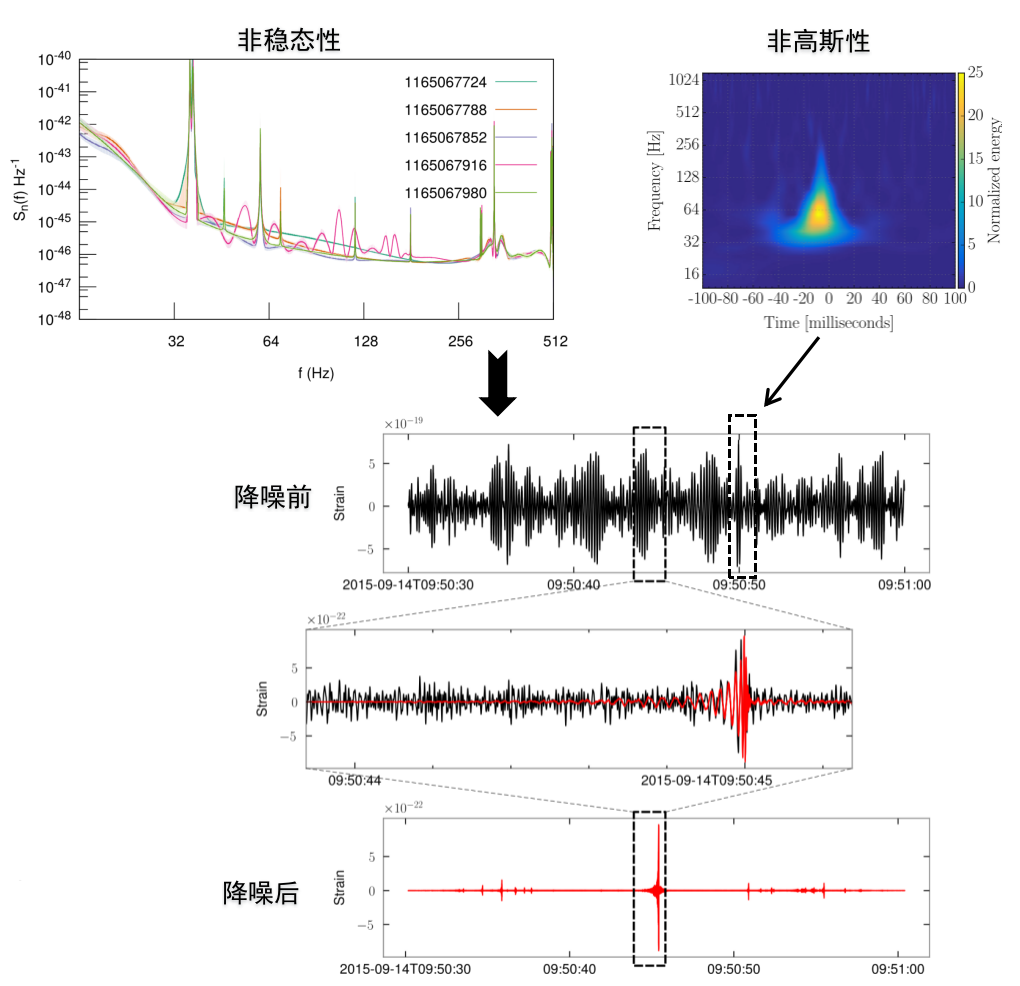
引力波观测数据
-
噪声: 非高斯 + 非稳态
-
(地面引力波探测) 信噪比极低,通常约为噪声幅度的1/100(-60分贝)
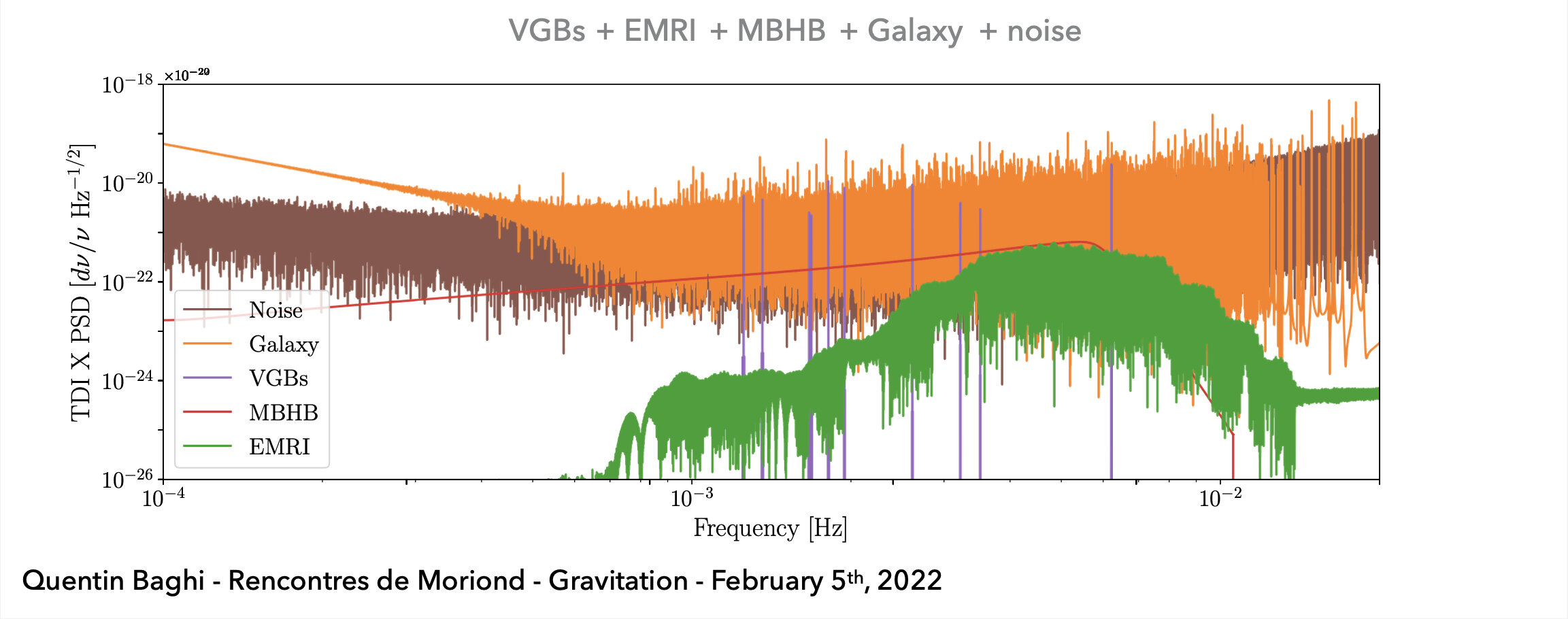
(空间引力波探测) 在任务观测期间接收到的所有引力波信号的叠加(例如:\(10^4\) 个双星黑洞系统,\(10\sim10^2\) 个超大质量黑洞,以及\(10\sim10^3\) 个极端质量比旋近系统等)。


LIGO-VIRGO-KAGRA
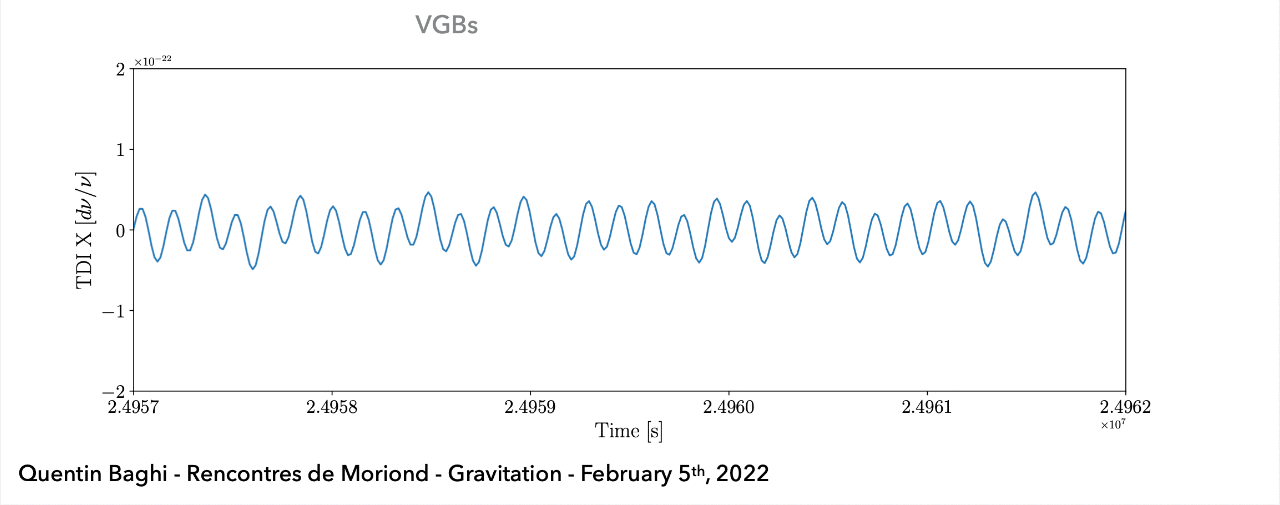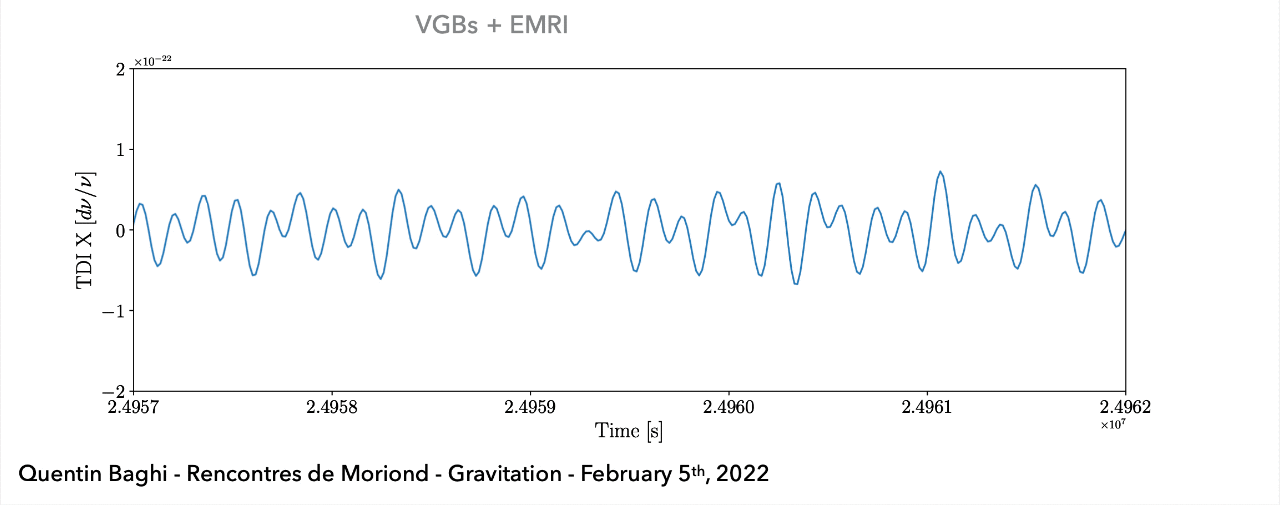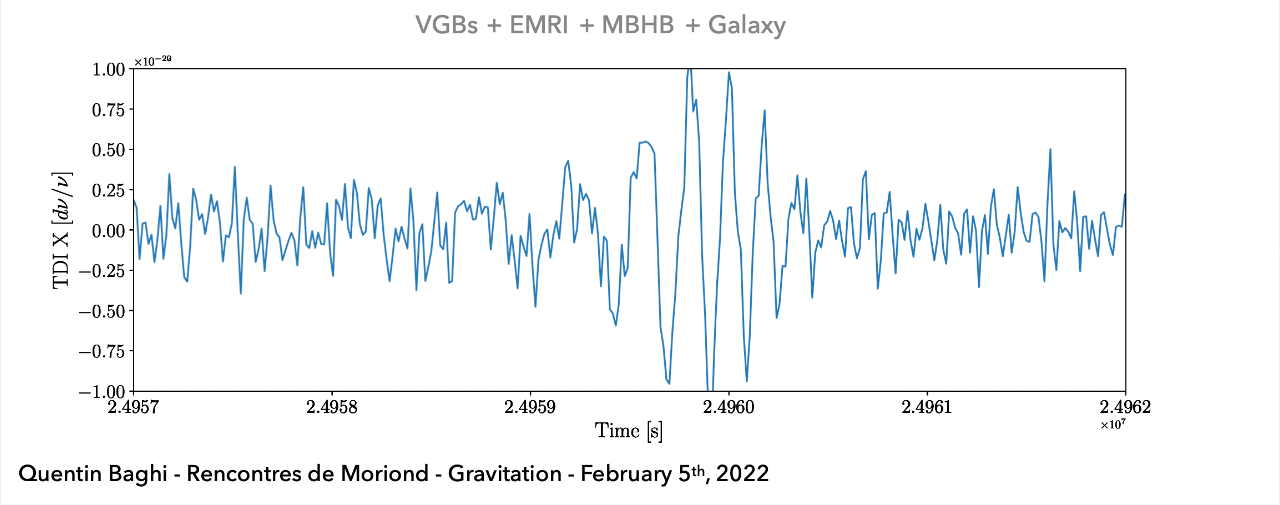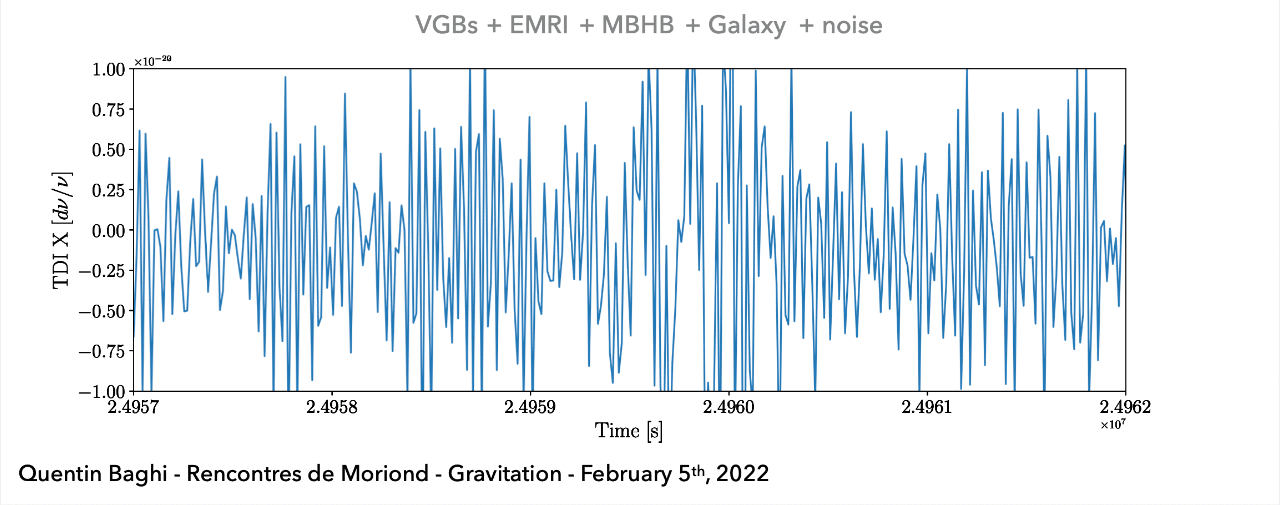
LISA / Taiji project

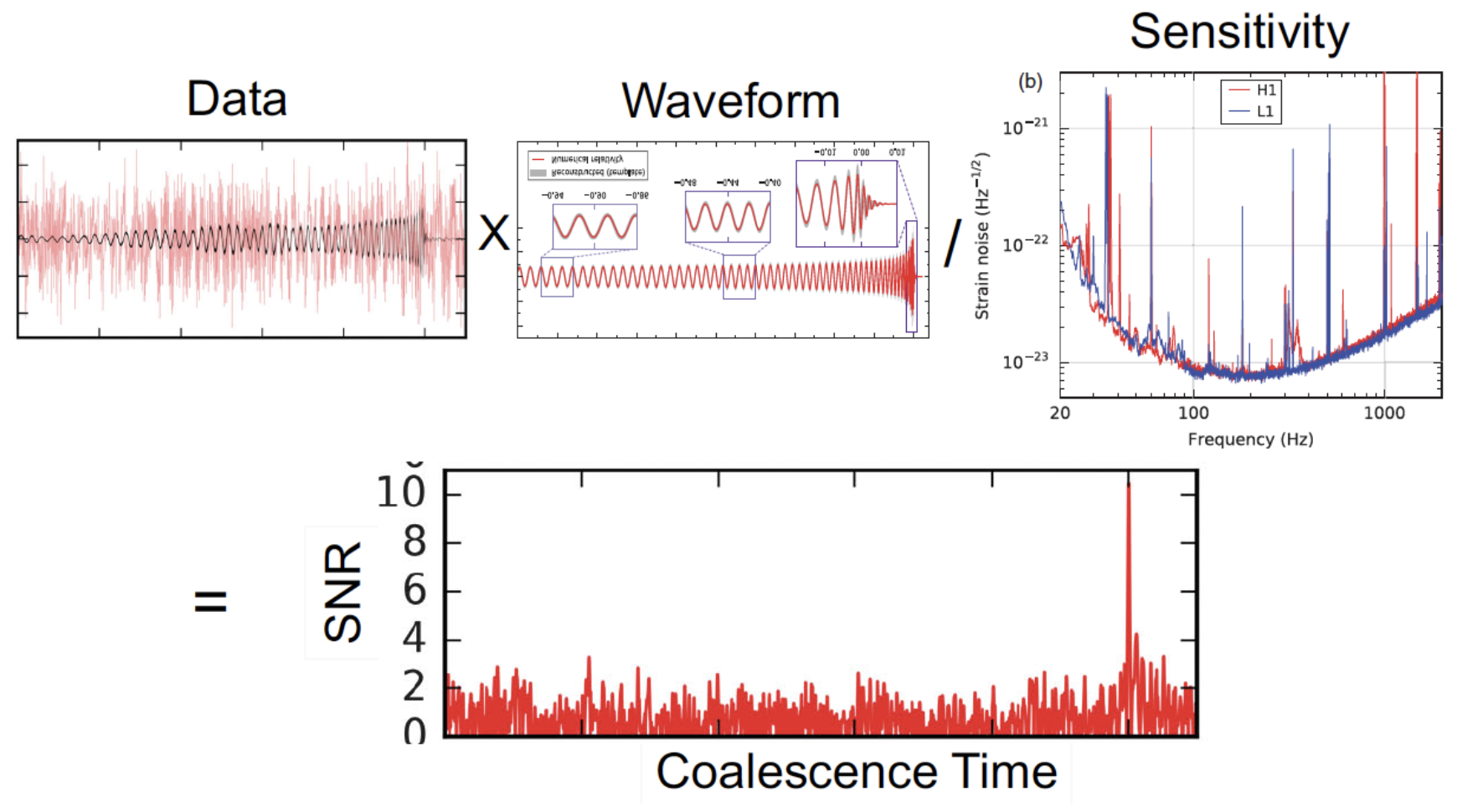
Matched filtering techniques (匹配滤波方法)
-
In Gaussian and stationary noise environments, the optimal linear algorithm for extracting weak signals
- Works by correlating a known signal model \(h(t)\) (template) with the data.
- Starting with data: \(d(t) = h(t) + n(t)\).
- Defining the matched-filtering SNR \(\rho(t)\):
\(\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2 \) , where \(\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df \) ,
\(\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df \), \(S_n(f)\) is noise power spectral density (one-sided).
Text

目录

- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery

科学智能:AI for Science
-
2016年,AlphaGo 第一版发表在了 Nature 杂志上
-
2021年,AI预测蛋白质结构登上 Science、Nature 年度技术突破,潜力无穷
-
2022年,DeepMind团队通过游戏训练AI发现矩阵乘法算法问题
-
《达摩院2022十大科技趋势》将 AI for Science 列为重要趋势
-
“人工智能成为科学家的新生产工具,催生科研新范式”
-
-
2023年,DeepMind发布AI工具GNoME (Nature),成功预测220万种晶体结构
-
AI for Science:为科学带来了模型与数据双驱动的新的研究范式
-
AI + 数学、AI + 化学、AI + 医药、AI + 量子、AI + 物理、AI + 天文 ...
-




AlphaGo 围棋机器人

AlphaTensor 发现矩阵算法

AlphaFold 蛋白质结构预测

验证数学猜想
Text

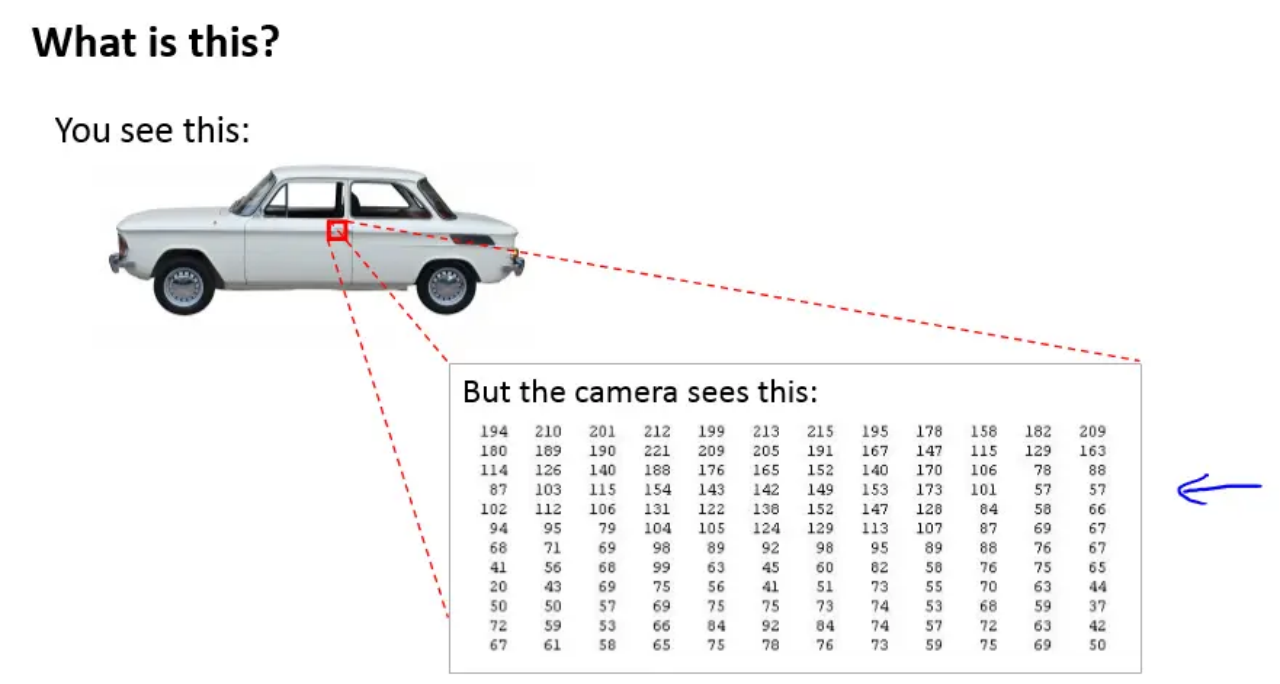
Pioneering works utilizing CNN
- The most common and direct approach, from Computer Vision (CV) to GW signal processing: pixel point \(\Rightarrow\) sampling point.
- Convolutional neural networks (CNN) can achieve comparable performance to Matched Filtering and surpass them in terms of execution speed (with GPU support) under Gaussian stationary noise.
AI for Science \(\rightarrow\) AI for GW Astronomy
- Artificial Intelligence (AI) has great potential to revolutionize gravitational wave astronomy by improving data analysis, modeling, and detector development.
- Representation and supervised learning crucially extract features from GW signals, autonomously identifying informative features and leveraging labeled data for accuracy.
Text
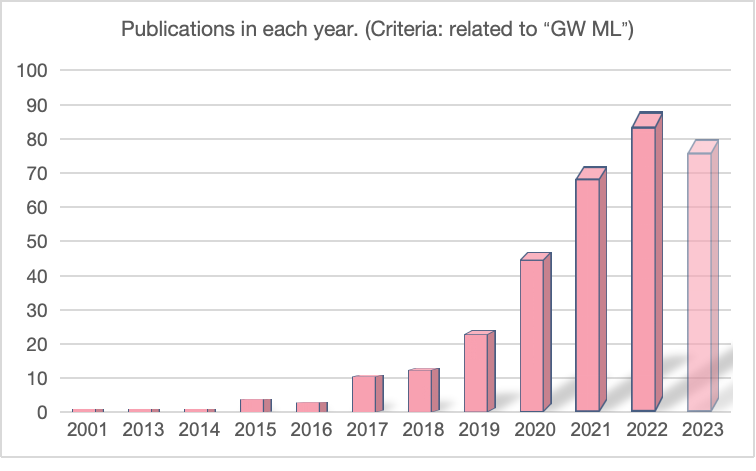
Exported: Oct, 2023 (in preparation)

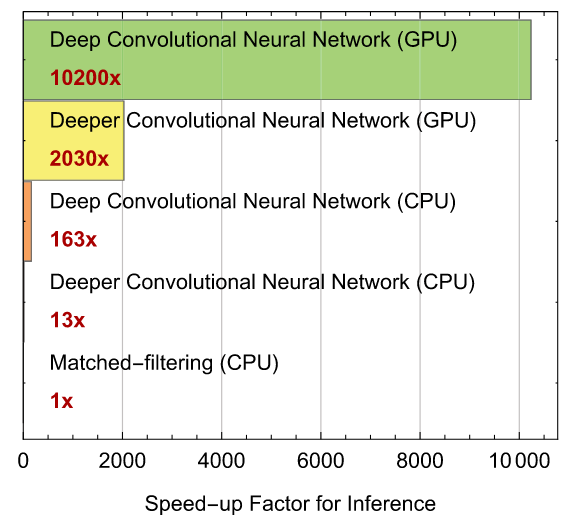
PRL, 2018, 120(14): 141103.
PRD, 2018, 97(4): 044039.
引力波数据处理:人工智能技术应用
Content




- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery


Matched-filtering Convolutional Neural Network (MFCNN)
Text
- GW templates can be utilized as recognizable features for signal detection.
- It is feasible to generalize both matched-filtering and neural networks.
- Linear filters (i.e., matched-filtering) in signal processing can be reformulated as neural layers (i.e., CNNs).
MLGWSC-1
-
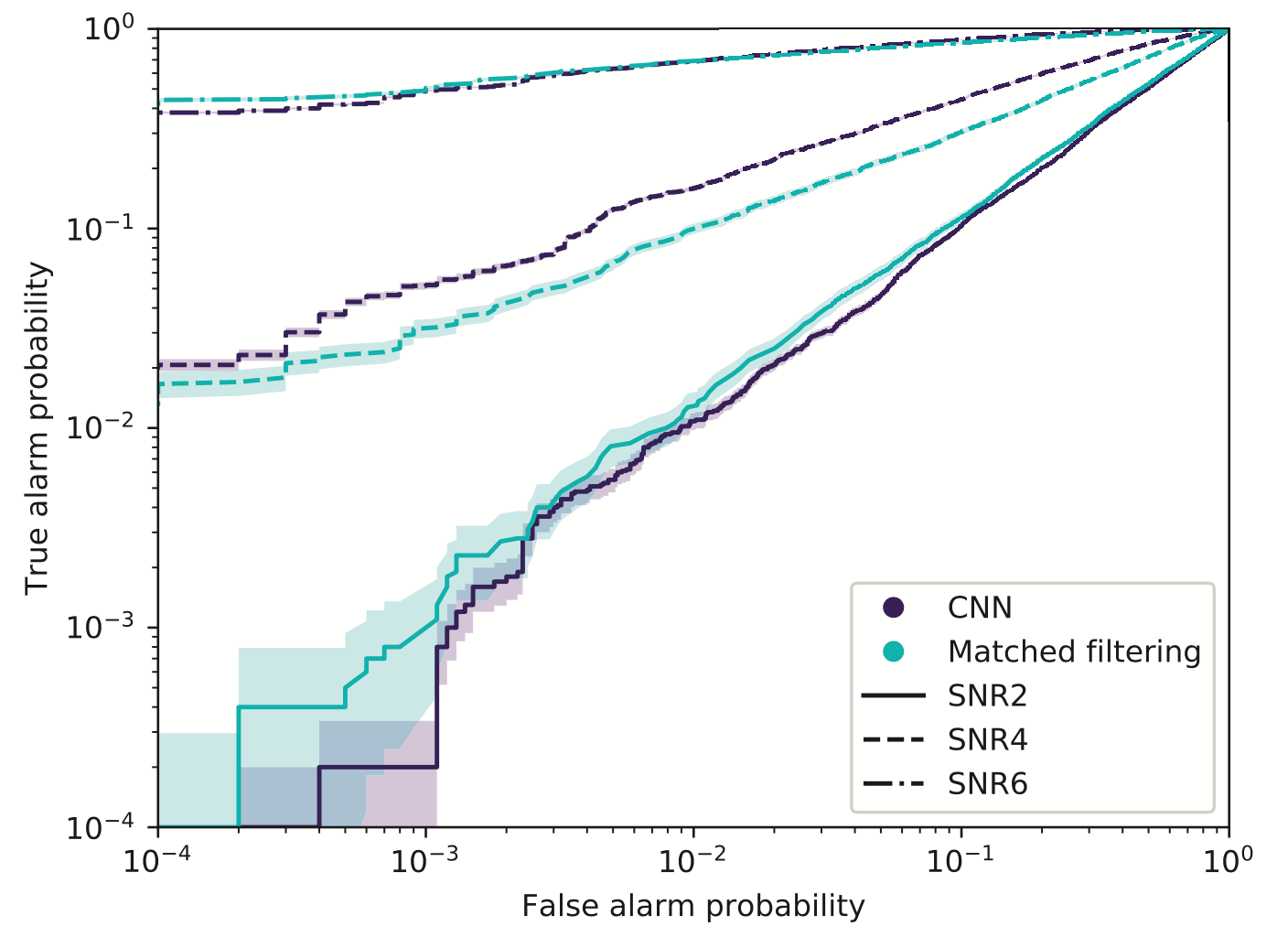
The majority of AI algorithms used for testing are highly sensitive to non-Gaussian real noise backgrounds, resulting in high false positive rates.
(MFCNN group) H.W., et al. PRD (2023)

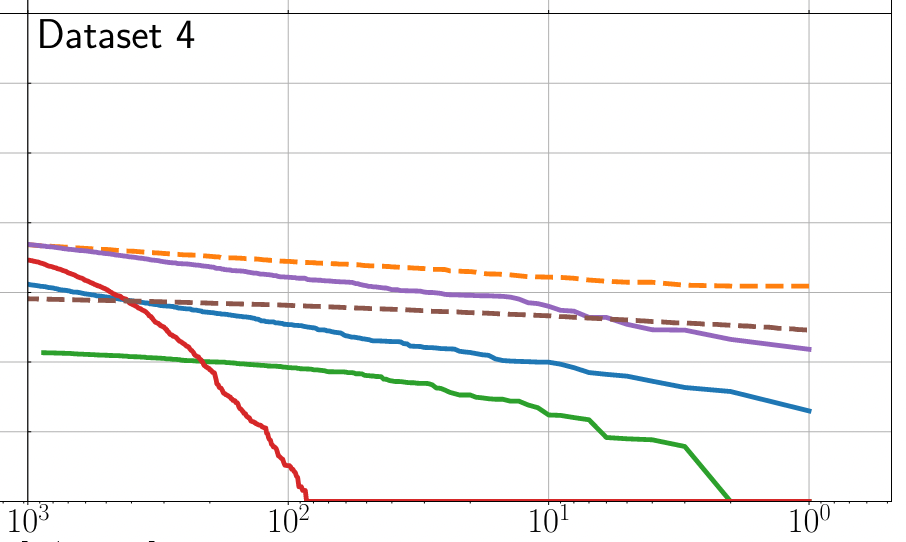
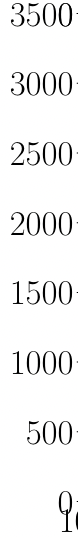
Text
CL.M., W.W., H.W., et al. PRD (2022)
Ensemble learning
-
Leverages statistical approaches to utilize more information for making informed decisions by combining multiple models.
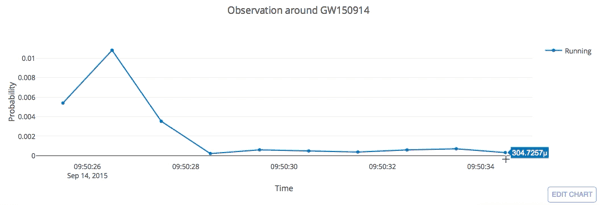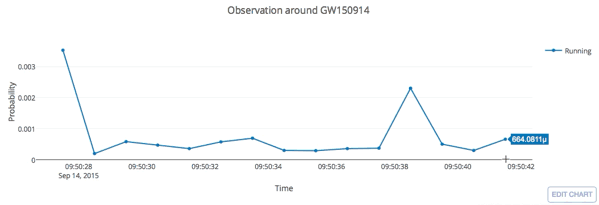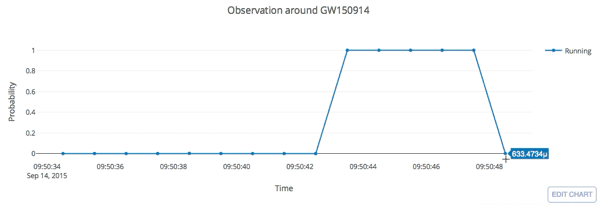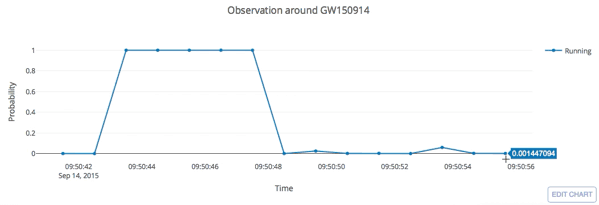
Real-time GW searches for GW150914
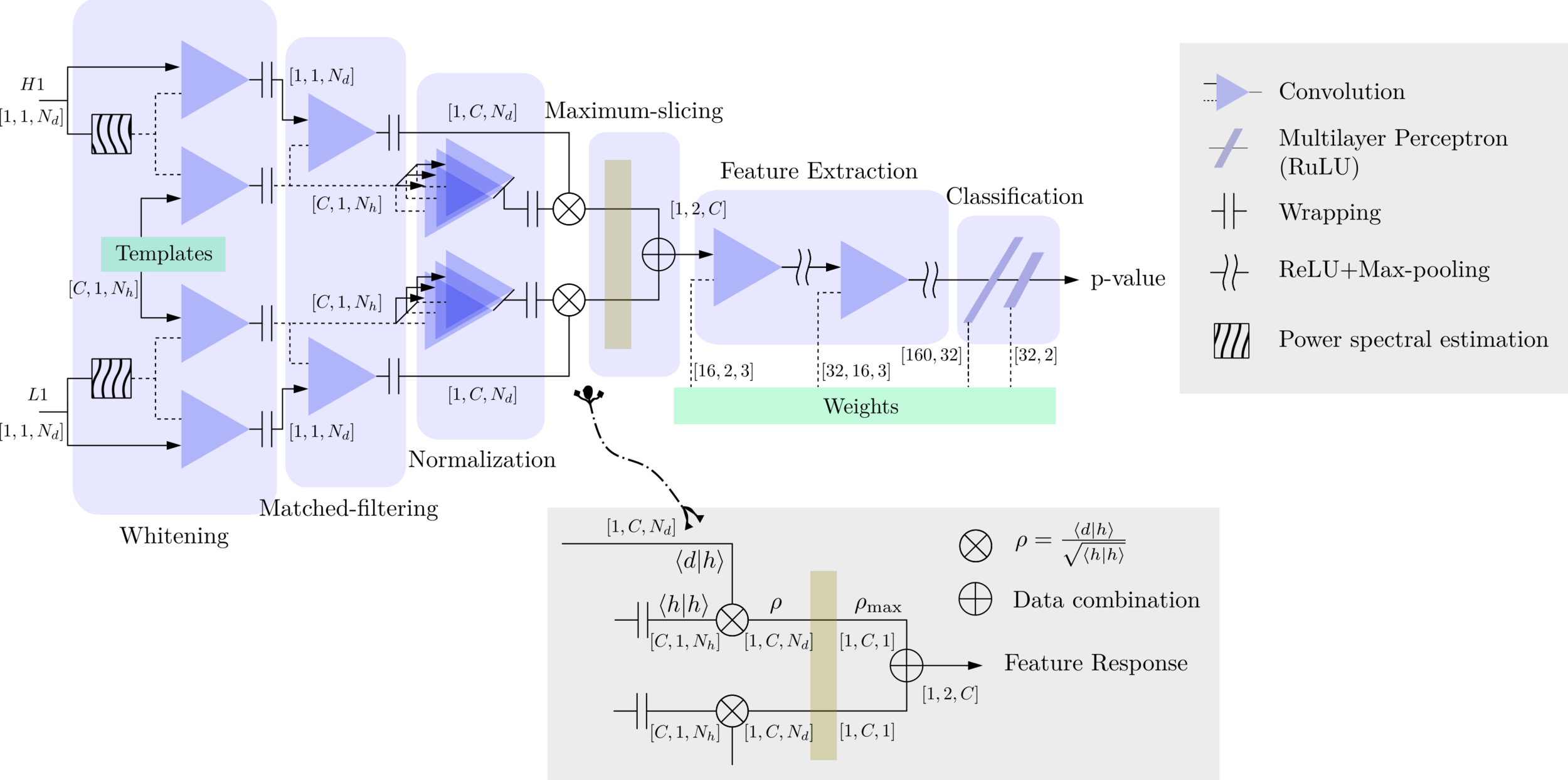
H.W., et al. PRD (2020)
Text
Expanding the dimension of the output
- is to call more information to make decisions in improving AI models.
Text
CL.M., W.W., H.W., et al. PRD (2023)
人工智能技术与引力波数据处理:信号探测
Text
Beyond Speed: Generalization and Discovery in GW Detection
- Leveraging our experience in signal modeling (MFCNN)
and noise modeling (WaveFormer), we are gradually
building an offline pipeline capable of searching for
signals in complete GW observation data and calculating
FARs.
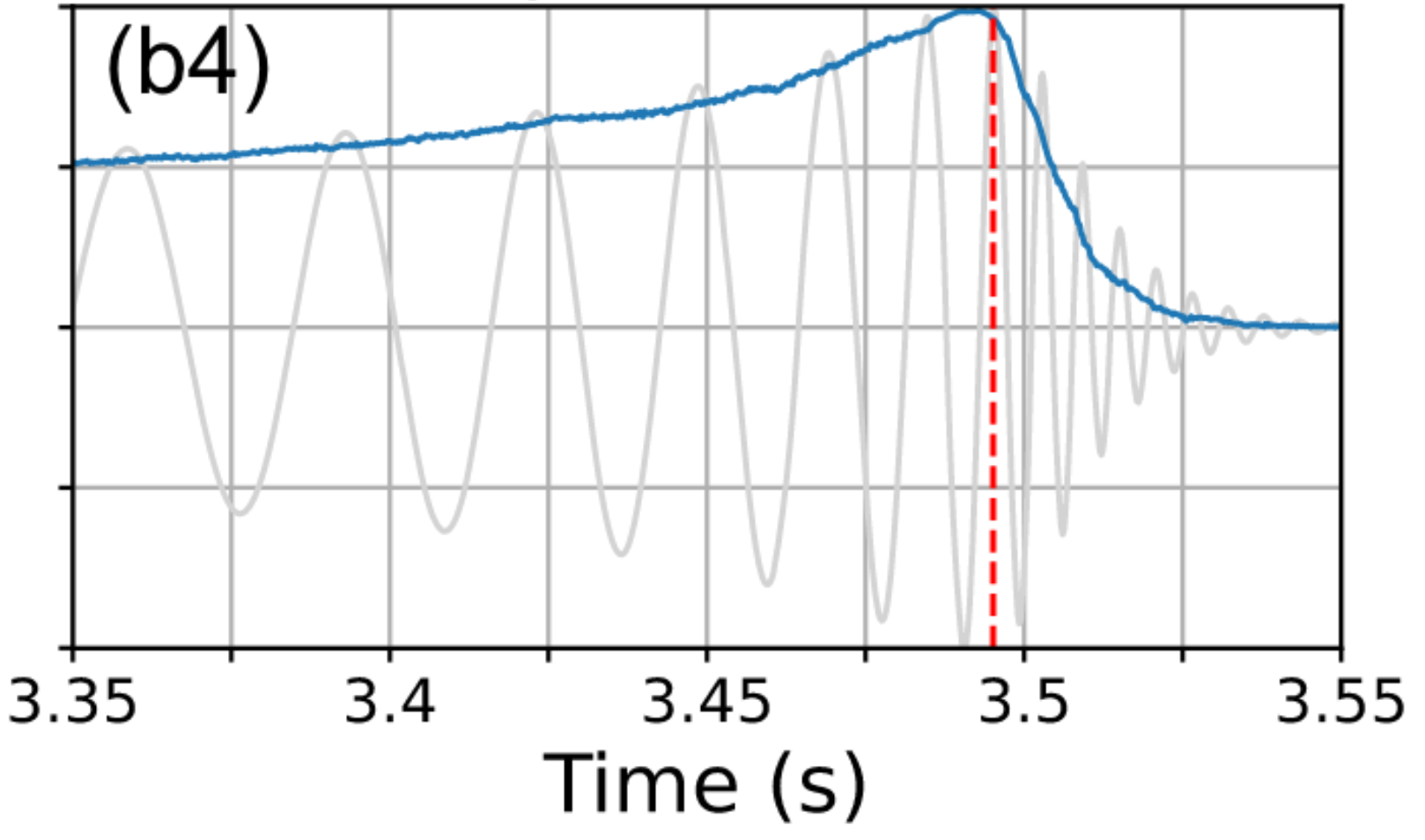
He Wang, et al. MLST. 5, 1 (2024): 015046.
人工智能技术与引力波数据处理:信号探测

Text
Challenges in Model Interpretability
- The black-box nature of AI models poses significant challenges in interpretability, making it difficult to compare AI-generated detection statistics with those derived from matched filtering chi-square distributions.
- Despite being able to identify potential gravitational wave signals, convincing the scientific community of the pipeline's validity and the statistical significance of new discoveries remains a hurdle.
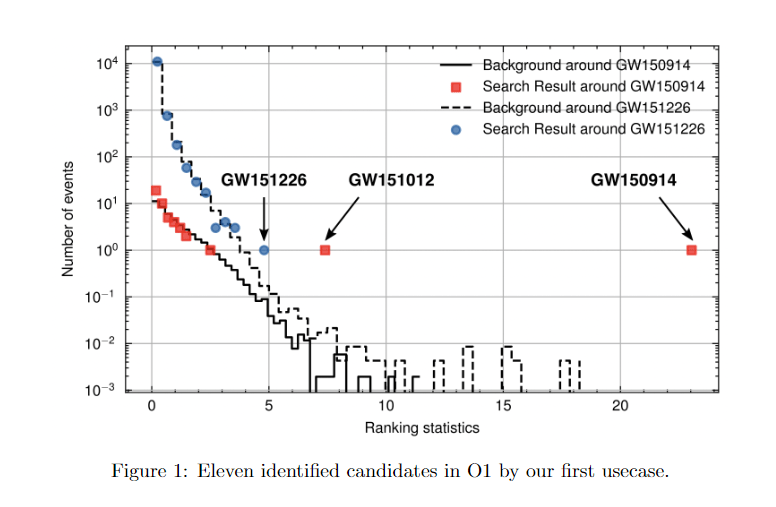
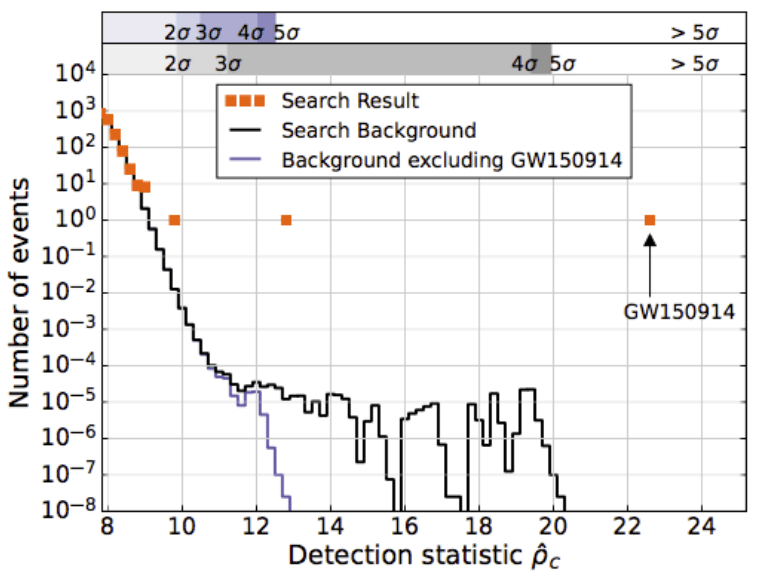
He Wang, et al. MLST. 5, 1 (2024): 015046.
GW151226
GW151012
LVK. arXiv:1602.03839
人工智能技术与引力波数据处理:信号探测

Text

Challenges in Model Interpretability
- The black-box nature of AI models poses significant challenges in interpretability, making it difficult to compare AI-generated detection statistics with those derived from matched filtering chi-square distributions.
- Despite being able to identify potential gravitational wave signals, convincing the scientific community of the pipeline's validity and the statistical significance of new discoveries remains a hurdle.

He Wang, et al. MLST. 5, 1 (2024): 015046.
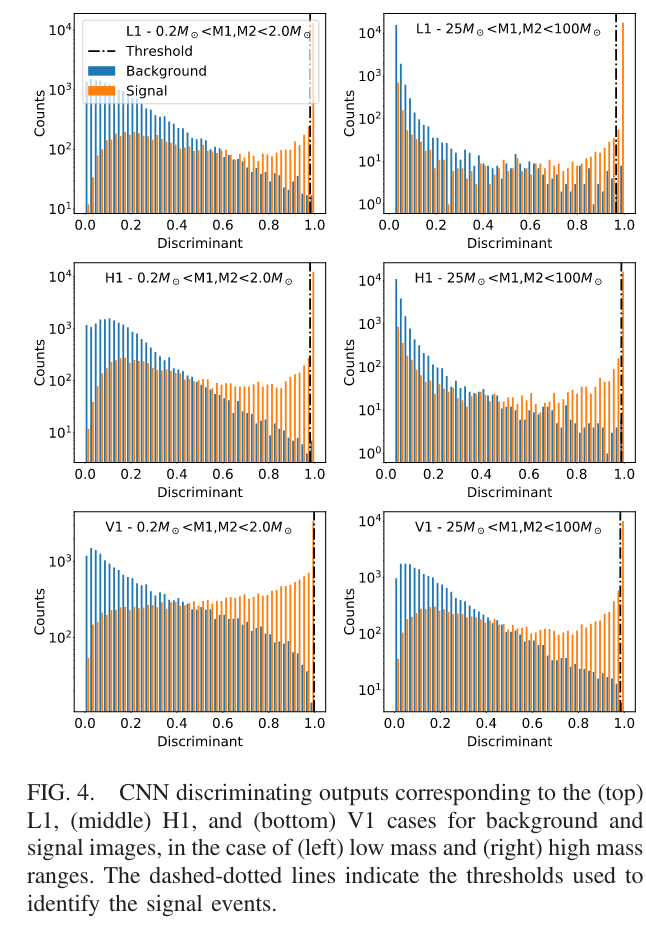
Menéndez-Vázquez A, et al. PRD 2021
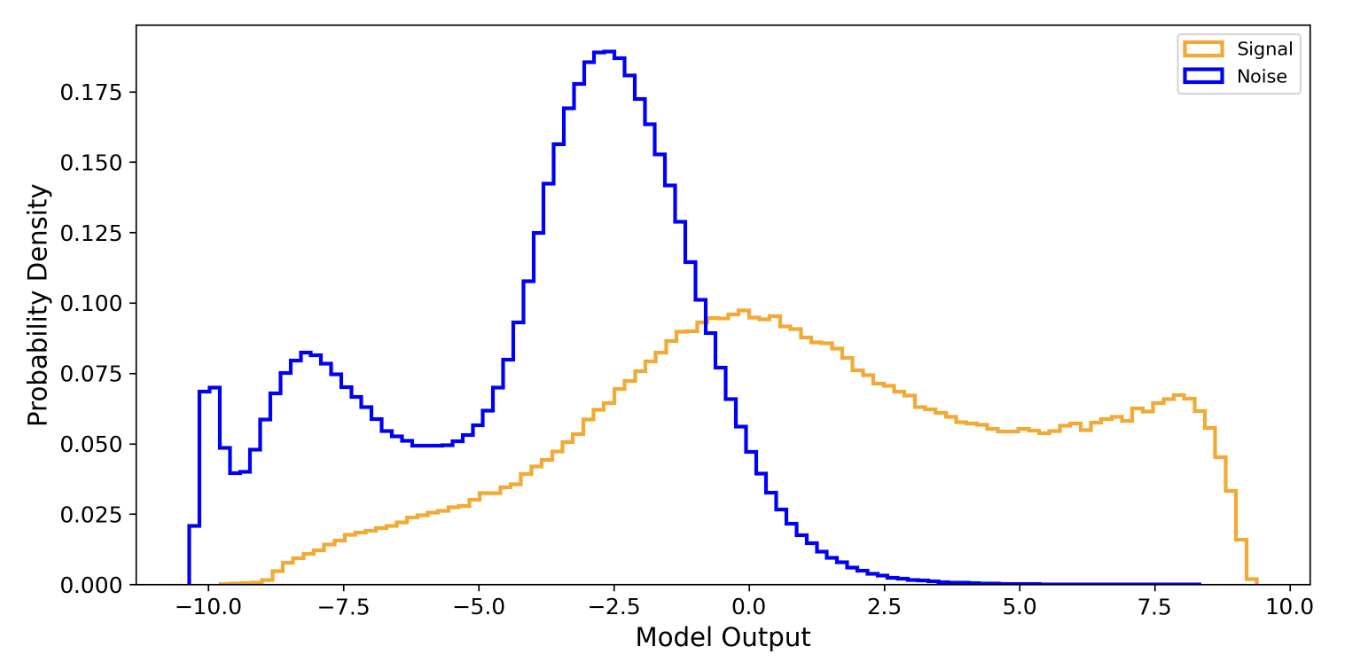
Alfaidi & Messerger. arXiv:2402.04589
The negative log-likelihood cost function always strongly penalizes the most active incorrect prediction. And the correctly classified examples will contribute little to the overall training cost."
—— I. Goodfellow, Y. Bengio, A. Courville. Deep Learning. 2016. (book)

noise
noise + signal

GW151226
GW151012
LVK. arXiv:1602.03839
人工智能技术与引力波数据处理:信号探测
Content



- GW Astronomy
- AI for Science · GW Data Analysis
- GW search · Pipeline
- Parameter estimation · Scientific discovery

Credit: LIGO Magazine.
人工智能技术与引力波数据处理:参数反演

-
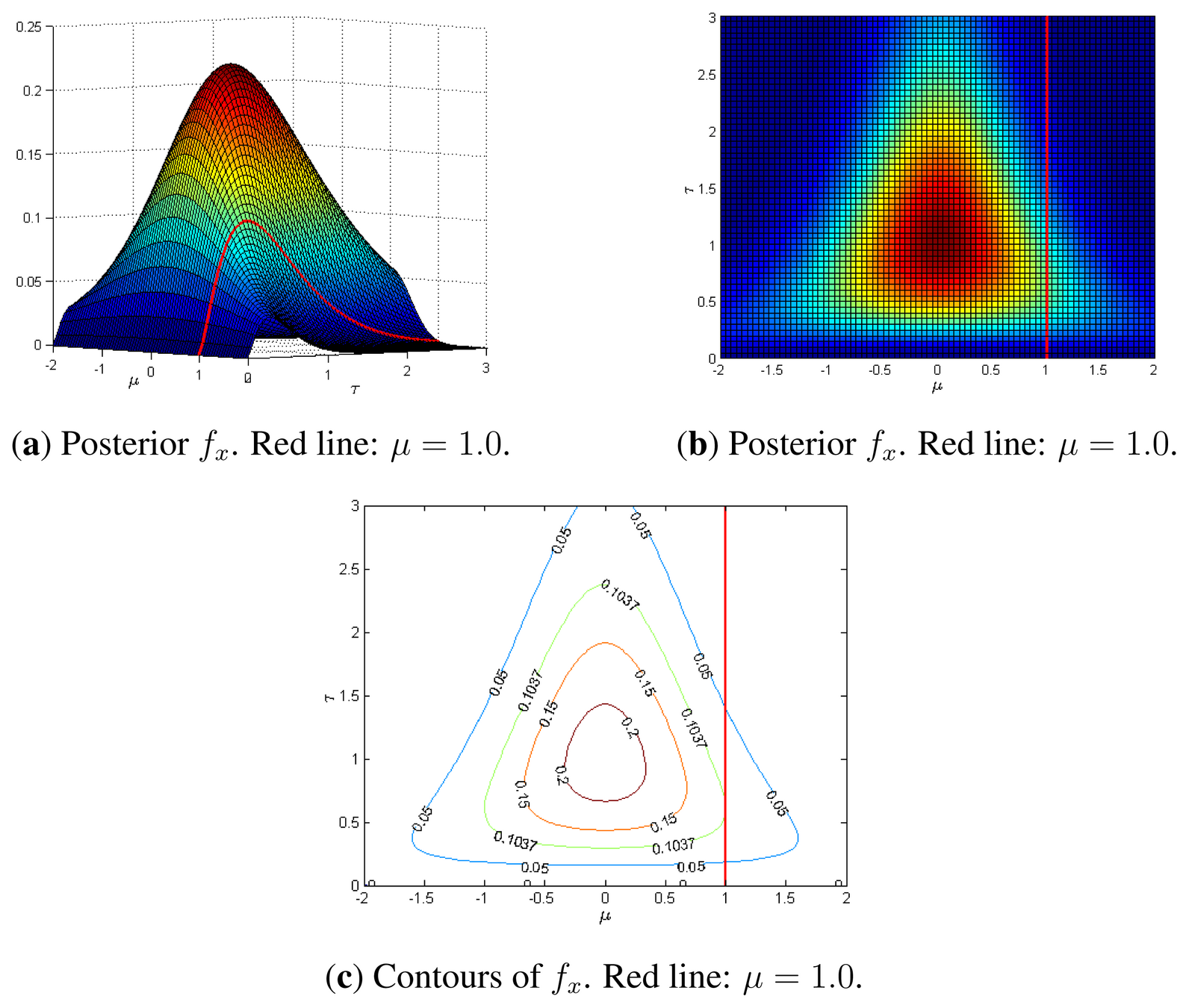
Traditional parameter estimation (PE) techniques rely on Bayesian analysis methods (posteriors + evidence)
- Computing the full 15-dimensional posterior distribution estimate is very time-consuming:
- Calculating likelihood function
- Template generation time-consuming
- Machine learning algorithms are expected to speed up!





Bayesian statistics
Data quality improvement
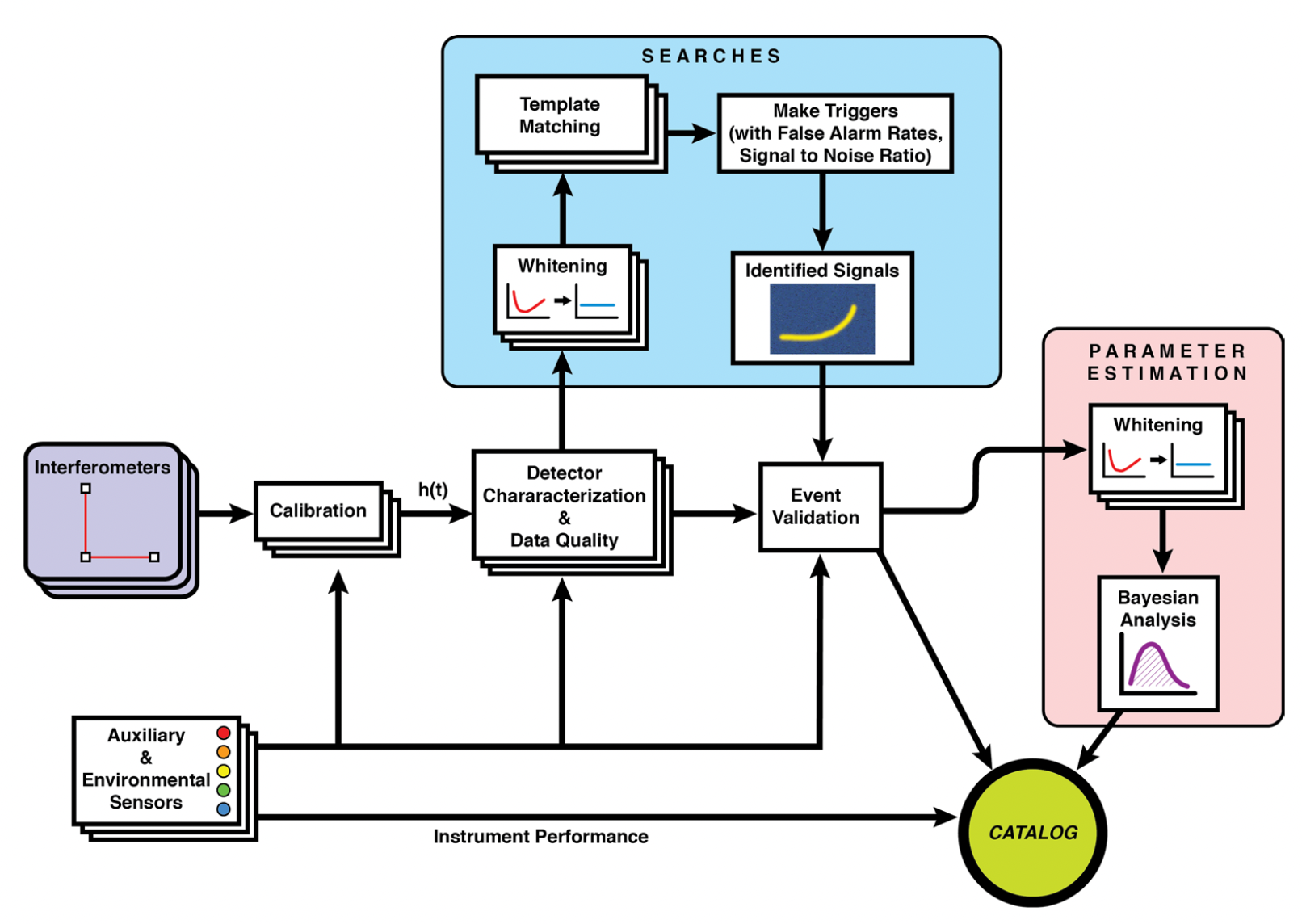
Credit: Marco Cavaglià
LIGO-Virgo data processing
GW searches
Astrophsical interpretation of GW sources
人工智能技术与引力波数据处理:参数反演
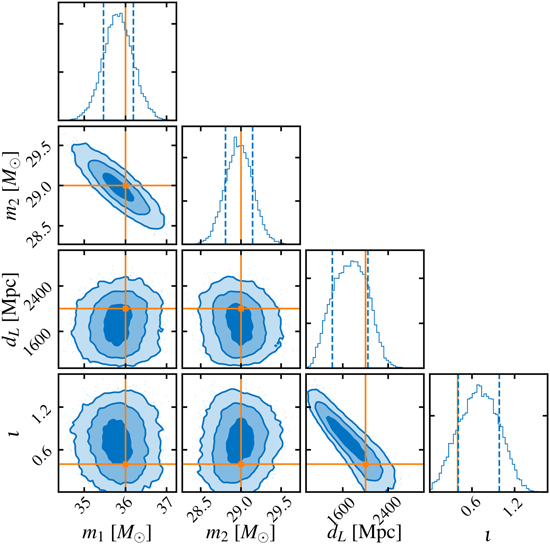
- A complete 15-dimensional posterior probability distribution, taking about 1 s (<< \(10^4\) s).
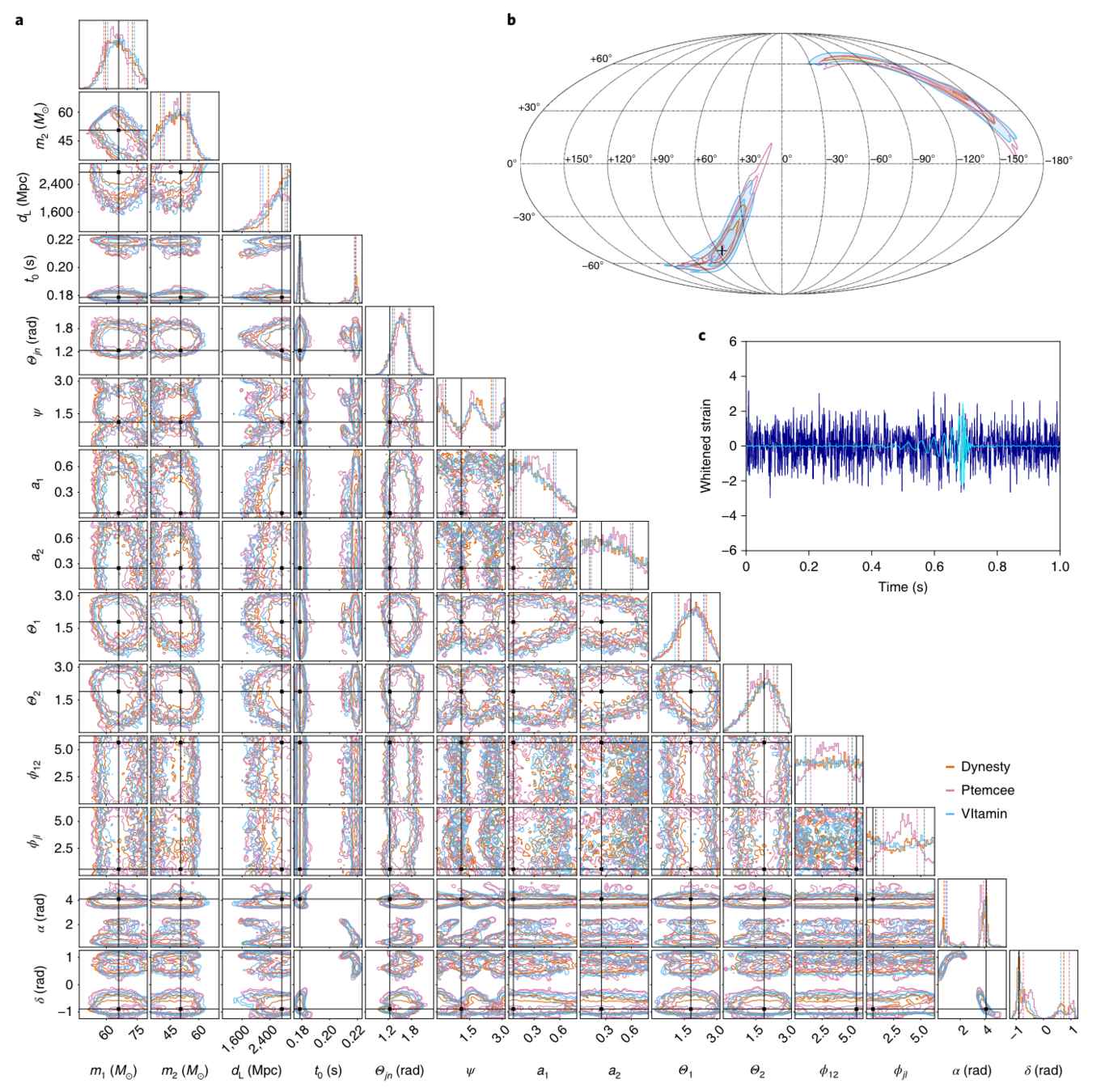
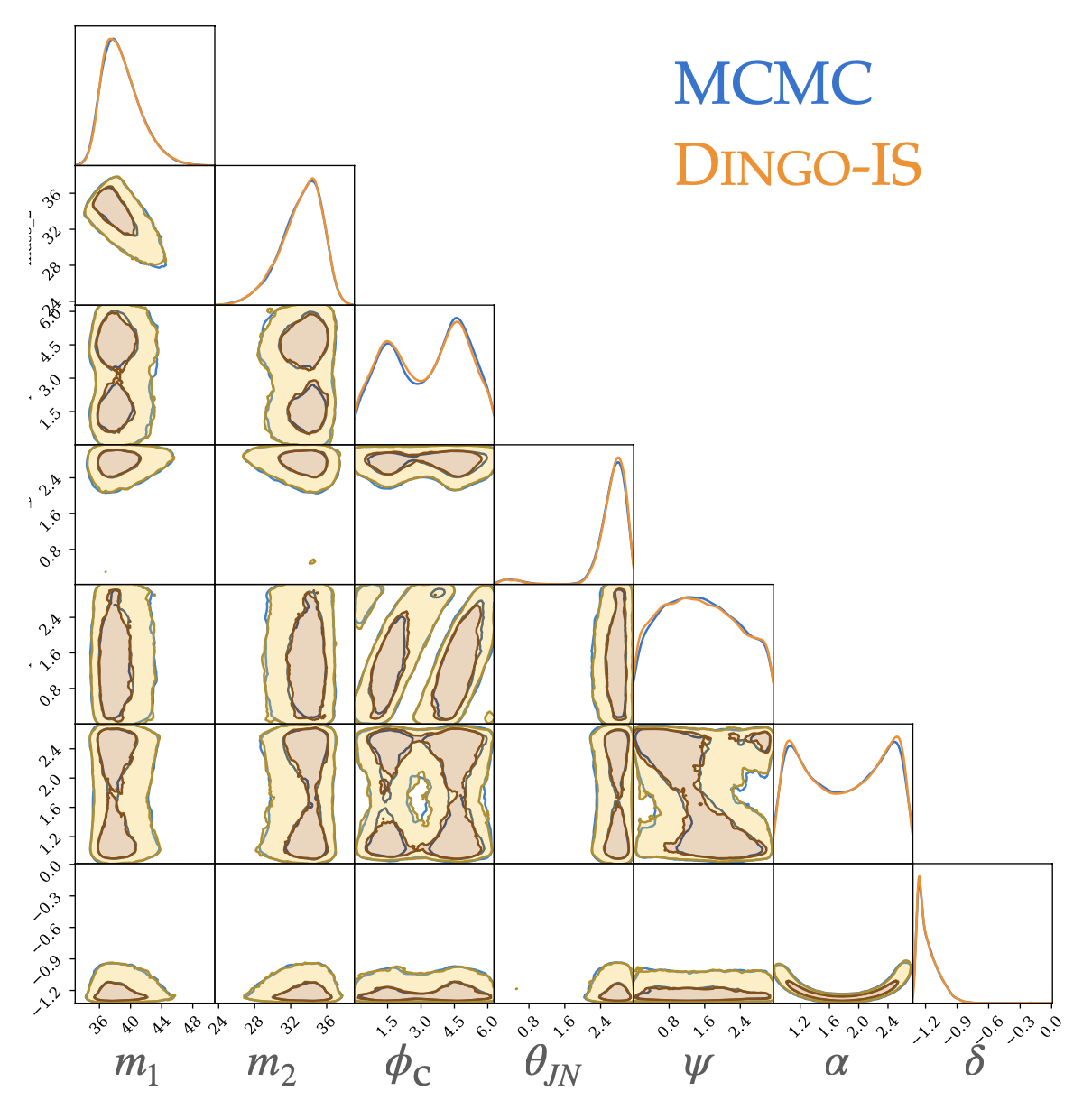
- Prior Sampling: 50,000 Posterior samples in approximately 8 Seconds.
- Capable of calculating evidence
- Processing time: (using 64 CPU cores)
- less than 1 hour with IMRPhenomXPHM,
- approximately 10 hours with SEOBNRv4PHM
PRL 127, 24 (2021) 241103.
PRL 130, 17 (2023) 171403.
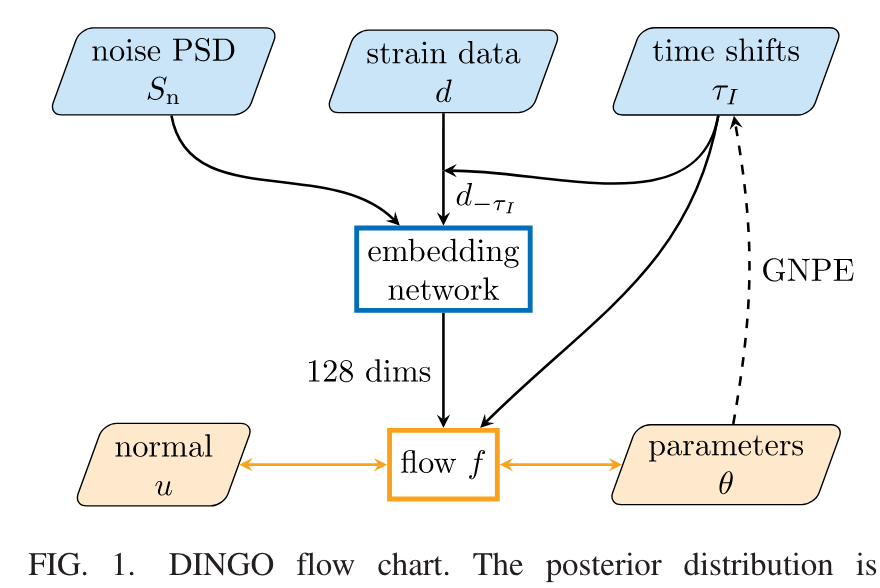
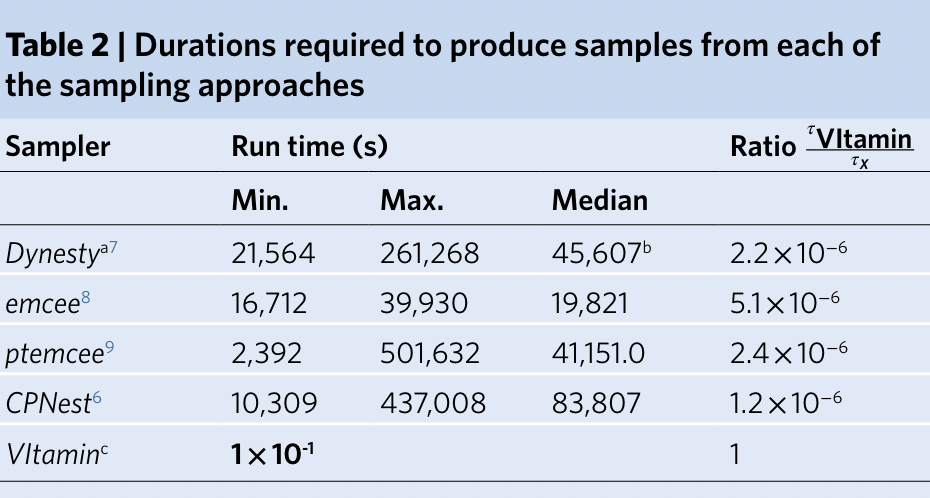
Nature Physics 18, 1 (2022) 112–17
HW, et al. Big Data Mining and Analytics 5, 1 (2021) 53–63.
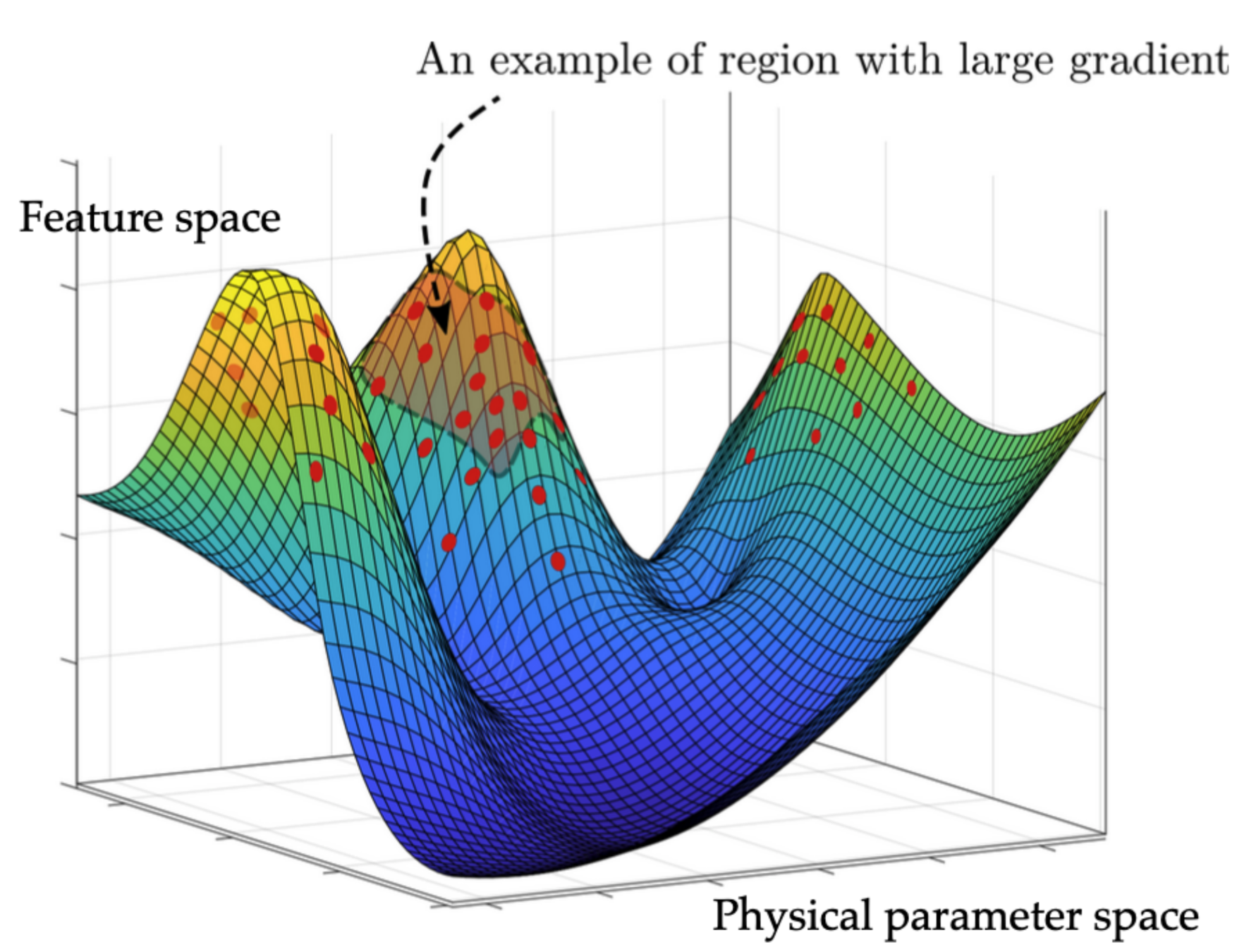
A diagram of prior sampling between feature space and physical parameter space
人工智能技术与引力波数据处理:参数反演
(Based on 1912.02762)

【【机器学习】白板推导系列(三十三) ~ 流模型(Flow based Model)】
Normalizing Flow Model (1/4)
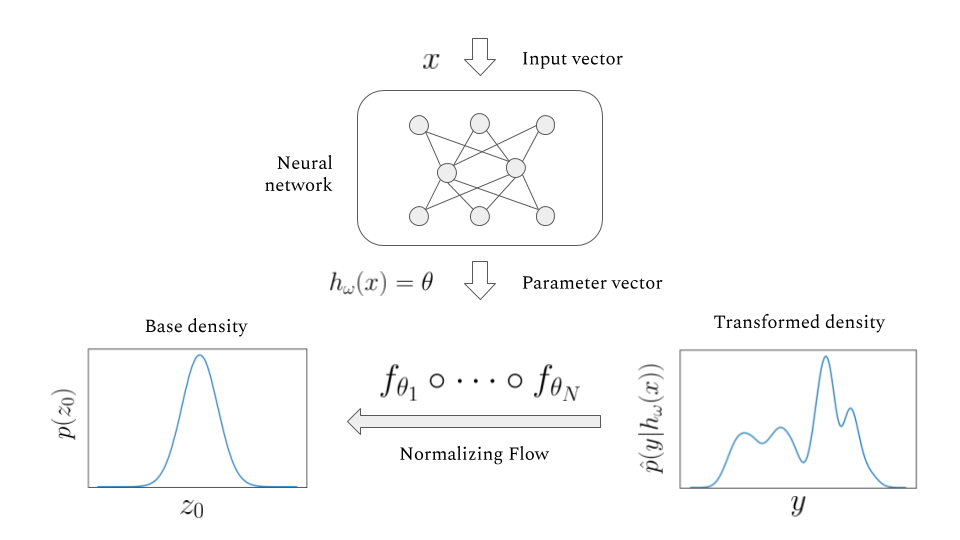
The main idea of flow-based modeling is to express \(\mathbf{y}\in\mathbb{R}^D\) as a transformation \(T\) of a real vector \(\mathbf{z}\in\mathbb{R}^D\) sampled from \(p_{\mathrm{z}}(\mathbf{z})\):
Note: The invertible and differentiable transformation \(T\) and the base distribution \(p_{\mathrm{z}}(\mathbf{z})\) can have parameters \(\{\boldsymbol{\phi}, \boldsymbol{\psi}\}\) of their own, i.e. \( T_{\phi} \) and \(p_{\mathrm{z},\boldsymbol{\psi}}(\mathbf{z})\).
Change of Variables:
Equivalently,
The Jacobia \(J_{T}(\mathbf{u})\) is the \(D \times D\) matrix of all partial derivatives of \(T\) given by:
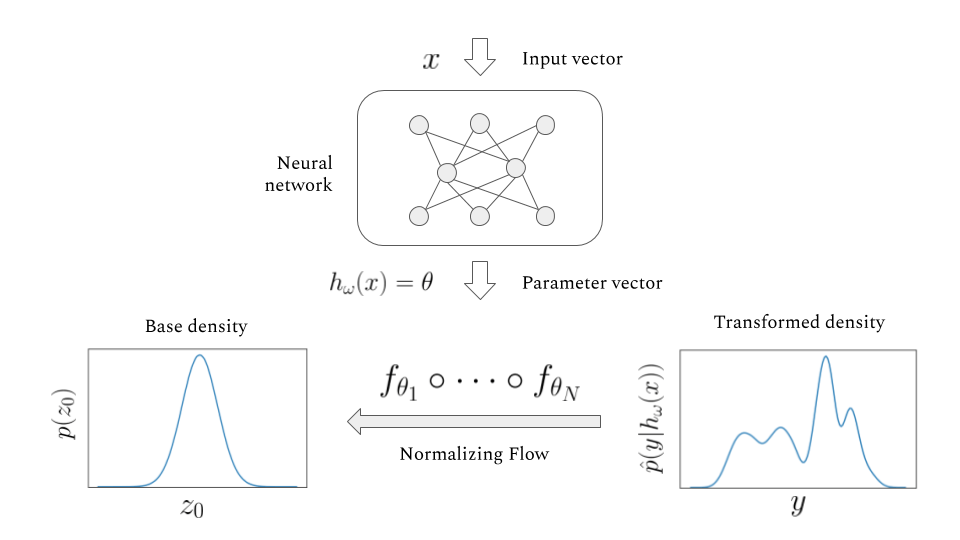

base density
target density

(Based on 1912.02762)
Normalizing Flow Model (2/4)
- Data: target data \(\mathbf{y}\in\mathbb{R}^{15}\) (with condition data \(\mathbf{x}\)).
- Task:
- Fitting a flow-based model \(p_{\mathrm{y}}(\mathbf{y} ; \boldsymbol{\theta})\) to a target distribution \(p_{\mathrm{y}}^{*}(\mathbf{y})\)
- by minimizing KL divergence with respect to the model’s parameters \(\boldsymbol{\theta}=\{\boldsymbol{\phi}, \boldsymbol{\psi}\}\),
- where \(\boldsymbol{\phi}\) are the parameters of \(T\) and \(\boldsymbol{\psi}\) are the parameters of \(p_{\mathrm{z}}(\mathbf{z})=\mathcal{N}(0,\mathbb{I})\).
- Loss function:
- Assuming we have a set of samples \(\left\{\mathbf{y}_{n}\right\}_{n=1}^{N}\sim p_{\mathrm{y}}^{*}(\mathbf{y})\),
Minimizing the above Monte Carlo approximation of the KL divergence is equivalent to fitting the flow-based model to the samples \(\left\{\mathbf{y}_{n}\right\}_{n=1}^{N}\) by maximum likelihood estimation.


base density
target density
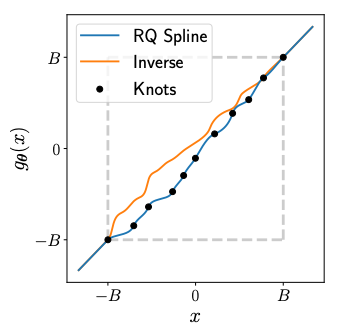
Rational Quadratic Neural Spline Flows
(RQ-NSF)

Train
nflow
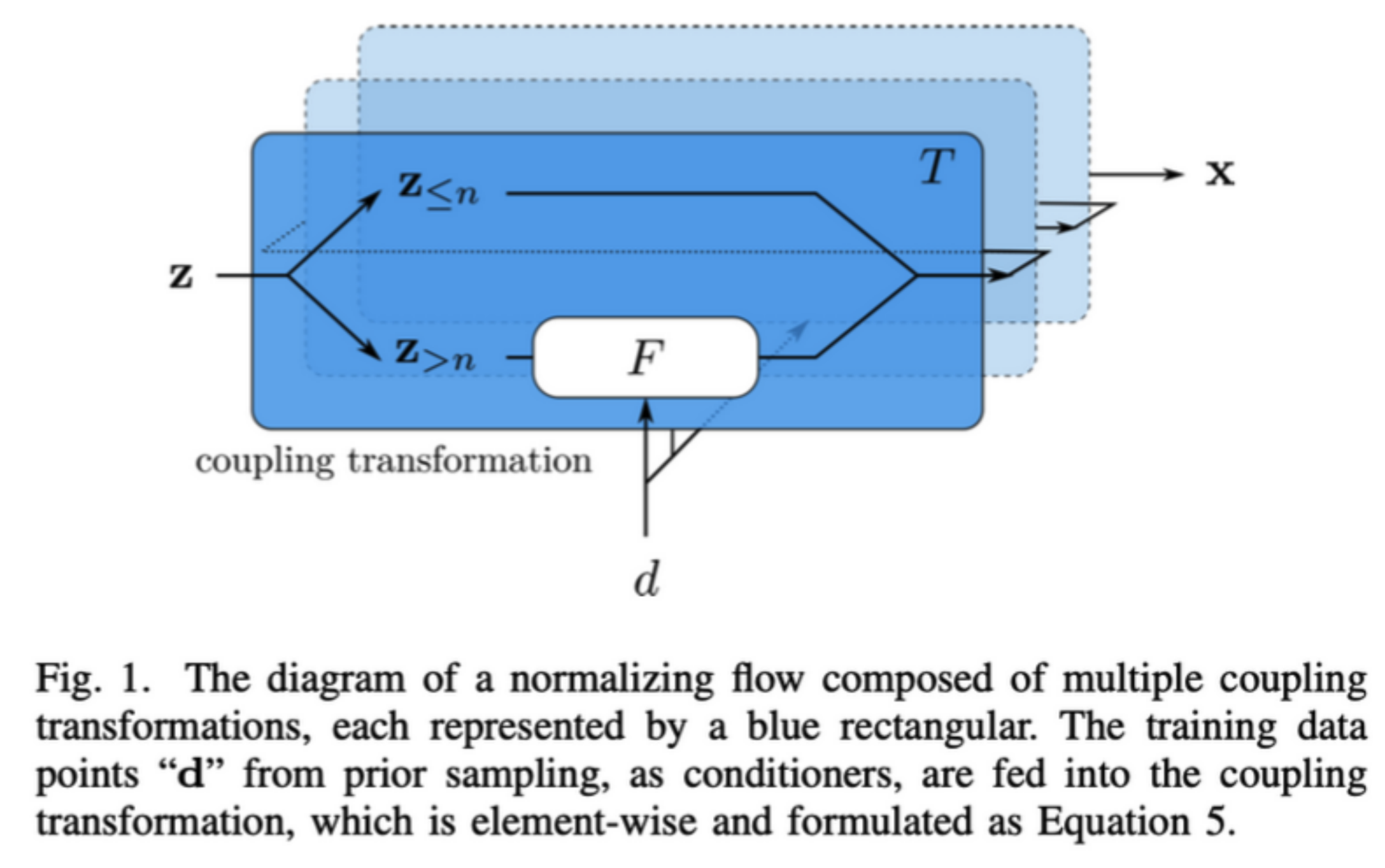
Normalizing Flow Model (3/4)

归一化流模型示意图

Test
nflow
Train
nflow
Normalizing Flow Model (4/4)
-
Bayesian inference, the Holy Grail of gravitational-wave data analysis,
enables astrophysical interpretation and scientific discoveries.
Simulation-Based Inference (SBI)
- SBI \(\Rightarrow\) Fast and precise parameter estimation.
- SBI \(\Rightarrow\) TGR / Cosmology / PTA ...

Text

PRL 127, 24 (2021) 241103.
PRL 130, 17 (2023) 171403.
Real-time gravitational wave science with neural posterior estimation
Sampling with prior knowledge for high-dimensional gravitational wave data analysis
He Wang, et al. Big Data Min. Anal. (2021)
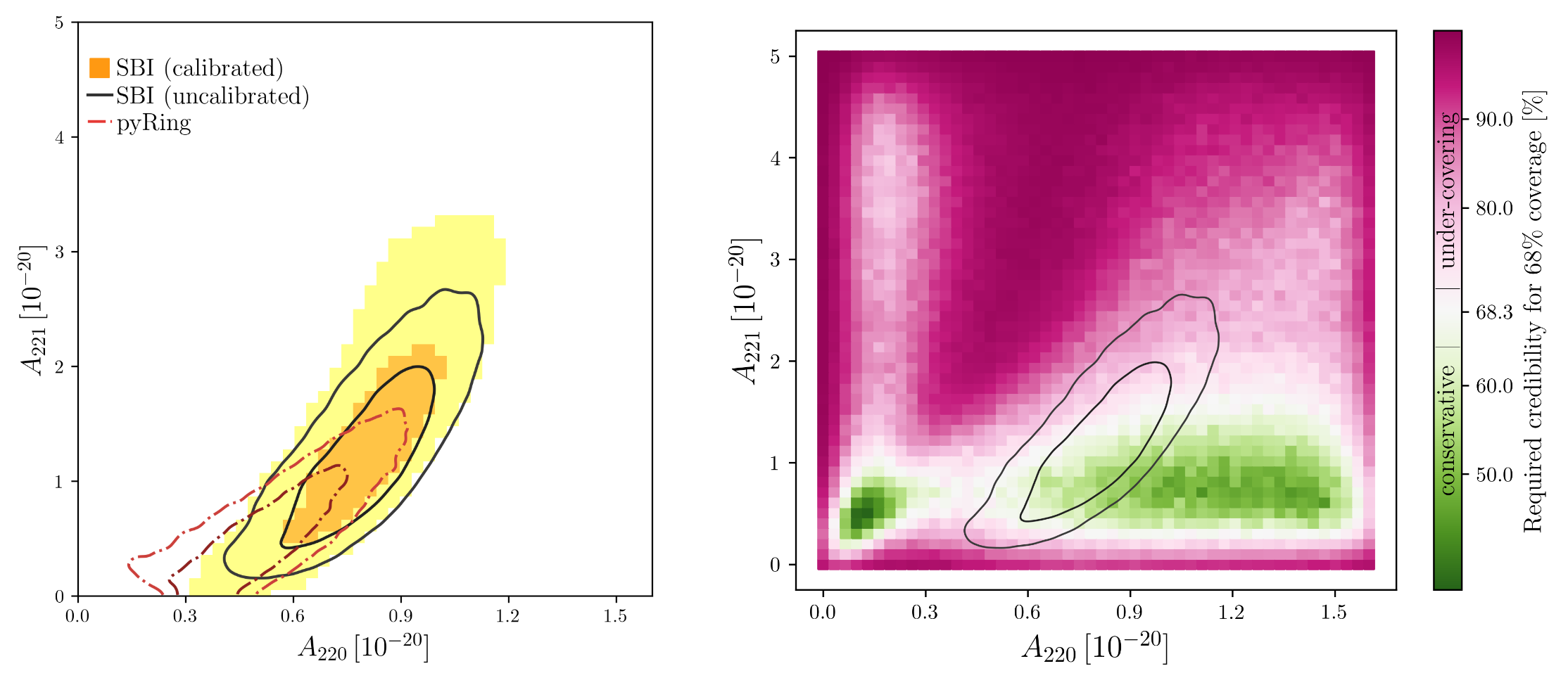
PRD 108, 4 (2023): 044029.
Neural Posterior Estimation with Guaranteed Exact Coverage: The Ringdown of GW150914
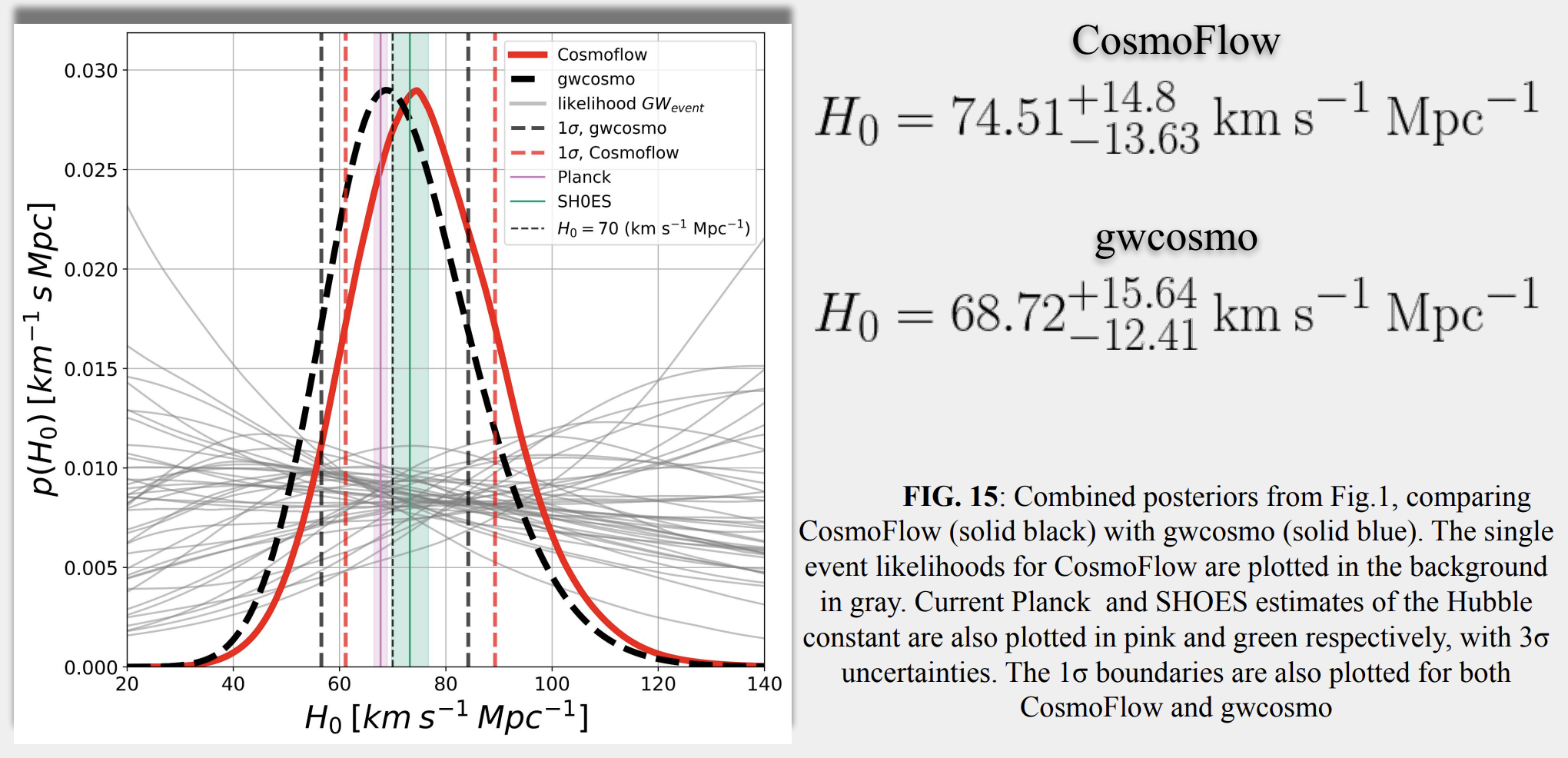
arXiv:2310.13405, LIGO-P2300306
Cosmological Inference using Gravitational Waves and Normalising Flows
Parameter estimation · Scientific discovery
Fast Parameter Inference on Pulsar Timing Arrays with Normalizing Flows
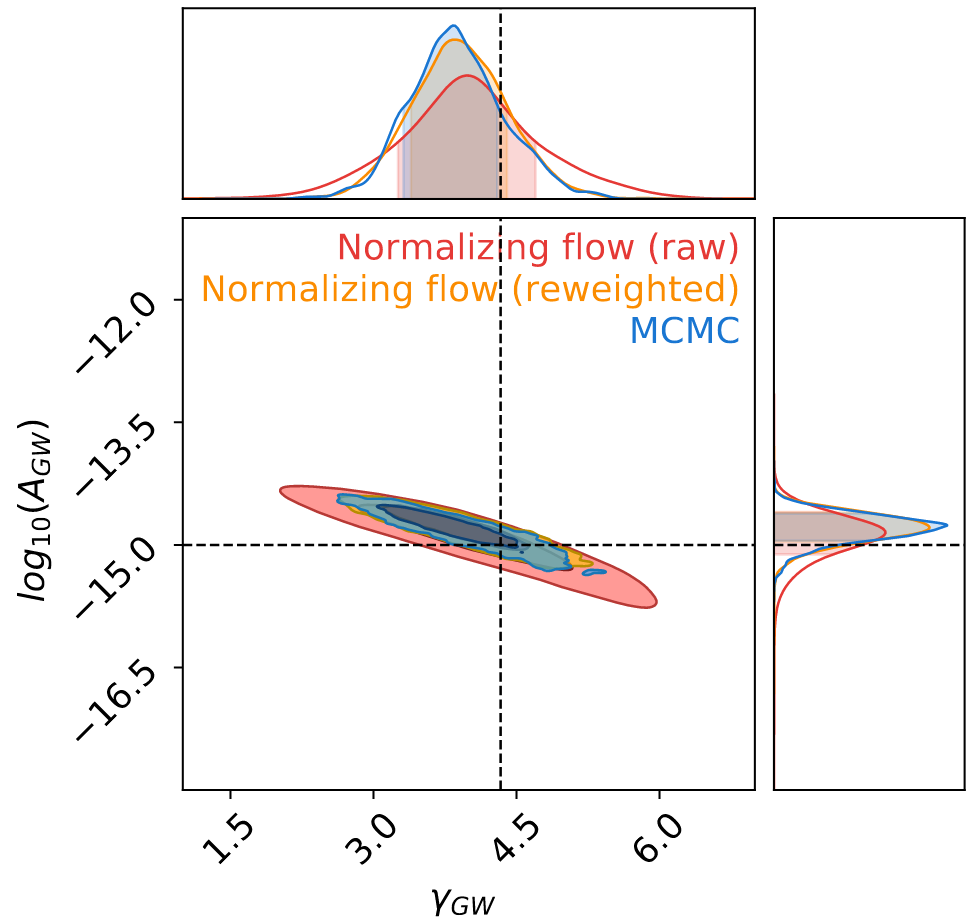
arXiv:2310.12209
He Wang, et al. (2024)
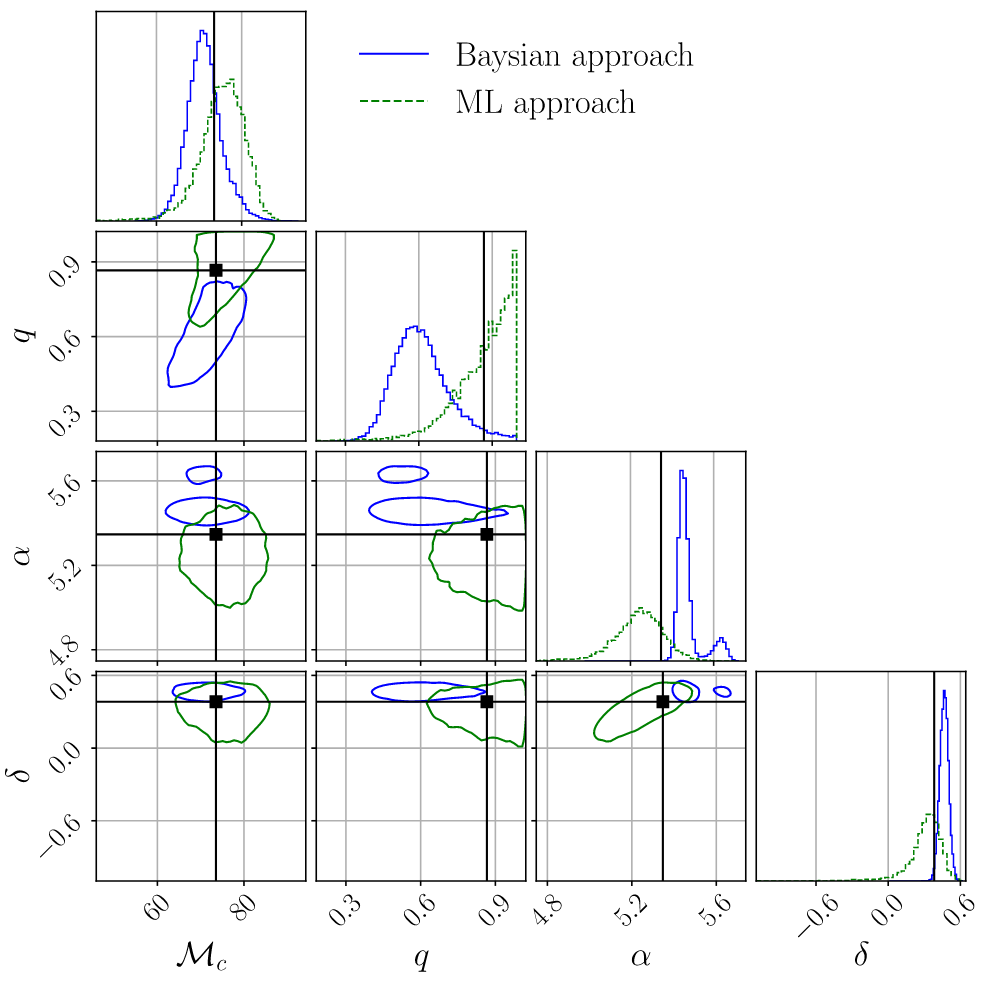
Normalizing Flows as an Avenue to Studying Overlapping Gravitational Wave Signals
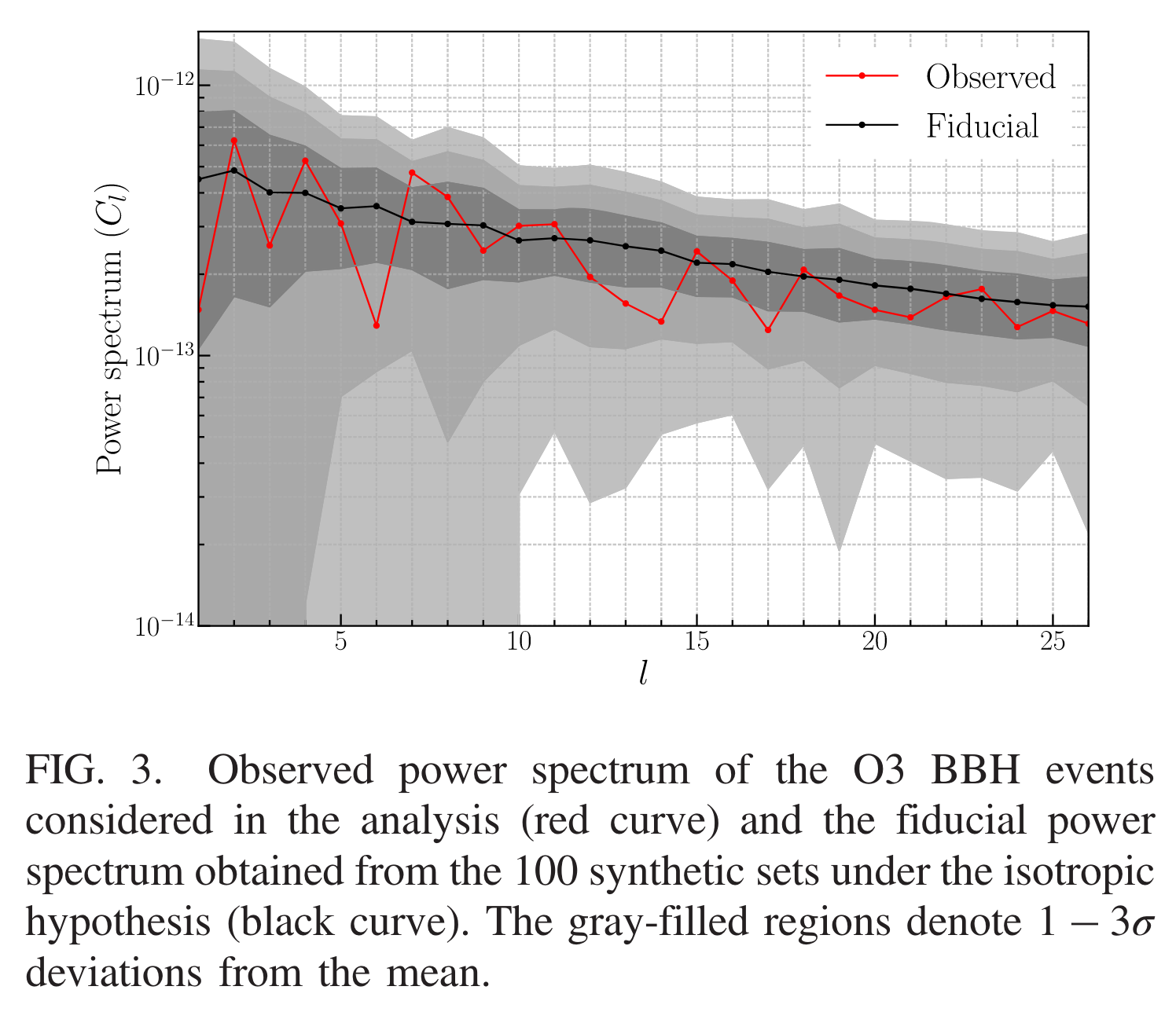
PRL 131, 17 (2023): 171403.
Angular Power Spectrum of Gravitational-Wave Transient Sources as a Probe of the Large-Scale Structure
Ongoing and Future Projects

| Pipeline | Targets | Programing Language (sampling method) | Comments |
|---|---|---|---|
|
GLASS (Littenberg&Cornish 2023) |
Noise, UCB, VGB, MBHB |
C / Python (TPMCMC / RJMCMC) | noise_mcmc+gb_mcmc+vb_mcmc+global_fit |
| Eryn | UCB | Python (TPMCMC / RJMCMC) | Mini code for UCB case |
| PyCBC-INFERENCE | MBHB | Python (?) | Unavailable |
| Bilby in Space / tBilby | MBHB / ? | ? / Python? (RJMCMC) | Unavailable |
| Strub et al. | UCB | ? (GP) | Unavailable / GPU-based |
| Zhang et al. (LZU) | UCB | ? (PSO) | MLP |
| Balrog | MBHB | ? |

(Sec.8.6 Red Book)
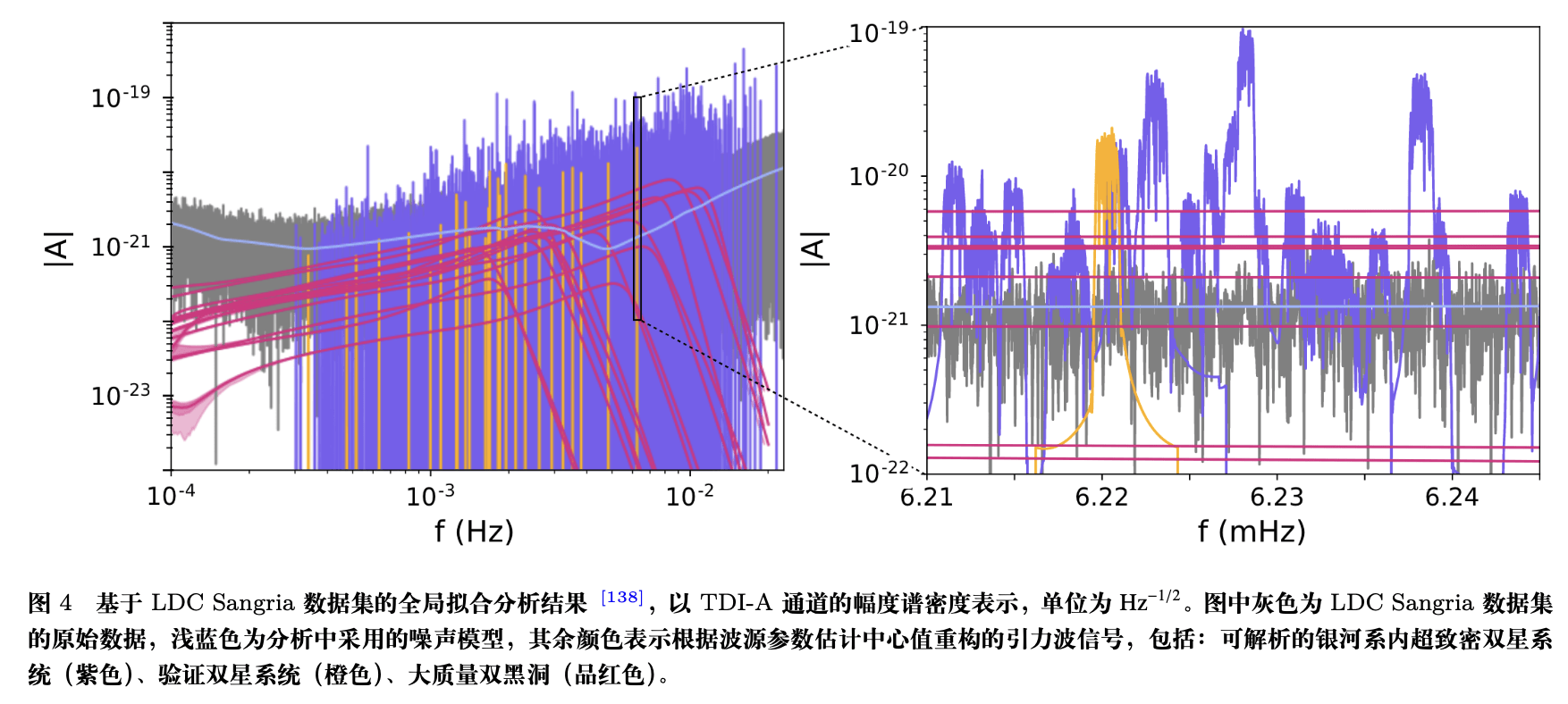
Global Fit
- The idea of the global fit method is to comprehensively model all astrophysical and instrumental features present in the space-borne gravitational wave data.
- This approach not only focuses on the signal from a single source, but attempts to capture the combined effects of all sources in the data, conducting a comprehensive analysis of the entire dataset to identify and model all potential signal and noise sources.
Technical challenges:
- High dimensional
- Highly correlated
- Multimodality
- Trans-dimensional
Text

Ongoing and Future Projects
Neural density estimation
-
Density fit for posterior distributions
- use the old posterior to form a proposal for the extended data.
-
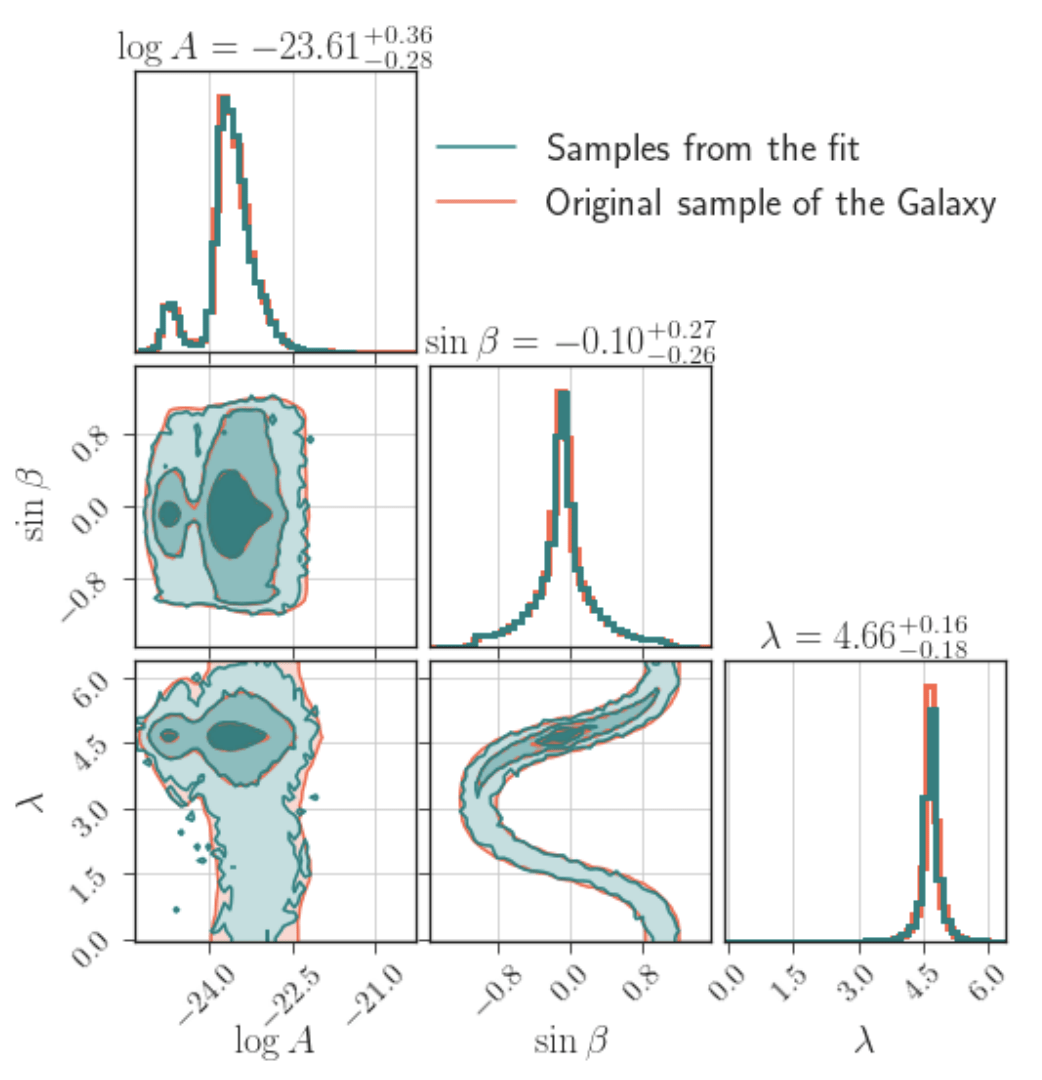
Density fit for the Galaxy
- fitt a Galaxy model for joint distribution for \((A, \beta, \lambda)\).
- ...
Text

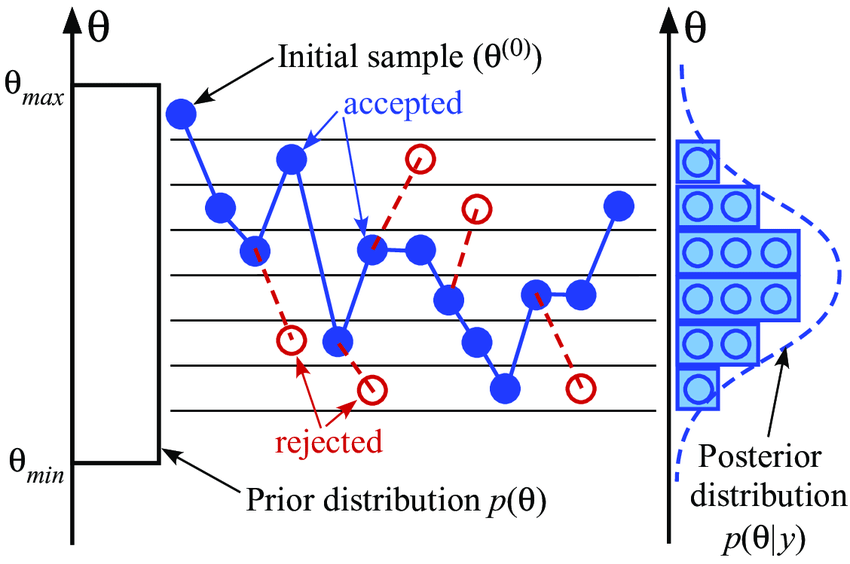
Disadvantages of MCMC
- Computational Intensity: MCMC can be computationally demanding, especially for large datasets or highly complex models.
- Difficulty in Tuning Parameters: Properly tuning MCMC algorithms can be challenging. Selecting the right step size or proposal distribution is crucial. Choosing the wrong tuning parameters can lead to inefficient sampling and inaccurate results.
- Challenges in Reaching Convergence: MCMC chains must converge to the true distribution; otherwise, the results are meaningless.
- Necessity for Appropriate Initial Values: The choice of initial values can affect the results.

Ref:
- Ashton, G, and C Talbot. MNRAS 507, no. 2 (2021): 2037–51.
- Korsakova, N, et al. (2402.13701)
- Wouters, T, et al. (2404.11397)
Ongoing and Future Projects
Neural density estimation
- Density fit for posterior distributions
- use the old posterior to form a proposal for the extended data.
- Density fit for the Galaxy
- fitt a Galaxy model for joint distribution for \((A, \beta, \lambda)\).
- ...
Text

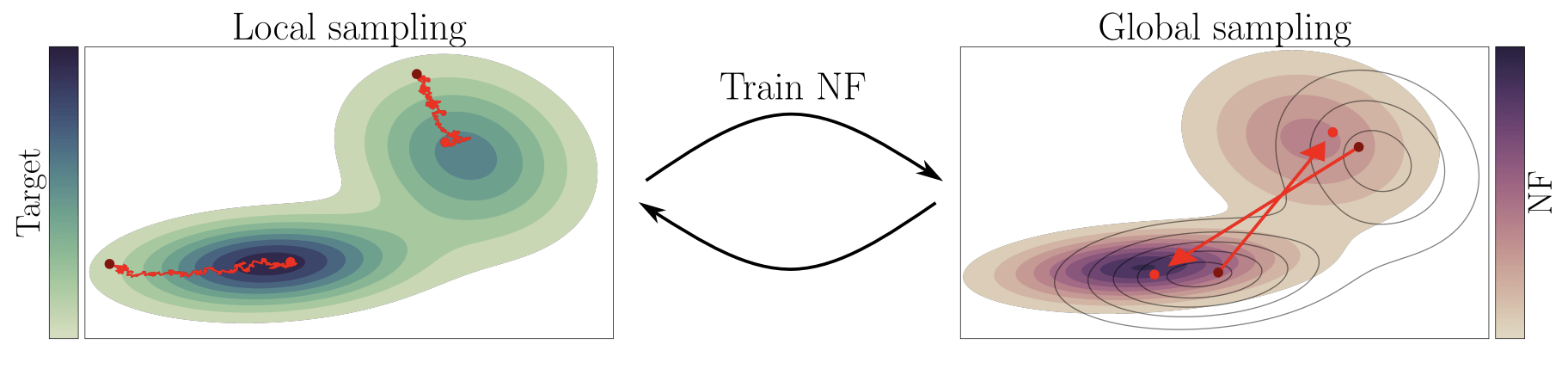
nflow


Ref:
- Ashton, G, and C Talbot. MNRAS 507, no. 2 (2021): 2037–51.
- Korsakova, N, et al. (2402.13701)
- Wouters, T, et al. (2404.11397)
Ongoing and Future Projects
Neural density estimation
- Density fit for posterior distributions
- use the old posterior to form a proposal for the extended data.
- Density fit for the Galaxy
- fitt a Galaxy model for joint distribution for \((A, \beta, \lambda)\).
- ...
Text


nflow



for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This slide: https://slides.com/iphysresearch/2024june_bua

AI Predicting the Universe: Opportunities and Challenges
-
Exploring the importance of understanding how AI models make predictions in scientific research.
- The critical role of generative models (生成模型是关键)
- Quantifying uncertainty: a key aspect (不确定性量化问题)
- Fostering controllable and reliable models (模型的可控可信问题)

AI or Bayes

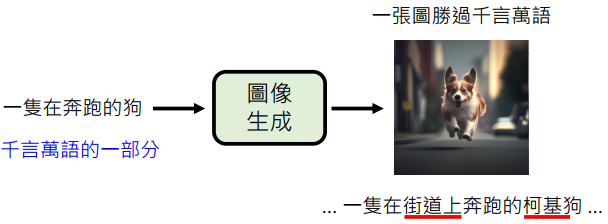
Text-to-image
"A running dog"
- The most common and direct approach, from Artificial Intelligence Generated Content (AIGC) to GW statistical inference: pixel point \(\Rightarrow\) inferred parameter.

AI Predicting the Universe: Opportunities and Challenges
-
Exploring the importance of understanding how AI models make predictions in scientific research.
- The critical role of generative models (生成模型是关键)
- Quantifying uncertainty: a key aspect (不确定性量化问题)
- Fostering controllable and reliable models (模型的可控可信问题)



AI or Bayes

Text-to-image
"A corgi running on the street"
A picture is worth a thousand words.
A fraction of a thousand words.
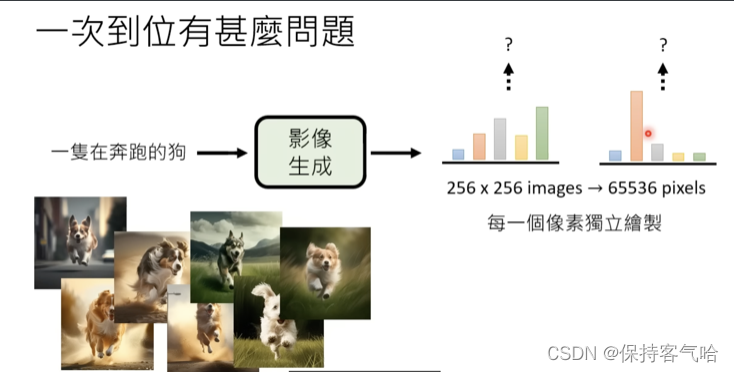
Credit: 李宏毅
"A running dog"
- The most common and direct approach, from Artificial Intelligence Generated Content (AIGC) to GW statistical inference: pixel point \(\Rightarrow\) inferred parameter.