Efficient Numerical Methods for Nonlinear Model Predictive Control with Applications in Adaptive Cruise Control

Ihno Schrot — Disputationsvortrag — 03. Juli 2025

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

MOTIVATION

Bildquellen: jcomp, bzw. rawpixel.com, auf Freepik

Adaptive Cruise Control (ACC)

  • Fahrassistenzsystem
  • Tempomat + Abstandshalter

Ecological ACC (EACC)

  • Variiert Abstand zum vorigen Fahrzeug (PP0)
  • Nutzt Verkehrs- und Streckeninfo \(\rightarrow\) Energiesparen

\(\rightarrow\) Nichtlineare Modellprädiktive Regelung (NMPC)

1/14

  • Umgang mit tabellarisierten Daten und externen Einflüssen
  • Wenig Rechenleistung auf Onboard-Hardware  

Herausforderungen für numerische NMPC Methoden

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

NICHTLINEARE MODELLPRÄDIKTIVE REGELUNG (NMPC)

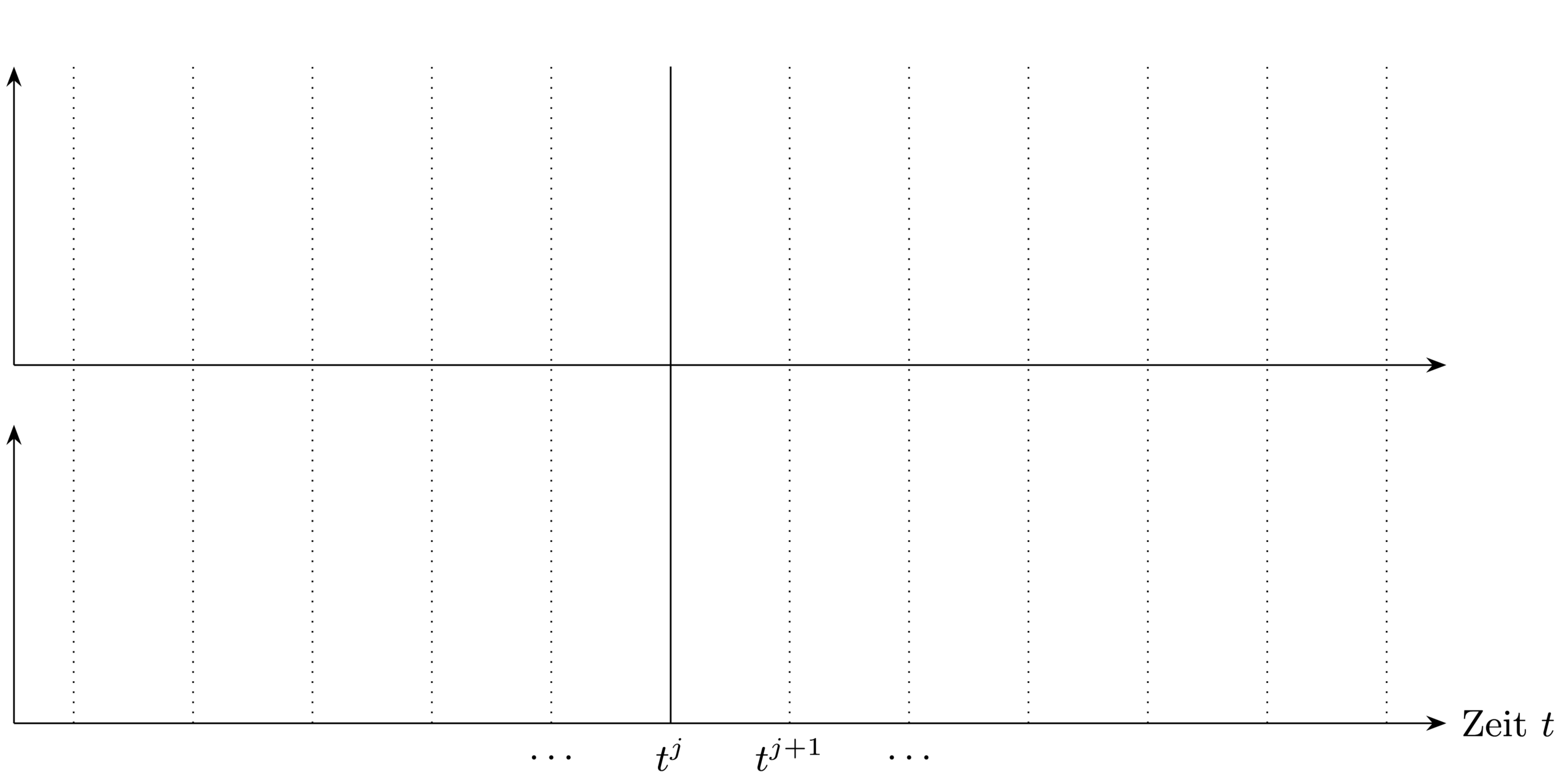
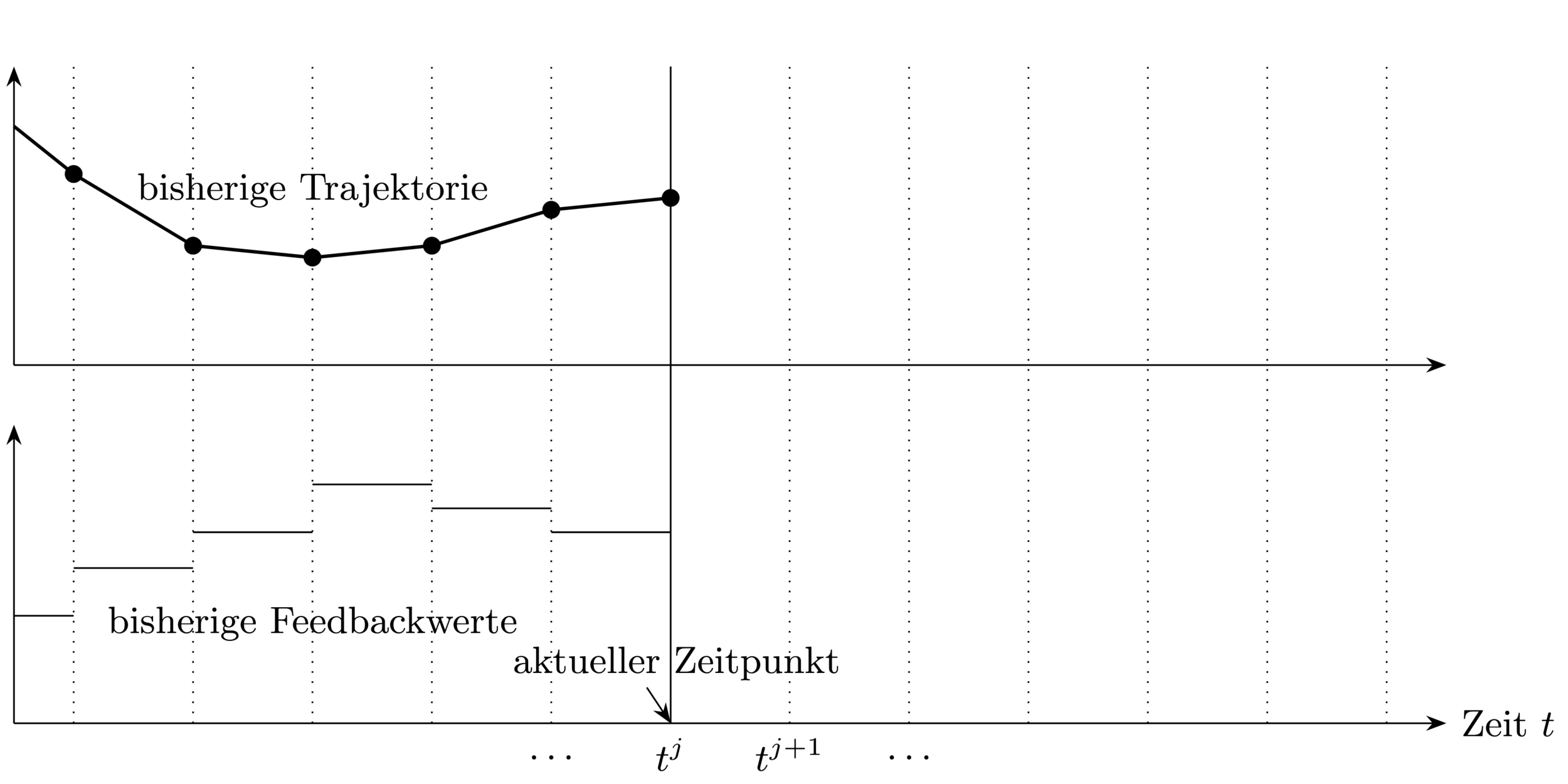
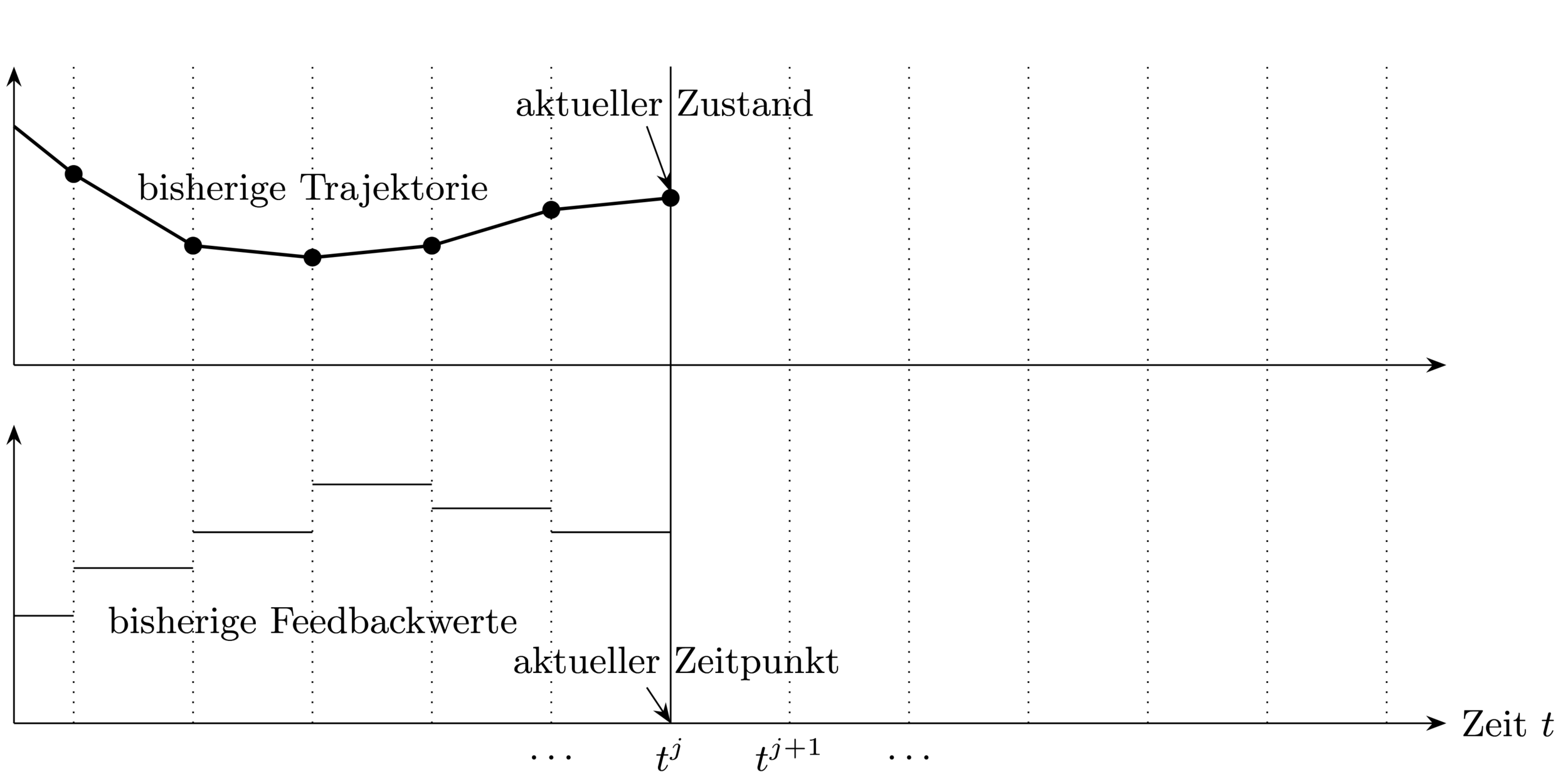
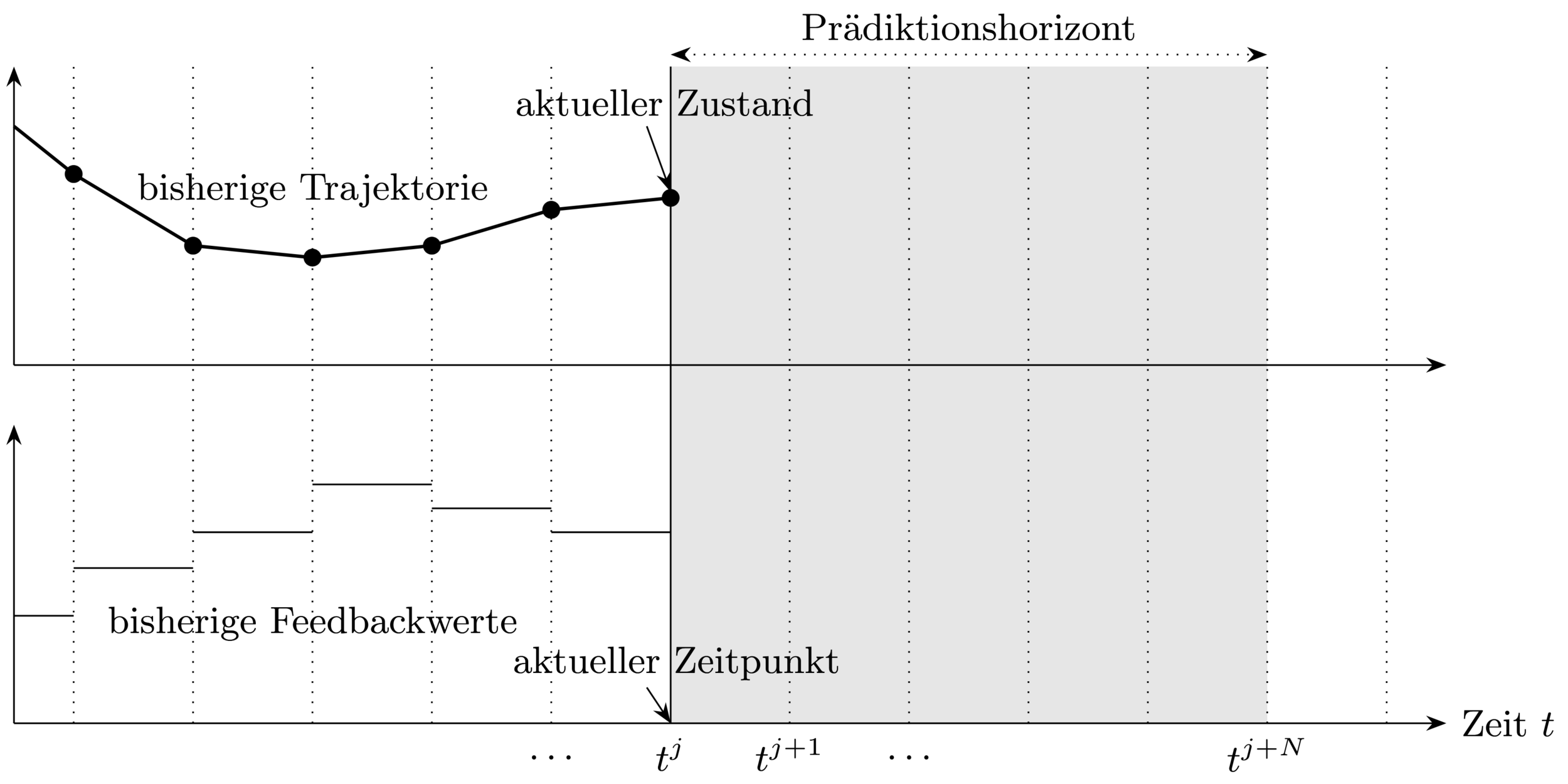
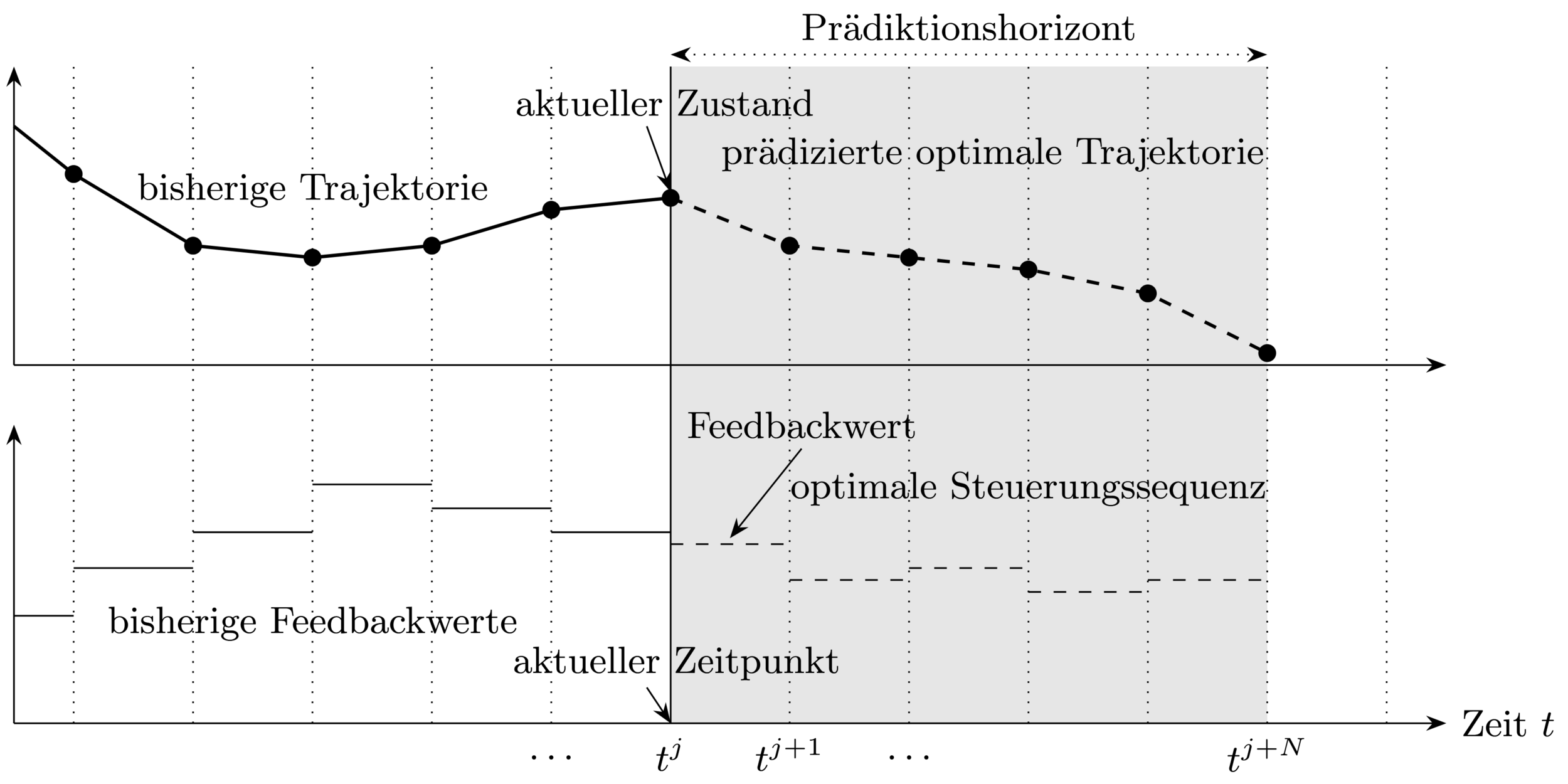
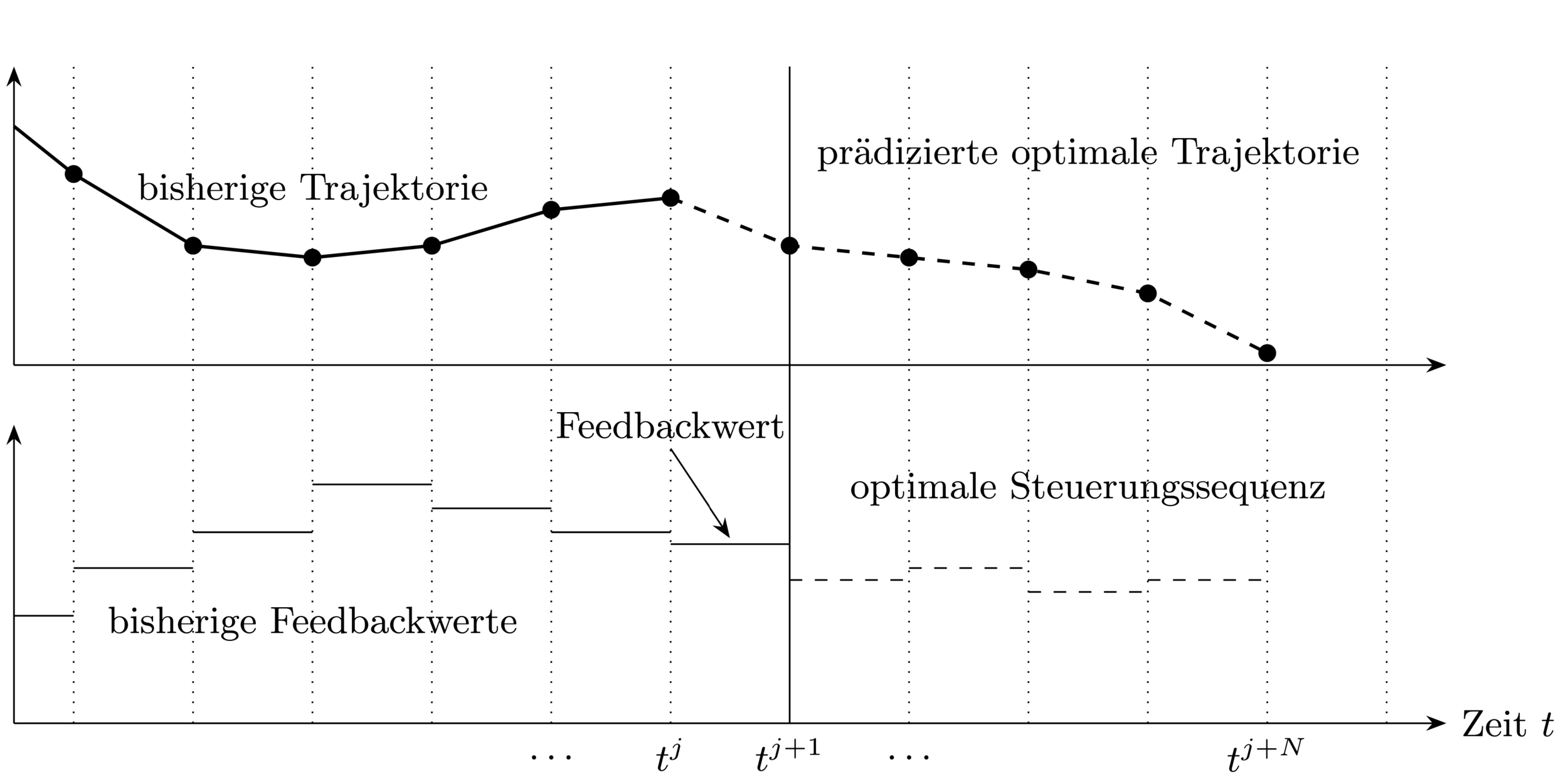
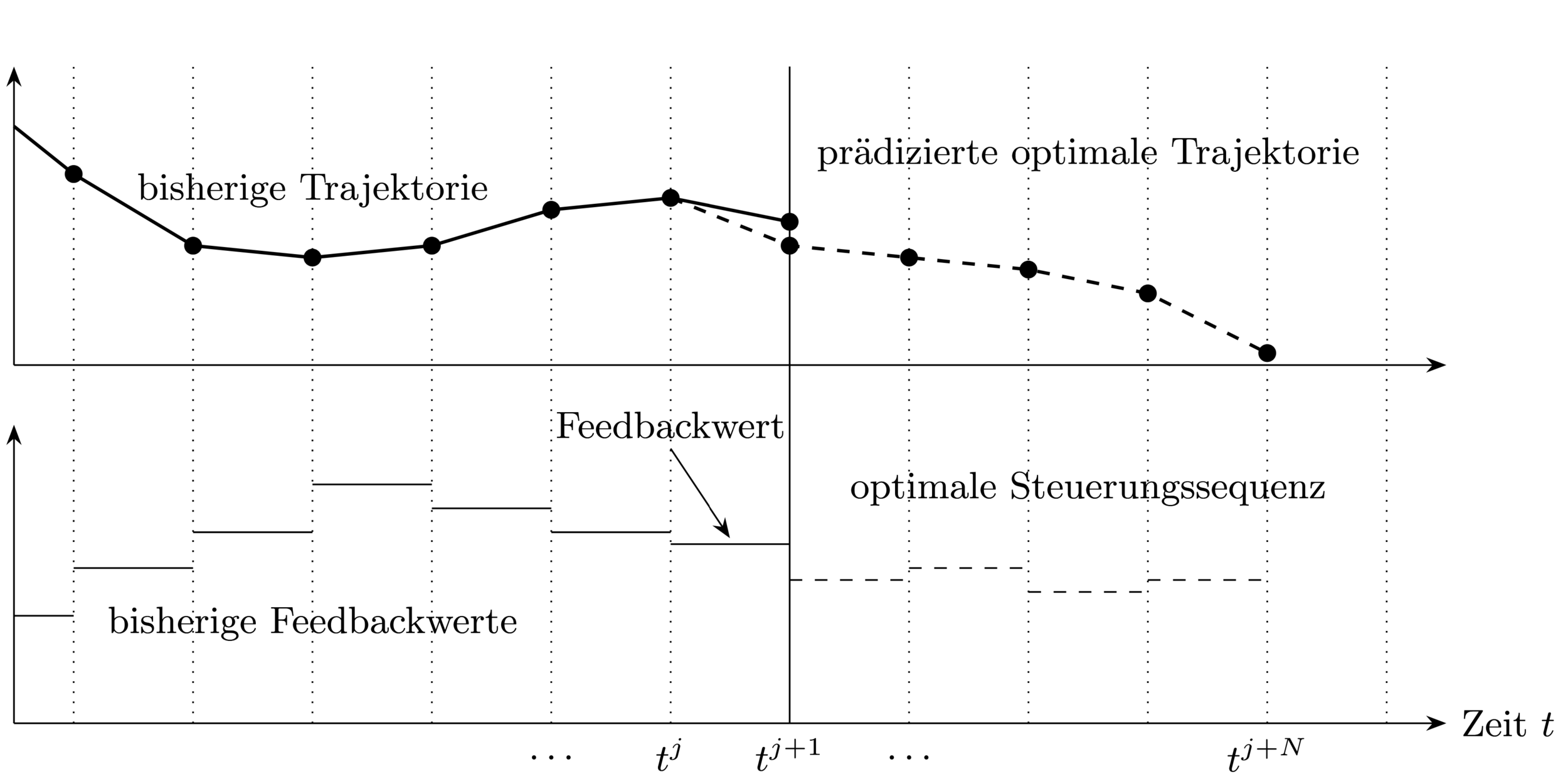
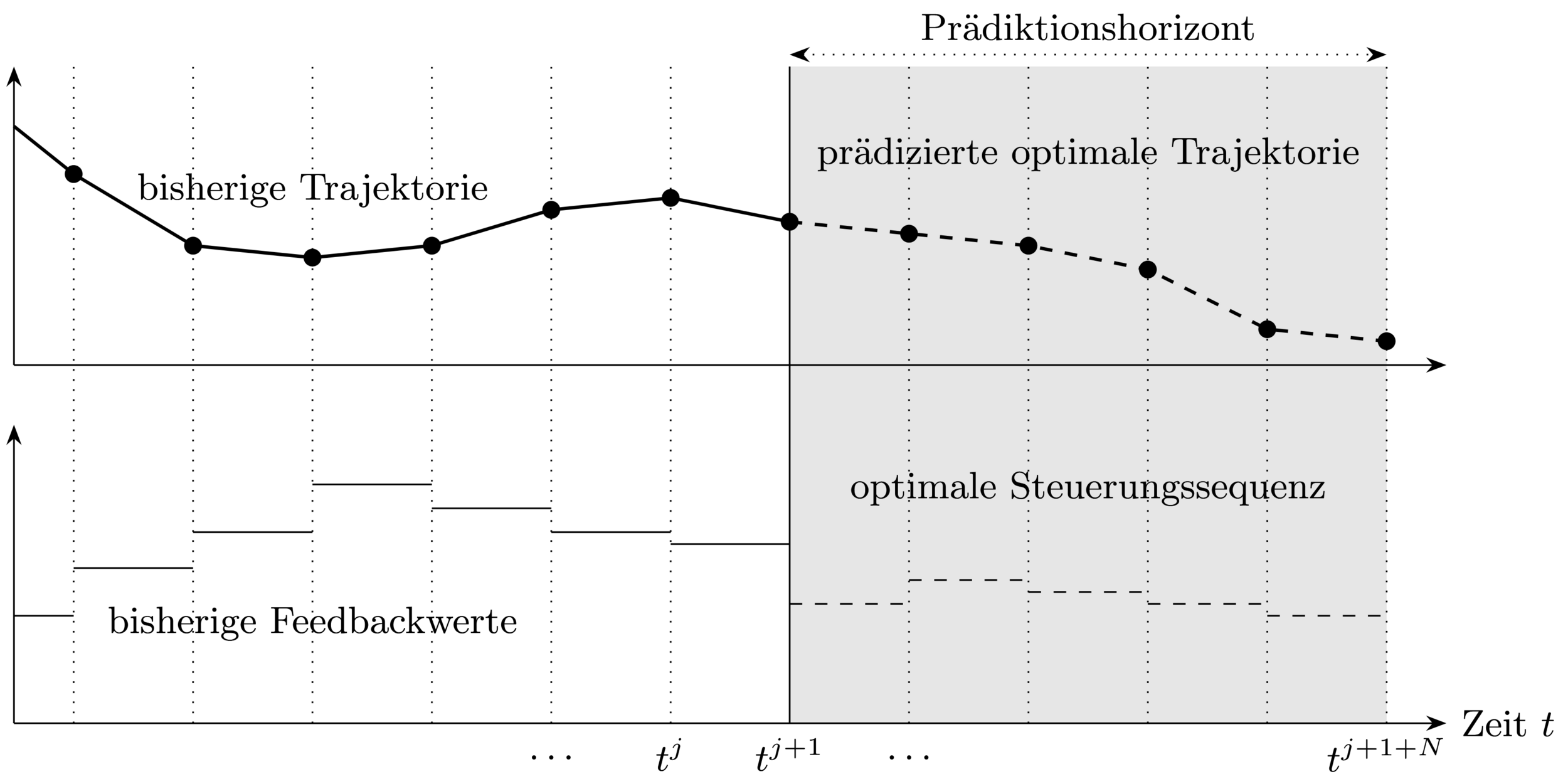
Bei jedem Samplingzeitpunkt:

1. Bestimme aktuellen Zustand

3. Verwende Feedbackwert bis zum nächsten

Samplingzeitpunkt

2. Löse Optimalsteuerungsproblem (OCP) über

Prädiktionshorizont

Closed-loop Steuerungsstrategie \(\rightarrow\) erlaubt auf Störungen zu reagieren

2/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

FRAMEWORK ZUM EFFIZIENTEN LÖSEN VON FOLGEN VON OCPs

\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min_{x(\cdot),u(\cdot)} & \int_{t^j}^{t^j+T} &\Psi\left(x(t),u(t)\right) \ud t + \Phi\left(x(t^j+T)\right)\\ &\quad\text{s.\,t. }& \dot{x}(t) &= f\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T],\\ && x(t^j) &= x^j,&&\\ && 0 &\leq h\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T],\\ && 0 &= r^{\mathrm{e}} \left(x(t^j),x(t^j+T)\right),\\ && 0 &\leq r^{\mathrm{i}} \left(x(t^j),x(t^j+T)\right). \end{aligned}

Systemzustand
und
Steuerung

Systemzustand
und
Steuerung

Laufende und terminale Kosten

Laufende und terminale Kosten

ODE Modell

ODE Modell

Gemischte Zustands- und Steuerungspfadnebenbedingungen

+

Randbedingungen

Modellierung

3/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

FRAMEWORK ZUM EFFIZIENTEN LÖSEN VON FOLGEN VON OCPs

\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min_{x(\cdot),u(\cdot)} & \int_{t^j}^{t^j+T_\mathrm{hor}} &\Psi\left(x(t),u(t)\right) \ud t + \Phi\left(x(t^j+T_\mathrm{hor})\right)\\ &\quad\text{s.\,t. }& \dot{x}(t) &= f\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T_\mathrm{hor}],\\ && x(t^j) &= x^j,&&\\ && 0 &\leq h\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T_\mathrm{hor}],\\ && 0 &= r^{\mathrm{e}} \left(x(t^j),x(t^j+T_\mathrm{hor})\right),\\ && 0 &\leq r^{\mathrm{i}} \left(x(t^j),x(t^j+T_\mathrm{hor})\right). \end{aligned}

\(\infty\) - dimensionales OCP

Modellierung

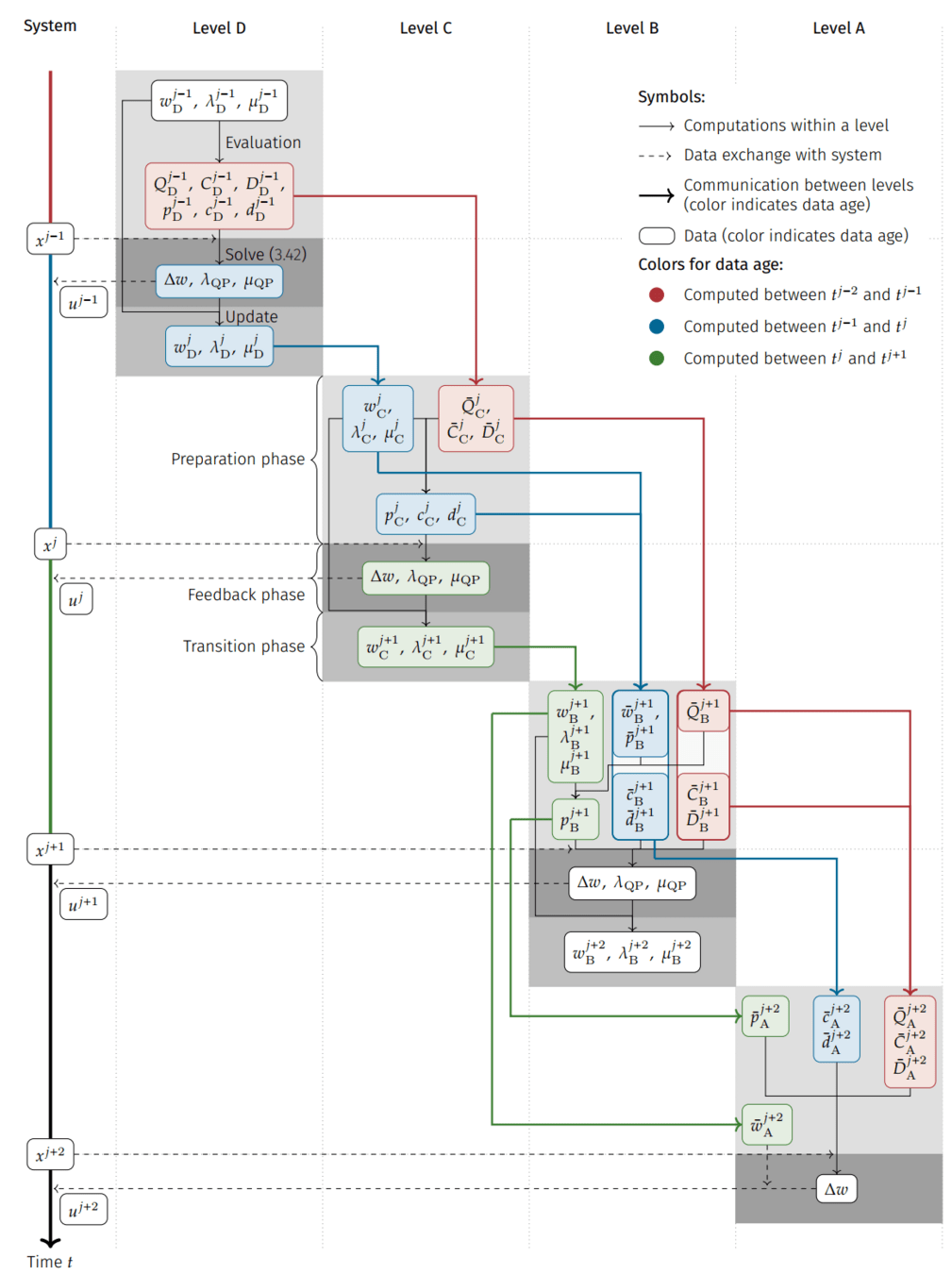
Multi-Level Iterations (MLI)
[Wirsching, 2018]

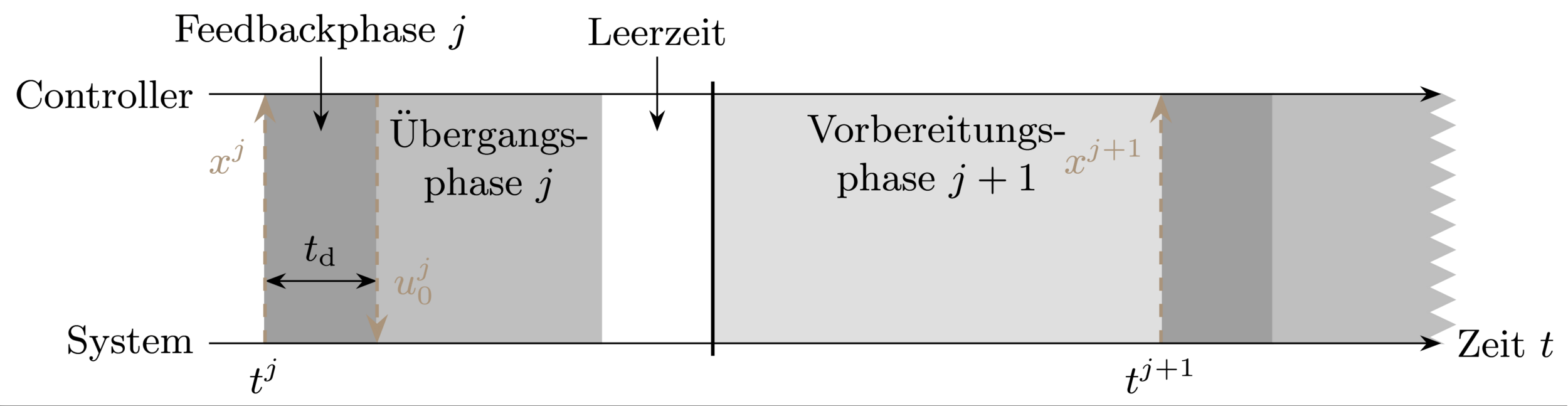
Real-Time Iterations (RTI)
[Diehl et. al, 2002]

\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min_{\substack{s\in\mathbb{R}^{n_s}\\q\in\mathbb{R}^{n_q}}} & \sum_{m=0}^{N-1} &\Psi_m\left(s_m,q_m\right) + \Phi\left(s_N\right)\\ &\quad\text{s.\,t. }& 0 &= x\left(\tau_{m+1};s_m,q_m\right)-s_{m+1},\quad m=0,\ldots,N-1,\\ && 0 &= x^j - s_0,&&\\ && 0 &\leq h\left(s_m,q_m\right),\quad m=0,\ldots,N-1,\\ && 0 &= r^{\mathrm{e}} \left(s_0,s_N\right),\\ && 0 &\leq r^{\mathrm{i}} \left(s_0,s_N\right). \end{aligned}

Nichtlineares Programm (NLP)

Direct Multiple Shooting (DMS)
[Bock, Plitt 1984]

Meine Beiträge

Theoretische Grundlagen

  • [Bock, Plitt, 1984] H. G. Bock and K. J. Plitt. “A Multiple Shooting Algorithm for Direct Solution of Optimal Control Problems”. In: IFAC Proceedings Volumes 17.2 (1984). 9th IFAC World Congress: A Bridge Between Control Science and Technology, Budapest, Hungary, 2-6 July 1984, pp. 1603–1608
  • [Diehl et. al., 2002] M. Diehl, H. G. Bock, J. P. Schlöder, R. Findeisen, Z. Nagy, and F. Allgöwer. “Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations”. In: Journal of Process Control 12.4 (2002), pp. 577–585
  • [Wirsching, 2018] L. Wirsching. “Multi-level iteration schemes with adaptive level choice for nonlinear model predictive control”. PhD thesis. Heidelberg University, 2018
\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min_{\substack{\Delta s\in\mathbb{R}^{n_s}\\\Delta q\in\mathbb{R}^{n_q}}} & &\frac{1}{2}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}^T\begin{pmatrix}B^{ss} & B^{sq} \\ B^{qs} & B^{qq}\end{pmatrix}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix} + \begin{pmatrix}b^s\\b^q\end{pmatrix}^T\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}\\ &\quad\text{s.\,t. }& 0 &= S_m^s\Delta s_m + S_m^q\Delta q_m - \Delta s_{m+1},\quad m=0,\ldots,M-1,\\ && 0 &= x^j - s_0 - \Delta s_0,&&\\ && 0 &\leq H_m^s\Delta s_m + H_m^q\Delta q_m + h_m,\quad m=0,\ldots,M-1,\\ && 0 &= R_{s_0}^\mathrm{e}\Delta s_0 + R_{s_M}^\mathrm{e}\Delta s_M + r^\mathrm{e},\\ && 0 &\leq R_{s_0}^\mathrm{i}\Delta s_0 + R_{s_M}^\mathrm{i}\Delta s_M + r^\mathrm{i}. \end{aligned}

Quadratisches Programm (QP)

Zugeschnittenes SQP-Verfahren

3/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

MEINE BEITRÄGE

1.

2.

3.

4.

ANWENDUNG:
EACC

  • Realistisches Testproblem mit realen Kennfeldern und Fahrdaten

  • Erfolgreiche numerische Tests

STABILITÄT BEI INEXAKTEM NMPC

  • OCP semilinear parabolischer PDEs

  • Beweis asymptotischer Stabilität der System-Optimierer-Dynamik

FORM-ERHALTENDE
INTERPOLATION

  • Klassifikation im multivariaten Fall

  • Methode zur multivariaten, form-erhaltenden, glatten Interpolation

  • Berücksichtigung externer Einflüsse bei DMS, RTI und MLI

  • Angepasste Condensing-Strategien

EXTERNE EINFLÜSSE

  • Szenariobasiertes Online-Feedback

  • Online-Aufwand: Matrix-Vektor-Multiplikation oder Lösen eines QPs

SensEIS
FEEDBACK

4/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

FORMERHALTENDE GLATTE INTERPOLATION

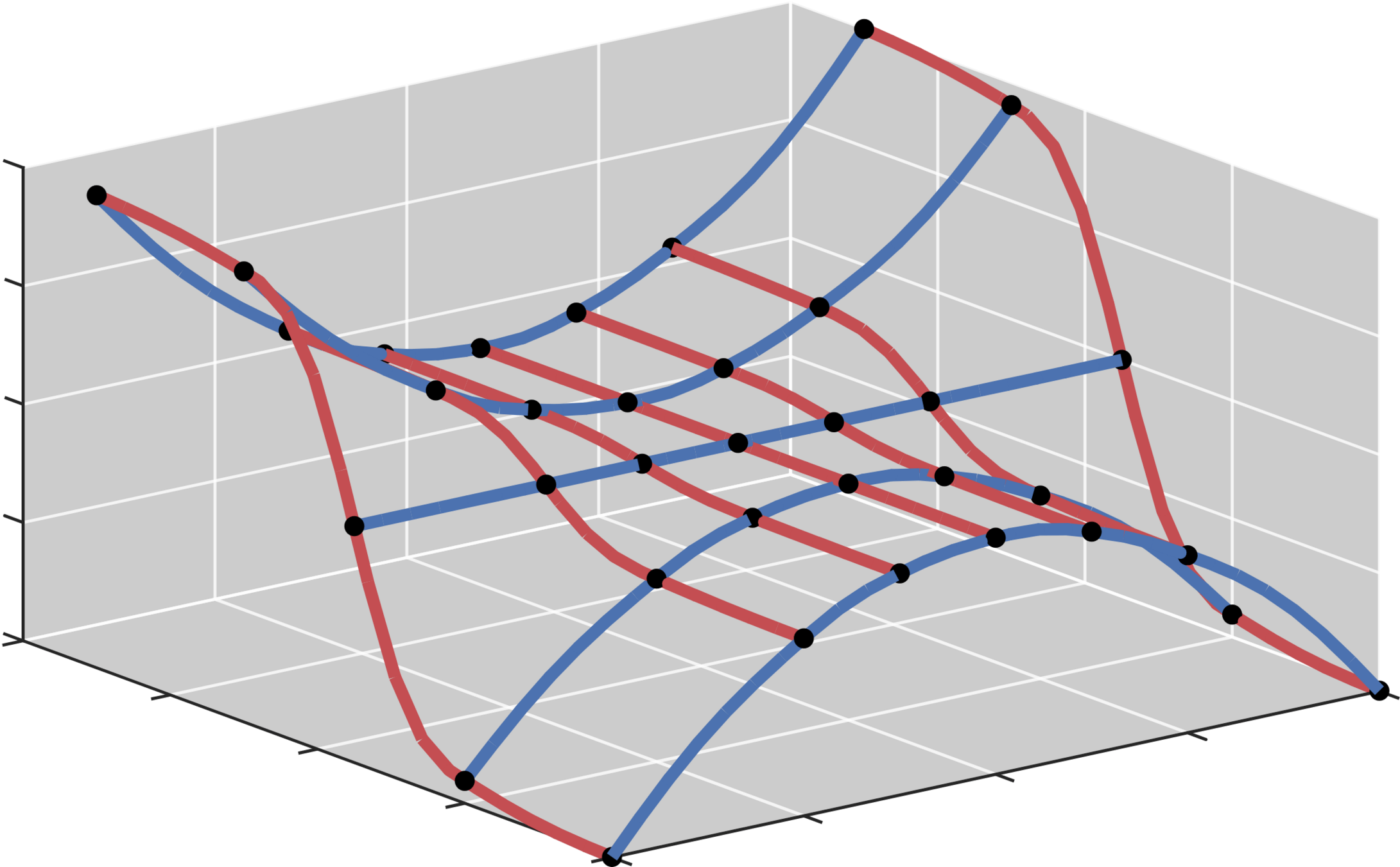
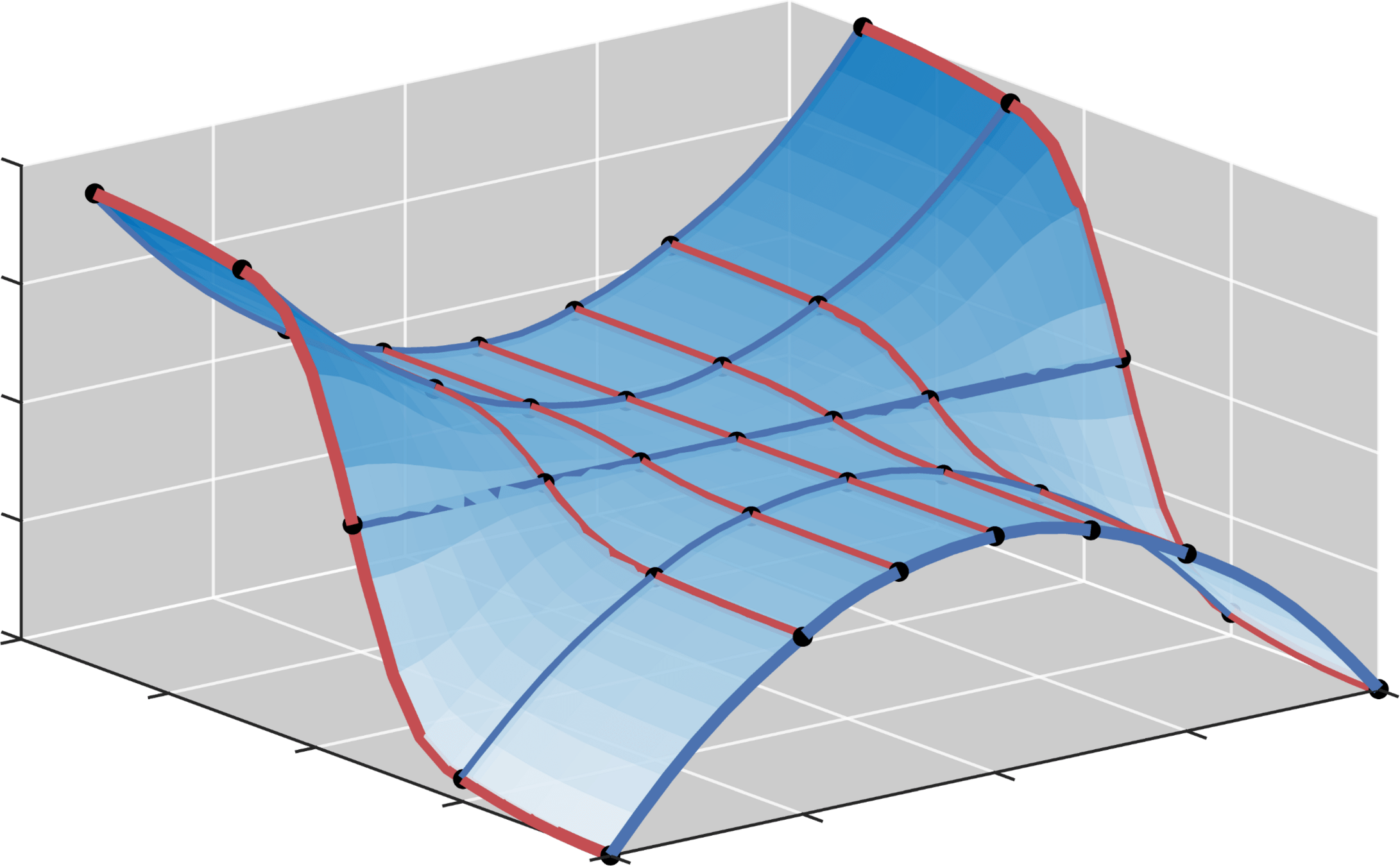
BESONDERHEITEN MEINER METHODE: 

  • Modularität: Univariate Methode frei wählbar
  • Erbt Glattheit, Formerhaltung und Lokalität der univariaten Methode
  • [Costantini, 1988] P. Costantini. “An algorithm for computing shape-preserving interpolating splines of arbitrary degree”. In: Journal of Computational and Applied Mathematics 22.1 (1988), pp. 89–136
  • [Coons, 1967] S. A. Coons. Surfaces for computer-aided design of space forms. Tech. rep. Project MAC-TR 41. USA: MIT, 1967

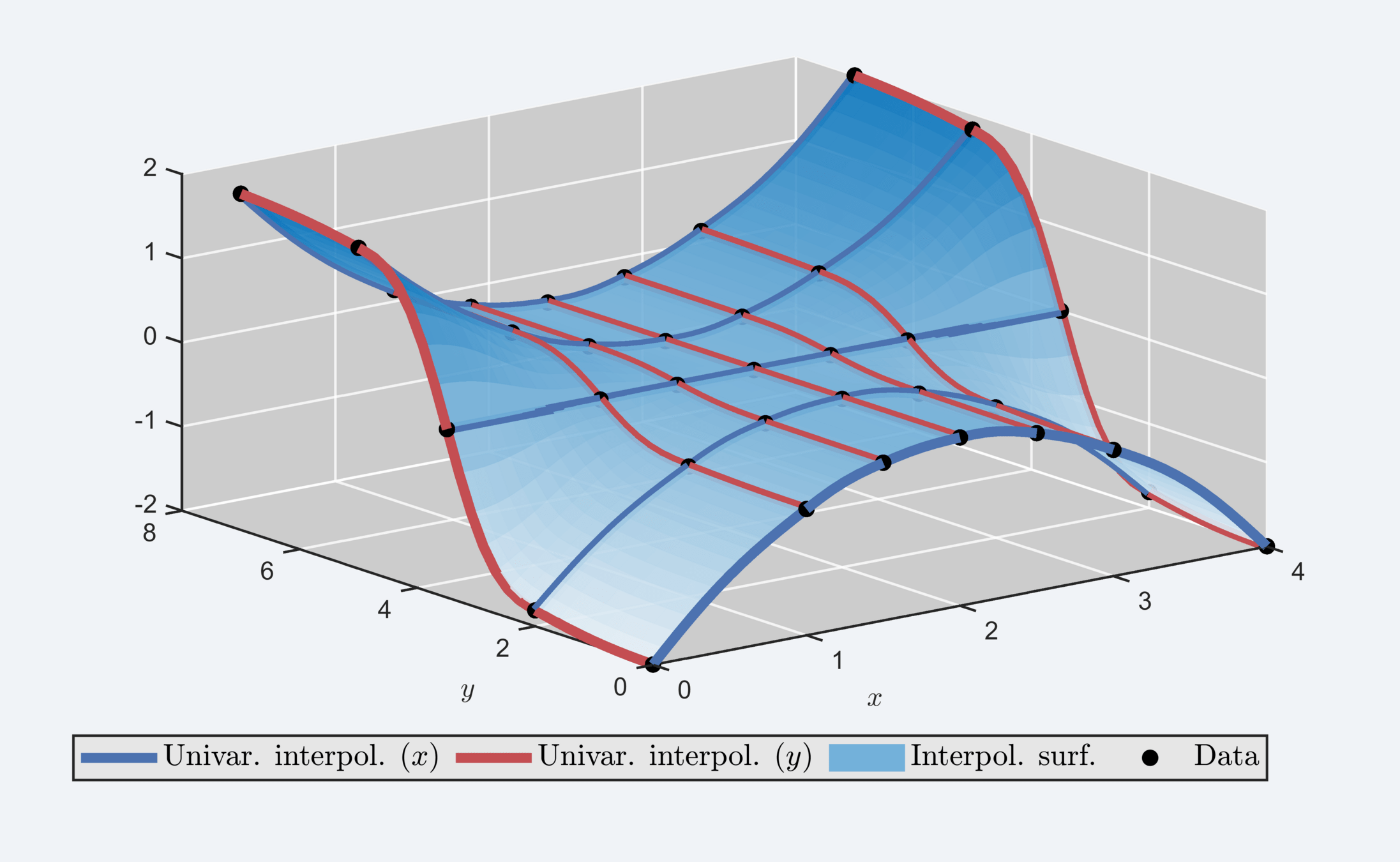
MEINE METHODE:

Schritt 1: Formerhaltende glatte univariate Interpolation entlang der Gitterlinien, bspw. mit [Costantini, 1988]

Schritt 2: Gewichtung der univariaten Interpolation durch höherdimensionale Erweiterung von Coons' Patches [Coons, 1967]

THEMA:  Interpolation multivariater tabellarisierter Daten (Kennfelder)

 

HERAUSFORDERUNGEN:

  • Aus Modellierung: Formerhaltung (Monotonie, Konvexität u. ä.)
  • Aus Optimierung: Glatte Interpolation (sonst Undifferenzierbarkeiten in OCP!)

5/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

MEINE BEITRÄGE

2.

ANWENDUNG:
EACC

  • Realistisches Testproblem mit realen Kennfeldern und Fahrdaten

  • Erfolgreiche numerische Tests

STABILITÄT BEI INEXAKTEM NMPC

  • OCP semilinear parabolischer PDEs

  • Beweis asymptotischer Stabilität der System-Optimierer-Dynamik

FORM-ERHALTENDE
INTERPOLATION

  • Klassifikation im multivariaten Fall

  • Methode zur multivariaten, form-erhaltenden, glatten Interpolation

  • Berücksichtigung externer Einflüsse bei DMS, RTI und MLI

  • Angepasste Condensing-Strategien

EXTERNE EINFLÜSSE

  • Szenariobasiertes Online-Feedback

  • Online-Aufwand: Matrix-Vektor-Multiplikation oder Lösen eines QPs

SensEIS
FEEDBACK

6/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

SensEIS FEEDBACK

MEINE METHODE:

...

Löse
OCP

Löse
OCP

Löse
OCP

THEMA:  Schnelles Online-Feedback

VARIANTEN MEINER METHODE: 

  • Feedbackmatrix: Nur Matrix-Vektor-Multiplikation als Online-Aufwand
  • Feedbackgenerierendes QP: Berücksichtigt Active-Set-Wechsel
  • Kombinierbar mit MLI oder eigenständige Methode

HERAUSFORDERUNGEN: 

  • Aus Anwendung: Möglichst geringer Online-Rechenwaufwand
  • Aus Optimierung: Kombinierbar mit MLI

Optimale Lösung &
Feedbackoperator

Optimale Lösung &
Feedbackoperator

Optimale Lösung &
Feedbackoperator

Offline-Phase

Online-Phase

Neue
Steuerung

Feedbackoperator
aus Szenario

Aktueller Systemzustand

Optimale Lösung aus  Szenario

7/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

SensEIS FEEDBACK - FEEDBACKGENERIERENDES QP

QP IM ZUGESCHNITTENEN SQP-VERFAHREN

NEUE KOMPONENTEN

\newcommand{\ud}{\mathrm{d}} % \definecolor{hlc}{HTML}{AA947B} \begin{aligned} &\quad\min_{\substack{\Delta s\in\mathbb{R}^{n_s}\\\Delta q\in\mathbb{R}^{n_q}}} \frac{1}{2}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}^T\begin{pmatrix}B^{ss} & B^{sq} \\ B^{qs} & B^{qq}\end{pmatrix}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix} \hspace{0.25cm} + \begin{pmatrix}b^s\\b^q\end{pmatrix}^T\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix} \hspace{0.4cm} + \begin{pmatrix}\Delta x^j \\ \Delta \rho^j \\ \Delta v^j\end{pmatrix}^T\begin{pmatrix}B^{\hat{x}s} & B^{\hat{x}q} \\ B^{\rho s} & B^{\rho q} \\ B^{v s} & B^{v q}\end{pmatrix}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}\\[2em] & \left\{ \quad\text{s.\,t. }\quad \begin{aligned} & 0 = -\Delta s_0 &&&& & \hspace{0.25cm} & +\Delta x^j &&&&\\ & 0 = S_m^s\Delta s_m - \Delta s_{m+1} &&+ S_m^q\Delta q_m && &&&& + S_m^\rho\Delta\rho^j &&+ S_m^v\Delta v^j,\\ & 0 \leq H_m^s\Delta s_m &&+ H_m^q\Delta q_m &&+ h_m &&&& + H_m^\rho\Delta\rho^j &&+ H_m^v\Delta v^j,\\ & 0 = R_{s_0}^\mathrm{e}\Delta s_0 + R_{s_M}^\mathrm{e}\Delta s_M &&&& &&&&+ R^{\mathrm{e}}_{\rho}\Delta\rho^j &&+ R^{\mathrm{e}}_{v_0}\Delta v_0^j + R^{\mathrm{e}}_{v_M}\Delta v_M^j,\\ & 0 \leq R_{s_0}^\mathrm{i}\Delta s_0 + R_{s_M}^\mathrm{i}\Delta s_M &&&&+ r^\mathrm{i} &&&&+ R^{\mathrm{i}}_{\rho}\Delta\rho^j &&+ R^{\mathrm{i}}_{v_0}\Delta v_0^j + R^{\mathrm{i}}_{v_M}\Delta v_M^j. \end{aligned} \right. \end{aligned}

Resi-duen

Linearisierung bzgl.
Zuständen u. Steuerung

Hesse-Matrix bzgl.
Zuständen und Steuerung

Gradient bzgl.
Zuständen und Steuerung

Lin. bzgl.
Parametern

Lin. bzgl. aktuellem Zustand

Linearisierung bzgl.
externen Einflüssen

Hesse-Matrix bzgl. aktuellem Zustand,
Parametern und externen Einflüssen dann Zuständen und Steuerungen

8/14

Variablen:
Zustände und Steuerungen

Linearisiert und ausgewertet in Szenario-lösung

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

SensEIS FEEDBACK - FEEDBACKGENERIERENDES QP

QP IM ZUGESCHNITTENEN SQP-VERFAHREN

NEUE KOMPONENTEN

Variablen:
Zustände und Steuerungen

\newcommand{\ud}{\mathrm{d}} % \definecolor{hlc}{HTML}{AA947B} \begin{aligned} &\quad\min_{\substack{\Delta s\in\mathbb{R}^{n_s}\\\Delta q\in\mathbb{R}^{n_q}}} \frac{1}{2}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}^T\begin{pmatrix}B^{ss} & B^{sq} \\ B^{qs} & B^{qq}\end{pmatrix}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix} \hspace{0.25cm} + \begin{pmatrix}b^s\\b^q\end{pmatrix}^T\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix} \hspace{0.4cm} + \begin{pmatrix}\Delta x^j \\ \Delta \rho^j \\ \Delta v^j\end{pmatrix}^T\begin{pmatrix}B^{\hat{x}s} & B^{\hat{x}q} \\ B^{\rho s} & B^{\rho q} \\ B^{v s} & B^{v q}\end{pmatrix}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}\\[2em] & \left\{ \quad\text{s.\,t. }\quad \begin{aligned} & 0 = -\Delta s_0 &&&& & \hspace{0.25cm} & +\Delta x^j &&&&\\ & 0 = S_m^s\Delta s_m - \Delta s_{m+1} &&+ S_m^q\Delta q_m && &&&& + S_m^\rho\Delta\rho^j &&+ S_m^v\Delta v^j,\\ & 0 \leq H_m^s\Delta s_m &&+ H_m^q\Delta q_m &&+ h_m &&&& + H_m^\rho\Delta\rho^j &&+ H_m^v\Delta v^j,\\ & 0 = R_{s_0}^\mathrm{e}\Delta s_0 + R_{s_M}^\mathrm{e}\Delta s_M &&&& &&&&+ R^{\mathrm{e}}_{\rho}\Delta\rho^j &&+ R^{\mathrm{e}}_{v_0}\Delta v_0^j + R^{\mathrm{e}}_{v_M}\Delta v_M^j,\\ & 0 \leq R_{s_0}^\mathrm{i}\Delta s_0 + R_{s_M}^\mathrm{i}\Delta s_M &&&&+ r^\mathrm{i} &&&&+ R^{\mathrm{i}}_{\rho}\Delta\rho^j &&+ R^{\mathrm{i}}_{v_0}\Delta v_0^j + R^{\mathrm{i}}_{v_M}\Delta v_M^j. \end{aligned} \right. \end{aligned}

Linearisiert und ausgewertet in Szenario-lösung

Lineare Approximation der Residuuen bzgl.
aktuellem Zustand, Parametern und externen Einflüssen

8/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

MEINE BEITRÄGE

3.

ANWENDUNG:
EACC

  • Realistisches Testproblem mit realen Kennfeldern und Fahrdaten

  • Erfolgreiche numerische Tests

STABILITÄT BEI INEXAKTEM NMPC

  • OCP semilinear parabolischer PDEs

  • Beweis asymptotischer Stabilität der System-Optimierer-Dynamik

FORM-ERHALTENDE
INTERPOLATION

  • Klassifikation im multivariaten Fall

  • Methode zur multivariaten, form-erhaltenden, glatten Interpolation

  • Berücksichtigung externer Einflüsse bei DMS, RTI und MLI

  • Angepasste Condensing-Strategien

EXTERNE EINFLÜSSE

  • Szenariobasiertes Online-Feedback

  • Online-Aufwand: Matrix-Vektor-Multiplikation oder Lösen eines QPs

SensEIS
FEEDBACK

9/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

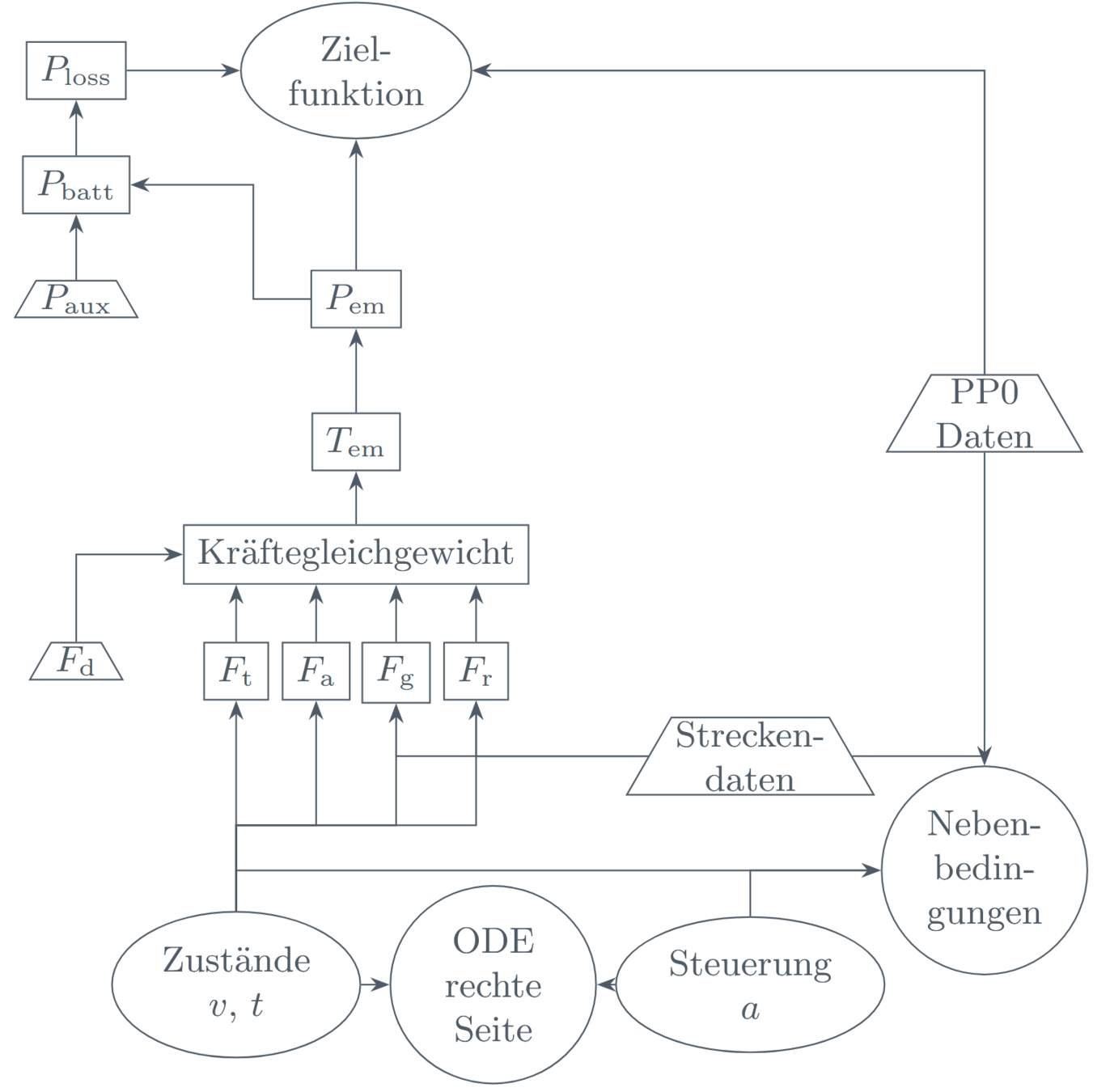
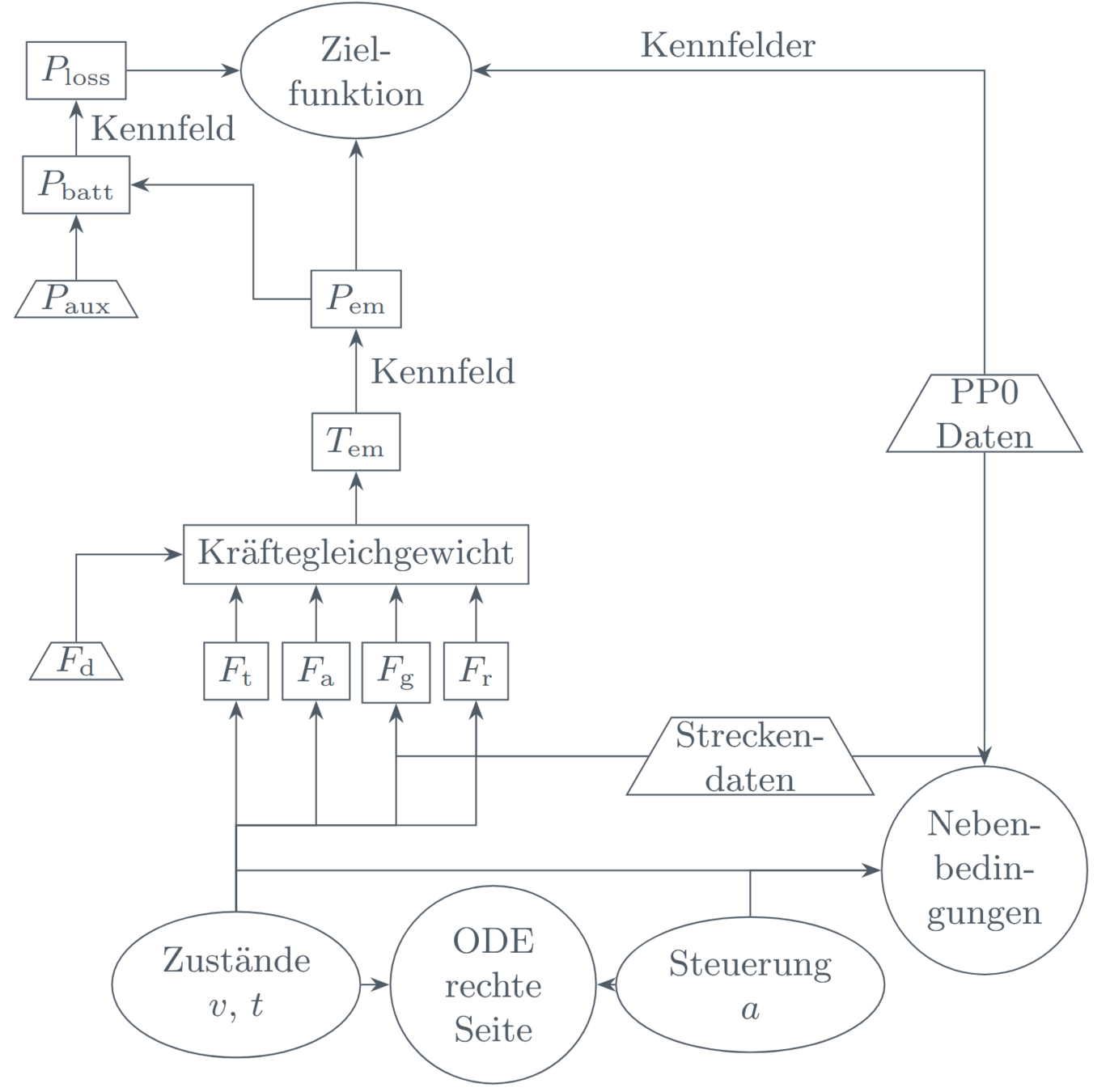
ECOLOGICAL ADAPTIVE CRUISE CONTROL (EACC)

MEINE REALISTISCHE EACC FORMULIERUNG:

  • Freie Variable: Strecke \(s\)

  • Zustände: Geschwindigkeit \(v\) und Zeit \(t\)

  • Steuerung: Beschleunigung \(a\)

\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min_{v(\cdot),\,t(\cdot),\,a(\cdot)} && \int_{s^j}^{s^j+S}\left[ w_0 P_\mathrm{em} + w_1 P_\mathrm{loss} + \sum_{i=1}^{k}w_{i+1}\Psi_i^\mathrm{c}\right]\ud s\\[1.35em] &\quad\text{s.\,t. }&& \begin{aligned} \begin{pmatrix}v'(s)\\t'(s) \end{pmatrix} &= \frac{1}{v(s)} \begin{pmatrix}a(s) \\ 1 \end{pmatrix},&& s\in[s^j,s^j+S],\\ \begin{pmatrix}v(s^j)\\t(s^j) \end{pmatrix} &= \begin{pmatrix} v^j\\t^j\end{pmatrix},&&\\[1.05em] a_\mathrm{min} &\leq a(s) \leq a_\mathrm{max},&& s\in[s^j,s^j+S],\\ 0 & < v(s) \leq v_\mathrm{max}(s),&& s\in[s^j,s^j+S],\\ 0 &\leq t(s) - t_\mathrm{PP0}(s) -\Delta t_\mathrm{min},&& s\in[s^j,s^j+S]. \end{aligned} \end{aligned}

Energieverbrauch und Komfortaspekte

Beschleunigungs-, und Geschwindigkeitsschranken
und Sicherheitsabstand

Energieverbrauch und Komfortaspekte

Beschleunigungs-, und Geschwindigkeitsschranken
und Sicherheitsabstand

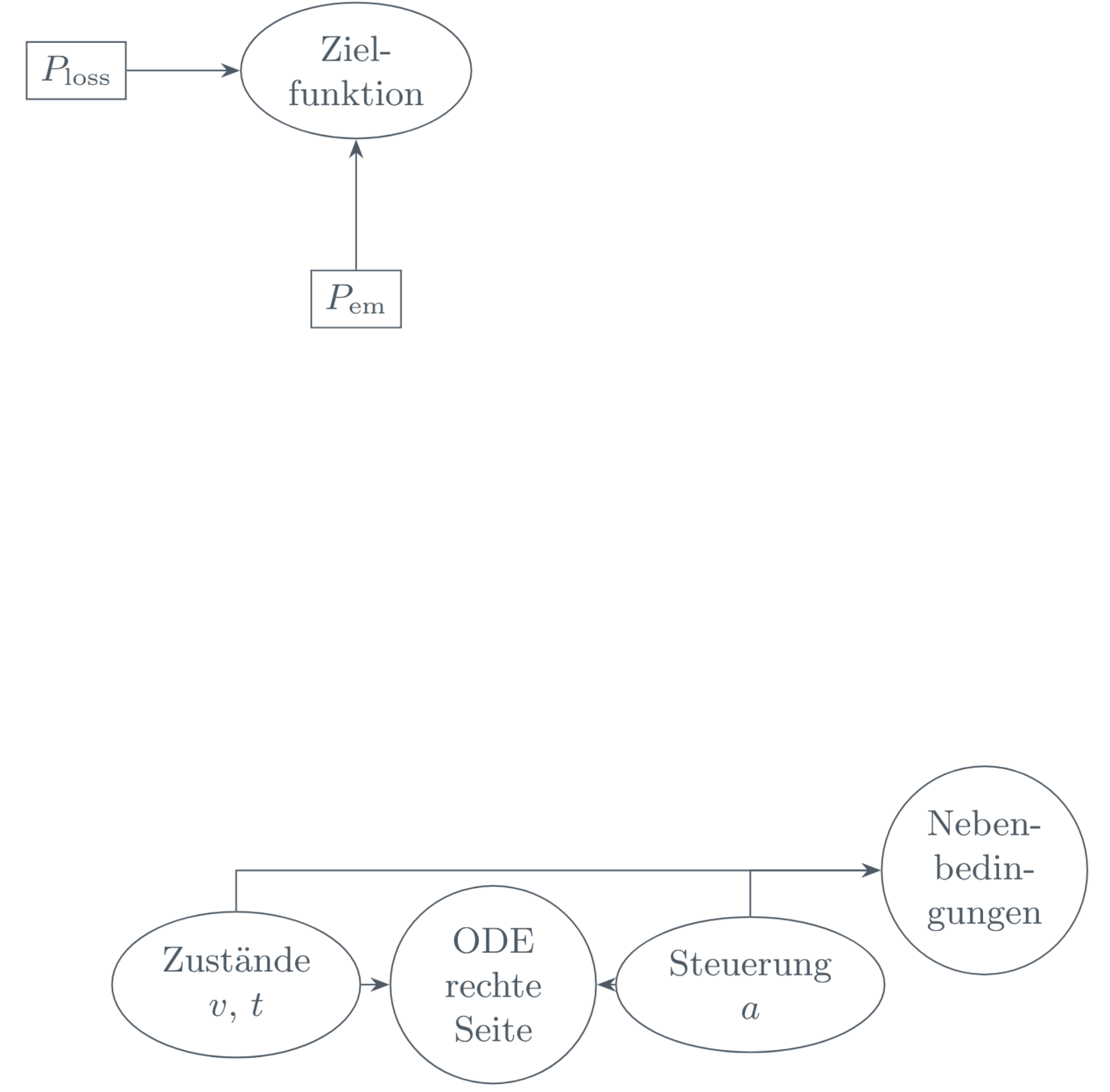
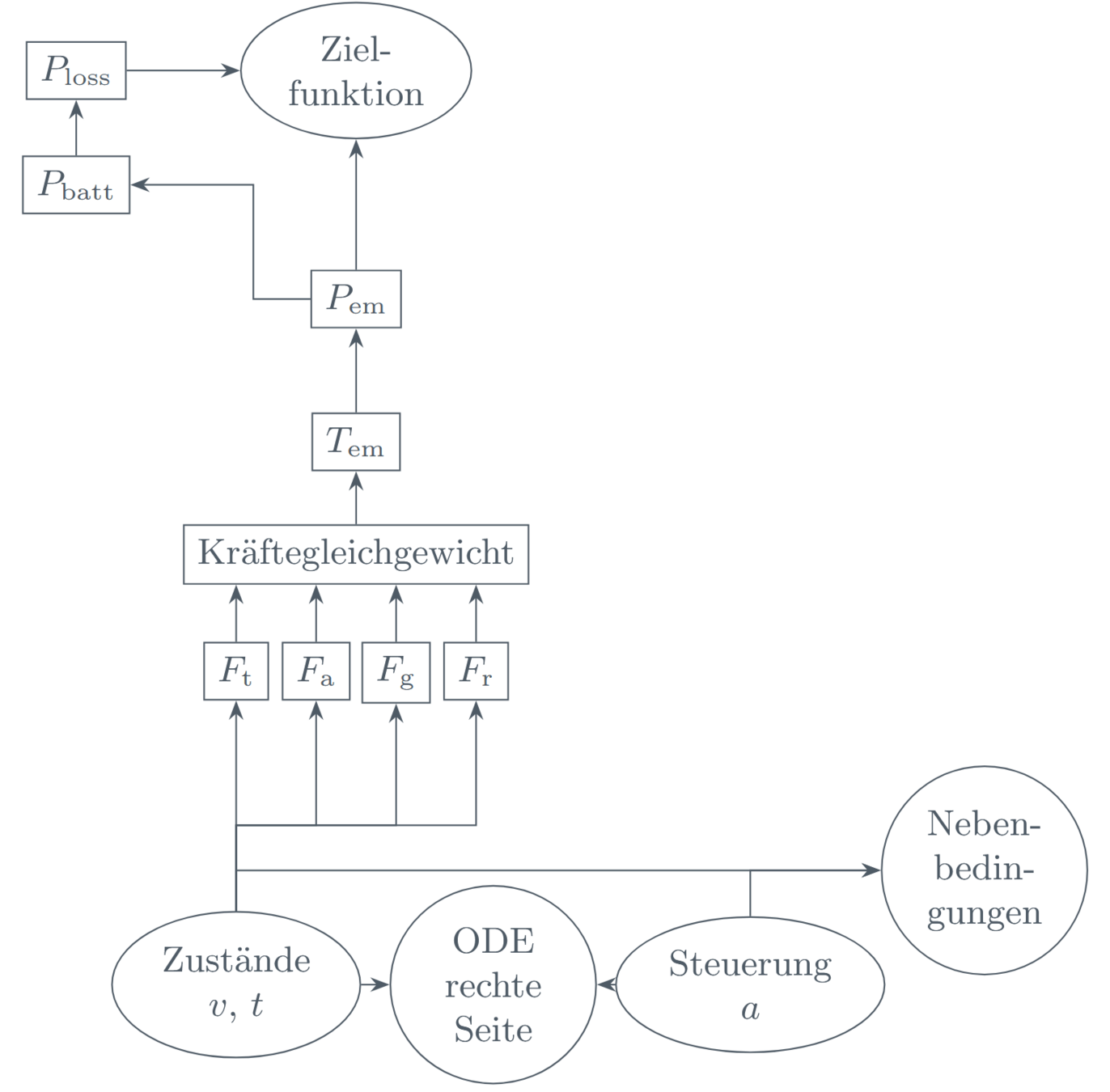
10/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

ECOLOGICAL ADAPTIVE CRUISE CONTROL (EACC) — RESULTATE

MEIN TESTSETUP:

  • Echtdaten einer Fahrt von 34,5km in Stuttgart

  • Reale Kennfelder vom Industriepartner

  • Interpolation der Kennfelder mit meiner neuen Methode

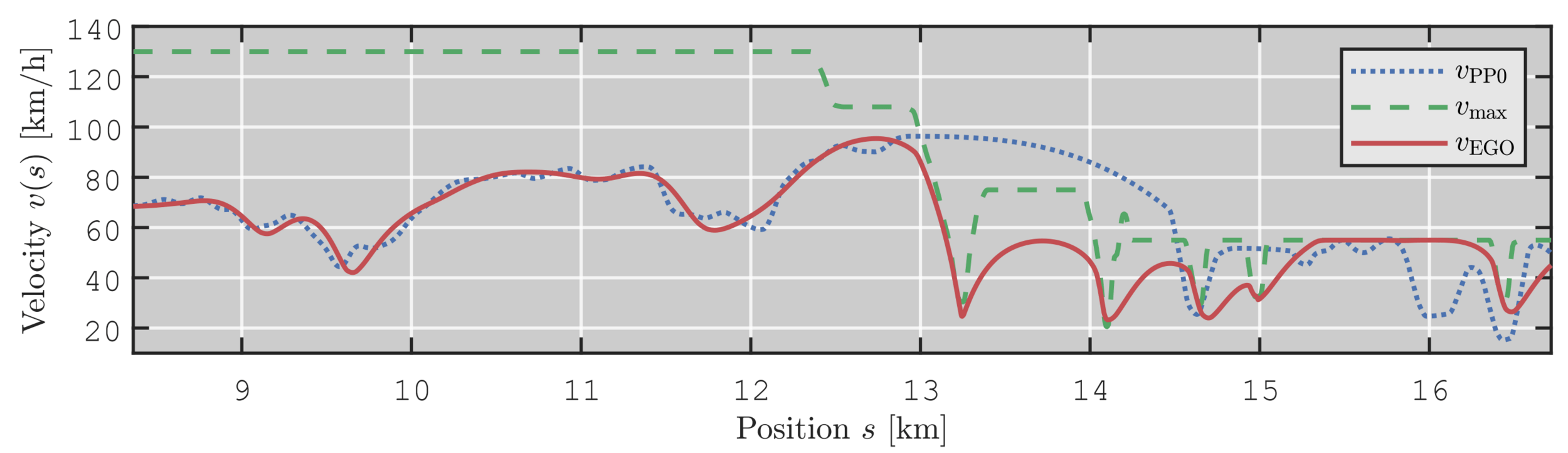
ENERGIEEINSPARUNGEN

  • Standard MLI:                            3,4%
  • MLI mit externen Einflüssen:  4,3%

PP0 verletzt
Tempolimit!

Energieeffizientes Befolgen
des Tempolimits

Energieeffizientes Verfolgen von PP0

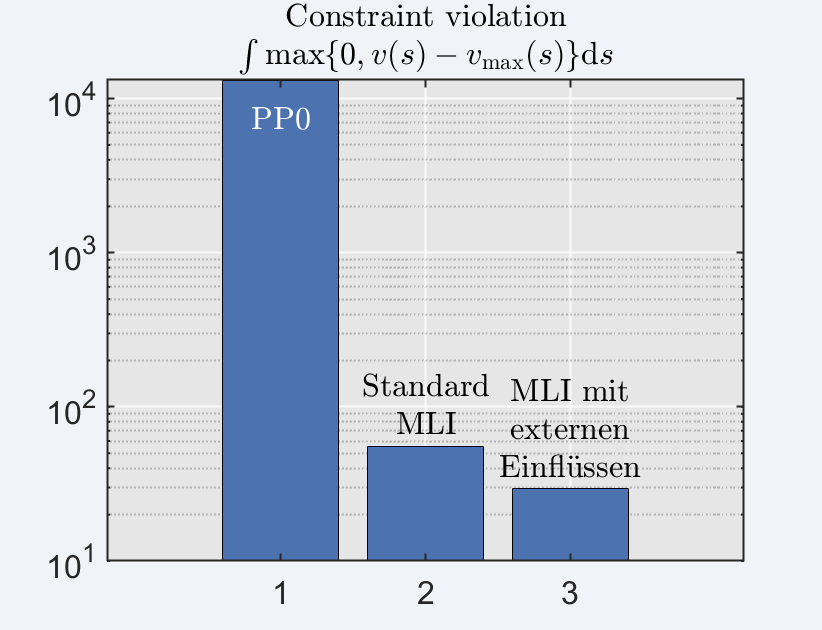
VIEL BESSERE EINHALTUNG DES TEMPOLIMITS!

11/14

Energieeffizientes Verfolgen von PP0

Energieeffizientes Befolgen
des Tempolimits

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

MEINE BEITRÄGE

4.

ANWENDUNG:
EACC

  • Realistisches Testproblem mit realen Kennfeldern und Fahrdaten

  • Erfolgreiche numerische Tests

STABILITÄT BEI INEXAKTEM NMPC

  • OCP semilinear parabolischer PDEs

  • Beweis asymptotischer Stabilität der System-Optimierer-Dynamik

FORM-ERHALTENDE
INTERPOLATION

  • Klassifikation im multivariaten Fall

  • Methode zur multivariaten, form-erhaltenden, glatten Interpolation

  • Berücksichtigung externer Einflüsse bei DMS, RTI und MLI

  • Angepasste Condensing-Strategien

EXTERNE EINFLÜSSE

  • Szenariobasiertes Online-Feedback

  • Online-Aufwand: Matrix-Vektor-Multiplikation oder Lösen eines QPs

SensEIS
FEEDBACK

12/14

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

STABILITÄT VON INEXAKTEM NMPC FÜR SEMILINEARE PARABOLISCHE PDEs

\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min_{x(\cdot),u(\cdot)} & \int_{t^j}^{t^j+T} &\Psi\left(x(t),u(t)\right) \ud t + \Phi\left(x(t^j+T)\right)\\ &\quad\text{s.\,t. }& \dot{x}(t) &= f\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T],\\ && x(t^j) &= x^j,&&\\ && 0 &\leq h\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T],\\ && 0 &= r^{\mathrm{e}} \left(x(t^j),x(t^j+T)\right),\\ && 0 &\leq r^{\mathrm{i}} \left(x(t^j),x(t^j+T)\right). \end{aligned}

ODE OPTIMALSTEUERUNGSPROBLEM

MOTIVATION: Stabilität Grundvoraussetzung für Sicherheit

ODE-FALL: Stabilität bewiesen, s. bspw. [Zanelli et. al, 2021]

  • [Zanelli et. al., 2021] A. Zanelli, Q. Tran-Dinh, and M. Diehl. “A Lyapunov function for the combined system-optimizer dynamics in inexact model predictive control”. In: Automatica 134 (2021), p. 109901
  • [Tröltzsch, 2009] Optimale Steuerung partieller Differentialgleichungen: Theorie, Verfahren und Anwendungen. 2., überarb. Aufl. Studium. Wiesbaden: Vieweg + Teubner, 2009
     

Semilineare parabolische PDE

Semilineare parabolische PDE

Rand-steuerung

(aus [Tröltzsch, 2009])

\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min & &\int_{\Omega}\Phi\left(x,y\left(x,T\right)\right)\ud x + \iint_{Q}\phi\left(x,y\left(x,t\right)\right)\ud x\ud t\\ & &&+\iint_{\Sigma}\Psi\left(x,y\left(x,t\right),u\left(x,t\right)\right)\ud x\ud t\\ &\text{over}&&y\in C\left(\bar{Q}\right),\,u\in L^s\left(\Sigma\right),\\ &\text{s.\,t.}&& \begin{aligned} \dot{y}-\Delta y + f\left(x,y\right)&=0&&\text{in}~Q,\\ y(0) &= y^j &&\text{in}~\Omega,\\ \partial_\nu y + g\left(x,y\right)&=u&&\text{in}~\Sigma,\\ u_\mathrm{l}(x)\leq u\left(x,t\right)&\leq u_\mathrm{u}(x)&&\text{a.\,e.}~\Sigma. \end{aligned} \end{aligned}

PDE OPTIMALSTEUERUNGSPROBLEM

13/14

MEIN BEITRAG:

Inexakte NMPC Methoden auch bei PDEs stabil

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

STABILITÄT VON INEXAKTEM NMPC FÜR SEMILINEARE PARABOLISCHE PDEs

  • [Tröltzsch, 2009] Optimale Steuerung partieller Differentialgleichungen: Theorie, Verfahren und Anwendungen. 2., überarb. Aufl. Studium. Wiesbaden: Vieweg + Teubner, 2009
     

SYSTEM-OPTIMIERER-DYNAMIK

y^j = y\left(T;y^{j-1},u^{j-1}\right)
u^{j} = \xi\left(y^j,u^{j-1}\right)

System-
verhalten

System-
verhalten

Optimierer-
iteration(en)

u^{j-1}
y^{j-1}

Systemzustand

Steuerung

Optimierer-
iteration(en)

MEIN THEOREM

Der Gleichgewichtspunkt \( \left(y^\ast, u^\ast\right) = \left(0,0\right)\in L^p\left(\Omega\right)\times L^s\left(\Sigma\right) \) ist asymptotisch stabil für die System-Optimierer-Dynamik.

(aus [Tröltzsch, 2009])

\newcommand{\ud}{\mathrm{d}} \begin{aligned} &\min & &\int_{\Omega}\Phi\left(x,y\left(x,T\right)\right)\ud x + \iint_{Q}\phi\left(x,y\left(x,t\right)\right)\ud x\ud t\\ & &&+\iint_{\Sigma}\Psi\left(x,y\left(x,t\right),u\left(x,t\right)\right)\ud x\ud t\\ &\text{over}&&y\in C\left(\bar{Q}\right),\,u\in L^s\left(\Sigma\right),\\ &\text{s.\,t.}&& \begin{aligned} \dot{y}-\Delta y + f\left(x,y\right)&=0&&\text{in}~Q,\\ y(0) &= y^j &&\text{in}~\Omega,\\ \partial_\nu y + g\left(x,y\right)&=u&&\text{in}~\Sigma,\\ u_\mathrm{l}(x)\leq u\left(x,t\right)&\leq u_\mathrm{u}(x)&&\text{a.\,e.}~\Sigma. \end{aligned} \end{aligned}

PDE OPTIMALSTEUERUNGSPROBLEM

13/14

MEIN BEITRAG:

Inexakte NMPC Methoden auch bei PDEs stabil

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

STABILITÄT VON INEXAKTEM NMPC FÜR SEMILINEARE PARABOLISCHE PDEs

SYSTEM-OPTIMIERER-DYNAMIK

y^j = y\left(T;y^{j-1},u^{j-1}\right)
u^{j} = \xi\left(y^j,u^{j-1}\right)

System-
verhalten

System-
verhalten

Optimierer-
iteration(en)

u^{j-1}
y^{j-1}

Systemzustand

Steuerung

Optimierer-
iteration(en)

MEIN THEOREM

Der Gleichgewichtspunkt \( \left(y^\ast, u^\ast\right) = \left(0,0\right)\in L^p\left(\Omega\right)\times L^s\left(\Sigma\right) \) ist asymptotisch stabil für die System-Optimierer-Dynamik.

WICHTIGE ZWISCHENSCHRITTE IM BEWEIS

Schritt 1: Zustände bleiben im Level-Set \(\mathcal{Y}_{\bar{V}}\) einer Lyapunov-Fkt. und Steuerungen im Kontraktionsgebiet des Optimierers

\begin{align*} &y^{0}\in\mathcal{Y}_{\bar{V}},&&u^{\mathrm{init}}\in\mathcal{B}_{\Sigma,s}\left(u^\ast\left(y^{0}\right),r_u\right)\\ \Rightarrow~ &y^{j+1}\in\mathcal{Y}_{\bar{V}},&&u^{j}\in\mathcal{B}_{\Sigma,s}\left(u^\ast\left(y^{j+1}\right),r_u\right) \end{align*}

Schritt 2: Abschätzungen für Kontraktion des Steuerungs-fehlers \(E^j\) und der modifizierten Lyapunov-Fkt. \(V^j\), wobei

\begin{gather*} E^j\coloneqq ||u^j-u^\ast\left(y^j\right)||_{L^s\left(\Sigma\right)},~V^j\coloneqq V\left(y^j\right)^{\frac{1}{q}} \end{gather*}

Schritt 3: Asymptotische Stabilität des positiven, linearen Systems für die oberen Schranken \(E^j_\mathrm{u}\), \(V^j_\mathrm{u}\) gegeben durch

\begin{gather*} \begin{pmatrix} V^{j+1}_{\mathrm{u}} \\ E^{j+1}_\mathrm{u}\end{pmatrix}=\begin{pmatrix}C_4 & C_3 \\ \kappa^k C_2 & \kappa^k C_1\end{pmatrix}\begin{pmatrix} V^{j}_{\mathrm{u}} \\ E^{j}_\mathrm{u}\end{pmatrix}~\text{mit}~\begin{pmatrix} V^{0}_{\mathrm{u}} \\ E^{0}_\mathrm{u}\end{pmatrix}=\begin{pmatrix} V^{0} \\ E^{0}\end{pmatrix} \end{gather*}

13/14

MEIN BEITRAG:

Inexakte NMPC Methoden auch bei PDEs stabil

Ihno Schrot — Efficient Numerical Methods for NMPC with Applications in ACC — Disputationsvortrag — 03. Juli 2025

MEINE BEITRÄGE

ANWENDUNG:
EACC

  • Realistisches Testproblem mit realen Kennfeldern und Fahrdaten

  • Erfolgreiche numerische Tests

STABILITÄT BEI INEXAKTEM NMPC

  • OCP semilinear parabolischer PDEs

  • Beweis asymptotischer Stabilität der System-Optimierer-Dynamik

FORM-ERHALTENDE
INTERPOLATION

  • Klassifikation im multivariaten Fall

  • Methode zur multivariaten, form-erhaltenden, glatten Interpolation

  • Berücksichtigung externer Einflüsse bei DMS, RTI und MLI

  • Angepasste Condensing-Strategien

EXTERNE EINFLÜSSE

  • Szenariobasiertes Online-Feedback

  • Online-Aufwand: Matrix-Vektor-Multiplikation oder Lösen eines QPs

SensEIS
FEEDBACK

14/14

Made with Slides.com