離散数学問4.5
石 立行
無向グラフの頂点被覆
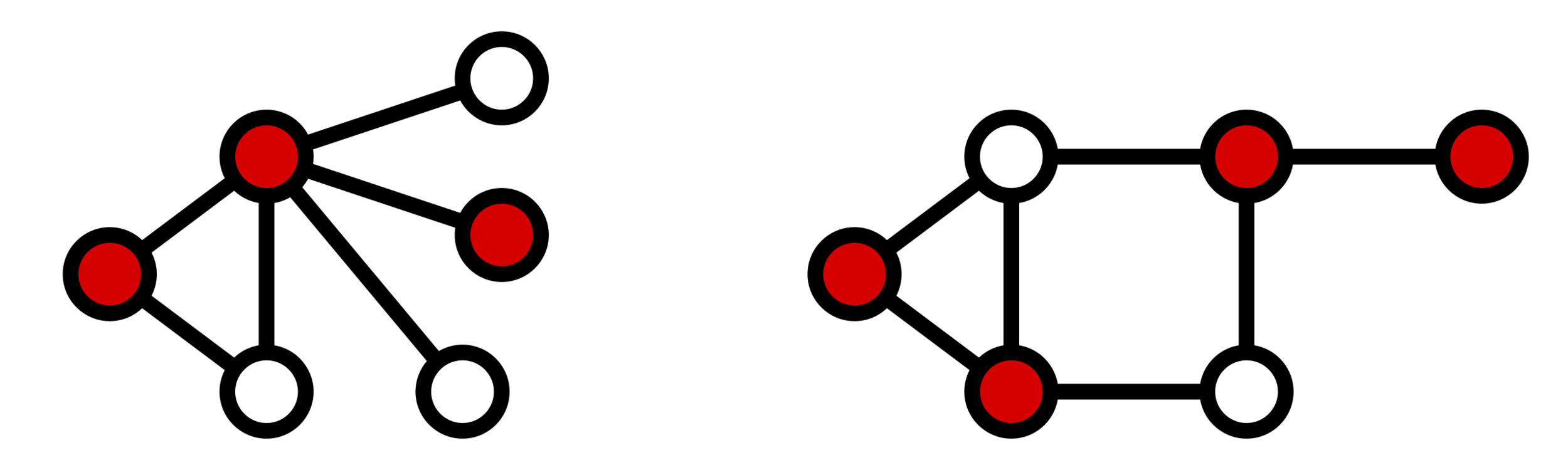
Wikipedia より
各辺について、被覆されている頂点が
少なくとも1つ以上
無向グラフの頂点被覆
(連続最適化問題版)
Wikipedia より一部改変

各辺について、2頂点の被覆の
「度合い」の和が1以上
(度合いは0以上1以下でなければならない)
無向グラフの頂点被覆
(連続最適化問題版)
最小化するもの:
\sum_{v \in V}
c_v x_v
各辺の重み(定数)
被覆の度合い
示したいこと
離散最適化問題の最適解
連続最適化問題の最適解
1 \leq
\leq 2
(a)
(b)
示したいこと
離散最適化問題の最適解
連続最適化問題の最適解
1 \leq
\leq 2
(a)
(b)
方針
(a) 離散最適化問題の解から連続の解を作る
(b) 連続最適化問題の解から離散の解を作る
離散最適化問題の最適解
連続最適化問題の最適解
1 \leq
(a)
離散最適化問題の最適解は
連続最適化問題の解にもなっている。
なので、連続最適化問題の最適解を
下回ることは不可能。
離散最適化問題の最適解
連続最適化問題の最適解
\leq 2
(b)
Q. 連続最適化問題の解から離散の解を作りたい。
A. 被覆度合いを四捨五入する
離散最適化問題の最適解
連続最適化問題の最適解
\leq 2
(b)
Q. 四捨五入した解は正しいか?
A.
各辺について、四捨五入前の2頂点の
被覆の「度合い」を \(a, b\) とする。
\( a + b \geq 1 \) より、\( a, b \) のいずれかは \( \frac{1}{2} \) 以上。
よって少なくともどちらかは1に丸められ
四捨五入後も頂点被覆となっている。
離散最適化問題の最適解
連続最適化問題の最適解
\leq 2
(b)
Q. その際のコストは?
A.
丸め上げた部分と切り捨てた部分に
分けて考える。
丸め上げた部分は高々2倍のコスト。
切り捨てた部分は0倍。
よって全部合わせても
2倍を超えることはない。