Probabilités et statistiques

Projet de

V. CARPE, S. EL AMRI, N. MENEUX, A. OBERTELLI, V. OSTERTAG, P. VALENTIN

PROMO 2018

20 JUIN 2016

Slide 1.2

Plan de la présentation

Group G1D - Probabilités et Statistiques
  • Rappel sur le sujet
  • Loi de Poisson et exponentielle
  • Simulation et nombres aléatoires
  • Simulation d'une station vélib'
  • Estimation des paramètres
  • Conclusion

Slide 1.3

Rappel du sujet

Group G1D - Probabilités et Statistiques

Etude, modélisation et simulation d'une station de vélib'

Approfondir nos connaissances sur le cours

Trouver la taille idéale d'une station

Trouver le nombre idéal de vélos par station

Certaines stations sont plus fréquentées que d'autres, déséquilibrant ainsi notre système et rendant la tâche difficile

Objectifs :

Slide 1.4

Modélisation

            Group G1D - Probabilités et Statistiques

Chaque station doit :

Avoir au moins un emplacement pour déposer un vélib'

Avoir au moins un vélib' lors de la venue d'un usager

Toutes les 6 heures, le nombre d'emplacements et de vélib' sont réinitialisés

P_{E}
PEP_{E}

Probabilité d'avoir toujours un emplacement libre pendant 6 heures

P_{V}
PVP_{V}

Probabilité d'avoir toujours un vélo libre pendant 6 heures

P_{E} = P_{V} = 90\%
PE=PV=90%P_{E} = P_{V} = 90\%

Slide 2.1

Group G1D - Probabilités et Statistiques

Loi de poisson

LOI EXPONENTIELLE

ET

Slide 2.2

Group G1D - Probabilités et Statistiques

Introduction

Établir des propriétés sur ces deux lois qui seront utiles dans notre modélisation

Notions abordées :

  • Variable aléatoire, moyenne, écart-type

  • Loi exponentielle

  • Loi poisson

Notations :

N(\tau)
N(τ)N(\tau)

Nombre de vélos arrivés pendant l'intervalle

\tau
τ\tau
p_{k}(\tau)
pk(τ)p_{k}(\tau)

Probabilité que k vélos soient arrivés pendant 

\tau
τ\tau

Temps entre l'arrivée de deux vélos

T

Slide 2.3

Group G1D - Probabilités et Statistiques

L’ESPÉRANCE 

L'espérance d'une variable aléatoire correspond au résultat qu'on s'attend le plus à trouver.

E(X) = \int_{-\infty}^{+\infty} xf(x)dx
E(X)=∫−∞+∞xf(x)dxE(X) = \int_{-\infty}^{+\infty} xf(x)dx

Soit X une variable aléatoire.

Si cette dernière est continue, on a alors :

Si elle est discrète :

E(X) = \sum_{i}P_{i}x_{i}
E(X)=∑iPixiE(X) = \sum_{i}P_{i}x_{i}

Slide 2.4

Group G1D - Probabilités et Statistiques

L’ESPÉRANCE 

Dans notre cas, en utilisant la deuxième définition, on obtient :

E(N(\tau)) = \lambda\tau
E(N(τ))=λτE(N(\tau)) = \lambda\tau

Intervalle de temps

Paramètre de

p_{k}(\tau)
pk(τ)p_{k}(\tau)

Interprétation

Il y a

\lambda\tau
λτ\lambda\tau

vélos arrivant pendant cet intervalle de temps en moyenne.

Slide 2.5

Group G1D - Probabilités et Statistiques

L'écart-type

L'écart-type mesure la dispersion d'une variable aléatoire.

Nous l'avons calculé à partir de la définition :

\sigma^2 = E(X^2) - E^2(X)
σ2=E(X2)−E2(X)\sigma^2 = E(X^2) - E^2(X)

Ce qui donne :

E(N(\tau)) = \sqrt{\lambda\tau}
E(N(τ))=λτE(N(\tau)) = \sqrt{\lambda\tau}

Slide 2.6

Group G1D - Probabilités et Statistiques

l'écart-type

Interprétation :

\lambda\tau
λτ\lambda\tau

68% du temps, on a un nombre de vélib' arrivant dans cet intervalle

+\sqrt{\lambda\tau}
+λτ+\sqrt{\lambda\tau}

95% du temps, on a un nombre de vélib' arrivant dans cet intervalle

99% du temps, on a un nombre de vélib' arrivant dans cet intervalle

Nombre de vélib'

Slide 2.7

Group G1D - Probabilités et Statistiques

Loi de poisson

Cette loi discontinue permet de décrire le nombre de fois qu'un événement se produira si l'on connait la moyenne de la fréquence d'apparition de ce dernier.

Siméon Denis Poisson

(1781 - 1840)

Mathématicien, physicien et géomètre

Connu pour ses très nombreux travaux (près de 400 publiés) et plus particulièrement pour la loi portant son nom. 

Slide 2.8

Group G1D - Probabilités et Statistiques

Loi de poisson

p_{k}(\tau)
pk(τ)p_{k}(\tau)

est donc une loi de poisson de paramètre 

\lambda\tau
λτ\lambda\tau

Résultats trouvés cohérents avec les valeurs vues en cours.

Soit

\lambda
λ\lambda

le nombre moyen d’occurrences, on a alors la probabilité suivante 

que l'événement se produise k fois :

p(k) = \frac{\lambda^k}{k!}e^{-\lambda}
p(k)=λkk!e−λp(k) = \frac{\lambda^k}{k!}e^{-\lambda}

Slide 2.9

Group G1D - Probabilités et Statistiques

Fonction de répartition

La fonction de répartition d'une variable est la probabilité d'obtenir l'événement {X<x}

Soit X, une variable aléatoire :

F_X(x) = p\{X < x \}
FX(x)=p{X<x}F_X(x) = p\{X < x \}

Dans le projet, on obtient :

F_T(\tau) = 1 - e^{-\lambda \tau}
FT(τ)=1−e−λτF_T(\tau) = 1 - e^{-\lambda \tau}

Interprétation

La probabilité que deux vélos arrivent espacés d'une durée inférieure à

\tau
τ\tau

est de

1 - e^{-\lambda \tau}
1−e−λτ1 - e^{-\lambda \tau}

Slide 2.10

Group G1D - Probabilités et Statistiques

Loi exponentielle

Cette loi permet de modéliser la durée de vie d'un phénomène sans usure.

Soit X une variable aléatoire et t une durée. On a :

f(t) = \alpha e^{-t\alpha}
f(t)=αe−tαf(t) = \alpha e^{-t\alpha}

T suit bien une loi exponentielle et nous retrouvons bien la fonction de répartition indiquée dans le cours

Slide 2.11

Group G1D - Probabilités et Statistiques

Propriété de cette loi

On retrouve bien :

E(T) = \frac{1}{\lambda}
E(T)=1λE(T) = \frac{1}{\lambda}
\sigma = \frac{1}{\lambda}
σ=1λ\sigma = \frac{1}{\lambda}

Espérance obtenue avec sa définition continue

Slide 2.12

Group G1D - Probabilités et Statistiques

Calcul de durées

t_{10\%} = \frac{-\ln(0.9)}{\lambda}
t10%=−ln(0.9)λt_{10\%} = \frac{-\ln(0.9)}{\lambda}
t_{90\%} = \frac{-\ln(0.1)}{\lambda}
t90%=−ln(0.1)λt_{90\%} = \frac{-\ln(0.1)}{\lambda}

Durée telle que 

P(T < t_{10\%}) = 0.1
P(T<t10%)=0.1P(T < t_{10\%}) = 0.1
P(T < t_{90\%}) = 0.9
P(T<t90%)=0.9P(T < t_{90\%}) = 0.9

et

Slide 2.13

Group G1D - Probabilités et Statistiques

Application

Flux d'arrivées et de sorties de vélos représenté par une loi de Poisson de 

et

\lambda_{in}
λin\lambda_{in}
\lambda_{out}
λout\lambda_{out}

de paramètres

\lambda_{in} > \lambda_{out}
λin>λout\lambda_{in} > \lambda_{out}

Plus d'arrivées de vélos que de sorties.

Si :

\lambda_{in} < \lambda_{out}
λin<λout\lambda_{in} < \lambda_{out}

Plus de sorties de vélos que d'arrivées

Le temps d'attente moyen pour un usager pour obtenir un vélo quand la station est vide est de

\frac{1}{2\lambda}
12λ\frac{1}{2\lambda}

Slide 3.1

Group G1D - Probabilités et Statistiques

Simulation

et

nombres aléatoires

Slide 3.2

Group G1D - Probabilités et Statistiques

Introduction

Nous allons tenter de générer des méthodes suivant les lois de Poisson et exponentielle vues précédemment

Notions abordées :

  • Générateur de nombres aléatoires

  • Méthodes de simulation modernes

  • Outils informatiques

Slide 3.3

Group G1D - Probabilités et Statistiques

Génération d'un nombre aléatoire

Génération par phénomènes imprévisibles

Comme les dés, la roulette, un tirage au sort, ...

Inconvénient : Souvent biaisées, pas assez sûres.

Génération par algorithme

Bien que déterministes, les programmes possèdent des opérations assez imprévisibles, utilisables pour cela.

Utilisation de phénomènes physiques

La radioactivité, les bruits thermiques, la mécanique quantique, ... permettent cela. 

Méthode la plus efficace mais ardue à mettre en place

Slide 3.4

Group G1D - Probabilités et Statistiques

Méthode de monte-Carlo

Nicholas Metropolis

(1915 - 1999)

Physicien

       A inventé en 1947 cette méthode avec Stanislaw Ulam

Employée pour le calcul d'intégrales et les simulations probabilistes. 

Principe :

On place aléatoirement des points sur un espace défini où se trouve la courbe.

La valeur de l'aire sous la courbe (l'intégrale) est proportionnelle au nombre de points sous la courbe. 

Slide 3.5

Group G1D - Probabilités et Statistiques

Méthode de monte-Carlo

Point placé aléatoirement

Slide 3.6

Group G1D - Probabilités et Statistiques

Génération d'une variable aléatoire

Elle suivra une loi exponentielle de paramètre lambda.

Possibilité de générer un nombre U aléatoirement entre 0 et 1

Outil à notre disposition

Nous sommes arrivés à la loi :

t_{u} = \frac{-\ln{(1-u)}}{\lambda}
tu=−ln(1−u)λt_{u} = \frac{-\ln{(1-u)}}{\lambda}

Si u=1, on obtiendra une erreur. Il faudra retirer un nombre aléatoire dans ce cas.

Slide 3.7

Group G1D - Probabilités et Statistiques

Application

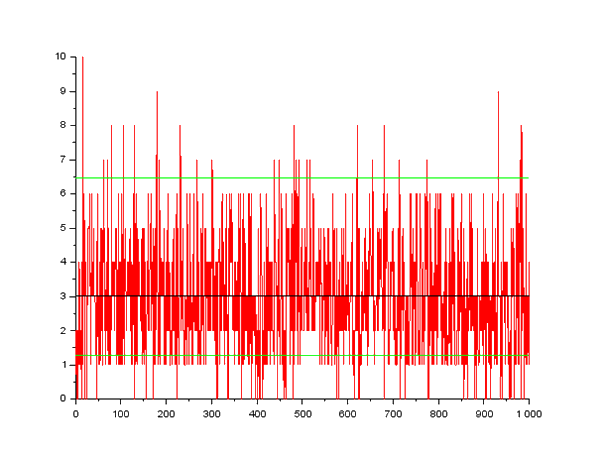
Moyenne

(=19,7)

t_{90\%}
t90%t_{90\%}
t_{10\%}
t10%t_{10\%}

(=46)

(=2,1)

T_k < t_{10\%}
Tk<t10%T_k < t_{10\%}
T_k > t_{90\%}
Tk>t90%T_k > t_{90\%}

8,5 % des échantillons

10,8 % des échantillons

Slide 3.8

Group G1D - Probabilités et Statistiques

Application (code)

//Génération de 1000 échantillons T avec une moyenne égale à 20s

t=-log(1-grand(1000,1,"def"))/0.05

//Recherche de la moyenne associée à T

E=0
for i=1:1000
	E=E+t(I,1)
end
E=E/1000
disp(E)

Permet d'obtenir 1000 nombres aléatoires entre 0 et 1

Slide 3.9

Group G1D - Probabilités et Statistiques

Génération de loi de poisson

Moyenne

(=3)

E+2\sigma
E+2σE+2\sigma

(=6,5)

E-\sigma
E−σE-\sigma

(=1,3)

N_k < E - \sigma
Nk<E−σN_k < E - \sigma

20,9% des échantillons

2,7% des échantillons

N_k > E + 2\sigma
Nk>E+2σN_k > E + 2\sigma

Slide 3.10

Group G1D - Probabilités et Statistiques

Histogramme de la densité

Valeurs théoriques

Valeurs empiriques

Slide 3.11

Group G1D - Probabilités et Statistiques

Histogramme de la densité

N > E+2\sigma
N>E+2σN > E+2\sigma
N < E-\sigma
N<E−σN < E-\sigma
  • { N < E− 𝜎} correspond à la moitié de la probabilité que l’événement soit en dehors d’une bande d’une largeur de deux écarts type centrée sur la moyenne.
  • {E+2 𝜎 } correspond à la moitié de la probabilité que l’événement soit en dehors d’une bande d’une largeur de quatre écarts type centrée sur la moyenne.

Slide 4.1

Group G1D - Probabilités et Statistiques

simulation

D'une station

Slide 4.2

Group G1D - Probabilités et Statistiques

Introduction

Vérifier les résultats obtenus lors d'études précédentes

Hypothèses :

  • Flux d'entrée et de sorties suivent une loi de Poisson aux paramètres connus.
  • Réinitialisation des flux tous les 
\Delta t
Δt\Delta t

On cherche à vérifier que le système est optimale pour :

(nombre de vélos dispo) soit égal à 22  

(nombre d'emplacements dispo) soit égal à 22  

soit égal à 6h  

\Delta t
Δt\Delta t
N_V(0)
NV(0)N_V(0)
N_E(0)
NE(0)N_E(0)

Slide 4.3

Group G1D - Probabilités et Statistiques

Relation

N_E(t) + N_V(t) = N_E(0) + N_V(0)
NE(t)+NV(t)=NE(0)+NV(0)N_E(t) + N_V(t) = N_E(0) + N_V(0)

Interprétation :

  • On voit que le nombre de vélos / d'emplacements ne peut dépasser la capacité de la station. 
  • Traduit la dépendance entre ces deux variables

Génération des données

Génération d'une suite d'instants d'arrivée

Génération d'une suite d'instants de sortie

 

  •  Reconstitution de la trame temporelle
  •  Déduction du nombre de vélos présents à chaque instant de modification

Slide 4.4

Group G1D - Probabilités et Statistiques

Extraction des données utiles

Limitation du cadre temporel de l'expérience : on ne garde que les valeurs concernées

Balayage des valeurs conservées pour repérer les cas extrêmes

Slide 4.5

Group G1D - Probabilités et Statistiques

Application

Slide 4.6

Group G1D - Probabilités et Statistiques

Démonstration sur Scilab

Slide 5.1

Group G1D - Probabilités et Statistiques

estimation des paramètres

Slide 5.2

Group G1D - Probabilités et Statistiques

Introduction

Déterminer les paramètres exprimés lors de la première partie du sujet.

Pour se faire, nous allons exploiter les données d'une station de vélib' du 31 mai 2013

Slide 5.3

Group G1D - Probabilités et Statistiques

Estimateur

Un estimateur permet d'évaluer un paramètre inconnu d'une loi de probabilité

La pertinence de l'estimation dépend de différents facteurs :

  • Sa convergence
  • Son biais
  • Son efficacité
  • Sa robustesse

Slide 5.3

Group G1D - Probabilités et Statistiques

Maximum de vraisemblance

Un estimateur peut être trouvé à l'aide de cette méthode.

Ronald Aylmer Fisher

(1890 - 1962)

Botaniste et statisticien

Un des fondateurs de la statistique moderne.

Principe :

  • On suppose que la variable nous intéressant suit une loi connue
  • On calcule sa vraisemblance qui mesure la probabilité que les observations connues suivent une loi donnée.
  • Le paramètre maximisant la ressemblance est l'estimateur cherché

Slide 5.4

Group G1D - Probabilités et Statistiques

Notre estimateur

En utilisant cette méthode, on obtient :

\hat{\lambda} = \frac{\sum_{k=1}^{n} X_k}{n}
λ^=∑k=1nXkn\hat{\lambda} = \frac{\sum_{k=1}^{n} X_k}{n}

échantillon k

nombre d'échantillons

C'est un estimateur sans biais et convergent.

Estimateur absolument convergent

Slide 5.5

Group G1D - Probabilités et Statistiques

Borne de Cramér-Rao

Borne permettant d'affirmer le caractère efficace d'un estimateur trouvé.

Estimateur

Dans notre cas :

Var(\hat{\lambda}) = \lambda
Var(λ^)=λVar(\hat{\lambda}) = \lambda

et

I(\lambda) = \frac{1}{\lambda}
I(λ)=1λI(\lambda) = \frac{1}{\lambda}

Notre estimateur est donc efficace.

Slide 5.6

Group G1D - Probabilités et Statistiques

Les intervalles de confiance

Nous renseigne sur la précision qu'a notre estimateur. Cet intervalle contient toujours la valeur réelle du paramètre.

Notre intervalle est le suivant :

\frac{1}{\tau}(\hat{a}-t(\sqrt{\frac{\hat{a}}{n}})) < \lambda < \frac{1}{\tau}(\hat{a}+t(\sqrt{\frac{\hat{a}}{n}}))
1τ(a^−t(a^n))<λ<1τ(a^+t(a^n))\frac{1}{\tau}(\hat{a}-t(\sqrt{\frac{\hat{a}}{n}})) < \lambda < \frac{1}{\tau}(\hat{a}+t(\sqrt{\frac{\hat{a}}{n}}))
\hat{a} = \hat{\lambda}\tau
a^=λ^τ\hat{a} = \hat{\lambda}\tau

Slide 5.7

Group G1D - Probabilités et Statistiques

Application

Démonstration sous Scilab

Conclusion

Slide 6.1

Group G1D - Probabilités et Statistiques
Made with Slides.com