\ f( n) \asymp g( n) \leftrightarrow f( n) \preceq g( n) \ \land \ f( n) \succeq g( n)\\
\\
\ f( n) \asymp g( n)\rightarrow f( n) \preceq g( n) \ \land \ f( n) \succeq g( n)
\begin{array}{l}0\leqslant a*g( n) \leqslant f( n)\Longrightarrow f( n) \succeq g( n)\\
\end{array}
\ f(n)⪯g(n) ∧ f(n)⪰g(n)\rightarrow{}f(n)≍g(n)
\begin{array}{l}
\Longrightarrow f( n) \asymp g( n)
\end{array}
\begin{array}{l}
f( n) \succeq g( n) \ \leftrightarrow \exists \ a >0\ \exists \ n_{0} \ \forall \ n\geqslant n_{0} :0\leqslant a\ *\ g( n) \leqslant f( n)\\
f( n) \preceq g( n) \ \leftrightarrow \exists \ b >0\ \exists \ n_{1} \ \forall \ n\geqslant n_{1} :0\leqslant f( n) \leqslant b\ *\ g( n)
\end{array}
\begin{array}{l}
0\leqslant f( n) \leqslant b*g( n) \Longrightarrow f( n) \preceq g( n)\\
\end{array}
\begin{array}{l}
\exists \ a >0\ \exists \ b >0\ \exists \ n_{0} \ \forall \ n\geqslant n_{0} :0\leqslant a\ *\ g( n) \leqslant f( n) \leqslant b\ *\ g( n)\\
\end{array}
\begin{array}{l}
\Longrightarrow \ f( n) \preceq g( n) \ \land \ f( n) \succeq g( n)
\end{array}
\begin{array}{l}
n_{2} =max( n_{0} ,n_{1})\\
\end{array}
\begin{array}{l}
\forall \ n\geqslant n_{2} \geqslant n_{0} :\ 0\leqslant \ a\ *\ g( n) \leqslant \ f( n)\\
\forall \ n\geqslant n_{2} \geqslant n_{1} :\ 0\leqslant f( n) \ \leqslant \ b\ *\ g( n)\\
\end{array}
\begin{array}{l}
\Longrightarrow \forall \ n\geqslant n_{2} :0\leqslant a\ *\ g( n) \leqslant f( n) \leqslant b\ *\ g( n)\\
\end{array}
Полезни свойства
Транзитивността\ на\ \asymp,\prec,\preceq,\succ,\succeq
\begin{array}{l}
f( n) \ =\ f_{1}( n) \pm f_{2}( n) \pm ...\pm f_{k}( n)\\
f_{1}( n) \succ f_{2}( n) ,\ f_{1}( n) \succ f_{3}( n) ,\ ...\ ,\ f_{1}( n) \succ f_{k}( n)\\
\Longrightarrow f( n) \asymp f_{1}( n)
\end{array}
f(n)=c * g(n) ⟹ f(n) ≍g(n)
Симетрията\ на\ \asymp
f( n) \asymp g( n) \Leftrightarrow f( n)^{k} \asymp g( n)^{k}
\lim _{n\rightarrow \infty }\frac{f( n)}{g( n)} =0\ \Leftrightarrow \ f( n) \prec g( n)
\lim _{n\rightarrow \infty }\frac{f( n)}{g( n)} =\infty \Leftrightarrow f( n) \succ g( n)
\lim _{n\rightarrow \infty }\frac{f( n)}{g( n)} =C >0\Rightarrow f( n) \asymp g( n)
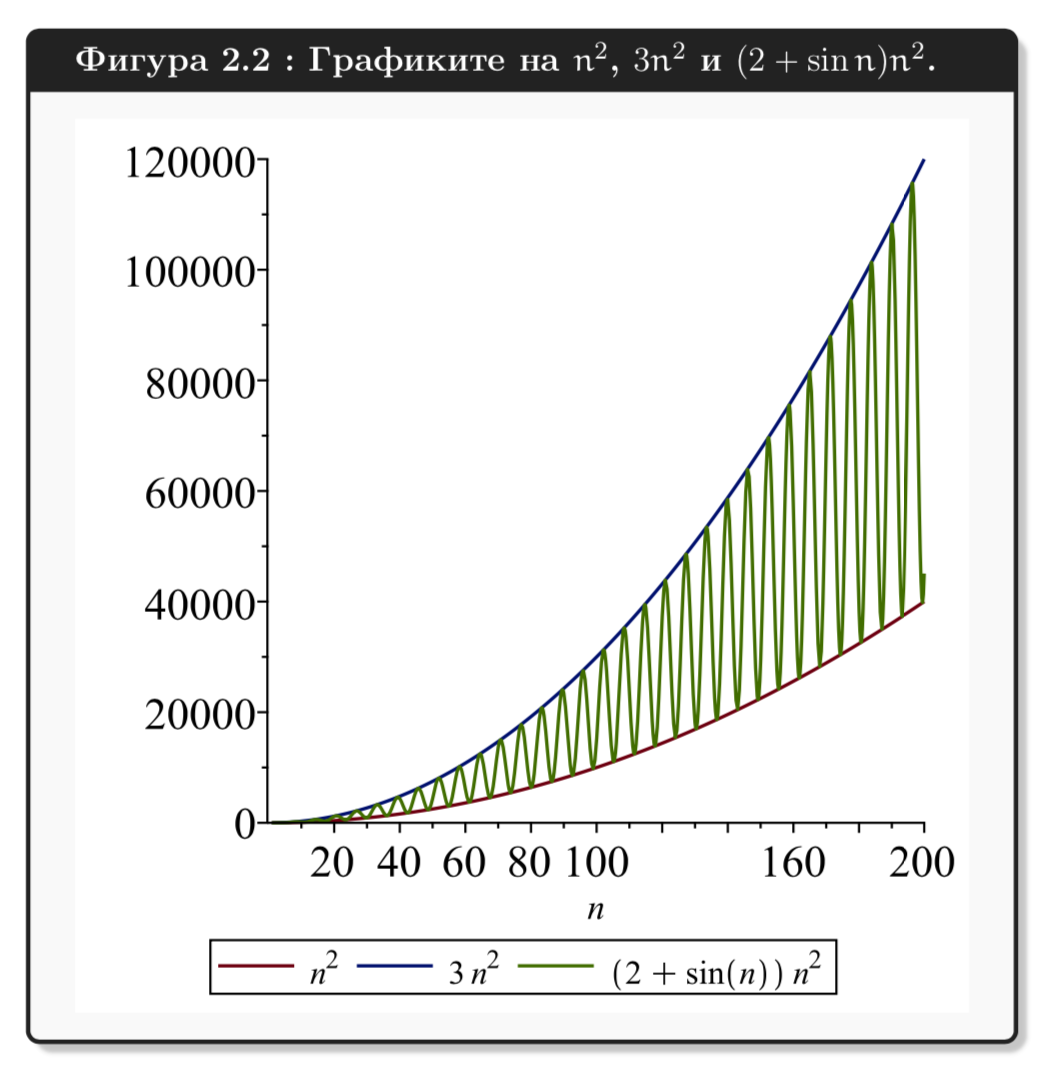
\begin{array}{l}
Ако\ g( n) \ e\ растяща\ и\ неограничена\ и\ a >1,\ то\\
f( n) \prec g( n) \ \Rightarrow a^{f( n)} \prec a^{g( n)}
\end{array}
\begin{array}{l}
Ако\ f( n) \ и\ g( n) \ са\ растящи\ и\ неограничени\ и\ a >1,\ то\\
a^{f( n)} \asymp a^{g( n)} \ \Rightarrow \ f( n) \asymp g( n) \
\end{array}
lg( f( n)) \prec lg( g( n)) \Rightarrow f( n) \prec g( n)
\begin{array}{l}
f( n) \asymp g( n) \ \Rightarrow lg( f( n)) \asymp lg( g( n))
\end{array}
\begin{array}{l}
Ако\ f( n) \ и\ g( n) \ са\ растящи\ и\ неограничени\ и\ a >1,\ то\\
a^{f( n)} \asymp a^{g( n)} \ \Rightarrow \ f( n) \asymp g( n) \
\end{array}
\exists c_{1}>0 \exists c_{2}>0 \exists n_{0}>0 \forall n>n_{0}: c_{1} \cdot a^{g(n)} \leqslant a^{f(n)} \leqslant c_{2} \cdot a^{g(n)}
\log _{a} c_{1}+g(n) \leqslant f(n) \leqslant \log _{a} c_{2}+g(n)

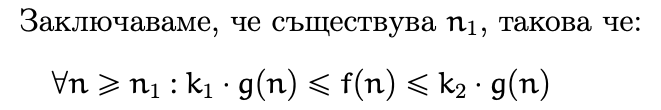
Апроксимация на Стирлинг
n!\sim \sqrt{2\pi n}\frac{n^{n}}{e^{n}} \ \Leftrightarrow \lim _{n\rightarrow \infty }\frac{\sqrt{2\pi n}\frac{n^{n}}{e^{n}}}{n!} =1
Важно\ следствие\ lg( n!) \asymp n\ lg( n)
\begin{array}{l}
По\ транзитивността\ на\ \asymp следва\ lg( n!) \asymp n\ lg( n)
\end{array}
lg\left(\sqrt{2\pi n}\frac{n^{n}}{e^{n}}\right) =lg\left(\sqrt{2\pi }\right) +\frac{1}{2} lg( n) +n\ lg( n) -n\ lg( e) \asymp n\ lg( n)
n!\asymp \sqrt{2\pi n}\frac{n^{n}}{e^{n}} \Longrightarrow lg( n!) \asymp lg\left(\sqrt{2\pi n}\frac{n^{n}}{e^{n}}\right)



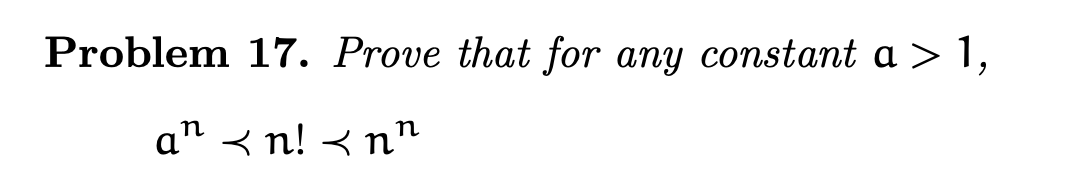
\begin{array}{l}
a^{n} \prec n!\\
n\asymp n\ lg( a) =lg\left( a^{n}\right) \prec lg( n!) \asymp n\ lg( n)
\end{array}
\begin{array}{l}
n!\prec n^{n}\\
\lim _{n\rightarrow \infty }\frac{n!}{n^{n}} =\lim _{n\rightarrow \infty }\left(\frac{n}{n} \ *\ \frac{n-1}{n} \ *\ ...\ *\ \frac{2}{n} \ *\ \frac{1}{n}\right) =0
\end{array}
\begin{aligned}
&\lim _{n \rightarrow \infty} \frac{n^{\epsilon}}{\left(\log _{a} n\right)^{k}}=\quad / / \text { полагаме } b \leftarrow \frac{\epsilon}{k}\\
&\lim _{n \rightarrow \infty} \frac{\left(n^{b}\right)^{k}}{\left(\log _{a} n\right)^{k}}=\\
&\lim _{n \rightarrow \infty}\left(\frac{n^{b}}{\log _{a} n}\right)^{k}=\quad / / k \text { е положително }\\
&\lim _{n \rightarrow \infty} \frac{n^{\mathrm{b}}}{\log _{a} \mathfrak{n}}=\quad / / \text { прилагаме правилото на l'Hôpital }\\
&\lim _{n \rightarrow \infty} \frac{b n^{b-1}}{\left(\frac{1}{\ln a}\right)\left(\frac{1}{n}\right)}=\\
&\lim _{n \rightarrow \infty}(\ln a) b n^{b}=\infty
\end{aligned}

Ако\ a >1\ и\ k >0,\ то\ n^{k} \prec a^{n}
lg\left( n^{k}\right) =k\ lg( n) \asymp lg( n)
lg\left( a^{n}\right) =n\ lg( a) \asymp n
lg( n) \prec n\ заради\ горното\ твърдение
lg\left( n^{k}\right) \asymp lg( n) \prec n\asymp lg\left( a^{n}\right) \Rightarrow n^{k} \prec a^{n}
Да\ се\ сравнят\ функциите\ ln( ln( n)) \ и\ ln( n)
\lim _{n\rightarrow \infty }\frac{ln( ln( n))}{ln( n)} =\ \ \ \ \ \ \ \ \ \ \ //по\ правилото\ на\ l'Hôpital
\lim _{n\rightarrow \infty }\frac{\frac{1}{ln( n)}( ln( n)) '}{( ln( n)) '} =
\lim _{n\rightarrow \infty }\frac{1}{ln( n)} =0
\Rightarrow ln( ln( n)) \prec ln( n)