The partial sums problem

Given a sequence of numbers, compute the sum of the numbers in any given range in the sequence

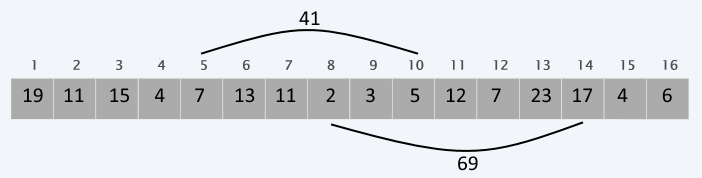
The naive approach

Go through each element between the start index and the end index and sum them.

Complexity is linear (O(n)) for each query and this is insufficient if we want to repeat this operation many times

instead

We can keep a separate list in which the element at each index keeps the sum up to that index. Now we can calculate the sum in O(1) with O(n) additional space

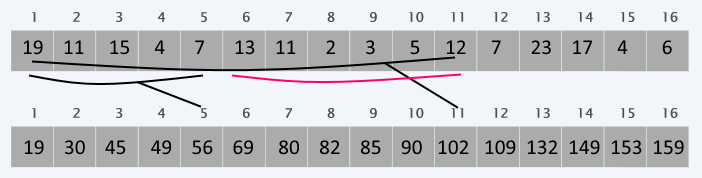
What about updates

If we want to be able to update a given element, we have to rebuild the list with the partial sums.

The complexity of this update is linear (O(n)) because we have to update every element past the updated index

Binary indexed tree

The binary indexed tree solves this problem.

It is represented by a complete binary tree where the leaves represent the sequence and each parent is the sum of its two children.

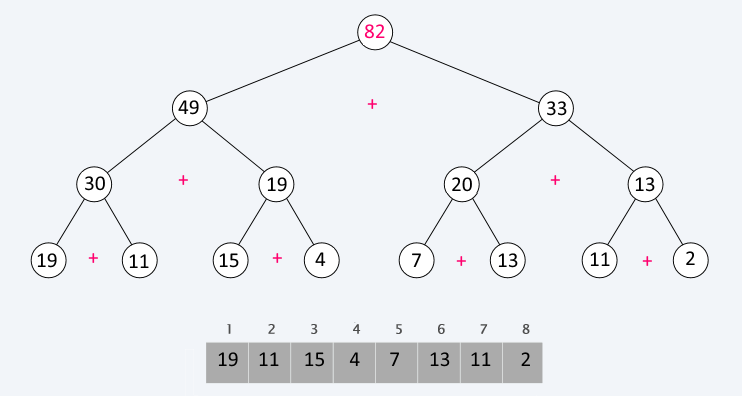
Binary indexed tree

The binary indexed tree uses O(n) additional memory but has O(log n) complexities for updating an item or querying a range.

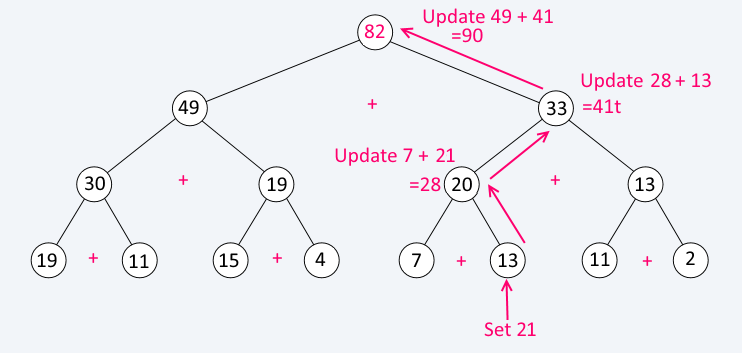
Update an element

To update an element, find its corresponding leaf node and update its value. Then go up through each parent and update its sum.

Query a range

The query uses the fact that each node actually represents a range of the sequence and the length of that range is a power of 2. As we know, each number can be represented by a sum of unique powers of 2. Therefore, we can use a single node from each level to construct the queried range.

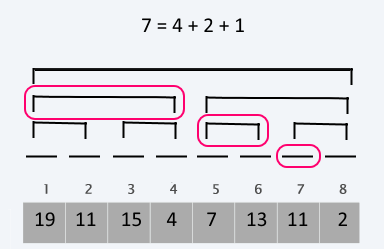
Query a range

We define the Query(i) method as the sum between 1 and i - 1.

Or in other words Query(i) = Sum [1;i) (we exclude the i for simplicity of the operations).

Steps:

Assign current = leaf_of(i)

sum = 0

WHILE current != root

     if is_right_child(current)

         sum+= left_sibling(current)

     current = parent(current)

         

Query a range

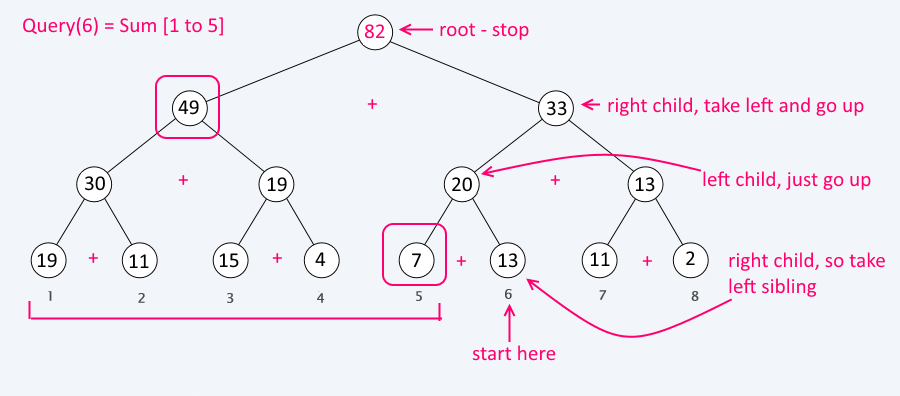
Things to consider

Representation - the indexed tree is always a complete binary tree of fixed size which never changes its structure. Therefore an array representation is more appropriate.

 

Size - the last level where we place the list always has a length which is a power of 2. If our list does not have a length which is a power of 2, we can extend it by adding zeroes.

 

Querying the whole range - the algorithm for querying cannot query the exact whole range, because it queries [1; i). To solve this, we can either add a check if we are querying the whole range and return the root, or we can extend our initial list to the next power of two.

Things to consider

Indices - lets say we are going to use array representation and we want to build the tree over a list of size N (N is an exact power of two)

• 1 is the index of the root
• There are N-1 non-leaf nodes placed on indices [1;N-1]
• N is the index of the first leaf (the first element of the list)
• N + i is the index of the i-th element of the original list (i is zero based)
• 2*N - 1 is the total number of nodes in the tree

Applications

The Binary Index Tree is usually used in other algorithms where calculating sums in ranges is necessary.

 

This can happen mainly in dynamic programming solutions where we need to sum the results of sub-tasks in a given range

 

The Binary Index Tree does not have many real world application but the idea behind it is a basic one in other structures and algorithms like:

• Segment tree
• RMQ (which in turn is used in LCA and LCP)

* I bet you like abbreviations :)