Binary search tree
The binary search tree is a binary tree which holds ordered data. The ordering rule is as follows:
the value in each node is greater than the value in its left child and less than the value in its right child.
Applications
The data in a BST is basically always kept sorted and this allows to quickly lookup existing elements. Insert and remove are also fast, having complexities proportional to the tree height.
- Data structures where data is constantly entering/leaving and a quick lookup is needed - map, set
- Used as a base structure for many database engines
- Used in computer graphics for determining object intersection
Representation
The operations in a BST often require redirecting pointers to parents or children, so the most effective representation is by using pointers
class Node
{
Key value;
Node leftChild;
Node rightChild;
}Operations
The Binary Search Tree supports the following operations:
- Insert element - O(log n)
- Remove element - O(log n)
- Lookup element - O(log n)
- Traverse in sorted order - O(n)
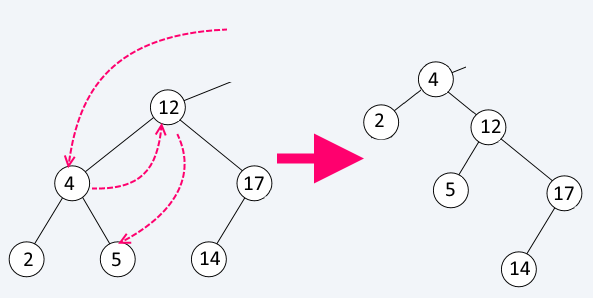
Insert
Insert starts from the root and compares the value of the element being inserted against the value of the existing node in order to decide in which subtree it should go. When there is no child at the link we should follow, insert the new element there
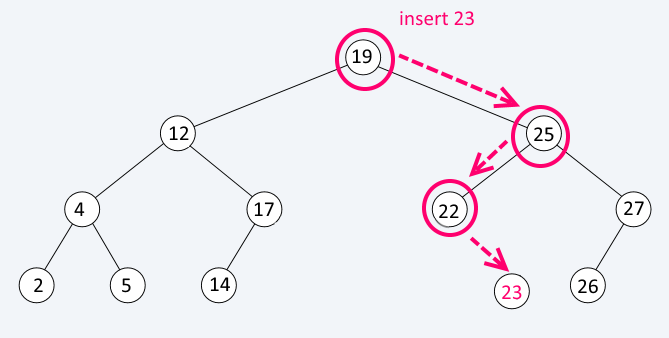
Insert
Insert(inserted value)
1. Assign current = root
2. Repeat
If: current.value > inserted value
If: has_left_child(current)
current = left_child(current), then goto 2
else:
create_left_child(current, inserted value)
If: current.value <= inserted value
If: has_right_child(current)
current = right_child(current), then goto 2
else:
create_right_child(current, inserted value)
Lookup
Lookup goes the same way as the insert - start from the root, compare values and follow one of the links.
Lookup(value)
Assign current = root
While current != null
If: current.value == value
return current
If: current.value > value
current = left_child(current)
If: current.value < value
current = right_child(current)
Remove
Remove first finds the element, then finds the leftmost node in its right sub-tree and swaps their values. Then executes Remove recursively for that leftmost node. If a node to be removed has only one child, we can just redirect the links. If a node to be removed does not have any children, just remove it.
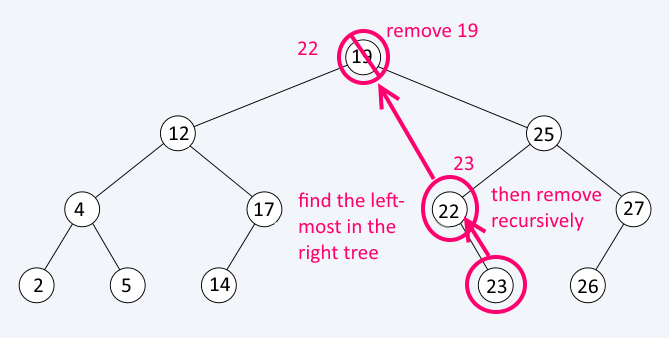
Remove
Remove(node) // should lookup the node before remove
current = node
If has_no_children(current)
remove_from_parent(current)
else if has_one_child(current)
replace_in_parent(current, only_child(current))
else
replacement = left_most_child(current.right)
current.value = replacement.value
Remove(replacement)
Traverse
Traversing a tree is basically going through each of its nodes in a specific order
Pre-order
go through the current, then through the left subtree, then through the right
Preorder-Traverse(node)
Print(node)
Preorder-Traverse(node.left)
Preorder-Traverse(node.right)
In-order
go through the left subtree, then through the current, then through the right
Preorder-Traverse(node)
Preorder-Traverse(node.left)
Print(node)
Preorder-Traverse(node.right)
*Note: this will gives us the sorted sequence
Post-order
go through the left subtree, then through the right, then through the current
Preorder-Traverse(node)
Preorder-Traverse(node.left)
Preorder-Traverse(node.right)
Print(node)
Balancing
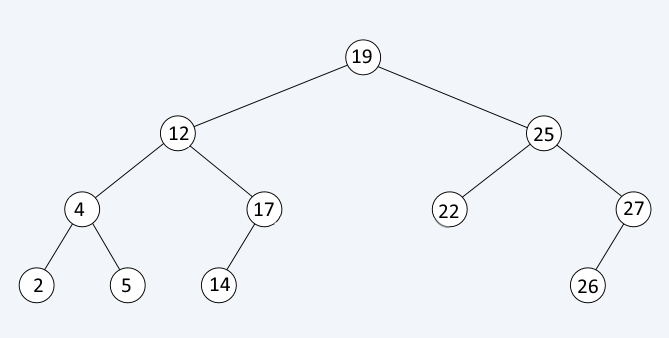
The shape of the binary tree depends on the input data. In the worst case (inserting sorted values) it will look like a list
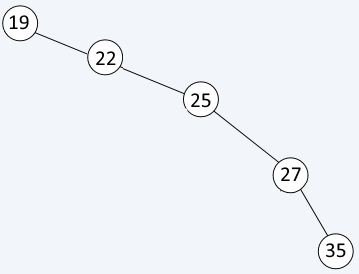
In this case operations will have complexity of O(n)
To resolve this issue, we need to balance the tree (on the figure - make 25 the root)
Balancing
Balancing turns out to be quite a complex task. There are different modifications of the BST which keep the data balanced. Some of them are:
- Red-black tree - marks some of the links as red and others as black and uses this to represent a 2,3-tree like a normal BST.
- AVL-tree - compares the heights of subtrees and applies rotations where needed. The first balanced BST invented.
- Treap - asigns random integers to nodes and tries to keep the heap rule for them (tree + heap = treap). Applies rotations to keep the heap rule.
Balancing - rotations
Rotation is a operation which keeps the BST rule but changes the height of subtrees. Rotations are used by Treap and AVL trees to keep the tree balanced. There are two types of rotation: left rotation and right rotation - bringing the left child or the right child up