Sort

根據定義來做
selection sort
insertion sort
merge sort
quick sort
std::sort

C++ swap

#include<algorithm>
交換兩個變數

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int main(){
    int a = 1, b = 2;
    swap(a, b);
    cout << a << ' ' << b << '\n';
    vector<int> va = {1,2,3}, vb = {4, 5};
    swap(va, vb);
    return 0;
}

自己寫 swap

還是要稍微會一下

#include<iostream>
using namespace std;
void swap(int &a, int &b){
    int t = a;
    a = b;
    b = t;
}
int main(){
    int a = 1, b = 2;
    swap(a, b);
    cout << a << ' ' << b << '\n';
    return 0;
}

Sort 排序

給一個長度為 \(n\) 陣列\(S\)，請你透過交換元素的方式使得：
- \(S_i \le S_{i+1}, \; 0 \le i < n-1\)

判斷陣列是否排序好\(O(n)\)

bool is_sorted(const vector<int> &S){
    int n = S.size();
    for (int i = 0; i + 1 < n; ++i)
        if (S[i] > S[i+1])
            return false;
    return true;
}

根據定義來做

void simple_sort(vector<int> &S){
    int n = S.size();
    while(!is_sorted(S)){
        for (int i = 0; i + 1 < n; ++i){
            if (S[i] > S[i+1])
                swap(S[i], S[i+1]);
        }
    }
}

簡化: bubble sort

void bubble_sort(vector<int> &S){
    int n = S.size();
    bool is_sorted;
    do{
        is_sorted = true;
        for (int i = 0; i + 1 < n; ++i){
            if (S[i] > S[i+1]){
                swap(S[i], S[i+1]);
                is_sorted = false;
            }
        }
    }while(is_sorted);
}

想一想

do while迴圈只會執行\(n-1\)次
為甚麼？

bubble sort: 無腦寫法\(O(n^2)\)

void bubble_sort(vector<int> &S){
    int n = S.size();
    for (int t = 0; t < n-1; ++t)
        for (int i = 0; i + 1 < n; ++i)
            if (S[i] > S[i+1])
                swap(S[i], S[i+1]);
}

Selection Sort

選擇排序

Selection Sort

找出最大的放最後

0	1	2	3	4
5	3	6	1	2

Selection Sort

找出最大的放最後

0	1	2	3	4
5	3	6	1	2

Selection Sort

找出最大的放最後

0	1	2	3	4
5	3	2	1	6

Selection Sort

找出最大的放最後

0	1	2	3	4
5	3	2	1	6

Selection Sort

找出最大的放最後

0	1	2	3	4
1	3	2	5	6

Selection Sort

找出最大的放最後

0	1	2	3	4
1	3	2	5	6

Selection Sort

找出最大的放最後

0	1	2	3	4
1	2	3	5	6

取得\(S_0\sim S_k\)中最大元素的編號

int find_max_id(const vector<int> &S, int k){
    int res = 0;
    for (int i = 1; i < k; ++i)
        if (S[i] > S[res])
            res = i;
    return res;
}

Selection Sort \(O(n^2)\)

int selection_sort(vector<int> &S){
    int n = S.size();
    for (int i = n-1; i > 0; --i){
        int max_id = find_max_id(S, i);
        swap(S[i], S[max_id]);
    }
}

延伸

Heap Sort

使用heap來做find_max_id操作
\(O(n \log n)\)

Insertion Sort

插入排序

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
5	3	6	1	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
5	3	6	1	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
5	3	6	1	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
3	5	6	1	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
3	5	6	1	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
3	5	6	1	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
3	5	1	6	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
3	1	5	6	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
1	3	5	6	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
1	3	5	6	2

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
1	3	5	2	6

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
1	3	2	5	6

Sorted

Insertion Sort

分為排序好以及未排序兩區域
不斷將元素從未排序加入排序好區域

0	1	2	3	4
1	2	3	5	6

Sorted

\(S_0\sim S_{k-1}\)已排序
現在要加入\(S_k\)

void insert(vector<int> &S, int k){
    while(k > 0){
        if (S[k] < S[k-1])
            swap(S[k], S[k-1]);
        --k;
    }
}

Insertion Sort \(O(n^2)\)

void insertion_sort(vector<int> &S){
    int n = S.size();
    for(int i = 0; i < n; ++i)
        insert(S, i);
}

Merge Sort

合併排序

想法

陣列S

想法

陣列S

陣列A

陣列B

分別對A,B進行排序

想法

陣列S

陣列A

陣列B

分別對A,B進行排序

陣列S

合併排序好的A,B

一直切割下去

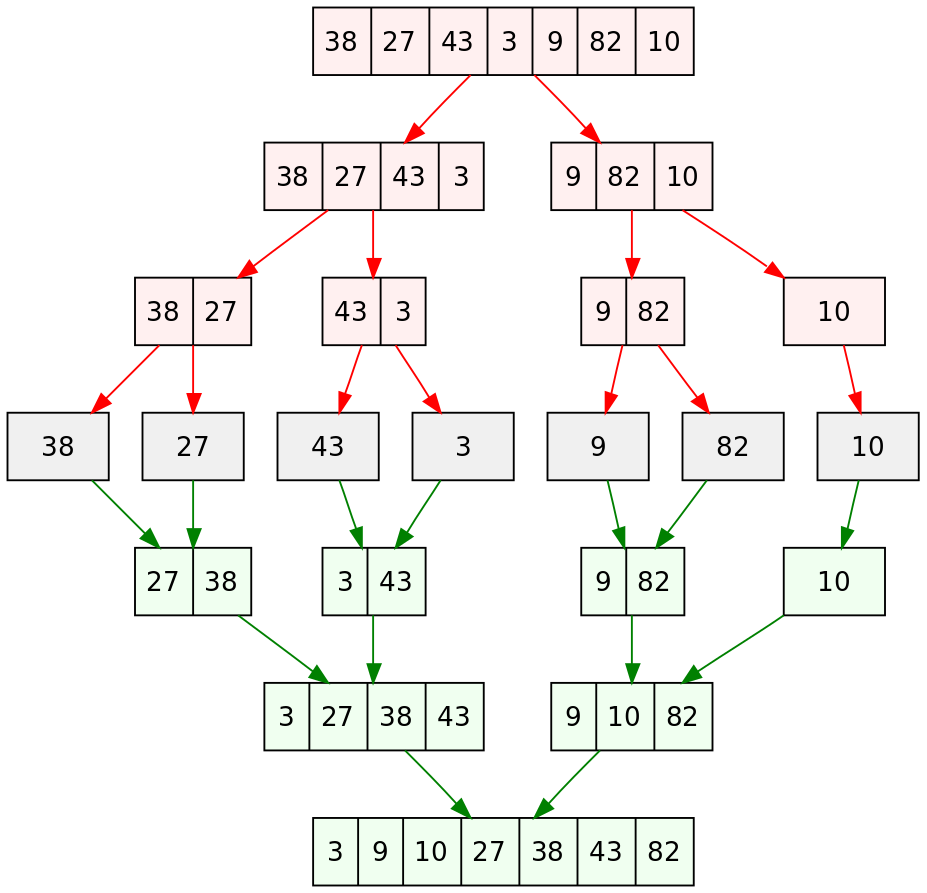
主要程式碼(遞迴)

vector<int> merge_sort(const vector<int> &S){
    if (S.size() <= 1)
        return S;
    int mid = S.size() / 2; //將陣列拆兩半
    vector<int> A(S.begin(), S.begin() + mid);
    vector<int> B(S.begin() + mid, S.end());
    A = merge_sort(A);
    B = merge_sort(B);
    return merge(A, B); // 怎麼做?
}

merge

2	3	7	10

1	4	5	6

merge

2	3	7	10

1	4	5	6

1

merge

2	3	7	10

1	4	5	6

1	2

merge

2	3	7	10

1	4	5	6

1	2	3

merge

2	3	7	10

1	4	5	6

1	2	3	4

merge

2	3	7	10

1	4	5	6

1	2	3	4	5

merge

2	3	7	10

1	4	5	6

1	2	3	4	5	6

merge

2	3	7	10

1	4	5	6

1	2	3	4	5	6	7

merge

2	3	7	10

1	4	5	6

1	2	3	4	5	6	7	10

merge \(O(n+m)\)

vector<int> merge(const vector<int> &A, const vector<int> &B){
    int n = A.size(), m = B.size(), i = 0, j = 0;
    vector<int> ans;
    while (i < n && j < m)
        if (B[j] < A[i])
            ans.push_back(B[j++]);
        else
            ans.push_back(A[i++]);
    while (i < n)
        ans.push_back(A[i++]);
    while (j < m)
        ans.push_back(B[j++]);
    return ans;
}

分析

時間
- \(T(n) = 2T(n/2) + O(n) = O(n\log n)\)
  - by master theorem
優點
- 時間複雜度好
缺點
- 需要大量額外空間

Inversion Count

逆序數對個數

定義: 逆序數對

給一個長度為 \(n\) 陣列\(S\)
定義逆序數對\((i,j)\)：
- \(S_i > S_j, \; 0 \le i < j < n\)

0	1	2	3	4
5	3	6	1	2

\(i\)

\(j\)

逆序數對個數

bubble sort, insertion sort
swap 執行的次數
暴力直接算 \(O(n^2)\)

int inversion_count(const vector<int> &S){
    int n = S.size(), cnt = 0;
    for(int i = 0; i < n; ++i)
        for(int j = i+1; j < n; ++j)
            if(S[i] > S[j]) ++cnt;
    return cnt;
}

分治想法

陣列S

陣列A

陣列B

分別計算A,B逆序數對數量

陣列S

計算B[i] > A[j]的數量

合併

merge

2	3	7	10

1	4	5	6

inversion count: 0

merge

2	3	7	10

1	4	5	6

1

inversion count: 4

merge

2	3	7	10

1	4	5	6

1	2

inversion count: 4

merge

2	3	7	10

1	4	5	6

1	2	3

inversion count: 4

merge

2	3	7	10

1	4	5	6

1	2	3	4

inversion count: 6

merge

2	3	7	10

1	4	5	6

1	2	3	4	5

inversion count: 8

merge

2	3	7	10

1	4	5	6

1	2	3	4	5	6

inversion count: 10

merge

2	3	7	10

1	4	5	6

1	2	3	4	5	6	7

inversion count: 10

merge

2	3	7	10

1	4	5	6

1	2	3	4	5	6	7	10

inversion count: 10

merge 時順便計算

int inversion_count;
vector<int> merge(const vector<int> &A, const vector<int> &B){
    int n = A.size(), m = B.size(), i = 0, j = 0;
    vector<int> ans;
    while (i < n && j < m)
        if (B[j] < A[i]){
            ans.push_back(B[j++]);
            inversion_count += n - i;
        }else
            ans.push_back(A[i++]);
    while (i < n)
        ans.push_back(A[i++]);
    while (j < m)
        ans.push_back(B[j++]);
    return ans;
}

merge 時順便計算

int inversion_count;
vector<int> merge(const vector<int> &A, const vector<int> &B){
    int n = A.size(), m = B.size(), i = 0, j = 0;
    vector<int> ans;
    while (i < n && j < m)
        if (B[j] < A[i]){
            ans.push_back(B[j++]);
            inversion_count += n - i;
        }else
            ans.push_back(A[i++]);
    while (i < n)
        ans.push_back(A[i++]);
    while (j < m)
        ans.push_back(B[j++]);
    return ans;
}

merge sort 時順便計算

int inversion_count(const vector<int> &S){
    inversion_count = 0;
    merge_sort(S);
    return inversion_count;
}

Quick Sort

快速排序

想法

隨機選一個位置 \(x\)
將陣列分成三份
- 小於 \(S_x\)
- 等於 \(S_x\)
- 大於 \(S_x\)
小於和大於的部分分別遞迴處理

想法

三分陣列(\(x = 1, S_x=3\))

0	1	2	3	4	5
6	3	5	1	3	2

1	2

3	3

6	5

\(<\)

\(>\)

\(=\)

quick sort

vector<int> quick_sort(const vector<int> &S){
    if(S.size() <= 1) return S;
    vector<int> less, equal, greater;
    int x = rand() % S.size();
    for(int i: S){
        if(i < S[x]) less.push_back(i);
        else if (i == S[x]) equal.push_back(i);
        else greater.push_back(i);
    }
    less = quick_sort(less);
    greater = quick_sort(greater);
    for(int i: equal)
        less.push_back(i);
    for(int i: greater)
        less.push_back(i);
    return less;
}

遞迴結構圖

複雜度

平均:
- \(O(n\log n)\)
最差(幾乎不會出現):
- \(O(n^2)\)

C++ Sort

std::sort
std::stable_sort

std::sort

#include <algorithm>
使用 introsort 實作
- quick sort + heap sort
- \(O(n\log n)\) 而且高效率

std::sort

用法
- sort(起始指標, 結束指標);
陣列用法(n是陣列長度)
- sort(S, S+n);
vector用法(n = S.size())
- sort(S.begin(), S.end());
- sort(S.begin(), S.begin() + n);

#include<algorithm>
using namespace std;
int main(){
    int A[] = {7,1,2,2,7,1,2,2};
    vector<int> B = {3,2,1,0};
    
    sort(A, A+4);
    // A = {1,2,2,7,7,1,2,2}
    
    sort(A, A+8);
    // A = {1,1,2,2,2,2,7,7}
    
    sort(B.begin(), B.begin()+2);
    // B = {2,3,1,0}
    
    sort(B.begin(), B.end());
    // B = {0,1,2,3}
    return 0;
}

std::stable_sort

#include <algorithm>
使用 merge sort 實作
- \(O(n\log n)\) 但稍慢

std::sort

用法
- 和sort一樣

#include<algorithm>
using namespace std;
int main(){
    int A[] = {7,1,2,2,7,1,2,2};
    vector<int> B = {3,2,1,0};
    
    stable_sort(A, A+4);
    // A = {1,2,2,7,7,1,2,2}
    
    stable_sort(A, A+8);
    // A = {1,1,2,2,2,2,7,7}
    
    stable_sort(B.begin(), B.begin()+2);
    // B = {2,3,1,0}
    
    stable_sort(B.begin(), B.end());
    // B = {0,1,2,3}
    return 0;
}

補充

Stooge Sort

臭皮匠排序
\(O(n^{\log 3 /\log 1.5}) \approx O(n^{2.71})\)

void stoogeSort(int s[], int L, int R){
    if (s[R] < s[L]) swap(s[L], s[R]);
    if (R-L <= 1) return;
    int p = (R-L+1) / 3;
    stoogeSort(s, L, R-p);
    stoogeSort(s, L+p, R);
    stoogeSort(s, L, R-p);
}

Sort

Sort

C++ swap

自己寫 swap

Sort 排序

判斷陣列是否排序好\(O(n)\)

根據定義來做

簡化: bubble sort

想一想

bubble sort: 無腦寫法\(O(n^2)\)

Selection Sort

選擇排序

Selection Sort

Selection Sort

Selection Sort

Selection Sort

Selection Sort

Selection Sort

Selection Sort

取得\(S_0\sim S_k\)中最大元素的編號

Selection Sort \(O(n^2)\)

延伸

Heap Sort

Insertion Sort

插入排序

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

Insertion Sort

\(S_0\sim S_{k-1}\)已排序 現在要加入\(S_k\)

Insertion Sort \(O(n^2)\)

Merge Sort

合併排序

想法

想法

想法

一直切割下去

主要程式碼(遞迴)

merge

merge

merge

merge

merge

merge

merge

merge

merge

merge \(O(n+m)\)

分析

Inversion Count

逆序數對個數

定義: 逆序數對

逆序數對個數

分治想法

merge

merge

merge

merge

merge

merge

merge

merge

merge

merge 時順便計算

merge 時順便計算

merge sort 時順便計算

Quick Sort

快速排序

想法

想法

quick sort

\(S_0\sim S_{k-1}\)已排序
現在要加入\(S_k\)

std::sort
std::stable_sort