Aim 3: Posterior Sampling and Uncertainty
March 28, 2023


Summary of contributions: \(K\)-RCPS
Provably minimize the mean interval length with:
- coverage of future samples from \(F(y)\)
- conformal risk control w.r.t. \(x\)
for any user-defined \(K\)-partition of the image.
For a stochastic sampler \(F:~\mathcal{Y} \to \mathcal{X}\) trained to retrieve a signal \(x\) given a low-quality observation \(y\)
Summary of contributions: \(K\)-RCPS
stochastic denoiser
\(F\)
calibration dataset
\(\mathcal{S}_{\text{cal}} = \{(x_i, y_i)\}_{i=1}^{n}\)
samples
\(\{\{F^{(k)}(y_i)\}_{k=1}^m\}_{i=1}^n\)
sample quantiles
\(\{[\hat{l}_{j,\alpha}, \hat{u}_{j,\alpha}]\}_{i=1}^n\)
\(K\)-RCPS
calibrated uncertainty maps
Summary of contributions: \(K\)-RCPS

Moving forward: image reconstruction
[Song, 22]
Data prior: forward SDE
\[\text{d}x = f(x, t) \text{d}t +g(t) \text{d}w\]
\[\implies x_t = \alpha(t) x_0 + \beta(t) z,~z \sim \mathcal{N}(0, \mathbb{I})\]
Measurement process (e.g., sparse-view CT, \(k\)-space MRI):
\[y = Ax + v,~v \sim \mathcal{N}(0, \sigma^2_0)\]
with
\[y \in \mathbb{R}^m,~x \in \mathbb{R}^n, m < n\]
and
\[A \in \R^{m \times n},~A = \mathcal{P}(\Lambda)T,~T \in \mathbb{R}^{n \times n}\]
Moving forward: image reconstruction
[Song, 22]
Consider
\[y_t = Ax_t + \alpha(t)v\]
\[\implies y_0 = Ax_0 + v = y~\quad(\alpha(0) = 1)\]
and
\[y_t = A[\alpha(t)x_0 + \beta(t)z] + \alpha(t)v = \alpha(t)y_0 + \beta(t)Az\]
Can easily generate \(\{y_t\}_{t \in [0,1]}\)
Moving forward: image reconstruction
[Song, 22]
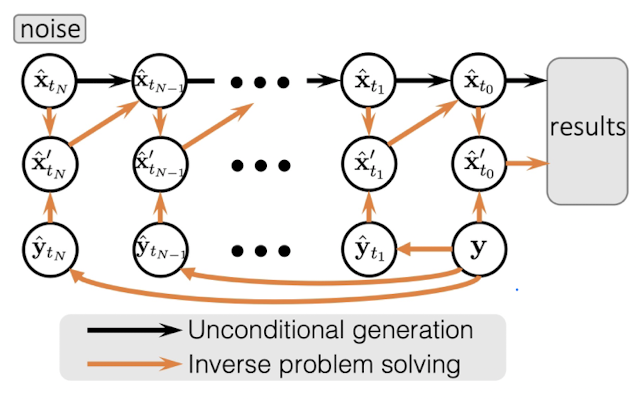
Proposed method: at every step \(t_i\)
1. Project \(x_{t_i}\) onto \(\{v \in \mathbb{R}^n:~Av = y_{t_i}\}\)
2. Call the unconditional score model to obtain \(x_{t_{i-1}}\)
Nonlinear measurement process
\[y = Be^{-A\mu} + v,~v \sim \mathcal{N}(0, K)\]
Open questions:
1. How to use an unconditional score network
2. How to guarantee data consistency
3. How to sample data efficiently