Aim 3: Posterior Sampling and Uncertainty

 

October 18, 2022

Score SDE (refresher)

[GitHub][paper]

0. Ito process

\text{d}x = f(x, t)\text{d}t + g(t)\text{d}w

1. [Anderson, 82] Reverse-time SDE

\text{d}x = [f(x, t) - g^2(t)~\nabla_x \log~p_t(x)]\text{d}t + g(t)\text{d}\bar{w}

\(\implies\)

2. [Song, 21] SDE Score Network

\theta^* = \arg \min \mathbb{E}_{(t,~x(0),~x(t) \mid x(0))}\left[\| s_\theta(x(t), t) - \nabla_x \log~p_{0t}(x(t)\mid x(0))\|_2^2\right]

Denoising Reverse-time SDE (no drift)

x_t = x_{t + 1} + g^2_{t + 1} \left[\nabla_x \log~p(x_{t+1}) + \nabla_x \log~p(y \mid x_{t+1})\right]~\Delta t + g_{t+1}z_{t+1}\sqrt{\Delta t}

Forward-time SDE

We use

\text{d}x = \sqrt{\frac{\text{d}}{\text{d}t}\sigma^2(t)} \text{d}w,~\sigma(t) = \sigma_{\min} \cdot \left(\frac{\sigma_{\max}}{\sigma_{\min}}\right)^t\\

\(x(0)\)

\(\sigma_{\min} = 0.01\)

\(x(T=1)\)

\(\sigma_{\max} = 1\)

Denoising reverse-time SDE (Euler)

We have

\nabla_x \log~p(y \mid x_t) = \frac{y - x_t}{\sigma^2_0 - \sigma^2_t}

Training a continuous-time score network on Abdomen CT

Model: U-net based on NCSNpp [GitHub] [paper]

Hardware: 8 NVIDIA RTX A5000 (24 GB of RAM each)

Sampling results

Original

Original

Perturbed

Samples

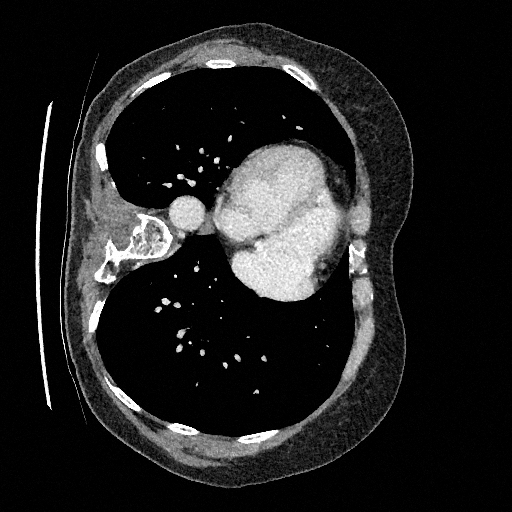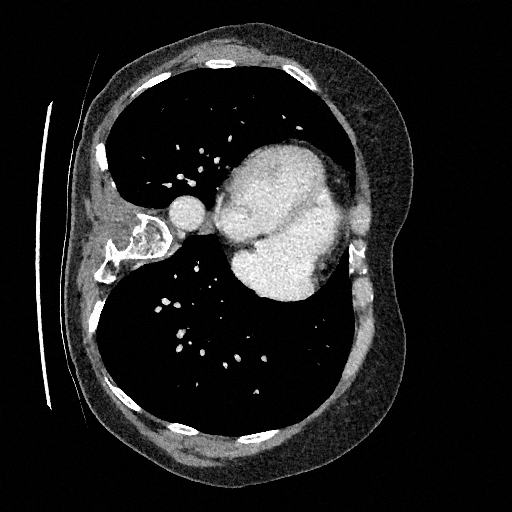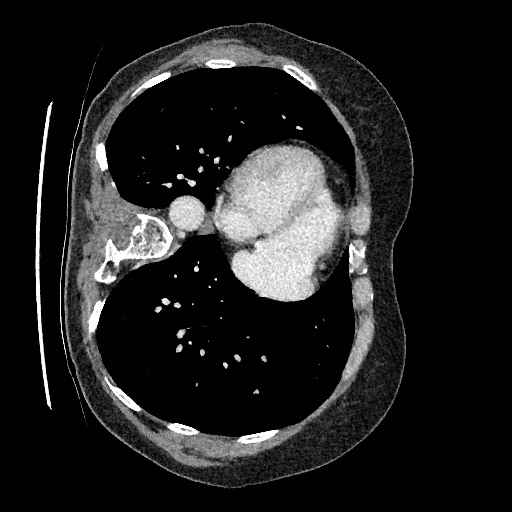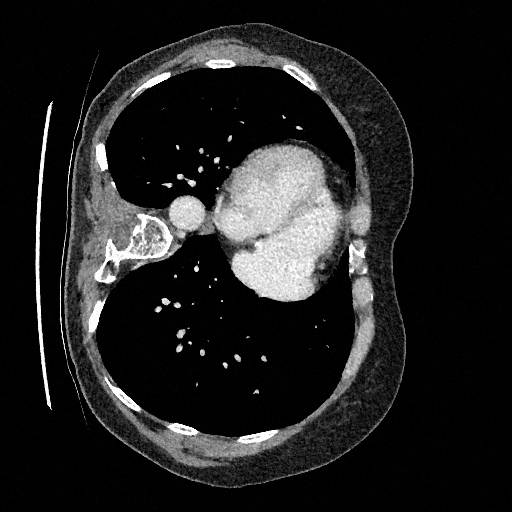
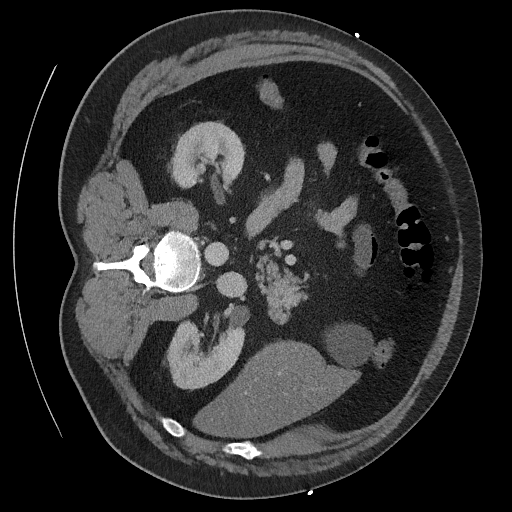
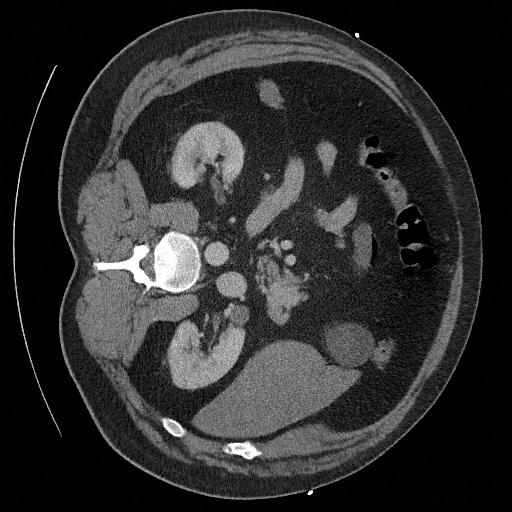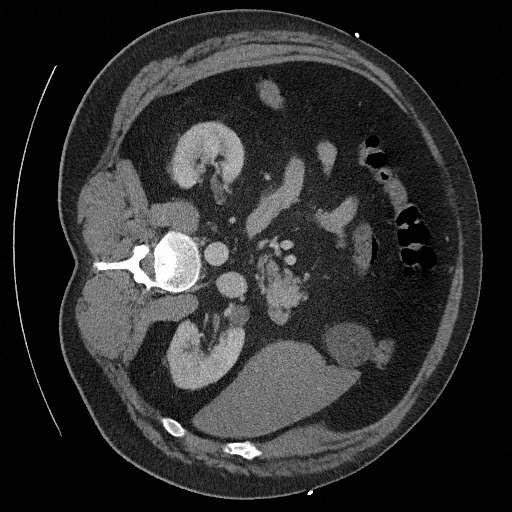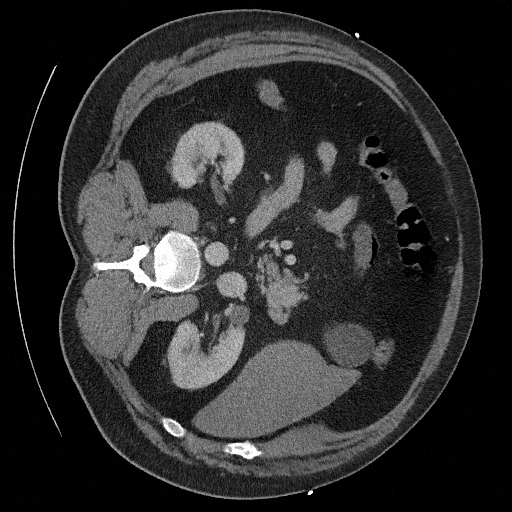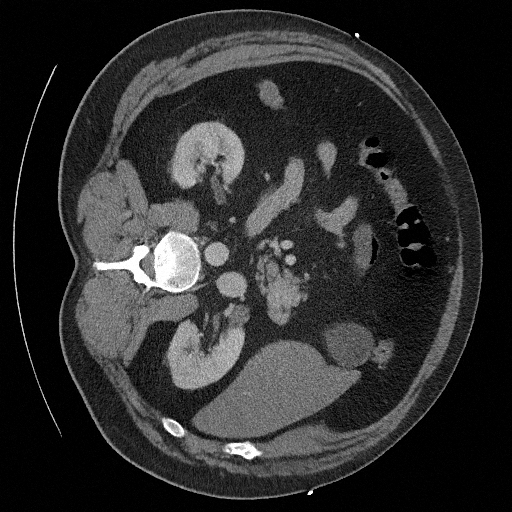
Sampling results

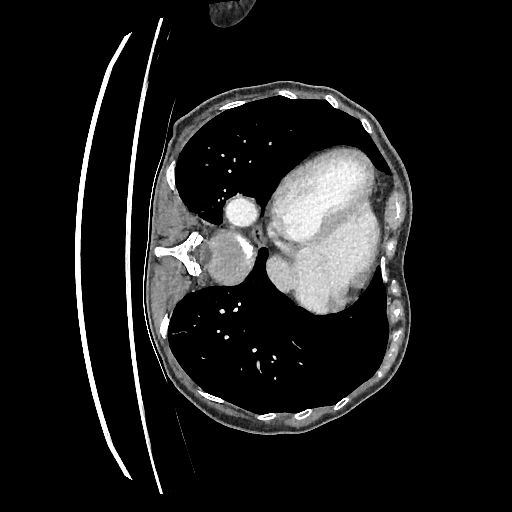
Original

Original

Perturbed

Sampled

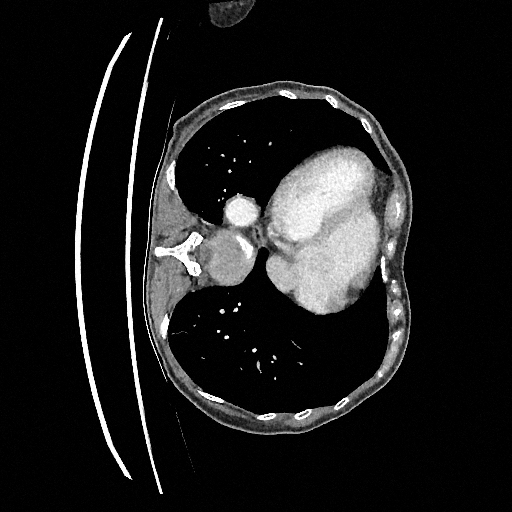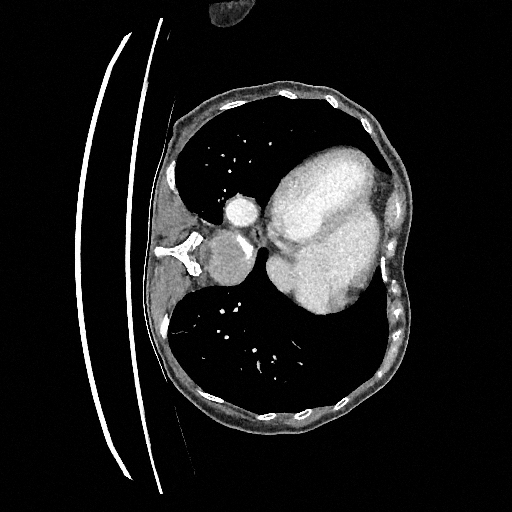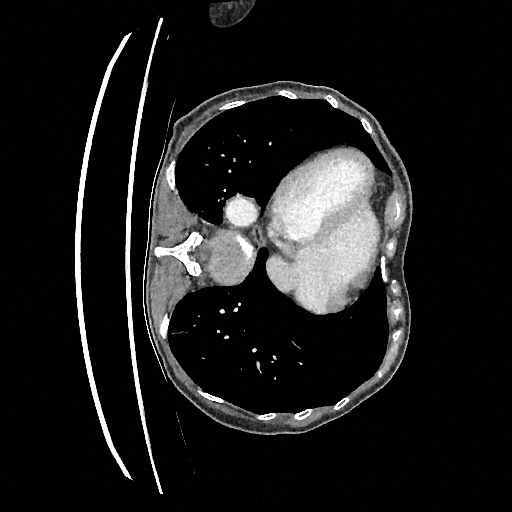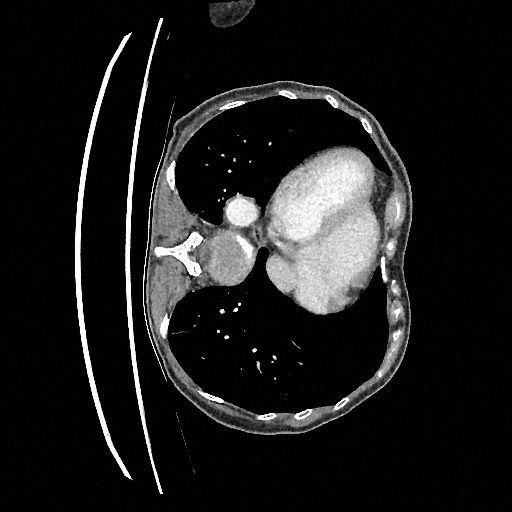
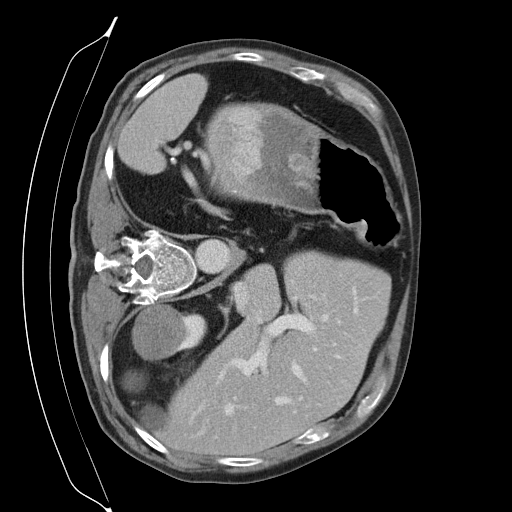
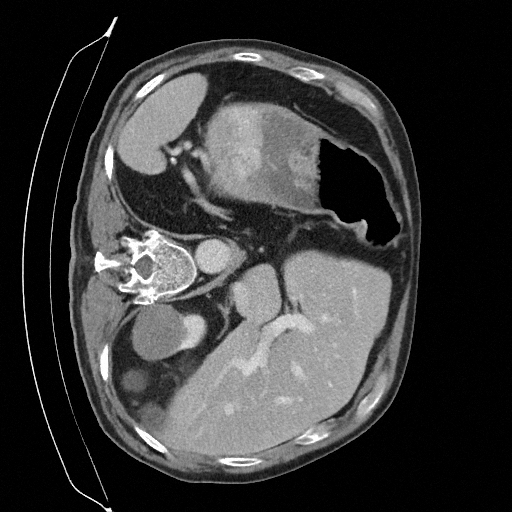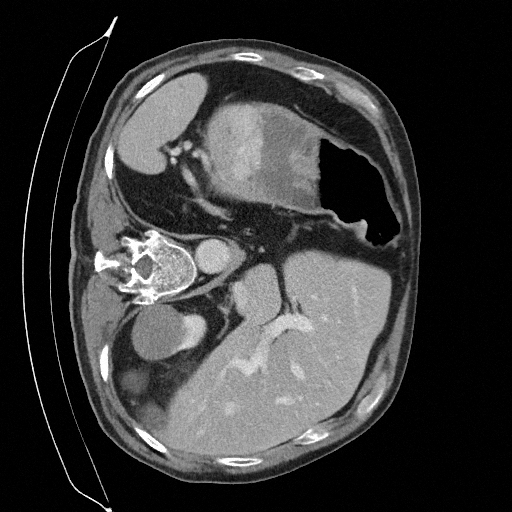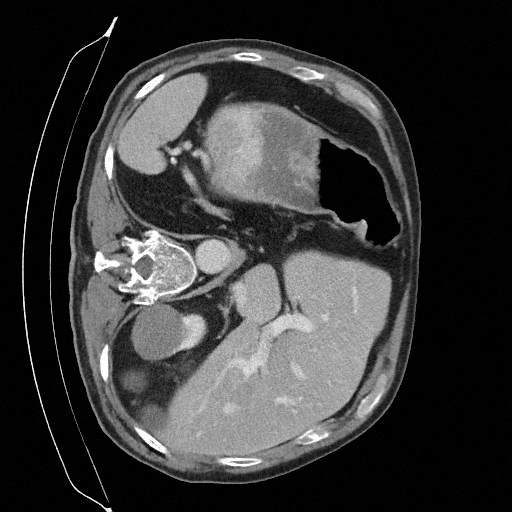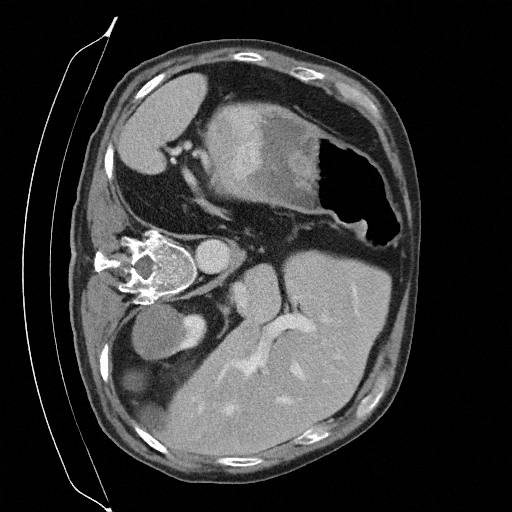
Sampling results

Some notions of uncertainty

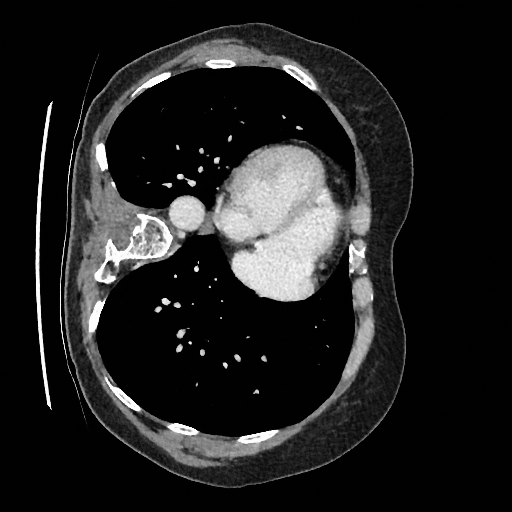
Mean

Standard Deviation

Quantile

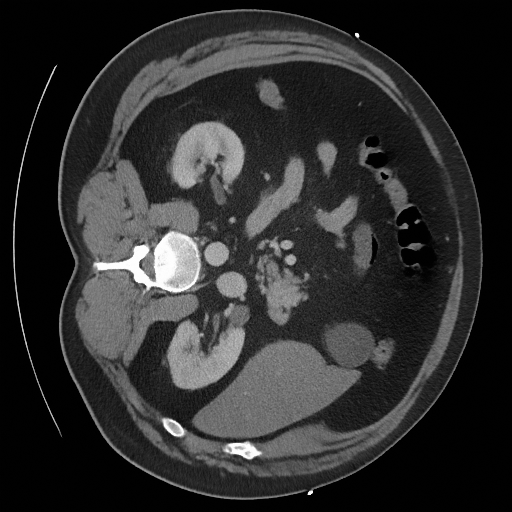
Some notions of uncertainty

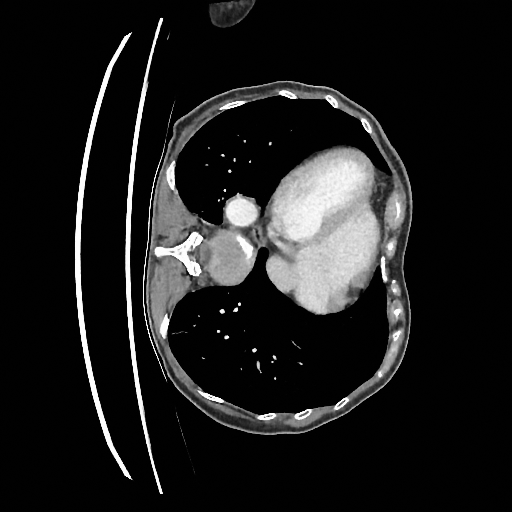
Mean

Standard Deviation

Quantile

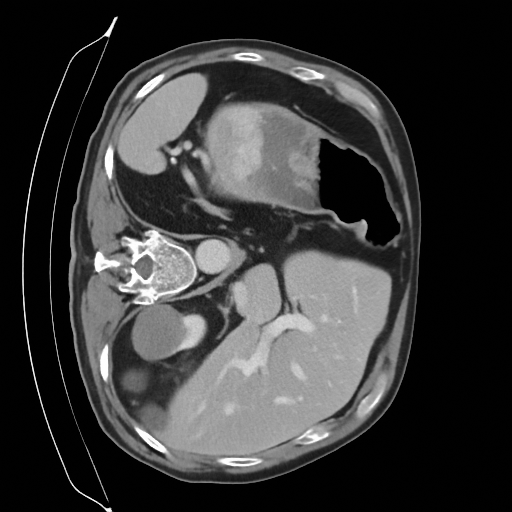
Next steps

How to grant these notions of uncertainty with guarantees? For example

    . "How far is the true image from a new sample?''

    . "How likely is it to observe an unrealistic sample?''

    . "How do we know if the computed empirical distribution contains the ground truth?''

 

Solving general linear inverse problems:

SNIPS [Kawar, 21]

y = Hx + z,~z \sim \mathcal{N}(0, \sigma^2_0 \mathbb{I})
\nabla_x \log~p(x)
\nabla_x \log~p(y \mid x)

Main idea: Sample in the SVD space of \(H\)

Solving general linear inverse problems:

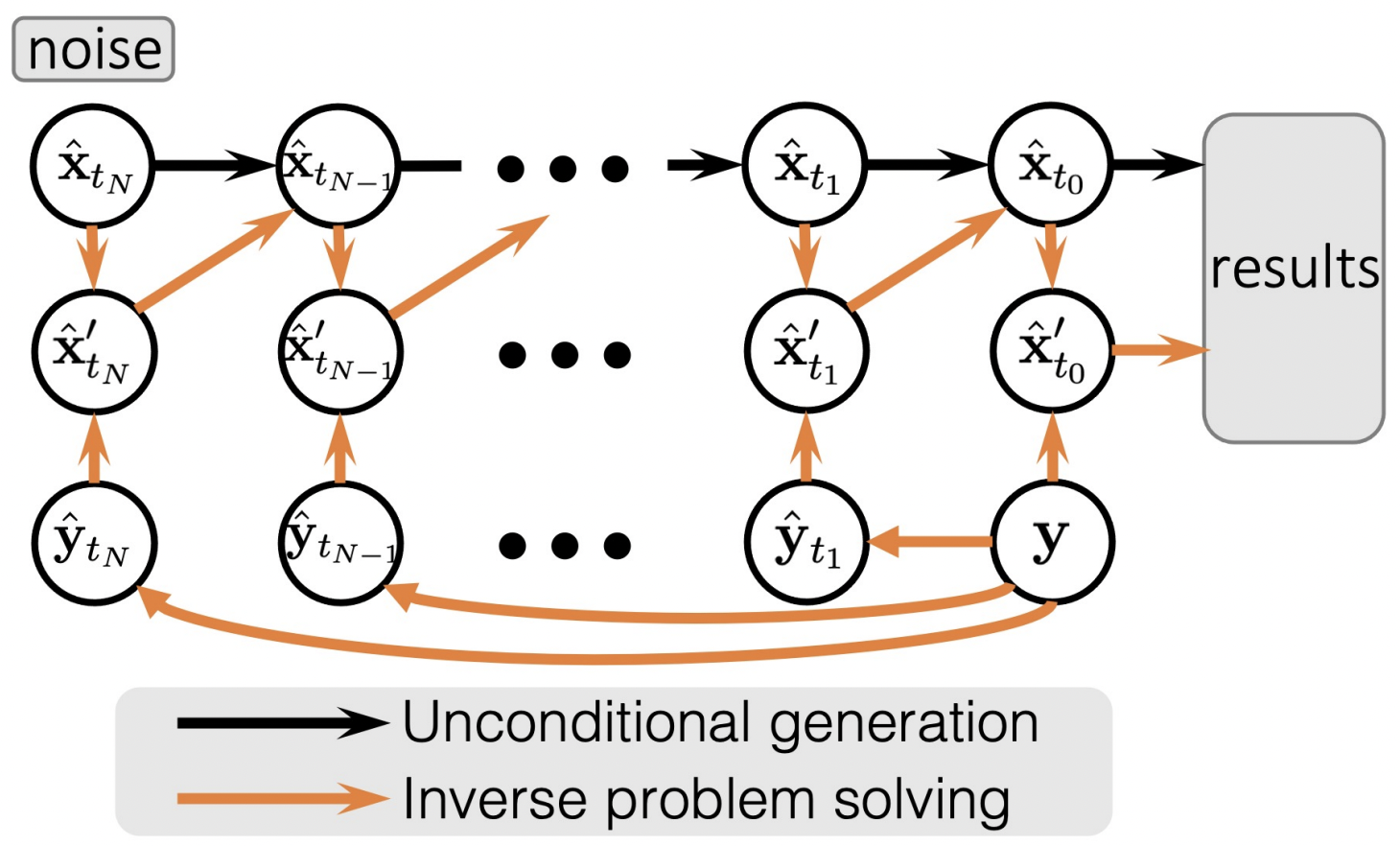
Solving Inverse Problems in Medical Imaging [Song, 22]

y = Ax + \epsilon,~\epsilon \sim \mathcal{N}(0, \sigma^2_0 \mathbb{I})

Main idea: Avoid the SVD decomposition by constructing \(\{\hat{y}_{t_i}\}_{i=0}^N\)

Made with Slides.com