Uncertainty Quantification in CT Denoising
Jacopo Teneggi, Matthew Tivnan, J. Webster Stayman, and Jeremias Sulam


57th Annual Conference on Information Science and Systems
Inverse problems in Image Processing

restoration
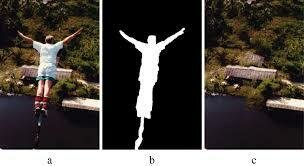
inpainting
CT reconstruction
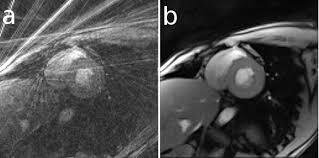
Inverse problems in Image Processing

restoration
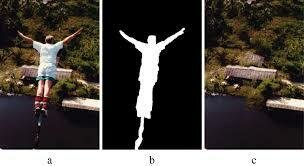
inpainting
CT reconstruction

CT Denoising
To retrieve the ground-truth signal \(x\) given a noisy observation \(y\) with
\[y = x + v,~v \sim \mathcal{N}(0, \mathbb{I})\]
Supervised Learning Approach
Given a set \(S = \{(x_i, y_i)\}_{i=1}^n\) train \(f:~\mathcal{Y} \to \mathcal{X}\) such that
\[\hat{f} = \arg\min~\frac{1}{n} \sum_{(x_i, y_i) \in S} \|x_i - f(y_i)\|^2\]

Original
Perturbed
Denoised
Supervised Learning Approach
Given a set \(S = \{(x_i, y_i)\}_{i=1}^n\) train \(f:~\mathcal{Y} \to \mathcal{X}\) such that
\[\hat{f} = \arg\min~\frac{1}{n} \sum_{(x_i, y_i) \in S} \|x_i - f(y_i)\|^2\]

Original
Perturbed
Denoised
Some disadvantages
- Loss of high-frequency information
- Point predictors
An Alternative Approach
Sample from the conditional posterior distribution
\[p(x \mid y)\]
by means of a stochastic function \(F:~\mathcal{Y} \to \mathcal{X}\).

Original
Perturbed
Sampled
An Alternative Approach
Sample from the posterior distribution
\[p(x \mid y)\]
by means of a stochastic function \(F:~\mathcal{Y} \to \mathcal{X}\)

Original
Perturbed
Sampled
Advantages
- Varied and high-quality samples
- Can be conditioned on several measurement models
Is the Model Right?




Is the Model Right?




Desired Guarantees
- How different will a new sample \(F(y)\) be?
- How far from the ground-truth signal \(x\)?
Entrywise Calibrated Quantiles
Fix \(y \in \mathbb{R}^d\) and sample \(m\) times from \(F(y) \in \mathbb{R}^d\)
Q: Where will the \((m+1)^{\text{th}}\) sample be?
Lemma (informal) For every feature \(j \in [d]\)
\[\mathcal{I}(y)_j = \left[\text{lower cal. quantile}, \text{upper cal. quantile}\right]\]
provides entrywise coverage, i.e.
\[\mathbb{P}\left[\text{next sample}_j \in \mathcal{I}(y)_j\right] \geq 1 - \alpha\]
Calibrated quantiles For a miscoverage level \(\alpha\)
\(0\)
\(1\)
\(\frac{\alpha}{2}\)
\(\frac{(1 -\alpha)}{2}\)
\(\frac{\lfloor(m+1)\alpha/2\rfloor}{m}\)
\(\frac{\lceil(m+1)(1 - \alpha/2)\rceil}{m}\)
Entrywise Calibrated Quantiles

Original
Perturbed
Lower
Upper
Interval size
Conformal Risk Control
For a pair \((x, y)\) sample from \(F(y)\) and compute \(\mathcal{I}(y)\)
Q: How many ground-truth features \(x_j\) are not in their respective intervals \(\mathcal{I}(y)_j\)?
Risk Controlling Prediction Sets (RCPS) For a risk level \(\epsilon\) and failure probability \(\delta\)
\[\mathbb{P}\left[\mathbb{E}\left[\text{number of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
RCPS Procedure
Procedure Define
\[\mathcal{I}_{\lambda}(y)_j = [\text{lower} - \lambda, \text{upper} + \lambda]\]
and choose
\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~\text{risk is controlled},~\forall \lambda' \geq \lambda\}\]
\(\lambda\)
\(R(\lambda)\)
\(\epsilon\)
\(\lambda^*\)
risk is controlled
RCPS Procedure
Procedure Define
\[\mathcal{I}_{\lambda}(y)_j = [\text{lower} - \lambda, \text{upper} + \lambda]\]
and choose
\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~\text{risk is controlled},~\forall \lambda' \geq \lambda\}\]
\(\lambda\)
\(R(\lambda)\)
\(\epsilon\)
\(\lambda^*\)
risk is controlled
Limitations
- Choosing a scalar \(\lambda\) may be suboptimal
- No explicit minimization of interval length
\(K\)-RCPS
For \(\bm{\lambda} \in \mathbb{R}^d\) define
\[\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{lower} - \lambda_j, \text{upper} + \lambda_j]\]
and minimize the mean interval length with risk control
\[\hat{\bm{\lambda}} = \arg\min~\sum_{j \in [d]} \lambda_j~\quad\text{s.t. risk is controlled}\]
THE CONSTRAINT SET IS NOT CONVEX
\[\downarrow\]
NEED FOR A CONVEX RELAXATION
\(K\)-RCPS
For \(\bm{\lambda} \in \mathbb{R}^d\) define
\[\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{lower} - \lambda_j, \text{upper} + \lambda_j]\]
and minimize the mean interval length with risk control
\[\bm{\lambda} = \arg\min~\sum_{j \in [d]} \lambda_j~\quad\text{s.t. risk is controlled}\]
THE CONSTRAINT SET IS NOT CONVEX
\[\downarrow\]
NEED FOR A CONVEX RELAXATION


\(K\)-RCPS
For any user-defined membership \(M \in \mathbb{R}^{d \times K}\) :
1. Solve
\[\tilde{\bm{\lambda}}_K = \arg\min~\sum_{k \in [K]}n_k\lambda_k~\quad\text{s.t. convex upper bound} \leq \epsilon\]
2. Choose
\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\text{risk is controlled},~\forall M\tilde{\bm{\lambda}}_K + \beta'\mathbb{1},~\beta' \geq \beta\}\]
\[\downarrow\]
\[\hat{\bm{\lambda}}_K = M\tilde{\bm{\lambda}}_K + \hat{\beta}\mathbb{1}\]
\(K\)-RCPS
For any user-defined membership \(M \in \mathbb{R}^{d \times K}\) :
1. Solve
\[\tilde{\bm{\lambda}}_K = \arg\min~\sum_{k \in [K]}n_k\lambda_k~\quad\text{s.t. convex upper bound} \leq \epsilon\]
2. Choose
\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\text{risk is controlled},~\forall M\tilde{\bm{\lambda}}_K + \beta'\mathbb{1},~\beta' \geq \beta\}\]
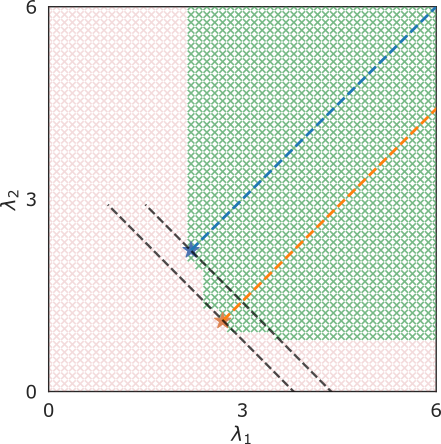
RCPS \((\lambda_1 = \lambda_2 = \lambda)\)
\(K\)-RCPS
gain
\(K\)-RCPS
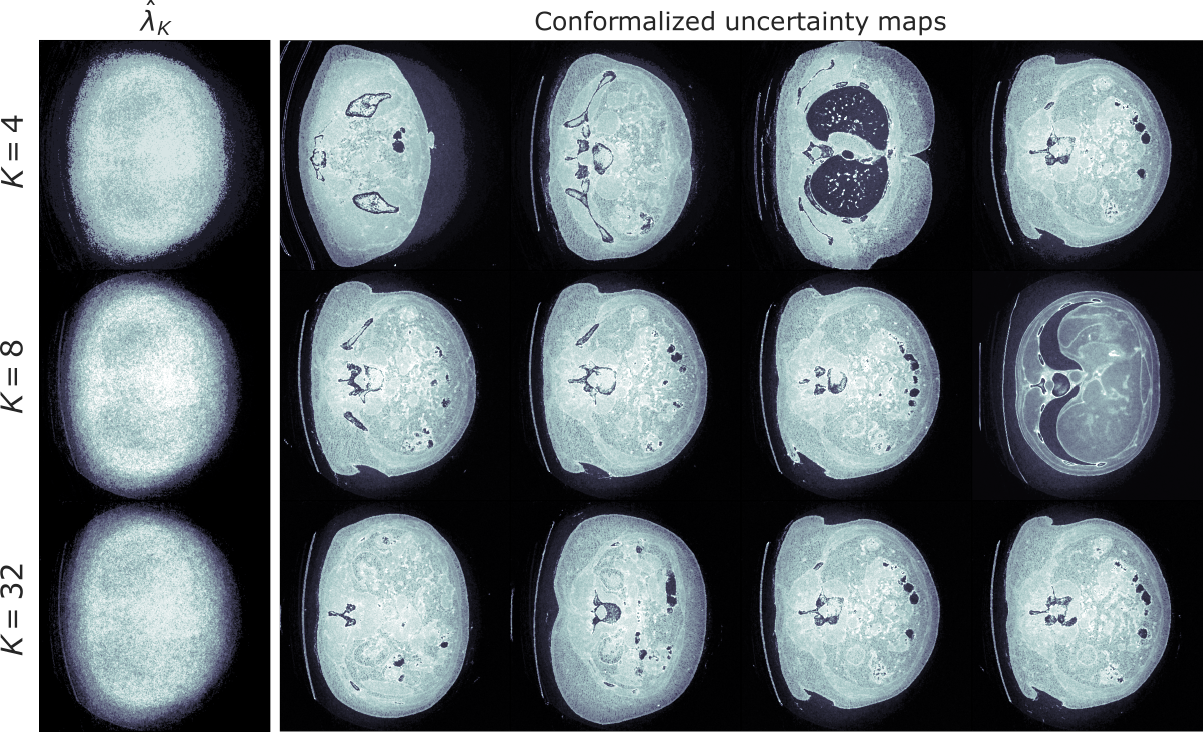
\(K\)-RCPS

Mean interval length
\[\text{RCPS}~\quad~\text{ }~0.1614 \pm 0.0020\]
\[K\text{-RCPS}~\quad~0.1391 \pm 0.0025\]
Thank you for your attention!




Jacopo Teneggi
Matt Tivnan
Web Stayman
Jeremias Sulam
Preprint:
GitHub repo: