Explainable ML
A brief overview with practical examples
Responsible ML
discriminative model
\(\rightarrow\)
input
prediction
Real-world
performance
Reproducibility
Explainability
Fairness
Privacy
\(\rightarrow\)
Responsible ML
discriminative model
\(\rightarrow\)
input
prediction
Real-world
performance
Reproducibility
Explainability
Fairness
Privacy
\(\rightarrow\)
Explaining model predictions
\(=\)
"hemorrhage"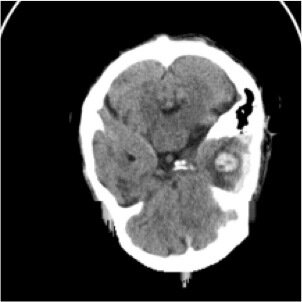
\(f\)
\((\)
\()\)
What are the important parts of
the image for this prediction?
\[\downarrow\]
A subset of features \(C\) with \(f(x_C) \approx f(x)\)
Local Explanation
Machine learning 🤝 linear models
Can we use the coefficients of a linear
model to explain its predictions?
Consider
\[f(x) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_dx_d\]
then
\[\beta_j = \frac{\partial f}{\partial x_j}\]
Machine learning 🤝 linear models
Definition (Conditional indepedence)
Let \(X, Y, Z\) be random variables
\[Y \perp \!\!\! \perp X \mid Z \iff p(y \mid x,z) = p(y \mid z)\]
For
\[y = f(x) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_dx_d\]
it holds that
\[\beta_j = 0 \iff Y \perp \!\!\! \perp X_j \mid X_{-j} \]
\[\downarrow\]
Linear models are inherently interpretable
Interpretable models vs explanations
Is there a tradeoff between inherently interpretable models and explanations?
Interpretable models
Explanation methods
- Gradients
LIME [Ribeiro, 16], CAM [Zhou, 16], GRAD-CAM [Selvaraju, 17]
- Information theory
RDE [Kolek, 22], V-IP [Chattopadhyay, 23]
- Game theory
SHAP [Lundberg, 17]
- Conditional independence
IRT [Burns, 20], XRT [T&B, 23]
- Semantic features
T-CAV [Kim, 18], PCBM [Yuksekgonul, 22]
🧐 What even is importance?
LIME [Ribeiro, 16]
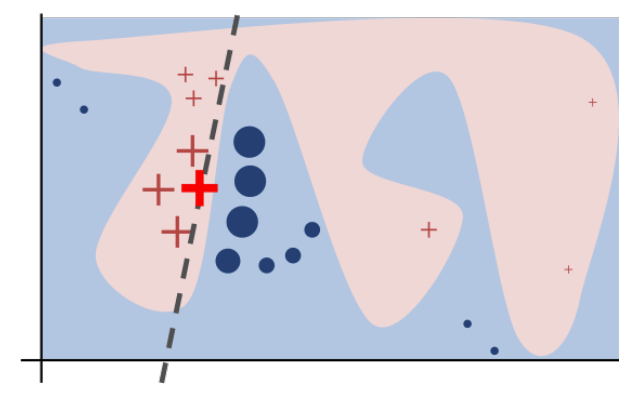
TLDR;
We know linear models, so let's train one!


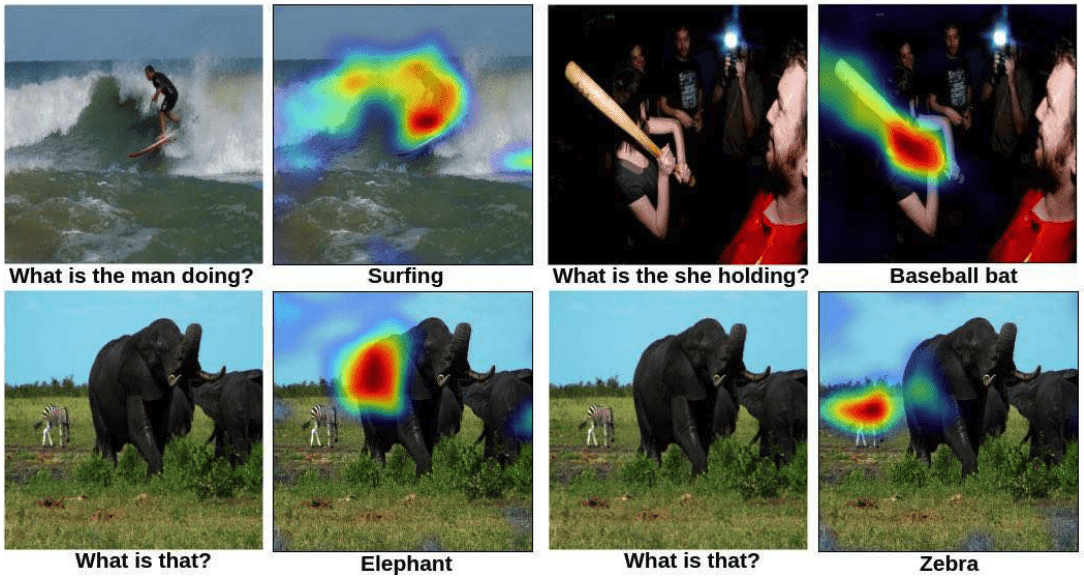
GRAD-CAM [Selvaraju, 17]
TLDR;
But automatic differentiation! Do a (fancy) backward pass
🧐 So why are we still talking about this?
Concerns on the validity of these methods [Aldebayo, 18]
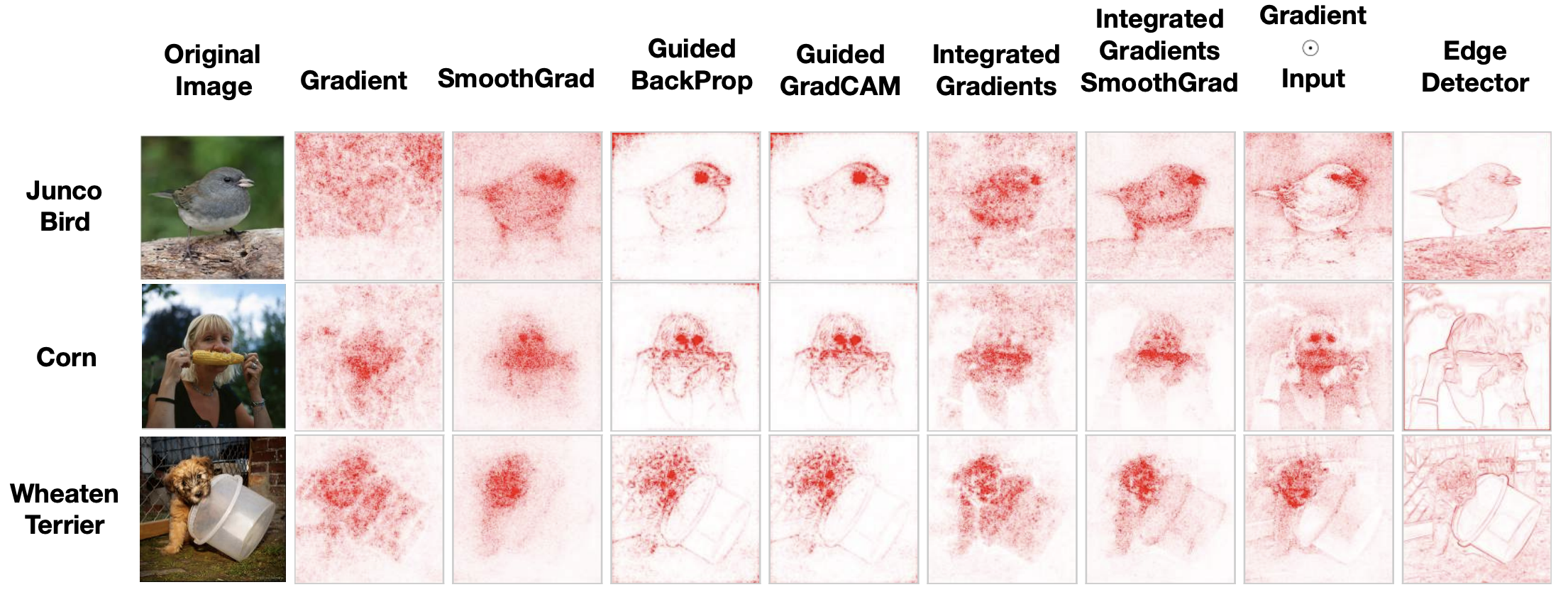
🧐 So why are we still talking about this?
Concerns on the robustness of these methods [Ghorbani, 19]
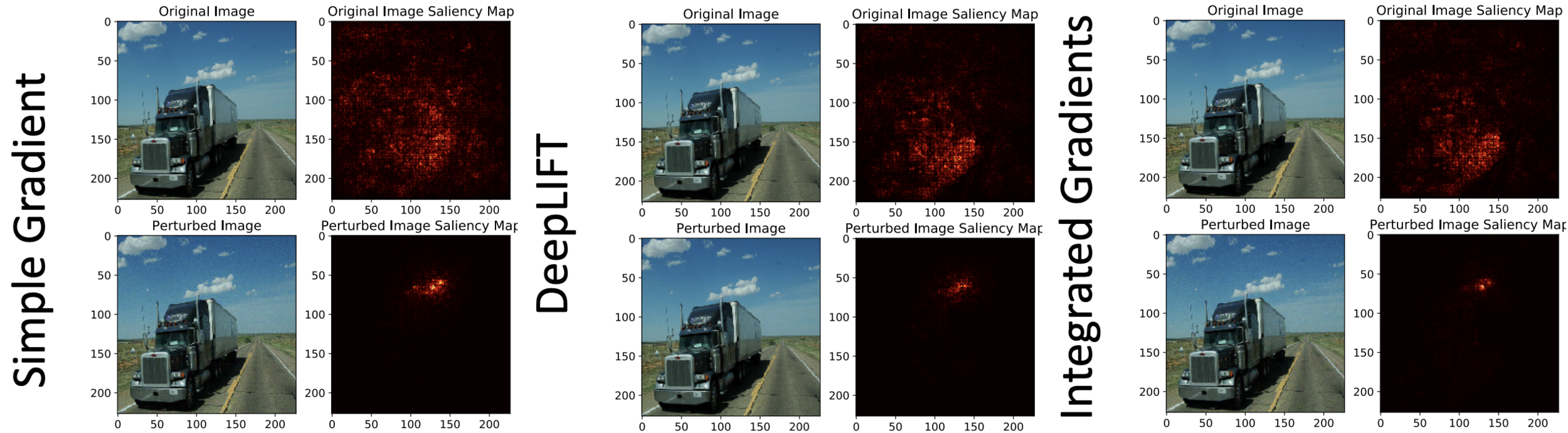
🧐 So why are we still talking about this?
Provably negative results on gradient explanations [Shah, 21]


SHAP [Lundbger, 17]
\[\uparrow\]
How much did player \(1\) contribute
to the outcome of the game?
Consider a game with \(d\) players
\[\dots\]
\(1\)
\(2\)
\(d\)
SHAP [Lundbger, 17]
How much did player \(1\) contribute
to the outcome of the game?
\[\downarrow\]
\[\phi_j = \sum_{C \subseteq [d] \setminus \{j\}} w_C \left[v(x_{C \cup \{j\}}) - v(x_C)\right]\]
Definition (Shapley value [Shapley, 53])
For a cooperative game with \(d\) players and characteristic function \(v:~2^{[d]} \to \mathbb{R}^+\), the Shapley value of player \(j\) is
\(\phi_j\) is the average marginalized contribution of
player \(j\) to all possible subsets of players
SHAP [Lundbger, 17]
\[\phi_j = \sum_{C \subseteq [d] \setminus \{j\}} w_C~\mathbb{E} \left[f(\widetilde{X}_{C \cup \{j\}}) - f(\widetilde{X}_C)\right]\]
For machine learning models
and
where
\[\widetilde{X}_C = [x_C, X_{-C}],\quad X_{-C} \sim \mathcal{D}_{X_C = x_C}\]
game \(v\)
\(\rightarrow\)
model \(f\)

\(x\)
\(x_C\)
\(\widetilde{X}_C\)
SHAP [Lundbger, 17]
\[\phi_j = \sum_{C \subseteq [d] \setminus \{j\}} w_C~\mathbb{E} \left[f(\widetilde{X}_{C \cup \{j\}}) - f(\widetilde{X}_C)\right]\]
and
where
\[\widetilde{X}_C = [x_C, X_{-C}],\quad X_{-C} \sim \mathcal{D}_{X_C = x_C}\]
game \(v\)
\(\rightarrow\)
model \(f\)
Sound theoretical
properties
1. Subsets are exponential
2. Need to sample
😍
😔
💡 Fast hierarchical games (h-Shap)
JT, Alexandre Luster, JS (2021) "Fast Hierarchical Games for Image Explanations", TPAMI
What do these problems
have in common?


sick cells
green lights
hemorrhage
Fast hierarchical games (h-Shap)
What do these problems
have in common?
\(\downarrow\)
If a part of the image is not important it cannot contain any important features
They all satisfy a Multiple Instance Learning assumption
\[f(x) = 1 \iff \exists C \subseteq [d]:~f(x_C) = 1\]
Fast hierarchical games (h-Shap)
If a part of the image is not important it cannot contain any important features

Fast hierarchical games (h-Shap)
If a part of the image is not important it cannot contain any important features

Fast hierarchical games (h-Shap)
If a part of the image is not important it cannot contain any important features

1. Runs in
\(O(k\log d)\)
2. Retrieves the correct Shapley values
Fast hierarchical games (h-Shap)
JT, Paul H Yi, JS (2023) "Examination-level Supervision for Deep Learning-based Intracranial Hemorrhage Detection on Head CT", Radiology: AI
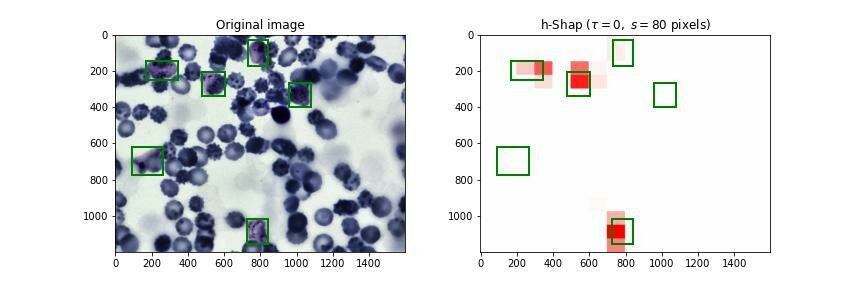
Fast hierarchical games (h-Shap)
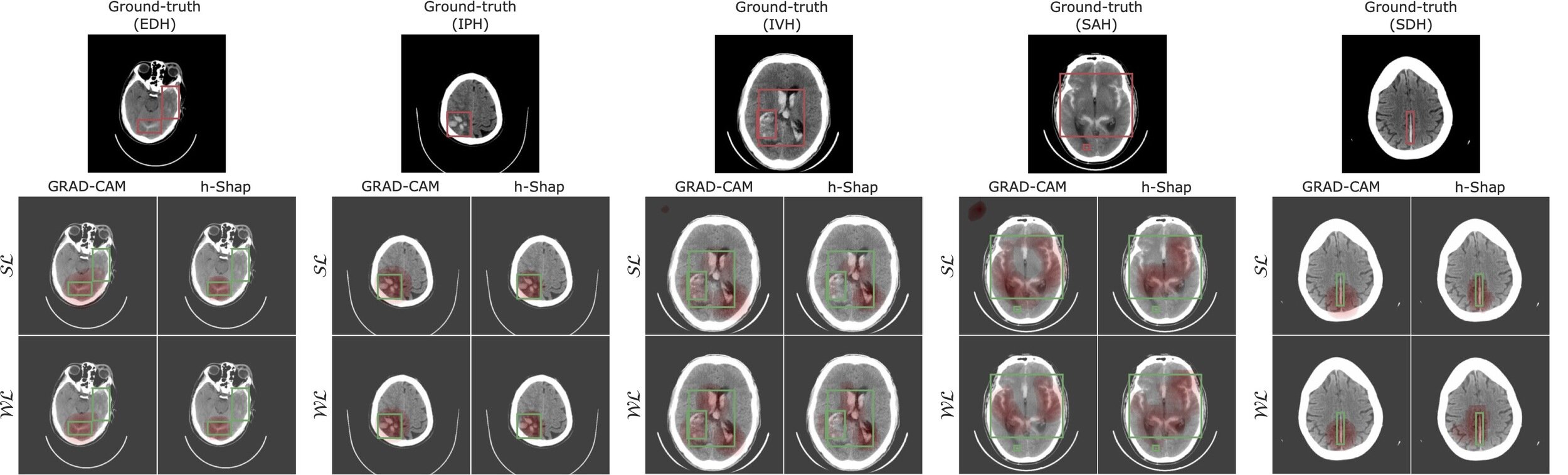
JT, Paul H Yi, JS (2023) "Examination-level Supervision for Deep Learning-based Intracranial Hemorrhage Detection on Head CT", Radiology: AI
Fast hierarchical games (h-Shap)
coding time!

🧐 What do large Shapley values mean?
Suppose
What do you report as
important, either or both?
\[\phi_1 = 0.25\]
\[\phi_2 = 0.35\]
and
\[\downarrow\]
Need to rigorously test for feature importance
💡 Conditional independence
Conditional independence null hypothesis
\[H_0:~Y \perp \!\!\! \perp X \mid Z\]
we can test for \(H_0\) with conditional randomization tests
reject \(H_0\) if \(\hat{p} \leq \alpha\)
\[\downarrow\]
\(p\)-values tell us the confidence we can
deem a feature important with
Definition (Type I error control)
If \(H_0\) is true, the probability of rejecting is below \(\alpha\)
\[\mathbb{P}_{H_0}[\hat{p} \leq \alpha] \leq \alpha\]
💡 Conditional independence
Conditional independence null hypothesis
\[H_0:~Y \perp \!\!\! \perp X \mid Z\]
we can test for \(H_0\) with conditional randomization tests
reject \(H_0\) if \(\hat{p} \leq \alpha\)
\[\downarrow\]
Definition (Type I error control)
If \(H_0\) is true, the probability of rejecting is below \(\alpha\)
\[\mathbb{P}_{H_0}[\hat{p} \leq \alpha] \leq \alpha\]
Can we test for a model's local
conditional independence?
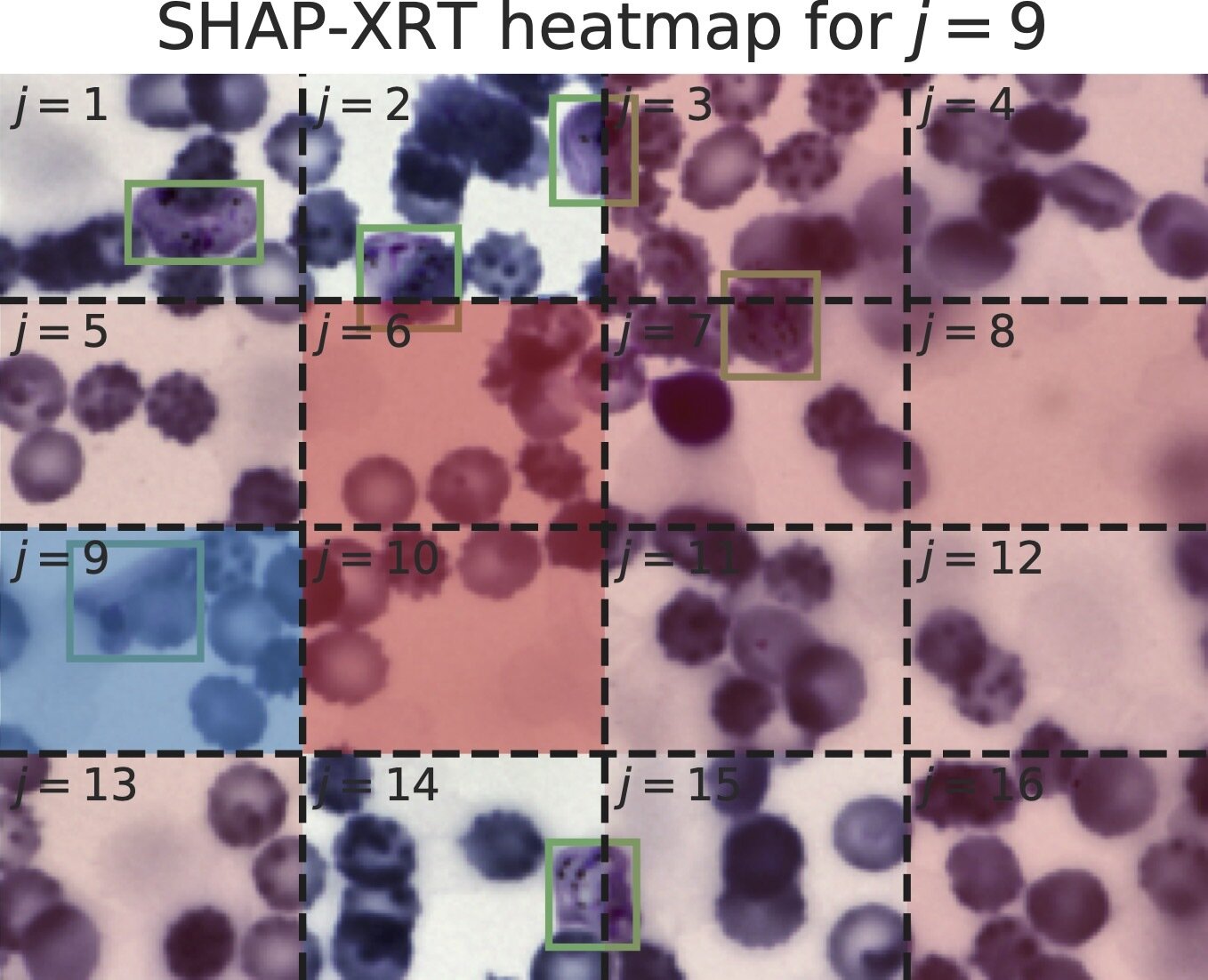
Explanation Randomization Test (XRT)
JT*, Beepul Bharti*, Yaniv Romano, JS (2023) "SHAP-XRT: The Shapley Value Meets Conditional Independence Testing", TMLR
model
feature
subset
\(f\)
\(j \in [d]\)
\(C \subseteq [d] \setminus \{j\}\)
\(x\)
input
\[H^{\text{XRT}}_{0,j,C}:~f(\widetilde{X}_{C \cup \{j\}}) \overset{d}{=} f(\widetilde{X}_C)\]
\[\downarrow\]
Reject the null hypothesis if the observed value of \(x_j\) changes the distribution of the response of the model
Explanation Randomization Test (XRT)
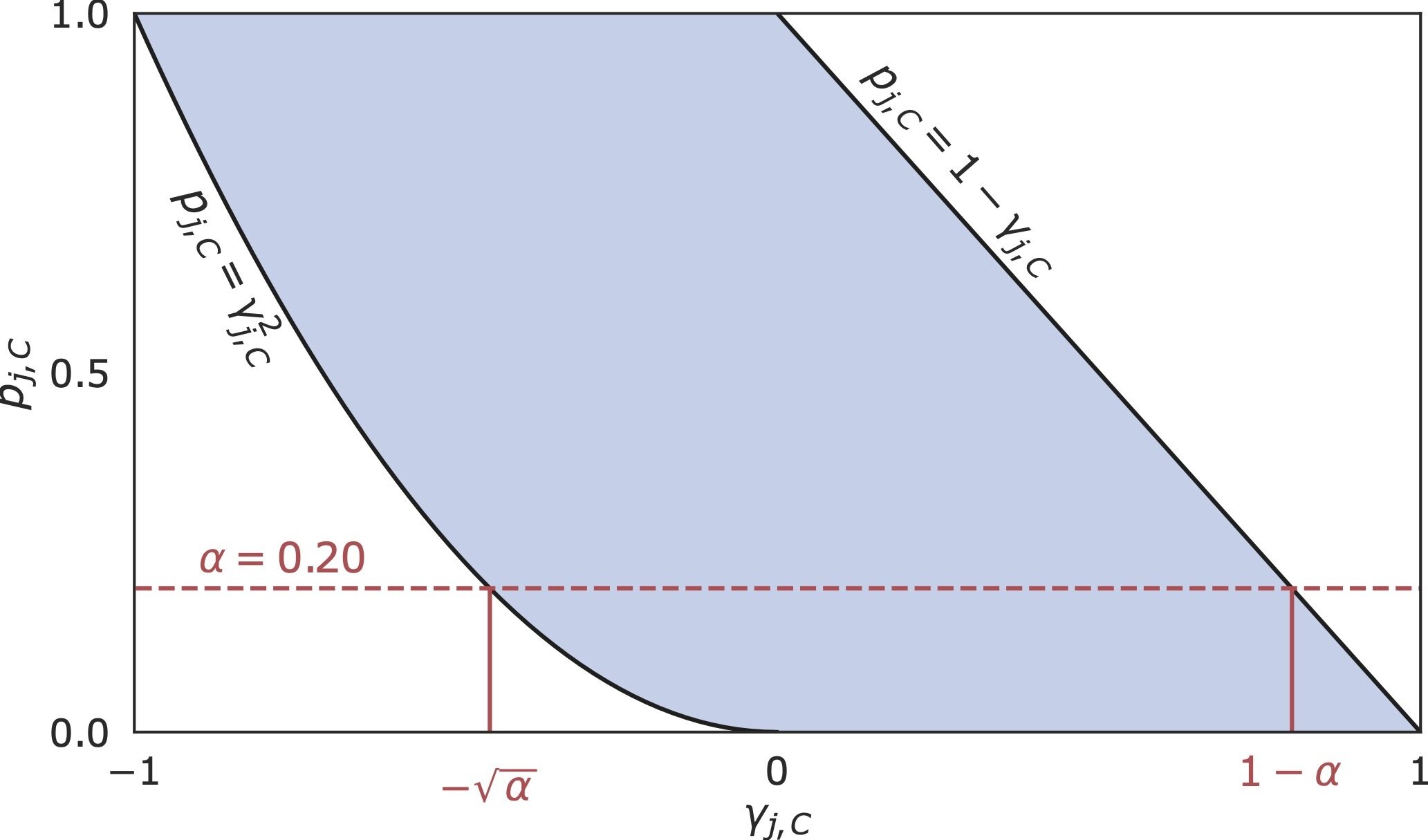
Recall
\[\phi_j = \sum_{C \subseteq [d] \setminus \{j\}} w_C~\mathbb{E} \left[f(\widetilde{X}_{C \cup \{j\}}) - f(\widetilde{X}_C)\right]\]
turns out that
\[\gamma_{j,C}^2 \leq p^{\text{XRT}}_{j,C} \leq 1 - \gamma_{j,C}\]
Explanation Randomization Test (XRT)
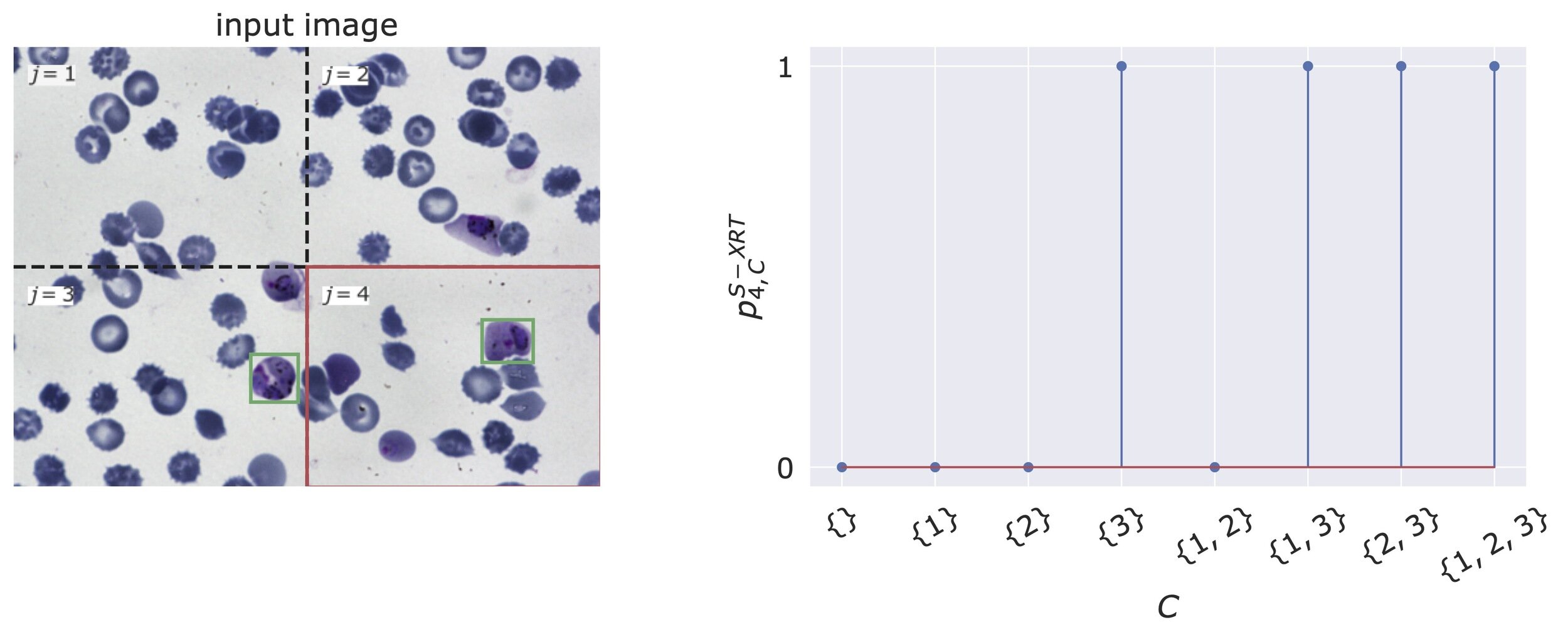
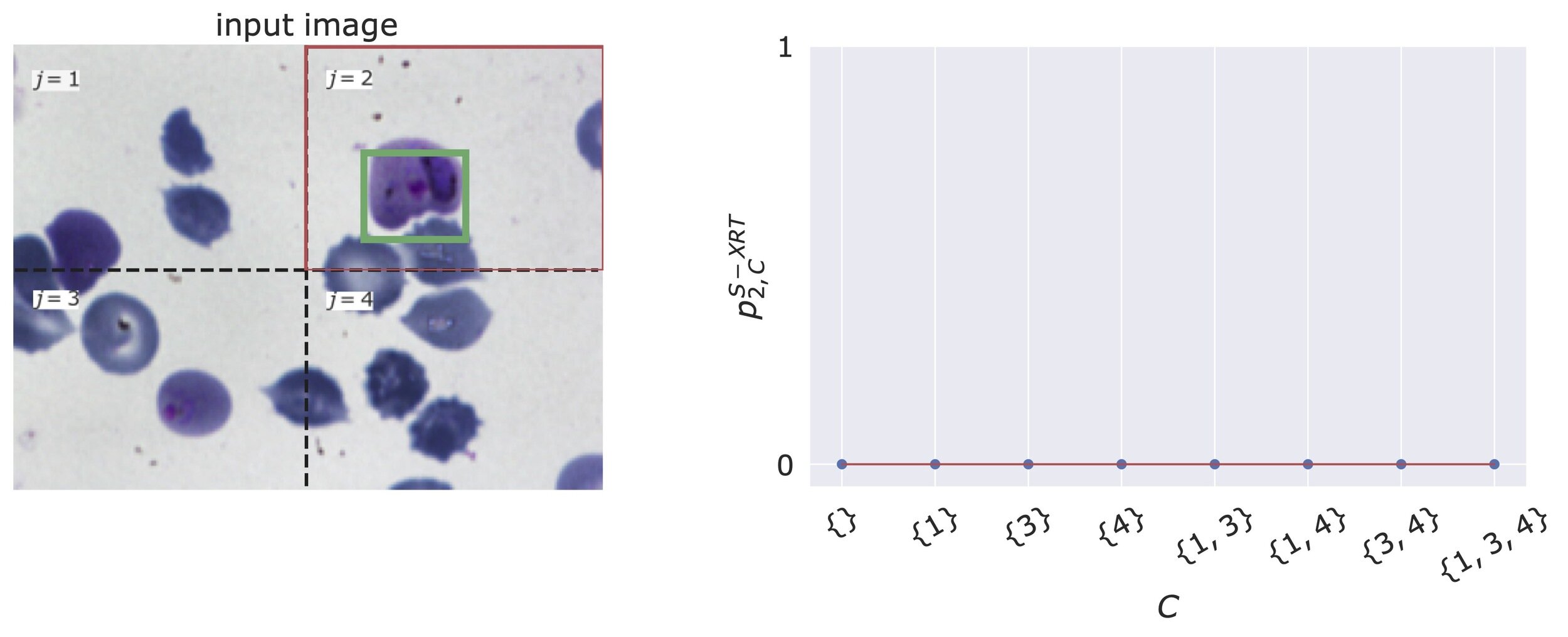
Explanation Randomization Test (XRT)
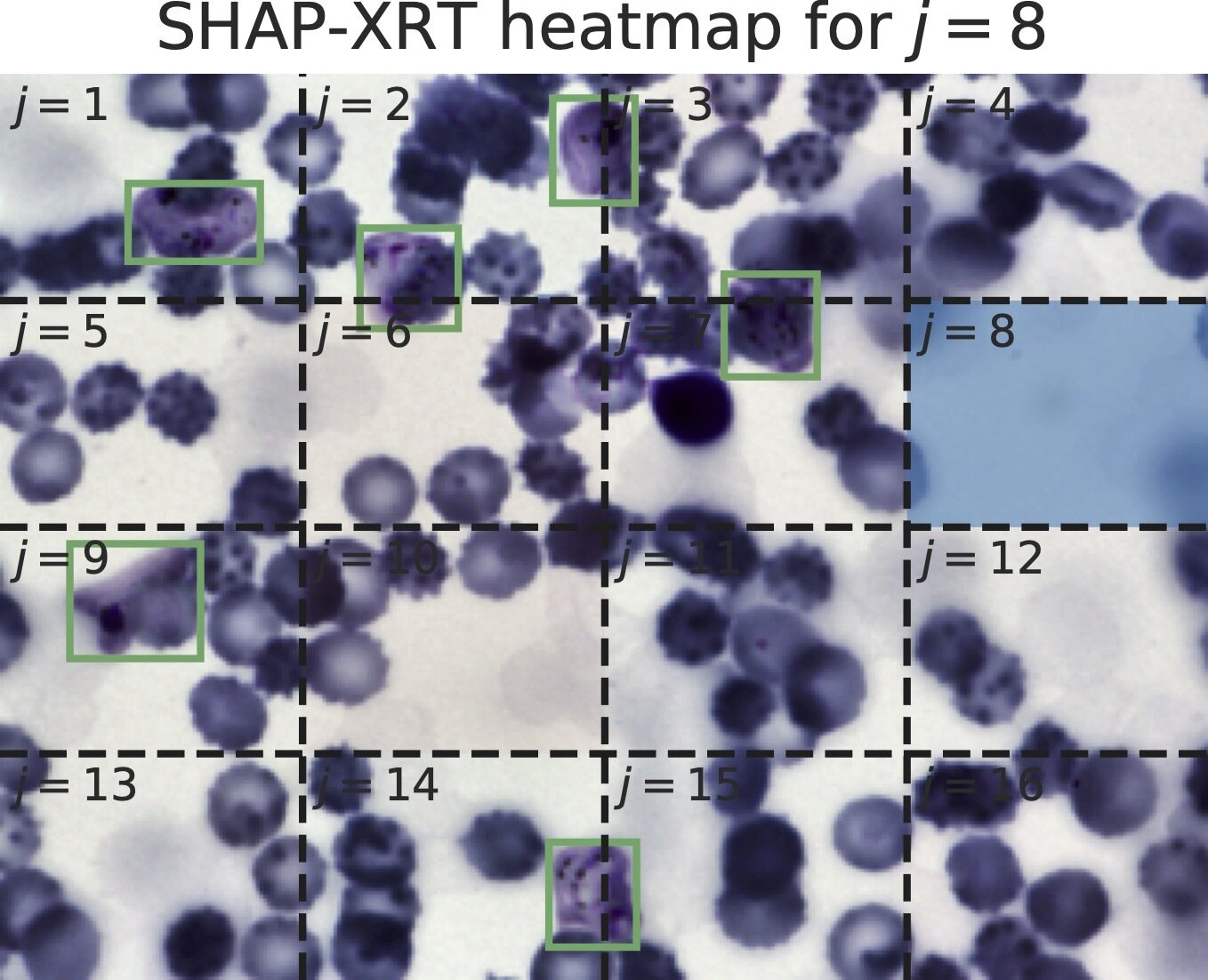
Thank you!




Beepul Bharti
Alexandre Luster
Yaniv Romano
Jeremias Sulam

XRT

h-Shap