微積分簡介

建國中學張均豪

被消失的2021四校寒訓

一些注意事項

本次課程內容為高中教材範圍，因為超過的講師也不會
內含大量唬爛，請斟酌參考
如果已經都會的可以上台把講師電爆沒有關係
大家一起愉快的聽課吧！

先備知識

函數的概念

函數?

相信大家都知道是什麼

以數學來說，是個表示「對應關係」的方式

\(f:\)

定義域

對應域

值域

常見函數的種類

多項式函數

\(f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)

一次函數：直線

\(f(x)=ax+b\)

二次函數：拋物線

\(f(x)=ax^2+bx+c\)

常見函數的種類

三角函數

\(\theta\)

\(c\)

\(a\)

\(b\)

\(sin(\theta)=\frac{b}{c}\)

\(cos(\theta)=\frac{a}{c}\)

\(tan(\theta)=\frac{b}{a}\)

\((cos\theta ,sin\theta)\)

(1,0)

(0,1)

\(\theta\)

常見函數的種類

指對數函數

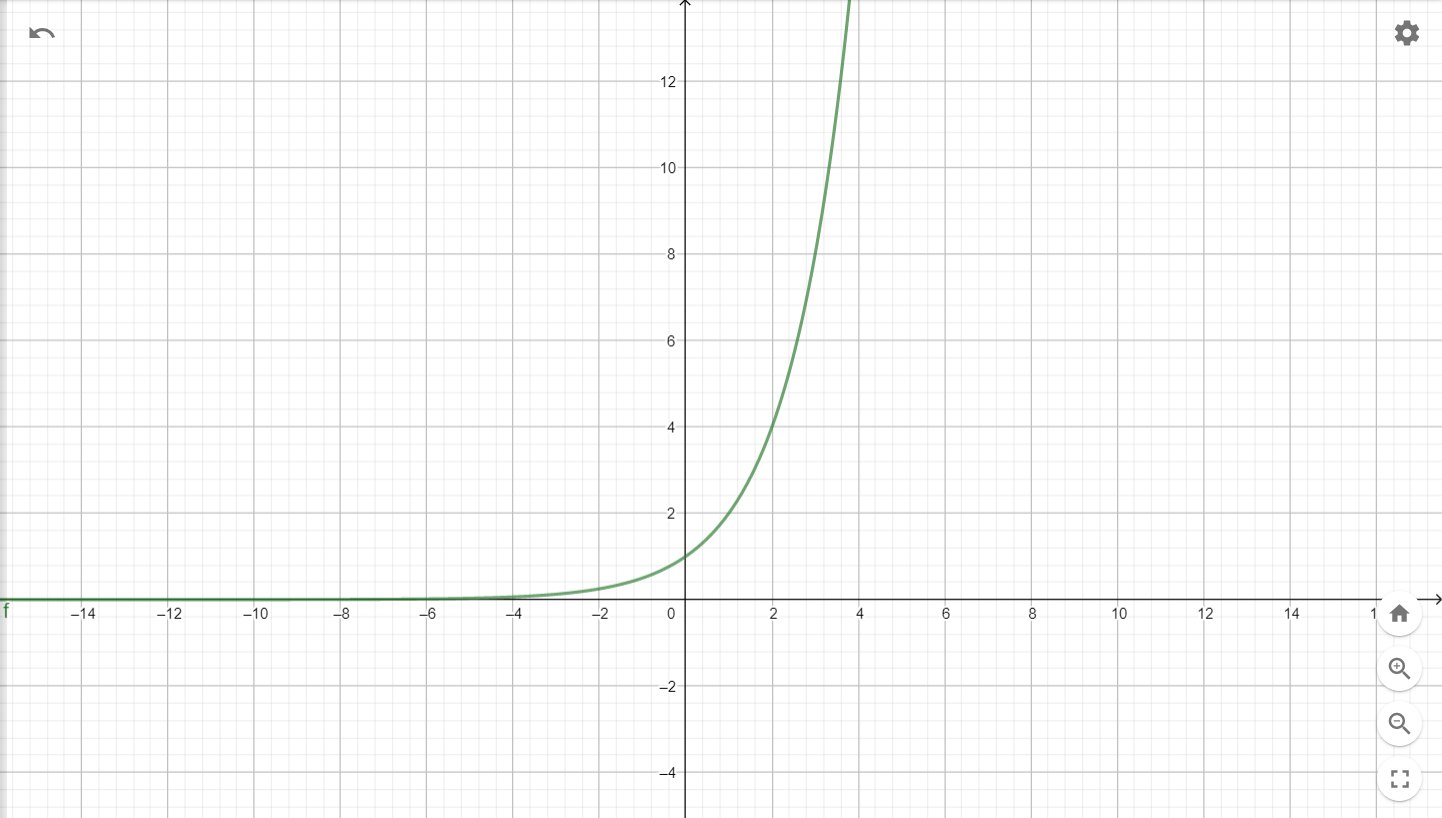
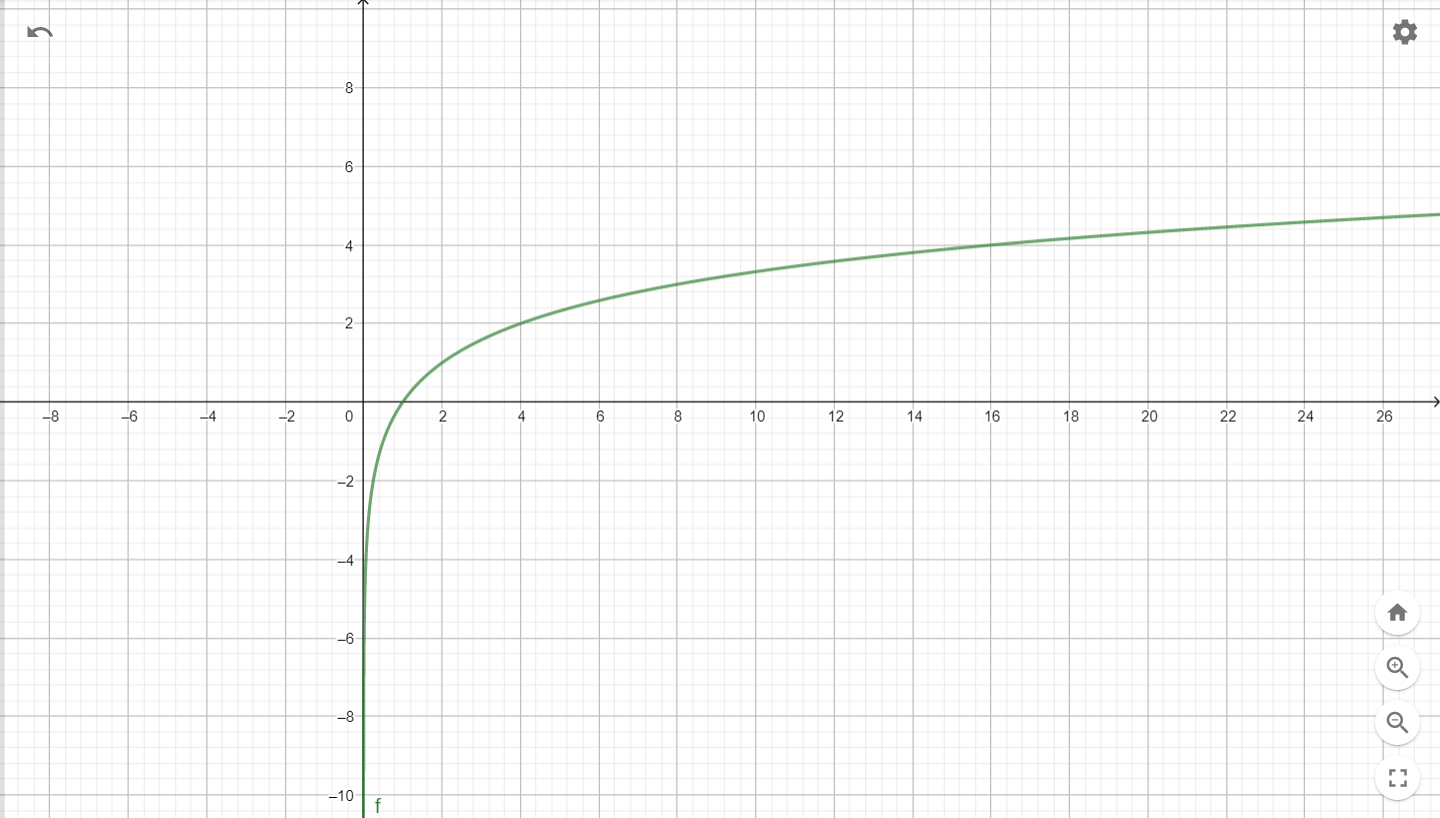
\(f(x)=2^x\)

\(f(x)=log_2x\)

常見函數的種類

其他長得奇形怪狀的東西

\(f(x)=\frac{1}{1+e^{-x}}\)

\(f(x)=\lfloor x\rfloor\)

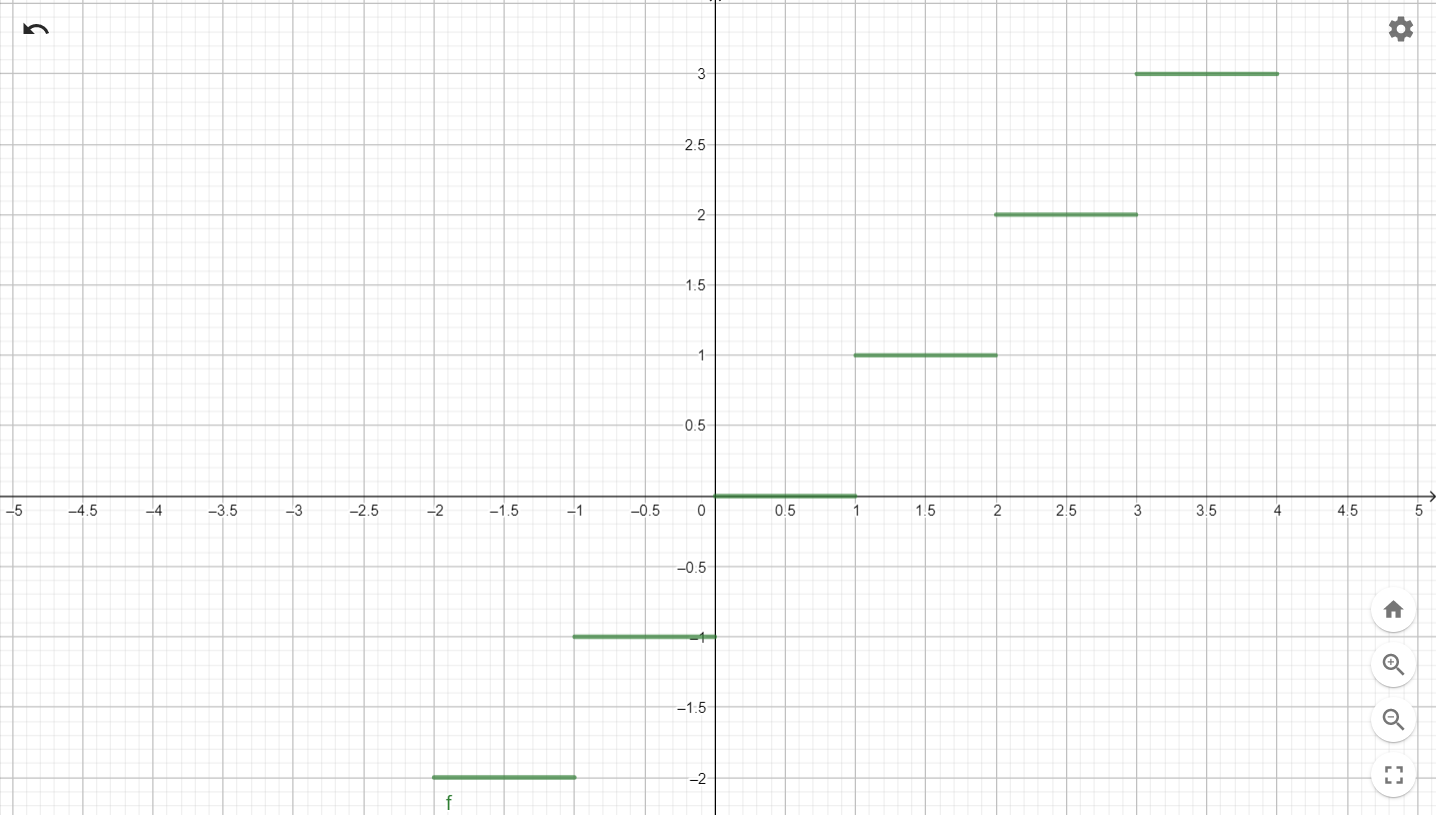
極限

函數的極限

有一個函數\(f\)，當\(x\)非常靠近某個\(a\)時，此時\(f(x)\)會非常接近某個值\(L\)，則稱\(L\)為\(f\)在\(a\)處的極限值，記為\(\lim\limits_{x\to a} f(x)=L\)

這個是高中教材的定義方式，不過有點不嚴謹(?

好啦真正的定義長這樣

若\(\lim\limits_{x\to a} f(x)=L\)

則對於任何\(\epsilon>0\)，都存在\(\delta>0\)，使得當\(0<|x-a|<\delta\)總有\(0<|f(x)-L|<\epsilon\)

看不懂沒關係，因為講師也沒看懂

總之先這樣

極限要怎麼找

打表

畫圖觀察

拿定義去做(我不會)

左極限與右極限

由左邊逼近的叫做左極限，記做\(\lim\limits_{x\to a^-} f(x)\)

由右邊逼近的叫做右極限，記做\(\lim\limits_{x\to a^+} f(x)\)

當\(\lim\limits_{x\to a}f(x)\)存在，\(\lim\limits_{x\to a}f(x)\) =\(\lim\limits_{x\to a^-}f(x)\) =\(\lim\limits_{x\to a^+}f(x)\)

極限值存在

極限值不存在

極限的四則運算

\(\lim\limits_{x\to a} (f(x)+g(x))=\lim\limits_{x\to a} f(x)+\lim\limits_{x\to a} g(x)\)

\(\lim\limits_{x\to a} (f(x)-g(x))=\lim\limits_{x\to a} f(x)-\lim\limits_{x\to a} g(x)\)

\(\lim\limits_{x\to a} (f(x)\cdot g(x))=\lim\limits_{x\to a} f(x)\cdot \lim\limits_{x\to a} g(x)\)

若 \(\lim\limits_{x\to a} g(x)\neq 0\)，則 \(\lim\limits_{x\to a} (\frac{f(x)}{g(x)})=\frac{\lim\limits_{x\to a} f(x)}{\lim\limits_{x\to a} g(x)}\)

反正就是他可以加減乘除(如果存在的話)

極限的運算

對大部分常見的函數，\(\lim\limits_{x\to a} f(x)=f(a)\)

不過有時候\(f(a)\)不存在

假如遇到\(\frac{定值}{\infty}\)，則結果為\(0\)

假如遇到\(\frac{\infty}{定值}\)或\(\frac{定值}{0}\)，則發散(極限不存在)

不過假如遇到\(\frac{0}{0},\frac{\infty}{\infty},\infty-\infty,0\cdot \infty\)等狀況

就需要另外處理

例：計算\(\lim\limits_{x\to 2}(\frac{x^2-5x+6}{x-2})\)

夾擠定理

若\(g(x)\leq f(x)\leq h(x)\)

且\(\lim\limits_{x\to a} g(x)=\lim\limits_{x\to a} h(x)=L\)

則\(\lim\limits_{x\to a} f(x)=L\)

大家可以直觀的感受一下，因為講師不會證明

這東西有時候會用得上

講點有趣的東西

自然對數的底數 \(e\)

\(e=\lim\limits_{x\to \infty} (1+\frac{1}{x})^x\)

會收斂至一個數字，約為2.71828

廢話講完了

接下來要進入到主要的部份

大家可以先休息一下

微分

微分是什麼

講微分之前要先講斜率

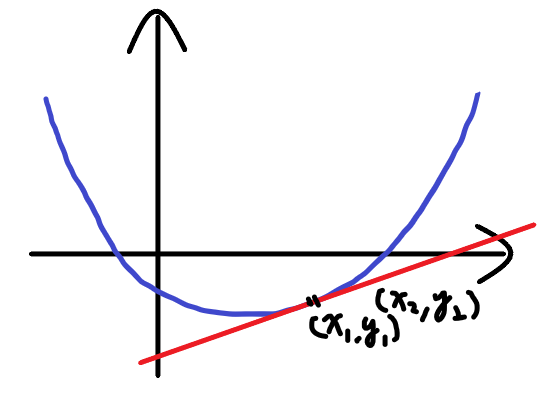
若一條直線通過\((x_1,y_1),(x_2,y_2)\)

則其斜率為\(\frac{y_2-y_1}{x_2-x_1}\)

(x2,y2)

(x1,y1)

微分是什麼

如果\((x_1,y_1),(x_2,y_2)\)是函數上的兩點

則這兩點連成的直線稱為一條割線

而這條直線的斜率就稱作割線斜率

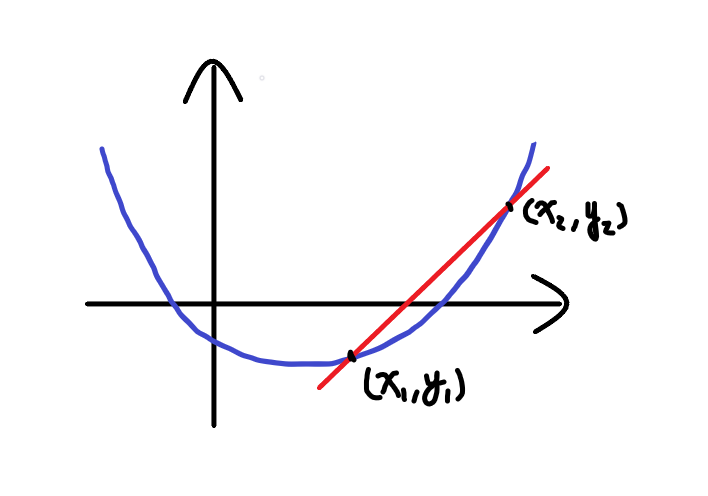
微分是什麼

現在我們將\((x_2,y_2)\)朝\((x_1,y_1)\)逼近

當他們之間的距離趨近於零時

此時兩點連成的直線稱為切線

其斜率就稱為切線斜率

微分是什麼

對於某個函數\(f(x)\)

我們可以對某個\(x=a\)求切線斜率

也就是\(\lim\limits_{h\to 0} \frac{f(a+h)-f(a)}{h}\)

稱作導數，也記做\(f'(a)\)

若此極限值存在，稱此函數\(f(x)\)「在\(a\)處可微分」

微分是什麼

若一個函數\(f(x)\)的每個\(x=a\)的導數皆存在

則此對應關係會形成一個新的函數

稱作\(f(x)\)的導函數，記作\(f'(x)\)，也記作\(\frac{df(x)}{dx}\)

即\(f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h}\)

而此計算過程稱作把函數\(f(x)\)微分

微分的性質

加減：\([f(x)\pm g(x)]'=f'(x)\pm g'(x)\)

係數積：\([af(x)]'=af'(x)\)

乘除？

微分的性質

[f(x)\cdot g(x)]'=\lim\limits_{h\to 0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}\\ =\lim\limits_{h\to 0}\frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h}\\ =\lim\limits_{h\to 0}\frac{f(x+h)g(x+h)-f(x)g(x+h)}{h}+\lim\limits_{h\to 0}\frac{f(x)g(x+h)-f(x)g(x)}{h}\\ =\lim\limits_{h\to 0}g(x+h)\cdot \frac{f(x+h)-f(x)}{h}+\lim\limits_{h\to 0}f(x)\cdot \frac{g(x+h)-g(x)}{h}\\ =f'(x)g(x)+f(x)g'(x)

微分的性質

[\frac{f(x)}{g(x)}]'=\lim\limits_{h\to 0}\frac{\frac{f(x+h)}{g(x+h)}-\frac{f(x)}{g(x)}}{h}\\ =\lim\limits_{h\to 0}\frac{f(x+h)g(x)-f(x)g(x+h)}{h\cdot g(x+h)g(x)}\\ =\lim\limits_{h\to 0}\frac{f(x+h)g(x)-f(x)g(x)+f(x)g(x)-f(x)g(x+h)}{h\cdot g(x+h)g(x)}\\ =\lim\limits_{h\to 0}\frac{g(x)\cdot \frac{f(x+h)-f(x)}{h}-f(x)\cdot \frac{g(x+h)-g(x)}{h}}{g(x+h)g(x)}\\ =\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}

除法的道理差不多

微分的性質

[f(g(x))]'=\lim\limits_{h\to 0}\frac{f(g(x+h))-f(g(x))}{h}\\ =\lim\limits_{h\to 0}\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}\\ =f'(g(x))\cdot g'(x)

連鎖律

有了這些東西就可以算微分了

常見函數的微分

常數函數\(f(x)=c\)

\(f'(x)=0\)

夠簡單吧XD

常見函數的微分

多項式函數

先處理最簡單的單項式

令\(f(x)=x^n\)，則\(f'(x)=?\)

常見函數的微分

f'(x)=\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h}\\ =\lim\limits_{h\to 0}\frac{(x+h)^n-x^n}{h}\\ =\lim\limits_{h\to 0}\frac{\sum_{k=0}^{n}C_k^nx^kh^{n-k}-x^n}{h}\\ =\lim\limits_{h\to 0}\frac{x^n+nx^{n-1}h+...-x^n}{h}\\ =nx^{n-1}

展開(二項式定理)

\(h\)的次數2以上的項都是0

常見函數的微分

f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_2x^2+a_1x+a_0\\ f'(x)=na_nx^{n-1}+(n-1)a_{n-1}x^{n-2}+...+2a_2x+a_1

然後再搭配前面的加法和係數積，就可以得到多項式的微分公式

微分的應用

求函數極值、凹向性

算極限(羅畢達法則)

物理：運動學

梯度下降(多變數微分)

etc.

積分

積分是什麼

講積分之前先要講面積

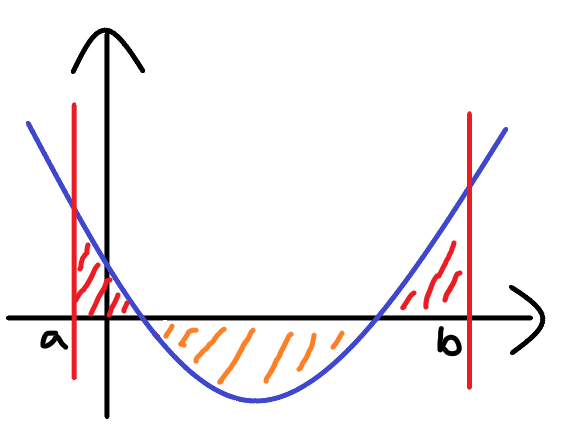
有一函數\(f(x)\)，定義此函數從\(a\)到\(b\)的定積分為函數圖形在區間\([a,b]\)內，"\(x\)軸上方面積-\(x\)軸下方面積"

以此圖形來說，就是紅色面積-橘色面積

定積分怎麼算

上和與下和

舉個簡單的例子

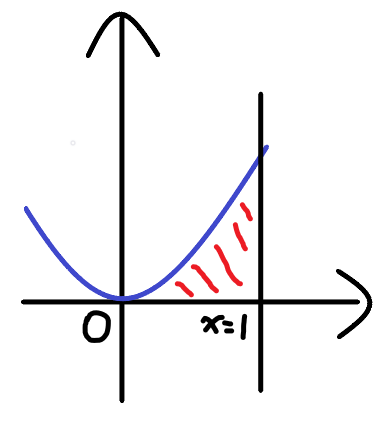
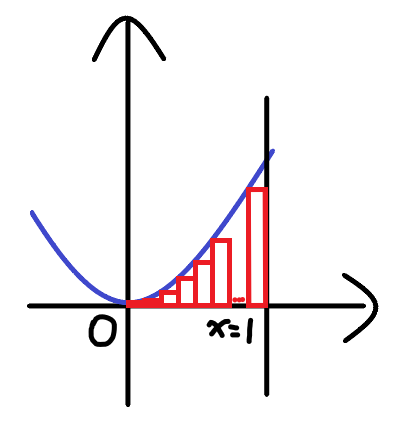
計算\(f(x)=x^2\)在\([0,1]\)之間的曲線下面積？

定積分怎麼算

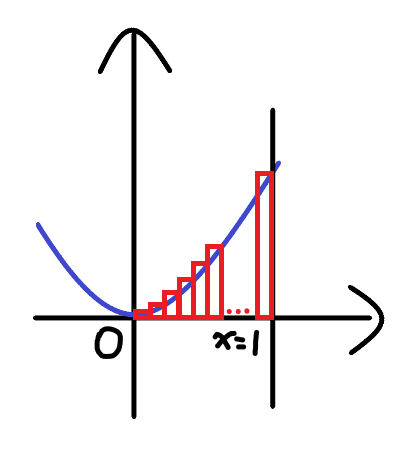
切成很多個小長方形相加，稱為黎曼和

將最小值當作高，稱為下和

反之將最大值當作高，稱為上和

則真正的面積會介於下和與上和之間

定積分怎麼算

將下和與上和以數學式表示

假設切成\(n\)塊，取\(n\)個等間隔的分割點

所以第\(k\)個分割點為\(a+k\cdot \Delta x\)，其中\(\Delta x=\frac{b-a}{n}\)

下和\(L_n=\sum_{k=1}^{n}f(c_k)\Delta x\)

上和\(U_n=\sum_{k=1}^{n}f(d_k)\Delta x\)

其中\(c_k\)與\(d_k\)分別表示第\(k\)小段\([x_{k-1},x_k]\)中，最小值與最大值發生的\(x\)座標

定積分怎麼算

回到剛剛的例子

區間為\([0,1]\)，所以\(\Delta x=\frac{1}{n}\)

因為該圖形遞增，所以最小值都會發生在左界，而最大值發生在右界，因此

下和\(L_n=\sum_{k=1}^{n}f(c_k)\Delta x=\frac{1}{n}\sum_{k=1}^{n}f(\frac{k-1}{n})\)

上和\(U_n=\sum_{k=1}^{n}f(d_k)\Delta x=\frac{1}{n}\sum_{k=1}^{n}f(\frac{k}{n})\)

定積分怎麼算

將\(n\)趨近於無限大

也就是算\(\lim\limits_{n\to \infty}L_n\)與\(\lim\limits_{n\to \infty}U_n\)

此時他們如果收斂至同一個值

且真實面積介於他們之間

根據夾擠定理，就可以得到答案

定積分怎麼算

來真正算一遍

L_n=\frac{1}{n}\sum_{k=1}^{n}f(\frac{k-1}{n})\\ =\frac{1}{n^3}\cdot [0^2+1^2+...+(n-1)^2]\\ =\frac{1}{n^3}\cdot \frac{(n-1)n(2n-1)}{6}=\frac{2n^2-3n+1}{6n^2}\\ U_n=\frac{1}{n}\sum_{k=1}^{n}f(\frac{k}{n})\\ =\frac{1}{n^3}\cdot [1^2+2^2...+n^2]\\ =\frac{1}{n^3}\cdot \frac{n(n+1)(2n+1)}{6}=\frac{2n^2+3n+1}{6n^2}

這裡用了一個大家可能不知道的結論，有興趣的可以自己證證看

定積分怎麼算

來真正算一遍

\lim\limits_{n\to \infty}L_n=\lim\limits_{n\to \infty}\frac{2n^2-3n+1}{6n^2}=\frac{1}{3}\\ \lim\limits_{n\to \infty}U_n=\lim\limits_{n\to \infty}\frac{2n^2+3n+1}{6n^2}=\frac{1}{3}

所以答案\(=\frac{1}{3}\)

定積分

我們將一個函數\(f(x)\)在區間\([a,b]\)內的曲線下面積

稱為\(f(x)\)在\([a,b]\)的定積分

表示為\(\int_a^bf(x)dx\)

如：\(\int_0^1x^2dx=\frac{1}{3}\)

定積分的運算性質

等等補

不定積分與反導函數

如果有一個函數\(F(x)\)，他的導函數(也就是微分後的結果)為\(f(x)\)

則稱\(F(x)\)為\(f(x)\)的反導函數，亦稱為不定積分

可以得知，\(F(x)+C\)也會是\(f(x)\)的一個反導函數

(\(C\)代表常數)

不定積分的運算性質

等等補

於是，神奇的事情發生了

微積分第一基本定理

有一函數\(f(x)\)，定義\(F(x)\)為\(\int_a^xf(x)dx\)

則\(F'(x)=f(x)\)

於是，神奇的事情發生了

微積分第二基本定理

令\(F(x)\)為\(f(x)\)的一個反導函數，則

\(\int_a^bf(x)dx=F(b)-F(a)=F(x)|_a^b\)

有關這兩個定理的證明附在下面

https://zh.wikipedia.org/wiki/%E5%BE%AE%E7%A7%AF%E5%88%86%E5%9F%BA%E6%9C%AC%E5%AE%9A%E7%90%86

他可以幹嘛

這兩個定理告訴我們，求定積分=找反導函數

所以我們算定積分的時候，就可以不用每次都作黎曼和，直接找反導函數就好了！

回到剛剛的例題：

\(\int_0^1x^2dx=\frac{1}{3}x^3|_0^1=\frac{1}{3}\)

秒殺ww

不過事情似乎沒有那麼簡單

積分不像微分，沒有辦法乘、除，也沒有連鎖律

因此，數學家們開發出了非常多的計算技巧，以應付複雜的積分形式(ex:變數代換、分部積分...)

不過因為講師也不會所以就不多講

積分的應用

算曲線下面積

算立體圖形的體積

物理上的應用(很多)

The end

廢話時間

因為今年寒訓消失的關係

等我回來之後會講剩下的原本寒訓預定教的課

敬請期待~