Preparing for the Qiskit developer certification exam

https://www.ibm.com/certify/exam?id=C1000-112

These slides at: https://slides.com/javafxpert/prep-qiskit-dev-cert-exam

Please note

IBM’s statements regarding its plans, directions, and intent are subject to change or withdrawal without notice and at IBM’s sole discretion.


Information regarding potential future products is intended to outline our general product direction and it should not be relied on in making a purchasing decision.


The information mentioned regarding potential future products is not a commitment, promise, or legal obligation to deliver any material, code or functionality. Information about potential future products may not be incorporated into any contract.


The development, release, and timing of any future features or functionality described for our products remains at our sole discretion.


Performance is based on measurements and projections using standard IBM benchmarks in a controlled environment. The actual throughput or performance that any user will experience will vary depending upon many factors, including considerations such as the amount of multiprogramming in the user’s job stream, the I/O configuration, the storage configuration, and the workload processed. Therefore, no assurance can be given that an individual user will achieve results similar to those stated here.

 

© 2021 IBM Corporation

About presenter Paul Kassebaum, Ph.D.

Partnership Developer

IBM Quantum

paul.kassebaum@ibm.com

linkedin.com/in/paulkassebaum

About presenter James Weaver

IBM Quantum Developer Advocate

Java Champion

Developer / Author / Speaker

james.weaver@ibm.com

@JavaFXpert

Getting the workforce quantum-ready

https://www.ibm.com/blogs/research/2021/03/quantum-developer-certification/

With our quantum developer certification, companies and research institutions will find a clear path to get their workforce quantum-ready. The certificate will help those hiring for classical programming and non-programming roles recognize holders of this certification as forward-thinking individuals willing to skill up for the future of the computing workforce.

The IBM Quantum Developer Certification is a 60-question certification exam offered on the Pearson VUE platform. Those who pass the exam will have demonstrated experience using Qiskit to create and execute quantum computing programs on IBM quantum computers and simulators, and the ability to perform these tasks with little to no assistance from product documentation, support, or peers.

What to expect from the exam

https://medium.com/qiskit/learn-more-about-the-ibm-quantum-developer-certification-and-how-to-take-it-for-free-d237f9765dc5

We figure that plenty of Qiskitters will be looking to take the certification exam, so we’ve put together a sneak peak of the exam’s structure, what’s going to be on it, and how to study for it. The test is going to be a 60-question exam, in English, offered on the Pearson VUE platform. The goal of the test is to certify that those who pass it can define, execute, and visualize quantum circuits using Qiskit, implement single and multi-qubit gates and understand their effects on quantum circuits, and leverage the fundamental features of Qiskit in order to write quantum programs.

Objectives of the exam

https://www.ibm.com/certify/exam?id=C1000-112

Preparing for the exam

https://www.ibm.com/certify/exam?id=C1000-112

Leveraging the IBM Quantum Composer

https://quantum-computing.ibm.com/composer

Create your first circuit walkthrough

Also, explore the Quantum Composer user guide, and Operations glossary

@JavaFXpert

Gain an intuitive understanding of the Bloch sphere and gate rotations with this web-based application known as Grok the Bloch Sphere

Bloch sphere playground

Studying the Qiskit Textbook

https://qiskit.org/textbook

Explore all of sections 1 and 2

Continue studying the Qiskit Textbook

https://qiskit.org/textbook

Explore the Defining Quantum Circuits section

Leveraging the IBM Quantum Lab

https://quantum-computing.ibm.com/lab/files/qiskit-tutorials/qiskit/start_here.ipynb

Explore the Qiskit Tutorials - Circuits Jupyter notebooks

The links shown above are in the start_here Jupyter notebook

Continue leveraging the IBM Quantum Lab

https://quantum-computing.ibm.com/lab/files/qiskit-tutorials/qiskit/start_here.ipynb

Explore the Qiskit Tutorials - Advanced circuit visualization Jupyter notebook

The Advanced circuit visualization link is in the start_here Jupyter notebook

More leveraging the IBM Quantum Lab

https://quantum-computing.ibm.com/lab/files/qiskit-tutorials/qiskit/start_here.ipynb

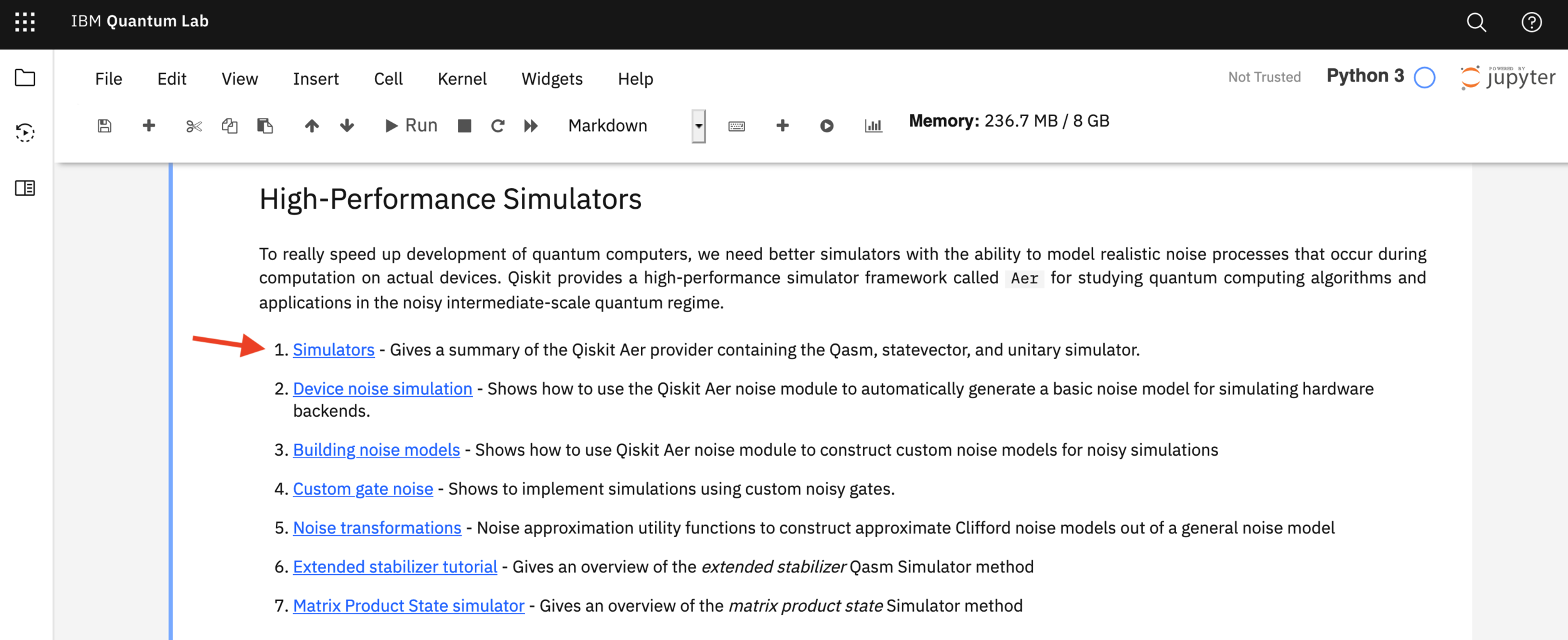
Explore the Qiskit Tutorials - Simulators Jupyter notebook

The Simulators link is in the start_here Jupyter notebook

Explore the Qiskit tutorials outside of a Jupyter notebook

https://qiskit.org/documentation/tutorials.html

Consulting the Qiskit API reference

https://qiskit.org/documentation/apidoc/terra.html

Working with OpenQASM

https://openqasm.com/

Consult qiskit.circuit.QiskitCircuit methods for using QASM within Qiskit

For example https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html#qiskit.circuit.QuantumCircuit.from_qasm_str

Consulting Quantum Computing StackExchange

https://quantumcomputing.stackexchange.com/questions/tagged/qiskit

Learn nuggets like this from other Qiskit developers

Working through the 20 sample questions

Each certification exam question falls into one of these objectives:

%qiskit_backend_overview
QiskitCircuit.from_qasm_str()

and string:

Access

Access

Access

... and understand

}

Working through sample question #1

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Familiarity with Qiskit API

✓

Working through sample question #2

https://javafxpert.github.io/grok-bloch/

Mental gymnastics on the Bloch sphere

✓

Working through sample question #3

✓

✓

✓

Familiarity with Qiskit API

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumRegister.html

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Working through sample question #4

✓

Familiarity with Qiskit API, measure vs. measure_all

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Working through sample question #5

https://qiskit.org/textbook/ch-gates/multiple-qubits-entangled-states.html

Entanglement and knowing the four Bell states

✓

https://en.wikipedia.org/wiki/Bell_state

Working through sample question #6

https://javafxpert.github.io/grok-bloch/

Gymnastics on the Bloch sphere, plot_bloch_multivector vs. plot_bloch_vector

✓

✓

Working through sample question #7

https://quantum-computing.ibm.com/composer/docs/iqx/operations_glossary

Gate operations

✓

Working through sample question #8

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Bell state, and initialize()

✓

✓

Working through sample question #9

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Familiarity with Qiskit API, multi-qubit gates

✓

https://qiskit.org/documentation/apidoc/circuit_library.html

Working though sample question #10

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Familiarity with Qiskit API, Toffoli gate

✓

https://qiskit.org/documentation/apidoc/circuit_library.html

Example Toffoli gate:

Working through sample question #11

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Familiarity with Qiskit API, barrier operation

✓

✓

Working through sample question #12

https://youtu.be/tS2CMOyWFMQ

Barrier operation, optimizing circuits

✓

Working through sample question #13

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html

Barrier operation, circuit depth

✓

Working though sample question #14

Using execute function parameters, coupling map, Aer qasm_simulator

✓

https://qiskit.org/documentation/tutorials/circuits/1_getting_started_with_qiskit.html

Working through sample question #15

https://qiskit.org/documentation/apidoc/execute.html

Using execute function parameters, coupling map, BasicAer qasm_simulator

✓

Example device gate map:

https://qiskit.org/documentation/apidoc/providers_basicaer.html

Working through sample question #16

https://qiskit.org/documentation/apidoc/providers_basicaer.html

BasicAer simulators

✓

✓

✓

Working through sample question #17

https://qiskit.org/documentation/tutorials/circuits/2_plotting_data_in_qiskit.html

Assigning BasicAer simulators

✓

Working through sample question #18

https://qiskit.org/documentation/stubs/qiskit.quantum_info.Operator.html

Quantum information, creating an Operator

✓

https://qiskit.org/textbook/ch-states/single-qubit-gates.html

Working through sample question #19

https://qiskit.org/documentation/apidoc/quantum_info.html

Familiarity with Qiskit quantum_info API, process and gate fidelity

✓

Working though sample question #20

Mentally calculating statevector from a quantum circuit

✓

Thanks for your attention! Any more questions?

https://www.ibm.com/certify/exam?id=C1000-112

ENIAC computer circa 1947

IBM Research quantum computer circa 2017

Backing up a little: History repeating itself

Massive hardware, limited bits, software infancy

Quantum computers make direct use of quantum-mechanical phenomena, such as superposition, interference and entanglement, to perform operations on data.

Feasible on classical computers

Feasible on quantum computers

Solutions to problems

Why use a quantum computer?

Some problems may be solved exponentially faster

@JavaFXpert

“Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.”

Simulating nature

complex chemical reactions, for example

Dr. Richard Feynman, 1981

@JavaFXpert

en.wikipedia.org/wiki/Richard_Feynman

bigbangtheory.wikia.com/wiki/Richard_Feynman

newscientist.com/article/mg22029445-100-my-quantum-algorithm-wont-break-the-internet-yet/

“If you start factoring 10-digit numbers then it’s going to start getting scary”

Breaking RSA crypto

someday maybe, using Shor's algorithm, formulated in 1994

Dr. Peter Shor, 2013

@JavaFXpert

“Programming a quantum computer is particularly interesting since there are multiple things happening in the same hardware simultaneously.  One needs to think like both a theoretical physicist and a computer scientist.”

Quickly searching unsorted data

using Grover's algorithm

Dr. Lov Grover, 2002

@JavaFXpert

outlookindia.com/magazine/story/ring-o-stars/220719

NISQ* era quantum computing domains

@JavaFXpert

Machine Learning

Optimization

Chemistry

Finance

*Noisy Intermediate Scale Quantum computers

Axioms of Quantum Mechanics

\vert\space\space\space\rangle

featuring grumpy cat (or is it grumpy ket)? 

@JavaFXpert

My microscopic cat is often grumpy

@JavaFXpert

\vert\space\space\space\rangle
\vert\space\space\space\rangle

sometimes he is actually happy

but I've never observed him in-between those states

desmos.com/calculator/0rpttswx6s​

Axiom 1: Superposition principle

@JavaFXpert

my cat can be in any combination of grumpy and happy

\vert\space\space\space\rangle
= \begin{bmatrix} 1 \\ 0 \end{bmatrix}
\vert\space\space\space\rangle
= \begin{bmatrix} 0 \\ 1 \end{bmatrix}
= \begin{bmatrix} \sqrt{\frac{1}{3}} \\ \sqrt{\frac{2}{3}} \end{bmatrix}
\sqrt{\frac{1}{3}}
\vert\space\space\space\rangle
+
\sqrt{\frac{2}{3}}
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle

Representing quantum states

geometrically, ket notation, and vectors

\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle

@JavaFXpert

\vert\space\space\space\rangle
\vert\space\space\space\rangle

Axiom 2: Unitary evolution

gates modeled as matrices

X

\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}

NOT gate (Pauli/X, bit-flip)

@JavaFXpert

\vert\space\space\space\rangle

Hadamard gate

great for putting cats in equal superpositions

H

\begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}

Hadamard gate

\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
+
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle

@JavaFXpert

\sqrt{\frac{1}{3}}
\vert\space\space\space\rangle
+
\sqrt{\frac{2}{3}}
\vert\space\space\space\rangle

Axiom 3: Measurement

probability is amplitude squared

When observed there is a:

\frac{1}{3}
\frac{2}{3}

probability of being grumpy

probability of being happy

@JavaFXpert

Multiple cats

\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
=
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
= \begin{bmatrix} 1 \\ 0 \end{bmatrix}
\otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix}

Composite quantum states

@JavaFXpert

= \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}

Multiple cats

\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
=
= \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}
= \begin{bmatrix} 1 \\ 0 \end{bmatrix}
\otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix}

Composite quantum states

\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle

@JavaFXpert

\sqrt{\frac{1}{2}}
+

Superpositions, evolution & measurement

putting the three axioms together

\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{2}}
\sqrt{\frac{1}{2}}
+
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{6}}
+
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{3}}
\vert\space\space\space\space\space\space\space\rangle

@JavaFXpert

quantum gates

quantum gates

measure

\downarrow
\downarrow
\downarrow
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle

with 1/2 probability

with 1/6 probability

with 1/3 probability

\vert\space\space\space\rangle

Quantum entanglement

spooky actions at a distance

H

Hadamard gate

\vert\space\space\space\rangle

CNOT gate

\sqrt{\frac{1}{2}}
+
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{2}}
\sqrt{\frac{1}{2}}
+
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{2}}

Mars - ESA

Alice Cat

Bob Cat

Venus - NASA

\vert\space\space\rangle
=
\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix}
\begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix}