Preparing for the Qiskit developer certification exam
These slides at: https://slides.com/javafxpert/prep-qiskit-dev-cert-exam
Please note
IBM’s statements regarding its plans, directions, and intent are subject to change or withdrawal without notice and at IBM’s sole discretion.
Information regarding potential future products is intended to outline our general product direction and it should not be relied on in making a purchasing decision.
The information mentioned regarding potential future products is not a commitment, promise, or legal obligation to deliver any material, code or functionality. Information about potential future products may not be incorporated into any contract.
The development, release, and timing of any future features or functionality described for our products remains at our sole discretion.
Performance is based on measurements and projections using standard IBM benchmarks in a controlled environment. The actual throughput or performance that any user will experience will vary depending upon many factors, including considerations such as the amount of multiprogramming in the user’s job stream, the I/O configuration, the storage configuration, and the workload processed. Therefore, no assurance can be given that an individual user will achieve results similar to those stated here.
© 2021 IBM Corporation
About presenter Paul Kassebaum, Ph.D.
About presenter James Weaver
IBM Quantum Developer Advocate
Java Champion
Developer / Author / Speaker
james.weaver@ibm.com
Getting the workforce quantum-ready
With our quantum developer certification, companies and research institutions will find a clear path to get their workforce quantum-ready. The certificate will help those hiring for classical programming and non-programming roles recognize holders of this certification as forward-thinking individuals willing to skill up for the future of the computing workforce.
The IBM Quantum Developer Certification is a 60-question certification exam offered on the Pearson VUE platform. Those who pass the exam will have demonstrated experience using Qiskit to create and execute quantum computing programs on IBM quantum computers and simulators, and the ability to perform these tasks with little to no assistance from product documentation, support, or peers.
What to expect from the exam
We figure that plenty of Qiskitters will be looking to take the certification exam, so we’ve put together a sneak peak of the exam’s structure, what’s going to be on it, and how to study for it. The test is going to be a 60-question exam, in English, offered on the Pearson VUE platform. The goal of the test is to certify that those who pass it can define, execute, and visualize quantum circuits using Qiskit, implement single and multi-qubit gates and understand their effects on quantum circuits, and leverage the fundamental features of Qiskit in order to write quantum programs.
Objectives of the exam
Preparing for the exam
Leveraging the IBM Quantum Composer
Create your first circuit walkthrough
Also, explore the Quantum Composer user guide, and Operations glossary
Gain an intuitive understanding of the Bloch sphere and gate rotations with this web-based application known as Grok the Bloch Sphere
Bloch sphere playground
Studying the Qiskit Textbook
Explore all of sections 1 and 2
Continue studying the Qiskit Textbook
Explore the Defining Quantum Circuits section
Leveraging the IBM Quantum Lab
Explore the Qiskit Tutorials - Circuits Jupyter notebooks
The links shown above are in the start_here Jupyter notebook
Continue leveraging the IBM Quantum Lab
Explore the Qiskit Tutorials - Advanced circuit visualization Jupyter notebook
The Advanced circuit visualization link is in the start_here Jupyter notebook
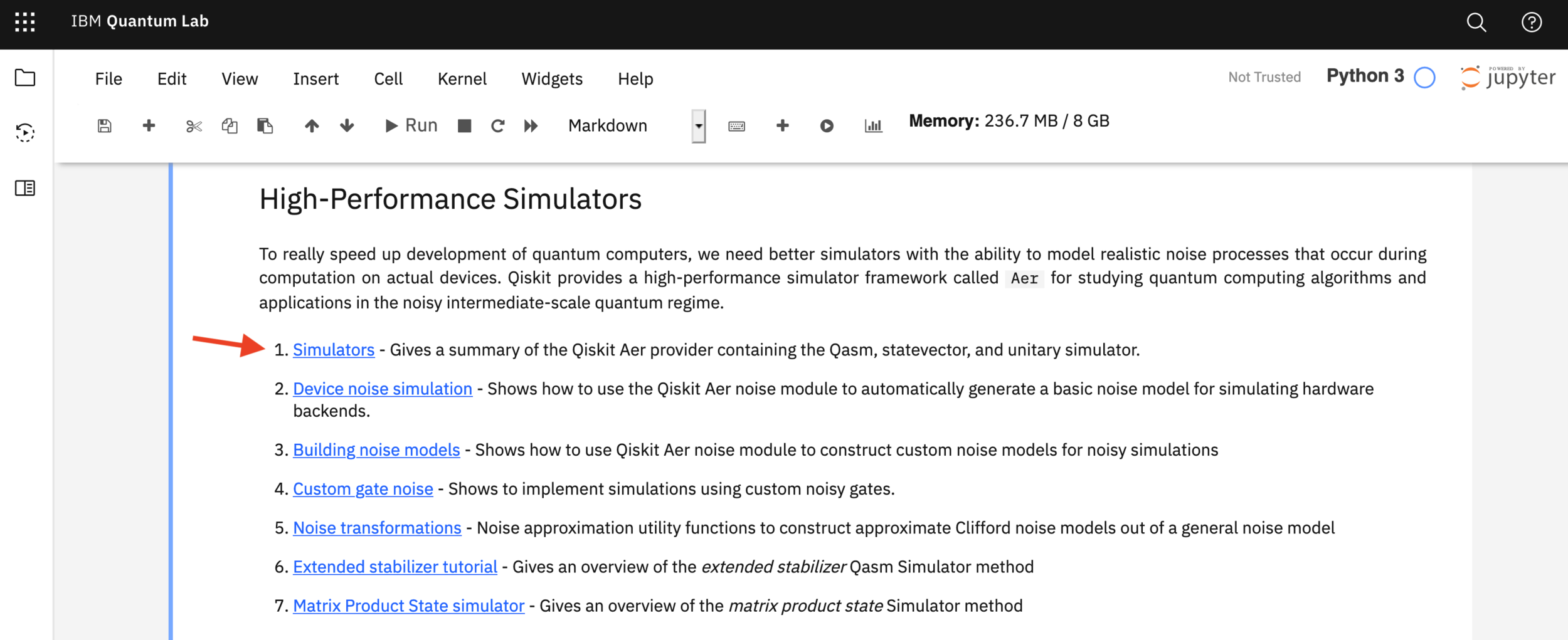
More leveraging the IBM Quantum Lab
Explore the Qiskit Tutorials - Simulators Jupyter notebook
The Simulators link is in the start_here Jupyter notebook
Explore the Qiskit tutorials outside of a Jupyter notebook
Consulting the Qiskit API reference
Working with OpenQASM
Consult qiskit.circuit.QiskitCircuit methods for using QASM within Qiskit
Consulting Quantum Computing StackExchange
Learn nuggets like this from other Qiskit developers
Working through the 20 sample questions
Each certification exam question falls into one of these objectives:
%qiskit_backend_overview
QiskitCircuit.from_qasm_str()
and string:
Access
Access
Access
... and understand
}
Working through sample question #1
Familiarity with Qiskit API
✓
Working through sample question #2
Mental gymnastics on the Bloch sphere
✓
Working through sample question #3
✓
✓
✓
Familiarity with Qiskit API
Working through sample question #4
✓
Familiarity with Qiskit API, measure vs. measure_all
Working through sample question #5
Entanglement and knowing the four Bell states
✓
Working through sample question #6
Gymnastics on the Bloch sphere, plot_bloch_multivector vs. plot_bloch_vector
✓
✓
Working through sample question #7
Gate operations
✓
Working through sample question #8
Bell state, and initialize()
✓
✓
Working through sample question #9
Familiarity with Qiskit API, multi-qubit gates
✓
Working though sample question #10
Familiarity with Qiskit API, Toffoli gate
✓
Example Toffoli gate:
Working through sample question #11
Familiarity with Qiskit API, barrier operation
✓
✓
Working through sample question #12
Barrier operation, optimizing circuits
✓
Working through sample question #13
Barrier operation, circuit depth
✓
Working though sample question #14
Using execute function parameters, coupling map, Aer qasm_simulator
✓
Working through sample question #15
Using execute function parameters, coupling map, BasicAer qasm_simulator
✓
Example device gate map:
Working through sample question #16
BasicAer simulators
✓
✓
✓
Working through sample question #17
Assigning BasicAer simulators
✓
Working through sample question #18
Quantum information, creating an Operator
✓
Working through sample question #19
Familiarity with Qiskit quantum_info API, process and gate fidelity
✓
Working though sample question #20
Mentally calculating statevector from a quantum circuit
✓
Thanks for your attention! Any more questions?
Backing up a little: History repeating itself
Massive hardware, limited bits, software infancy
Quantum computers make direct use of quantum-mechanical phenomena, such as superposition, interference and entanglement, to perform operations on data.
Feasible on classical computers
Feasible on quantum computers
Solutions to problems
Why use a quantum computer?
Some problems may be solved exponentially faster
“Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.”
Simulating nature
complex chemical reactions, for example
Dr. Richard Feynman, 1981
“If you start factoring 10-digit numbers then it’s going to start getting scary”
Breaking RSA crypto
someday maybe, using Shor's algorithm, formulated in 1994
Dr. Peter Shor, 2013
“Programming a quantum computer is particularly interesting since there are multiple things happening in the same hardware simultaneously. One needs to think like both a theoretical physicist and a computer scientist.”
Quickly searching unsorted data
using Grover's algorithm
Dr. Lov Grover, 2002
NISQ* era quantum computing domains
Machine Learning
Optimization
Chemistry
Finance
*Noisy Intermediate Scale Quantum computers
Axioms of Quantum Mechanics
\vert\space\space\space\rangle
featuring grumpy cat (or is it grumpy ket)?
My microscopic cat is often grumpy
\vert\space\space\space\rangle
\vert\space\space\space\rangle
sometimes he is actually happy
but I've never observed him in-between those states
Axiom 1: Superposition principle
my cat can be in any combination of grumpy and happy
\vert\space\space\space\rangle
=
\begin{bmatrix}
1 \\
0
\end{bmatrix}
\vert\space\space\space\rangle
=
\begin{bmatrix}
0 \\
1
\end{bmatrix}
=
\begin{bmatrix}
\sqrt{\frac{1}{3}} \\
\sqrt{\frac{2}{3}}
\end{bmatrix}
\sqrt{\frac{1}{3}}
\vert\space\space\space\rangle
+
\sqrt{\frac{2}{3}}
\vert\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
Representing quantum states
geometrically, ket notation, and vectors
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
Axiom 2: Unitary evolution
gates modeled as matrices
X
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
1 \\
0
\end{bmatrix}
=
\begin{bmatrix}
0 \\
1
\end{bmatrix}
NOT gate (Pauli/X, bit-flip)
\vert\space\space\space\rangle
Hadamard gate
great for putting cats in equal superpositions
H
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
\cdot
\begin{bmatrix}
1 \\
0
\end{bmatrix}
=
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}}
\end{bmatrix}
Hadamard gate
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
+
\sqrt{\frac{1}{2}}
\vert\space\space\space\rangle
\sqrt{\frac{1}{3}}
\vert\space\space\space\rangle
+
\sqrt{\frac{2}{3}}
\vert\space\space\space\rangle
Axiom 3: Measurement
probability is amplitude squared
When observed there is a:
\frac{1}{3}
\frac{2}{3}
probability of being grumpy
probability of being happy
Multiple cats
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
=
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
=
\begin{bmatrix}
1 \\
0
\end{bmatrix}
\otimes
\begin{bmatrix}
1 \\
0
\end{bmatrix}
Composite quantum states
=
\begin{bmatrix}
1 \\
0 \\
0 \\
0
\end{bmatrix}
Multiple cats
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\rangle
\vert\space\space\space\rangle
=
=
\begin{bmatrix}
0 \\
1 \\
0 \\
0
\end{bmatrix}
=
\begin{bmatrix}
1 \\
0
\end{bmatrix}
\otimes
\begin{bmatrix}
0 \\
1
\end{bmatrix}
Composite quantum states
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{2}}
+
Superpositions, evolution & measurement
putting the three axioms together
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{2}}
\sqrt{\frac{1}{2}}
+
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{6}}
+
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{3}}
\vert\space\space\space\space\space\space\space\rangle
quantum gates
quantum gates
measure
\downarrow
\downarrow
\downarrow
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
with 1/2 probability
with 1/6 probability
with 1/3 probability
\vert\space\space\space\rangle
Quantum entanglement
spooky actions at a distance
H
Hadamard gate
\vert\space\space\space\rangle
CNOT gate
\sqrt{\frac{1}{2}}
+
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{2}}
\sqrt{\frac{1}{2}}
+
\vert\space\space\space\space\space\space\space\rangle
\vert\space\space\space\space\space\space\space\rangle
\sqrt{\frac{1}{2}}
Mars - ESA
Alice Cat
Bob Cat
Venus - NASA
\vert\space\space\rangle
=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
Preparing to take the Qiskit developer certification exam
By javafxpert
Preparing to take the Qiskit developer certification exam
Preparing to take the Qiskit developer certification exam, entitled Fundamentals of Quantum Computation Using Qiskit v0.2X Developer
