Statistics: Probability



Aim:
Understand how to use words and numbers to name and calculate different probabilities.
How you'll know that you've been learning today:
Can calculate simple probabilities using
P(‘X’) = P(event ‘X’)/P(all events).
Date:
Time Remaining:
Describing Probability with Words (Qualitative)
An event's probability is a prediction of how LIKELY it is to occur e.g.
impossible unlikely 50/50 likely certain
Settings Troubleshooting
There might be some issues with using Mentimeter on iPads.
You will need to 'enable cookies'. And update to the latest iPadOS version.
Go to iPad settings, scroll down to 'Safari', and under the 'Privacy & Security' settings disable "Prevent Cross-Site Tracking" and disable "Block all Cookies."
If you are blocked from editing iPad settings, you'll need to show your parents this Slide and ask for permission to change the settings, so that you can use it interactively for class.
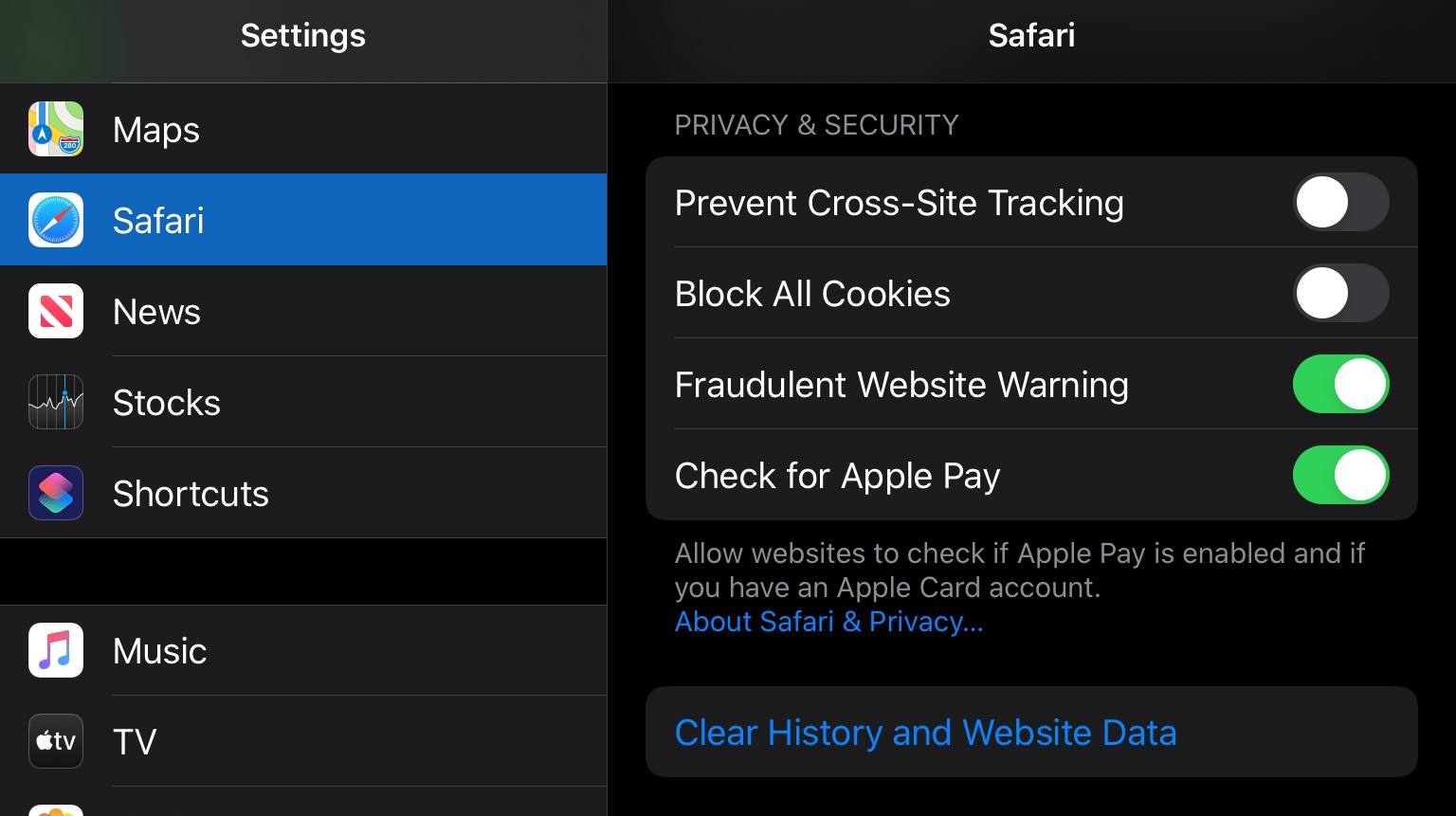
Click this to Show Settings Screenshot
Poll Bakcup (input code: 42 45 74) :
Feedback: Class Results
Hidden link to the poll dashboard (need to be logged-in as me to view/edit):https://www.mentimeter.com/s/8fe39ce2dc46b1bec09d3d01c59b319f/a254d7ffe01e/edit
Estimate the Likleyhood of Different Events
Take 5 minutes. Invent your own events. Locate their probability on the scale using words, numbers, and labels. Volunteer to your favorite one.
Describing Probability with Numbers (Quantitative)
COPY:
·Probability is a number between 0–1, with no units.
·It can be written as a percentage, as a fraction, or as a decimal.
·We should always simplify fractions (e.g. the probability 6/15 = 2/5)
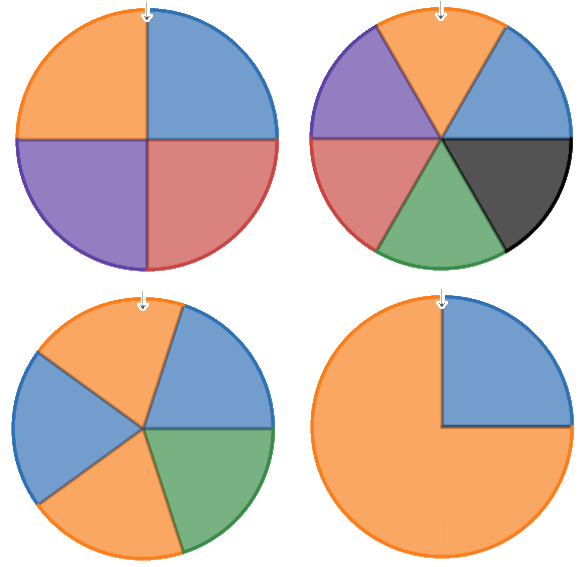
Calculate Probabilities Using Frequency
To compare probabilities, we need a fair way to measure them (to put numbers on them).
COPY:
Calculate
P(Rolling a 6 on a Dice)
There is only one '6' out of the 6 sides of a dice, there is only one 'blue' side on a fully-solved Rubik's cube.
Count the Number of Possible Cases
💰Coin flip / 🎲Dice / 🥚Egg Carton
🚚Truck Wheels / 🤸♀️Spinners


How to Write Probability Equations
We can write a probability in an equation:
"The probability of event 'X' happening is 1."
becomes
"P(event 'X') = 1"
or even shorter
P(X)=1
Complete Exercise 2 page 161 Questions 1-6 (15 min)
Easier vs. Harder Dice Games
Take a dice game where you win if you roll 5 or 6, and lose otherwise. Is it more likely to win this game or to lose it?
Compare this probability to a game where you only win if you roll a 6.
\(\frac{2}{6} > \frac{1}{6}\)
\(\frac{1}{3} > \frac{1}{6}\)
\(33.3\% > 16.67\% \)
Opposite Probabilities
If P(A) is the probability that A happens, the opposite probability (the probability that A does NOT happen) is calculated using 1-P(A) .
For example, Page 161 Question 6:
4 marbles, 1 blue 3 red. P(blue) = \(\frac{1}{4}\) P(red) = \(\frac{3}{4}\)
P(red)+P(blue)=1
so
P(blue) = 1-P(red) = 1\(-\frac{3}{4}\) = \(\frac{1}{4}\)