Aim:

Understand the relation between the shape of \(f’(x)\) and \(f(x)\), how one connects with the other.

Success Looks Like:

Can plot Curve Tables of functions to identify their shape, and can use these to plot the graph of \(f’(x)\) for a given \(f(x)\).

Date:
Time Remaining:

https://cuckoo.team/jaytch_ea

Every value of \(a\) that makes \(f’(a)=0\) is called a “stationary point”

When \(f’(x)\) is negative, \(f(x)\) is decreasing.

When \(f’(x)\) is \(0, f(x)\) is stationary.

When \(f’(x)\) is positive, \(f(x)\) is increasing.

Minimum: - 0 + “min” for “minus” Maximum: + 0 - "max" has ‘x’→ ‘+’ \ _ / / ‾ \

Steps for Constructing ‘Curve Tables” to Analyze Graphs using the Derivative Graph:

1. Differentiate

2. Solve for Zeroes

3. Assign sign of zones (by plugging-in values, visually from the graph, or from patterns)

4. Identify as either minimum, maximum, or turning point.

LINK to DESMOS grapher to help visualize things (same as on next page)

The parabola \(f(x)=x^2-5x\) differentiates to \(f’(x)=2x-5\), with maximum at \(x=\frac{5}{2}\).

The parabola \(f(x)=-\frac{1}{4}(x+2)(x-4)\) differentiates to \(f’(x)=-\frac{1}{2}x+\frac{1}{8}\), with maximum at \(x=1\).

COMPLETE:

pg104 Exercises 6L 2–8 finding where functions are positive/negative

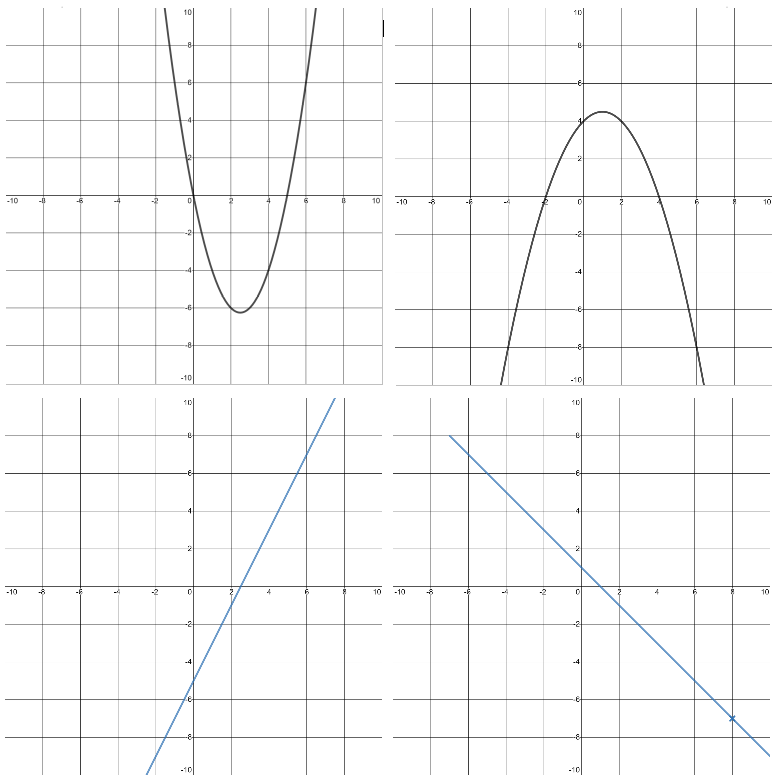
To sketch the graph of \(f’(x)\) from \(f(x)\):

1. Find the stationary and turning points,
2. Assign the sign for each zone, and

3. Connect-up all the details.

COMPLETE:

pg 110 Exercises 6P sketching graph of derivatives

Settings Troubleshooting

There might be some issues with using Mentimeter on iPads.

You will need to 'enable cookies'. And update to the latest iPadOS version.

Go to iPad settings, scroll down to 'Safari', and under the 'Privacy & Security' settings disable "Prevent Cross-Site Tracking" and disable "Block all Cookies."

If you are blocked from editing iPad settings, you'll need to show your parents this Slide and ask for permission to change the settings, so that you can use it interactively for class.

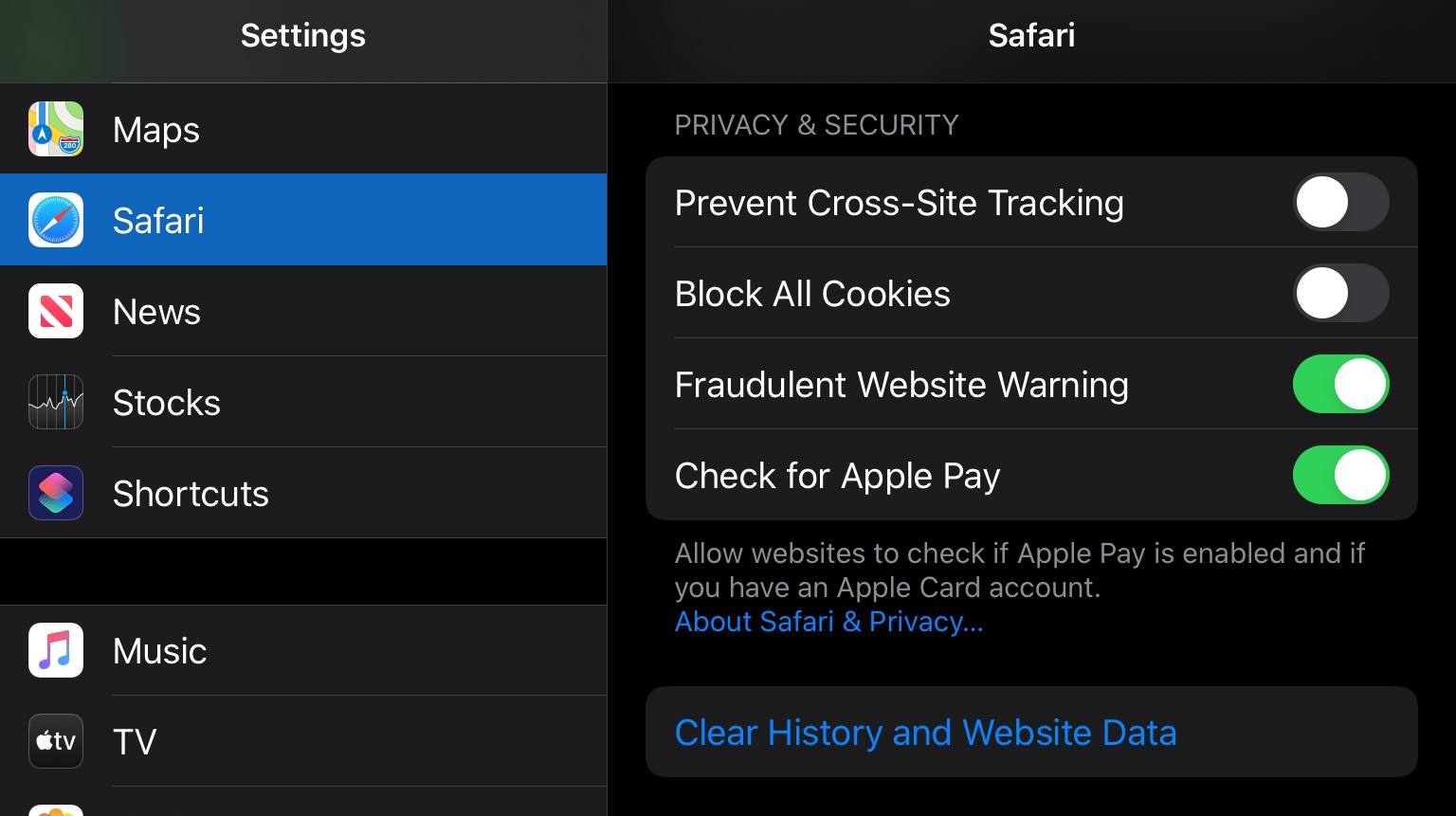
Click this to Show Settings Screenshot

Poll Bakcup

RESULTS

Calculus Differentiation Chain Rule

photo credit

\begin{array}{ r c c c } \frac{d}{dx} (ax+b)^{3} & & & \\ ax+b & → & ⬚ ^{3} & \\ & \searrow & & \\ a & \times & 3⬚^{2} & \\ =\ a3(ax+b)^{2} & & & \end{array}

\begin{array}{ r c c c } \frac{d}{dx} (ax+b)^{3} & & & \\ ax+b & → & ⬚ ^{3} & \\ & \searrow & & \\ a & \times & 3⬚ ^{2} & \\ =\ a3(ax+b)^{2} & & & \end{array}\\ \\ \\ \\ \begin{array}{ c c c c c c l } & & & & & & \frac{d}{dx} (cos^{8}\left( 2x^{2} +1\right) )\\ & & & & & & \\ 2x^{2} +1 & → & cos(⬚ ) & → & ⬚ ^{8} & = & cos^{8}\left( 2x^{2} +1\right)\\ & \searrow & & \searrow & & & \\ 2\times 2x & \times & -sin(⬚ ) & \times & 8⬚ ^{7} & = & 2\times 2x\times \left( -sin\left( 2x^{2} +1\right)\right) \times \left( 8\left( cos\left( 2x^{2} +1\right)\right)^{7}\right)\\ & & & & & & \end{array}

Calculus Tangents and Stationary Points

photo credit