Calculus Tangents and Stationary Points

photo credit

Aim:

Understand the meaning of the derivative — that f’(a) equals the gradient of tangent line at (a,f(a)), and use this understanding to identify properties of f(x).

Success Looks Like:

Can reliably calculate derivatives of simple polynomials, equations of lines between two points, evaluate f’(a) for various ‘a’, and identify +,-,0 regions of f(x) using f’(x).

Date:
Time Remaining:

https://cuckoo.team/jaytch_ea

Settings Troubleshooting

There might be some issues with using Mentimeter on iPads.

You will need to 'enable cookies'. And update to the latest iPadOS version.

Go to iPad settings, scroll down to 'Safari', and under the 'Privacy & Security' settings disable "Prevent Cross-Site Tracking" and disable "Block all Cookies."

If you are blocked from editing iPad settings, you'll need to show your parents this Slide and ask for permission to change the settings, so that you can use it interactively for class.

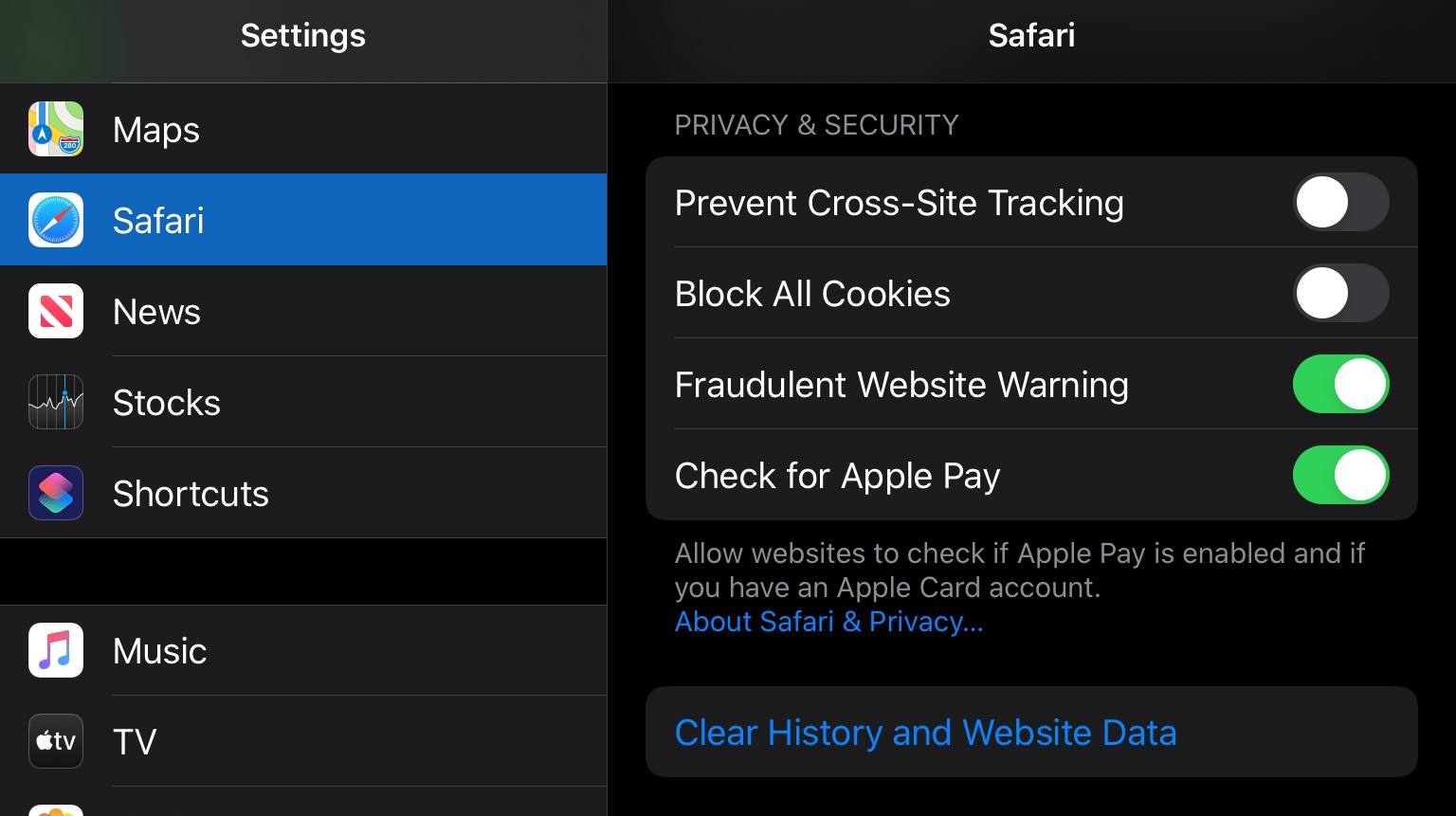
Click this to Show Settings Screenshot

Poll Bakcup (input code: 68 36 6) :

Feedback: Class Results

Hidden link to the poll dashboard (need to be logged-in as me to view/edit):https://www.mentimeter.com/s/9138f916d5560aabf59330fc0ef16d1d/1ea5f6c9df7a/edit

Recap: Basic Differentiation Rules

$\frac{d}{dx}( f(x) ) = f’(x) = df/dx$ The derivative of a function is the instantaneous rate of change of that function at each point.

$\frac{d}{dx}( x^n ) = nx^{n-1}$

To differentiate: multiply by the old power, decrease the power by one.

$\frac{d}{dx}(a) = 0$ The derivative of a constant is zero.

$\frac{d}{dx}( ax^n ) = a\frac{d}{dx} (x^n) = anx^{n-1}$

When differentiating a constant times a power of x, extract the constant and multiply it from the outside.

$\frac{d}{dx}( f(x)+g(x) ) = f’(x)+g’(x)$

The derivative of a sum of functions is the sum of their derivatives.

\begin{array} {lrclccccll}\mathbb{N} & y & = & 2\times(8)^3 & & & y & = & \phantom{-}1024 & \\ \mathbb{Z} & y & = & 2\times(-8)^3 & & & y & = & -1024 & \text{Inverse of }+\text{ requires Negative Numbers} \\ \mathbb{Q} & y & = & 2\times(-8)^{-3} & & & y & = & -\frac{1}{512} & \text{Inverse of }×\text{ requires Rational Numbers} \\ \mathbb{R} & y & = & 2\times(8)^{\frac{1}{6}} & & & y & = & 2\sqrt{2} & \text{Inverse of }\hat{} \: \text{ requires Real Numbers} \\ \mathbb{C} & -2 & = & 2\times(x)^2 & & & y & = & \sqrt{-1} & \sqrt{\text{Negatives}} \text{ requires Complex Numbers} \end{array}

Recap: Finding the equation of a line between two points

Find $m = \frac{Δy}{Δx}$

Put this into $y=mx+c$

Put a coordinate-pair into the equation to solve for $c$

Re-write $y=mx+c$ with values for $m$ and $c$

Example: Find the equation of the line passing through (2,4) , (3,9)

Differentiating from First Principles

We construct a crude tangent line between two points on $f(x)$

The first point has coordinates $(a, f(a) )$

The second point is shifted-over by $h$, with coordinates

$(a+h, f(a+h) )$

$y = mx+c$ $m = \frac{f(a+h)-f(a)}{(a+h)-(a)}$ $c = f(a)-ma$

What is the pattern as we zoom in and make $h$ shrink? (Discuss in pairs)

Experiment with some real numbers: $a=2$ and $h=1$, decreasing $h$ to 0.5, 0.25, 0.1 etc.

Conclusion:

shrinking $h$ gives a better-and-better fit to the $f(x)$ graph

We aren’t ‘dividing by zero’ because

1. $h$ cancels-out from the top and bottom, and

2. we never actually go to $h=0$, we just go near it → problem dodged 👌!

The slope of the tangent line $m$ at any point on $f(x)$ EQUALS the value of $f’(x)$ for that point

This expression for $m$ is the DEFINITION of ‘Differentiating’:

$$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$$

(If you’re keen, ask me after for the proof for how it works for x^n)

We can now use $f’(x)$ to gain knowledge about changes in $f(x)$

Task: Sketch $f(x)=x^2$ ,

on another pair of axes below it sketch $f’(x)$,

below this sketch a table horizontally of $f’(-2),f’(-1),f’(0),f’(1),f’(2)$,

evaluate $f’(x)$ at those points.

If the result is positive/negative/zero, below it write +/-/0

What’s the pattern (Discuss):

When $f’(x)$ is negative, $f(x)$ is decreasing.

When $f’(x)$ is positive, $f(x)$ is increasing, when $f’(x)$ is $0, f(x)$ is stationary.

Answers from this link: https://ssddproblems.com/differentiate-y-fx/

Every value of $a$ that makes $f’(a)=0$ is called a “stationary point”

Does the stationary point always line up with the minimum/maximum of the parabola? Re-write these parabolas in point-intercept form to investigate!

●$f(x)=x²+4x+4$ ●$p(x)=-x²-8x$ ●$s(x)=x²+6x-3$

Write these in the form $y=a(x+b)²+h$ to check if the parabola maximum/minimum matches up with the stationary point. After doing it by hand, you can check your results by typing them into today’s Desmos graph.

Extra Exercises: page 102 Ex. 2,3,4 Page103-104 Examples16–18, 6L2 🤓

Feedback: Class Results

Hidden link to the poll dashboard (need to be logged-in as me to view/edit):https://www.mentimeter.com/embed/9138f916d5560aabf59330fc0ef16d1d/0ce8f9acfcad

Aim:

Understand the meaning of the derivative — that f’(a) equals the gradient of tangent line at (a,f(a)), and use this understanding to identify properties of f(x).

Success Looks Like:

Can reliably calculate derivatives of simple polynomials, equations of lines between two points, evaluate f’(a) for various ‘a’, and identify +,-,0 regions of f(x) using f’(x).

Settings Troubleshooting

Poll Bakcup (input code: 68 36 6) :

Feedback: Class Results

Recap: Basic Differentiation Rules

Recap: Finding the equation of a line between two points

Differentiating from First Principles

What is the pattern as we zoom in and make \(h\) shrink? (Discuss in pairs)

The slope of the tangent line \(m\) at any point on \(f(x)\) EQUALS the value of \(f’(x)\) for that point

We can now use \(f’(x)\) to gain knowledge about changes in \(f(x)\)

Every value of \(a\) that makes \(f’(a)=0\) is called a “stationary point”

Extra Exercises: page 102 Ex. 2,3,4 Page103-104 Examples16–18, 6L2 🤓

Feedback: Class Results