Reconstrucción de Superficies 3D

Text

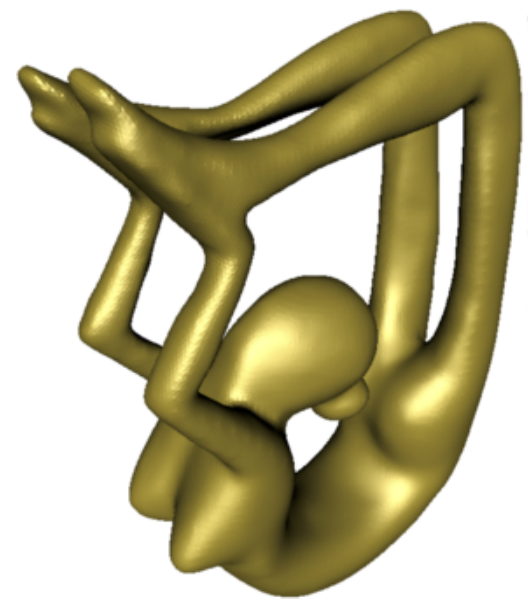
Para qué?

• Restauración y preservación de objetos de interés cultural
• Prototipado rápido
  • Objeto => modelo CAD
• Medicina
  • Diseño y manufactura de prótesis
  • Planeo de cirugias
• Animación
  • Aplicaciones recientes en AR para gamification 
• Ciencia
  • Monitoreo de sitios de excavación arqueológica

...

Adquisición

Reconstrucción

Visualización

Adquisición

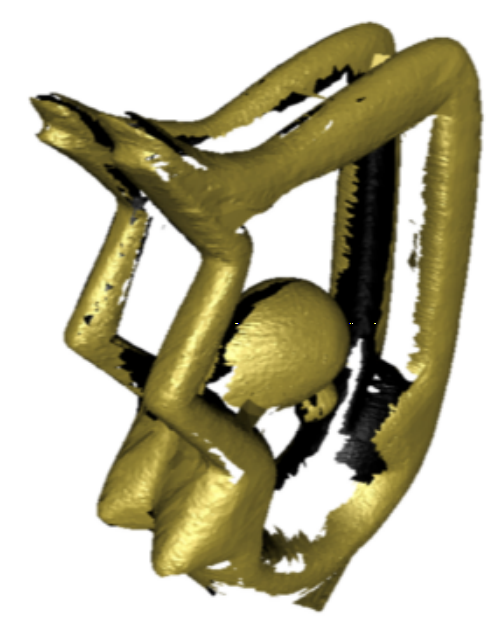
Equipos

Proyección y Fotos con

Luz Estructurada

Nube de Puntos

Camaras

Proyector

Registrado

Dos nubes de puntos, una mostrada en rojo y otra en verde

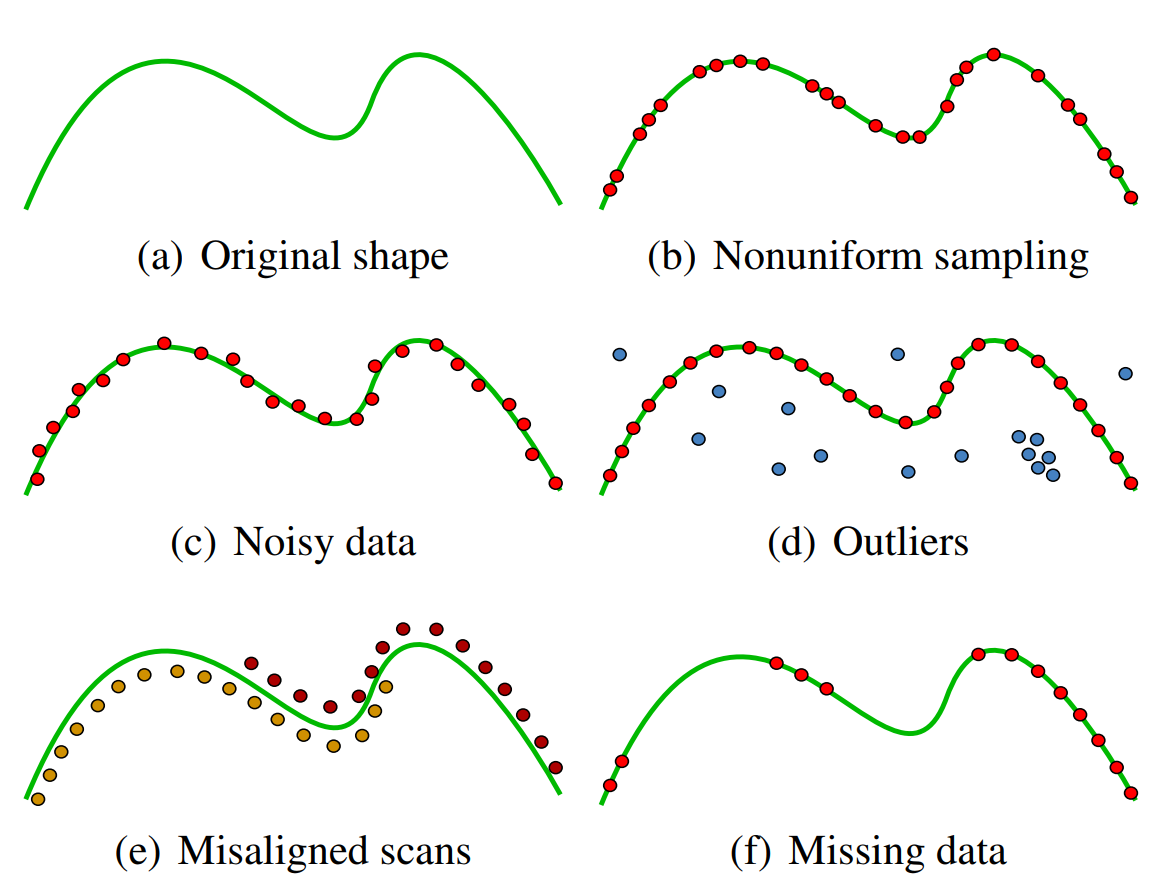
Nubes de Puntos Orientadas

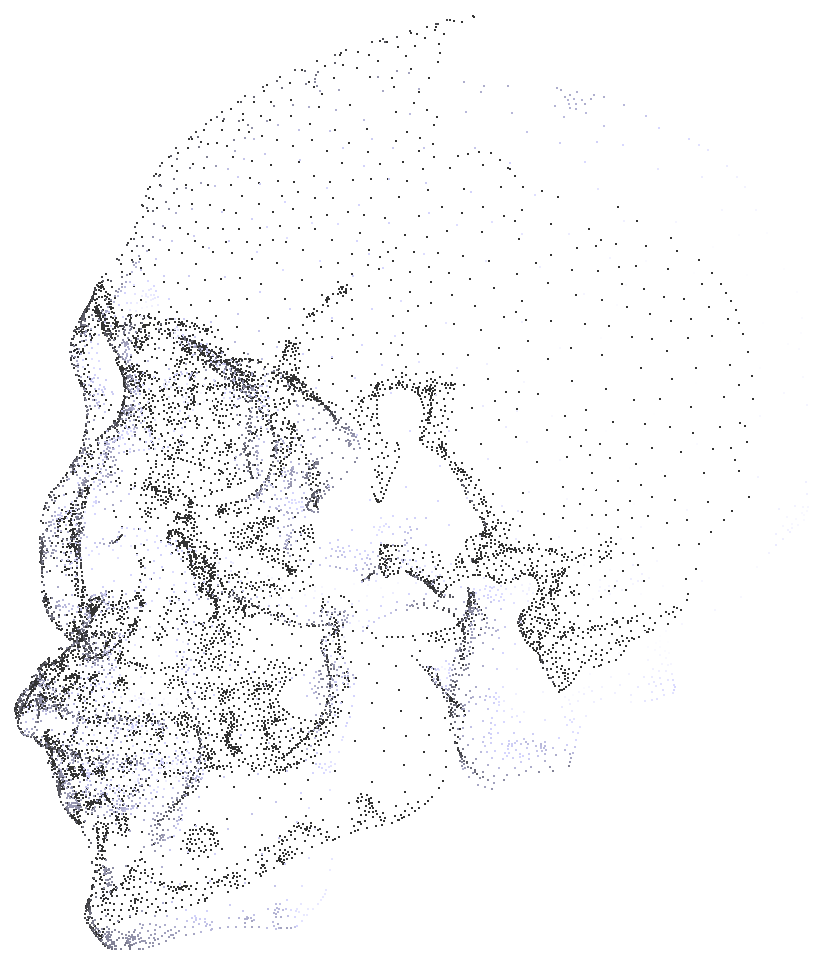
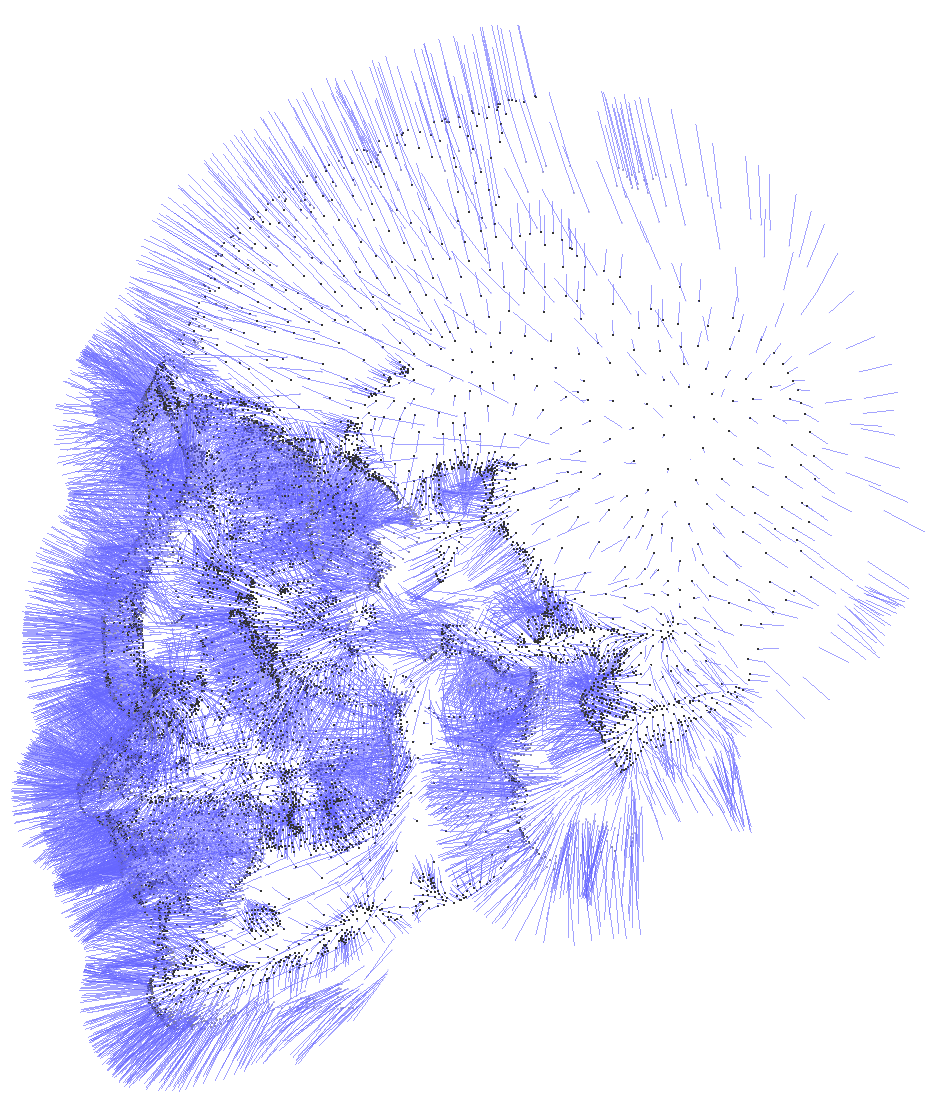
"Hacia dónde es el adentro/afuera"

Reconstrucción

Por qué?

• Las representaciones matemáticas de superficies tienen información importante sobre ellas:
  • Hacia a dónde es el adentro y el afuera
  • Si estamos en una zona plana o curva
  • Etcétera
• Más versatilidad
• Múltiples aplicaciones
• Hay muchas formas de representar superficies, cada una con ciertas ventajas para distintos usos.

Representación de Superficies

• Paramétricas
  • \( f : \Omega \to \mathcal{S},  \Omega \subset \mathbb{R}^2 \)
  • \( f(\Omega) = \mathcal{S} \subset \mathbb{R}^3 \)
  • Ejemplo: \( f_r(t) = (r \cos(t), r \sin(t)), 0 < t \leq 2 \pi \)
    • "Coordenadas Polares"
• Implícitas
  • \( f : \mathbb{R}^3 \to \mathbb{R} \)
  • \( S = \{ \mathbf{x} \in \mathbb{R^3} |  f(\mathbf{x}) = 0\} \)
  • Ejemplo: \( f(\mathbf{x}) = || \mathbf{x} ||_2 - 1 \)

Funciones de Distancia con Signo (SDF)

• \( f(\mathbf{x}) < 0 \iff \mathbf{x} \in \mathcal{S}^c \)
• \( f(\mathbf{x}) = 0 \iff \mathbf{x} \in \partial \mathcal{S} \)
• \( f(\mathbf{x}) > 0 \iff \mathbf{x} \in \mathcal{S} \)

• \( \max\{ f(\mathbf{x}), g(\mathbf{x}) \} \equiv \mathcal{S} \cup \mathcal{S}' \)
• \( \min\{ f(\mathbf{x}), g(\mathbf{x}) \} \equiv \mathcal{S} \cap \mathcal{S}' \)
• \( -f(\mathbf{x}) \equiv \mathcal{S} ^c \)

...

Muchísimo poder!

• Se pueden armar árboles que representan figuras k-dimensionales
• Llevado al extremo:

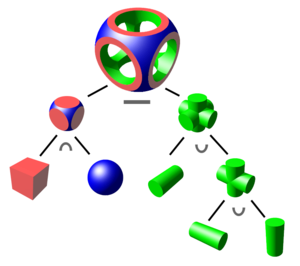
Ejemplos típicos:

• CAD
• Animaciones rápidas

Visualización

En general...

• Las computadoras usan mallas poligonales para representar superficies, en particular triangulares
• Por qué?
  • Más rápidas para muchas aplicaciones prácticas
  • 30 años de tecnología dedicada
• Sin embargo
  • Menos información a priori
  • Menos flexible
  • Es adicional a la reconstrucción

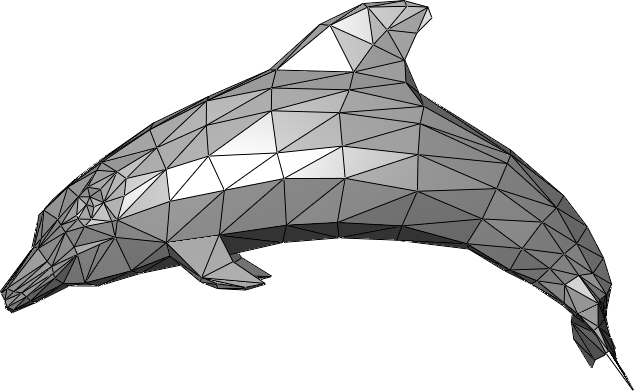
Isoextracción

• Necesitamos pasar de una SDF \( f : \mathbb{R}^3 \to \mathbb{R} \) a una malla poligonal
• Se usa Marching Squares / Cubes
  • Entrada: una grilla de evaluaciones de \( f \) en \( d \) dimensiones
  • Salida:
    • En 2D, lineas
    • En 3D, triangulos
• Lineal en el tamaño de la grilla
• Depende de la resolución

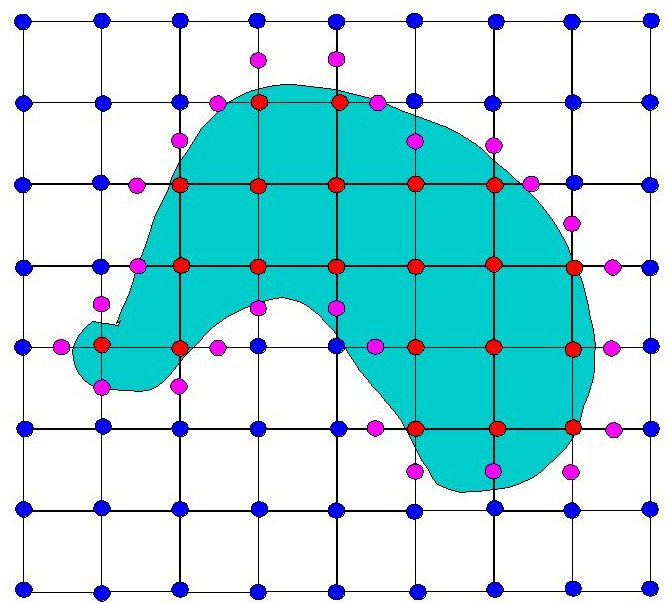
Aportes

• Demostraciones de varias propiedades de la Non-Convex Hull (NCH).
• Explicación de los vínculos entre la NCH y la Medial Axis Transform (MAT).
• Establecimos nuevos vínculos con el Power Diagram y el Multiplicatively Weighted Voronoi Diagram.
• Arreglamos problemas de Shrinking Ball (SB).

Aportes

• Desarrollamos Shrinking Planes (SP), para aproximar la NCH
  • Mejora de complejidad \( \Theta(N^2) \) a \( \mathcal{O}(N \log N) \).
• Proponemos una forma de comparar entre NCHs
• Experimentamos sobre los algoritmos propuestos y aplicamos la comparación anterior
  • Mucho más rápidos
  • Aproximan muy bien
• Experimentamos con la NCH para reconstrucción de superficies y comparamos con el estado del arte
  • Resultados muy prometedores, con lugar para mejora

Cápsula No-Convexa

o NCH (Non-Convex Hull)

Convexidad

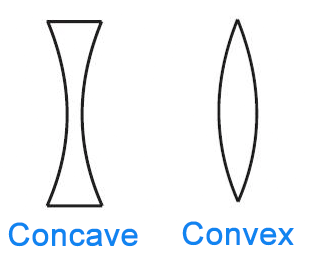
Conjunto Concavo

Conjunto Convexo

Convexo: todo par de puntos en el conjunto se une por una recta

Concavo: todo conjunto no convexo!

Cápsula Convexa

Convex Hull

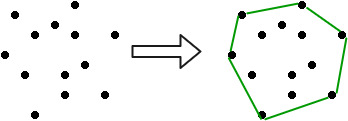
El conjunto convexo más chico que contiene a un conjunto de puntos

Cápsula Convexa Orientada

Oriented Convex Hull

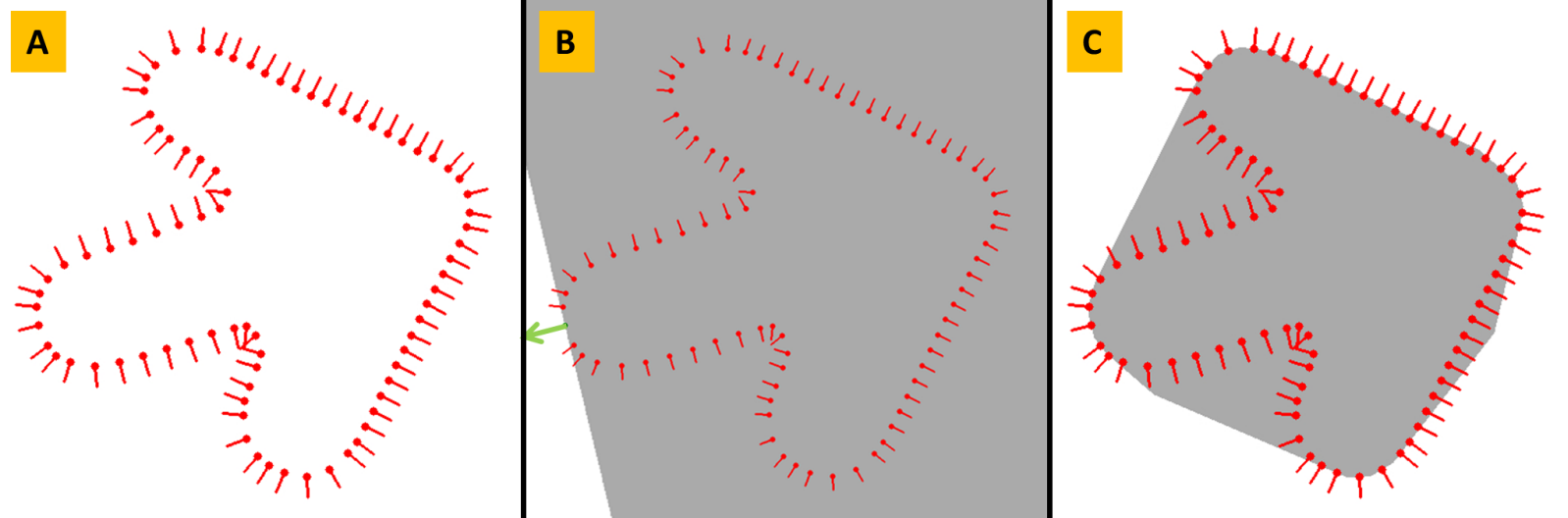
Cápsula No-Convexa

Non-Convex Hull

NCH SDF

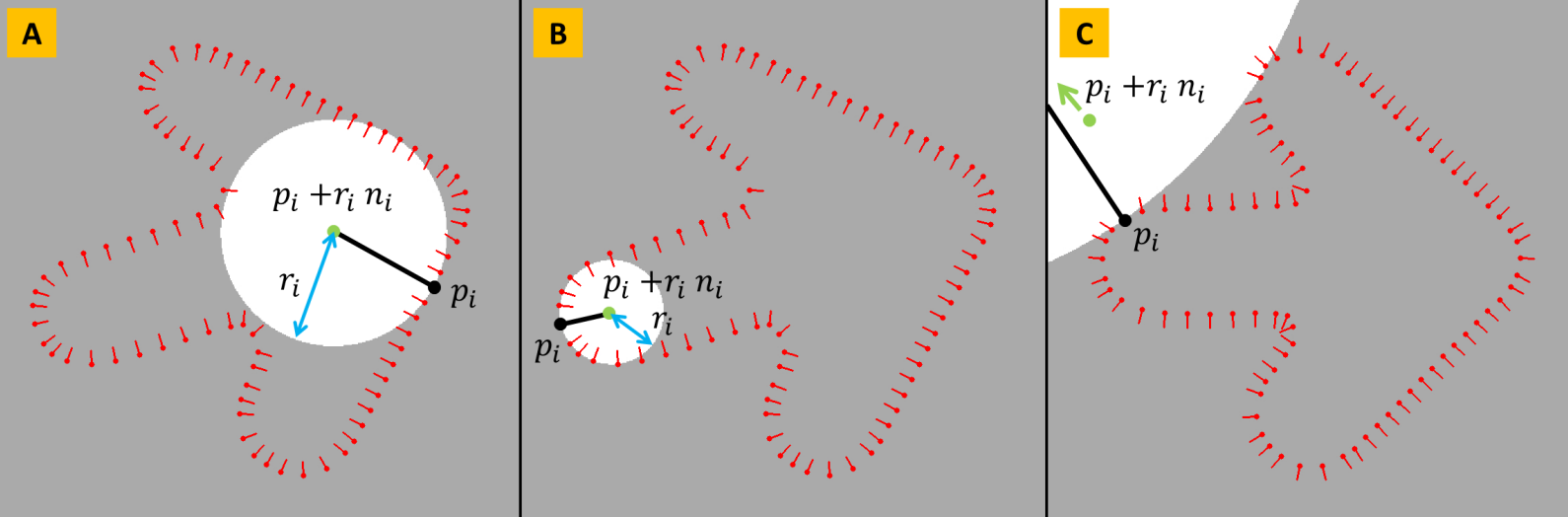
• Si \( \rho_i = 0 \), \( f_i(\mathbf{x}) \) es una SDF para un plano
• Si \( \rho_i > 0 \), \( f_i(\mathbf{x}) \) es una SDF para una esfera, centrada en \( \mathbf{p_i} + r_i \mathbf{n_i} \) y de radio \( r_i = \frac{1}{2 \rho_i}\)

Una sola elección: \( \rho_i \)

• Dijimos qué objeto matemático estamos usando.
• No cómo encontrarlo.
• 4 reglas
  • \( f_i(\mathbf{p_i}) = 0\)
  • \( \nabla f_i (\mathbf{p_i}) = \mathbf{n_i} \)
  • \( f_i(\mathbf{p_j}) \leq 0 \) para todo otro punto
  • \( \rho_i \geq 0 \) y además es maximal
• Si pedimos esas 4 propiedades, \( \rho_i \) queda univocamente determinado:

\( \rho_i = \max_{1 \leq j \leq N, j != i} \frac{\langle \mathbf{n_i}, \mathbf{p_j} - \mathbf{p_i} \rangle}{|| \mathbf{p_j} - \mathbf{p_i} ||^2} \)

En código...

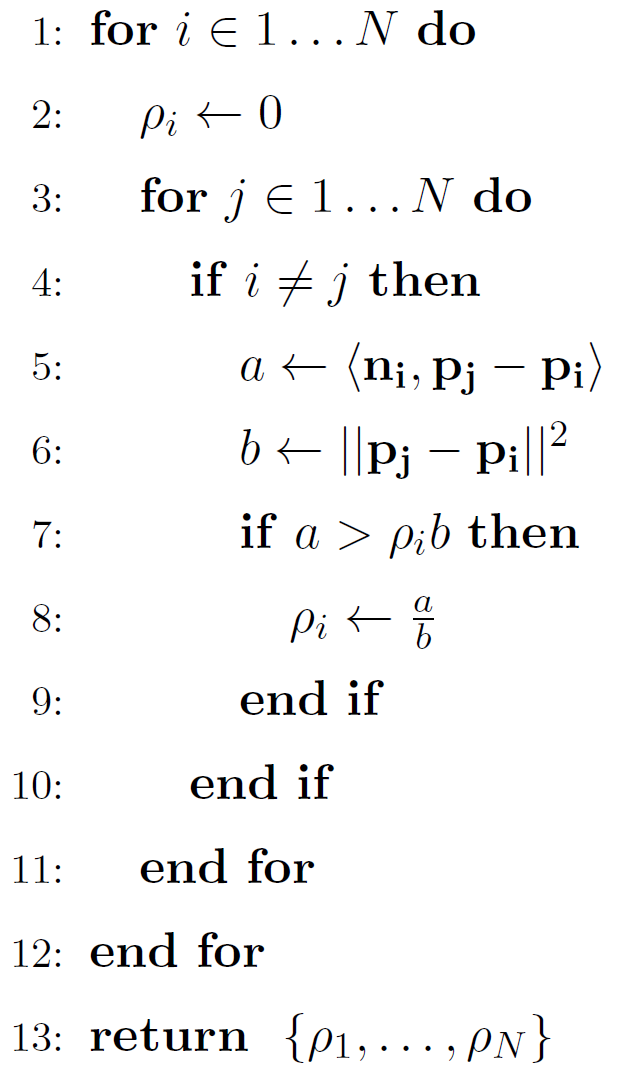
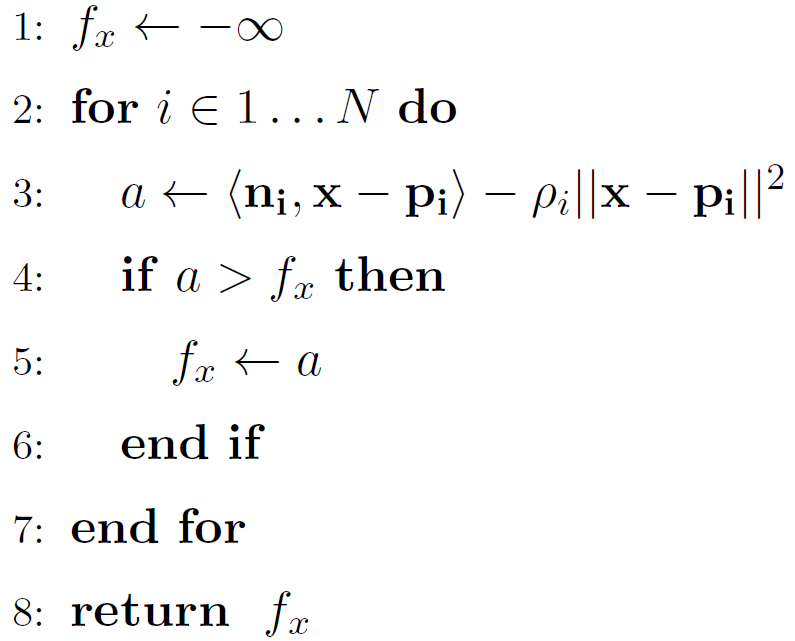
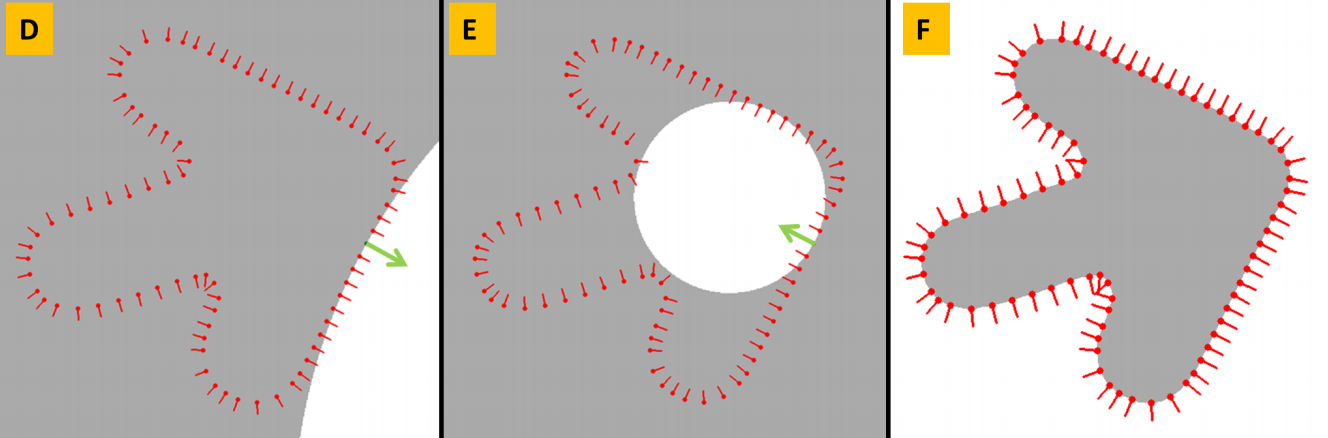
Estimar

SDF para \( \mathbf{x} \)

La intuición es...

1. Poner un plano en el punto, apuntando según su normal
2. Por cada punto distinto del actual:
   1. Si no está del lado de la normal:
      1. Saltearlo, ir al otro
   2. Reemplazar lo que haya por la esfera más grande que lo deje afuera o en el borde.

• Ponemos un plano o esfera que:
  • Deja a todos los puntos afuera o en el borde
  • Toca al punto actual
  • El "centro" está en la línea determinada por \( \mathbf{p_i} \) y \( \mathbf{n_i} \)

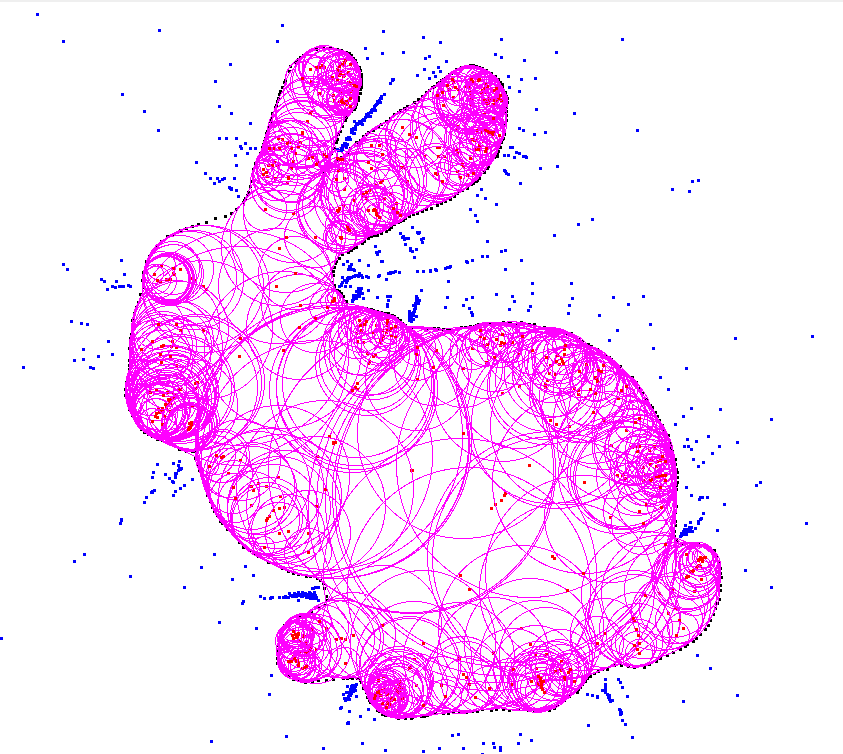
Naïve Non-Convex Hull

• Estimación de \( \rho_i \) como describimos
  • Fácil de programar (son 20 lineas!)
  • Trivialmente paralelizable
  • \( \Theta(N^2) \), con \( N \) la cantidad de puntos (lento!)
• Con condiciones sobre los puntos, reconstrucción sin error
• Invariante a roto-traslación, y predecible al escalar un objeto (menos mal!)

Hacia adentro

"Inner NCH"

Hacia afuera

"Outer NCH"

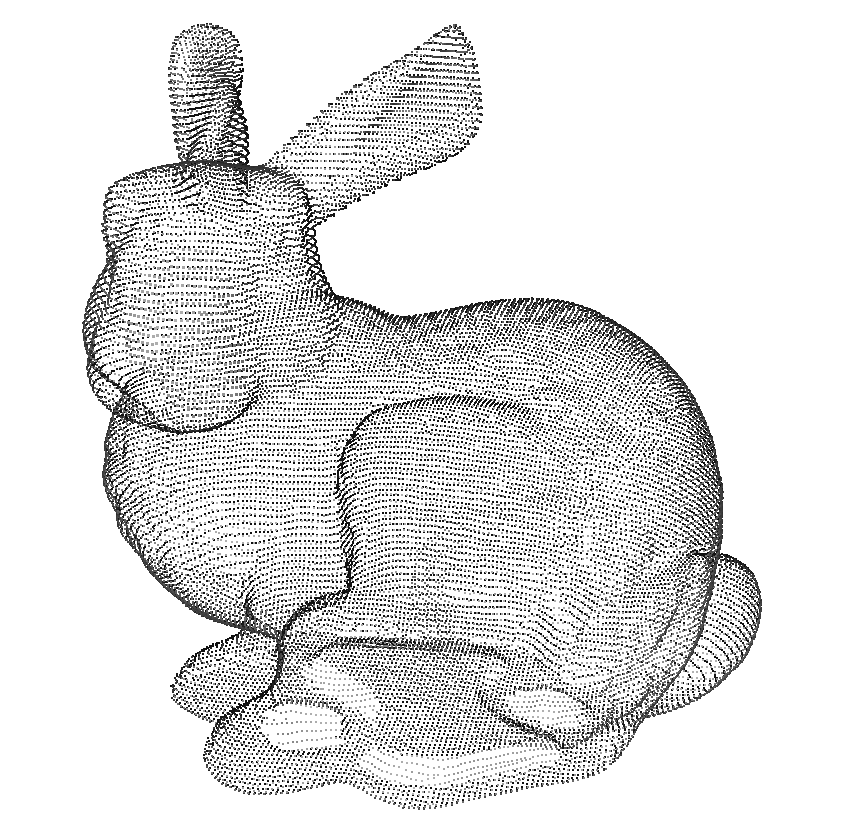
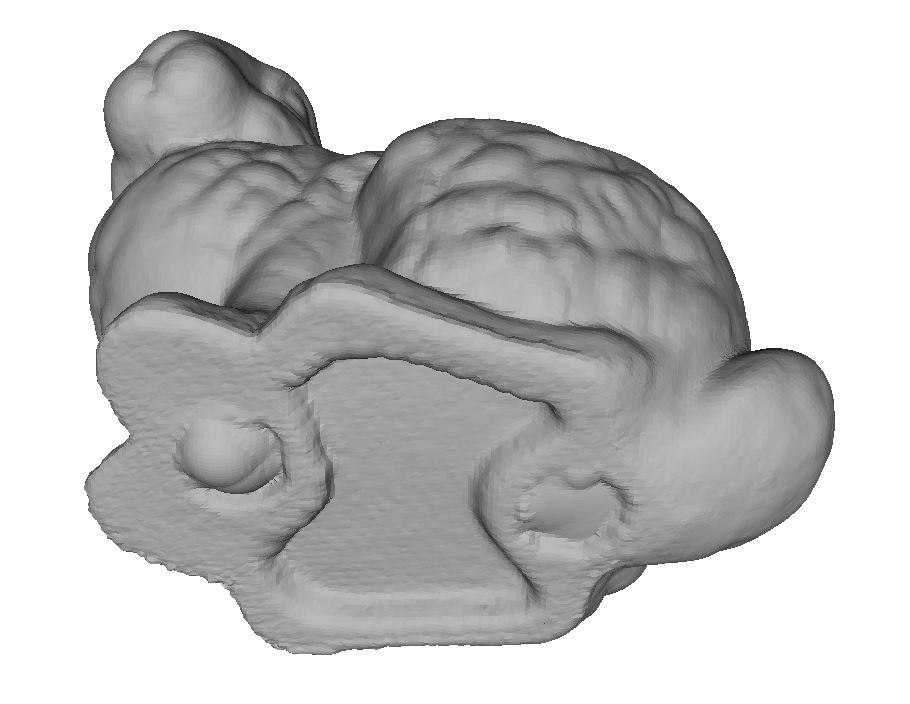
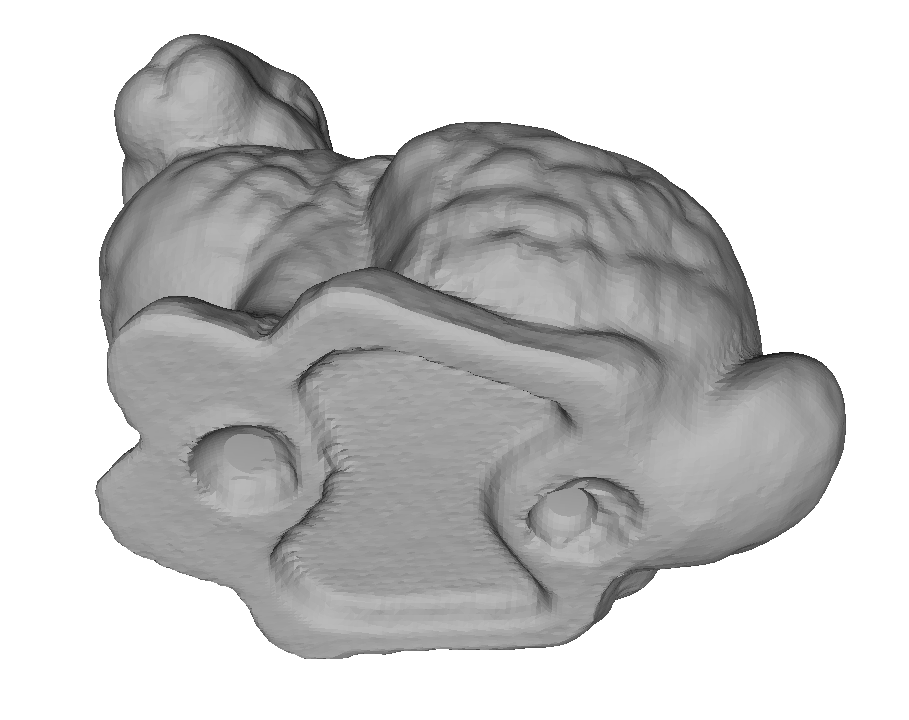
Nube de Puntos

Symmetric NCH

• En la práctica las normales se estiman y se orientan automáticamente
• No queremos que la reconstrucción dependa de la orientación
• Entonces:

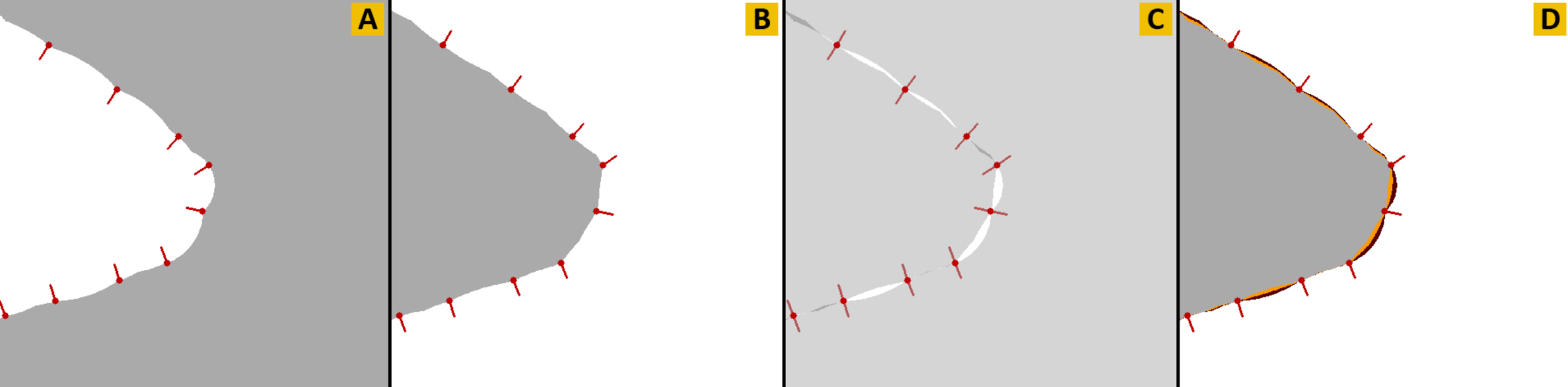
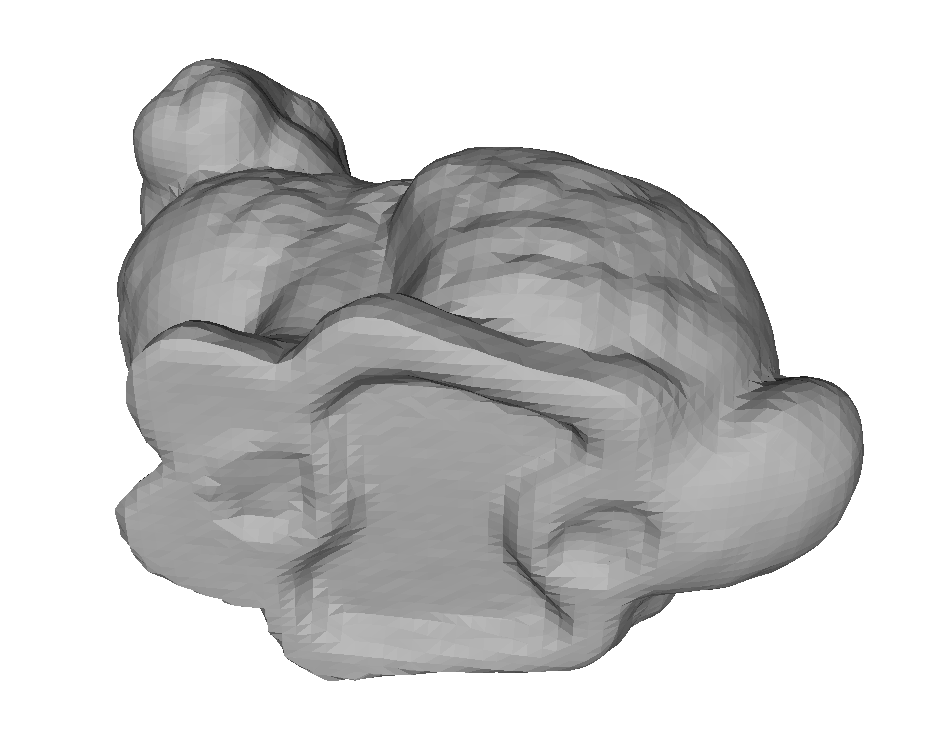
Shrinking Ball

para aproximación de la MAT

Medial Axis Transform

• Representación de una superficie como una unión de bolas k-dimensionales.
  • Unir los centros es el "esqueleto" de la figura
  • Cada bola es maximal (no puede agrandarse sin salir del objeto)
  • Toca por lo menos dos puntos de la superficie
  • ...

NCH = MAT

Cuando \( \rho_i > 0 \forall i\)

... Y hacia afuera...

• Podemos poner planos!
• Deja de ser equivalente, y produce reconstrucciones distintas
• Outer NCH es mucho mejor para aproximar bordes filosos
  • La MAT necesita infinitas bolas!

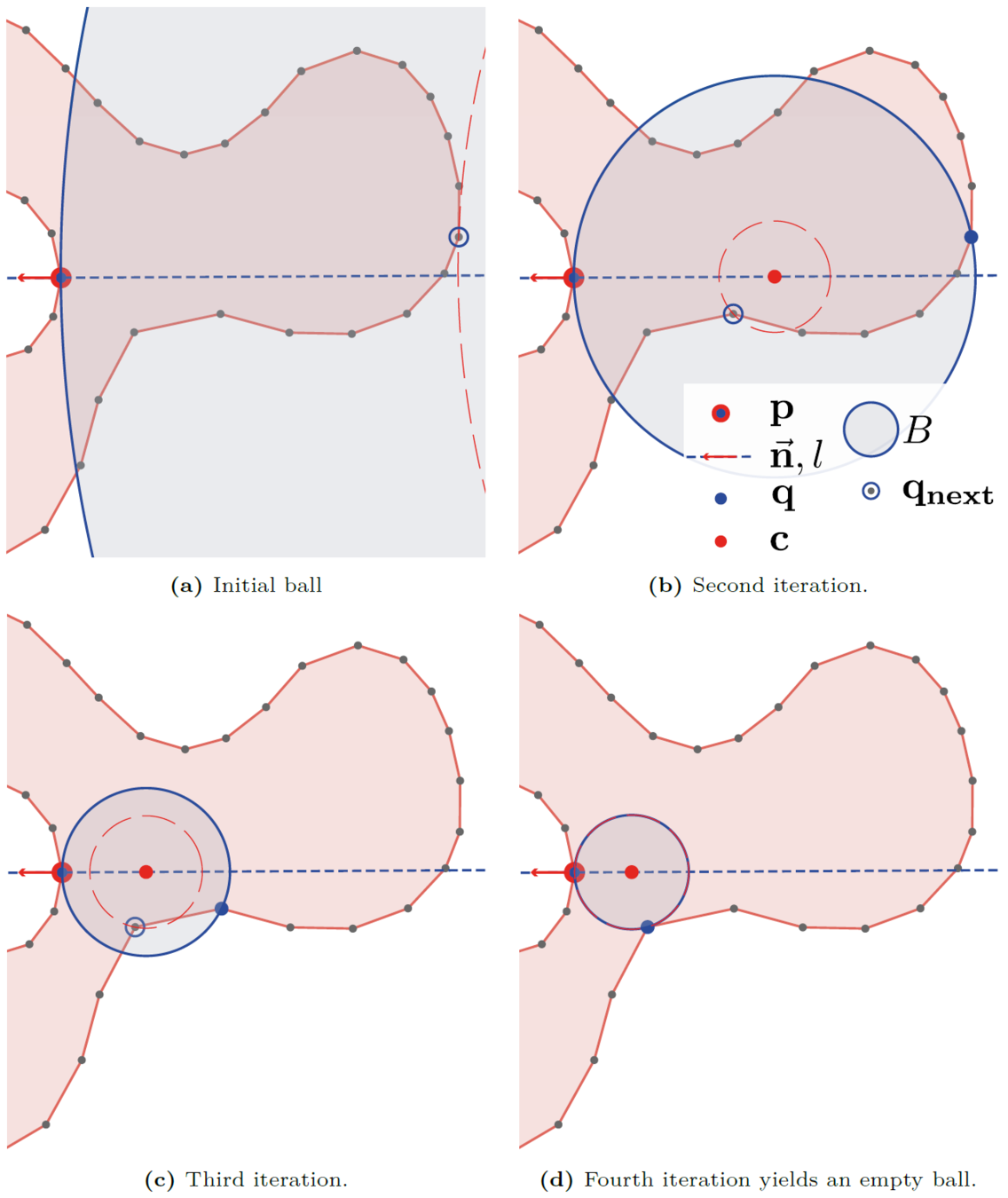
En código...

Cómo encontrar al vecino: K-D Tree

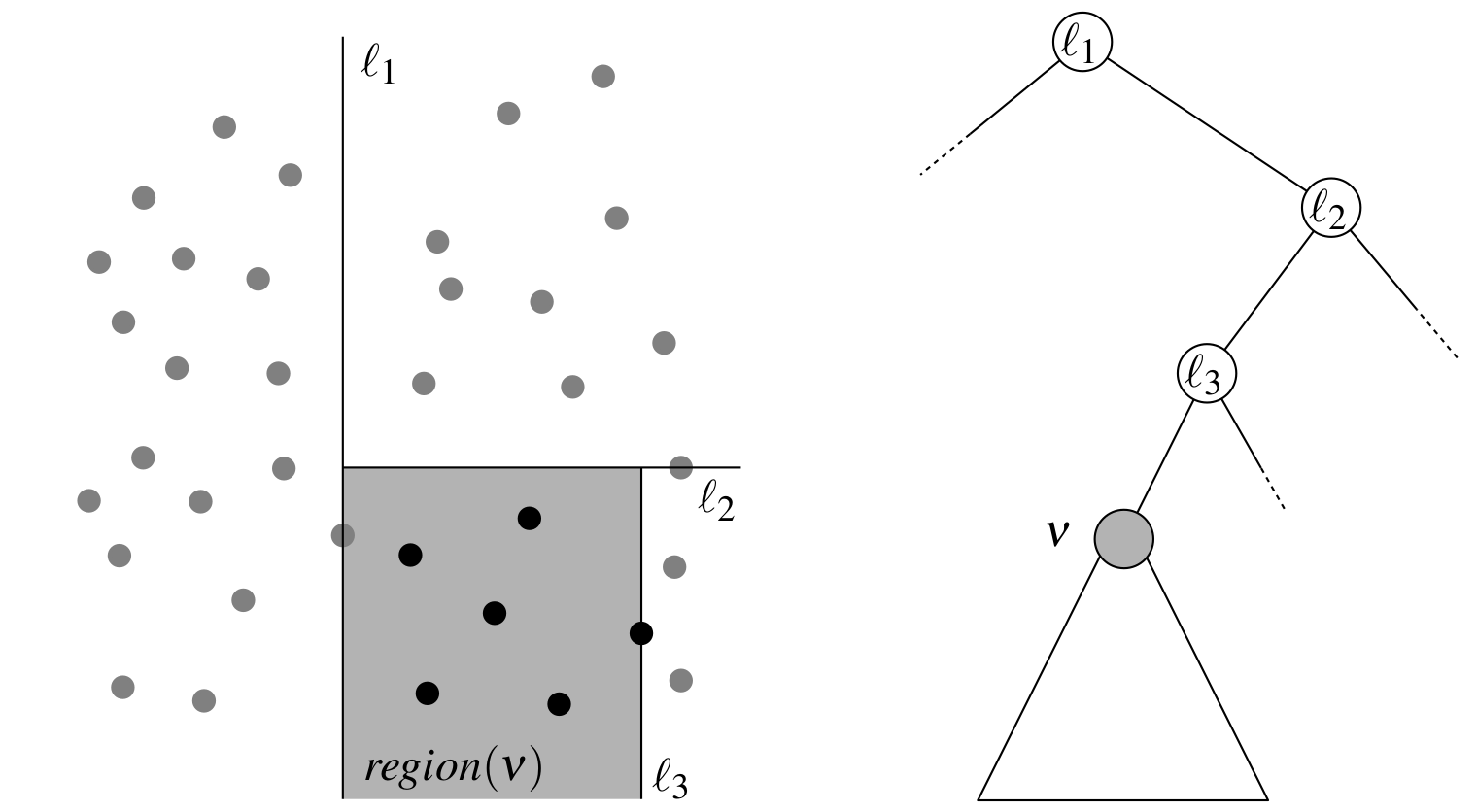
Construcción \( \mathcal{O}(N \log N) \)

Vecino más cercano, esperado \( \mathcal{O}(\log N) \), peor caso \( \mathcal{O}(N) \) 

Búsqueda por centro y radio, peor caso \( \mathcal{O}(N) \) 

En la práctica:

• Aproximados
• Muy rápidos

Pero esto tiene un problema...

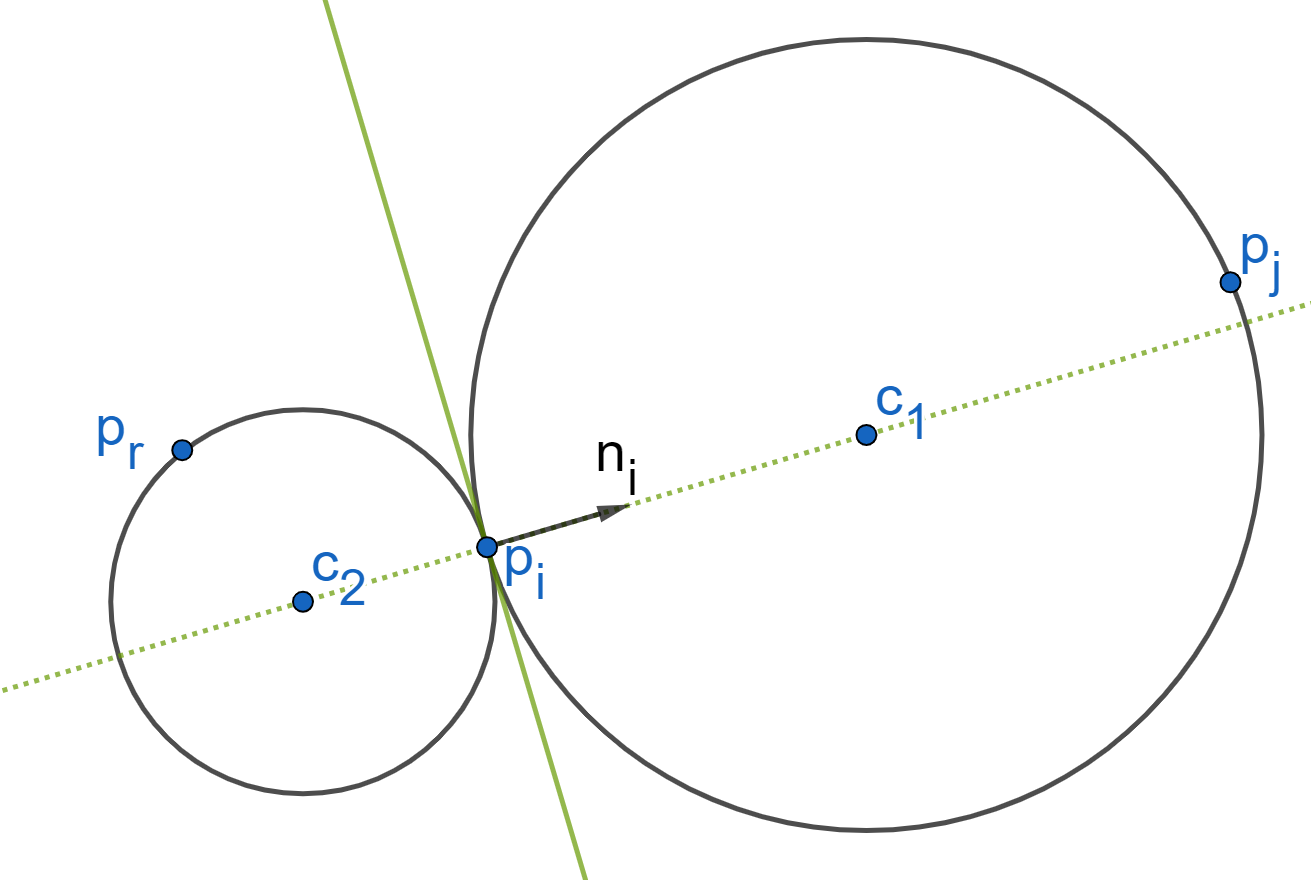
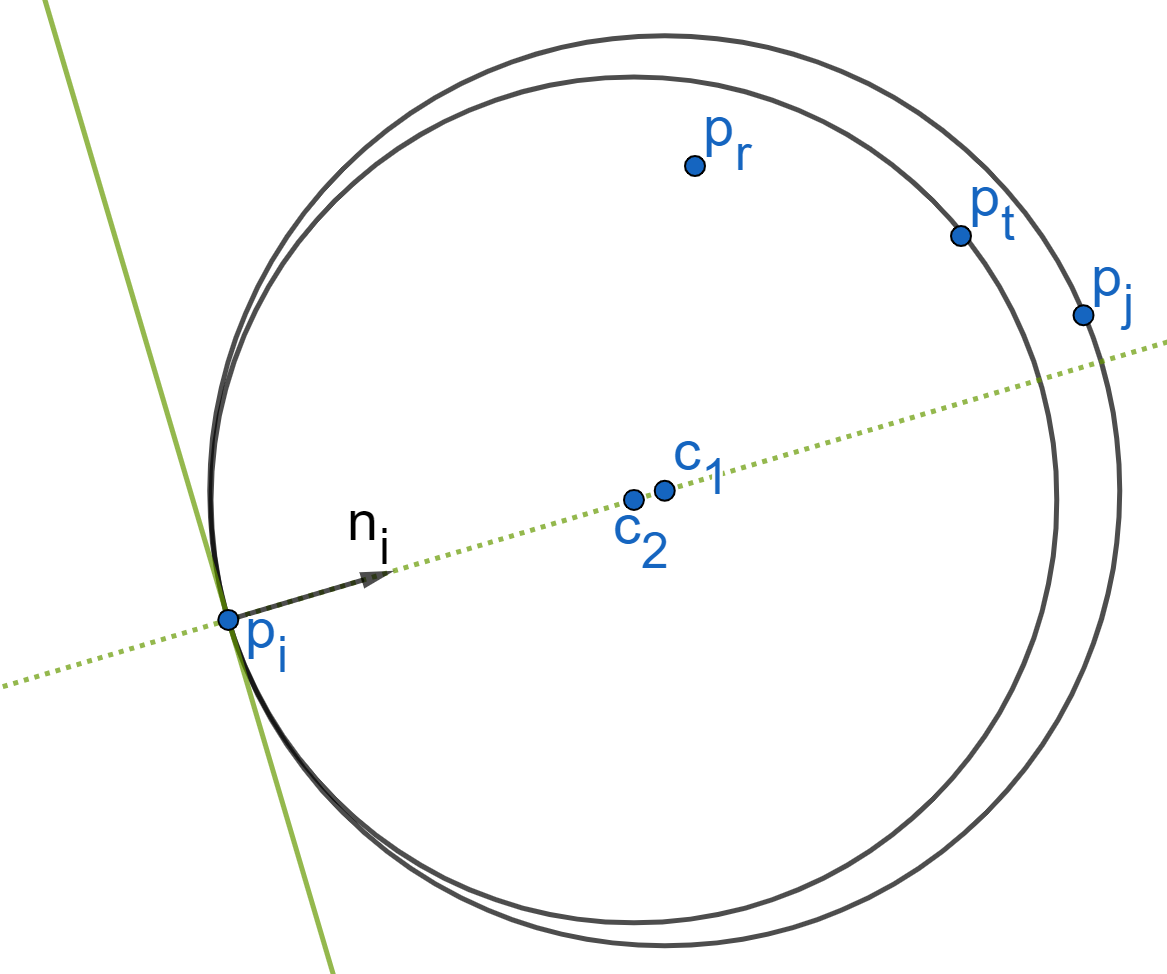
Es aproximado!, puede devolver \(p_r\), aunque deba devolver \(p_i\) o \(p_j\)

Pero esto tiene un problema...

En código...

Shrinking Ball

• Aproxima a un subconjunto de la MAT
  • Todas las bolas son maximales
  • Tocan en el punto
  • Los centros están en la dirección de la normal
• Cuando la densidad de muestreo tiende a infinito, converge a la MAT.
• Tiempo esperado \( \mathcal{O}(N \log N) \), peor caso \( \mathcal{O}(N^2) \)
  • En la práctica corre linearithmic

Shrinking Planes

para aproximación de la NCH

NCH = MAT + Planos

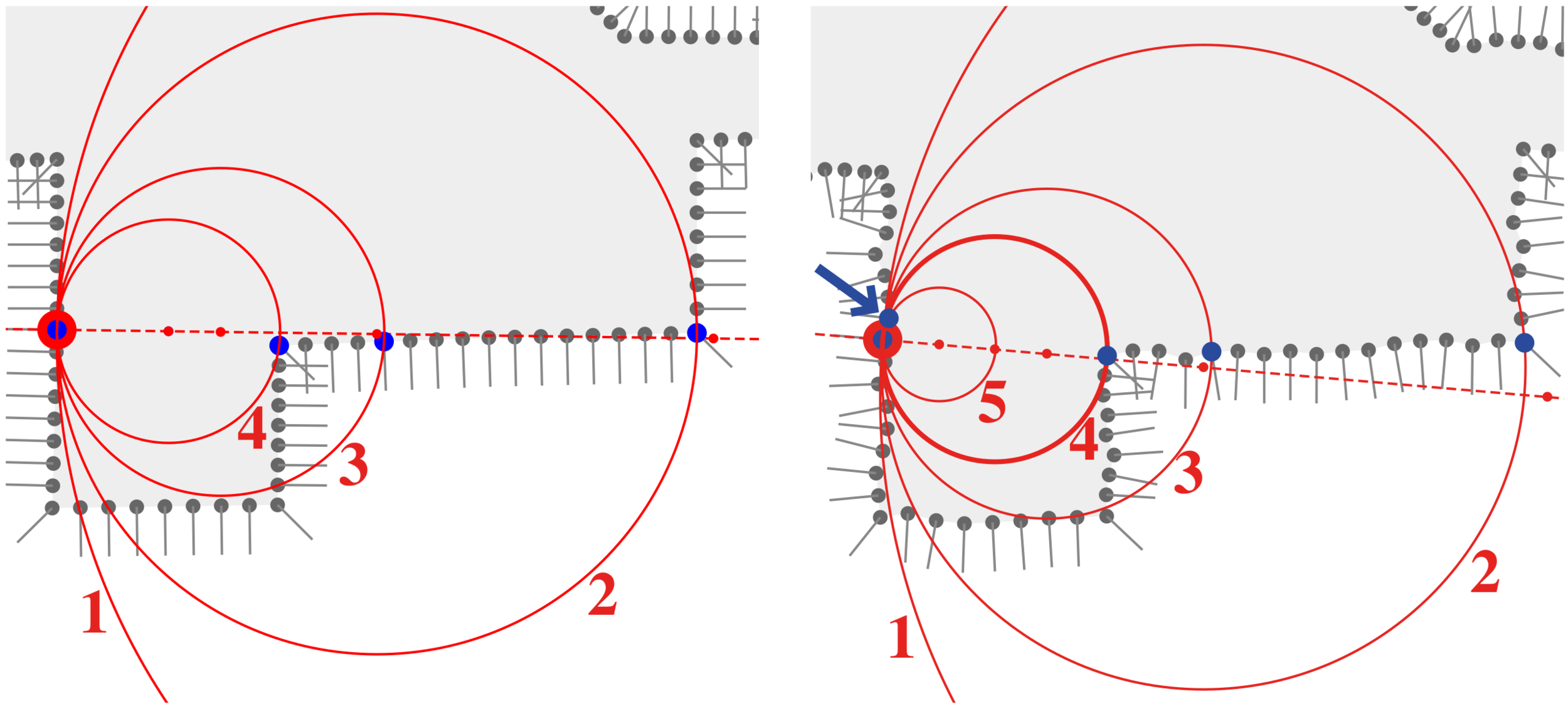
1. Empezamos con un radio inicial excesivamente grande, a propósito
2. Intentamos achicarlo usando Shrinking Ball
3. Pudimos achicarlo?
   1. Sí. Entonces, \( \rho_i = \frac{1}{2 r_i} \), con \( r_i \) el radio
   2. No. Entonces \( \rho_i = 0 \), ponemos un plano

En código...

En la practica...

• Funciona muy bien para la mayoría de los casos
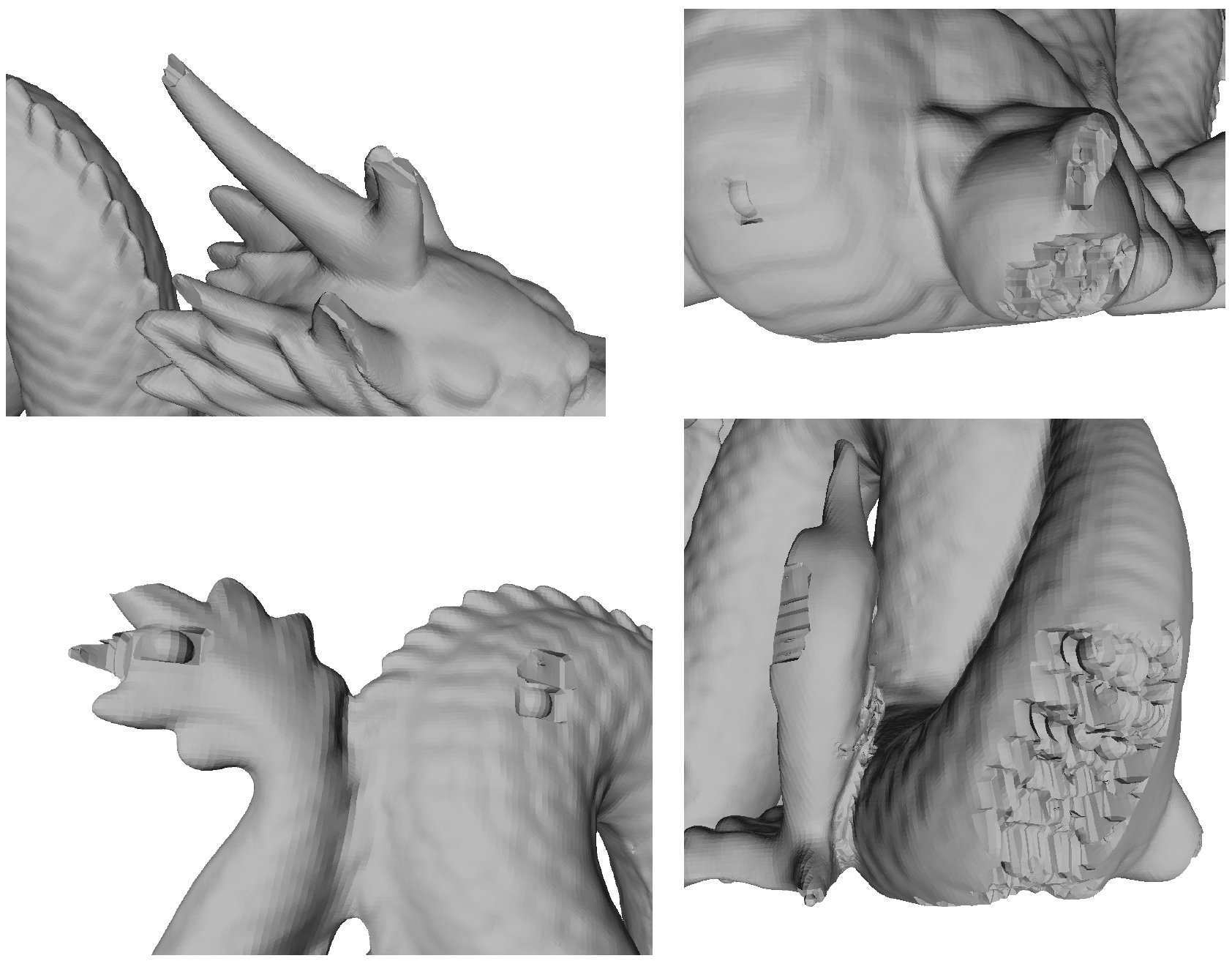
• Tiene problemas en ciertos casos, en general figuras complicadas:

Por qué?

• Los radios se vuelven cada vez más chicos.
  • La diferencia en general también
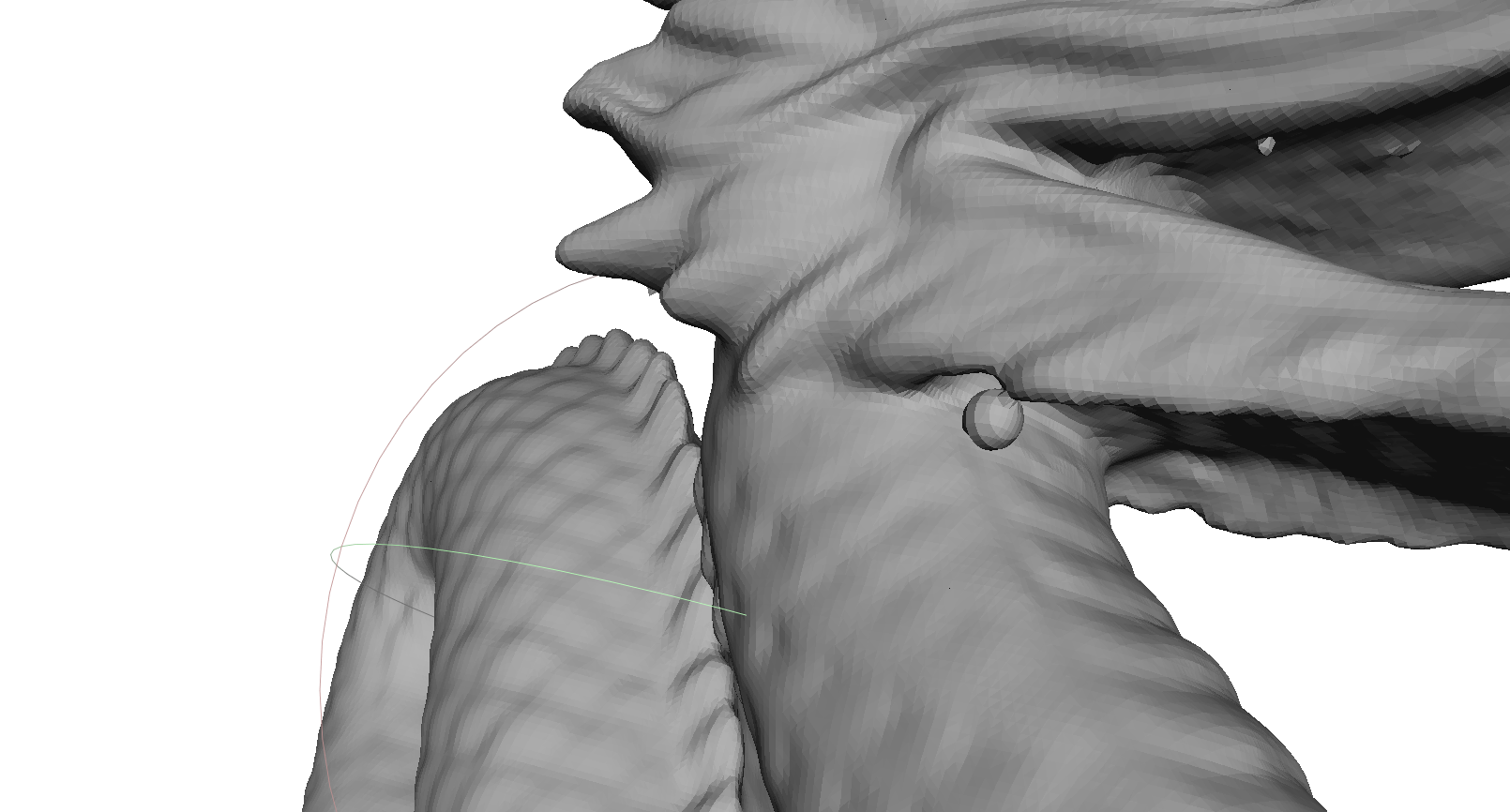
  • A veces, una diferencia muy chica entre un radio y el próximo hace que cortemos sin converger

En código...

La intuición es...

• Queremos evitar que haya puntos adentro
  • Bola muy grande, puntos muy dispersos
  • Como NCH, pero sobre menos puntos
• Shrinking Ball genera una bola razonablemente chica. Entonces:
  1. Hacer una búsqueda por radio
  2. Achicar sólo usando los que están adentro
  3. Repetir hasta que no pase más
• Si no limitamos la cantidad de resultados de la búsqueda, el algoritmo es equivalente a NNCH
• Cuadrático de vuelta
  • En la práctica funciona parecido a Shrinking Ball

Observaciones

• Ninguno de los algoritmos puede, a priori, obtener una mejor representación que NNCH
• Si SP o SB tienen error, sólo puede ser porque no achicaron lo suficiente
• Todos estos algoritmos van a hacer overfitting al ruido

Resultados

Cómo experimentamos

1

2

3

4

Malla Poligonal

Nube de Puntos

Estimación de Normales

Reconstrucción e Isoextracción

Qué medimos

Nos interesa comparar qué tan buenos somos desde múltiples puntos de vista:

• Velocidad
• Uso de recursos
• Calidad de reconstrucción
  • Sobre la aproximación de la NCH
• Calidad de la visualización
  • Sobre la superficie final, si la malla se ve parecida al original
  • En general, podemos modificar el algoritmo de isoextracción para obtener mejor calidad

Calidad de Aproximación

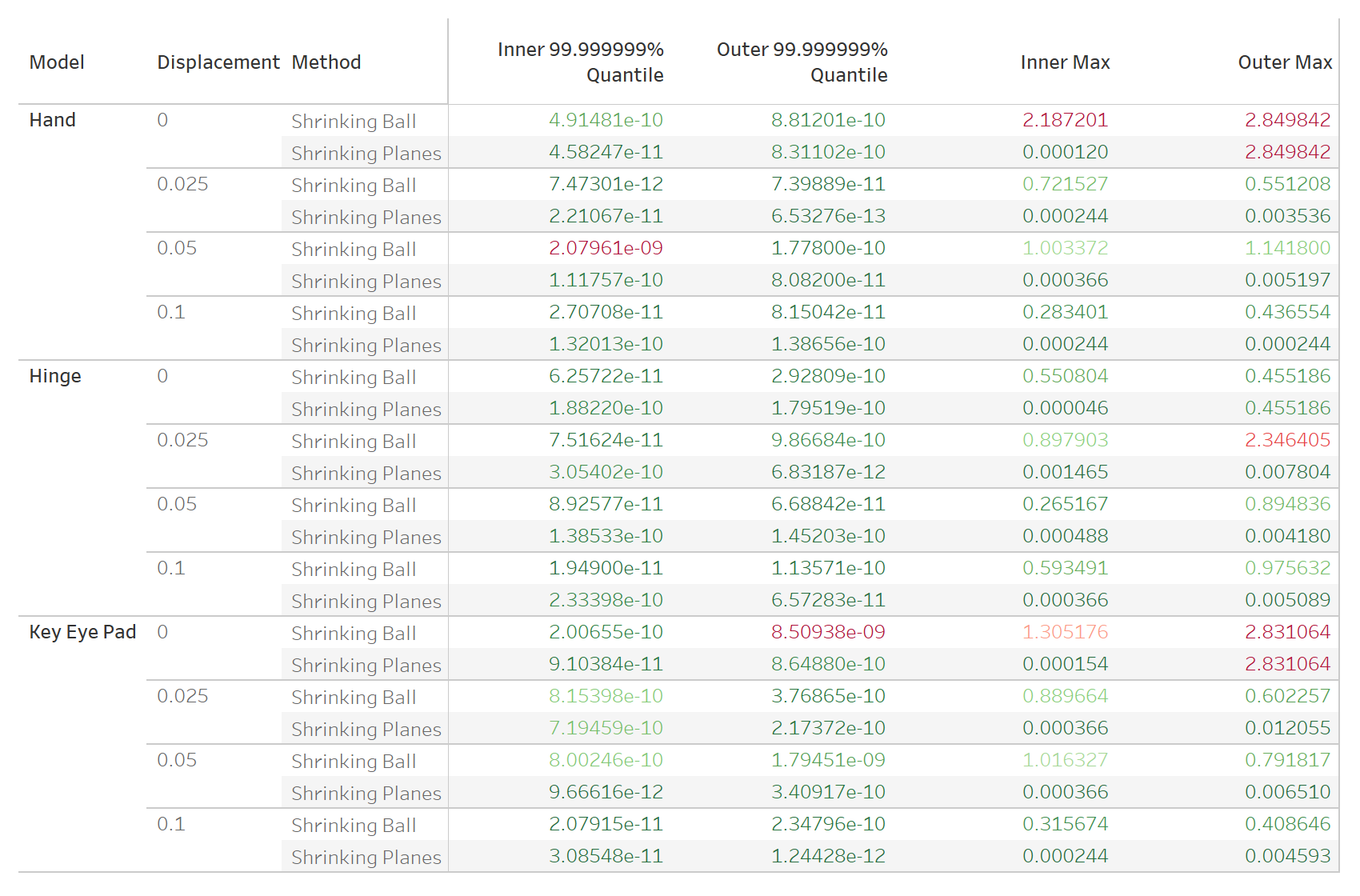
Si miramos \( | \rho_i^{+, \text{NNCH}} - \rho_i^{-, \text{SP}} | \), la distribución nos permite entender qué tan bien o mal aproximamos a la NCH, comparado con NNCH

En general, logramos errores menores a \( 10^{-11} \) en todos excepto 1 punto.

Además, SP es ordenes de magnitud mejor que SB

Calidad de Visualización

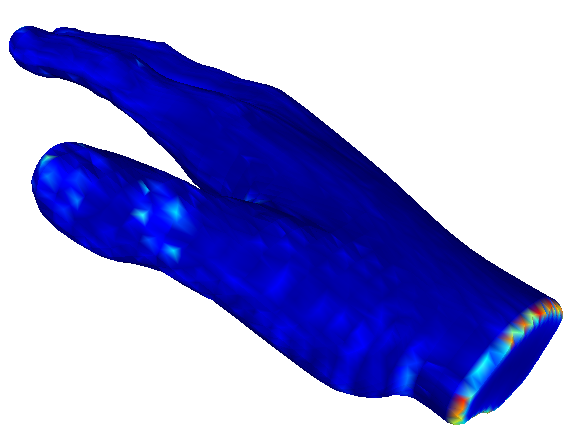
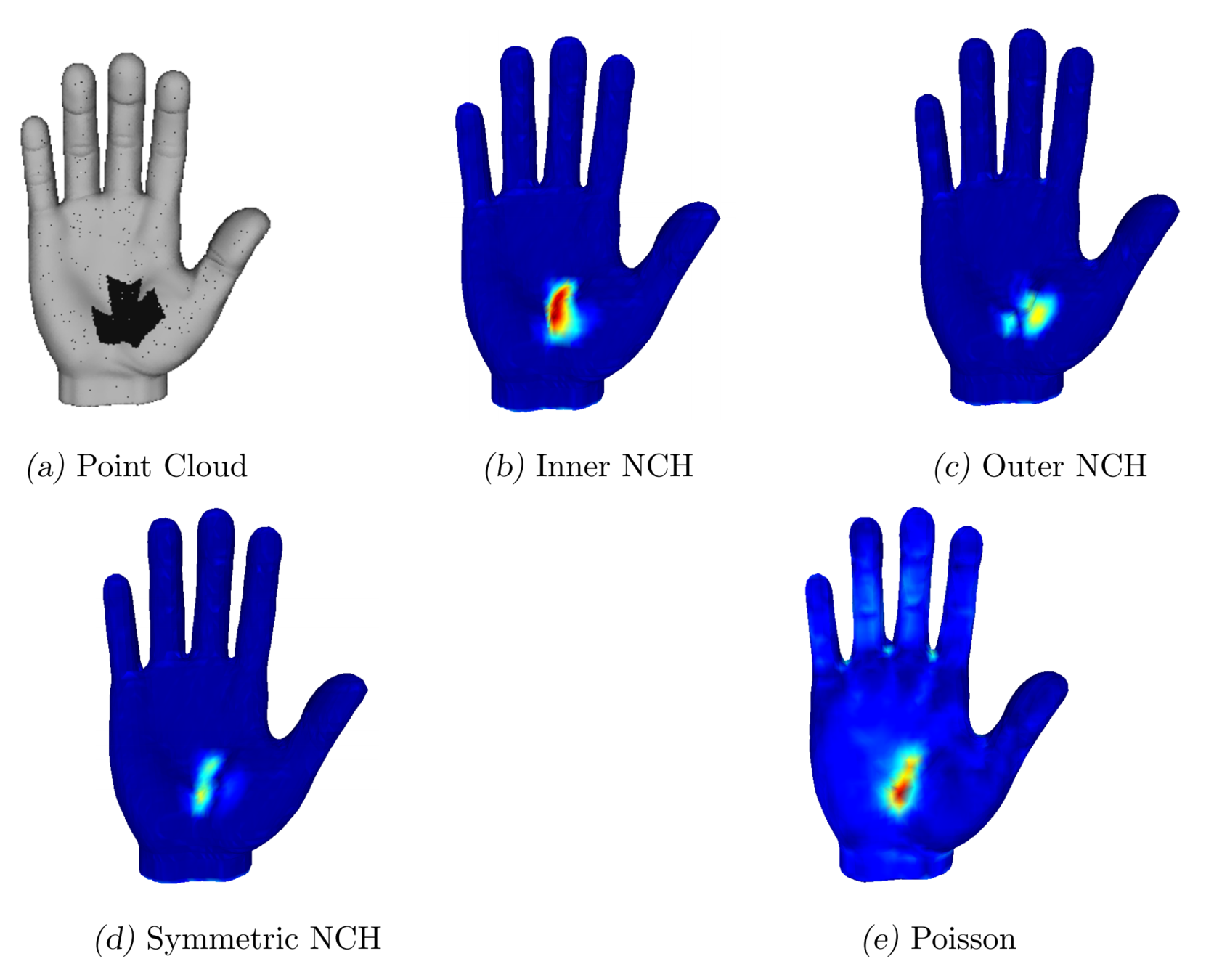
Experimentos con Ruido

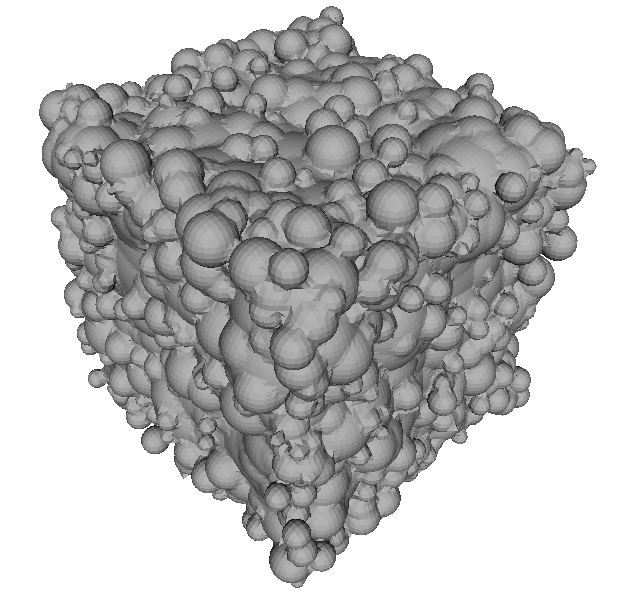
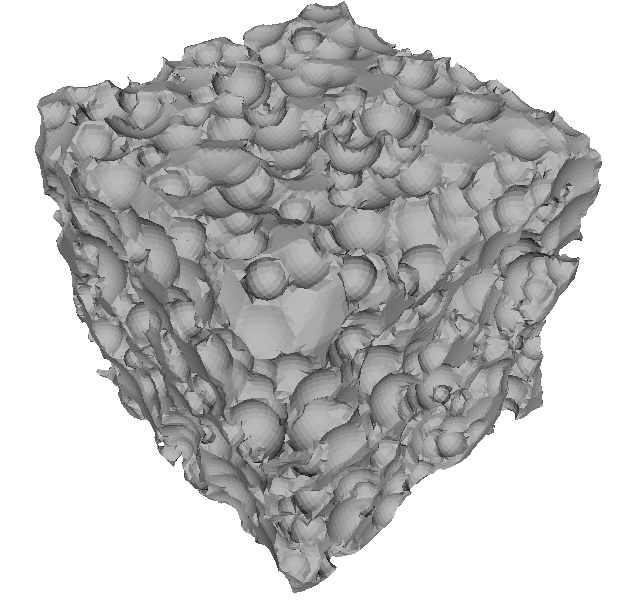
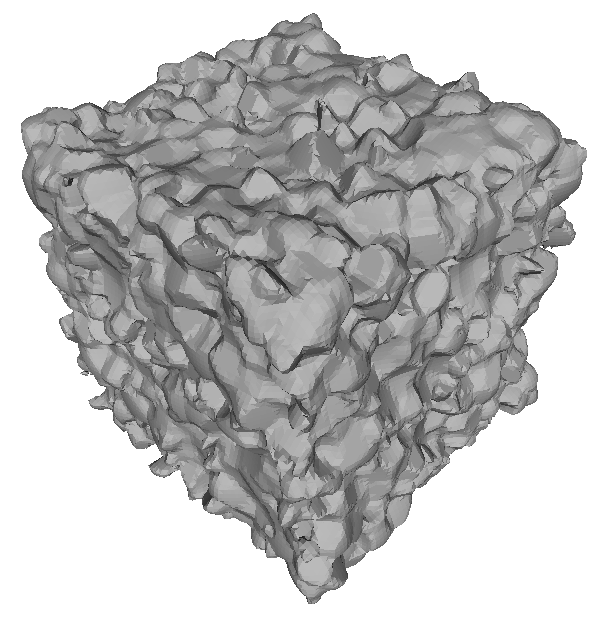
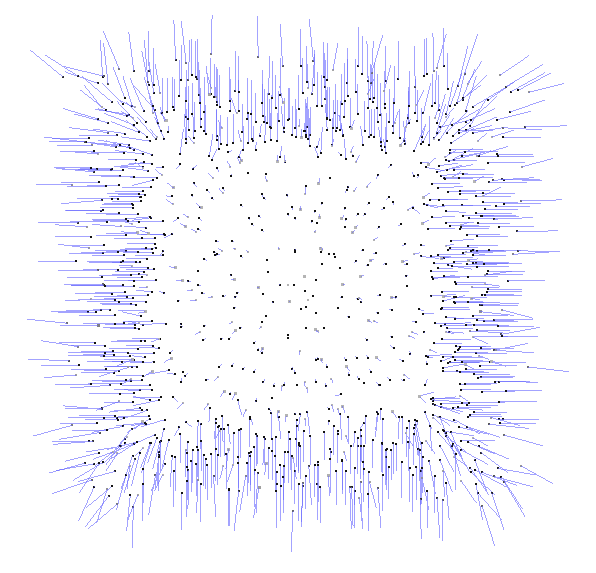
Inner NCH

Outer NCH

Symmetric NCH

Entrada

Estado del Arte

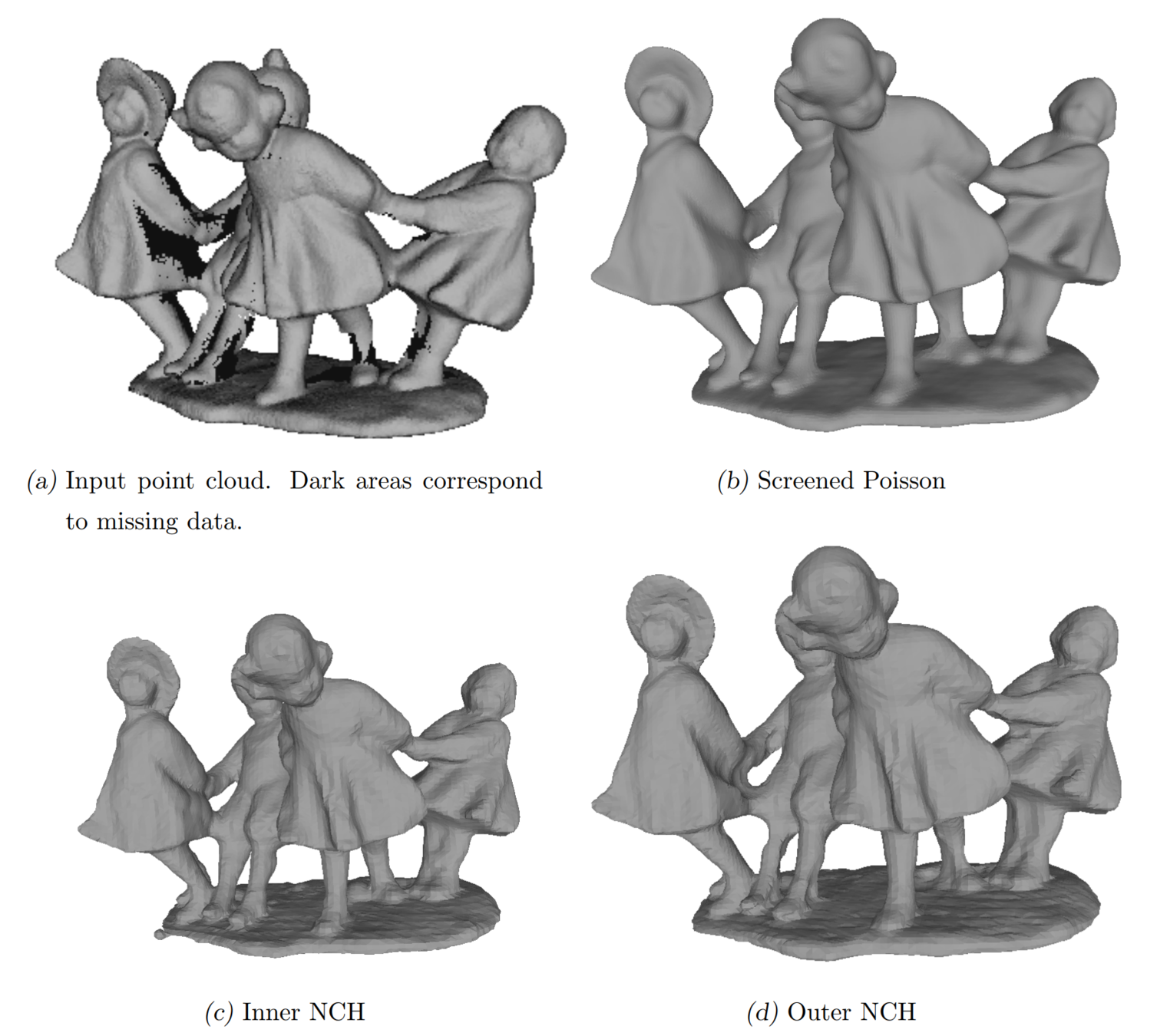
Experimentos con Falta de Datos

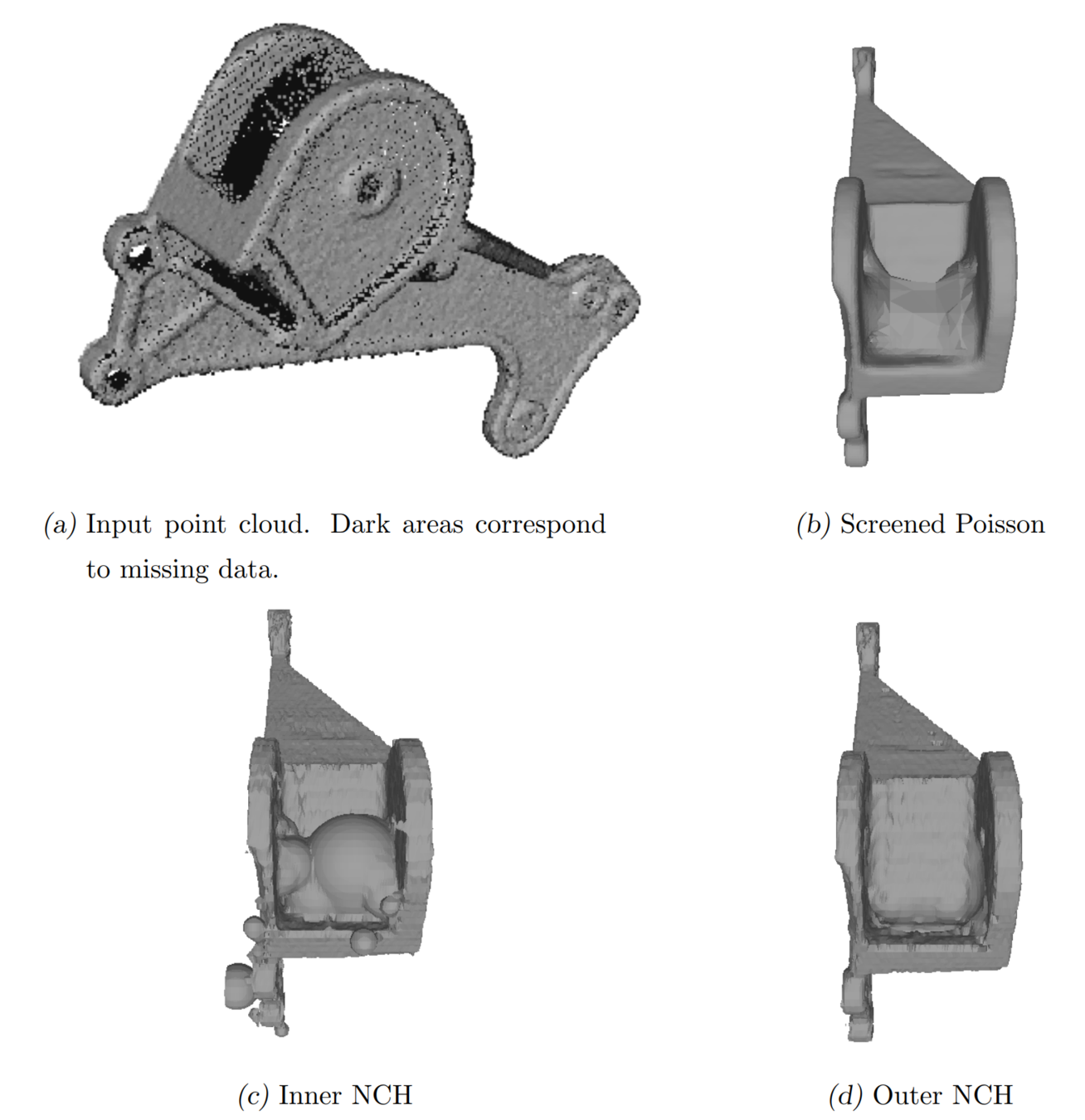
Experimentos con Escaneos Simulados

Experimentos con Escaneos Simulados

Uso de Memoria

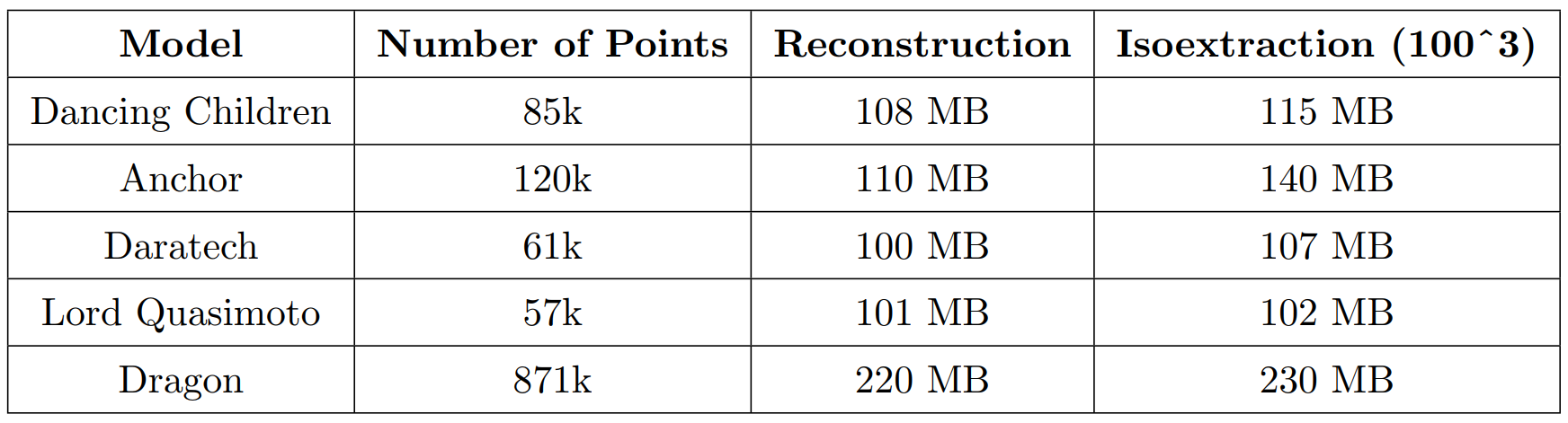
• Uso de memoria MUY bajo
• Además, \( \mathcal{O}(N) \)
• Ideal para:
  • GPUs, donde la cantidad de memoria es comparativamente restringida
  • Procesamiento de nubes de puntos a gran escala (i.e. cientos de millones)

Performance

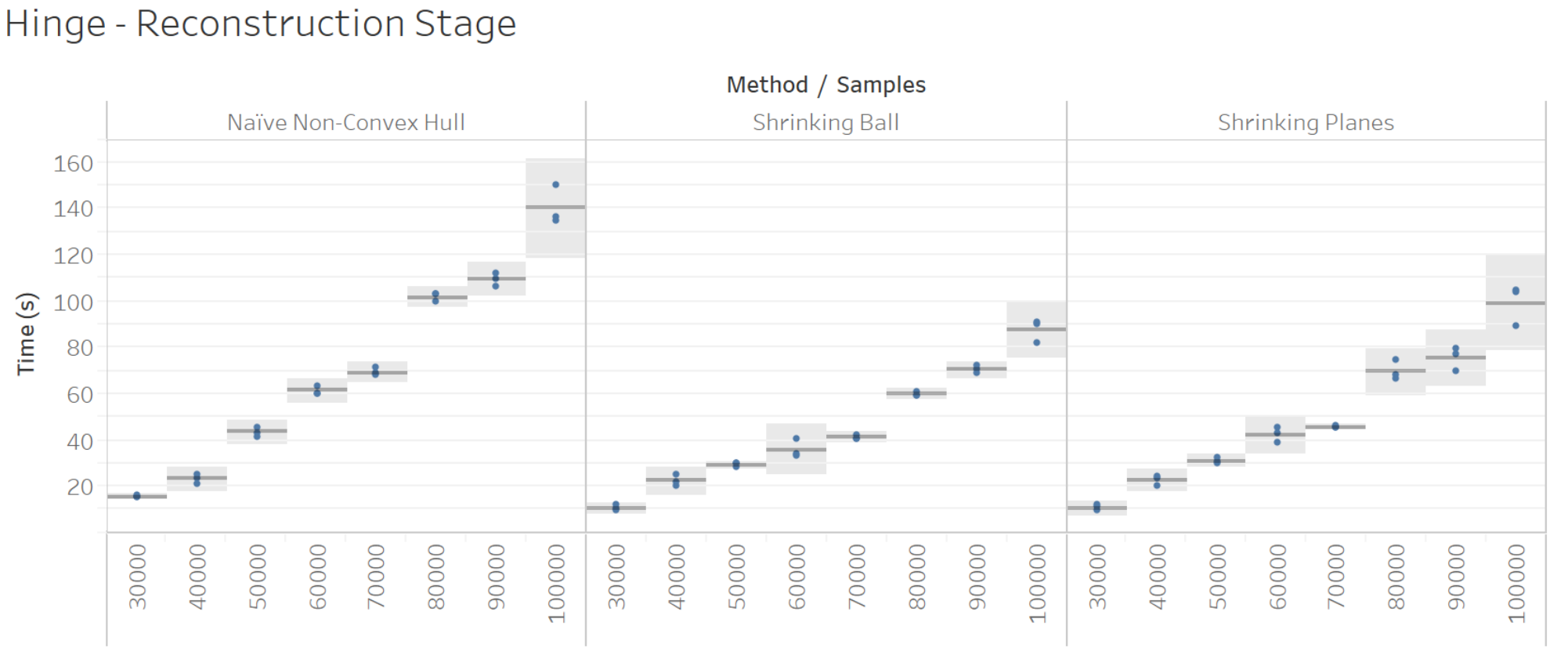
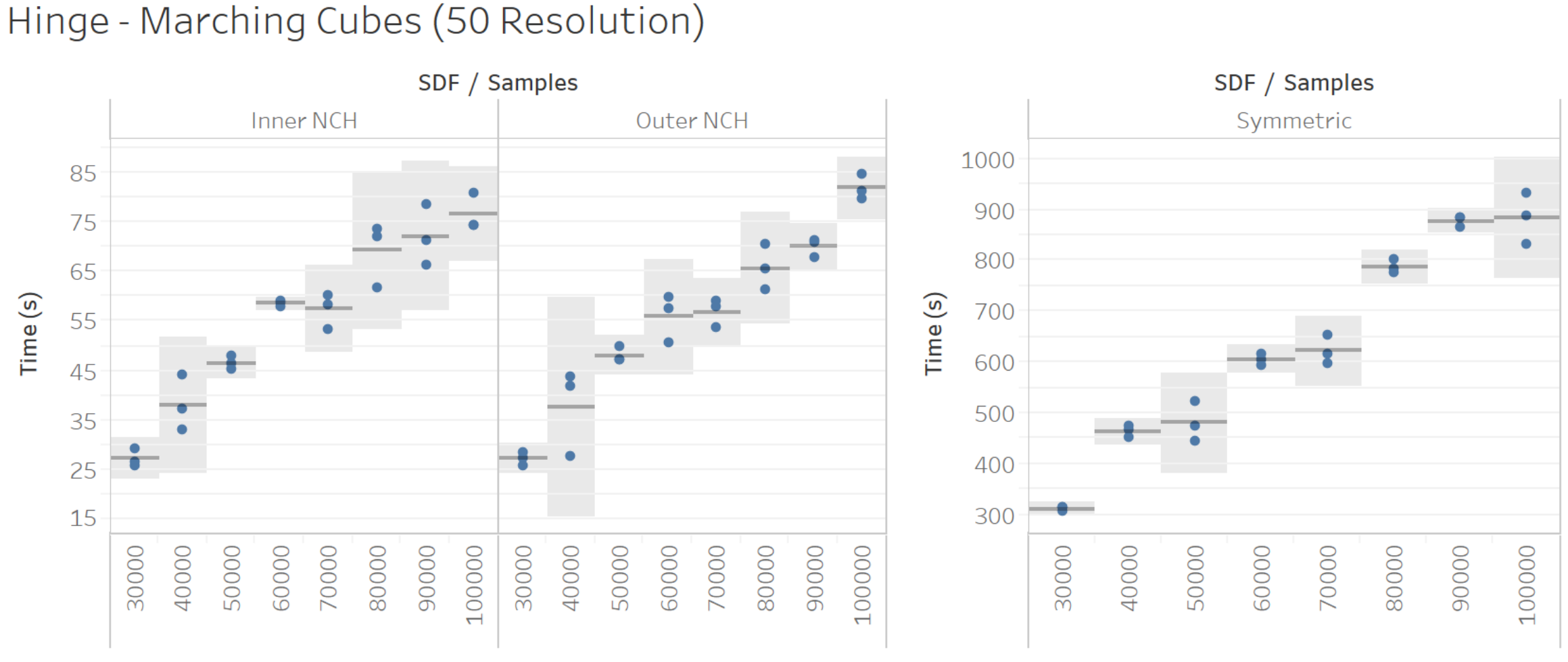
Conclusiones & Trabajo Futuro

Conclusiones

• Los nuevos métodos son sustancialmente más rápidos que NNCH
• Continúan siendo "embarrassingly parallel"
  • Amenos a GPU y multiprocesamiento
  • Muy bajo uso de recursos
• Vimos:
  • Calidad superior de Outer NCH relativo a Inner
  • La mejoría de la simétrica con respecto a ambos en presencia de ruido
• Las reconstrucciones son buenas cuando no hay ruido, pero la calidad empeora sustancialmente cuando sí lo hay

Trabajo a Futuro

• Implementación en GPU
  • Vimos que los algoritmos son paralelizables
  • Se puede bajar la velocidad de procesamiento al orden de decenas de milisegundos en la GPU
• Implementación Out-Of-Core
  • Para procesar nubes de puntos muy grandes, es necesario poder tener la información guardada en disco
• Reconstrucción adaptiva
  • En general, podemos eliminar puntos donde no necesitamos mayor nivel de detalle
• Isoextracción suave
  • El problema del ruido es la suavidad, y hay formas de evitarlo
• ... Y muchas más!, leer la tesis