How I learned to stop worrying and love the Gaussian Process
Jeriek Van den Abeele
Higgs&DM Meeting
Oslo – March 20, 2020

Correlation length-scale
Gaussian process prediction with uncertainty
Estimate from data! (kernels)
Global fits and the need for speed
Idea: consistent comparison of theories to all available data
- High-dimensional parameter space with varying phenomenology (e.g. MSSM-24)
- Quick prediction of next-to-leading order cross sections is crucial!
- Existing tools have drawbacks (Prospino: slow, NLL-fast: limited validity)
\(\mathcal{L} = \mathcal{L}_\mathsf{collider} \times \mathcal{L}_\mathsf{Higgs} \times \mathcal{L}_\mathsf{DM} \times \mathcal{L}_\mathsf{EWPO} \times \mathcal{L}_\mathsf{flavour} \times \ldots\)

Global fits and the need for speed
Idea: consistent comparison of theories to all available data
- High-dimensional parameter space with varying phenomenology (e.g. MSSM-24)
- Quick prediction of next-to-leading order cross sections is crucial!
- Existing tools have drawbacks (Prospino: slow, NLL-fast: limited validity)
\(\mathcal{L} = \mathcal{L}_\mathsf{collider} \times \mathcal{L}_\mathsf{Higgs} \times \mathcal{L}_\mathsf{DM} \times \mathcal{L}_\mathsf{EWPO} \times \mathcal{L}_\mathsf{flavour} \times \ldots\)

[GAMBIT, 1705.07919]

Fast estimate of SUSY (strong) production cross sections at NLO, and uncertainties from
- regression itself
- renormalisation scale
- PDF variation
- \(\alpha_s\) variation
Goal
$$ pp\to\tilde g \tilde g,\ \tilde g \tilde q_i,\ \tilde q_i \tilde q_j, $$
$$\tilde q_i \tilde q_j^{*},\ \tilde b_i \tilde b_i^{*},\ \tilde t_i \tilde t_i^{*}$$
Interface
Method
Pre-trained, distributed Gaussian processes
Stand-alone Python code, also implemented in GAMBIT
Processes
at \(\mathsf{\sqrt{s}=7/8/13/14}\) TeV
Soon public on GitHub!

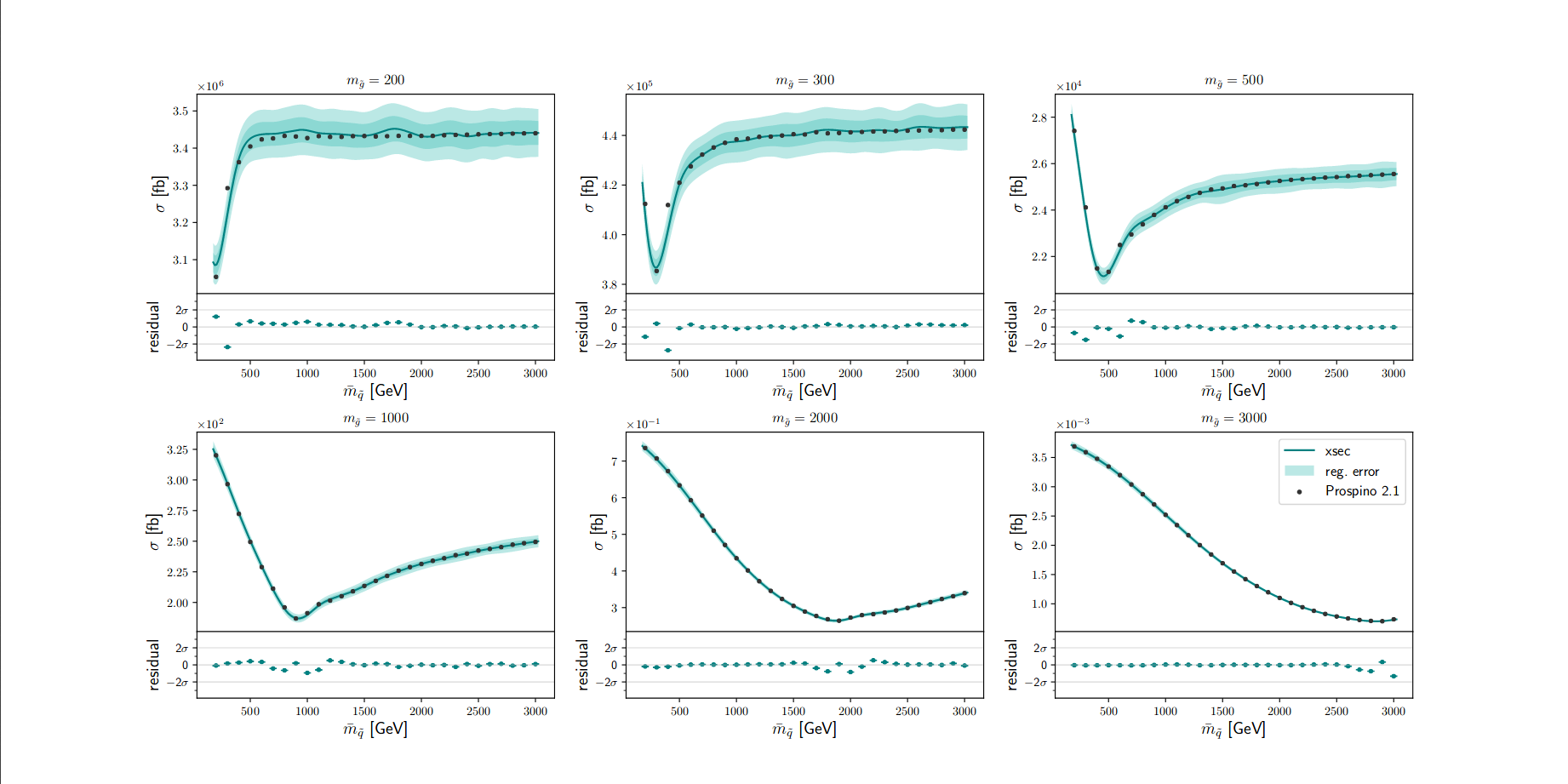
A quick example: gluino pair production at 13 TeV

Gaussian Processes 101
Radial Basis Function kernel
prior distribution over all functions
with the estimated smoothness
posterior distribution over functions
with updated \(m(\vec x)\)
data
Gaussian Processes 101

Matérn kernel
prior distribution over all functions
with the estimated smoothness
posterior distribution over functions
with updated \(m(\vec x)\)
data
All the scary math
Regression problem, with 'measurement' noise:
\(y=f(\vec x) + \varepsilon, \ \varepsilon\sim \mathcal{N}(0,\sigma_\varepsilon^2) \quad \rightarrow \quad \) infer \(f\), given data \(\mathcal{D} = \{\vec X, \vec y\}\)
Assume covariance structure expressed by a kernel function, like
Consider the data as a sample from a multivariate Gaussian distribution.
\([\vec x_1, \vec x_2, \ldots]\)
\([y_1, y_2, \ldots]\)
signal kernel
white-noise kernel
All the scary math
Regression problem, with 'measurement' noise:
\(y=f(\vec x) + \varepsilon, \ \varepsilon\sim \mathcal{N}(0,\sigma_\varepsilon^2) \quad \rightarrow \quad \) infer \(f\), given data \(\mathcal{D} = \{\vec X, \vec y\}\)
Training: optimise kernel hyperparameters by maximising the marginal likelihood
Posterior predictive distribution at a new point \(\vec x_*\) :
with
Implicit integration over points not in \(\vec X\)
[
All the scary math
Regression problem, with 'measurement' noise:
\(y=f(\vec x) + \varepsilon, \ \varepsilon\sim \mathcal{N}(0,\sigma_\varepsilon^2) \quad \rightarrow \quad \) infer \(f\), given data \(\mathcal{D} = \{\vec X, \vec y\}\)
Training: optimise kernel hyperparameters by maximising the marginal likelihood
Posterior predictive distribution at a new point \(\vec x_*\) :
with
Implicit integration over points not in \(\vec X\)
[

My kingdom for a good kernel ...
GPs allow us to use probabilistic inference to learn a function from data, in an interpretable, analytical, yet non-parametric Bayesian framework.
A GP model is fully specified once the mean function, kernel and its hyperparameters are chosen.
The probabilistic interpretation only holds under the assumption that the chosen kernel accurately describes the true correlation structure.
e.g. correlation length scales
My kingdom for a good kernel ...
The choice of kernel allows for great flexibility. But once chosen, it fixes the type of functions likely under the GP prior and determines the kind of structure captured by the model, e.g., periodicity and differentiability.


My kingdom for a good kernel ...
The choice of kernel allows for great flexibility. But once chosen, it fixes the type of functions likely under the GP prior and determines the kind of structure captured by the model, e.g., periodicity and differentiability.

My kingdom for a good kernel ...
The choice of kernel allows for great flexibility. But once chosen, it fixes the type of functions likely under the GP prior and determines the kind of structure captured by the model, e.g., periodicity and differentiability.
My kingdom for a good kernel ...
For our multi-dimensional case of cross-section regression, we get good results by multiplying Matérn (\(\nu = 3/2\)) kernels over the different mass dimensions:
The different lengthscale parameters \(l_d\) lead to automatic relevance determination for each feature: short-range correlations for important features over which the latent function varies strongly.
This is an anisotropic, stationary kernel. It allows for functions that are less smooth than with the standard squared-exponential kernel.

... with good hyperparameters


Short lengthscale, small noise
Long lengthscale, large noise
Underfitting, almost linear
Overfitting of fluctuations,
can lead to large uncertainties!
Typically, kernel hyperparameters are estimated by maximising the (log) marginal likelihood \(p( \vec y\ |\ \vec X, \vec \theta) \), aka the empirical Bayes method.
Alternative: MCMC integration over a range of \(\vec \theta\).
Gradient-based optimisation is widely used, but can get stuck in local optima and plateaus. Multiple initialisations can help, or global optimisation methods like differential evolution.
... with good hyperparameters
Typically, kernel hyperparameters are estimated by maximising the (log) marginal likelihood \(p( \vec y\ |\ \vec X, \vec \theta) \), aka the empirical Bayes method.
Alternative: MCMC integration over a range of \(\vec \theta\).
Gradient-based optimisation is widely used, but can get stuck in local optima and plateaus. Multiple initialisations can help, or global optimisation methods like differential evolution.
Global optimum: somewhere in between

The standard approach systematically underestimates prediction errors.
After accounting for the additional uncertainty from learning the hyper-parameters, the prediction error increases when far from training points.
... with good hyperparameters
[Wågberg+, 1606.03865]

... with good hyperparameters
Other tricks to improve the numerical stability of training:
- Normalising features and target values (avoid meaningful zero prior)
- Factoring out known behaviour from the target values
- Training on log-transformed targets, for extreme values and/or a large range, or to ensure positive predictions
Sometimes, a curious problem arises: negative predictive variances!
It is due to numerical errors when computing the inverse of the covariance matrix \(K\). When \(K\) contains many training points, there is a good chance that some of them are similar:
Nearly equal columns make \(K\) ill-conditioned. One or more eigenvalues \(\lambda_i\) are close to zero and \(K\) can no longer be inverted reliably. The number of significant digits lost is roughly the \(\log_{10}\) of the condition number
This becomes problematic when \(\kappa \gtrsim 10^8 \). In the worst-case scenario,
signal-to-noise ratio
number of points
GP Regularisation
GP Regularisation
- Use the Moore-Penrose matrix pseudo-inverse
- Disregard redundant points, averaging with zero uncertainty at repeated points
- Add a nugget/jitter term to the kernel
- White noise, can compute minimal value that reduces \(\kappa\) below \(\kappa_\mathsf{max}\)
- Can model discrepancy between GP model and latent function, e.g., regarding assumptions of stationarity and differentiability
- Avoid a large S/N ratio by adding a likelihood penalty term guiding the optimisation
- Nearly noiseless data is problematic ... Artificially increasing the noise level may be necessary, degrading the model a bit
[Mohammadi+, 1602.00853]
Workflow
Generating data
Random sampling
SUSY spectrum
Cross sections
Optimise kernel hyperparameters
Training GPs
GP predictions
Input parameters
Linear algebra
Cross section
estimates
Compute covariances
Training scales as \(\mathcal{O}(n^3)\), prediction as \(\mathcal{O}(n^2)\)

A balancing act
Mix of random samples with different priors in mass space
Evaluation speed
Sample coverage
Need to cover a large parameter space
Distributed Gaussian processes

[Liu+, 1806.00720]
Generalized Robust Bayesian Committee Machines
Aggregation model for dealing with large datasets
- Split the data into 1 global communication set \(\mathcal D_c\) and any number of local expert sets \(\mathcal D_i\)
- Train a separate GP on each data set
- Augment \(\mathcal D_i\) with \(\mathcal D_c\) , without re-training
- Combine predictions from the separate GPs, giving larger weight to experts with small uncertainty

Fast estimate of SUSY (strong) production cross sections at NLO, and uncertainties from
- regression itself
- renormalisation scale
- PDF variation
- \(\alpha_s\) variation
Goal
$$ pp\to\tilde g \tilde g,\ \tilde g \tilde q_i,\ \tilde q_i \tilde q_j, $$
$$\tilde q_i \tilde q_j^{*},\ \tilde b_i \tilde b_i^{*},\ \tilde t_i \tilde t_i^{*}$$
Interface
Method
Pre-trained, distributed Gaussian processes
Stand-alone Python code, also implemented in GAMBIT
Processes
at \(\mathsf{\sqrt{s}=7/8/13/14}\) TeV
Soon public on GitHub!
