Accelerating new physics searches with XSEC

Jeriek Van den Abeele

Spåtind 2020

Skeikampen – January 6

Based on work with A. Buckley,

I.A.V. Holm, A. Kvellestad,

A. Raklev, P. Scott,

J.V. Sparre

@JeriekVda

$$$

Time is money

Interpolation ...

Interpolation ... doesn't give prediction uncertainty!

Correlation length-scale

Correlation length-scale

Correlation length-scale

Correlation length-scale

Correlation length-scale

Correlation length-scale

Correlation length-scale

Correlation length-scale

Correlation length-scale

Estimate from data! (kernels)

Correlation length-scale

Estimate from data! (kernels)

Correlation length-scale

Gaussian process prediction with uncertainty

Estimate from data! (kernels)

Correlation length-scale

Gaussian process prediction with uncertainty

Estimate from data! (kernels)

Gaussian Processes 101

prior over all functions

with the estimated smoothness

posterior over functions

\mathcal{N}(\vec 0, \Sigma^2)

data

\mathcal{N}(\vec{\mu}', \Sigma'^2)

Radial Basis Function kernel

Gaussian Processes 101

prior over all functions

with the estimated smoothness

posterior over functions

\mathcal{N}(\vec 0, \Sigma^2)

data

\mathcal{N}(\vec{\mu}', \Sigma'^2)

Matérn kernel

New physics? Yes, please!

Global fits and the need for speed

Idea: consistent comparison of theories to all available data

  • High-dimensional parameter space with varying phenomenology             (e.g. MSSM-24)
  • Quick prediction of next-to-leading order cross sections is crucial!
  • Existing tools have drawbacks  (Prospino: slow, NLL-fast: limited validity)

\(\mathcal{L} = \mathcal{L}_\mathsf{collider} \times  \mathcal{L}_\mathsf{Higgs} \times  \mathcal{L}_\mathsf{DM} \times  \mathcal{L}_\mathsf{EWPO} \times  \mathcal{L}_\mathsf{flavour} \times \ldots\)

Global fits and the need for speed

Idea: consistent comparison of theories to all available data

  • High-dimensional parameter space with varying phenomenology             (e.g. MSSM-24)
  • Quick prediction of next-to-leading order cross sections is crucial!
  • Existing tools have drawbacks  (Prospino: slow, NLL-fast: limited validity)

\(\mathcal{L} = \mathcal{L}_\mathsf{collider} \times  \mathcal{L}_\mathsf{Higgs} \times  \mathcal{L}_\mathsf{DM} \times  \mathcal{L}_\mathsf{EWPO} \times  \mathcal{L}_\mathsf{flavour} \times \ldots\)

[GAMBIT, 1705.07919]

CMSSM

Fast estimate of SUSY (strong) production cross sections at NLO, and uncertainties from

  • regression itself
  • renormalisation scale
  • PDF variation
  • \(\alpha_s\) variation

Goal

$$ pp\to\tilde g \tilde g,\ \tilde g \tilde q_i,\ \tilde q_i \tilde q_j, $$

$$\tilde q_i \tilde q_j^{*},\ \tilde b_i \tilde b_i^{*},\ \tilde t_i \tilde t_i^{*}$$

Interface

Method

Pre-trained, distributed Gaussian processes

Stand-alone Python code, also implemented in GAMBIT

Processes

at \(\mathsf{\sqrt{s}=7/8/13/14}\) TeV

Soon public on GitHub!

Workflow

Generating data

Random sampling

SUSY spectrum

Cross sections

Optimise kernel hyperparameters

Training GPs

GP predictions

Input parameters

Linear algebra

Cross section

estimates

Compute covariances

Workflow

Generating data

Random sampling

SUSY spectrum

Cross sections

Optimise kernel hyperparameters

Training GPs

GP predictions

Input parameters

Linear algebra

Cross section

estimates

Compute covariances

XSEC

Training scales as \(\mathcal{O}(n^3)\), prediction as \(\mathcal{O}(n^2)\)

A balancing act

Mix of random samples with different priors in mass space

Evaluation speed

Sample coverage

Need to cover a large parameter space

Distributed Gaussian processes

Training scales as \(\mathcal{O}(n^3)\), prediction as \(\mathcal{O}(n^2)\)

A balancing act

Mix of random samples with different priors in mass space

Evaluation speed

Sample coverage

Need to cover a large parameter space

Distributed Gaussian processes

[Liu+, 1806.00720]

Generalized Robust Bayesian Committee Machine

Plots, plots, plots

XSEC: the cross-section evaluation code

\tilde g \tilde g

XSEC: the cross-section evaluation code

\tilde g \tilde g

XSEC: the cross-section evaluation code

\tilde g \tilde g

XSEC: the cross-section evaluation code

\tilde q \tilde q

XSEC: the cross-section evaluation code

\tilde g \tilde q
\tilde g \tilde q

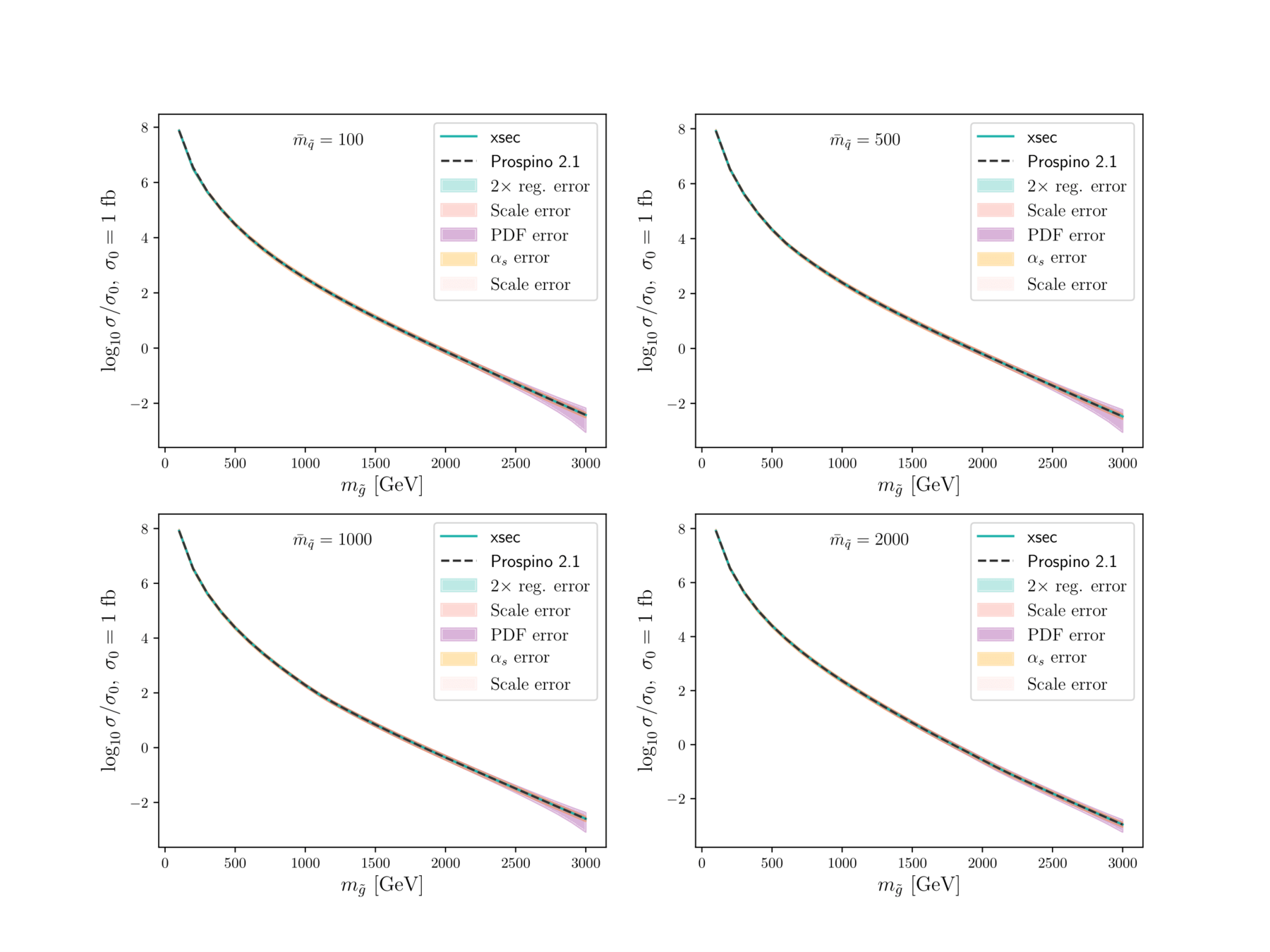
XSEC: the cross-section evaluation code

Thank you!

Backup slides

Gaussian Processes 101 (non-parametric regression)

prior over functions

The covariance matrix controls smoothness.

Assume it is given by a kernel function, like

k(x_1, x_2) = \exp\!\left(-\frac{|x_2-x_1|^2}{2\mathcal{l}^2}\right).

posterior over functions

Bayesian approach to estimate  \( y_* = f(x_*) \) :

y_* | \mathbf{y} \sim \mathcal{N}(K_* K^{-1}\mathbf{y},\ K_{**}-K_*K^{-1}K_*^T)

Consider the data as a sample from a multivariate Gaussian distribution.

\begin{pmatrix} \mathbf{y} \\ y_{*} \end{pmatrix} \sim \mathcal{N}{\left( \begin{pmatrix} \mathbf{0} \\ 0 \end{pmatrix} , \begin{bmatrix} K & K_{*}\\ K_{*}^T & K_{**}\\ \end{bmatrix} \right)}
K_{ij} = k(x_i, x_j) \\ K_{*i}= k(x_*,x_i) \\ K_{**} = k(x_*,x_*)

data

mean

covariance

Gaussian Processes 101 (non-parametric regression)

prior over functions

The covariance matrix controls smoothness.

Assume it is given by a kernel function, like

k(x_1, x_2) = \exp\!\left(-\frac{|x_2-x_1|^2}{2\mathcal{l}^2}\right).

posterior over functions

Bayesian approach to estimate  \( y_* = f(x_*) \) :

y_* | \mathbf{y} \sim \mathcal{N}(K_* K^{-1}\mathbf{y},\ K_{**}-K_*K^{-1}K_*^T)

Consider the data as a sample from a multivariate Gaussian distribution.

\begin{pmatrix} \mathbf{y} \\ y_{*} \end{pmatrix} \sim \mathcal{N}{\left( \begin{pmatrix} \mathbf{0} \\ 0 \end{pmatrix} , \begin{bmatrix} K & K_{*}\\ K_{*}^T & K_{**}\\ \end{bmatrix} \right)}
K_{ij} = k(x_i, x_j) \\ K_{*i}= k(x_*,x_i) \\ K_{**} = k(x_*,x_*)

data

mean

covariance

Radial Basis Function kernel

prior over functions

The covariance matrix controls smoothness.

Assume it is given by a kernel function, like

k(x_1, x_2) = \exp\!\left(-\frac{|x_2-x_1|^2}{2\mathcal{l}^2}\right).

posterior over functions

Bayesian approach to estimate  \( y_* = f(x_*) \) :

y_* | \mathbf{y} \sim \mathcal{N}(K_* K^{-1}\mathbf{y},\ K_{**}-K_*K^{-1}K_*^T)

Consider the data as a sample from a multivariate Gaussian distribution.

\begin{pmatrix} \mathbf{y} \\ y_{*} \end{pmatrix} \sim \mathcal{N}{\left( \begin{pmatrix} \mathbf{0} \\ 0 \end{pmatrix} , \begin{bmatrix} K & K_{*}\\ K_{*}^T & K_{**}\\ \end{bmatrix} \right)}
K_{ij} = k(x_i, x_j) \\ K_{*i}= k(x_*,x_i) \\ K_{**} = k(x_*,x_*)

data

mean

covariance

Matérn kernel

Gaussian Processes 101 (non-parametric regression)

XSEC: the cross section evaluation code

\tilde g \tilde q

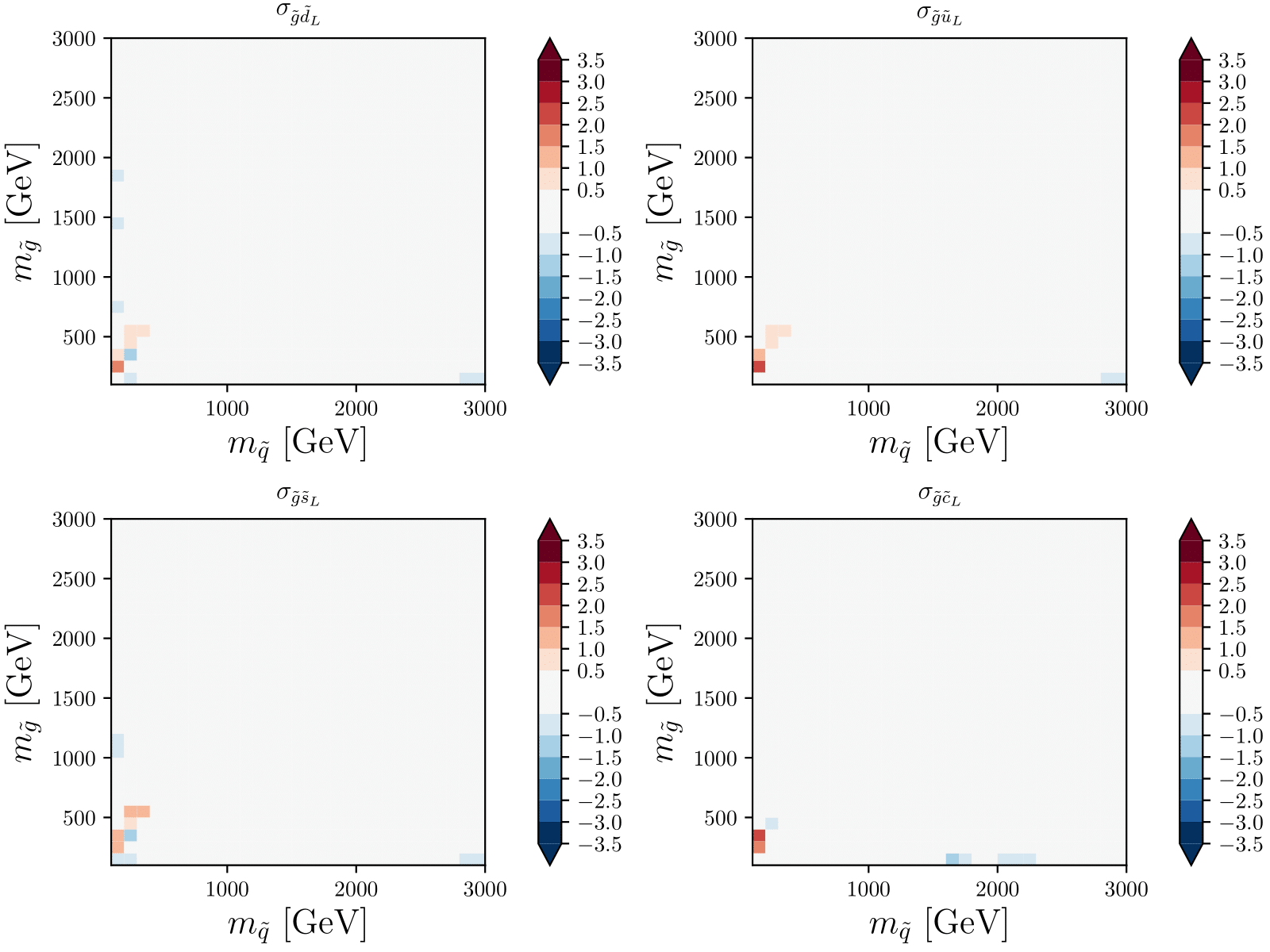
Image: Claire David (CERN)

Scale-dependence of LO/NLO

[Beenakker+, hep-ph/9610490]

Made with Slides.com