Distancia entre dos puntos
Distancia de un punto a una recta
Bienvenidos chicos!
Distancia entre dos puntos
La distancia entre dos elementos del plano, es la misma distancia existente entre sus puntos..
Fórmula:

ó

Ejemplo
Demuestre que el triangulo A=(2,1); B=(7,2) y C=(3,3) es isosceles.
*Procedemos a calcular las distancias entre los puntos del triangulo

Rpta: El triangulo es isosceles, ya que dos de sus lados son iguales.




Distancia de un punto a una recta
Esta relacionada con la perperdicular a esta que pase por los puntos

Ejemplo
Calcula la distancia del punto P=(5,2) a la recta r que pasa por el punto A=(2,-3), y tiene vector director u=(1,4)

*Planteamos con los datos dados la ecuación vectorial de la recta.
Ec.Vectorial

Ec.Parametrtica
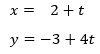
Reemplazamos los valores de P y Us en la Ec. continua y obtenemos la Ec. genaral de la recta.

El vector unitario de r es Ur=(1,4), por lo tanto, el vector unitario de s es Us= (-4,1)
Calculamos H, reemplazando x=2+t ; y=-3+4t en x+4y-13=0 las ecuaciones.
2+t+4(-3+4t)-13=0
2+t-12+16t-13=0
t=23/17
Conociendo t,reemplazamos en las ecuaciones: x=2+t ; y=-3+4t
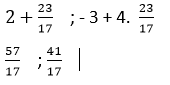
Por ultimo:


GRACIAS POR SU ATENCIÓN.