Introduction to Functional Programming

Content

Recursion
High order function
Closure & lexical scope
Partial application & currying
Delay evaluation

Intro: Put an elephant into a fridge

Imperative paradigm:

print 'open the fridge'
print 'put elephant into the fridge'
print 'close the fridge'

Put an elephant into a fridge

OO paradigm:

class Fridge:
    def open(self):
        print 'open the fridge'

    def put(self, something):
        print 'put %s into the fridge' % something

    def close(self):
        print 'close the fridge'

fridge = Fridge()
fridge.open()
fridge.put('elephant')
fridge.close()

Put an elephant into a fridge

Functional paradigm:

def open(something):
    print 'open the %s' % something
    return something

def put(object, container):
    print 'put %s into the %s' % (object, container)
    return container

def close(something):
    print 'close the %s' % something
    return something 
close(put('elephant', open('fridge')))

1. Recursion

In order to understand recursion,

you must first understand recursion.

Why recursion?

Wikipedia:

In computer science, functional programming is a programming paradigm, a style of building the structure and elements of computer programs, that:

Treats computation as the evaluation of mathematical functions
Avoid state and mutable data

Treats computation as the evaluation of mathematical functions

Functions: take in values and return values

Statements do something:

>>>i = i + 1
>>>

Use statements? No!

Expression produce value:

>>>i + 1
43
>>>

Use expression? Yes!

Avoid state and mutable data

Loops:

def fac(n):
    n = 1 #mutation
    for i in range(n): #states
        n = n * (i + 1) #mutation
    return n

Recursion:

def fac(n):
    if n == 0:
        return 1
    else:
        return n * fac(n - 1)

So how to write recursion?

How to compute exponential of a given number?

b^n = b * b * b ... * b (b occurs n times)

So:

def exp(b, n):
    result = 1
    for _ in range(n):
        result *= b
    return result

So how to write recursion?

How to compute exponential of a given number?

b^n = b * b^(n - 1)b^0 = 1

So:

def exp(b, n):
    if n:
        return b * exp(b, n - 1)
    else:
        return 1

So how to write recursion?

How to compute exponential more efficiently?

b^n = b^(n/2) * b^(n/2)  (if n is even)
b^n = b * b^(n-1) (if n is odd)
b^0 = 1

def exp(b, n):
    if n%2:
        return b * exp(b, n - 1)
    elif n:
        return exp(b, n/2) * exp(b, n/2)
    else:
        return 1

Another example

Fibonacci sequence

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n - 1) + fib(n - 2)

However, this solution has a big problem

If we trace call chain of recursive fib(n)

fib(4) called [#1]
--fib(3) called [#2]
----fib(2) called [#3]
------fib(1) called [#4]
------fib(1) returned 1 [#4]
------fib(0) called [#5]
------fib(0) returned 0 [#5]
----fib(2) returned 1 [#3]
----fib(1) called [#6]
----fib(1) returned 1 [#6]
--fib(3) returned 2 [#2]
--fib(2) called [#7]
----fib(1) called [#8]
----fib(1) returned 1 [#8]
----fib(0) called [#9]
----fib(0) returned 0 [#9]
--fib(2) returned 1 [#7]
fib(4) returned 3 [#1]

fib(4) called fib() 9 times

fib(5) called fib() 15 times

fib(6) called fib() 25 times

...

Tail Recursion

Convert recursive process to iterative process.

def fib(n):
    def fib_iter(a, b, n):
        if n:
            return fib_iter(b, a + b, n - 1)
        else:
            return a
    return fib_iter(0, 1, n)

track state by function arguments
reduce length of call stack and improve efficiency
(not supported in python yet)

2. First class

function

First class function

First class function means functions are treated as first class element by programming language. Like objects in OOP.

Privileges of first class elements includes

They may be named by variables.
They may be passed as arguments to functions.
They may be returned as the results of procedures.
They may be included in data structures.

Functions can be named by variables

Anonymous function:

>>> (lambda x: x * x)(2)
4

Function s can be assigned to variables:

>>> square = lambda x: x * x
>>> square(2)
4

Or make alias easily:

>>> sq = square
>>> sq(2)
4

Function passed as arguments

The well known build in functions

map(), filter(), reduce()

sorted()

>>> name = ['Leonardo DiCaprio', 'Johnny Depp', 'Tom Cruise']
>>> sorted(name) #sort by full name
['Johnny Depp', 'Leonardo DiCaprio', 'Tom Cruise']
>>> sorted(name, key = lambda x: x.split(' ')[1]) #sort by last name
['Tom Cruise', 'Johnny Depp', 'Leonardo DiCaprio']
>>> sorted(name, key = lambda x: len(x)) #sort by name length
['Tom Cruise', 'Johnny Depp', 'Leonardo DiCaprio']

get_cursors_if

get_cursors_if(source, satisfy_func, transform_func)

Function as return value

A tiny example:

>>> def addn(n):
	def add(m):
		return m + n
	return add

>>> add2 = addn(2)
>>> add2(3)
5

Memoization

Memoization

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n - 1) + fib(n - 2)

Recall the recursive version of fib(),it is in very low efficient because of redundant computation. What if it can store the computed result?

Memoization

def memoize(f):
    cache = {}
    def g(x):
        if x not in cache:
            cache[x] = f(x)
        return cache[x]
    return g

fib = memoize(fib) >>> fib(5)
fib(5) called [#1]
 fib(4) called [#2]
  fib(3) called [#3]
   fib(2) called [#4]
    fib(1) called [#5]
    fib(1) returned 1 [#5]
    fib(0) called [#6]
    fib(0) returned 0 [#6]
   fib(2) returned 1 [#4]
  fib(3) returned 2 [#3]
 fib(4) returned 3 [#2]
fib(5) returned 5 [#1]

Trace

High order function that can trace function call.

__report_indent = [0]

def trace(fn):
    def wrap(*params,**kwargs):
        call = wrap.callcount = wrap.callcount + 1

        indent = ' ' * __report_indent[0]
        fc = "%s(%s)" % (fn.__name__, ', '.join(
            [a.__repr__() for a in params] +
            ["%s = %s" % (a, repr(b)) for a,b in kwargs.items()]
        ))

        print "%s%s called [#%s]"\
            % (indent, fc, call)
        __report_indent[0] += 1
        ret = fn(*params,**kwargs)
        __report_indent[0] -= 1
        print "%s%s returned %s [#%s]"\
            % (indent, fc, repr(ret), call)

        return ret
    wrap.callcount = 0
    return wrap

Decorator

Special syntax in Python:

fib = memorize(fib)

can be written as:

@memorize
def fib(n):
    ...

3. Closure

and lexical scope

Closure

A closure, like an object instance, is a way of carrying around a bundle of data and functionality, wrapped up together.

Lexical scope is a nature way to implement closure.

Closure

def addx(x):
    def func(y):
        return x + y
    return func
foo = addx(5)
x = 3
>>>foo(10) 
15 # in lexical scope, 5 is bind to x in foo

In lexical scope, the body of a function is evaluated in the environment where the function is defined, not the environment where the function is called. By working in this way, it binds data with functions.

Alternative to closure

#Argument passingdef addx(x):
    def func(a, b = x):
        return a + b
    return func
>>> a = addx(2)
>>> a(3)
5

#use objectclass addx():
    def __init__(self, x):
        self.x = x

    def __call__(self, y):
        return self.x + y
>>> a = addx(2)
>>> a(3)
5

Anything done with closure can be done without closure.

But closure provides a more clear and simple solution.

Alternative to closure

The venerable master was walking with his student. The student said "Master, I have heard that objects are a very good thing - is this true?" Master looked pityingly at his student and replied, "Foolish pupil - objects are merely a poor man's closures."
On his next walk with master, student said "Master, I have diligently studied the matter, and now understand that objects are truly a poor man's closures." Master responded by hitting student with his stick, saying "When will you learn? Closures are a poor man's object." At that moment, the student became enlightened.

http://people.csail.mit.edu/gregs/ll1-discuss-archive-html/msg03277.html

Special notice for python

Reassign closure variable of immutable type inside function will lead to unexpected result.

def counter():
    count = 0
    def func():
        count += 1
        return count
    return func
>>> count = counter()
>>> count()
Traceback (most recent call last):
  File "", line 1, in 
    count()
  File "C:/Users/JC/Desktop/a.py", line 152, in func
    count += 1
UnboundLocalError: local variable 'count' referenced before assignment

Special notice for python

A common solution is to replace immutable objectwith mutable object

def counter():
    count = [0]
    def func():
        count[0] += 1
        return count[0]
    return func
>>> count = counter()
>>> count()
1
>>> count()
2

4. Partial application and

Currying

Partial application

Partial function application is about fixing some arguments of a given function to yield another function with fewer arguments.

get_cursors_if

get_cursors_if(source, satisfy_func, transform_func)
get_cursor_names_if = partial(get_cursors_if,    transform_func = lambda c: c.displayname)
get_class_cursor = partial(get_cursors_if,    satisfy_func = lambda c: c.kind == CursorKind.CXX_CLASS,    transform_func = lambda c: c)

Partial application

Consider the following Ackermann function which computes hyperoperations of 2.

def Ackermann(x, y):
    if not y:
        return 0
    elif not x:
        return 2 * y
    elif y == 1:
        return 2
    else:
        return A(x - 1, A(x, y - 1))

Hyperoperations

Partial application

Ackermann(x, y) computes y times hyper(x - 2) of base 2


>>> Ackermann(0, 4)
8                      #hyper 2  multipication 2 * 4
>>> Ackermann(1, 4)
16                     #hyper 3 exponentiation 2 ^ 4>>> Ackermann(2, 3)
16                     #hyper 4 tetration  2 ^^ 3
>>> Ackermann(2, 4)
65536                  # 2 ^^ 4

Partial application

With partial application, we can generate functions to compute hyper n

def partial_Ack(n):
    def func(b):
        return Ackermann(n, b)
    return func
multiply2 = partial_Ack(0)
exp2 = partial_Ack(1)
teration2 = partial_Ack(2)

partial() function provided by functools provides a move convenient way for partial application

from functools import partial

multiply = partial(Ackermann, 0)

Partial application

Why partial application?

Convenience
Bind data with function to build more specific function
Encapsulation and detail hidding

Currying

Transforming a function that takes multiple arguments (or a tuple of arguments) in such a way that it can be called as a chain of functions

def func(a, b, c):
    return a + b + c

def curried_func(a):
    return lambda b: lambda c: a + b + c

>>> print func('a', 'b', 'c')
abc
>>> print curried_func('a')('b')('c')
abc

Currying

Currying is close related to partial application
Currying can transfer multiple argument function to a chain of single argument function which is very useful in old days when functions can only take in one argument.
Nowadays, currying is generally considered as language support for partial application. It can be replaced by partial application, thus it is seldom used in languages that doesn't support currying.
A Haskell example. Haskell has language syntax that support currying

computation a b c d = (a + b^2+ c^3 + d^4)

fillOne   = computation 1 
fillTwo   = fillOne 2     
fillThree = fillTwo 3     
answer    = fillThree 5   
-- Result: answer == 657

5. Delay evaluation

Implementing my_if()

Python do not support ternary operator like ( ? : ) in C++, what if we want to write if statement in one line?

one solution: use "and" and "or"

#a ? b : c
(a and b) or c

an other solution: implement an my_if function

#a ? b : c
my_if(a, b, c)

Implementing my_if()

def my_if(a, b, c):

if a:

return b

else:

return c

This solution looks just like syntax sugar of if statement.

However, it does not work.

Implementing my_if()

Consider the following situation:

def bad_exp():
    while True:
        pass

The If statement works well:

if True:
    good_exp()
else:
    bad_exp()

But my_if() will run into infinity loop:

my_if(True, good_exp(), bad_exp())

Because function arguments will be evaluated first.

Delay evaluation

In order to delay evaluation of statements, we can wrap statements into functions. Functions are evaluated to themselves and let function call evaluated to statements.

Modified my_if():

def my_if(a, b, c):
    if a:
        return b()
    else:
        return c()

To call my_if():

my_if(a, lambda : b, lambda : c)

Delay evaluation

Delay the evaluation of parameter by putting it into a wrapper function. Then call the function to get the value of parameter. The wrapping process is called ‘thunk’.

However, if use delay evaluation, parameter will be computed every time when it is used.

Stream

If we need a sequence but we don't know exactly how long is needed. We can delay the evaluation of sequence, and evaluate it one by one when needed. This kind of object is called stream

def fib():
    def stream(a, b):
        return (a, lambda : stream(a + b, a))
    return stream(1, 0)

above if a stream than generates Fibonacci numbers. Every time when fib() is called, it generate a tuple of fib number and delayed fib() for next element.

Stream

To get first element of stream:

>>> fib()[0]
1

To get the second one:

>>> fib()[1]()[0]
1

To get the nth:

def get_nth(stream, n):
    val, next_str = stream()
    if n != 1:
        return get_nth(next_str, n - 1)
    else:
        return val >>> get_nth(fib, 10)
55

Stream example: twin prime

Twin prime means two prime that one prime is different with the other by two, for example (3, 5), (17, 19). There is said to have infinity number of twin primes.

def isprime(n):
    for x in xrange(2, int(n**0.5)+1):
        if n % x == 0:
            return False
    return True

def prime():
    def stream(n):
        if isprime(n):
            return (n, lambda : stream(n + 1))
        else:
            return stream(n + 1)
    return stream(2)

Stream example: twin prime

def twin_prime():
    def stream(n):
        if isprime(n) and isprime(n + 2):
            return ((n, n + 2), lambda : stream(n + 1))
        else:
            return stream(n + 1)
    return stream(2)

>>> for i in range(1, 5):
. . . 	print get_nth(twin_prime, i)

(3, 5)
(5, 7)
(11, 13)
(17, 19)

Generator

Generator object provided by python is also very suitable for generating sequence of infinity length.

def gen_prime():
    n = 2
    def gen(n):
        if isprime(n):
            return n
        else:
            return gen(n + 1)
    while True:
        n = gen(n)
        yield n
        n += 1

Generator

Generation version of twin_prime:

def gen_twin_prime():
    prime = gen_prime()
    a = prime.next()
    def gen(a):
        b = prime.next()
        if b - a == 2:
            return (a, b)
        else:
            return gen(b)
    while True:
        tmp = gen(a)
        a = tmp[1]
        yield tmp

Ideas of stream and generator are almost the same.

Generator has more language support.

PF and OOP

Let's go back to the fridge example.

Suppose we want to put elephant into the zoo.

OOP:

class Zoo:
    def open(self):
        ...
    def put(self, object):
        ...
    def close(self):
        ...

PF and OOP

Let's go back to the fridge example.

Suppose we want to put elephant into the zoo.

FP:

def open(something):
    if something == 'fridge':
        ...
    elif something == 'zoo':
        ...

def put
    if... 
def close    if...

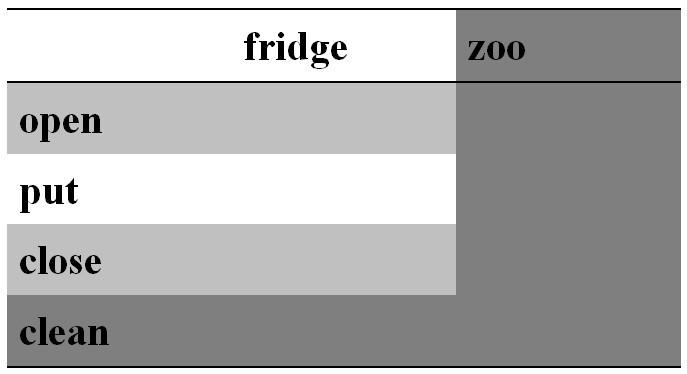
PF and OOP

Now, we want to add clean() method for fridge and zoo

OOP:

class Fridge:
    ...
    def clean(self):
        print 'clean the fridge'

class Zoo:
    ...
    def clean(self):
        print 'clean the zoo'

PF and OOP

Now, we want to add clean() method for fridge and zoo

FP:

def clean(something):
    if something == 'fridge':
        print 'clean the fridge'
    elif something == 'zoo':
        print 'clean the zoo'
    return something