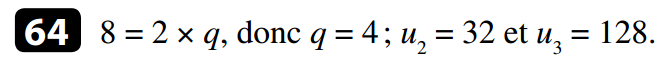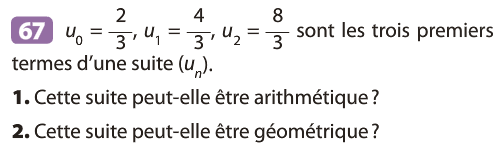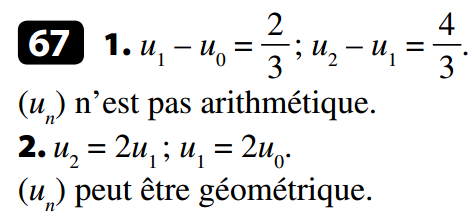Suites Numériques
Act 1 p 95 (Nathan


Suites Numériques
1. Notion de suite numérique
1.1 Définition
Définition :
Une suite numérique est une liste indexée de nombres.
Elle a un premier terme, un deuxième terme, etc.
Exemples :
- La suite des multiples de 7 : 0, 7, 14, ....
- La suite des nombres entiers impairs : 1, 3, 5, 7, . . .
- La suite définie par
Notations :
- On utilise généralement les lettres u, v, w, . . . pour caractériser une suite.
- est appelé terme d’indice n (ou de rang n) de la suite.
- La suite dans sa globalité est notée
Remarque :
Dans beaucoup de cas, on commencera l’indexation à l’indice zéro. Dans ce cas :
est le premier terme ;
est le deuxième terme ;
est le troisième terme ; etc.
Il ne faut pas confondre le terme d’indice n et le terme.
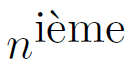
1.2 Définition à l'aide d’une formule explicite
Exemple :
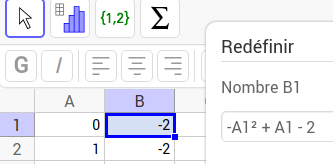
Soit la suite définie par :
On a :
Remarque : La suite est donc de la forme , où f est une fonction.
On peut donc représenter graphiquement la suite comme on représenterait la fonction f, mais en se limitant aux images des entiers naturels (et donc sans relier les points obtenus).
Calcul des premiers termes et représentation graphique (nuage de points) avec GeoGebra
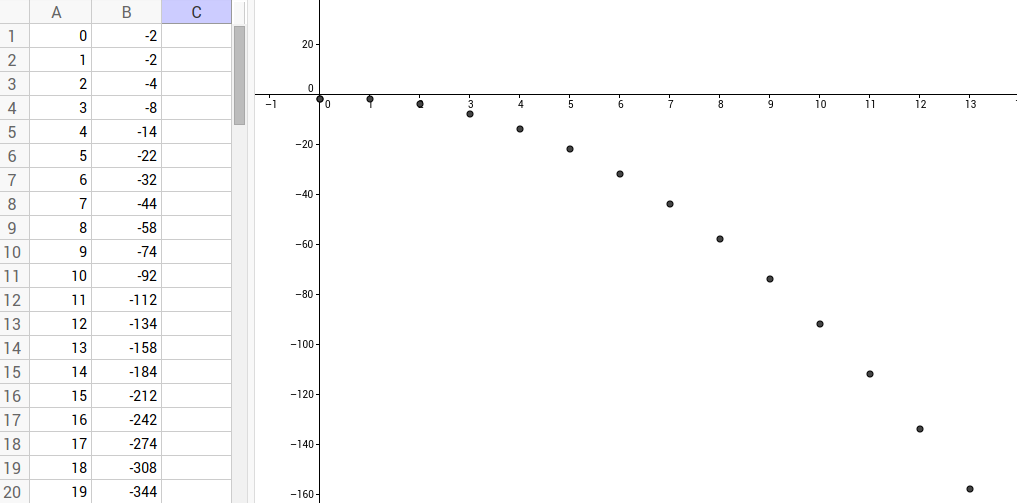
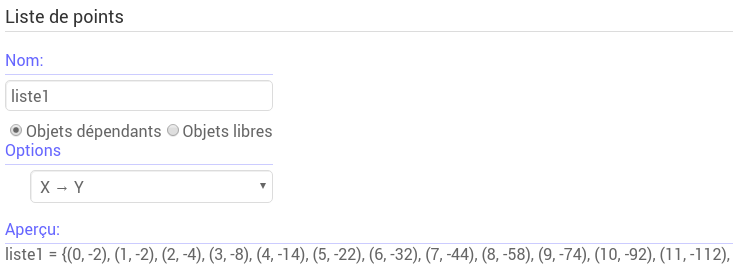

1.3 Définition à l'aide d’une formule de récurrence
Exemples :
Soit la suite de premier terme et dont le terme suivant est obtenu en ajoutant 3 puis en divisant par 2.
On a :
et plus généralement
Remarque :
- Dans ce cas, chaque terme est calculé à partir du terme précédent. On calcule donc les termes de proche en proche (avant de calculer , il faut déjà avoir calculé etc.).
- On notera la suite de la façon suivante :
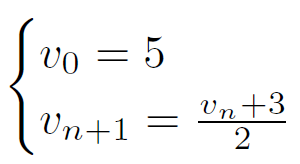
On a donc
avec
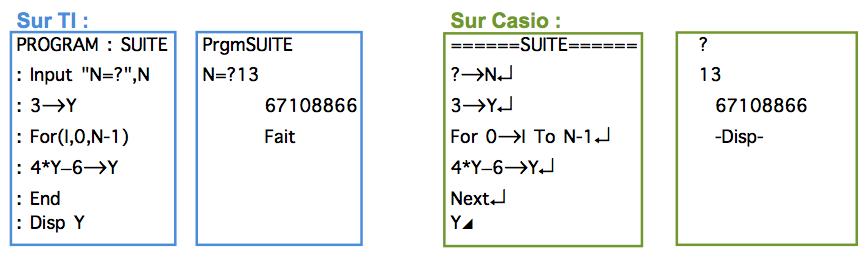
On définit la suite (vn) par v0 = 3 et pour tout n de ℕ , vn+1 = 4vn - 6
Calculer le terme v13 à l'aide d'une calculatrice :
Algorithme de calcul d'un terme d'une suite définie par récurrence :





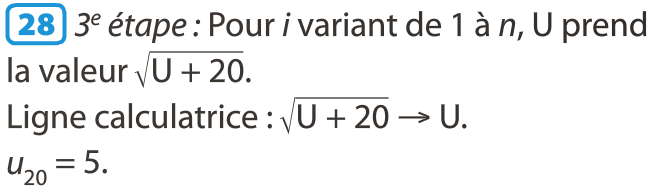
Le mode suite de la calculatrice :


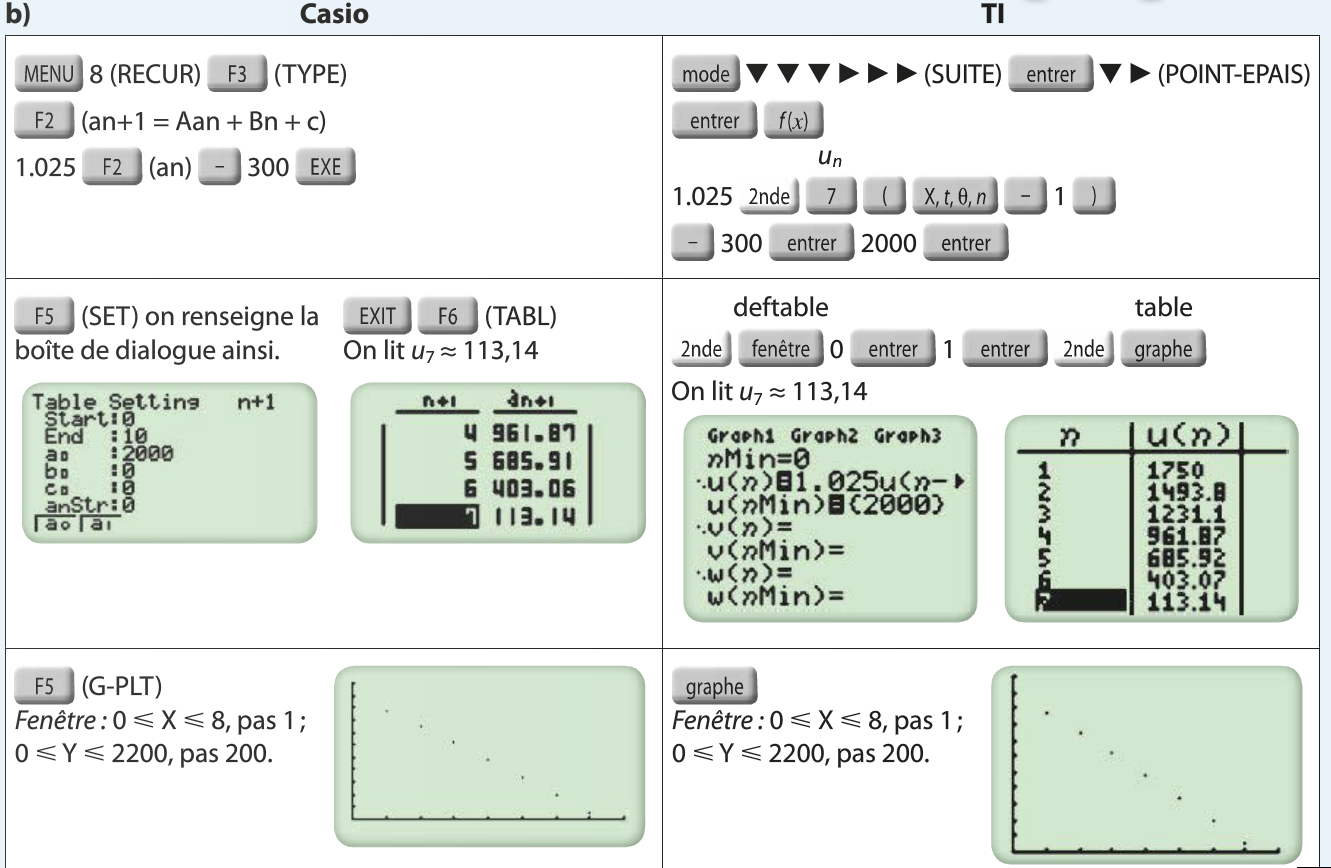
Représentation graphique d'une suite définie par récurrence :
f est une fonction affine, sa représentation graphique est la droite d'équation :
On construit ensuite la droite d'équation y = x
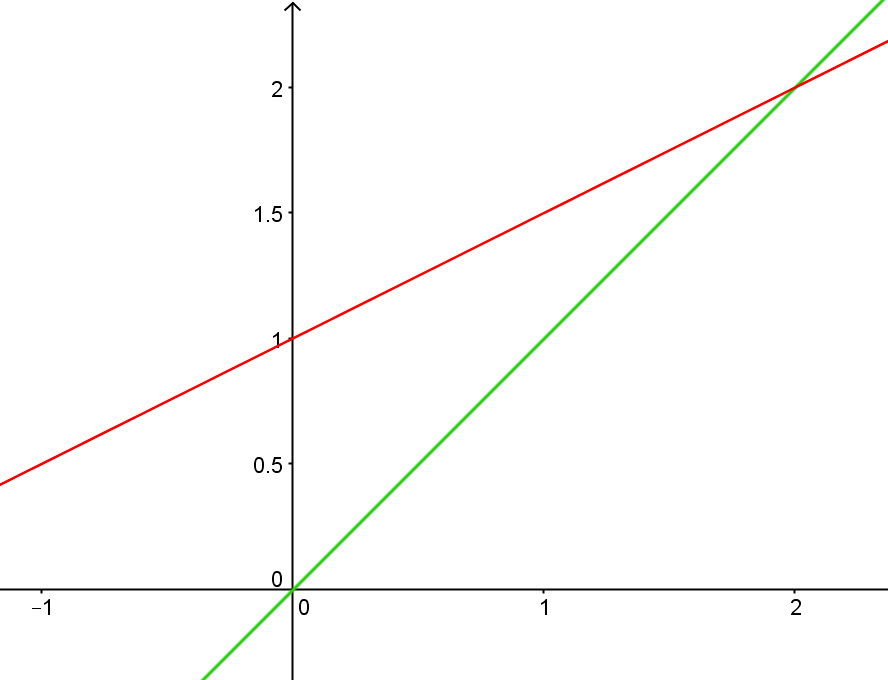
On repère u0 sur l'axe des abscisses
On reporte ensuite u1 sur l'axe des abscisses

On recommence...
2. Sens de variation d'une suite
Définition :
- Une suite (un) est croissante si, pour tout entier naturel n, on a :
- Une suite (un) est décroissante si, pour tout entier naturel n, on a :
On peut aussi définir une suite strictement croissante, strictement décroissante ou constante.
Propriété : Pour étudier les variations de la suite (un), il suffit d’étudier le signe de :
- Si pour tout n, alors (un) est croissante.
- Si pour tout n, alors (un) est décroissante.
Exemples :
- Soit (un) la suite définie par
Par suite :
donc pour tout n
On en déduit que la suite (un) est strictement décroissante.
- Soit (vn) la suite définie par
Par suite :
donc pour tout n
On en déduit que la suite (vn) est strictement décroissante.
Propriété : Soit Un une suite définie par
- Si la fonction f est croissante sur [0 ; +∞[, alors la suite (un) est croissante.
- Si la fonction f est décroissante sur [0 ; +∞[, alors la suite (un) est décroissante.
Remarque : La réciproque de cette propriété est fausse.
Exemple : Soit (un) la suite définie par
On a un = f (n) avec
L'étude du signe de la dérivée de f nous donne les variations suivantes :

f est décroissante sur [0 ; +∞[. La suite (un) est donc décroissante.
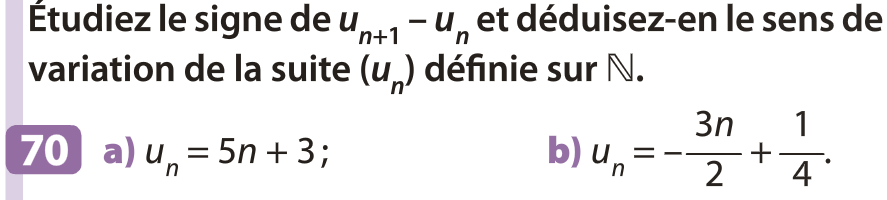

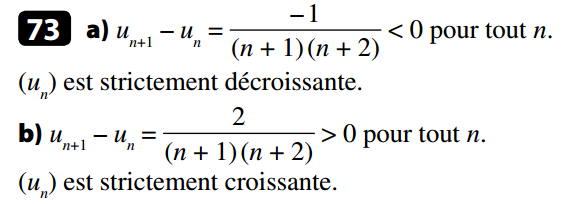
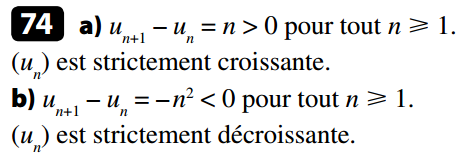
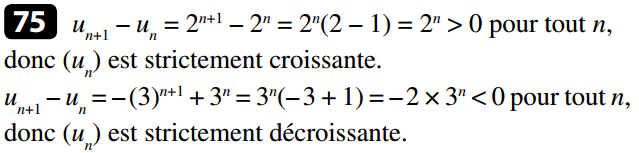

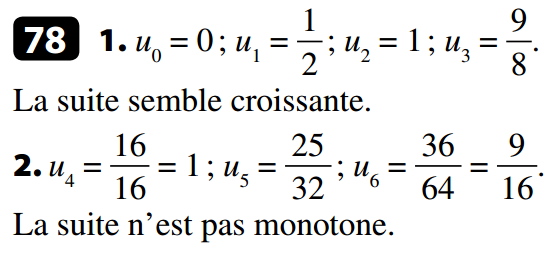


3. Suites arithmétiques
3.1 Définition, exemples
Définition : On dit qu’une suite (un) est arithmétique si on passe d’un terme au suivant en ajoutant toujours le même nombre réel r.
On a donc :
Le réel r est alors appelé raison de la suite.
Exemples :
- La suite : 1, 6, 11, 16, 21, . . . est arithmétique de raison 5.
- La suite définie par : est arithmétique de raison (−3).
- La suite des entiers naturels : 0, 1, 2, 3,4, 5, . . . est arithmétique de raison 1.
- La suite des entiers naturels impairs est arithmétique de raison 2.
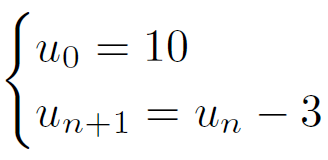
Propriété : Une suite (un) est arithmétique si et seulement si la différence est constante pour tout entier n.
Dans ce cas, la constante trouvée est la raison de la suite.
- Soit w la suite définie par :
Exemples :
- Soit u la suite définie par un = 3n − 2.
un+1 − un = 3 (n + 1) − 2 − (3n − 2) = 3n + 3 − 2 − 3n + 2 = 3
- Soit v la suite définie par vn = n².
vn+1 − vn = (n + 1)² − n² = n² + 2n + 1 − n² = 2n + 1
Le résultat dépend de n, la suite n’est donc pas arithmétique.
La suite est donc arithmétique de raison
La suite est donc arithmétique de raison 3 et de premier terme u0 = −2.
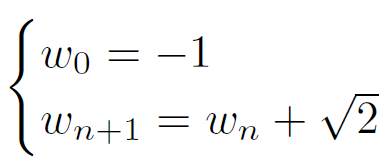
On a immédiatement :
3.2 Formule explicite
Soit (un) une suite arithmétique de raison r.
On a :
u1 = u0 + r
u2 = u1 + r = u0 + 2r
u3 = u2 + r = u0 + 2r + r = u0 + 3r
Plus généralement, on a le résultat suivant :
Propriété : Soit (un) une suite arithmétique de raison r. Alors :
Plus généralement, si (un) est une suite arithmétique de raison r et si n et p sont deux entiers naturels, on a :
Remarque :
Exemples :
- Soit (un) la suite arithmétique de premier terme u0 = 7 et de raison r = −2.
On a : un = u0 + nr = 7 + n × (−2) = 7 − 2n.
En particulier : u50 = 7 − 2 × 50 = 7 − 100 = −93.
3.3 Représentation graphique et sens de variation
Propriétés : Soit (un) une suite arithmétique de raison r.
- Dans un repère, les points de coordonnées (n ; un) sont alignés.
- La suite (un) est croissante si r > 0, décroissante si r < 0 et constante si r = 0.
- Soit (vn) la suite arithmétique telle que v4 = 3 et de raison r = 5.
Calcul de v10 :
Calcul de v0 :
Exemples :

Les suites arithmétiques correspondent à des évolutions linéaires.
4. Suites géométriques
4.1 Définition, exemples
Définition : On dit qu’une suite (un) est géométrique si on passe d’un terme au suivant en multipliant toujours par le même nombre réel q.
On a donc :
Le réel q est alors appelé raison de la suite.
Exemples :
- La suite : 1, 2, 4, 8, 16, . . . est géométrique de raison 2.
- La suite définie par : est géométrique de raison
- La suite définie par est géométrique de raison -1.
- On augmente tous les ans une quantité de 5%. La suite obtenue est C’est donc une suite géométrique de raison 1, 05.
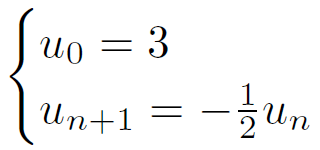
Méthode : Montrer qu'une suite est géométrique
Pour montrer qu’une suite est géométrique, on essaiera de mettre son terme général sous la forme :
Exemples :
- Soit u la suite définie par
La suite est donc géométrique de raison 3 et de premier terme
- Soit v la suite définie par
La suite est donc géométrique de raison et de premier terme
4.2 Formule explicite
Soit (un) une suite géométrique de raison q.
On a :
Plus généralement, on a le résultat suivant :
Théorème : Soit (un) une suite géométrique de raison q. Alors :
Plus généralement, si (un) est une suite géométrique de raison q et si n et p sont deux entiers naturels, on a :
Remarque :
Exemples :
- Soit (un) la suite géométrique de premier terme u0 = 5 et de raison q = 2.
- Soit (vn) la suite géométrique telle que v4 = -7 et de raison q = 3.
On a :
On a :
Calcul de v10 :
On a :
Calcul de v0 :
En particulier :
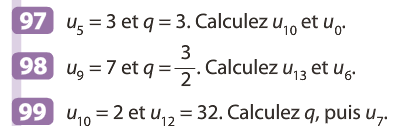
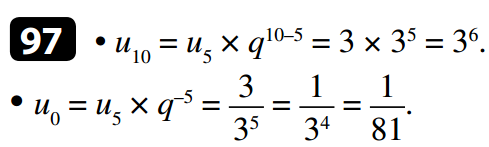
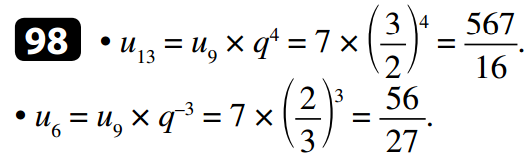
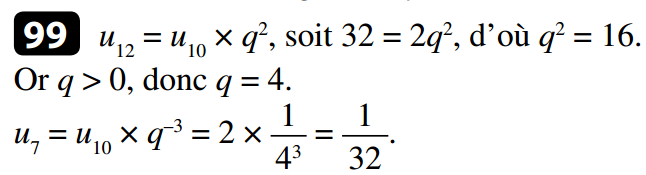


a) Formule explicite de (un) :
a) Formule explicite de (un) :
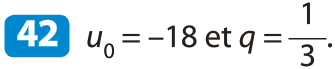
a) Formule explicite de (un) :
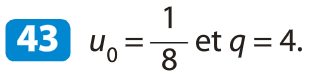
a) Formule explicite de (un) :
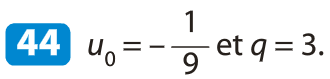
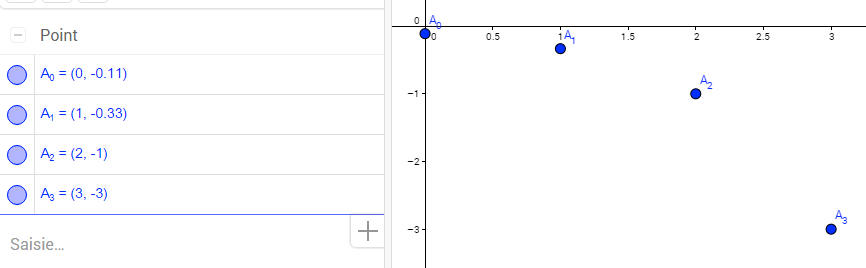

On en déduit que (un) est une suite géométrique de raison 5 et de premier terme u0=3.
Rappel : Pour montrer qu’une suite (un) est géométrique, on essaiera de démontrer que pour tout n :
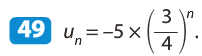
On en déduit que (un) est une suite géométrique de raison et de premier terme u0 = -5.
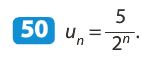
On en déduit que (un) est une suite géométrique de raison et de premier terme u0 = 5.
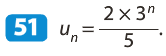
On en déduit que (un) est une suite géométrique de raison 3 et de premier terme u0 =
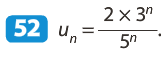
On en déduit que (un) est une suite géométrique de raison et de premier terme u0 = 2.


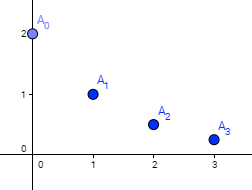
4.3 Représentation graphique et sens de variation
Propriété : Soit (un) la suite géométrique définie par
avec q > 0. (Un) est croissante si q > 1, décroissante si 0 < q < 1 et constante si q = 1.

Les suites géométriques correspondent à des évolutions exponentielles.
Exemples : (cas où u0 > 0)
Remarque : Si u0 < 0 et q > 1 alors est décroissante.
Si u0 < 0 et 0 < q < 1 alors est croissante.

Pour montrer qu’une suite (un) est géométrique, on peut également mettre un sous la forme